The Laplace Transform

The Laplace Transform

Laplace transforms take us into a world where calculus operations become algebraic operations.

In this new world, solving a differential equation is reduced to the problem of solving an algebraic equation.

Today, we learn how to navigate back and forth between these two worlds.

Once we're able to do this, we will be able to solve equations in a new and powerful way.

The Laplace Transform

The Laplace Transform of $f(t)$ is defined to be $$ \mathscr{L}\{f(t)\}=\int_0^{\infty}e^{-st}f(t)\,dt=F(s) $$ Notice that we are "integrating out" the variable $t$ and getting back a function $F(s)$ in $s.$

$f(t)$ lives in the $t$-domain, and $F(s)$ lives in the $s$-domain.

As we shall see in the next section, calculus operations in the $t$-domain turn into algebraic operations in the $s$-domain.

$\mathscr{L}$ is an operator since it eats functions in $t$ and spits out functions in $s.$

A Note on Notation

The Laplace transform of a function $f$ of $t$ is typically denoted by its corresponding capital letter $F$ as a function of $s.$

For example, $$ \begin{array}{c} \mathscr{L}\{f(t)\}=F(s)\\\\ \mathscr{L}\{g(t)\}=G(s)\\\\ \mathscr{L}\{h(t)\}=H(s)\\\\ \mbox{etc.} \end{array} $$

The Big Idea

$$ \begin{array}{ccc} \color{magenta}{t\mbox{-domain}}&& \color{blue}{s\mbox{-domain}}\\ \color{magenta}{\mbox{differential equation in } x(t)} & \overset{\Large{\mathscr{L}}}{\LARGE{\longrightarrow}} & \color{blue}{\mbox{algebraic equation in }X(s)}\\ \color{magenta}{calculus}\,\,\,\, \LARGE{\big\downarrow}& & \color{blue}{algebra}\,\,\,\, \LARGE{\big\downarrow} \\ \color{magenta}{\mbox{obtain solution } x(t)} & \underset{\Large{\mathscr{L}^{-1}}}{\LARGE{\longleftarrow}} & \color{blue}{\mbox{algebraic solution }X(s)}\\ \end{array} $$

Example

Compute $ \mathscr{L}\{ 1 \}. $

$$ \begin{array}{lll} \displaystyle \mathscr{L}\{ 1 \}&\displaystyle=\int_0^{\infty}e^{-st}\cdot 1\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\infty}e^{-st}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[-\frac{1}{s}e^{-st}\right]_0^{\infty} &\mbox{}\\ \displaystyle &\displaystyle=\lim_{t\rightarrow \infty}\left[-\frac{1}{s}e^{-st}\right]-\left[-\frac{1}{s}e^{-s\cdot 0}\right] &\mbox{}\\ \displaystyle &\displaystyle=0-\left[-\frac{1}{s}\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{s} &\mbox{}\\ \end{array} $$

Example

Compute $ \mathscr{L}\{ e^{-at} \}. $

$$ \begin{array}{lll} \displaystyle \mathscr{L}\{ e^{-at} \}&\displaystyle=\int_0^{\infty}e^{-st}\cdot e^{-at}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\infty}e^{-st-at}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\infty}e^{-(s+a)t}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[-\frac{1}{s+a}e^{-(s+a)t}\right]_0^{\infty} &\mbox{}\\ \displaystyle &\displaystyle=\lim_{t\rightarrow \infty}\left[-\frac{1}{s+a}e^{-(s+a)t}\right]-\left[-\frac{1}{s+a}e^{-(s+a)\cdot 0}\right] &\mbox{}\\ \displaystyle &\displaystyle=0-\left[-\frac{1}{s+a}\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{s+a} &\mbox{}\\ \end{array} $$

Example

Compute $ \mathscr{L}\{ t \}. $

$$ \begin{array}{lll} \displaystyle \mathscr{L}\{ t \}&\displaystyle=\int_0^{\infty}e^{-st}\cdot t\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\infty}te^{-st}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[\frac{1}{(-s)^2}(-st-1)e^{-st}\right]_0^{\infty} &\mbox{by parts (or by entry #42 in integral table)}\\ \displaystyle &\displaystyle=\left[\frac{1}{s^2}(-st-1)e^{-st}\right]_0^{\infty} &\mbox{}\\ \displaystyle &\displaystyle=\lim_{t\rightarrow \infty}\left[\frac{1}{s^2}(-st-1)e^{-st}\right]-\left[\frac{1}{s^2}(-s\cdot 0-1)e^{-s\cdot 0}\right] &\mbox{}\\ \displaystyle &\displaystyle=0-\left[\frac{1}{s^2}(-1)\right] &\mbox{by L'Hôpital}\\ \displaystyle &\displaystyle=\frac{1}{s^2} &\mbox{}\\ \end{array} $$

Example

Compute $ \mathscr{L}\{ \sin(\omega t) \}. $

$$ \begin{array}{lll} \displaystyle \mathscr{L}\{ \sin(\omega t) \}&\displaystyle=\int_0^{\infty}e^{-st}\cdot \sin(\omega t)\,dt &\mbox{}\\ %\displaystyle &\displaystyle=\int_0^{\infty}te^{-st}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[\frac{e^{-st}}{s^2+\omega^2}(-s\sin(\omega t)-\omega \cos(\omega t))\right]_0^{\infty} &\mbox{by parts (or by entry #44 in integral table)}\\ %\displaystyle &\displaystyle=\left[\frac{1}{s^2}(-st-1)e^{-st}\right]_0^{\infty} &\mbox{}\\ \displaystyle &\displaystyle=\lim_{t\rightarrow \infty}\left[\frac{e^{-st}}{s^2+\omega^2}(-s\sin(\omega t)-\omega \cos(\omega t))\right]-\left[\frac{e^{-s\cdot 0}}{s^2+\omega^2}(-s\sin(\omega \cdot 0)-\omega \cos(\omega \cdot 0))\right] &\mbox{}\\ \displaystyle &\displaystyle=0-\left[\frac{1}{s^2+\omega}(-\omega)\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\omega}{s^2+\omega^2} &\mbox{}\\ \end{array} $$

An Amazing Bonus

The Laplace transform plays very nice with many functions, including those with jump discontinuities.

One function we'll be spending a lot of time with is the unit step function $u(t)$ defined below.

$u(t)=\begin{cases}0 & \mbox{if }\,\,\,\, t\lt 0\\ 1 & \mbox{if }\,\,\,\, t\geq 0\\ \end{cases}$

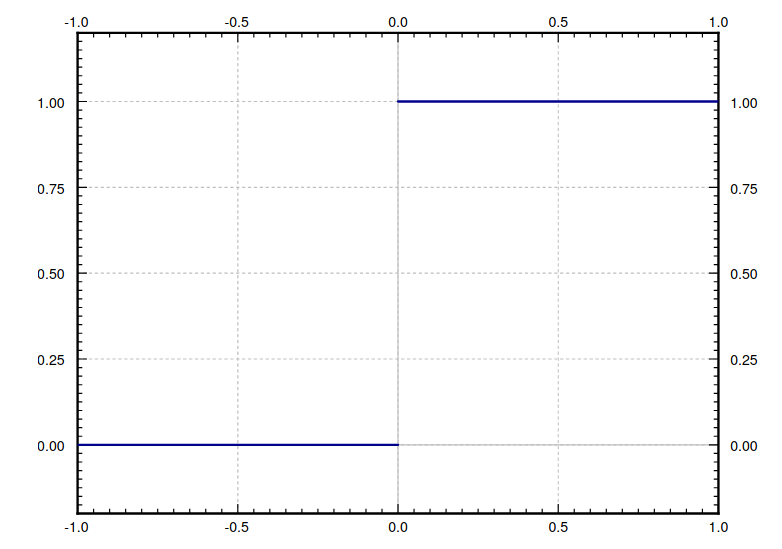
Functions with jump discontinuities do occur often in applications, especially in electronics where forcing functions can take on an "on"-or-"off" nature.

Special Note: The unit step function is also known as the Heaviside function.

Example

Compute $ \mathscr{L}\{ u(t-a) \}. $

$$ \begin{array}{lll} \displaystyle \mathscr{L}\{ u(t-a) \}&\displaystyle=\int_0^{\infty}e^{-st}\cdot u(t-a)\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_a^{\infty}e^{-st}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[-\frac{1}{s}e^{-st}\right]_a^{\infty} &\mbox{}\\ \displaystyle &\displaystyle=\lim_{t\rightarrow \infty}\left[-\frac{1}{s}e^{-st}\right]-\left[-\frac{1}{s}e^{-s\cdot a}\right] &\mbox{}\\ \displaystyle &\displaystyle=0-\left[-\frac{1}{s}e^{-as}\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{e^{-as}}{s} &\mbox{}\\ \end{array} $$

A Modest Table of Laplace Transforms

$$ \begin{array}{cc|cc} \hline f(t) & F(s)=\mathscr{L}\{f(t)\} & f(t) & F(s)=\mathscr{L}\{f(t)\}\\ \hline \displaystyle 1 & \displaystyle \frac{1}{s} & \displaystyle e^{-at}& \displaystyle \frac{1}{s+a} \\ \hline \displaystyle C & \displaystyle \frac{C}{s} & \displaystyle e^{at}& \displaystyle \frac{1}{s-a} \\ \hline \displaystyle t & \displaystyle \frac{1}{s^2} & \displaystyle \sin(\omega t) & \displaystyle \frac{\omega}{s^2+\omega^2}\\ \hline \displaystyle t^2 & \displaystyle \frac{2}{s^3}& \displaystyle \cos(\omega t)& \displaystyle \frac{s}{s^2+\omega^2} \\ \hline \displaystyle t^3 & \displaystyle \frac{6}{s^4} & \displaystyle \sinh(\omega t) & \displaystyle \frac{\omega}{s^2-\omega^2}\\ \hline \displaystyle t^n, \,\,\,\,t=1,2,3,\ldots & \displaystyle \frac{n!}{s^{n+1}}& \displaystyle \cosh(\omega t)& \displaystyle \frac{s}{s^2-\omega^2} \\ \hline \displaystyle t^{r},\,\,\,\,r\gt -1& \displaystyle \frac{\Gamma(r+1)}{s^{r+1}}& \displaystyle u(t-a)& \displaystyle \frac{e^{-as}}{s}\\ \hline \end{array} $$

More Good News!

$\mathscr{L}$ is a linear operator!

That is, for any functions $f(t)$ and $g(t)$ $$ \mathscr{L}\{f(t)+g(t)\}=\mathscr{L}\{f(t)\}+\mathscr{L}\{g(t)\} $$ and $$ \mathscr{L}\{cf(t)\}=c\mathscr{L}\{g(t)\} $$

$$ \begin{array}{lll} \displaystyle \mathscr{L}\{f(t)+g(t)\}&\displaystyle=\int_0^{\infty}e^{-st}(f(t)+g(t))\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\infty}e^{-st}f(t)+e^{-st}g(t)\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\infty}e^{-st}f(t)\,dt+\int_0^{\infty}e^{-st}g(t)\,dt &\mbox{by linearity of the integral}\\ \displaystyle &\displaystyle=\mathscr{L}\{f(t)\}+\mathscr{L}\{g(t)\} &\mbox{}\\ \end{array} $$ $$ \begin{array}{lll} \displaystyle \mathscr{L}\{cf(t)\}&\displaystyle=\int_0^{\infty}e^{-st}cf(t)\,dt &\mbox{}\\ \displaystyle &\displaystyle=c\int_0^{\infty}e^{-st}f(t)\,dt &\mbox{by linearity of the integral}\\ \displaystyle &\displaystyle=c\mathscr{L}\{f(t)\}&\mbox{}\\ \end{array} $$

Example

Compute $ \displaystyle \mathscr{L}\left\{t^2-2t+3+\frac{1}{2}\sin(2t)+3e^{-3t} \right\}. $

$$ \begin{array}{lll} \displaystyle \mathscr{L}\left\{t^2-2t+3+\frac{1}{2}\sin(2t)+3e^{-3t} \right\}&\displaystyle=\mathscr{L}\left\{t^2\right\}-\mathscr{L}\left\{2t\right\}+\mathscr{L}\left\{3\right\}+\mathscr{L}\left\{\frac{1}{2}\sin(2t)\right\}+\mathscr{L}\left\{3e^{-3t} \right\} &\mbox{by linearity}\\ \displaystyle &\displaystyle=\mathscr{L}\left\{t^2\right\}-2\mathscr{L}\left\{t\right\}+3\mathscr{L}\left\{1\right\}+\frac{1}{2}\mathscr{L}\left\{\sin(2t)\right\}+3\mathscr{L}\left\{e^{-3t} \right\} &\mbox{by linearity}\\ \displaystyle &\displaystyle=\frac{2}{s^3}-2\frac{1}{s^2} +3\frac{1}{s}+\frac{1}{2}\frac{2}{s^2+4}+3\frac{1}{s+3}&\mbox{using table}\\ \displaystyle &\displaystyle=\frac{2}{s^3}-\frac{2}{s^2} +\frac{3}{s}+\frac{1}{s^2+4}+\frac{3}{s+3}&\mbox{}\\ \end{array} $$

Dire Warning

$$ \color{red}{\mathscr{L}\{f(t)g(t)\}\neq \mathscr{L}\{f(t)\}\mathscr{L}\{g(t)\}} $$ The Laplace transform of a product is not the product of the transforms!

Example: Let $f(t)=t$ and $g(t)=t.$ Then $$ \begin{array}{lll} \displaystyle \mathscr{L}\{f(t)g(t)\}&\displaystyle=\mathscr{L}\{t\cdot t\} &\mbox{}\\ \displaystyle &\displaystyle=\mathscr{L}\{t^2\} &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{s^3} &\mbox{}\\ \displaystyle &\displaystyle\color{red}{\neq}\frac{1}{s^4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{s^2}\cdot \frac{1}{s^2} &\mbox{}\\ \displaystyle &\displaystyle=\mathscr{L}\{t\}\cdot\mathscr{L}\{t\} &\mbox{}\\ \displaystyle &\displaystyle=\mathscr{L}\{f(t)\}\cdot\mathscr{L}\{g(t)\} &\mbox{}\\ \end{array} $$

The Fine Print

Definition

A function $f(t)$ is of exponential order if $ f(t)\leq Me^{ct} $ for some constant $M$ for all $t$ greater than some $t_0.$

Theorem (Existence)

If $f(t)$ is of exponential order, then $F(s)=\mathscr{L}\{f(t)\}$ exists and is defined for all $s \gt c.$

Theorem (Uniqueness)

Let $f(t)$ and $g(t)$ be continuous and of exponential order. Also, suppose that for some constant $C$ we have $F(s)=G(s)$ for all $s\gt C.$ Then $f(t)=g(t)$ for all $t\geq 0.$

The Inverse Laplace Transform

Taking a trip to the $s$-domain is not so bad.

However, we have to get home to the $t$-domain at some point.

For that return trip, we need the inverse Laplace transform, $\mathscr{L}^{-1}$

The Inverse Laplace Transform

Suppose $$ \mathscr{L}\{f(t)\}=F(s) $$ Then, $$ \mathscr{L}^{-1}\{F(s)\}=f(t) $$

Example

Find $\displaystyle \mathscr{L}^{-1}\left\{\frac{s}{s^2+4}\right\}.$

Here we may simply use our table!

$$ \displaystyle \mathscr{L}^{-1}\left\{\frac{s}{s^2+4}\right\}=\displaystyle \mathscr{L}^{-1}\left\{\frac{s}{s^2+2^2}\right\}=\cos(2t) $$

More Good News!

The inverse Laplace transform is also a linear operator!

That is, for any functions $F(s)$ and $G(s)$ in the $s$-domain, $$ \mathscr{L}^{-1}\{F(s)+G(s)\}=\mathscr{L}^{-1}\{F(s)\}+\mathscr{L}^{-1}\{G(s)\} $$ and $$ \mathscr{L}^{-1}\{cF(s)\}=c\mathscr{L}^{-1}\{F(s)\} $$

Example

Compute $ \displaystyle \mathscr{L}^{-1}\left\{\frac{s^2+s+1}{s^3+s}\right\}. $

We first re-express $\displaystyle \frac{s^2+s+1}{s^3+s}$ in the form $\displaystyle \frac{A}{s}+\frac{Bs+C}{s^2+1}.$ $$ \begin{array}{lll} &\displaystyle\frac{s^2+s+1}{s^3+s}=\frac{A}{s}+\frac{Bs+C}{s^2+1} &\mbox{}\\ \implies &\displaystyle \frac{s^2+s+1}{s^3+s}\color{magenta}{s(s^2+1)}=\frac{A}{s}\color{magenta}{s(s^2+1)}+\frac{Bs+C}{s^2+1}\color{magenta}{s(s^2+1)} &\mbox{}\\ \implies &\displaystyle s^2+s+1=A(s^2+1)+(Bs+C)s &\mbox{}\\ \implies &\displaystyle s^2+s+1=As^2+A+Bs^2+Cs &\mbox{}\\ \implies &\displaystyle s^2+s+1=(A+B)s^2+Cs+A &\mbox{}\\ \implies &\displaystyle \begin{cases} A&+B&&=1\\ && C&=1 \\ A&&&=1 \\ \end{cases} &\mbox{}\\ \end{array} $$ Solving by inspection, $A=1,$ $B=0,$ and $C=1.$

Thus, $$ \frac{s^2+s+1}{s^3+s}=\frac{1}{s}+\frac{1}{s^2+1} $$ We may now compute the inverse transform. $$ \begin{array}{lll} \displaystyle \mathscr{L}^{-1}\left\{\frac{s^2+s+1}{s^3+s}\right\}&\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s}+\frac{1}{s^2+1}\right\} &\mbox{}\\ \displaystyle &\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s}\right \}+\mathscr{L}^{-1}\left\{\frac{1}{s^2+1}\right\} &\mbox{by linearity}\\ \displaystyle &\displaystyle=1+\sin(t) &\mbox{using table}\\ \end{array} $$

The First Shifting Property of $\mathscr{L}$

Suppose $\mathscr{L}\{f(t)\}=F(s).$ Then, $$ \mathscr{L}\{e^{-at}f(t)\}=F(s+a) $$ Another useful way of writing the first shifting property is $$ e^{-at}f(t)=\mathscr{L}^{-1}\{F(s+a)\} $$

Example

Compute $ \displaystyle \mathscr{L}^{-1}\left\{\frac{1}{s^2+4s+8}\right\}. $

First We massage the the expression $ \displaystyle \mathscr{L}^{-1}\left\{\frac{1}{s^2+4s+8}\right\}. $ into a form so that we can use the property $\mathscr{L}\{e^{-at}f(t)\}=F(s+a)$ with our table of transforms.

We do so by completing the square. $$ \begin{array}{lll} \displaystyle \frac{1}{s^2+4s+8}&\displaystyle=\frac{1}{s^2+4s\color{magenta}{+4-4}+8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{\color{blue}{s^2+4s+4}-4+8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{\color{blue}{(s+2)^2}+4} &\mbox{}\\ \end{array} $$ This form looks a lot like $\displaystyle \frac{\omega}{s^2+\omega^2}$ from our table of transforms where $\omega=2.$

That is, $$ \mathscr{L}\{\sin(2t)\}=\frac{2}{s^2+4} $$

We now have everything we need to compute the inverse transform. $$ \begin{array}{lll} &\displaystyle \mathscr{L}\{\sin(2t)\}=F(s)=\frac{2}{s^2+4} &\mbox{}\\ \implies &\displaystyle \mathscr{L}\{\sin(2t)\}=F(s)=2\frac{1}{s^2+4}&\mbox{}\\ \implies &\displaystyle \mathscr{L}\{e^{-2t}\sin(2t)\}=F(s+2)=2\frac{1}{(s+2)^2+4}&\mbox{by the 1st shifting property}\\ \implies &\displaystyle \frac{1}{2}\mathscr{L}\{e^{-2t}\sin(2t)\}=\frac{1}{s^2+4s+4}&\mbox{}\\ \implies &\displaystyle \mathscr{L}\left\{\frac{1}{2}e^{-2t}\sin(2t)\right\}=\frac{1}{s^2+4s+4}&\mbox{by linearity of the transform}\\ \end{array} $$ Thus, applying the inverse transform to both sides of the last equation, we see that $$ \mathscr{L}^{-1}\left\{\frac{1}{s^2+4s+8}\right\}=\frac{1}{2}e^{-2t}\sin(2t) $$