Today we reap the rewards for learning how to solve non-homogeneous equations!
We consider problems involving mass spring systems with external forces and circuits with variable voltage sources.
Special Note
The notation we use here will differ slightly from the book.
There are several places where we have opted to use a more standard notation.
Mass Spring System Model
The mass spring system consisting of mass $m$ in kilograms attached to a spring with spring constant $k$ newtons per meter and damping coefficient $c$ is governed by the equation $$ mx''+bx'+kx=F(t) $$ where $F(t)$ is any external force $F(t)$ at time $t.$
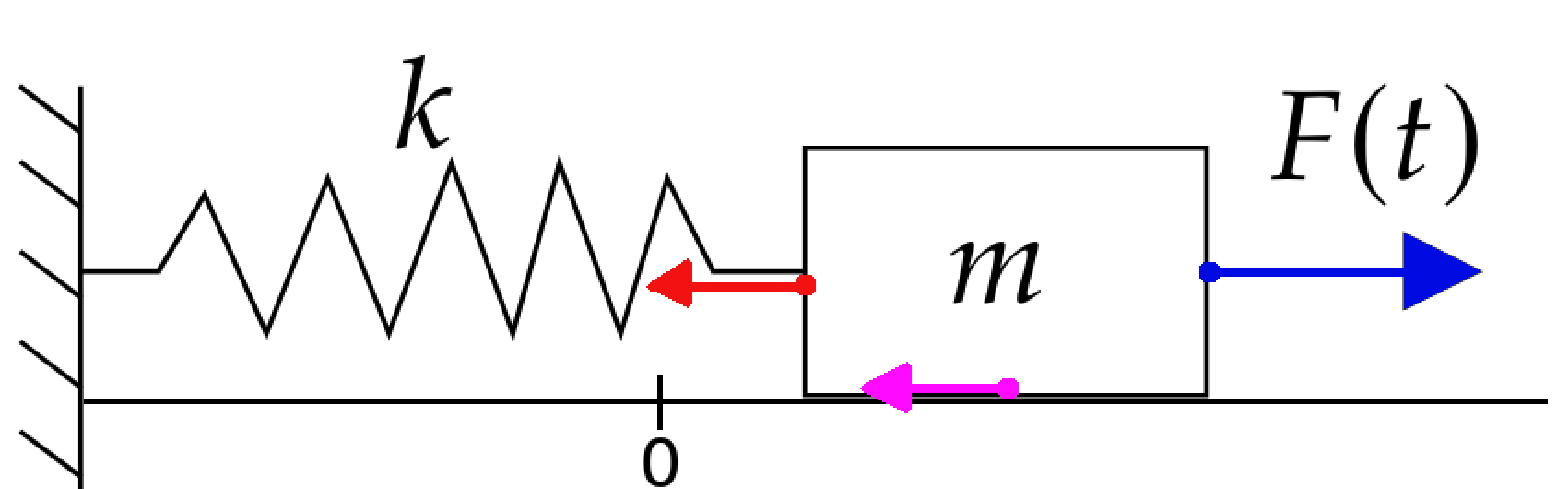
Part I
Undamped Forced Motion
Undamped Forced Motion
Undamped Forced Oscillations
The equation for undamped forced oscillation is $$ mx''+kx=F_0\cos(\omega t) $$ As before, we divide through by $m$ to obtain an equation of the form $$ x''+\omega_0^2x=\frac{F_0}{m}\cos(\omega t) $$ The homogeneous solution is $$ x_h(t)=C_1\cos(\omega_0 t)+C_2\sin(\omega_0 t) $$ To find the general solution, we must find a particular solution.
There are two cases to consider: $\omega_0 \neq \omega,$ and $\omega_0=\omega.$
Finding a Particular Solution When $\omega_0\neq\omega$
Since there is no damping, the original equation contains only second derivatives.
Thus, we may assume a particular solution of the form $x_p=C\cos(\omega t).$
Letting it rip....
Finding a Particular Solution When $\omega_0\neq\omega$ $$ \begin{array}{lll} &\displaystyle x''+\omega_0^2x=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle (C\cos(\omega t))''+\omega_0^2(C\cos(\omega t))=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle -C\omega^2\cos(\omega t)+C\omega_0^2\cos(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle (-C\omega^2+C\omega_0^2)\cos(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle (C\omega_0^2-C\omega^2)\cos(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle C(\omega_0^2-\omega^2)\cos(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \end{array} $$ We conclude that $C(\omega_0^2-\omega^2)=\frac{1}{m}F_0$ from which it follows that $$ C=\frac{F_0}{m(\omega_0^2-\omega^2)} $$
Undamped Forced Oscillations When $\omega_0\neq \omega$
Assuming that $\omega_0\neq \omega,$ we obtain a particular solution $$ x_p=\frac{F_0}{m(\omega_0^2-\omega^2)}\cos(\omega t) $$ Thus, the general solution to the equation for undamped forced oscillation is $$ x(t)=C_1\cos(\omega_0 t)+C_2\sin(\omega_0 t)+\frac{F_0}{m(\omega_0^2-\omega^2)}\cos(\omega t) $$ which we may also write in the form $$ x(t)=A\cos(\omega_0 t-\phi)+\frac{F_0}{m(\omega_0^2-\omega^2)}\cos(\omega t) $$ where $A=\sqrt{C_1^2+C_2^2}$ is the amplitude and $\phi$ is the phase shift.
Example
Suppose a $0.5$ kilogram mass is attached to a spring with constant $8$ newtons per meter.
Starting from rest, a periodic force $F(t)=10\cos(3t)$ is applied.
Find the equation of motion.
In this case, $F_0=10,$ $m=0.5,$ $k=8,$ $\displaystyle \omega_0=\sqrt{\frac{k}{m}}=\sqrt{\frac{8}{0.5}}=4$ and $\omega=3,$ so
the system is described by equation
$$
x''+16x=10\cos(3t),\,\,\,\,x(0)=0,\,\,\,\,x'(0)=0
$$
Our solution has the form
$$
\begin{array}{ll}
x(t)&=\displaystyle C_1\cos(\omega_0 t)+C_2\sin(\omega_0 t)+\frac{F_0}{m(\omega_0^2-\omega^2)}\cos(\omega t)\\
&=\displaystyle C_1\cos(4 t)+C_2\sin(4 t)+\frac{10}{0.5(4^2-3^2)}\cos(3 t)\\
&=\displaystyle C_1\cos(4 t)+C_2\sin(4 t)+\frac{20}{7}\cos(3 t)\\
\end{array}
$$
Applying the first initial condition,
$$
\begin{array}{lll}
&\displaystyle x(0)=0&\mbox{}\\
\implies &\displaystyle C_1\cos(4 \cdot 0)+C_2\sin(4 \cdot 0)+\frac{20}{7}\cos(3 \cdot 0)=0&\mbox{}\\
\implies &\displaystyle C_1+\frac{20}{7}=0&\mbox{}\\
\implies &\displaystyle C_1=-\frac{20}{7}&\mbox{}\\
\end{array}
$$
Since,
$$
x'(t)=-4C_1\sin(4 t)+4C_2\cos(4 t)-\frac{60}{7}\sin(3 t)=-\frac{80}{7}\sin(4 t)+4C_2\cos(4 t)-\frac{60}{7}\sin(3 t)
$$
we now apply the second initial condition
$$
\begin{array}{lll}
&\displaystyle x'(0)=0&\mbox{}\\
\implies &\displaystyle -\frac{80}{7}\sin(4 \cdot 0)+4C_2\cos(4 \cdot 0)-\frac{60}{7}\sin(3 \cdot 0)=0&\mbox{}\\
\implies &\displaystyle 4C_2=0&\mbox{}\\
\implies &\displaystyle C_2=0&\mbox{}\\
\end{array}
$$
The solution to the IVP governing our system is then
$$
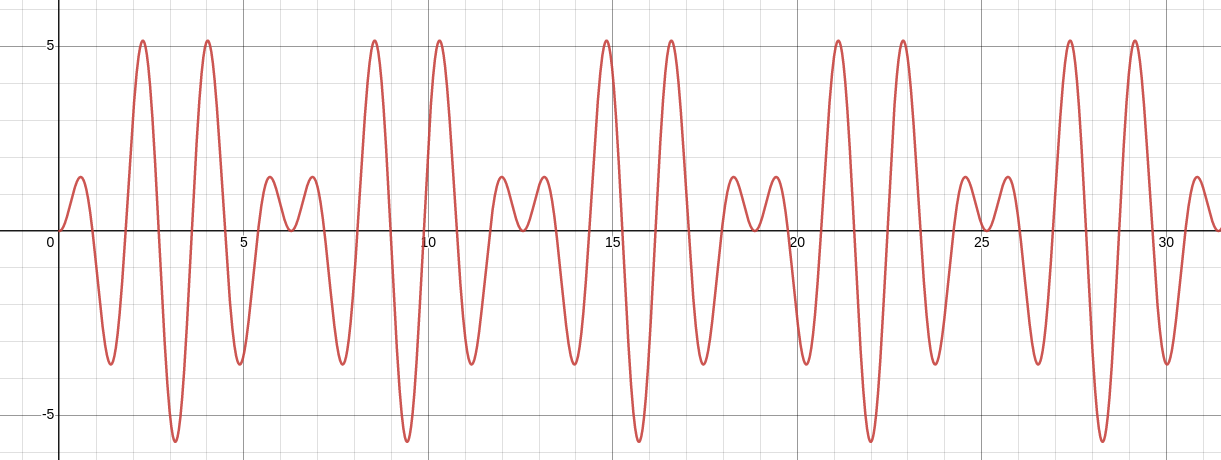
x(t)=-\frac{20}{7}\cos(4 t)+\frac{20}{7}\cos(3 t)
$$
The graph is given below.
A Nice Fun Bonus
The above solution $$ x(t)=-\frac{20}{7}\cos(4 t)+\frac{20}{7}\cos(3 t) $$ exhibits "beating" behavior.
That is, when a higher frequency wave's amplitude is modulated by a lower frequency wave.
To understand this more clearly, we may rewrite the the above using the identity $$ \cos y-\cos x =2\sin\left(\frac{x-y}{2}\right)\sin\left(\frac{x+y}{2}\right) $$ Our solution becomes $$ \begin{array}{lll} \displaystyle x(t)&\displaystyle=-\frac{20}{7}\cos(4 t)+\frac{20}{7}\cos(3 t) &\mbox{}\\ \displaystyle &\displaystyle=\frac{20}{7}(\cos(3 t)-\cos(4t)) &\mbox{}\\ \displaystyle &\displaystyle=\frac{20}{7}\cdot 2\sin\left(\frac{4t-3t}{2}\right)\sin\left(\frac{4t+3t}{2}\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{40}{7}\sin\left(\frac{1}{2}t\right)\sin\left(\frac{7}{2}t\right) &\mbox{}\\ \end{array} $$ In this case the amplitude of the higher frequency wave $\displaystyle \sin\left(\frac{7}{2}t\right)$ is modulated by the lower frequency wave $\displaystyle \frac{40}{7}\sin\left(\frac{1}{2}t\right)$ as seen below.


A Nice Fun Bonus
The above solution $$ x(t)=-\frac{20}{7}\cos(4 t)+\frac{20}{7}\cos(3 t) $$ exhibits "beating" behavior.
That is, when a higher frequency wave's amplitude is modulated by a lower frequency wave.
To understand this more clearly, we may rewrite the the above using the identity $$ \cos y-\cos x =2\sin\left(\frac{x-y}{2}\right)\sin\left(\frac{x+y}{2}\right) $$ Our solution becomes $$ \begin{array}{lll} \displaystyle x(t)&\displaystyle=-\frac{20}{7}\cos(4 t)+\frac{20}{7}\cos(3 t) &\mbox{}\\ \displaystyle &\displaystyle=\frac{20}{7}(\cos(3 t)-\cos(4t)) &\mbox{}\\ \displaystyle &\displaystyle=\frac{20}{7}\cdot 2\sin\left(\frac{4t-3t}{2}\right)\sin\left(\frac{4t+3t}{2}\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{40}{7}\sin\left(\frac{1}{2}t\right)\sin\left(\frac{7}{2}t\right) &\mbox{}\\ \end{array} $$ In this case the amplitude of the higher frequency wave $\displaystyle \sin\left(\frac{7}{2}t\right)$ is modulated by the lower frequency wave $\displaystyle \frac{40}{7}\sin\left(\frac{1}{2}t\right)$ as seen below.

Finding a Particular Solution When $\omega_0=\omega$
We now consider the case when $\omega_0=\omega.$
In this case our equation becomes $$ x''+\omega^2x=\frac{F_0}{m}\cos(\omega t) $$ To find a particular solution using undetermined coefficients, we can't assume a solution of the form $C\cos(\omega t)$ since this solves the homogeneous equation.
Therefore, we will try a solution of the form $x_p=t[C\cos(\omega t)+D\sin(\omega t)].$
The reason the more complicated form is because if we chose $x_p=Ct\cos(\omega t),$ then $x_p''$ would contain terms involving sines.
Let's see what happens...
Finding a Particular Solution When $\omega_0=\omega$
$$ \begin{array}{lll} &\displaystyle x''+\omega^2x=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle (t[C\cos(\omega t)+D\sin(\omega t)])''+\omega^2(t[C\cos(\omega t)+D\sin(\omega t)])=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle (C\cos(\omega t)+D\sin(\omega t)+t[-C\omega\sin(\omega t)+D\omega\cos(\omega t)])'+C\omega^2 t\cos(\omega t)+D\omega^2t\sin(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle (-C\omega\sin(\omega t)+D\omega\cos(\omega t)-C\omega\sin(\omega t)+D\omega\cos(\omega t)+t[-C\omega^2\cos(\omega t)-D\omega^2\sin(\omega t)])+C\omega^2 t\cos(\omega t)+D\omega^2t\sin(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle -C\omega\sin(\omega t)+D\omega\cos(\omega t)-C\omega\sin(\omega t)+D\omega\cos(\omega t)\underbrace{-C\omega^2t\cos(\omega t)-D\omega^2t\sin(\omega t)}+\underbrace{C\omega^2 t\cos(\omega t)+D\omega^2t\sin(\omega t)}=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle -C\omega\sin(\omega t)+D\omega\cos(\omega t)-C\omega\sin(\omega t)+D\omega\cos(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle -C\omega\sin(\omega t)+D\omega\cos(\omega t)-C\omega\sin(\omega t)+D\omega\cos(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \implies &\displaystyle 2D\omega\cos(\omega t)-2C\omega\sin(\omega t)=\frac{F_0}{m}\cos(\omega t)&\mbox{}\\ \end{array} $$
Finding a Particular Solution When $\omega_0=\omega$
Equating coefficients, $$ 2D\omega=\frac{F_0}{m} \,\,\,\,\mbox{and}\,\,\,\,2C\omega=0 $$ Thus, $$ D=\frac{F_0}{2m\omega} $$ and our particular solution is $$ x_p=t[C\cos(\omega t)+D\sin(\omega t)]=\frac{F_0}{2m\omega}t\sin(\omega t) $$
Finding a Particular Solution When $\omega_0=\omega$
The general solution to $$ x''+\omega^2x=\frac{F_0}{m}\cos(\omega t) $$ is $$ x(t)=C_1\cos(\omega t)+C_2\sin(\omega t)+\frac{F_0}{2m\omega}t\sin(\omega t) $$ which we may also write in the form $$ x(t)=A\cos(\omega t-\phi)+\frac{F_0}{2m\omega}t\sin(\omega t) $$ where $A=\sqrt{C_1^2+C_2^2}$ is the amplitude and $\phi$ is the phase shift.
Before we do an example, are there any thoughts on how we can interpret this solution?
Example
Suppose a $0.5$ kilogram mass is attached to a spring with constant $8$ newtons per meter.
Starting from rest, a periodic force $F(t)=10\cos(4t)$ is applied.
Find the equation of motion.
The system is described by $$ x''+16x=10\cos(4t),\,\,\,\,x(0)=0,\,\,\,\,x'(0)=0 $$ Our solution has the form $$ x(t)=C_1\cos(\omega t)+C_2\sin(\omega t)+\frac{F_0}{2m\omega}t\sin(\omega t) $$
In this case, $F_0=10,$ $m=0.5,$ $k=8,$ and $\omega_0=\omega=4,$ so $$ x_p=\frac{F_0}{2m\omega}t\sin(\omega t)=\frac{10}{2(0.5)\cdot 4}t\sin(4 t)=\frac{5}{2}t\sin(4 t) $$ Thus, $$ x(t)=C_1\cos(4 t)+C_2\sin(4 t)+\frac{5}{2}t\sin(4 t) $$ Applying the first initial condition, $$ \begin{array}{lll} &\displaystyle x(0)=0&\mbox{}\\ \implies &\displaystyle C_1\cos(\omega \cdot 0)+C_2\sin(\omega \cdot 0)+\frac{5}{2}t\sin(4 \cdot 0)=0&\mbox{}\\ \implies &\displaystyle C_1=0&\mbox{}\\ \end{array} $$ We then have $$ x(t)=C_2\sin(4 t)+\frac{5}{2}t\sin(4 t) $$ so that $$ x'(t)=4C_2\cos(4t)+\frac{5}{2}(\sin(4t)+ 4t\cos(4t)) $$ Applying the second initial condition, $$ \begin{array}{lll} &\displaystyle x'(0)=0&\mbox{}\\ \implies &\displaystyle 4C_2\cos(0)+\frac{5}{2}(\sin(0)+ 4\cdot 0\cdot \cos(0))=0&\mbox{}\\ \implies &\displaystyle 4C_2=0&\mbox{}\\ \implies &\displaystyle C_2=0&\mbox{}\\ \end{array} $$
The solution is then $$ x(t)=\frac{5}{2}t\sin(4 t) $$ the graph is given below.
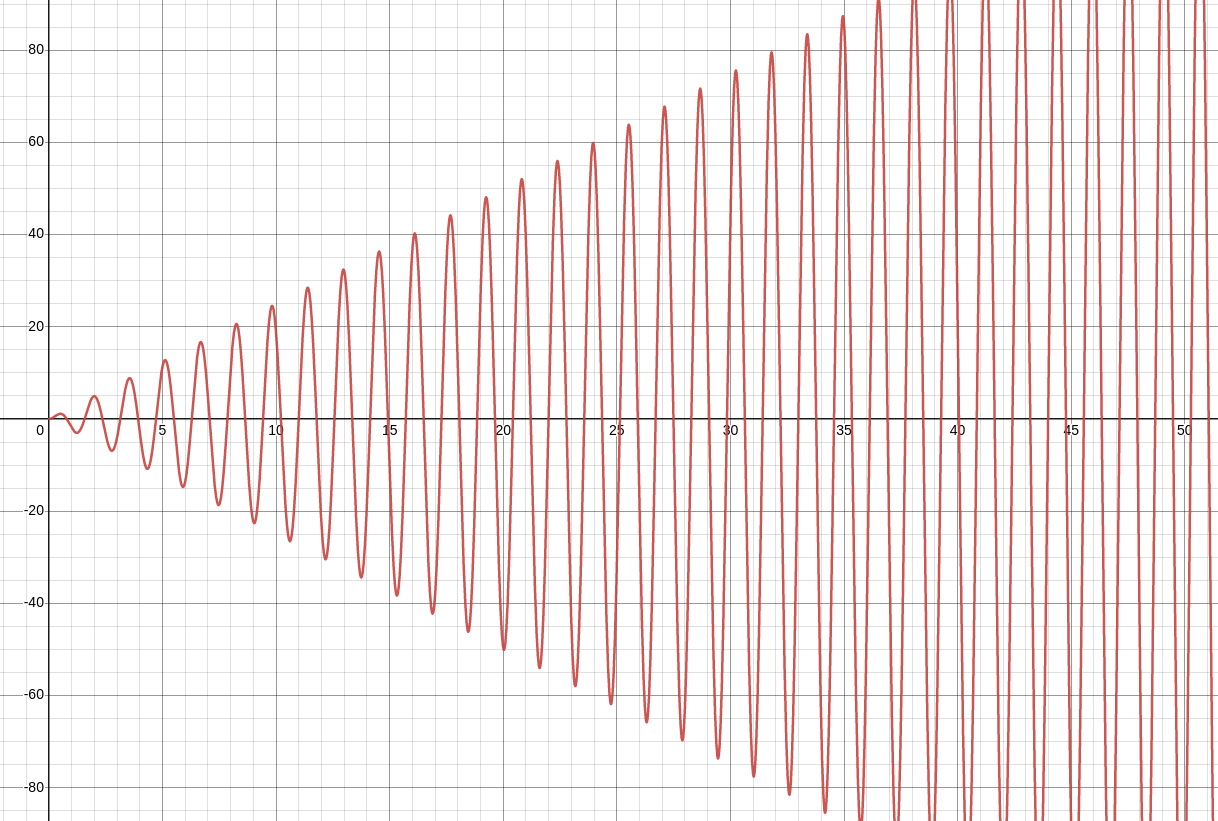
Resonance
The mass-spring model has predicted a phenomenon called resonance.
Resonance
Comparing both examples we have looked at, the first models what happens when the an oscillatory external force is "out of sync" with the frequency the system "wants" to oscillate.
In the second example oscillatory external force is "in perfect sync" with the frequency the system "wants" to oscillate. Energy is always being added to the system.


$x''+16x=10\cos(3t)$$x''+16x=10\cos(4t)$
Familiar Examples of Resonance
An example of resonance we have likely all experienced as kids on a school playground is swinging on a swing set.
Applying energy at just the right time causes us to swing ever higher.
On the other hand, if our timing is off, we won't swing very high.
Familiar Examples of Resonance and Beating Behavior
Another example some of us may be familiar with is sound.
If you've ever heard objects vibrate in a room as a result of a strong tone, this is an example of resonance.
On the other hand, if two "tones" have frequencies which are "slightly out of sync", we can hear the periodic "beats" when the tones add.
Resonance
Undesirable examples of resonance occur when human made structures vibrate at "just the right" frequency causing violent, and sometimes destructive, behavior.
As an example, you may know that soldiers are instructed to never march in step when crossing a bridge. The Angers Bridge in France was destroyed when a battalion marched across it in $1850.$

Part II
Damped Forced Motion
Damped Forced Motion
Damped Forced Motion
Systems without damping technically do not exist in real life.
This is not to say that an undamped model can't be a good at capturing the behavior of a system.
However, we also need to consider situations when damping cannot be ignored.
Damped Forced Oscillations
We begin by considering the general equation for damped, forced oscillation. $$ mx''+bx'+kx=F_0\cos(\omega t) $$ As usual, we divide through by $m$ to get $$ x''+2px'+\omega_0^2x=\frac{F_0}{m}\cos(\omega t) $$ where $\displaystyle p=\frac{b}{2m}$ and $\displaystyle \omega_0=\sqrt{\frac{k}{m}}.$
Damped Forced Oscillations
Solving the characteristic equation $$ r^2+2pr+\omega_0^2=0 $$ we obtain $$ r_1=-p+\sqrt{p^2-\omega_0^2}\,\,\,\,\mbox{and}\,\,\,\,r_2=-p-\sqrt{p^2-\omega_0^2} $$ so that $3$ possible general homogeneous solutions are $$ x_h(t)= \begin{cases} C_1e^{r_1 t}+C_2e^{r_2t} & \mbox{ if }\,\,b^2-4km\gt 0\\ C_1e^{-p}+C_2te^{-pt} & \mbox{ if }\,\,b^2 -4km=0\\ e^{-pt}(C_1\cos(\omega_1 t)+C_2\sin(\omega_1 t)) & \mbox{ if }\,\,b^2-4km\lt 0\\ \end{cases} $$ where $\omega_1=\sqrt{\omega_0^2-p^2}.$
Damped Forced Oscillations
Using the method of undetermined coefficients, we try a particular solution $$ x_p(t)=A\cos(\omega t)+B\sin(\omega t) $$ Plugging this into our equation and another round of algebra we get...
Damped Forced Oscillations
$$ ((\omega_0^2-\omega^2)B-2\omega p A)\sin(\omega t)+((\omega_0^2-\omega^2)A-2\omega p B)\cos(\omega t)=\frac{F_0}{m}\cos(\omega t) $$ Solving the system for $A$ and $B$ we get $$ A=\frac{(\omega_0^2-\omega^2)F_0}{m(2\omega p)^2+m(\omega_0^2-\omega^2)^2} \,\,\,\,\mbox{and}\,\,\,\, B=\frac{2\omega p F_0}{m(2\omega p)^2+m(\omega_0^2-\omega^2)^2} $$
Damped Forced Oscillations
Our particular solution is then $$ x_p(t)=\frac{(\omega_0^2-\omega^2)F_0}{m(2\omega p)^2+m(\omega_0^2-\omega^2)^2}\cos(\omega t) +\frac{2\omega p F_0}{m(2\omega p)^2+m(\omega_0^2-\omega^2)^2}\sin(\omega t) $$ which we may then phrase as a single cosine $$ x_p(t)=\frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}}\cos(\omega t-\phi) $$ where $\displaystyle \tan(\phi)=\frac{B}{A}=\frac{2\omega p}{\omega_0^2-\omega^2}$ for the the phase shift $\phi$ and $\displaystyle \frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}}=\sqrt{A^2+B^2}$ is the amplitude.
More About Phase Shift
Letting $\displaystyle M=\frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}},$ and using the cosine difference identity $$ \begin{array}{lll} \displaystyle x_p(t)&\displaystyle=M\cos(\omega t-\phi) &\mbox{}\\ \displaystyle &\displaystyle=M\cos (\omega t) \cos \phi + M\sin (\omega t) \sin \phi &\mbox{}\\ \displaystyle &\displaystyle=M\cos \phi\cos (\omega t) + M\sin \phi \sin (\omega t) &\mbox{}\\ \end{array} $$ we see that $$ A=\frac{(\omega_0^2-\omega^2)F_0}{m(2\omega p)^2+m(\omega_0^2-\omega^2)^2} \,\,\,\,\mbox{and}\,\,\,\, \cos(\phi)\,\,\,\mbox{must have the same sign} $$ and $$ B=\frac{2\omega p F_0}{m(2\omega p)^2+m(\omega_0^2-\omega^2)^2} \,\,\,\,\mbox{and}\,\,\,\, \sin(\phi) \,\,\,\mbox{must have the same sign} $$
More About Phase Shift
For $\displaystyle A=\frac{(\omega_0^2-\omega^2)F_0}{m(2\omega p)^2+m(\omega_0^2-\omega^2)^2}$ and $\displaystyle B=\frac{2\omega p F_0}{m(2\omega p)^2+m(\omega_0^2-\omega^2)^2},$ we have $\displaystyle \frac{B}{A}=\frac{2\omega p}{\omega_0^2-\omega^2}$ and
$$ \begin{array}{lll} A\gt 0 \,\,\,\,\mbox{and}\,\,\,\, B \gt 0,\,\,\,\, &\displaystyle\phi=\tan^{-1}\left(\frac{B}{A}\right)\,\,\,\,&\mbox{($\phi$ in Quadrant 1)}\\ A\lt 0 \,\,\,\,\mbox{and}\,\,\,\, B \gt 0,\,\,\,\, &\displaystyle\phi=\tan^{-1}\left(\frac{B}{A}\right)+\pi\,\,\,\,&\mbox{($\phi$ in Quadrant 2)}\\ A\lt 0 \,\,\,\,\mbox{and}\,\,\,\, B \lt 0,\,\,\,\, &\displaystyle\phi=\tan^{-1}\left(\frac{B}{A}\right)+\pi\,\,\,\,&\mbox{($\phi$ in Quadrant 3)}\\ A\gt 0 \,\,\,\,\mbox{and}\,\,\,\, B \lt 0,\,\,\,\, &\displaystyle \phi=\tan^{-1}\left(\frac{B}{A}\right)\,\,\,\,&\mbox{($\phi$ in Quadrant 4)}\\ \end{array} $$
Example
Suppose a $1$ kilogram mass is attached to a spring with constant $1$ newton per meter.
Furthermore, the mass is subject to friction which translates to a damping coefficient of $0.7.$
A periodic force $F(t)=\cos(1.1 t)$ is applied.
Find the general equation of motion.
For this example, $m=1,$ $k=1,$ $b=0.7,$ $F_0=1,$ and $\omega=1.1.$
Since $b^2-4km=0.7^2-4(1)(1)=-3.51\lt 0$ we know our homogeneous solution will have the form $$ x_h(t)=e^{-pt}(C_1\cos(\omega_1 t)+C_2\sin(\omega_1 t)) $$ Now, $\displaystyle p=\frac{b}{2m}=\frac{0.7}{2(1)}=0.35$ and $ \displaystyle \omega_0=\sqrt{\frac{k}{m}}=\sqrt{\frac{1}{1}}=1 $ so that $\omega_1=\sqrt{\omega_0^2-p^2}=\sqrt{1^2-0.35^2}=\sqrt{0.8775}.$
Thus, the homogeneous solution is $$ x_h(t)=e^{-0.35t}(C_1\cos(\sqrt{0.8775}t)+C_2\sin(\sqrt{0.8775}t)) $$ Now, the sign of $A\lt 0$ since it is the same as $\omega_0^2-\omega^2=1^2-1.1^2\lt 0,$ and the sign of $B$ is positive.
Thus, the phase angle $\phi$ must lie in Quadrant $2.$ It follows that $$ \begin{array}{ll} \displaystyle \phi&=\displaystyle\tan^{-1}\left(\frac{B}{A}\right)+\pi\\ &=\displaystyle\tan^{-1}\left(\frac{2\omega p}{\omega_0^2-\omega^2}\right)+\pi\\ &=\displaystyle\tan^{-1}\left(\frac{2(1.1)(0.35)}{1^2-1.1^2}\right)+\pi\\ &=\displaystyle\tan^{-1}\left(-\frac{11}{3}\right)+\pi\\ &\approx 1.837048376\\ \end{array} $$ The particular solution is then $$ \begin{array}{lll} \displaystyle x_p(t)&\displaystyle=\frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}}\cos(\omega t-\phi) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{(1)\sqrt{(2(1.1)0.35)^2+((1)^2-(1.1)^2)^2}}\cos(1.1 t-1.837048376) &\mbox{}\\ \displaystyle &\displaystyle=1.252940028\cos(1.1 t-1.837048376) &\mbox{}\\ \end{array} $$ and the general equation of motion for our system is then $$ \begin{array}{ll} x(t)&=x_h(t)+x_p(t)\\ &=e^{-0.35t}(C_1\cos(\sqrt{0.8775}t)+C_2\sin(\sqrt{0.8775}t))+1.252940028\cos(1.1 t-1.837048376)\\ \end{array} $$ The graphs of solutions with varying initial conditions are along with the particular solution $\color{#cd5754}{x_p(t)=1.252940028\cos(1.1 t-1.837048376)}$ are shown below.
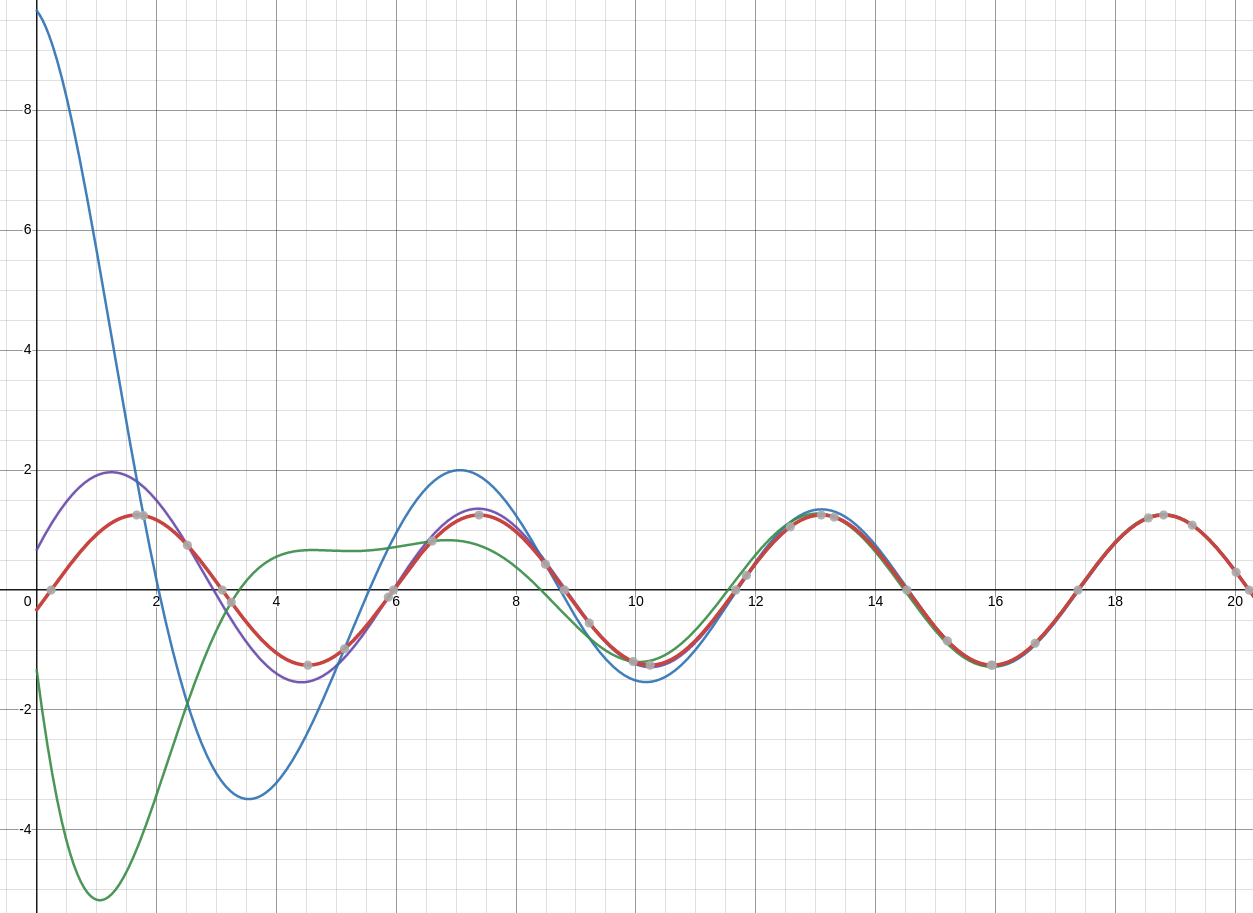
Since $b^2-4km=0.7^2-4(1)(1)=-3.51\lt 0$ we know our homogeneous solution will have the form $$ x_h(t)=e^{-pt}(C_1\cos(\omega_1 t)+C_2\sin(\omega_1 t)) $$ Now, $\displaystyle p=\frac{b}{2m}=\frac{0.7}{2(1)}=0.35$ and $ \displaystyle \omega_0=\sqrt{\frac{k}{m}}=\sqrt{\frac{1}{1}}=1 $ so that $\omega_1=\sqrt{\omega_0^2-p^2}=\sqrt{1^2-0.35^2}=\sqrt{0.8775}.$
Thus, the homogeneous solution is $$ x_h(t)=e^{-0.35t}(C_1\cos(\sqrt{0.8775}t)+C_2\sin(\sqrt{0.8775}t)) $$ Now, the sign of $A\lt 0$ since it is the same as $\omega_0^2-\omega^2=1^2-1.1^2\lt 0,$ and the sign of $B$ is positive.
Thus, the phase angle $\phi$ must lie in Quadrant $2.$ It follows that $$ \begin{array}{ll} \displaystyle \phi&=\displaystyle\tan^{-1}\left(\frac{B}{A}\right)+\pi\\ &=\displaystyle\tan^{-1}\left(\frac{2\omega p}{\omega_0^2-\omega^2}\right)+\pi\\ &=\displaystyle\tan^{-1}\left(\frac{2(1.1)(0.35)}{1^2-1.1^2}\right)+\pi\\ &=\displaystyle\tan^{-1}\left(-\frac{11}{3}\right)+\pi\\ &\approx 1.837048376\\ \end{array} $$ The particular solution is then $$ \begin{array}{lll} \displaystyle x_p(t)&\displaystyle=\frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}}\cos(\omega t-\phi) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{(1)\sqrt{(2(1.1)0.35)^2+((1)^2-(1.1)^2)^2}}\cos(1.1 t-1.837048376) &\mbox{}\\ \displaystyle &\displaystyle=1.252940028\cos(1.1 t-1.837048376) &\mbox{}\\ \end{array} $$ and the general equation of motion for our system is then $$ \begin{array}{ll} x(t)&=x_h(t)+x_p(t)\\ &=e^{-0.35t}(C_1\cos(\sqrt{0.8775}t)+C_2\sin(\sqrt{0.8775}t))+1.252940028\cos(1.1 t-1.837048376)\\ \end{array} $$ The graphs of solutions with varying initial conditions are along with the particular solution $\color{#cd5754}{x_p(t)=1.252940028\cos(1.1 t-1.837048376)}$ are shown below.

Transient and Steady Periodic Solutions
In the above example, the homogeneous solution $ x_h(t)=e^{-0.35t}(C_1\cos(\sqrt{0.8775}t)+C_2\sin(\sqrt{0.8775}t)) $ is called the transient solution and the particular solution $ \color{#cd5754}{x_p(t)=1.252940028\cos(1.1 t-1.837048376)} $ is called the steady periodic solution.

Transient and Steady Periodic Solutions
The more damping a system has, the shorter the effect of the transient solution since the factor $e^{-pt}$ decays to $0$ faster.
On the other hand, as the damping gets smaller and smaller, that is, $b\rightarrow 0,$ our solutions approach the kind we saw in the first two examples; the effect of the homogeneous solution "lasts forever."

Resonance in Damped Systems
We now discuss the how the long-term behavior damped systems (i.e., steady periodic solutions) is influenced by the choice of the frequency $\omega$ of our forcing function $F(t)=F_0\cos(\omega t).$
Our particular (steady periodic) solution is in general $$ x_p(t)=\frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}}\cos(\omega t-\phi) $$ We shall presently focus on the amplitude of the the above. $$ \frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}} $$
Resonance in Damped Systems
The amplitude $M$ of $x_p$ depends on the frequency $\omega$ of the forcing function $F(t)=F_0\cos(\omega t).$
We then write $$ M(\omega)=\frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}} $$ For a particular system, we allow the input frequency $\omega$ to vary.
The resulting curve is called the frequency response curve.
The $\omega$ which yields the largest amplitude $M(\omega)$ is called the resonant frequency of the system.
Resonance in Damped Systems
To find the resonant frequency $\omega$ which gives the maximum amplitude $M(\omega),$ we solve the equation $$ M'(\omega)=0. $$ which becomes $$ \frac{-2\omega(2p^2+\omega^2-\omega_0^2)F_0}{m((2\omega p)^2+(\omega^2-\omega_0^2)^2)^{3/2}}=0 $$ It follows that $$ \begin{array}{lll} &\displaystyle \omega(2p^2+\omega^2-\omega_0^2)=0&\mbox{}\\ \implies &\displaystyle \omega=0\,\,\,\,\mbox{or}\,\,\,\, 2p^2+\omega^2-\omega_0^2=0&\mbox{}\\ \end{array} $$ But $\omega=0$ would result in a non-oscillatory input, so we discard this root and conclude that our resonant frequency is $$ \omega=\sqrt{\omega_0^2-2p^2} $$
Example
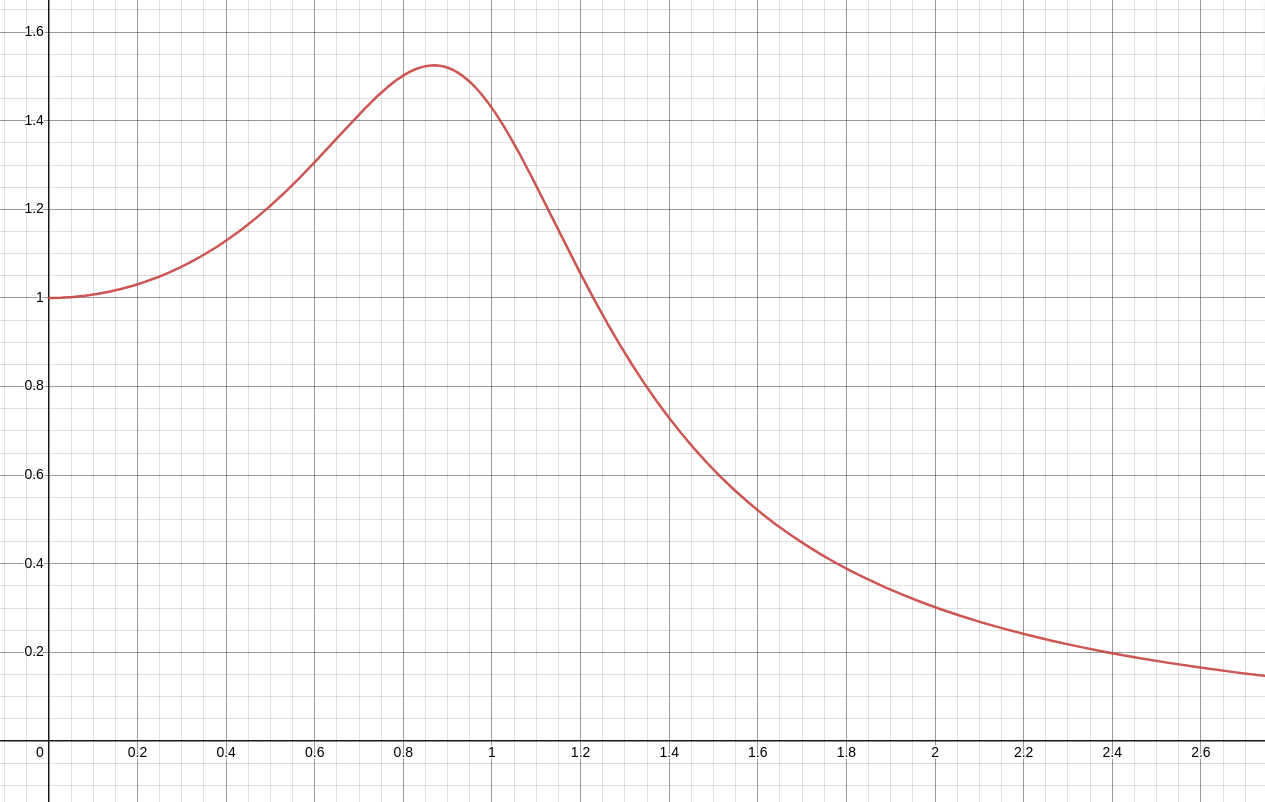
For the above system, $m=1,$ $k=1,$ $b=0.7,$ $F_0=1.$ The frequency response curve is $$ M(\omega)=\frac{F_0}{m\sqrt{(2\omega p)^2+(\omega_0^2-\omega^2)^2}} =\frac{1}{1\cdot\sqrt{(2\omega \cdot 0.35)^2+(1^2-\omega^2)^2}} =\frac{1}{\sqrt{(0.7\omega)^2+(1-\omega^2)^2}} $$
Example
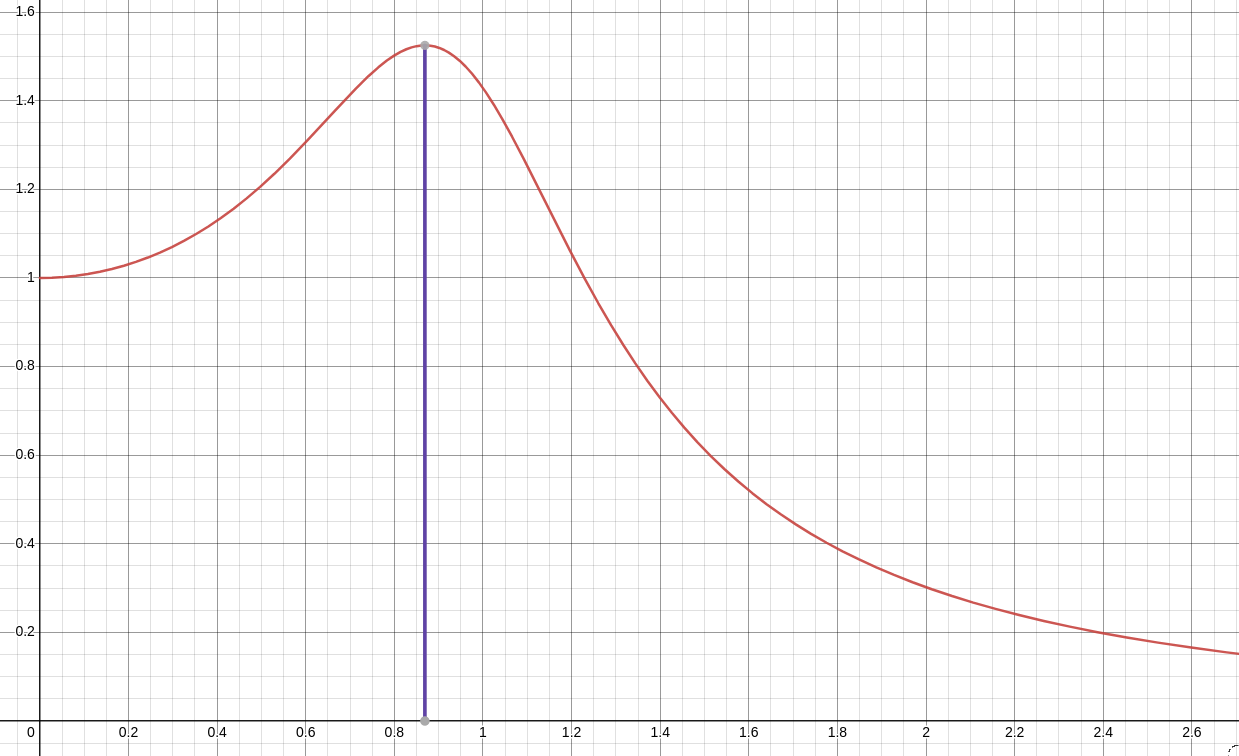
For the above system, $m=1,$ $k=1,$ $b=0.7,$ $F_0=1.$ The resonant frequency is $$ \omega=\sqrt{\omega_0^2-2p^2}=\sqrt{1^2-2(0.35)^2}\approx 0.8689073598 $$
Example
For the above system, $m=1,$ $k=1,$ $b=0.7,$ $F_0=1.$ The maximal amplitude is $$ M(\omega)=M(0.8689073598)=\frac{1}{\sqrt{(0.7(0.8689073598))^2+(1-(0.8689073598)^2)^2}}\approx 1.525030036 $$

Resonance in Damped Systems
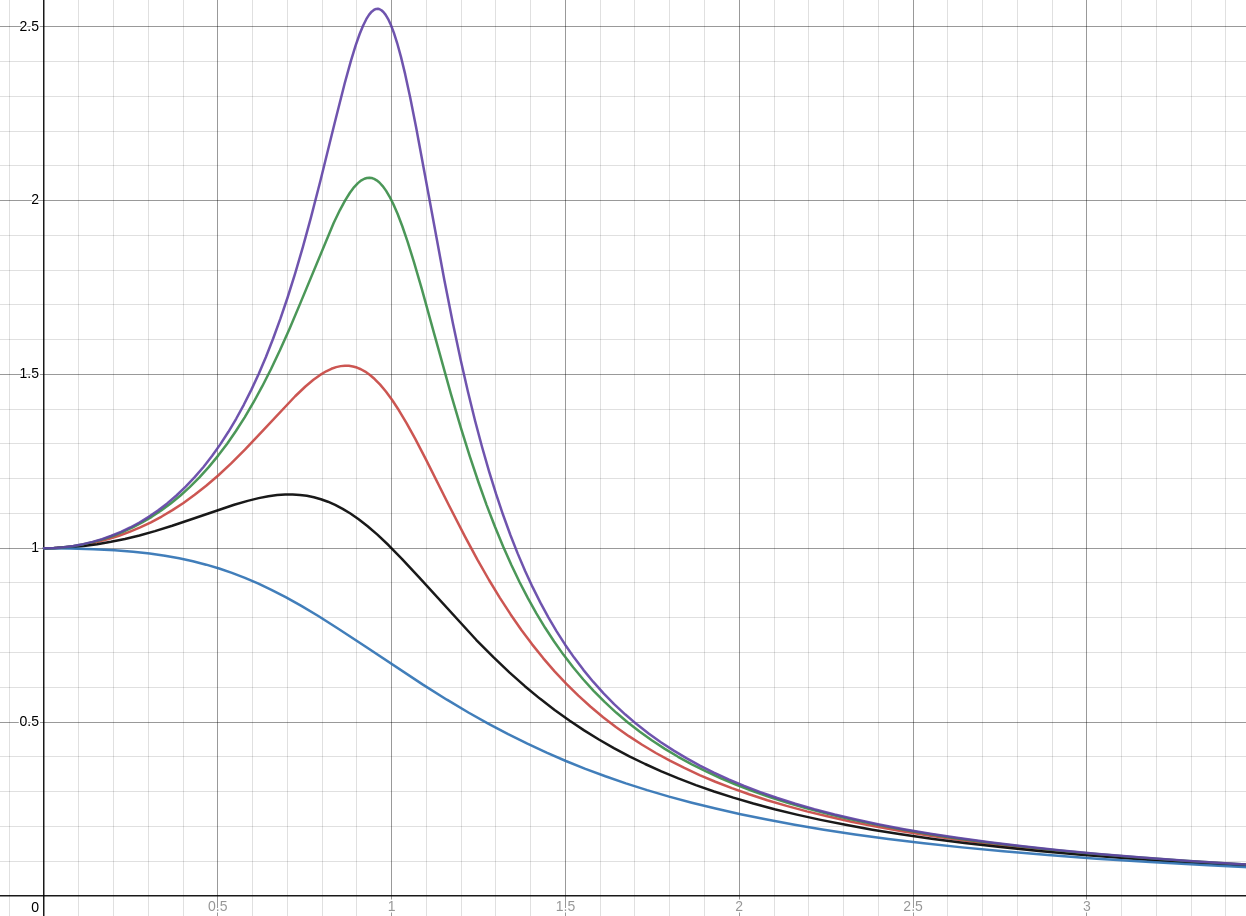
It is also illuminating to allow the damping coefficient $b$ to vary. For each value of the damping coefficient we get a different frequency response curve.
Resonance in Damped Systems
The graph below is for the values $\color{#417eba}{b=1.5},$ $\color{black}{b=1},$ $\color{#cc5652}{b=0.7},$ $\color{#4b9758}{b=0.5},$ and $\color{#6f54ae}{b=0.4}.$

Resonance in Damped Systems
As the damping coefficient decreases, the amplitude at the resonance frequency increases.

Resonance in Damped Systems
As seen above, resonance in damped systems does occur, but not to the degree we observed in the undamped case.
There is a bound on the amplitude of a solution when damping is present.
That said, engineers must pay very careful attention to "mass-spring-like" systems which have a relatively small damping coefficient as this allows for the possibility for large oscillations when a periodic forcing function's frequency is close to the resonance frequency of the system.
The resonance we have studied in damped mass spring systems is what the author of our text calls practical resonance.