Last time we solved equations of the form $$y'=f(x)$$ and their solutions can be stated simply as antiderivatives.
In stark contrast, a general first-order differential equation has the form $$ y'=f(x,y) $$ and there is no general method for solving this equation for an arbitrary function $f(x,y).$
What shall we do?
An Idea
Consider the equation $y'=xy.$
The slope of a solution curve $y(x)$ which passes through the point $(x,y)$ is given by multiplying the $x$ and $y$ coordinates.
For example, the slope of the curve which passes through the point $(2,1.5)$ is $2\cdot 1.5=3.$
Let's plot this slope in the plane...
An Idea
The slope of the curve $y(x)$ which passes through the point $(2,1.5)$ is $2\cdot 1.5=3.$
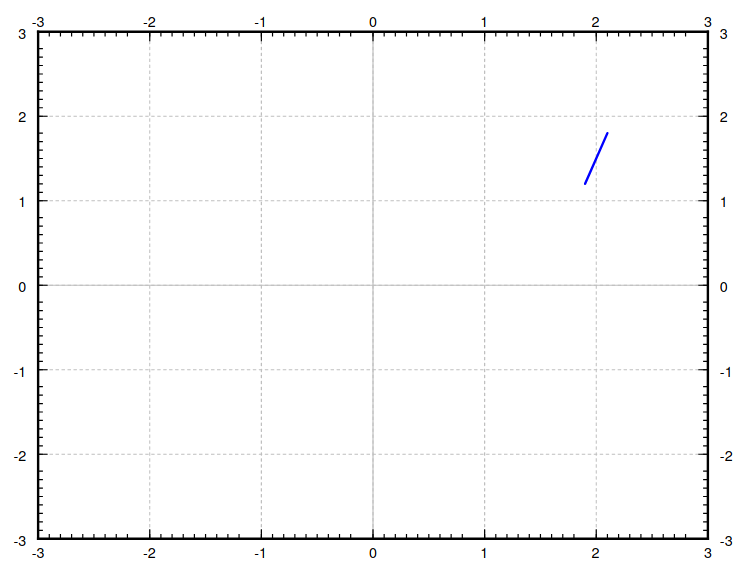
We shall now do this for many points...
Slope Fields
The representation below is called the slope field of $y'=xy.$
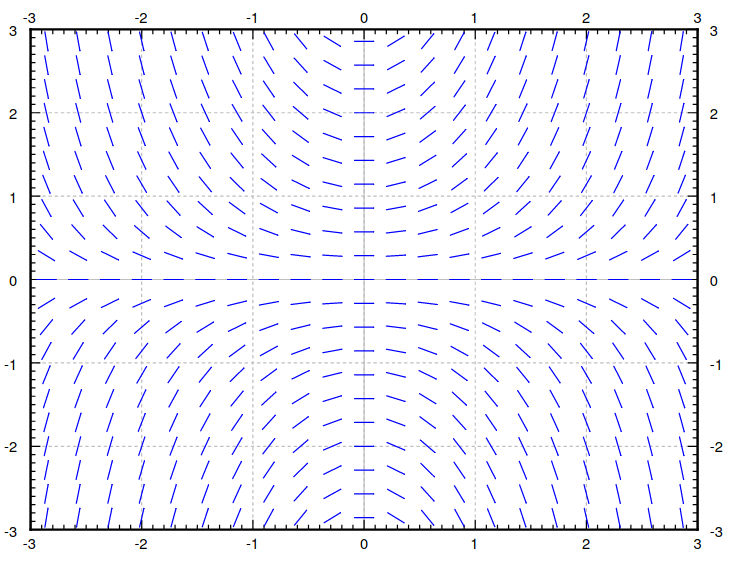
From the slope field we are able to glean important qualitative features of solutions to the equation without even having to solve the equation!
Example
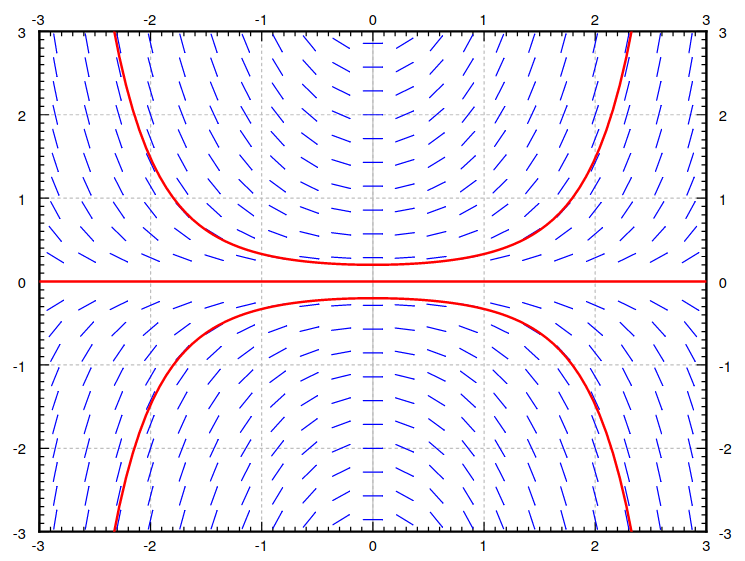
Using the slope field for $y'=xy,$ sketch solution curves satisfying the initial conditions $y(0)=0.2,$ $y(0)=0,$ and $y(0)=-0.2.$

Existence and Uniqueness of Solutions to First-Order Equations
Now that we can visualize the qualitative behavior of any first-order equation, we ask ourselves two questions:
1) Does a solution exist?
2) If a solution exists, is it unique?
Although these questions might seem important to theorists only, the answers to these questions have practical significance.
Existence and Uniqueness of Solutions to First-Order Equations
Suppose you develop a predictive model for some phenomenon which involves a differential equation.
Furthermore, suppose the equation which supposedly describes your system had no solution.
What would you conclude?
Your model sucks.
On the other hand, suppose you found solutions, but there are more than one with the same initial condition.
What would you conclude then?
Your model sucks.
For these reasons, the next theorem offers us great clarity for when we can expect existence and uniqueness.
Picard's Theorem (Existence & Uniqueness)
If $f(x,y)$ is a continuous function of two variables and $\displaystyle \frac{\partial f}{\partial y}$ is continuous near a point $(x_0,y_0),$ then the initial value problem $$ y'=f(x,y), \,\,\,\,\, y(x_0)=y_0 $$ has a solution (at least for $x$ in some small interval) and is unique.
Émile Picard

Jean-Luc Picard's Theorem (Existence & Uniqueness)
If a differential-equation model doesn't have any solutions or the solutions to initial value problems aren't unique, the model probably sucks.

From the hypothesis it follows that the model lacks predictive value.
The conclusion follows. $\square$
Example
The equation $y'=xy$ satisfies Picard's Theorem since $xy$ is everywhere continuous and $\displaystyle \frac{\partial }{\partial y}xy=x$ is continuous near any any initial point $(x_0,y_0).$

Notice that, for example $y(0)=y_0$ is unique for every $y_0.$ That is, the solution curves never intersect.
Example
Consider the equation $$y'=2\sqrt{|y|}.$$ Although $2\sqrt{|y|}$ may be continuous, $\displaystyle \frac{\partial }{\partial y}\left(2\sqrt{|y|}\right)$ doesn't exist at $y=0$ and cannot be continuous there.
Thus, Picard's Theorem has nothing to say about the existence or uniqueness of solutions to this equation.
It turns out that solutions do exist, but at $y=0,$ solutions might not be unique...
Example
The equation $y'=2\sqrt{|y|}$ has two solutions satisfying the initial condition $y(0)=0.$
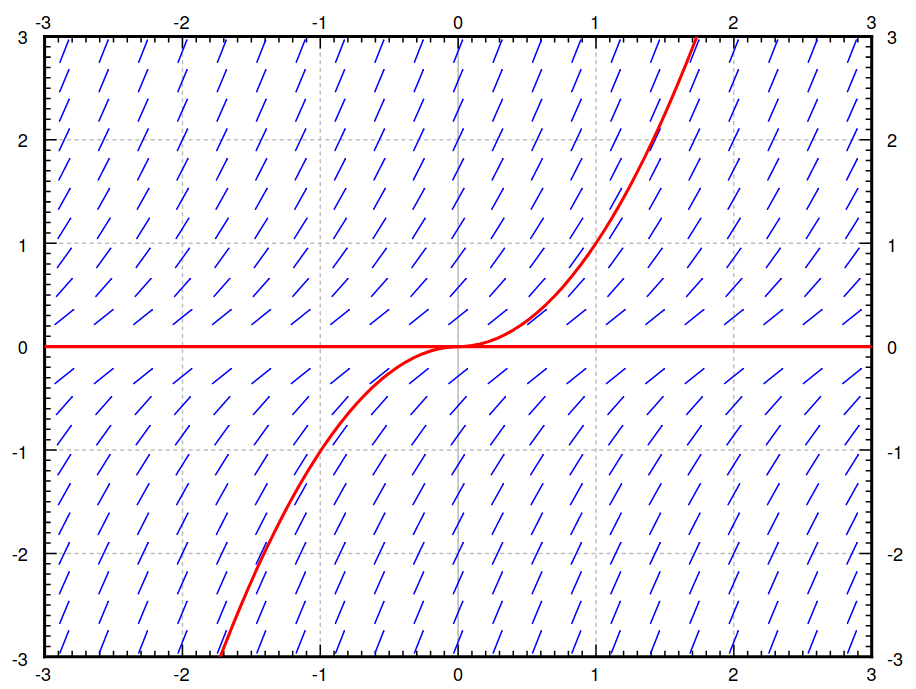
The two solutions are $y(x)=0$ and $y(x)=\begin{cases}x^2 & x \geq 0\\ -x^2 & x \lt 0\end{cases}$
Example
Sketch the slope field for $y'=y^3.$

Recall that we solved this equation in the last section. $$ y=0 \,\,\,\mbox{ or }\,\,\, y=\pm\sqrt{\frac{1}{C-2x}}=\pm\frac{1}{\sqrt{C-2x}} $$ is the general solution.
For the initial condition $y(0)=1$ we obtained $\displaystyle y=\frac{1}{\sqrt{1-2x}}.$

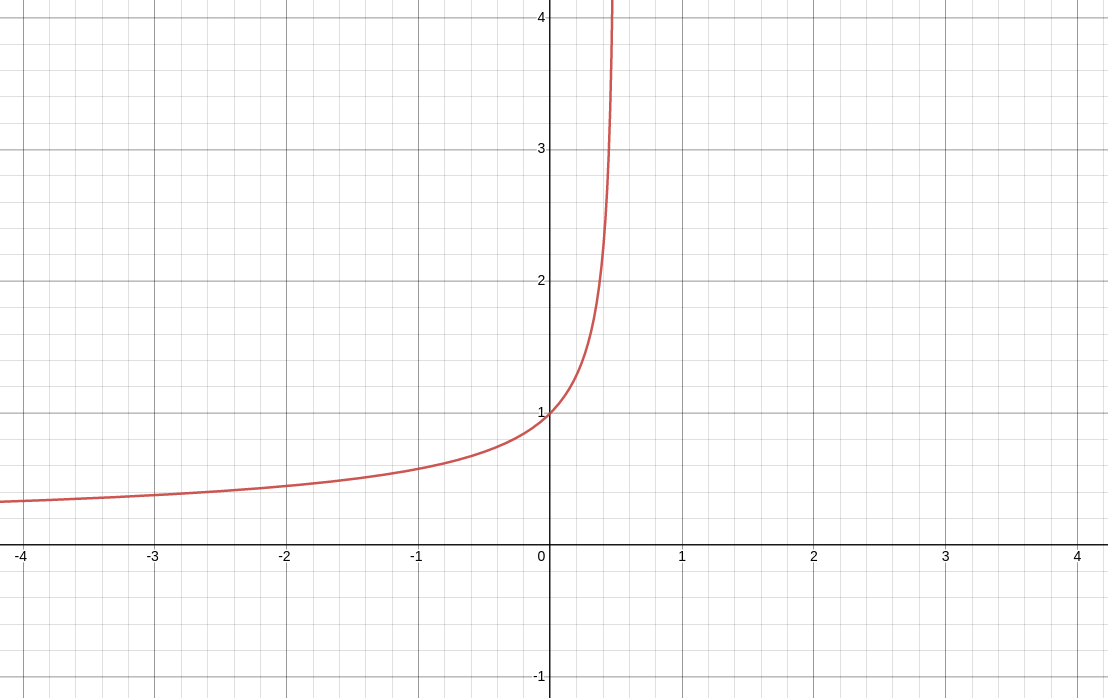
Final Thought
Most, if not all, of the time we will be dealing with equations for which existence and uniqueness holds.
This is especially true for the applications we will be studying.