With the new machinery we've developed over the last two sections (curl, divergence, and surface/flux integrals), we may now generalize Green's Theorem to three dimensions.
The generalization of the circulation form of Green's Theorem is called Stokes' Theorem.
Stokes' Theorem
Let $S$ be a piecewise smooth oriented surface with a boundary that is a simple closed curve $C$ with positive orientation. If ${\bf F}$ is a vector field with component functions that have continuous partial derivatives on an open region containing $S,$ then $$ \displaystyle \oint_{C} {\bf F}\cdot d{\bf r} = \iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} $$
Various Notations of Stokes' Theorem $$ \begin{array}{ll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &= \displaystyle \oint_{C} {\bf F}\cdot {\bf T} \, ds\\ &=\displaystyle \iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \,dS \\ &=\displaystyle \iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S}\\ &=\displaystyle \iint_{S} \nabla \times {\bf F} \cdot {\bf N} \, dS \\ &=\displaystyle \iint_{S} \nabla \times {\bf F} \cdot d{\bf S} \\ \end{array} $$
In Words
$\displaystyle \iint_{S} \color{red}{\mbox{curl }{\bf F}} \cdot \color{blue}{{\bf N}}\, dS=\color{magenta}{\oint_{C} {\bf F}\cdot d{\bf r}}$


The sum of normal components of the circulation densities over a surface is equal to the total circulation along the boundary.
Example
Verify that Stokes' theorem is true for vector field ${\bf F} = \langle 2z + y, 2x + z, 2y + x \rangle$ and surface $S$ which is the upwardly oriented portion of the graph of by $z=x^2+y^2$ for $0\leq z \leq 4.$
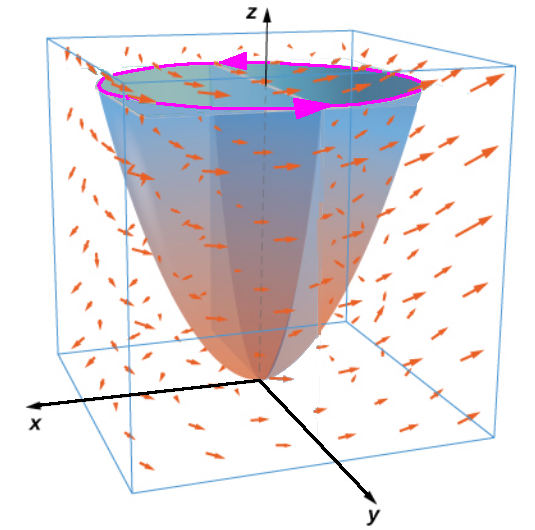
We first compute the line integral directly.
We parameterize the boundary is where $z=x^2+y^2$ intersects the plane $z=4.$
That is, our boundary curve is $x^2+y^2=4,$ or a circle of radius $2.$
Since the surface is oriented upward, the curve must be positively oriented (counterclockwise).
We parameterize this curve as ${\bf r}(t)=\langle 2\cos t, 2\sin t, 4\rangle.$
Then ${\bf r}'(t)=\langle -2\sin t, 2\cos t, 0\rangle.$
We now compute the line integral as $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r}&\displaystyle= \oint_{C} {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \langle 2z(t) + y(t), 2x(t) + z(t), 2y(t) + x(t) \rangle \cdot \langle -2\sin t, 2\cos t, 0\rangle \, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \langle 2 \cdot 4 + 2\sin t, 2\cdot 2 \cos t + 4, 2\cdot 2\sin t + \cos t \rangle \cdot \langle -2\sin t, 2\cos t, 0\rangle \, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \langle 8 + 2\sin t, 4 \cos t + 4, 4\sin t + \cos t \rangle \cdot \langle -2\sin t, 2\cos t, 0\rangle \, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} (8 + 2\sin t)(-2\sin t)+(4 \cos t + 4)(2\cos t)+ (4\sin t + \cos t)\cdot 0 \, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -16\sin t -4\sin^2 t+ 8\cos^2 t + 8\cos t \, dt &\mbox{}\\ \displaystyle &\displaystyle=\left[-16(-\cos t) -4\left(\frac{1}{2}t-\frac{1}{4}\sin (2t)\right)+ 8\left(\frac{1}{2}t+\frac{1}{4}\sin (2t)\right) + 8\sin t\right]_0^{2\pi} &\mbox{table!}\\ \displaystyle &\displaystyle=\left[16\cos t -2t+\sin (2t)+ 4t+2\sin (2t) + 8\sin t\right]_0^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=\left[16\cos t +3\sin (2t)+ 2t + 8\sin t\right]_0^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=16\cos 2\pi +3\sin (4\pi)+ 4\pi + 8\sin (2\pi)-\left(16\cos 0 +3\sin (2\cdot 0)+ 2\cdot 0 + 8\sin 0\right) &\mbox{}\\ \displaystyle &\displaystyle=16 +0+ 4\pi + 0-\left(16 +0 + 0\right) &\mbox{}\\ \displaystyle &\displaystyle=16 +4\pi -16 &\mbox{}\\ \displaystyle &\displaystyle=4\pi &\mbox{}\\ \end{array} $$
We shall now use Stokes' Theorem to calculate the line integral as a surface integral.
First, we assemble all the pieces we need to do the calculation.
Parameterizing the surface, we have ${\bf r}(s,t)=\langle s,t,s^2+t^2\rangle$ over the $s,t$-region $s^2+t^2\leq 4.$
Then $$ \begin{array}{ll} {\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle 1& 0 \displaystyle &2s \displaystyle \\0&1&2t\end{array}\right|\\ &=(0-2s){\bf i}-(2t-0){\bf j}+(1-0){\bf k}\\ &=-2s{\bf i}-2t{\bf j}+{\bf k}\\ \end{array} $$ We now calculate the curl of ${\bf F}.$ $$ \begin{array}{ll} \displaystyle \mbox{curl }{\bf F}&= \nabla \times {\bf F}\\ &=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\2z+y&2x+z&2y+x\end{array}\right|\\ &=(2-1){\bf i}-(1-2){\bf j}+(2-1){\bf k} & \\ &={\bf i}+{\bf j}+{\bf k} & \\ \end{array} $$ We now calculate the line integral as a flux integral with Stokes' Theorem.
Since the surface is oriented upward, $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \, dS &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \mbox{curl }{\bf F}({\bf r}(s,t)) \cdot ({\bf r}_s\times {\bf r}_t)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \langle 1,1,1 \rangle \cdot \langle -2s,-2t,1 \rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} -2s-2t+1 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^2 \int_{-\sqrt{4-s^2}}^{\sqrt{4-s^2}} -2s-2t+1 \, dt \, ds &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{2} (-2r \cos \theta-2r \sin \theta +1) r \, dr \, d\theta &\mbox{convert to polar coordinates}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{2} -2r^2 \cos \theta-2r^2 \sin \theta +r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \left[ -\frac{2}{3}r^3 \cos \theta-\frac{2}{3}r^3 \sin \theta +\frac{1}{2}r^2 \right]_{0}^{2}\, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} -\frac{16}{3} \cos \theta-\frac{16}{3} \sin \theta +2 \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\left[-\frac{16}{3} \sin \theta+\frac{16}{3} \cos \theta +2\theta \right]_{0}^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=-\frac{16}{3} \sin(2\pi)+\frac{16}{3} \cos (2\pi) +2(2\pi) -\left(-\frac{16}{3} \sin 0+\frac{16}{3} \cos 0 +2(0) \right) &\mbox{}\\ \displaystyle &\displaystyle=-0+\frac{16}{3} +4\pi -\left(-0+\frac{16}{3} \right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{16}{3} +4\pi -\frac{16}{3} &\mbox{}\\ \displaystyle &\displaystyle=4\pi&\mbox{}\\ \end{array} $$
We parameterize the boundary is where $z=x^2+y^2$ intersects the plane $z=4.$
That is, our boundary curve is $x^2+y^2=4,$ or a circle of radius $2.$
Since the surface is oriented upward, the curve must be positively oriented (counterclockwise).
We parameterize this curve as ${\bf r}(t)=\langle 2\cos t, 2\sin t, 4\rangle.$
Then ${\bf r}'(t)=\langle -2\sin t, 2\cos t, 0\rangle.$
We now compute the line integral as $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r}&\displaystyle= \oint_{C} {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \langle 2z(t) + y(t), 2x(t) + z(t), 2y(t) + x(t) \rangle \cdot \langle -2\sin t, 2\cos t, 0\rangle \, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \langle 2 \cdot 4 + 2\sin t, 2\cdot 2 \cos t + 4, 2\cdot 2\sin t + \cos t \rangle \cdot \langle -2\sin t, 2\cos t, 0\rangle \, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \langle 8 + 2\sin t, 4 \cos t + 4, 4\sin t + \cos t \rangle \cdot \langle -2\sin t, 2\cos t, 0\rangle \, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} (8 + 2\sin t)(-2\sin t)+(4 \cos t + 4)(2\cos t)+ (4\sin t + \cos t)\cdot 0 \, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -16\sin t -4\sin^2 t+ 8\cos^2 t + 8\cos t \, dt &\mbox{}\\ \displaystyle &\displaystyle=\left[-16(-\cos t) -4\left(\frac{1}{2}t-\frac{1}{4}\sin (2t)\right)+ 8\left(\frac{1}{2}t+\frac{1}{4}\sin (2t)\right) + 8\sin t\right]_0^{2\pi} &\mbox{table!}\\ \displaystyle &\displaystyle=\left[16\cos t -2t+\sin (2t)+ 4t+2\sin (2t) + 8\sin t\right]_0^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=\left[16\cos t +3\sin (2t)+ 2t + 8\sin t\right]_0^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=16\cos 2\pi +3\sin (4\pi)+ 4\pi + 8\sin (2\pi)-\left(16\cos 0 +3\sin (2\cdot 0)+ 2\cdot 0 + 8\sin 0\right) &\mbox{}\\ \displaystyle &\displaystyle=16 +0+ 4\pi + 0-\left(16 +0 + 0\right) &\mbox{}\\ \displaystyle &\displaystyle=16 +4\pi -16 &\mbox{}\\ \displaystyle &\displaystyle=4\pi &\mbox{}\\ \end{array} $$
We shall now use Stokes' Theorem to calculate the line integral as a surface integral.
First, we assemble all the pieces we need to do the calculation.
Parameterizing the surface, we have ${\bf r}(s,t)=\langle s,t,s^2+t^2\rangle$ over the $s,t$-region $s^2+t^2\leq 4.$
Then $$ \begin{array}{ll} {\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle 1& 0 \displaystyle &2s \displaystyle \\0&1&2t\end{array}\right|\\ &=(0-2s){\bf i}-(2t-0){\bf j}+(1-0){\bf k}\\ &=-2s{\bf i}-2t{\bf j}+{\bf k}\\ \end{array} $$ We now calculate the curl of ${\bf F}.$ $$ \begin{array}{ll} \displaystyle \mbox{curl }{\bf F}&= \nabla \times {\bf F}\\ &=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\2z+y&2x+z&2y+x\end{array}\right|\\ &=(2-1){\bf i}-(1-2){\bf j}+(2-1){\bf k} & \\ &={\bf i}+{\bf j}+{\bf k} & \\ \end{array} $$ We now calculate the line integral as a flux integral with Stokes' Theorem.
Since the surface is oriented upward, $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \, dS &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \mbox{curl }{\bf F}({\bf r}(s,t)) \cdot ({\bf r}_s\times {\bf r}_t)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \langle 1,1,1 \rangle \cdot \langle -2s,-2t,1 \rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} -2s-2t+1 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^2 \int_{-\sqrt{4-s^2}}^{\sqrt{4-s^2}} -2s-2t+1 \, dt \, ds &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{2} (-2r \cos \theta-2r \sin \theta +1) r \, dr \, d\theta &\mbox{convert to polar coordinates}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{2} -2r^2 \cos \theta-2r^2 \sin \theta +r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \left[ -\frac{2}{3}r^3 \cos \theta-\frac{2}{3}r^3 \sin \theta +\frac{1}{2}r^2 \right]_{0}^{2}\, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} -\frac{16}{3} \cos \theta-\frac{16}{3} \sin \theta +2 \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\left[-\frac{16}{3} \sin \theta+\frac{16}{3} \cos \theta +2\theta \right]_{0}^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=-\frac{16}{3} \sin(2\pi)+\frac{16}{3} \cos (2\pi) +2(2\pi) -\left(-\frac{16}{3} \sin 0+\frac{16}{3} \cos 0 +2(0) \right) &\mbox{}\\ \displaystyle &\displaystyle=-0+\frac{16}{3} +4\pi -\left(-0+\frac{16}{3} \right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{16}{3} +4\pi -\frac{16}{3} &\mbox{}\\ \displaystyle &\displaystyle=4\pi&\mbox{}\\ \end{array} $$
The Advantages of Stokes' Theorem
One of the great advantages of Stokes' Theorem is that it gives us options.
For example, calculating a messy line integral $\displaystyle \oint_C {\bf F}\cdot d{\bf r}$ could be greatly simplified by calculating the flux integral $\displaystyle \iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S}$ instead.
Example
Use Stokes' Theorem to calculate line integral $\displaystyle \oint_C {\bf F}\cdot d{\bf r}$ where ${\bf F} = \langle z, x, y \rangle$ and $C$ is oriented counterclockwise (positively) and is the boundary of a triangle with vertices $(0, 0, 2),$ $(3, 0, 0),$ and $(0, 2, 0).$
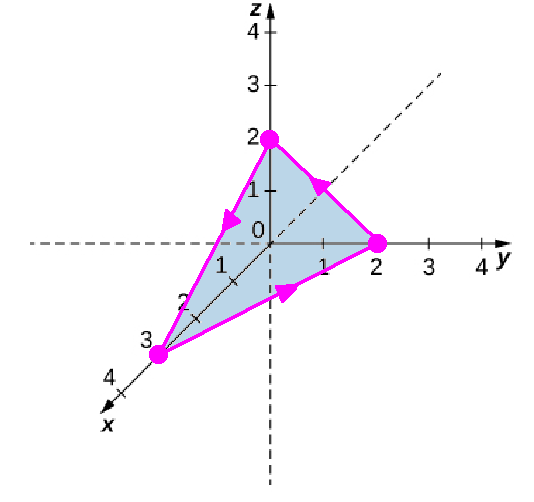
We could calculate the line integral directly, but this would involve breaking up our curve into three separate pieces.
Is there any hope?
This is a job for Stokes' Theorem!
As before, we assemble all the pieces we need to do the calculation.
Parameterizing the surface, we have $\displaystyle {\bf r}(s,t)=\left \langle s,t,2-\frac{2}{3}s-t\right \rangle$ where $\displaystyle 0\leq s \leq 3$ and $\displaystyle 0\leq t \leq 2-\frac{2}{3}s.$
Then $$ \begin{array}{ll} {\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle 1& 0 \displaystyle &-\frac{2}{3} \displaystyle \\0&1&-1\end{array}\right|\\ &=\displaystyle \left(0-\left(-\frac{2}{3}\right)\right){\bf i}-\left(-1-0\right){\bf j}+(1-0){\bf k}\\ &=\displaystyle \frac{2}{3}{\bf i}+{\bf j}+{\bf k}\\ \end{array} $$ We now calculate the curl of ${\bf F}.$ $$ \begin{array}{ll} \displaystyle \mbox{curl }{\bf F}&= \nabla \times {\bf F}\\ &=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\z&x&y\end{array}\right|\\ &=(1-0){\bf i}-(-1){\bf j}+(1-0){\bf k} & \\ &={\bf i}+{\bf j}+{\bf k} & \\ \end{array} $$ We now calculate the line integral with Stokes' Theorem. $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \, dS &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \mbox{curl }{\bf F}({\bf r}(s,t)) \cdot ({\bf r}_s\times {\bf r}_t)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \langle 1,1,1 \rangle \cdot \left\langle \frac{2}{3},1,1 \right\rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \frac{2}{3}+1+1 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \frac{8}{3} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\iint_{D} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}\int_{0}^{2-\frac{2}{3}s} \, dt \, ds &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}[t]_{0}^{2-\frac{2}{3}s} \, ds &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}2-\frac{2}{3}s \, ds &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left[2s-\frac{1}{3}s^2 \right]_{0}^{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left(2\cdot 3-\frac{1}{3}\cdot 3^2 \right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left(6-3 \right) &\mbox{}\\ \displaystyle &\displaystyle=8 &\mbox{}\\ \end{array} $$ A Nice Fun Shortcut
Recall that the flux integral $\displaystyle \iint_S {\bf G}\cdot d{\bf S}$ over a surface $S$ given by $z=g(x,y)$ can be calculated as $\displaystyle \iint_D -Pg_x-Q g_x+R \, dA$ where $P,$ $Q,$ and $R$ are the components of ${\bf G}.$
Taking $\displaystyle z=g(x,y)=2-\frac{2}{3}x-y,$ then $\displaystyle g_x=-\frac{2}{3}$ and $\displaystyle g_y=-1$ so that the above calculation could have been more expediently performed as $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} -Pg_x-Q g_y+R \, dA &\mbox{here $P,$ $Q,$ and $R$ are the components of ${\bf G}=\mbox{curl }{\bf F}$}\\ \displaystyle &\displaystyle=\iint_{D} -1\left(-\frac{2}{3}\right)-1(-1)+1(1) \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \frac{2}{3}+1+1 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \frac{8}{3} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\iint_{D} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}\int_{0}^{2-\frac{2}{3}x} \, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}[y]_{0}^{2-\frac{2}{3}x} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}2-\frac{2}{3}x \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left[2x-\frac{1}{3}x^2 \right]_{0}^{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left(2\cdot 3-\frac{1}{3}\cdot 3^2 \right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left(6-3 \right) &\mbox{}\\ \displaystyle &\displaystyle=8 &\mbox{}\\ \end{array} $$ We note that we could have used the same result for the previous example as well.
Is there any hope?
This is a job for Stokes' Theorem!
As before, we assemble all the pieces we need to do the calculation.
Parameterizing the surface, we have $\displaystyle {\bf r}(s,t)=\left \langle s,t,2-\frac{2}{3}s-t\right \rangle$ where $\displaystyle 0\leq s \leq 3$ and $\displaystyle 0\leq t \leq 2-\frac{2}{3}s.$
Then $$ \begin{array}{ll} {\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle 1& 0 \displaystyle &-\frac{2}{3} \displaystyle \\0&1&-1\end{array}\right|\\ &=\displaystyle \left(0-\left(-\frac{2}{3}\right)\right){\bf i}-\left(-1-0\right){\bf j}+(1-0){\bf k}\\ &=\displaystyle \frac{2}{3}{\bf i}+{\bf j}+{\bf k}\\ \end{array} $$ We now calculate the curl of ${\bf F}.$ $$ \begin{array}{ll} \displaystyle \mbox{curl }{\bf F}&= \nabla \times {\bf F}\\ &=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\z&x&y\end{array}\right|\\ &=(1-0){\bf i}-(-1){\bf j}+(1-0){\bf k} & \\ &={\bf i}+{\bf j}+{\bf k} & \\ \end{array} $$ We now calculate the line integral with Stokes' Theorem. $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \, dS &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \mbox{curl }{\bf F}({\bf r}(s,t)) \cdot ({\bf r}_s\times {\bf r}_t)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \langle 1,1,1 \rangle \cdot \left\langle \frac{2}{3},1,1 \right\rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \frac{2}{3}+1+1 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \frac{8}{3} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\iint_{D} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}\int_{0}^{2-\frac{2}{3}s} \, dt \, ds &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}[t]_{0}^{2-\frac{2}{3}s} \, ds &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}2-\frac{2}{3}s \, ds &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left[2s-\frac{1}{3}s^2 \right]_{0}^{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left(2\cdot 3-\frac{1}{3}\cdot 3^2 \right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left(6-3 \right) &\mbox{}\\ \displaystyle &\displaystyle=8 &\mbox{}\\ \end{array} $$ A Nice Fun Shortcut
Recall that the flux integral $\displaystyle \iint_S {\bf G}\cdot d{\bf S}$ over a surface $S$ given by $z=g(x,y)$ can be calculated as $\displaystyle \iint_D -Pg_x-Q g_x+R \, dA$ where $P,$ $Q,$ and $R$ are the components of ${\bf G}.$
Taking $\displaystyle z=g(x,y)=2-\frac{2}{3}x-y,$ then $\displaystyle g_x=-\frac{2}{3}$ and $\displaystyle g_y=-1$ so that the above calculation could have been more expediently performed as $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} -Pg_x-Q g_y+R \, dA &\mbox{here $P,$ $Q,$ and $R$ are the components of ${\bf G}=\mbox{curl }{\bf F}$}\\ \displaystyle &\displaystyle=\iint_{D} -1\left(-\frac{2}{3}\right)-1(-1)+1(1) \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \frac{2}{3}+1+1 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \frac{8}{3} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\iint_{D} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}\int_{0}^{2-\frac{2}{3}x} \, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}[y]_{0}^{2-\frac{2}{3}x} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\int_{0}^{3}2-\frac{2}{3}x \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left[2x-\frac{1}{3}x^2 \right]_{0}^{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left(2\cdot 3-\frac{1}{3}\cdot 3^2 \right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{3}\left(6-3 \right) &\mbox{}\\ \displaystyle &\displaystyle=8 &\mbox{}\\ \end{array} $$ We note that we could have used the same result for the previous example as well.
The Advantages of Stokes' Theorem
On the other hand, Stokes' Theorem allows us to restate a complicated flux integral $\displaystyle \iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S}$ as a line integral which may be simpler.
Example
Use Stokes' Theorem to calculate surface integral $\displaystyle \iint_S \mbox{curl } {\bf F} \cdot d{\bf S}$ as a line integral $\displaystyle \oint_C {\bf F}\cdot d{\bf r}$ where ${\bf F} = \langle z, x, y \rangle,$ $S$ is the surface as shown in the figure below oriented outwardly.
To obtain an outward surface orientation, we orient boundary curve, $C,$ clockwise (negatively).
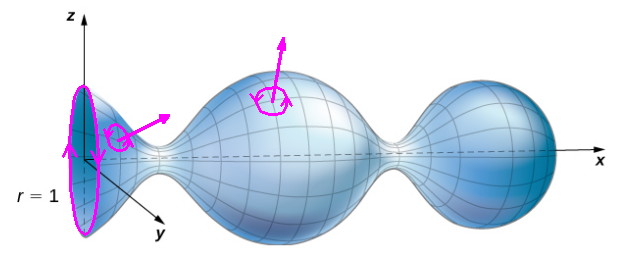
Using Stokes' Theorem in the other direction, we can calculate the surface integral of over our wacky surface by calculating the line integral at the boundary.
The boundary curve is $y^2+z^2=1,$ so we'll parameterize the curve as ${\bf r}(t)=\langle 0, \cos (-t), \sin (-t) \rangle=\langle 0, \cos t, -\sin t \rangle$ over $0 \leq t \leq 2\pi$ for our clockwise orientation.
Then ${\bf r}'(t)=\langle 0, -\sin t, -\cos t \rangle.$ $$ \begin{array}{lll} \displaystyle \iint_S \mbox{curl } {\bf F} \cdot d{\bf S}&\displaystyle= \oint_C {\bf F}\cdot d{\bf r}&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \langle z(t),x(t),y(t) \rangle \cdot \langle 0, -\sin t, \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \langle -\sin t, 0, \cos t \rangle \cdot \langle 0, -\sin t, -\cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} -\cos^2 t\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\int_{0}^{2\pi} \cos^2 t\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\left[\frac{1}{2}t+\frac{1}{4}\sin (2t)\right]_{0}^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=-\left(\frac{1}{2}(2\pi)+\frac{1}{4}\sin (4\pi)-\left(\frac{1}{2}(0)+\frac{1}{4}\sin(0)\right)\right) &\mbox{}\\ \displaystyle &\displaystyle=-(\pi+0-\left(0\right)) &\mbox{}\\ \displaystyle &\displaystyle=-\pi&\mbox{}\\ \end{array} $$

Using Stokes' Theorem in the other direction, we can calculate the surface integral of over our wacky surface by calculating the line integral at the boundary.
The boundary curve is $y^2+z^2=1,$ so we'll parameterize the curve as ${\bf r}(t)=\langle 0, \cos (-t), \sin (-t) \rangle=\langle 0, \cos t, -\sin t \rangle$ over $0 \leq t \leq 2\pi$ for our clockwise orientation.
Then ${\bf r}'(t)=\langle 0, -\sin t, -\cos t \rangle.$ $$ \begin{array}{lll} \displaystyle \iint_S \mbox{curl } {\bf F} \cdot d{\bf S}&\displaystyle= \oint_C {\bf F}\cdot d{\bf r}&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \langle z(t),x(t),y(t) \rangle \cdot \langle 0, -\sin t, \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \langle -\sin t, 0, \cos t \rangle \cdot \langle 0, -\sin t, -\cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} -\cos^2 t\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\int_{0}^{2\pi} \cos^2 t\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\left[\frac{1}{2}t+\frac{1}{4}\sin (2t)\right]_{0}^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=-\left(\frac{1}{2}(2\pi)+\frac{1}{4}\sin (4\pi)-\left(\frac{1}{2}(0)+\frac{1}{4}\sin(0)\right)\right) &\mbox{}\\ \displaystyle &\displaystyle=-(\pi+0-\left(0\right)) &\mbox{}\\ \displaystyle &\displaystyle=-\pi&\mbox{}\\ \end{array} $$
An Astonishing Consequence of Stokes' Theorem
Stokes' Theorem tells us that the flux of $\mbox{curl } {\bf F}$ through a surface $S$ depends ONLY on the boundary curve.
That is, for ANY surface $S$ having the same boundary curve $C,$ the value of $\displaystyle \iint_S \mbox{curl } {\bf F} \cdot d{\bf S}$ will ALWAYS be the same!
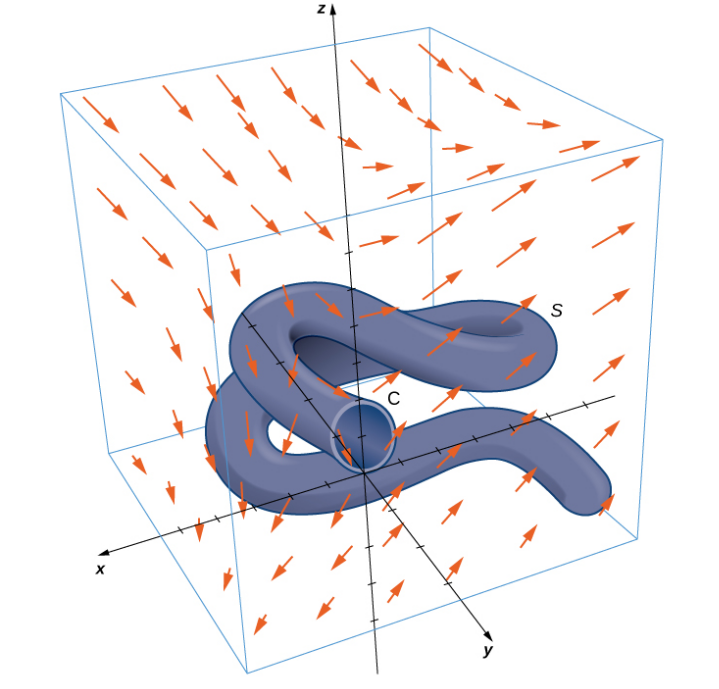
Example
Let ${\bf F} = \langle 2z + y, 2x + z, 2y + x \rangle.$
Verify that the value of $\displaystyle \iint_S \mbox{curl } {\bf F} \cdot d{\bf S}$ is unchanged for the upwardly oriented surfaces determined by $z=x^2+y^2$ and $z=4,$ both of which have the oriented boundary curve $C$ given by ${\bf r}(t)=\langle 2\cos t, 2\sin t, 4\rangle.$
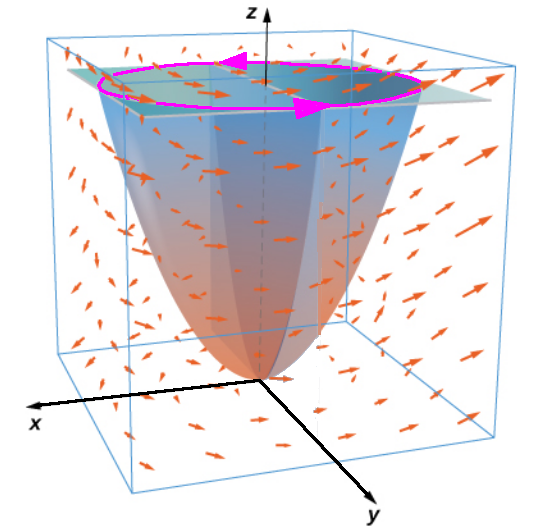
In our first example we saw that over the paraboloid surface that
$$
\iint_{S} \mbox{curl }{\bf F}\cdot d{\bf S}=4\pi
$$
We now calculate $\displaystyle \iint_{S'} \mbox{curl }{\bf F}\, d{\bf S}$
where $S'$ is the surface $z=4$ which we may parameterized as
${\bf r}(s,t)=\langle s,t,4\rangle$ over the region $s^2+t^2\leq 4.$
Then $$ \begin{array}{ll} {\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle 1& 0 \displaystyle &0 \displaystyle \\0&1&0\end{array}\right|\\ &=\displaystyle 0{\bf i}-0{\bf j}+(1-0){\bf k}\\ &=\displaystyle {\bf k}\\ \end{array} $$ Also, we recall from our first example that $\mbox{curl }{\bf F}=\langle 1,1,1 \rangle$
We now calculate the surface integral directly. $$ \begin{array}{lll} %\displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle \iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \, dS &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \mbox{curl }{\bf F}({\bf r}(s,t)) \cdot ({\bf r}_s\times {\bf r}_t)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \langle 1,1,1 \rangle \cdot \langle 0,0,1 \rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} 1 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^2 \int_{-\sqrt{4-s^2}}^{\sqrt{4-s^2}} \, dt \, ds &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{2} r \, dr \, d\theta &\mbox{convert to polar coordinates}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\left[\frac{1}{2}r^2 \right]_{0}^{2}\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}2\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\cdot 2\pi &\mbox{}\\ \displaystyle &\displaystyle=4\pi&\mbox{}\\ \end{array} $$ The answer agrees!
Thus, we could have chosen a much easier surface to work with from the beginning!
Then $$ \begin{array}{ll} {\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle 1& 0 \displaystyle &0 \displaystyle \\0&1&0\end{array}\right|\\ &=\displaystyle 0{\bf i}-0{\bf j}+(1-0){\bf k}\\ &=\displaystyle {\bf k}\\ \end{array} $$ Also, we recall from our first example that $\mbox{curl }{\bf F}=\langle 1,1,1 \rangle$
We now calculate the surface integral directly. $$ \begin{array}{lll} %\displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle \iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \, dS &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \mbox{curl }{\bf F}({\bf r}(s,t)) \cdot ({\bf r}_s\times {\bf r}_t)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \langle 1,1,1 \rangle \cdot \langle 0,0,1 \rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} 1 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^2 \int_{-\sqrt{4-s^2}}^{\sqrt{4-s^2}} \, dt \, ds &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{2} r \, dr \, d\theta &\mbox{convert to polar coordinates}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\left[\frac{1}{2}r^2 \right]_{0}^{2}\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}2\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\cdot 2\pi &\mbox{}\\ \displaystyle &\displaystyle=4\pi&\mbox{}\\ \end{array} $$ The answer agrees!
Thus, we could have chosen a much easier surface to work with from the beginning!
Analogies
Flux integrals of curl vector fields are surface independent in the same way that line integrals of gradient fields are path independent. That is, their values are determined by the original function values on the boundaries.
 |  |
| $\displaystyle \int_C \nabla f \cdot d{\bf r}=f({\bf r}(b))-f({\bf r}(a))$ | $\displaystyle \iint_{S} \nabla \times {\bf F} \cdot d{\bf S} =\oint_{C} {\bf F}\cdot d{\bf r}$ |
Corollary to Stokes' Theorem: The flux of a curl field through a closed surface is $0.$
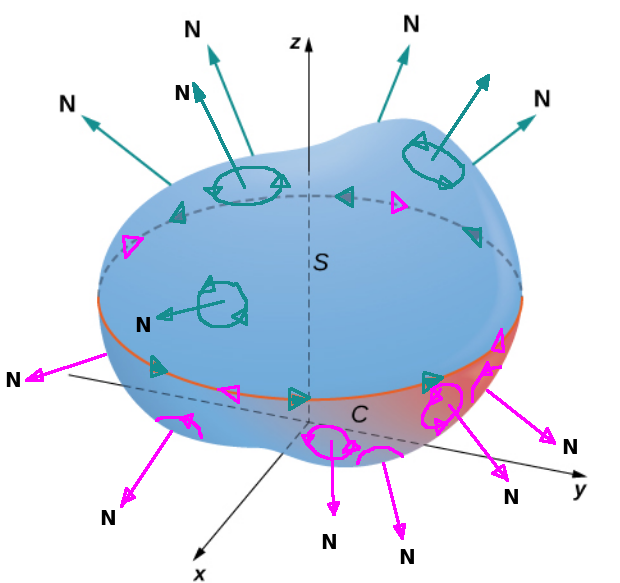
The boundary curves for the upper and lower halves cancel out to $0.$
Analogous Theorems
$$ \begin{array}{cc} \mbox{Gradient Field}&\mbox{Curl Field}\\ %\displaystyle \oint_C \nabla f \cdot \,d{\bf r}=0 & \displaystyle \,{\large \bigcirc}\kern-1.54em \iint_S \nabla \times {\bf F} \cdot \,d{\bf S}=0\\ \displaystyle \oint_C \nabla f \cdot \,d{\bf r}=0 & \displaystyle \,{\large \subset\!\!\supset}\kern-1.7em \iint_S \nabla \times {\bf F} \cdot \,d{\bf S}=0\\ \end{array} $$
The first says that the line integral of a closed loop in a gradient field is $0.$
The second says that the flux integral through a closed surface in a curl field is $0.$
Also Notice: The gradient vector points in the direction of the greatest rate of change whereas the curl points in the direction of the greatest angular change.
Example
Let ${\bf F} = \langle 2z + y, 2x + z, 2y + x \rangle.$
Verify that $\displaystyle \iint_S \mbox{curl } {\bf F} \cdot d{\bf S}=0$ over the sphere of radius $1$ centered at the origin (a closed surface).
We will parameterize the unit sphere as ${\bf r}(\theta,\phi)= \langle \sin \phi \cos \theta, \sin \phi \sin \theta, \cos \phi \rangle$
over the region $0 \leq \theta \leq 2\pi$ and $0 \leq \phi \leq \pi$
so that
$$
\begin{array}{ll}
{\bf r}_{\theta}\times {\bf r}_{\phi}&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ -\sin \phi \sin \theta & \sin \phi \cos \theta & 0 \\ \cos \phi \cos \theta & \cos \phi \sin \theta & -\sin \phi \end{array}\right|\\
&=\displaystyle (-\sin^2 \phi \cos \theta-0){\bf i}-(\sin^2 \phi \sin \theta-0){\bf j}+(-\sin \phi \cos \phi \sin^2 \theta-\sin\phi \cos \phi \cos^2 \theta){\bf k}\\
&=\displaystyle -\sin^2 \phi \cos \theta\,{\bf i}-\sin^2 \phi \sin \theta\,{\bf j}-\sin \phi \cos \phi (\sin^2 \theta +\cos^2 \theta){\bf k}\\
&=\displaystyle -\sin^2 \phi \cos \theta\,{\bf i}-\sin^2 \phi \sin \theta\,{\bf j}-\sin \phi \cos \phi \,{\bf k}\\
\end{array}
$$
Also, we recall from our first example that $\mbox{curl }{\bf F}=\langle 1,1,1 \rangle$
We now calculate the surface integral directly. $$ \begin{array}{lll} %\displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle \iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \, dS &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \mbox{curl }{\bf F}({\bf r}(\theta,\phi)) \cdot ({\bf r}_{\theta}\times {\bf r}_{\phi})\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \langle 1,1,1 \rangle \cdot \langle -\sin^2 \phi \cos \theta,-\sin^2 \phi \sin \theta,-\sin \phi \cos \phi \rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} -\sin^2 \phi \cos \theta-\sin^2 \phi \sin \theta-\sin \phi \cos \phi \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{\pi} -\sin^2 \phi \cos \theta-\sin^2 \phi \sin \theta-\sin \phi \cos \phi \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=-\int_{0}^{2\pi}\int_{0}^{\pi} \sin^2 \phi \cos \theta \, d\phi \, d\theta-\int_{0}^{2\pi}\int_{0}^{\pi}\sin^2 \phi \sin \theta \, d\phi \, d\theta -\int_{0}^{2\pi}\int_{0}^{\pi} \sin \phi \cos \phi \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=-\int_{0}^{2\pi} \cos \theta \left(\int_{0}^{\pi} \sin^2 \phi \, d\phi\right) \, d\theta-\int_{0}^{2\pi}\sin \theta \left(\int_{0}^{\pi}\sin^2 \phi \, d\phi\right) \, d\theta -\int_{0}^{2\pi}\left(\int_{0}^{\pi} \frac{1}{2}\sin (2\phi) \, d\phi \right)\, d\theta &\mbox{}\\ \displaystyle &\displaystyle=-\left(\int_{0}^{\pi} \sin^2 \phi \, d\phi\right)\left(\int_{0}^{2\pi} \cos \theta \, d\theta\right)-\left(\int_{0}^{\pi}\sin^2 \phi \, d\phi\right)\left(\int_{0}^{2\pi}\sin \theta \, d\theta\right) -\left(\int_{0}^{\pi} \frac{1}{2}\sin (2\phi) \, d\phi \right)\left(\int_{0}^{2\pi} \, d\theta\right) &\mbox{}\\ \displaystyle &\displaystyle=-\left(\int_{0}^{\pi} \sin^2 \phi \, d\phi\right)\cdot 0-\left(\int_{0}^{\pi}\sin^2 \phi \, d\phi\right)\cdot 0 -0 \cdot 2\pi &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$
We now calculate the surface integral directly. $$ \begin{array}{lll} %\displaystyle \oint_{C} {\bf F}\cdot d{\bf r} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\mbox{}\\ \displaystyle \iint_{S} \mbox{curl }{\bf F} \cdot d{\bf S} &\displaystyle=\iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \, dS &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \mbox{curl }{\bf F}({\bf r}(\theta,\phi)) \cdot ({\bf r}_{\theta}\times {\bf r}_{\phi})\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} \langle 1,1,1 \rangle \cdot \langle -\sin^2 \phi \cos \theta,-\sin^2 \phi \sin \theta,-\sin \phi \cos \phi \rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_{D} -\sin^2 \phi \cos \theta-\sin^2 \phi \sin \theta-\sin \phi \cos \phi \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{\pi} -\sin^2 \phi \cos \theta-\sin^2 \phi \sin \theta-\sin \phi \cos \phi \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=-\int_{0}^{2\pi}\int_{0}^{\pi} \sin^2 \phi \cos \theta \, d\phi \, d\theta-\int_{0}^{2\pi}\int_{0}^{\pi}\sin^2 \phi \sin \theta \, d\phi \, d\theta -\int_{0}^{2\pi}\int_{0}^{\pi} \sin \phi \cos \phi \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=-\int_{0}^{2\pi} \cos \theta \left(\int_{0}^{\pi} \sin^2 \phi \, d\phi\right) \, d\theta-\int_{0}^{2\pi}\sin \theta \left(\int_{0}^{\pi}\sin^2 \phi \, d\phi\right) \, d\theta -\int_{0}^{2\pi}\left(\int_{0}^{\pi} \frac{1}{2}\sin (2\phi) \, d\phi \right)\, d\theta &\mbox{}\\ \displaystyle &\displaystyle=-\left(\int_{0}^{\pi} \sin^2 \phi \, d\phi\right)\left(\int_{0}^{2\pi} \cos \theta \, d\theta\right)-\left(\int_{0}^{\pi}\sin^2 \phi \, d\phi\right)\left(\int_{0}^{2\pi}\sin \theta \, d\theta\right) -\left(\int_{0}^{\pi} \frac{1}{2}\sin (2\phi) \, d\phi \right)\left(\int_{0}^{2\pi} \, d\theta\right) &\mbox{}\\ \displaystyle &\displaystyle=-\left(\int_{0}^{\pi} \sin^2 \phi \, d\phi\right)\cdot 0-\left(\int_{0}^{\pi}\sin^2 \phi \, d\phi\right)\cdot 0 -0 \cdot 2\pi &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$
Special Note: Since $$\displaystyle \mbox{curl }{\bf F} \cdot {\bf k} %=\left| %\begin{array}{ccc} %{\bf i} &{\bf j} &{\bf k}\\ %\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ %P & Q & R\\ %\end{array} %\right|\cdot {\bf k} %=\left(\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right){\bf i}-\left(\frac{\partial R}{\partial x}-\frac{\partial P}{\partial z}\right){\bf j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right){\bf k}\right)\cdot {\bf k} =\left(\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right){\bf i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right){\bf j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right){\bf k}\right)\cdot {\bf k} =\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}, $$ we may restate the circulation form of Green's Theorem in vector form: $$\displaystyle \oint_{C} {\bf F}\cdot d{\bf r}=\iint_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA = \iint_{D} \mbox{curl }{\bf F} \cdot {\bf k} \,dA$$
Scenic Vista: Stokes' Theorem is a generalization of the circulation (tangential) form of Green's Theorem. $$ \begin{array}{ll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r}=\displaystyle \oint_{C} {\bf F}\cdot {\bf T} \, ds = \iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \,dS& \mbox{Stokes' Theorem} \end{array} $$


Stokes' Theorem is Green's Theorem over a bumpy blanket!
Application
When a magnetic field changes with time, it induces an electric field. Conversely, a changing electric field induces a magnetic field.
Application
One of Maxwell's equations, called Faraday's Law, describes the interaction between changing electric and magnetic fields, and it has two forms: an integral form and differential form.
| Integral Form | Differential Form |
| $$\oint_{\partial S} {\bf E} \cdot d{\bf r}=-\frac{d}{dt}\iint_{S} {\bf B} \cdot d{\bf S} $$ | $$\mbox{curl } {\bf E}=-\frac{\partial {\bf B}}{\partial t}$$ |
Stokes' Theorem helps us to understand how the integral form is derived from the differential form.
Let's begin with the differential form
$$
\mbox{curl } {\bf E}=-\frac{\partial {\bf B}}{\partial t}
$$
Taking the surface integral of both sides
$$
\iint_{S} \mbox{curl } {\bf E} \cdot d{\bf S}= \iint_{S}-\frac{\partial {\bf B}}{\partial t} \cdot d{\bf S}
$$
By Stokes' Theorem, we may rewrite the left hand side as a line integral along the boundary of $S,$ that is,
$\displaystyle \oint_{\partial S} {\bf E}\cdot d{\bf r}.$
Assuming that the surface $S$ does not change with time, we may use the special case of the Leibniz Integral Rule and interchange the derivative and the integral so that the right hand side can be expressed as $\displaystyle -\frac{d}{dt} \iint_{S} {\bf B} \cdot d{\bf S}.$
From the above, the previous equation may be rewritten as $$ \oint_{\partial S} {\bf E} \cdot d{\bf r} =- \frac{d}{dt} \iint_{S} {\bf B} \cdot d{\bf S} $$ which is the integral form of Faraday's Law.
Assuming that the surface $S$ does not change with time, we may use the special case of the Leibniz Integral Rule and interchange the derivative and the integral so that the right hand side can be expressed as $\displaystyle -\frac{d}{dt} \iint_{S} {\bf B} \cdot d{\bf S}.$
From the above, the previous equation may be rewritten as $$ \oint_{\partial S} {\bf E} \cdot d{\bf r} =- \frac{d}{dt} \iint_{S} {\bf B} \cdot d{\bf S} $$ which is the integral form of Faraday's Law.
