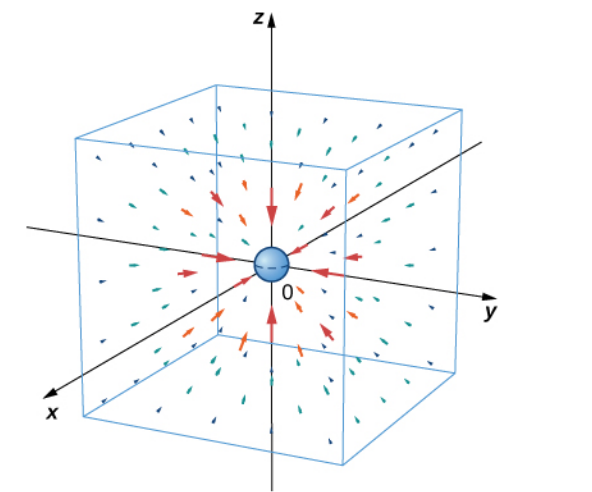
In the previous topic we saw that the flux density at each point measures how "expansive/contractive" a vector field and the circulation density measures how "swirly" a vector field is.
Today, we look at the generalization of both of these ideas to three dimensions.
We also saw how Green's Theorem can save time by expressing a messy line integral as a simpler double integral.
The divergence and curl will enable us to state higher-dimensional versions of Green's Theorem (which itself is a higher-dimensional version of the Fundamental Theorem of Calculus).
The Divergence of a Vector Field
The divergence of a vector field ${\bf F}=\langle P,Q,R\rangle$, denoted $\mbox{div }{\bf F}$ is given by $$ \mbox{div }{\bf F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} $$
The Divergence of a Vector Field
Another notation for $\mbox{div }{\bf F}$ is $\nabla \cdot {\bf F}.$
Taking $\displaystyle \nabla=\left \langle\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\right \rangle,$ we have $$ \nabla \cdot {\bf F}=\left \langle\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\right \rangle \cdot \langle P,Q,R\rangle=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=\mbox{div }{\bf F} $$ This notation is often used in physics as well.
Interpreting Divergence
Notice the similarity of the divergence, $\displaystyle \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z},$ to the two-dimensional flux density $\displaystyle \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}.$
The divergence is simply the three-dimensional version of flux density, and is sometimes even called that.
$\mbox{div }{\bf F}$ measures how expansive/contractive, a three-dimensional field is at a point.
Interpreting Divergence
Again, if we think of a vector field as a fluid flow, the divergence ($3$D flux density) at a point is the tendency of the fluid to leave or exit from that point.
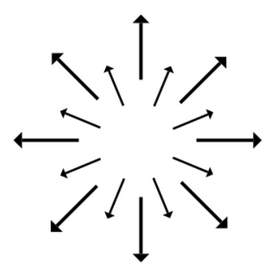 | 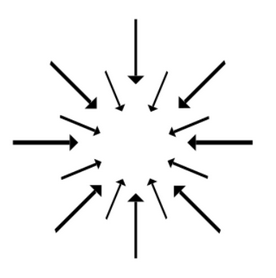 |
| $\mbox{div }{\bf F}\gt 0$ | $\mbox{div }{\bf F}\lt 0$ |
The sign of the the divergence positive when fluid is leaving (a source) and is negative when fluid is coming in (a sink).
The divergence is zero when the fluid leaving the same as the fluid coming in.
Interpreting Divergence: Three Examples
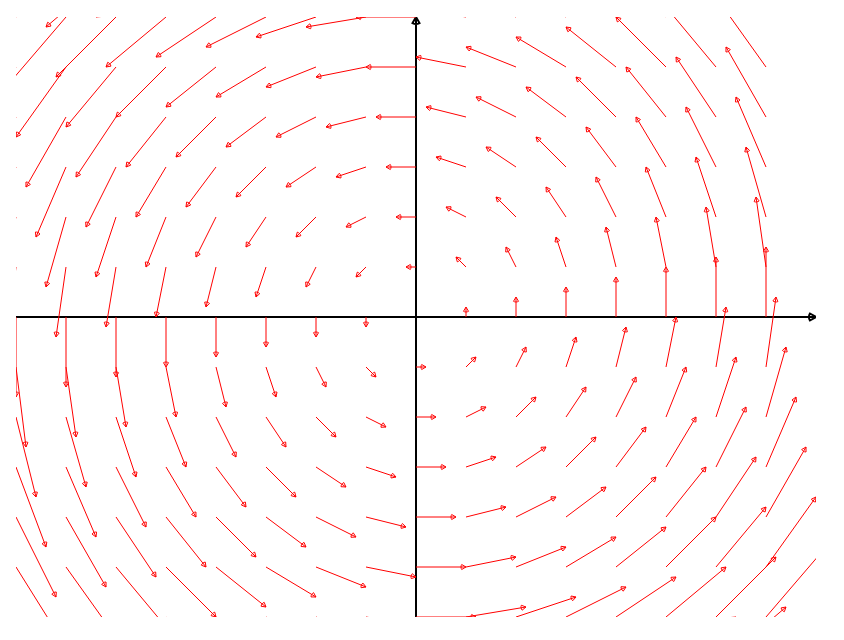 | 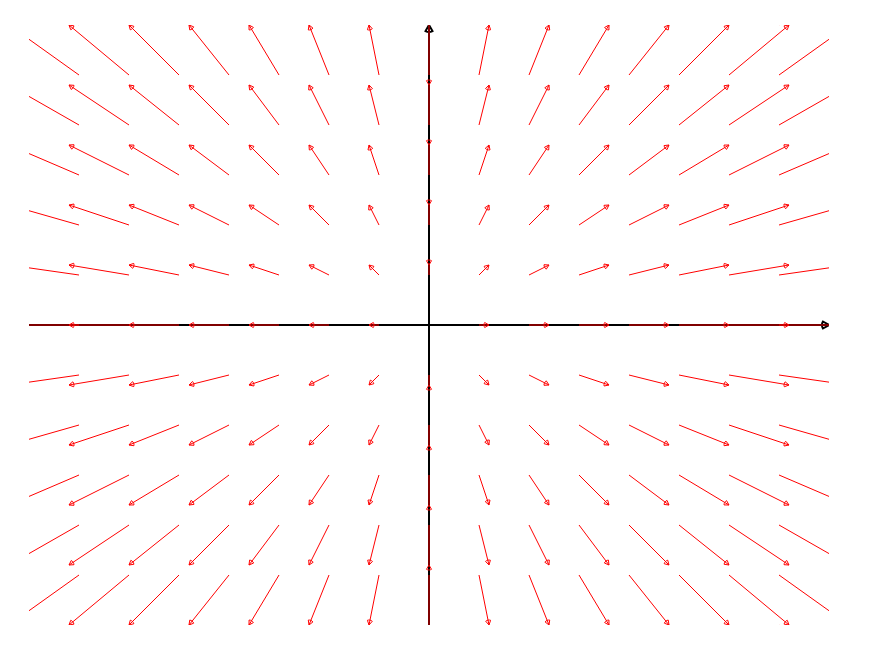 | 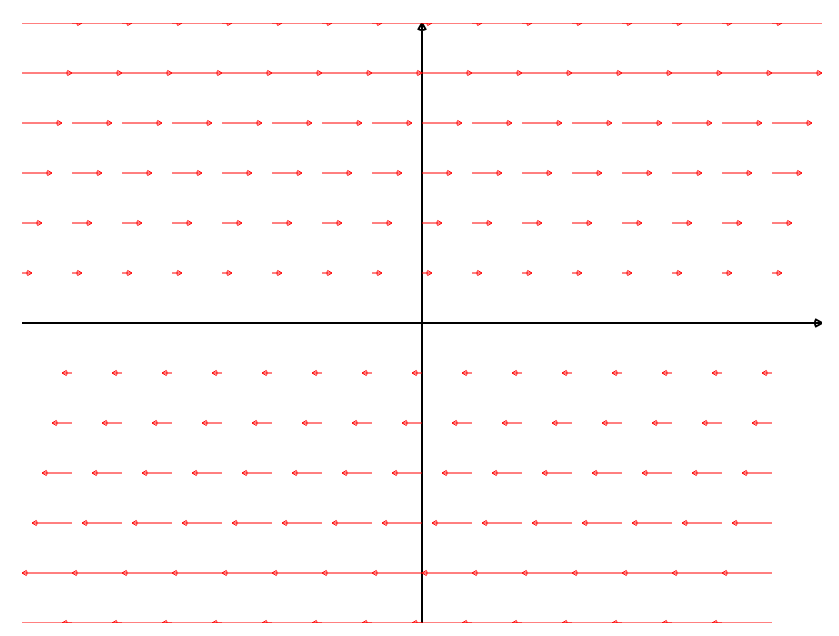 |
| ${\bf F}(x, y) = \langle -y, x \rangle=-y\,{\bf i}+x\,{\bf j}$ $\displaystyle \mbox{div }{\bf F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=0+0=0$ | ${\bf F}(x, y) = \langle x, y \rangle=x\,{\bf i}+y\,{\bf j}$ $\displaystyle \mbox{div }{\bf F} =\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=1+1=2$ | ${\bf F}(x, y) = \langle y, 0 \rangle=y\,{\bf i}$ $\displaystyle \mbox{div }{\bf F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=0+0$ |
Example
Consider the vector field ${\bf F}(x, y, z) = x^2 \,{\bf i} + xy\,{\bf j} + x^3 y^3 \,{\bf k}.$
Compute $\mbox{div }{\bf F}$ at the points $(1,1,1)$ and $(-1,-1,1).$ Interpret the results as if ${\bf F}$ were a fluid flow.
$$
\begin{array}{lll}
\displaystyle \mbox{div }{\bf F}&\displaystyle=\nabla \cdot {\bf F} &\mbox{}\\
\displaystyle &\displaystyle= \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} &\mbox{}\\
\displaystyle &\displaystyle= \frac{\partial }{\partial x}x^2+\frac{\partial }{\partial y}xy+\frac{\partial }{\partial z}x^3y^3 &\mbox{}\\
\displaystyle &\displaystyle= 2x+x+0 &\mbox{}\\
\displaystyle &\displaystyle= 3x &\mbox{}\\
\end{array}
$$
At the point $(1,1,1),$ $\mbox{div }{\bf F}=3\cdot 1=3.$
We may interpret this to mean that the fluid is flowing out of this point at a rate of three units volume per unit time.
At the point $(-1,-1,-1),$ $\mbox{div }{\bf F}=3\cdot (-1)=-3.$ We may interpret this to mean that the fluid is flowing into this point at a rate of three units volume per unit time.
At the point $(-1,-1,-1),$ $\mbox{div }{\bf F}=3\cdot (-1)=-3.$ We may interpret this to mean that the fluid is flowing into this point at a rate of three units volume per unit time.
Electricity and Magnetism
In addition to fluid mechanics, we shall see that divergence and curl are indispensable to the mathematical description of electricity and magnetism.
For instance, one of Maxwell's Equations says that for any magnetic field ${\bf B},$ it must be true that $$\mbox{div }{\bf B}=\nabla \cdot {\bf B}=0.$$ That is, any field ${\bf F}$ for which $\mbox{div }{\bf F}\neq 0$ could not be a magnetic field.
Another way of saying this is that a magnetic field cannot have sources or sinks.
That is, it must be source-free! (solenoidal)
Example
Consider the vector field ${\bf F}(x, y, z) = x^2 \,{\bf i} + xy\,{\bf j} + x^3 y^3 \,{\bf k}.$
Could ${\bf F}$ be a magnetic field?

Since $\mbox{div }{\bf F}=3x,$ the field ${\bf F}$ could not possibly a magnetic field.
Special Note
If we take ${\bf F}=\langle P(x,y),Q(x,y),0\rangle,$ then $$ \mbox{div }{\bf F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}, $$ so that the flux form of Green's Theorem can now be stated as $$ \oint_C {\bf F}\cdot {\bf N}\, ds=\iint_D \mbox{div }{\bf F} \, dA $$
We now extend the notion of circulation density to three dimensions.
This time, however, the circulation density in three dimensions is a vector quantity called the curl.
The Curl of a Vector Field
The curl of a vector field ${\bf F}=\langle P,Q,R\rangle$, denoted $\mbox{curl }{\bf F}$ is given by $$ \mbox{curl }{\bf F} =\left\langle \frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z},\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x},\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right\rangle =\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right){\bf i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right){\bf j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right){\bf k} $$
The Curl of a Vector Field
Another notation for $\mbox{curl }{\bf F}$ is $\nabla \times {\bf F}.$
Again, taking $\displaystyle \nabla=\left \langle\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\right \rangle,$ we have $$ \nabla \times {\bf F} =\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\P&Q&R\end{array}\right| =\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right){\bf i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right){\bf j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right){\bf k} $$ This notation is often used in physics as well.
Interpreting the Curl
Notice that we can embed a two-dimensional vector field, $\langle P(x,y),Q(x,y)\rangle,$ in $\mathbb{R}^3$ by the construction $\displaystyle {\bf F}=\langle P(x,y),Q(x,y),0\rangle.$ Then, $$ \mbox{curl }{\bf F} =\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right){\bf i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right){\bf j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right){\bf k} =\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right){\bf k} $$ That is, magnitude of $\mbox{curl }{\bf F}$ is the circulation density of the two dimensional field $\langle P(x,y),Q(x,y)\rangle.$
In other words, the curl is simply the three-dimensional version of circulation density.
Interpreting the Curl
If we think of a vector field as a fluid flow and we place a little paddle wheel in the fluid, the curl at a point is the tendency of the paddle wheel to spin.
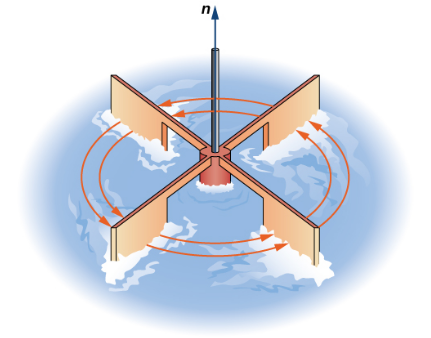
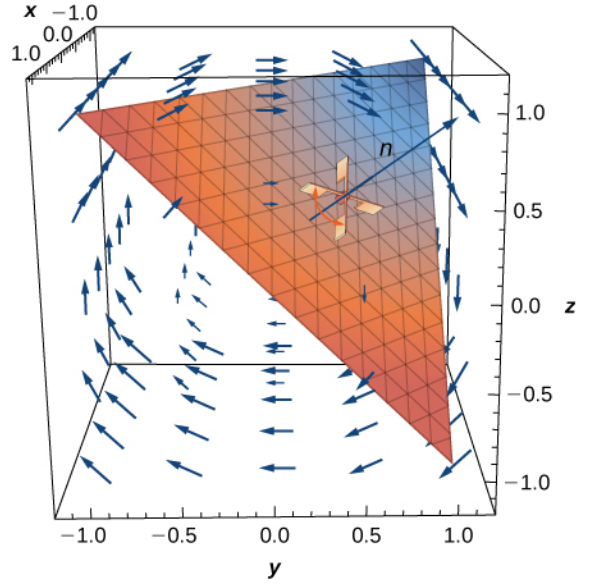
The sign of the the curl is the direction: positive is counterclockwise and negative is clockwise.
Interpreting The Curl: Three Examples
 |  |  |
| ${\bf F}(x, y) = \langle -y, x \rangle=-y\,{\bf i}+x\,{\bf j}$ $\displaystyle \mbox{curl }{\bf F}= \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=1-(-1)=2$ | ${\bf F}(x, y) = \langle x, y \rangle=x\,{\bf i}+y\,{\bf j}$ $\displaystyle \mbox{curl }{\bf F}=\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0-0=0$ | ${\bf F}(x, y) = \langle y, 0 \rangle=y\,{\bf i}$ $\displaystyle \mbox{curl }{\bf F}=\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0-1=-1$ |
Example
Consider the vector field ${\bf F}(x, y, z) = x^2 \,{\bf i} + xy\,{\bf j} + x^3 y^3 \,{\bf k}.$
Compute $\mbox{curl }{\bf F}$ at the points $(1,1,1)$ and $(-1,-1,1).$ Interpret the results as if ${\bf F}$ were a fluid flow.

$$
\begin{array}{ll}
\displaystyle \mbox{curl }{\bf F}&= \nabla \times {\bf F}\\
&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\P&Q&R\end{array}\right|\\
&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\x^2&xy&x^3y^3\end{array}\right|\\
&=(3x^3y^2-0){\bf i}-(3x^2y^3-0){\bf j}+(y-0){\bf k}\\
&=3x^3y^2{\bf i}-3x^2y^3{\bf j}+y{\bf k}\\
\end{array}
$$
At $(1,1,1),$ $$\mbox{curl }{\bf F}=3(1)^3(1)^2{\bf i}-3(1)^2(1)^3{\bf j}+(1){\bf k}=3{\bf i}-3{\bf j}+{\bf k}$$
At $(-1,-1,-1),$ $$\mbox{curl }{\bf F}=3(-1)^3(1)^2{\bf i}-3(-1)^2(-1)^3{\bf j}+(-1){\bf k}=-3{\bf i}+3{\bf j}-{\bf k}$$
At $(-1,-1,-1),$ $$\mbox{curl }{\bf F}=3(-1)^3(1)^2{\bf i}-3(-1)^2(-1)^3{\bf j}+(-1){\bf k}=-3{\bf i}+3{\bf j}-{\bf k}$$
Example
Consider a gravitational vector field $$ {\bf F}(x,y,z)=\left \langle\frac{-Gm_1 m_2x}{(x^2+y^2+z^2)^{3/2}},\frac{-Gm_1 m_2y}{(x^2+y^2+z^2)^{3/2}},\frac{-Gm_1 m_2z}{(x^2+y^2+z^2)^{3/2}}\right \rangle $$ Compute $\mbox{curl }{\bf F}.$
$$
\begin{array}{ll}
\displaystyle \mbox{curl }{\bf F}&= \nabla \times {\bf F}\\
&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\P&Q&R\end{array}\right|\\
&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\ \displaystyle \frac{-Gm_1 m_2x}{(x^2+y^2+z^2)^{3/2}}& \displaystyle \frac{-Gm_1 m_2y}{(x^2+y^2+z^2)^{3/2}}&\displaystyle\frac{-Gm_1 m_2z}{(x^2+y^2+z^2)^{3/2}}\end{array}\right|\\
&=\left(\displaystyle \frac{\partial }{\partial y}\frac{-Gm_1 m_2z}{(x^2+y^2+z^2)^{3/2}}-\frac{\partial }{\partial z}\frac{-Gm_1 m_2y}{(x^2+y^2+z^2)^{3/2}}\right){\bf i}-\left(\displaystyle \frac{\partial }{\partial x}\frac{-Gm_1 m_2z}{(x^2+y^2+z^2)^{3/2}}-\frac{\partial }{\partial z}\frac{-Gm_1 m_2x}{(x^2+y^2+z^2)^{3/2}}\right){\bf j}+\left(\displaystyle \frac{\partial }{\partial x}\frac{-Gm_1 m_2y}{(x^2+y^2+z^2)^{3/2}}-\frac{\partial }{\partial y}\frac{-Gm_1 m_2x}{(x^2+y^2+z^2)^{3/2}}\right){\bf k}\\
&=\left(\displaystyle \frac{-3(-Gm_1 m_2z)}{2(x^2+y^2+z^2)^{5/2}}\cdot 2y-\displaystyle \frac{-3(-Gm_1 m_2y)}{2(x^2+y^2+z^2)^{5/2}}\cdot 2z\right){\bf i}-\left(\displaystyle \frac{-3(-Gm_1 m_2z)}{2(x^2+y^2+z^2)^{5/2}}\cdot 2x-\displaystyle \frac{-3(-Gm_1 m_2x)}{2(x^2+y^2+z^2)^{5/2}}\cdot 2z\right){\bf j}+\left(\displaystyle \frac{-3(-Gm_1 m_2y)}{2(x^2+y^2+z^2)^{5/2}}\cdot 2x-\displaystyle \frac{-3(-Gm_1 m_2x)}{2(x^2+y^2+z^2)^{5/2}}\cdot 2y\right){\bf k}\\
&=\left(\displaystyle \frac{3Gm_1 m_2yz}{(x^2+y^2+z^2)^{5/2}}-\displaystyle \frac{3Gm_1 m_2yz}{(x^2+y^2+z^2)^{5/2}} \right){\bf i}-\left(\displaystyle \frac{3Gm_1 m_2xz}{(x^2+y^2+z^2)^{5/2}}-\displaystyle \frac{3Gm_1 m_2xz}{2(x^2+y^2+z^2)^{5/2}}\right){\bf j}+\left(\displaystyle \frac{3Gm_1 m_2xy}{(x^2+y^2+z^2)^{5/2}}-\displaystyle \frac{3Gm_1 m_2xy}{(x^2+y^2+z^2)^{5/2}}\right){\bf k}\\
&=0{\bf i}-0{\bf j}+0{\bf k}\\
&={\bf 0}\\
\end{array}
$$
Special Note
Since $$\displaystyle \mbox{curl }{\bf F} \cdot {\bf k} %=\left| %\begin{array}{ccc} %{\bf i} &{\bf j} &{\bf k}\\ %\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ %P & Q & R\\ %\end{array} %\right|\cdot {\bf k} %=\left(\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right){\bf i}-\left(\frac{\partial R}{\partial x}-\frac{\partial P}{\partial z}\right){\bf j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right){\bf k}\right)\cdot {\bf k} =\left(\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right){\bf i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right){\bf j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right){\bf k}\right)\cdot {\bf k} =\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}, $$ we may restate the circulation form of Green's Theorem in vector form: $$\displaystyle \oint_{C} {\bf F}\cdot d{\bf r}=\oint_C {\bf F}\cdot {\bf T}\, ds=\iint_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA = \iint_{D} \mbox{curl }{\bf F} \cdot {\bf k} \,dA$$
How Divergence and Curl Relate to One Another
Since we can take the divergence of a vector field, we can take the divergence of the curl of a vector field $$ \mbox{div}(\mbox{curl }{\bf F})=\nabla \cdot (\nabla \times {\bf F}) $$ Any guesses for what will happen?
As long as the second partials are continuous, we have
$$
\begin{array}{lll}
\displaystyle \mbox{div}(\mbox{curl }{\bf F})&\displaystyle= \nabla \cdot (\nabla \times {\bf F})&\mbox{}\\
\displaystyle &\displaystyle=\left \langle \frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}\right \rangle \cdot \left \langle \frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}, \frac{\partial P}{\partial z}-\frac{\partial R}{\partial x},\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right\rangle &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial }{\partial x}\left( \frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)+\frac{\partial }{\partial y}\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)+\frac{\partial }{\partial z}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial^2 R}{\partial x \partial y}-\frac{\partial^2 Q}{\partial x\partial z}+\frac{\partial^2 P}{\partial y \partial z}-\frac{\partial^2 R}{\partial y\partial x}+\frac{\partial^2 Q}{\partial z\partial x}-\frac{\partial^2 P}{\partial z \partial y} &\mbox{}\\
\displaystyle &\displaystyle=0 &\mbox{by Clairaut!}\\
\end{array}
$$
Divergence of the Curl
Let ${\bf F} = \langle P, Q, R \rangle$ be a vector field in $\mathbb{R}^3$ such that the component functions all have continuous second-order partial derivatives. Then, $$ \mbox{div}(\mbox{curl }{\bf F})=\nabla \cdot (\nabla \times {\bf F}) =0 $$ In words: a curl field is divergence free. That is, it has no sources or sinks (is source-free!).
Corollary: Non-Zero Divergence Implies Not a Curl Field
The above result gives us a way to test if a field ${\bf G}$ is not curl field.
If a field ${\bf G}$ is a curl field, then ${\bf G}=\mbox{curl }{\bf F}$ for some field ${\bf F}.$ Then, $$ \mbox{div } {\bf G}=\mbox{div}(\mbox{curl }{\bf F})=\nabla \cdot (\nabla \times {\bf F}) =0 $$ We may represent this fact as $$ \mbox{${\bf G}$ is a curl field}\implies \mbox{div } {\bf G}=0 $$ In practice, however, we use the contrapositive of the above statement. $$ \mbox{div } {\bf G} \neq 0 \implies \mbox{${\bf G}$ is not a curl field} $$
Example
Is it possible for ${\bf G}(x, y, z) = \langle \sin x, \cos y, \sin(xyz) \rangle$ to be the curl of some vector field ${\bf F}?$
$$
\begin{array}{lll}
\displaystyle \mbox{div } {\bf G}&\displaystyle= \nabla \cdot {\bf G}&\mbox{}\\
\displaystyle &\displaystyle= \frac{\partial }{\partial x}\sin x+\frac{\partial }{\partial y}\cos y+\frac{\partial }{\partial z}\sin(xyz)&\mbox{}\\
\displaystyle &\displaystyle= \cos x-\sin y+xy\cos(xyz)&\mbox{}\\
\displaystyle &\displaystyle\neq 0&\mbox{}\\
\end{array}
$$
Thus ${\bf G}$ cannot be a curl field.
The Curl of a Gradient Field
Since we can find the curl of a vector field, we can take the curl of the gradient of function $f.$ That is, we may compute $$ \mbox{curl}(\nabla f)=\nabla \times \nabla f $$ Any guesses for what will happen?
Again, if the mixed partials continuous,
$$
\begin{array}{lll}
\displaystyle \mbox{curl}(\nabla f) &\displaystyle= \nabla \times \nabla f&\mbox{}\\
\displaystyle &\displaystyle= \nabla \times \left\langle \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\right\rangle &\mbox{}\\
\displaystyle &\displaystyle= \left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\\displaystyle \frac{\partial f}{\partial x}&\displaystyle \frac{\partial f}{\partial y}&\displaystyle \frac{\partial f}{\partial z}\end{array}\right| &\mbox{}\\
\displaystyle &\displaystyle= \left \langle \frac{\partial }{\partial y}\frac{\partial f}{\partial z}-\frac{\partial }{\partial z}\frac{\partial f}{\partial y},-\left(\frac{\partial }{\partial x}\frac{\partial f}{\partial z}-\frac{\partial }{\partial z}\frac{\partial f}{\partial x}\right),\frac{\partial }{\partial x}\frac{\partial f}{\partial y}-\frac{\partial }{\partial y}\frac{\partial f}{\partial x} \right \rangle&\mbox{}\\
\displaystyle &\displaystyle= \left \langle \frac{\partial^2 f}{\partial y \partial z}-\frac{\partial^2 f}{\partial z \partial y},-\left(\frac{\partial^2 f}{\partial x \partial z}-\frac{\partial^2 f}{\partial z \partial x}\right),\frac{\partial^2 f}{\partial x \partial y}-\frac{\partial^2 f}{\partial y\partial x} \right \rangle&\mbox{}\\
\displaystyle &\displaystyle= \left \langle 0,0,0 \right \rangle&\mbox{by Clairaut!}\\
\displaystyle &\displaystyle= {\bf 0}&\mbox{}\\
\end{array}
$$
The Curl of a Gradient Field
Let ${\bf F} = \langle P, Q, R \rangle$ be a vector field in $\mathbb{R}^3$ such that the component functions all have continuous second-order partial derivatives. Then, $$ \mbox{curl}(\nabla f)=\nabla \times \nabla f={\bf 0} $$ In words: a gradient field is curl free (or irrotational, conservative).
Corollary: Conservative Field Implies Zero Curl
If ${\bf F} = \langle P, Q, R \rangle$ is conservative, then $\mbox{curl }{\bf F} ={\bf 0}.$
Implications for Gravitational Fields
Gravitational fields are curl free since they are conservative (gradient) fields.
Note: We showed this this directly already.
Implications for Electricity and Magnetism
Since unchanging electric fields are also gradient fields, we have that unchanging electric fields are also curl free.
How Many of You Remember This Clunky Old Thing?
Let ${\bf F}$ be a vector field in two or three dimensions such that the component functions of ${\bf F}$ have continuous second- order mixed-partial derivatives on the domain of ${\bf F}.$
If ${\bf F}(x,y)=\langle P(x,y),Q(x,y)\rangle$ is a conservative vector field in $\mathbb{R}^2,$ then $\displaystyle \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}.$
If ${\bf F}(x,y,z)=\langle P(x,y,z),Q(x,y,z),R(x,y,z)\rangle$ is a conservative vector field in $\mathbb{R}^3,$ then
$$ \begin{array}{l} \displaystyle \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\\ \displaystyle \frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}\\ \displaystyle \frac{\partial R}{\partial x}=\frac{\partial P}{\partial z} \end{array} $$ Do you notice anything???
How Many of You Remember This?
Let ${\bf F} = \langle P, Q, R \rangle$ be a vector field on an open, simply connected region $D.$
Then, $$ \begin{array}{ll} \displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}, &\\ \displaystyle \frac{\partial P}{\partial z} = \frac{\partial R}{\partial x}, &\mbox{ and }\\ \displaystyle \frac{\partial Q}{\partial z} = \frac{\partial R}{\partial y} &\\ \end{array} $$ throughout $D$ if and only if ${\bf F}$ is conservative.
Translation?
Curl Test for a Conservative Field
Let ${\bf F} = \langle P, Q, R \rangle$ be a vector field in space on a simply connected domain.
Then $\mbox{curl }{\bf F}={\bf 0}$ implies that ${\bf F}$ is conservative.
From the above considerations we have an even stronger result.
Zero Curl is Equivalent to Conservative Field on Simply Connected Domain
Let ${\bf F} = \langle P, Q, R \rangle$ be a vector field in space on a simply connected domain.
Then $\mbox{curl }{\bf F}={\bf 0}$ if and only if ${\bf F}$ is conservative.
Example
Use the curl test to determine whether ${\bf F}(x, y, z) = \langle yz, xz, xy \rangle$ is conservative.
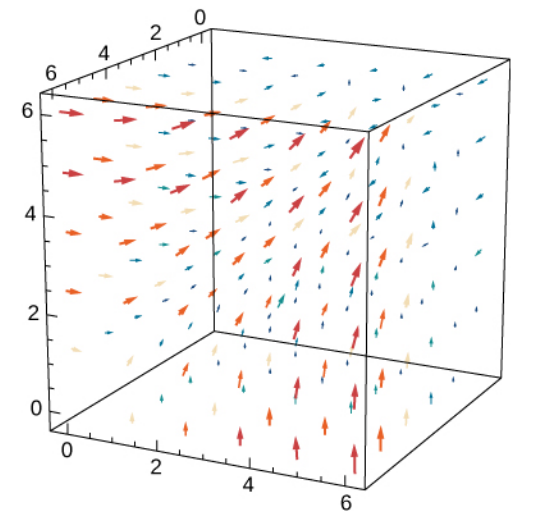
${\bf F}(x, y, z) = \langle yz, xz, xy \rangle$ is a field defined on the simply connected domain $\mathbb{R}^3.$
So, the curl test applies. $$ \begin{array}{ll} \displaystyle \mbox{curl }{\bf F}&= \nabla \times {\bf F}\\ %&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\P&Q&R\end{array}\right|\\ &=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\yz&xz&xy\end{array}\right|\\ &=(x-x){\bf i}-(y-y){\bf j}+(z-z){\bf k} & \\ &=0{\bf i}-0{\bf j}+0{\bf k} & \\ &={\bf 0}& \\ \end{array} $$ By the curl test we may conclude that ${\bf F}$ is a conservative field.
So, the curl test applies. $$ \begin{array}{ll} \displaystyle \mbox{curl }{\bf F}&= \nabla \times {\bf F}\\ %&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\P&Q&R\end{array}\right|\\ &=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\yz&xz&xy\end{array}\right|\\ &=(x-x){\bf i}-(y-y){\bf j}+(z-z){\bf k} & \\ &=0{\bf i}-0{\bf j}+0{\bf k} & \\ &={\bf 0}& \\ \end{array} $$ By the curl test we may conclude that ${\bf F}$ is a conservative field.
Another Bit of Notation
We shall introduce a bit more notation.
$$ \mbox{div }(\nabla f)=\nabla \cdot \nabla f=\nabla^2 f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2} $$ in two dimensions and $$ \mbox{div }(\nabla f)=\nabla \cdot \nabla f=\nabla^2 f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}+\frac{\partial^2 f}{\partial z^2} $$ in three dimensions.
With this in mind...
The Heat and Wave Equations
The heat equation can be expressed in either two or three dimensions as $$ \frac{\partial f}{\partial t}=k\nabla^2 f $$ where $k$ is the thermal conductivity. Note that similar "reaction-diffusion" equations model other phenomena, such as population growth over space and time.
The wave equation can be expressed in either two or three dimensions as $$ \frac{\partial^2 f}{\partial t^2}=c^2\nabla^2 f $$ where $c$ is the propagation speed of the wave.
Recall: Laplace's Equation
Recall that Laplace's Equation is the partial differential equation $$ \nabla^2 f=0 $$ Also recall that solutions to Laplace's Equation are called harmonic functions.
Harmonic Functions
Harmonic functions appear often in physics. Two examples are:
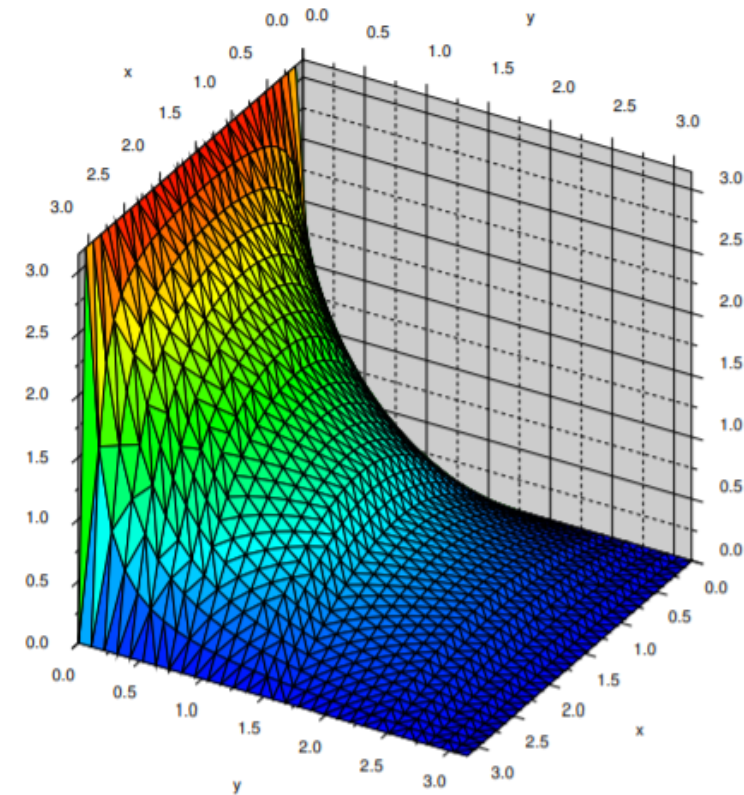 |  |
| Steady-State Temperature Distributions | Electric Potential for Unchanging Electric Fields in regions with no charge |
Example
Which of the functions $$ f (x, y) = x^2 + x - y $$ or $$ f (x, y) = x^2 - y^2 + x $$ is a possible potential function of an electrostatic field?
For $f (x, y) = x^2 + x - y,$
$$
\begin{array}{lll}
\displaystyle \nabla^2 f &\displaystyle=\nabla \cdot \nabla f &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial^2 f}{\partial x^2} +\frac{\partial^2 f}{\partial y^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial^2 }{\partial x^2}(x^2 + x - y) +\frac{\partial^2 }{\partial y^2}(x^2 + x - y) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}(2x+1) +\frac{\partial }{\partial y}(-1) &\mbox{}\\
\displaystyle &\displaystyle=2 +0 &\mbox{}\\
\displaystyle &\displaystyle\neq 0 &\mbox{}\\
\end{array}
$$
Thus $f (x, y) = x^2 + x - y$ is not harmonic and cannot be the potential function of an electrostatic field.
For $f (x, y) = x^2 - y^2 + x,$ $$ \begin{array}{lll} \displaystyle \nabla^2 f &\displaystyle=\nabla \cdot \nabla f &\mbox{}\\ \displaystyle &\displaystyle=\frac{\partial^2 f}{\partial x^2} +\frac{\partial^2 f}{\partial y^2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\partial^2 }{\partial x^2}(x^2 - y^2 + x) +\frac{\partial^2 }{\partial y^2}(x^2 - y^2 + x) &\mbox{}\\ \displaystyle &\displaystyle=\frac{\partial}{\partial x}(2x+1) +\frac{\partial }{\partial y}(-2y) &\mbox{}\\ \displaystyle &\displaystyle= 2+(-2) &\mbox{}\\ \displaystyle &\displaystyle= 0 &\mbox{}\\ \end{array} $$ Thus $f (x, y) = x^2 + x - y$ is harmonic, it could be the potential function of an electrostatic field.
For $f (x, y) = x^2 - y^2 + x,$ $$ \begin{array}{lll} \displaystyle \nabla^2 f &\displaystyle=\nabla \cdot \nabla f &\mbox{}\\ \displaystyle &\displaystyle=\frac{\partial^2 f}{\partial x^2} +\frac{\partial^2 f}{\partial y^2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\partial^2 }{\partial x^2}(x^2 - y^2 + x) +\frac{\partial^2 }{\partial y^2}(x^2 - y^2 + x) &\mbox{}\\ \displaystyle &\displaystyle=\frac{\partial}{\partial x}(2x+1) +\frac{\partial }{\partial y}(-2y) &\mbox{}\\ \displaystyle &\displaystyle= 2+(-2) &\mbox{}\\ \displaystyle &\displaystyle= 0 &\mbox{}\\ \end{array} $$ Thus $f (x, y) = x^2 + x - y$ is harmonic, it could be the potential function of an electrostatic field.
Summary of Formulas and Results $$ \begin{array}{rl} \mbox{Divergence:} &\displaystyle \mbox{div }{\bf F}=\nabla \cdot {\bf F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\\ \mbox{Curl:} &\displaystyle \mbox{curl }{\bf F}=\nabla \times {\bf F}=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle \frac{\partial }{\partial x}& \displaystyle \frac{\partial }{\partial y}& \displaystyle \frac{\partial }{\partial z}\\P&Q&R\end{array}\right|\\ \mbox{Curl Fields are Divergence Free:} & \displaystyle \mbox{div}(\mbox{curl }{\bf F})=\nabla \cdot (\nabla \times {\bf F})=0\\ \mbox{$\mbox{div }{\bf G}\neq 0$ Implies Not a Curl Field:} & \displaystyle \mbox{div } {\bf G} \neq 0 \implies \mbox{${\bf G}$ is not a curl field}\\ \mbox{Gradient Fields are Curl Free:} & \displaystyle \mbox{curl}(\nabla f)=\nabla \times \nabla f={\bf 0}\\ \mbox{Conservative Field Implies Zero Curl:} &\mbox{Conservative Field $\implies$ $\mbox{curl }{\bf F}={\bf 0}$}\\ \mbox{Curl Test for a Conservative Field:} & \displaystyle \mbox{curl }{\bf F}={\bf 0} \mbox{ on Simply Connected $D$} \implies \mbox{${\bf F}$ is Conservative on $D$} \\ \mbox{Harmonic Functions:} & \displaystyle \nabla^2 f=\nabla \cdot \nabla f=\mbox{div}(\nabla f)=0\\ \mbox{Vector Form of Green's Theorem:} & \displaystyle \oint_C {\bf F}\cdot {\bf N} \,ds=\iint_D \mbox{div }{\bf F} \, dA \,\,\mbox{ (Flux Form)}\\ \mbox{Vector Form of Green's Theorem:} & \displaystyle \displaystyle \oint_{C} {\bf F}\cdot {\bf T}\, ds= \iint_{D} \mbox{curl }{\bf F} \cdot {\bf k} \,dA \,\,\mbox{ (Circulation Form)}\\ \end{array} $$
Summary of Physical Examples
Magnetic fields and fluid flows of incompressible fluids are divergence free. That is, no point is a source or sink; the net flow in or out is $0$ at every point.
For the above reasons, divergence-free fields are called solenoidal, incompressible, or source-free fields.
Unchanging electric fields and gravitational fields are curl free. Interpreting a curl-free field as a fluid flow, a tiny paddle wheel placed in the flow would not spin. For this reason, curl-free fields are sometimes called irrotational fields.
Conservative and Source Free Fields in $3$ Dimensions
Let $D$ be a simply connected domain in $\mathbb{R}^3.$
A field $F=\langle P,Q,R \rangle$ is conservative in $D$ precisely when $\nabla \times {\bf F}=\mbox{curl } {\bf F}=0.$
A field $F=\langle P,Q,R \rangle$ is source-free in $D$ precisely when $\nabla \cdot {\bf F}=\mbox{div } {\bf F}=0.$
If a field $F=\langle P,Q,R \rangle$ is simultaneously conservative and source-free in $D$, then $P,$ $Q,$ and $R$ are harmonic functions.
The potential function $f$ for ${\bf F}$ is also harmonic.
STOP TAKING NOTES NOW!
Food for Thought
Recall that the gradient operator $\nabla$ is a kind of generalized derivative. In fact, for any multivariable functions $f$ and $g,$ the following properties hold $$ \begin{array}{ll} \nabla (f+g)=\nabla f + \nabla g&\mbox{Linearity Property of Gradient}\\ \nabla (cf)=c\nabla f&\mbox{Linearity Property of Gradient}\\ \nabla (fg)=g\nabla f+f\nabla g&\mbox{Product Rule}\\ \displaystyle \nabla\left(\frac{f}{g}\right)=\frac{g\nabla f-f\nabla g}{g^2}&\mbox{Quotient Rule}\\ \end{array} $$
Food for Thought
The divergence operator $\nabla \cdot$ and curl operator $\nabla \times$ are also generalized derivatives on three-dimensional vector fields.
Food for Thought
$$ \begin{array}{ll} \nabla \cdot({\bf F}+{\bf G})=\nabla \cdot{\bf F}+\nabla \cdot{\bf G}&\mbox{Linearity Property of Divergence}\\ \nabla \cdot(c{\bf F})=c\,\nabla \cdot{\bf F}&\mbox{Linearity Property of Divergence}\\ \nabla \times({\bf F}+{\bf G})=\nabla \times{\bf F}+\nabla \times{\bf G}&\mbox{Linearity Property of the Curl}\\ \nabla \times(c{\bf F})=c\,\nabla \times{\bf F}&\mbox{Linearity Property of the Curl}\\ \nabla \cdot(f{\bf F})=(\nabla f )\cdot{\bf F}+f (\nabla \cdot{\bf F}) & \mbox{Divergence of a Product of Scalar Function and Vector Field}\\ \nabla \times(f{\bf F})=(\nabla f )\times{\bf F}+f (\nabla \times{\bf F}) & \mbox{Curl of a Product of Scalar Function and Vector Field}\\ \nabla \cdot({\bf F}\times{\bf G})=(\nabla \times {\bf F})\cdot {\bf G}-{\bf F}\cdot (\nabla \times {\bf G})&\mbox{Divergence of a Cross Product}\\ \end{array} $$