The Fundamental Theorem for Line Integrals can be a sanity-saving shortcut, especially if the path is difficult or cumbersome to describe.
However, what do we do if we are working with a field which is not conservative???
Green's Theorem offers an elegant, time-saving shortcut when the path of integration is a closed loop.
Green's Theorem restates a closed-loop line integral as a double integral.
Green's Theorem (Circulation Form)
Let $D$ be an open, simply connected region with a boundary curve $C$ that is a piecewise smooth, simple closed curve oriented counterclockwise (positively). Let ${\bf F} = \langle P, Q \rangle$ be a vector field with component functions that have continuous partial derivatives on $D.$ Then, $$\displaystyle \oint_{C} {\bf F}\cdot d{\bf r}=\iint_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA$$
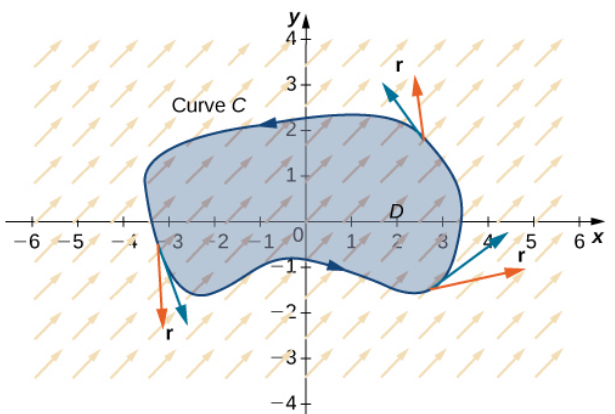
Green's Theorem (Circulation Form)
Green's Theorem allows us to restate a line integral over a closed loop $C$ as a double integral over the region $D$ enclosed by $C.$

That is, $C=\partial D.$
Example
Let ${\bf F}(x, y) = \langle P(x, y), Q(x, y) \rangle = \langle x-2y, y-x \rangle=(x-2y){\bf i}+(y-x)\,{\bf j}$ and let $C$ is be a rectangle with vertices $(0, 0),$ $(2, 0),$ $(2, 1),$ and $(0, 1)$ oriented counterclockwise (positively). Calculate the line integral $\displaystyle \oint_{C} {\bf F}\cdot d{\bf r}.$
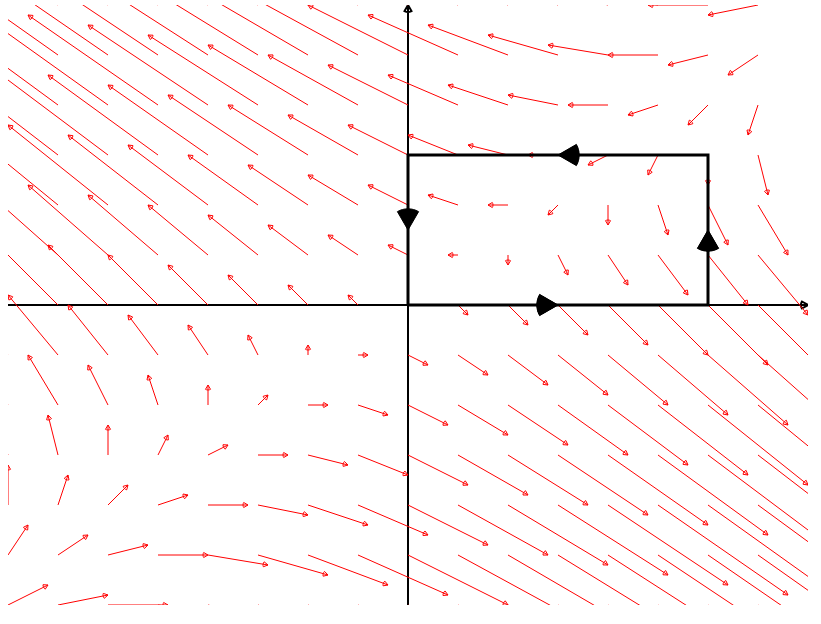
By Green's Theorem,
$$
\begin{array}{lll}
\displaystyle \oint_{C} {\bf F}\cdot d{\bf r}&\displaystyle=\oint_{\partial D} {\bf F}\cdot d{\bf r} &\mbox{}\\
\displaystyle &\displaystyle= \iint_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{2}\int_{0}^{1} -1-(-2) \,dy\,dx&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{2}\int_{0}^{1} \,dy\,dx&\mbox{}\\
\displaystyle &\displaystyle= 2&\mbox{}\\
\end{array}
$$
Not bad, eh?
It's especially nice if you compare the above to what we had to do earlier to compute the same integral...
We had to break up our curve into $4$ pieces and parameterize each curve separately. $$ \begin{array}{lll} \displaystyle C_1:&\displaystyle {\bf r}_1(t)=\langle t,0\rangle &\mbox{over $0\leq t\leq 2$}\\ \displaystyle C_2:&\displaystyle {\bf r}_2(t)=\langle 2,t\rangle &\mbox{over $0\leq t\leq 1$}\\ \displaystyle C_3:&\displaystyle {\bf r}_3(t)=\langle 2-t,1\rangle &\mbox{over $0\leq t\leq 2$}\\ \displaystyle C_4:&\displaystyle {\bf r}_4(t)=\langle 0,1-t \rangle &\mbox{over $0\leq t\leq 1$}\\ \end{array} $$ Then, $$ \begin{array}{lll} \displaystyle \int_{C} {\bf F}\cdot d{\bf r}&\displaystyle= \int_{C_1+C_2+C_3+C_4} {\bf F}\cdot d{\bf r}&\mbox{}\\ \displaystyle &\displaystyle= \int_{C_1} {\bf F}\cdot d{\bf r}_1+\int_{C_2} {\bf F}\cdot d{\bf r}_2+\int_{C_3} {\bf F}\cdot d{\bf r}_3+\int_{C_4} {\bf F}\cdot d{\bf r}_4&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2} {\bf F}({\bf r}_1)\cdot \frac{d{\bf r}_1}{dt}\,dt+\int_{0}^{1} {\bf F}({\bf r}_2)\cdot \frac{d{\bf r}_2}{dt}\,dt+\int_{0}^{2} {\bf F}({\bf r}_3)\cdot \frac{d{\bf r}_3}{dt}\,dt+\int_{0}^{1} {\bf F}({\bf r}_4)\cdot \frac{d{\bf r}_4}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2} \langle x_1(t)-2y_1(t),y_1(t)-x_1(t) \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle x_2(t)-2y_2(t),y_2(t)-x_2(t) \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle x_3(t)-2y_3(t),y_3(t)-x_3(t) \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle x_4(t)-2y_4(t),y_4(t)-x_4(t) \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2} \langle t-2\cdot 0,0-t \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle 2-2t,t-2 \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle 2-t-2\cdot 1,1-(2-t) \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle 0-2(1-t),1-t-0 \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2} \langle t,-t \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle 2-2t,t-2 \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle -t,t-1 \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle 2t-2,1-t \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2} t \,dt+\int_{0}^{1} t-2 \,dt+\int_{0}^{2} t\,dt+\int_{0}^{1} t-1\,dt&\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{1}{2}t^2\right]_{0}^{2} + \left[\frac{1}{2}t^2-2t\right]_{0}^{1}+\left[\frac{1}{2}t^2\right]_{0}^{2}+\left[\frac{1}{2}t^2-t\right]_{0}^{1}&\mbox{}\\ \displaystyle &\displaystyle= (2)+\left(\frac{1}{2}-2\right)+(2)+\left(\frac{1}{2}-1\right)&\mbox{}\\ \displaystyle &\displaystyle= 2+\left(-\frac{3}{2}\right)+2+\left(-\frac{1}{2}\right)&\mbox{}\\ \displaystyle &\displaystyle= 2&\mbox{}\\ \end{array} $$
Not bad, eh?
It's especially nice if you compare the above to what we had to do earlier to compute the same integral...
We had to break up our curve into $4$ pieces and parameterize each curve separately. $$ \begin{array}{lll} \displaystyle C_1:&\displaystyle {\bf r}_1(t)=\langle t,0\rangle &\mbox{over $0\leq t\leq 2$}\\ \displaystyle C_2:&\displaystyle {\bf r}_2(t)=\langle 2,t\rangle &\mbox{over $0\leq t\leq 1$}\\ \displaystyle C_3:&\displaystyle {\bf r}_3(t)=\langle 2-t,1\rangle &\mbox{over $0\leq t\leq 2$}\\ \displaystyle C_4:&\displaystyle {\bf r}_4(t)=\langle 0,1-t \rangle &\mbox{over $0\leq t\leq 1$}\\ \end{array} $$ Then, $$ \begin{array}{lll} \displaystyle \int_{C} {\bf F}\cdot d{\bf r}&\displaystyle= \int_{C_1+C_2+C_3+C_4} {\bf F}\cdot d{\bf r}&\mbox{}\\ \displaystyle &\displaystyle= \int_{C_1} {\bf F}\cdot d{\bf r}_1+\int_{C_2} {\bf F}\cdot d{\bf r}_2+\int_{C_3} {\bf F}\cdot d{\bf r}_3+\int_{C_4} {\bf F}\cdot d{\bf r}_4&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2} {\bf F}({\bf r}_1)\cdot \frac{d{\bf r}_1}{dt}\,dt+\int_{0}^{1} {\bf F}({\bf r}_2)\cdot \frac{d{\bf r}_2}{dt}\,dt+\int_{0}^{2} {\bf F}({\bf r}_3)\cdot \frac{d{\bf r}_3}{dt}\,dt+\int_{0}^{1} {\bf F}({\bf r}_4)\cdot \frac{d{\bf r}_4}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2} \langle x_1(t)-2y_1(t),y_1(t)-x_1(t) \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle x_2(t)-2y_2(t),y_2(t)-x_2(t) \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle x_3(t)-2y_3(t),y_3(t)-x_3(t) \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle x_4(t)-2y_4(t),y_4(t)-x_4(t) \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2} \langle t-2\cdot 0,0-t \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle 2-2t,t-2 \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle 2-t-2\cdot 1,1-(2-t) \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle 0-2(1-t),1-t-0 \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2} \langle t,-t \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle 2-2t,t-2 \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle -t,t-1 \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle 2t-2,1-t \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2} t \,dt+\int_{0}^{1} t-2 \,dt+\int_{0}^{2} t\,dt+\int_{0}^{1} t-1\,dt&\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{1}{2}t^2\right]_{0}^{2} + \left[\frac{1}{2}t^2-2t\right]_{0}^{1}+\left[\frac{1}{2}t^2\right]_{0}^{2}+\left[\frac{1}{2}t^2-t\right]_{0}^{1}&\mbox{}\\ \displaystyle &\displaystyle= (2)+\left(\frac{1}{2}-2\right)+(2)+\left(\frac{1}{2}-1\right)&\mbox{}\\ \displaystyle &\displaystyle= 2+\left(-\frac{3}{2}\right)+2+\left(-\frac{1}{2}\right)&\mbox{}\\ \displaystyle &\displaystyle= 2&\mbox{}\\ \end{array} $$
Thank you, Green's Theorem!
We love you!
But Seriously...
Wow! this is magic.. right?
Answer
At first glance, it sure seems like it.
But it isn't. We're going take a closer look at what makes Green's Theorem tick.
The key to understanding why Green's Theorem works lies in measuring how rotational, or "swirly", a field is at a point.
This measure is called the circulation density.
Circulation Density
| $\mbox{Circulation}$ | $=$ | $\mbox{bottom}$ | $+$ | $\mbox{right}$ | $+$ | $\mbox{top}$ | $+$ | $\mbox{left}$ |
| $\approx$ | $\color{red}{{\bf F}(x,y)}\cdot\color{blue}{{\bf i}}\,\Delta x$ | $+$ | $\color{red}{{\bf F}(x+\Delta x,y)}\cdot \color{blue}{{\bf j}}\,\Delta y$ | $+$ | $\color{red}{{\bf F}(x+\Delta x,y+\Delta y)}\cdot\color{blue}{({\bf -i})} \,\Delta x$ | $+$ | $\color{red}{{\bf F}(x,y+\Delta y)}\cdot\color{blue}{({\bf -j})}\,\Delta y$ | |
| $=$ | $P(x,y)\, \Delta x$ | $+$ | $Q(x+\Delta x,y)\, \Delta y$ | $-$ | $P(x+\Delta x,y+\Delta y)\, \Delta x$ | $-$ | $Q(x,y+\Delta y)\, \Delta y$ |
$$ \begin{array}{ll} \mbox{Circulation Density}&=\displaystyle\frac{\mbox{Circulation}}{\mbox{Area}}\\ &=\displaystyle\frac{\mbox{Circulation}}{\Delta x \Delta y}\\ &\approx\displaystyle\frac{P(x,y)\,\Delta x+Q(x+\Delta x)\,\Delta y-P(x+\Delta x,y+\Delta y)\,\Delta x-Q(x,y+\Delta y)\,\Delta y}{\Delta x \Delta y}\\ &=\displaystyle\frac{Q(x+\Delta x)\,\Delta y-Q(x,y+\Delta y)\,\Delta y-[P(x+\Delta x,y+\Delta y)\,\Delta x-P(x,y)\,\Delta x]}{\Delta x \Delta y}\\ &=\displaystyle\frac{Q(x+\Delta x)\,\Delta y-Q(x,y+\Delta y)\,\Delta y}{\Delta x \Delta y}-\frac{P(x+\Delta x,y+\Delta y)\,\Delta x-P(x,y)\,\Delta x}{\Delta x \Delta y}\\ &=\displaystyle\frac{Q(x+\Delta x)-Q(x,y+\Delta y)}{\Delta x}-\frac{P(x+\Delta x,y+\Delta y)-P(x,y)}{\Delta y}\\ &\approx \displaystyle \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\\ \end{array} $$
Thus, the circulation density $$ \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} $$ quantifies how rotational, or "swirly", a field is at a point $(x,y)$ in the plane.
More formally, if the field is a fluid flow, the circulation density measures a fluid particle's tendency to spin.
A positive circulation density indicates counterclockwise spin, and negative circulation density indicates clockwise spin.
$$\mbox{Circulation}\approx \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,\Delta x \, \Delta y$$
Green's Theorem (Circulation Form): $\displaystyle \oint_{C} {\bf F}\cdot {\bf T} \,ds=\oint_{C} {\bf F}\cdot d{\bf r}\approx \sum_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,\Delta x \, \Delta y$
Green's Theorem (Circulation Form)
Let $D$ be an open, simply connected region with a boundary curve $C$ that is a piecewise smooth, simple closed curve oriented counterclockwise (positively). Let ${\bf F} = \langle P, Q \rangle$ be a vector field with component functions that have continuous partial derivatives on $D.$ Then, $$\displaystyle \oint_{\partial D} {\bf F}\cdot {\bf T} \,ds=\oint_{C} {\bf F}\cdot d{\bf r}=\oint_C P\,dx+Q\,dy=\iint_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA$$ In Words: The sum of the circulation densities over the interior of a region is equal to the total circulation at the boundary.

Interpreting Circulation Density
If we think of a vector field as a fluid flow and we place a little paddle wheel in the fluid, the circulation density at a point is the tendency of the paddle wheel to spin.
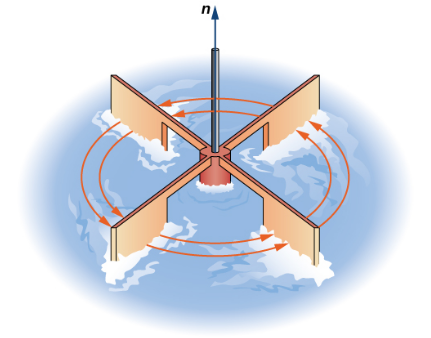
The sign of the the circulation density is the direction: positive is counterclockwise and negative is clockwise.
Interpreting Circulation Density: Three Examples
 |  |  |
| ${\bf F}(x, y) = \langle -y, x \rangle=-y\,{\bf i}+x\,{\bf j}$ $\displaystyle \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=1-(-1)=2$ | ${\bf F}(x, y) = \langle x, y \rangle=x\,{\bf i}+y\,{\bf j}$ $\displaystyle \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0-0=0$ | ${\bf F}(x, y) = \langle y, 0 \rangle=y\,{\bf i}$ $\displaystyle \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0-1=-1$ |
Green's Theorem (Flux Form)
Let $D$ be an open, simply connected region with a boundary curve $C$ that is a piecewise smooth, simple closed curve that is oriented counterclockwise (positively). Let ${\bf F} = \langle P, Q \rangle$ be a vector field with component functions that have continuous partial derivatives on an open region containing $D.$ Then, $$\oint_C {\bf F} \cdot {\bf N}\,ds=\oint_C -Q\, dx + P \,dy=\iint_D \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)\, dA$$
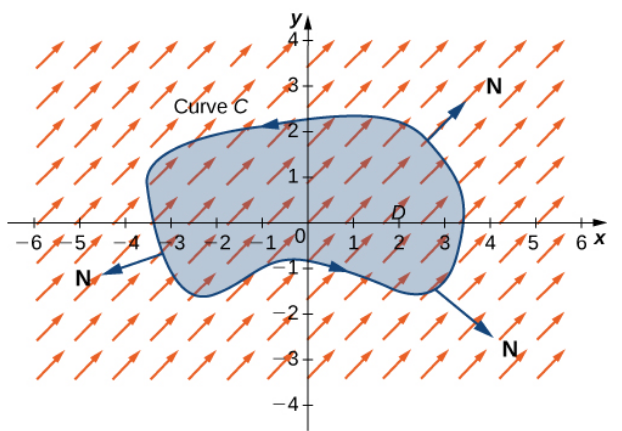
Example Let ${\bf F}(x, y) = \langle -y, x-y \rangle=-y\,{\bf i}+(x-y)\,{\bf j}$ and let $C$ the unit circle oriented counterclockwise (positively).
Calculate the outward flux $\displaystyle \oint_C {\bf F}\cdot {\bf N} \,ds.$

Using the flux form of Green's Theorem,
$$
\begin{array}{lll}
\displaystyle \oint_C {\bf F}\cdot {\bf N} \,ds& \displaystyle\oint_{\partial D} {\bf F}\cdot {\bf N} \,ds &\mbox{}\\
\displaystyle &\displaystyle=\iint_D \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)\, dA &\mbox{}\\
\displaystyle &\displaystyle=\iint_D -1\, dA &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{1} -1\cdot r\,dr\, d\theta &\mbox{using polar coordinates}\\
\displaystyle &\displaystyle=-\int_{0}^{2\pi}\left[\frac{1}{2}r^2\right]_{0}^{1}\, d\theta &\mbox{}\\
\displaystyle &\displaystyle=-\int_{0}^{2\pi}\frac{1}{2}\, d\theta &\mbox{}\\
\displaystyle &\displaystyle=-\frac{1}{2}\int_{0}^{2\pi}\, d\theta &\mbox{}\\
\displaystyle &\displaystyle=-\frac{1}{2}\cdot 2\pi &\mbox{}\\
\displaystyle &\displaystyle=-\pi &\mbox{}\\
\end{array}
$$
Again, in comparison the above is substantially easier than our earlier calculation where we had to (1) parameterize the curve, ${\bf r}(t)=\langle \cos t,\sin t \rangle,$ (2) take its derivative, ${\bf r}'(t)=\langle -\sin t, \cos t \rangle,$ and then (3) finally, $$ \begin{array}{lll} \displaystyle \oint_C {\bf F}\cdot{\bf N}\,ds&\displaystyle= \int_0^{2\pi} {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle -y(t),x(t)-y(t) \rangle\cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle -\sin t,\cos t-\sin t \rangle \cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} -\sin t \cos t +\cos t \sin t -\sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\int_0^{2\pi} \sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\int_0^{2\pi} \frac{1-\cos(2t)}{2}\,dt&\mbox{trig identity!}\\ \displaystyle &\displaystyle= -\frac{1}{2}\int_0^{2\pi} 1-\cos(2t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\frac{1}{2}\left[t-\frac{1}{2}\sin(2t)\right]_0^{2\pi}&\mbox{}\\ \displaystyle &\displaystyle= -\pi&\mbox{}\\ \end{array} $$
Again, in comparison the above is substantially easier than our earlier calculation where we had to (1) parameterize the curve, ${\bf r}(t)=\langle \cos t,\sin t \rangle,$ (2) take its derivative, ${\bf r}'(t)=\langle -\sin t, \cos t \rangle,$ and then (3) finally, $$ \begin{array}{lll} \displaystyle \oint_C {\bf F}\cdot{\bf N}\,ds&\displaystyle= \int_0^{2\pi} {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle -y(t),x(t)-y(t) \rangle\cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle -\sin t,\cos t-\sin t \rangle \cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} -\sin t \cos t +\cos t \sin t -\sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\int_0^{2\pi} \sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\int_0^{2\pi} \frac{1-\cos(2t)}{2}\,dt&\mbox{trig identity!}\\ \displaystyle &\displaystyle= -\frac{1}{2}\int_0^{2\pi} 1-\cos(2t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\frac{1}{2}\left[t-\frac{1}{2}\sin(2t)\right]_0^{2\pi}&\mbox{}\\ \displaystyle &\displaystyle= -\pi&\mbox{}\\ \end{array} $$
Flux Density
The key to understanding why the flux form of Green's Theorem works lies in measuring how radial, or "expansive/contractive", a field is at a point.
This measure is called the flux density.
Flux Density
| $\mbox{Outward Flux}$ | $=$ | $\mbox{bottom}$ | $+$ | $\mbox{right}$ | $+$ | $\mbox{top}$ | $+$ | $\mbox{left}$ |
| $\approx$ | $\color{red}{{\bf F}(x,y)}\cdot\color{blue}{({\bf -j})}\,\Delta x$ | $+$ | $\color{red}{{\bf F}(x+\Delta x,y)}\cdot\color{blue}{{\bf i}}\,\Delta y$ | $+$ | $\color{red}{{\bf F}(x+\Delta x,y+\Delta y)}\cdot\color{blue}{{\bf j}}\,\Delta x$ | $+$ | $\color{red}{{\bf F}(x,y+\Delta y)}\cdot\color{blue}{({\bf -i})}\,\Delta y$ | |
| $=$ | $-Q(x,y)\, \Delta x$ | $+$ | $P(x+\Delta x,y)\, \Delta y$ | $+$ | $Q(x+\Delta x,y+\Delta y)\, \Delta x$ | $-$ | $P(x,y+\Delta y)\, \Delta y$ |
$$ \begin{array}{ll} \mbox{Flux Density}&=\displaystyle\frac{\mbox{Outward Flux}}{\mbox{Area}}\\ &=\displaystyle\frac{\mbox{Outward Flux}}{\Delta x \Delta y}\\ &\approx\displaystyle\frac{-Q(x,y)\,\Delta x+P(x+\Delta x)\,\Delta y+Q(x+\Delta x,y+\Delta y)\,\Delta x-P(x,y+\Delta y)\,\Delta y}{\Delta x \Delta y}\\ &=\displaystyle\frac{P(x+\Delta x)\,\Delta y-P(x,y+\Delta y)\,\Delta y+Q(x+\Delta x,y+\Delta y)\,\Delta x-Q(x,y)\,\Delta x}{\Delta x \Delta y}\\ &=\displaystyle\frac{P(x+\Delta x)\,\Delta y-P(x,y+\Delta y)\,\Delta y}{\Delta x \Delta y}+\frac{Q(x+\Delta x,y+\Delta y)\,\Delta x-Q(x,y)\,\Delta x}{\Delta x \Delta y}\\ &=\displaystyle\frac{P(x+\Delta x)-P(x,y+\Delta y)}{\Delta x}+\frac{Q(x+\Delta x,y+\Delta y)-Q(x,y)}{\Delta y}\\ &\approx \displaystyle \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\\ \end{array} $$
Thus, the flux density $$ \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} $$ quantifies how radial, or "expansive/contractive" a field is at a point $(x,y)$ in the plane.
$$\mbox{Outward Flux}\approx \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)\,\Delta x \, \Delta y$$
Green's Theorem (Flux Form): $\displaystyle \oint_C {\bf F} \cdot {\bf N}\,ds\approx \sum_D \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)\, \Delta x \,\Delta y$
Green's Theorem (Flux Form)
Let $D$ be an open, simply connected region with a boundary curve $C$ that is a piecewise smooth, simple closed curve that is oriented counterclockwise (positively). Let ${\bf F} = \langle P, Q \rangle$ be a vector field with component functions that have continuous partial derivatives on an open region containing $D.$ Then, $$\oint_{\partial D} {\bf F} \cdot {\bf N}\,ds=\oint_C -Q\, dx + P \,dy=\iint_D \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)\, dA$$ In Words: The sum of the flux densities over the interior of a region is equal to the total outward flux at the boundary.
Interpreting Flux Density
Again, if we think of a vector field as a fluid flow, the flux density at a point is the tendency of the fluid to leave or exit from that point.
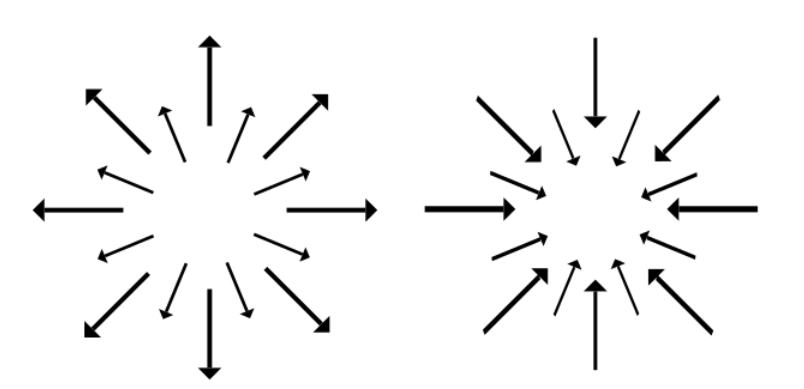
The sign of the the flux density positive when fluid is leaving (a "source") and is negative when fluid is coming in (a "sink").
Flux density is zero when the fluid leaving the same as the fluid coming in.
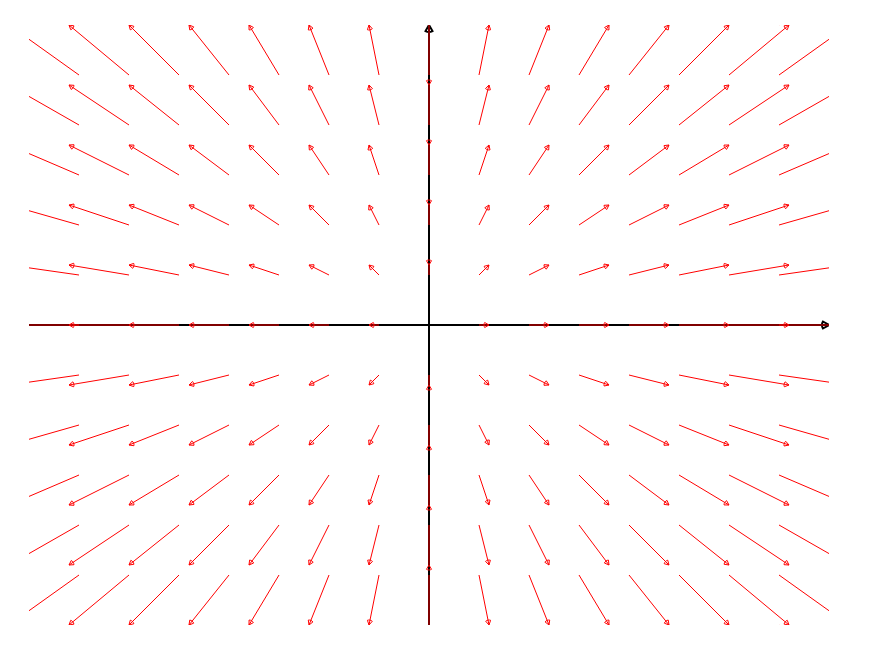
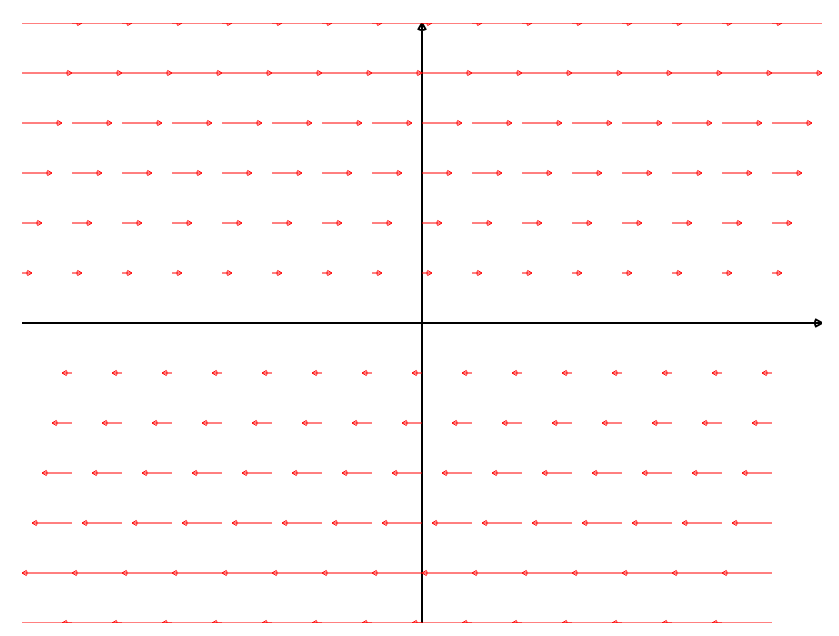
Interpreting Flux Density: Three Examples
 |  |  |
| ${\bf F}(x, y) = \langle -y, x \rangle=-y\,{\bf i}+x\,{\bf j}$ $\displaystyle \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=0+0=0$ | ${\bf F}(x, y) = \langle x, y \rangle=x\,{\bf i}+y\,{\bf j}$ $\displaystyle \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=1+1=2$ | ${\bf F}(x, y) = \langle y, 0 \rangle=y\,{\bf i}$ $\displaystyle \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=0+0=0$ |
Example
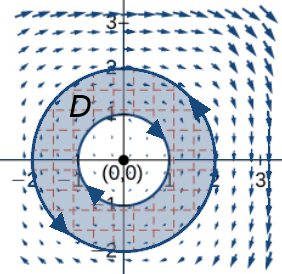
Let ${\bf F}(x, y) = \langle y^3, -x^3 \rangle= y^3\,{\bf i}-x^3\,{\bf j}$ and let $C$ be the two circles of centered at the origin with radius $2$ oriented counterclockwise (positively) and radius $1$ oriented clockwise (negatively).
Calculate: (a) $\displaystyle \oint_{\partial D} {\bf F}\cdot d{\bf r}$ and (b) $\displaystyle \oint_{\partial D} {\bf F}\cdot {\bf N} \,ds.$
Whoa There, Tiger!
Electric Kitty reminds us that we must be careful with heavy machinery.

Electric Kitty has a big question for you...
Big Question
As it's stated, Green's Theorem works for simply connected regions.
Can we apply Green's Theorem to a region with holes in it?
Big Answer
Electric Kitty says "Yes!"

Here's how...
Electric Kitty Says...
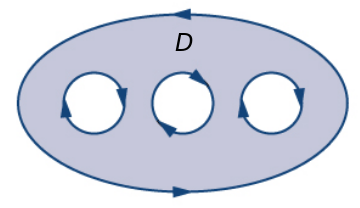
Just break up your swiss-cheese region $D$ into simply-connected pieces!
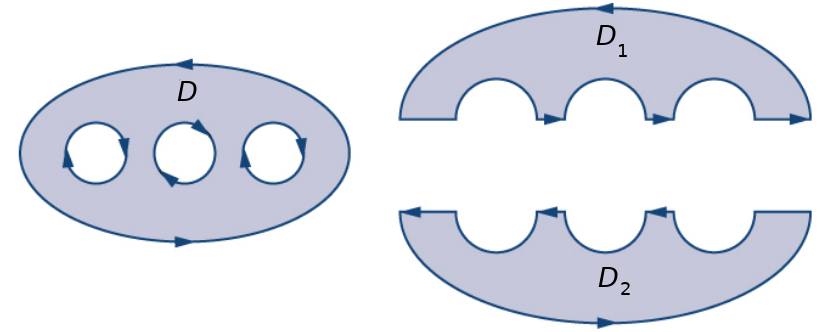
For example, the region below can be broken up into two regions $D_1$ and $D_2$ so that $$D=D_1 \cup D_2.$$
Electric Kitty Says...
Now we may apply Green's Theorem (circulation form) to the simply-connected pieces! $$ \begin{array}{lll} \displaystyle \int_{\partial D} {\bf F}\cdot d{\bf r} &=\displaystyle \oint_{\partial D_1} {\bf F}\cdot d{\bf r} + \oint_{\partial D_2} {\bf F}\cdot d{\bf r}&\mbox{}\\ &=\displaystyle \iint_{D_1} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA+\iint_{D_2} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA&\mbox{Green's Theorem now applies!}\\ &=\displaystyle \iint_{D_1\cup D_2} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA&\mbox{by properties of double integrals}\\ &=\displaystyle \iint_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA&\mbox{since $D=D_1 \cup D_2$}\\ \end{array} $$

Electric Kitty Says...
We may also apply the flux form of Green's Theorem to the simply-connected pieces! $$ \begin{array}{lll} \displaystyle \int_{\partial D} {\bf F}\cdot {\bf N} \,ds &=\displaystyle \oint_{\partial D_1} {\bf F}\cdot {\bf N} \,ds + \oint_{\partial D_2} {\bf F}\cdot {\bf N} \,ds&\mbox{}\\ &=\displaystyle \iint_{D_1} \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right) \,dA+\iint_{D_2} \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right) \,dA&\mbox{Green's Theorem now applies!}\\ &=\displaystyle \iint_{D_1\cup D_2} \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right) \,dA&\mbox{by properties of double integrals}\\ &=\displaystyle \iint_{D} \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right) \,dA&\mbox{since $D=D_1 \cup D_2$}\\ \end{array} $$

Electric Kitty Says...
We can take any reasonable swiss-cheese region and break it up into as many pieces as we need to make Green's Theorem work.
So, for the region in from the above example,
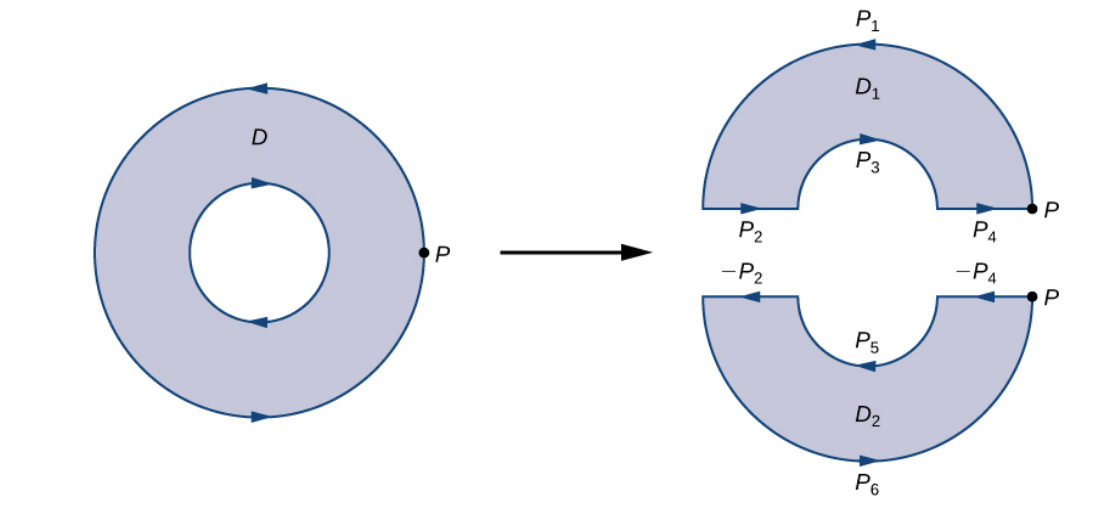
Electric Kitty Says...
You may now return to your regularly-scheduled example.

Thank you, Electric Kitty!
We love you too!
Example
Let ${\bf F}(x, y) = \langle y^3, -x^3 \rangle= y^3\,{\bf i}-x^3\,{\bf j}$ and let $C$ be the two circles of centered at the origin with radius $2$ oriented counterclockwise (positively) and radius $1$ oriented clockwise (negatively).
Calculate: (a) $\displaystyle \oint_{\partial D} {\bf F}\cdot d{\bf r}$ and (b) $\displaystyle \oint_{\partial D} {\bf F}\cdot {\bf N} \,ds.$

Using Green's Theorem,
$$
\begin{array}{lll}
\displaystyle \oint_{\partial D} {\bf F}\cdot d{\bf r}&\displaystyle= \oint_{\partial D} {\bf F}\cdot {\bf T} \, ds&\mbox{reminder of tangential form}\\
\displaystyle &\displaystyle= \oint_{\partial D} y^3\,dx-x^3 \,dy&\mbox{reminder of scalar differential form}\\
\displaystyle &\displaystyle= \iint_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA&\mbox{}\\
\displaystyle &\displaystyle= \iint_{D} -3x^2-3y^2 \,dA&\mbox{}\\
\displaystyle &\displaystyle= -3\iint_{D} x^2+y^2 \,dA&\mbox{}\\
\displaystyle &\displaystyle= -3\int_{0}^{2\pi}\int_{1}^{2} r^2 \cdot r \, dr \, d\theta&\mbox{convert to polar coordinates}\\
\displaystyle &\displaystyle= -3\int_{0}^{2\pi}\left[\frac{1}{4}r^4\right]_{1}^{2} \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= -3\int_{0}^{2\pi} \frac{1}{4}(2)^4-\frac{1}{4}(1)^4\, d\theta&\mbox{}\\
\displaystyle &\displaystyle= -3\int_{0}^{2\pi} 4-\frac{1}{4}\, d\theta&\mbox{}\\
\displaystyle &\displaystyle= -3\int_{0}^{2\pi} \frac{15}{4}\, d\theta&\mbox{}\\
\displaystyle &\displaystyle= -3\cdot \frac{15}{4}\int_{0}^{2\pi} \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= -\frac{45}{4}\cdot 2\pi&\mbox{}\\
\displaystyle &\displaystyle= -\frac{45\pi}{2}&\mbox{}\\
\end{array}
$$
and
$$
\begin{array}{lll}
\displaystyle \oint_{\partial D} {\bf F}\cdot {\bf N} \,ds&\displaystyle= \oint_C -Q\, dx + P \,dy&\mbox{reminder of scalar differential form}\\
\displaystyle &\displaystyle= \oint_{\partial D} x^3 \, dx+y^3 \, dy&\mbox{}\\
\displaystyle &\displaystyle= \iint_D \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)\, dA&\mbox{}\\
\displaystyle &\displaystyle= \iint_D 0+0\, dA&\mbox{}\\
\displaystyle &\displaystyle= 0&\mbox{}\\
\end{array}
$$
Example
For $\displaystyle {\bf F}(x, y)=\langle P,Q \rangle = \left\langle\frac{y}{x^2+y^2},\frac{-x}{x^2+y^2}\right \rangle,$ compute $\displaystyle \oint_{C} {\bf F}\cdot d{\bf r}$ where $C$ is the unit circle oriented centered at the origin and oriented counterclockwise (positively).
First, we do a little prep.
$$
\begin{array}{lll}
\displaystyle \frac{\partial P}{\partial y}&\displaystyle=\frac{\partial }{\partial y}\frac{y}{x^2+y^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{(x^2+y^2)\cdot 1-y\cdot 2y}{(x^2+y^2)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{x^2+y^2-2y^2}{(x^2+y^2)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{x^2-y^2}{(x^2+y^2)^2} &\mbox{}\\
\end{array}
$$
and
$$
\begin{array}{lll}
\displaystyle \frac{\partial Q}{\partial x}&\displaystyle=\frac{\partial }{\partial x}\frac{-x}{x^2+y^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{(x^2+y^2)\cdot (-1)-(-x)\cdot 2x}{(x^2+y^2)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-x^2-y^2+2x^2}{(x^2+y^2)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{x^2-y^2}{(x^2+y^2)^2} &\mbox{}\\
\end{array}
$$
Then, using Green's Theorem, $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r}&\displaystyle=\oint_{\partial D} {\bf F}\cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \frac{x^2-y^2}{(x^2+y^2)^2}-\frac{x^2-y^2}{(x^2+y^2)^2}\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D 0\, dA &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$
Then, using Green's Theorem, $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r}&\displaystyle=\oint_{\partial D} {\bf F}\cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \frac{x^2-y^2}{(x^2+y^2)^2}-\frac{x^2-y^2}{(x^2+y^2)^2}\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D 0\, dA &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$
And the crowd goes nuts!
Let's take a victory lap!
WHEN YOU APPLY GREEN'S THEOREM WHERE IT HAS NO BUSINESS BEING APPLIED,
YOU GET WRONG ANSWERS!
AND YOU MAKE KITTY ANGRY!!!!!!!!!!!!!!!!!!

AND YOU MAKE KITTY ANGRY!!!!!!!!!!!!!!!!!!

Whoa There, Tiger!
Electric Kitty reminds us (AGAIN!) that we must be careful with heavy machinery.

Remember that the hypotheses of a theorem must be satisfied before unleashing it.
Electric Kitty asks you: why does Green's Theorem not apply?
$\displaystyle {\bf F}(x, y)=\langle P,Q \rangle = \left\langle\frac{y}{x^2+y^2},\frac{-x}{x^2+y^2}\right \rangle$
is not continuous at the origin since ${\bf F}$ is undefined there.
Thus the partial derivatives of $P$ and $Q$ are also not continuous at $(0,0).$
Since the region $D$ contained $(0,0),$ the hypotheses of Green's Theorem (continuous partials!) weren't all satisfied.
Also, recall that we computed this line integral earlier.
Letting ${\bf r}(t)=\langle \cos t, \sin t\rangle$ over $0 \leq t \leq 2\pi,$ we have ${\bf r}'(t)=\langle -\sin t, \cos t\rangle$ so that $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_0^{2\pi} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\frac{y(t)}{x(t)^2+y(t)^2},\frac{-x(t)}{x(t)^2+y(t)^2}\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\frac{\sin t}{\cos^2 t+\sin^2 t},\frac{-\cos t}{\cos^2 t+\sin^2 t}\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\sin t,-\cos t\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -\sin^2 t-\cos^2 t \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -1 \,dt &\mbox{}\\ \displaystyle &\displaystyle=-2\pi &\mbox{}\\ \end{array} $$ Fun Fact
For any simply closed curve $C$ bounding a region $D,$ $$ \oint_{C} {\bf F} \cdot d{\bf r}=\oint_{\partial D} {\bf F} \cdot d{\bf r} = \begin{cases} 0 & \mbox{ if } (0,0)\not \in D \\ -2\pi & \mbox{ if } (0,0) \in D \end{cases} $$
Thus the partial derivatives of $P$ and $Q$ are also not continuous at $(0,0).$
Since the region $D$ contained $(0,0),$ the hypotheses of Green's Theorem (continuous partials!) weren't all satisfied.
Also, recall that we computed this line integral earlier.
Letting ${\bf r}(t)=\langle \cos t, \sin t\rangle$ over $0 \leq t \leq 2\pi,$ we have ${\bf r}'(t)=\langle -\sin t, \cos t\rangle$ so that $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_0^{2\pi} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\frac{y(t)}{x(t)^2+y(t)^2},\frac{-x(t)}{x(t)^2+y(t)^2}\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\frac{\sin t}{\cos^2 t+\sin^2 t},\frac{-\cos t}{\cos^2 t+\sin^2 t}\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\sin t,-\cos t\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -\sin^2 t-\cos^2 t \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -1 \,dt &\mbox{}\\ \displaystyle &\displaystyle=-2\pi &\mbox{}\\ \end{array} $$ Fun Fact
For any simply closed curve $C$ bounding a region $D,$ $$ \oint_{C} {\bf F} \cdot d{\bf r}=\oint_{\partial D} {\bf F} \cdot d{\bf r} = \begin{cases} 0 & \mbox{ if } (0,0)\not \in D \\ -2\pi & \mbox{ if } (0,0) \in D \end{cases} $$
Public Service Announcement
Electric Kitty reminds us that even when we mess up, Electric Kitty still loves us... as long as we keep feeding Electric Kitty.

Application: Work
A particle starts at point $(-2, 0),$ moves along the $x$-axis to $(2, 0),$ and then travels along semicircle $y = 4 - x^2$ to the starting point.
Use Green's theorem to find the work done on this particle by force field ${\bf F}(x,y) = x\,{\bf i} + (x^3 + 3xy^2){\bf j}.$
The work done on the particle is calculated as the line integral $\displaystyle \oint_{C} {\bf F} \cdot d{\bf r}.$
Since the hypotheses of Green's Theorem are satisfied, let's use Green's Theorem.
The region we're integrating over is shown below,
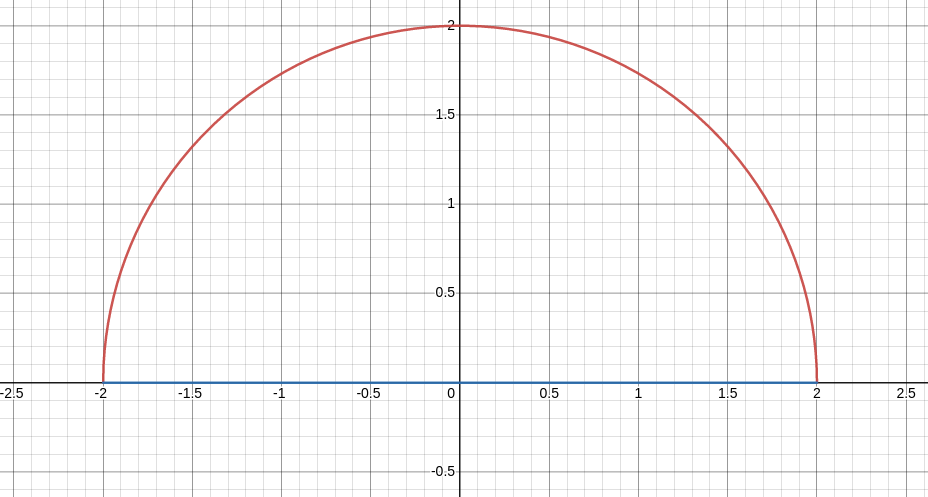
Then $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r}&\displaystyle=\oint_{\partial D} {\bf F}\cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D 3x^2+3y^2-0\, dA &\mbox{}\\ \displaystyle &\displaystyle=3\iint_D x^2+y^2\, dA &\mbox{}\\ \displaystyle &\displaystyle=3\int_{0}^{\pi} \int_{0}^{2} r^2\, r \,dr\,d\theta &\mbox{converting to cuddly polar coordinates}\\ \displaystyle &\displaystyle=3\int_{0}^{\pi} \int_{0}^{2} r^3\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=3\int_{0}^{\pi} \left[\frac{1}{4}r^4\right]_{0}^{2}\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=3\int_{0}^{\pi} 4\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=12\int_{0}^{\pi} \,d\theta &\mbox{}\\ \displaystyle &\displaystyle=12\pi &\mbox{}\\ \end{array} $$
Since the hypotheses of Green's Theorem are satisfied, let's use Green's Theorem.
The region we're integrating over is shown below,

Then $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F}\cdot d{\bf r}&\displaystyle=\oint_{\partial D} {\bf F}\cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D 3x^2+3y^2-0\, dA &\mbox{}\\ \displaystyle &\displaystyle=3\iint_D x^2+y^2\, dA &\mbox{}\\ \displaystyle &\displaystyle=3\int_{0}^{\pi} \int_{0}^{2} r^2\, r \,dr\,d\theta &\mbox{converting to cuddly polar coordinates}\\ \displaystyle &\displaystyle=3\int_{0}^{\pi} \int_{0}^{2} r^3\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=3\int_{0}^{\pi} \left[\frac{1}{4}r^4\right]_{0}^{2}\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=3\int_{0}^{\pi} 4\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=12\int_{0}^{\pi} \,d\theta &\mbox{}\\ \displaystyle &\displaystyle=12\pi &\mbox{}\\ \end{array} $$
Turning Green's Theorem on its Ear
If line and flux integrals can be converted to double integrals, then...
a double integral can be converted to a line integral.
In particular, we will use the above idea to express the area of a region $D$ as a line integral.
Turning Green's Theorem on its Ear
We note that for the field $\displaystyle {\bf F}=\left \langle -\frac{y}{2},\frac{x}{2}\right \rangle,$ we have $$ \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=Q_x-P_y=\frac{1}{2}-\left(-\frac{1}{2}\right)=1. $$ Conclusion?????????????
Using Green's Theorem to Find an Area
The area of a region $D$ can now be expressed as $$ \begin{array}{lll} A(D) &=\displaystyle \iint_D\,dA&\mbox{}\\ &=\displaystyle \oint_{\partial D} {\bf F} \cdot d{\bf r}&\mbox{stealthy reverse application of Green's Theorem}\\ &=\displaystyle \oint_{\partial D} \left \langle -\frac{y}{2},\frac{x}{2}\right \rangle \cdot \left\langle dx,dy\right \rangle&\mbox{since $\displaystyle {\bf F}=\left \langle -\frac{y}{2},\frac{x}{2}\right \rangle$ to make double integrand $1$}\\ &=\displaystyle \oint_{\partial D} -\frac{y}{2}\, dx + \frac{x}{2}\,dy &\mbox{}\\ &=\displaystyle \frac{1}{2}\oint_{\partial D} -y\, dx + x\,dy &\mbox{}\\ \end{array} $$
Using Green's Theorem to Find an Area
Notice that $\displaystyle {\bf F}=\left \langle -\frac{y}{2},\frac{x}{2}\right \rangle$ is not unique way to to get $$ \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=1 $$ Other fields like $\displaystyle {\bf F}=\left \langle 0,x\right \rangle$ and $\displaystyle {\bf F}=\left \langle -y,0\right \rangle$ also do the trick.
Thus, the following line integrals all express the same area $A(D).$ $$ A(D)=\iint_D\,dA=\oint_{\partial D} x \,dy=-\oint_{\partial D} y \, dx= \frac{1}{2}\oint_{\partial D} -y\, dx + x\,dy $$
Using Green's Theorem to Find an Area
Use Green's theorem to find the area of the region enclosed by the curve $$ {\bf r}(t)=t^2\,{\bf i}+\left(\frac{t^3}{3}-t\right)\,{\bf j},\,\,\,\,\,-\sqrt{3}\leq t \leq \sqrt{3} $$
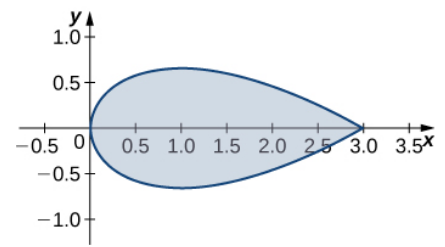
We shall use the scalar differential form shortcut.
First, we note that since ${\bf r}(t)=t^2\,{\bf i}+\left(\frac{t^3}{3}-t\right)\,{\bf j}$ we may say that $x(t)=t^2$ and $\displaystyle y(t)=\frac{1}{3}t^3-t.$
Then $$ \begin{array}{lll} \displaystyle A(D)&\displaystyle= \iint_D\,dA&\mbox{}\\ \displaystyle &\displaystyle=\oint_{\partial D} x \,dy &\mbox{}\\ \displaystyle &\displaystyle=\int_{-\sqrt{3}}^{\sqrt{3}} x(t) \,\frac{dy}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{-\sqrt{3}}^{\sqrt{3}} t^2 (t^2-1)\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{-\sqrt{3}}^{\sqrt{3}} t^4-t^2\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[ \frac{1}{5}t^5-\frac{1}{3}t^3\right]_{-\sqrt{3}}^{\sqrt{3}} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\left(\sqrt{3}\right)^5-\frac{1}{3}\left(\sqrt{3}\right)^3-\left(\frac{1}{5}\left(-\sqrt{3}\right)^5-\frac{1}{3}\left(-\sqrt{3}\right)^3\right) &\mbox{}\\ \displaystyle &\displaystyle=2\cdot \frac{1}{5}\left(\sqrt{3}\right)^5-2\cdot \frac{1}{3}\left(\sqrt{3}\right)^3 &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{5}\cdot 9\cdot \sqrt{3}-\frac{2}{3}\cdot 3 \sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{18}{5} \sqrt{3}-2\sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{18}{5} \sqrt{3}-2\sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{5} \sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle\approx 2.771281292 &\mbox{}\\ \end{array} $$ For giggles, and to check our work, let's compute the area as $$ \begin{array}{lll} \displaystyle A(D)&\displaystyle= \iint_D\,dA&\mbox{}\\ \displaystyle &\displaystyle=-\oint_{\partial D} y \,dx &\mbox{}\\ \displaystyle &\displaystyle=-\int_{-\sqrt{3}}^{\sqrt{3}} y(t) \,\frac{dx}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\int_{-\sqrt{3}}^{\sqrt{3}} \left(\frac{1}{3}t^3-t\right)\cdot 2t\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\int_{-\sqrt{3}}^{\sqrt{3}} \frac{2}{3}t^4-2t^2\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\left[ \frac{2}{15}t^5-\frac{2}{3}t^3\right]_{-\sqrt{3}}^{\sqrt{3}} &\mbox{}\\ \displaystyle &\displaystyle=-\left[ \frac{2}{15}\left(\sqrt{3}\right)^5-\frac{2}{3}\left(\sqrt{3}\right)^3-\left(\frac{2}{15}\left(-\sqrt{3}\right)^5-\frac{2}{3}\left(-\sqrt{3}\right)^3\right)\right] &\mbox{}\\ \displaystyle &\displaystyle= -\frac{2}{15}\left(\sqrt{3}\right)^5+\frac{2}{3}\left(\sqrt{3}\right)^3+\frac{2}{15}\left(-\sqrt{3}\right)^5-\frac{2}{3}\left(-\sqrt{3}\right)^3 &\mbox{}\\ \displaystyle &\displaystyle= -\frac{2}{15}\left(\sqrt{3}\right)^5+\frac{2}{3}\left(\sqrt{3}\right)^3-\frac{2}{15}\left(\sqrt{3}\right)^5+\frac{2}{3}\left(\sqrt{3}\right)^3 &\mbox{}\\ \displaystyle &\displaystyle= -\frac{4}{15}\left(\sqrt{3}\right)^5+\frac{4}{3}\left(\sqrt{3}\right)^3 &\mbox{}\\ \displaystyle &\displaystyle= -\frac{4}{15}\cdot 9 \cdot \sqrt{3}+\frac{4}{3}\cdot 3 \cdot \sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle= -\frac{4}{5}\cdot 3 \cdot \sqrt{3}+4\sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle= -\frac{12}{5} \sqrt{3}+\frac{20}{5}\sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle= \frac{8}{5} \sqrt{3} &\mbox{}\\ \end{array} $$
First, we note that since ${\bf r}(t)=t^2\,{\bf i}+\left(\frac{t^3}{3}-t\right)\,{\bf j}$ we may say that $x(t)=t^2$ and $\displaystyle y(t)=\frac{1}{3}t^3-t.$
Then $$ \begin{array}{lll} \displaystyle A(D)&\displaystyle= \iint_D\,dA&\mbox{}\\ \displaystyle &\displaystyle=\oint_{\partial D} x \,dy &\mbox{}\\ \displaystyle &\displaystyle=\int_{-\sqrt{3}}^{\sqrt{3}} x(t) \,\frac{dy}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{-\sqrt{3}}^{\sqrt{3}} t^2 (t^2-1)\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{-\sqrt{3}}^{\sqrt{3}} t^4-t^2\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[ \frac{1}{5}t^5-\frac{1}{3}t^3\right]_{-\sqrt{3}}^{\sqrt{3}} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\left(\sqrt{3}\right)^5-\frac{1}{3}\left(\sqrt{3}\right)^3-\left(\frac{1}{5}\left(-\sqrt{3}\right)^5-\frac{1}{3}\left(-\sqrt{3}\right)^3\right) &\mbox{}\\ \displaystyle &\displaystyle=2\cdot \frac{1}{5}\left(\sqrt{3}\right)^5-2\cdot \frac{1}{3}\left(\sqrt{3}\right)^3 &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{5}\cdot 9\cdot \sqrt{3}-\frac{2}{3}\cdot 3 \sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{18}{5} \sqrt{3}-2\sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{18}{5} \sqrt{3}-2\sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{8}{5} \sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle\approx 2.771281292 &\mbox{}\\ \end{array} $$ For giggles, and to check our work, let's compute the area as $$ \begin{array}{lll} \displaystyle A(D)&\displaystyle= \iint_D\,dA&\mbox{}\\ \displaystyle &\displaystyle=-\oint_{\partial D} y \,dx &\mbox{}\\ \displaystyle &\displaystyle=-\int_{-\sqrt{3}}^{\sqrt{3}} y(t) \,\frac{dx}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\int_{-\sqrt{3}}^{\sqrt{3}} \left(\frac{1}{3}t^3-t\right)\cdot 2t\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\int_{-\sqrt{3}}^{\sqrt{3}} \frac{2}{3}t^4-2t^2\,dt &\mbox{}\\ \displaystyle &\displaystyle=-\left[ \frac{2}{15}t^5-\frac{2}{3}t^3\right]_{-\sqrt{3}}^{\sqrt{3}} &\mbox{}\\ \displaystyle &\displaystyle=-\left[ \frac{2}{15}\left(\sqrt{3}\right)^5-\frac{2}{3}\left(\sqrt{3}\right)^3-\left(\frac{2}{15}\left(-\sqrt{3}\right)^5-\frac{2}{3}\left(-\sqrt{3}\right)^3\right)\right] &\mbox{}\\ \displaystyle &\displaystyle= -\frac{2}{15}\left(\sqrt{3}\right)^5+\frac{2}{3}\left(\sqrt{3}\right)^3+\frac{2}{15}\left(-\sqrt{3}\right)^5-\frac{2}{3}\left(-\sqrt{3}\right)^3 &\mbox{}\\ \displaystyle &\displaystyle= -\frac{2}{15}\left(\sqrt{3}\right)^5+\frac{2}{3}\left(\sqrt{3}\right)^3-\frac{2}{15}\left(\sqrt{3}\right)^5+\frac{2}{3}\left(\sqrt{3}\right)^3 &\mbox{}\\ \displaystyle &\displaystyle= -\frac{4}{15}\left(\sqrt{3}\right)^5+\frac{4}{3}\left(\sqrt{3}\right)^3 &\mbox{}\\ \displaystyle &\displaystyle= -\frac{4}{15}\cdot 9 \cdot \sqrt{3}+\frac{4}{3}\cdot 3 \cdot \sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle= -\frac{4}{5}\cdot 3 \cdot \sqrt{3}+4\sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle= -\frac{12}{5} \sqrt{3}+\frac{20}{5}\sqrt{3} &\mbox{}\\ \displaystyle &\displaystyle= \frac{8}{5} \sqrt{3} &\mbox{}\\ \end{array} $$
Source-Free Fields
An important class of vector fields are Source-Free fields.
A good hip-pocket example of source-free fields are incompressible fluid flows.
In this way, source-Free fields can be thought of as the fluid-flow foil to conservative (irrotational, gradient) fields.
Special Note: Source-Free fields are also called solenoidal fields.
Two important examples of source-free fields include
1. Magnetic Fields
2. Incompressible Fluid Flows
Source-Free Fields
Properties which characterize source-free fields include:
1. The flux $\displaystyle \oint_{C} {\bf F}\cdot {\bf N} \, ds=0$ for any closed curve $C.$
2. If $C_1$ and $C_2$ are curves lying entirely in the domain of ${\bf F}$ with the same starting points and endpoints, then $\displaystyle \int_{C_1} {\bf F}\cdot {\bf N} \, ds=\int_{C_2} {\bf F}\cdot {\bf N} \, ds.$ that is, flux is also independent of path!
3. There is a stream function $g(x, y)$ for ${\bf F}.$ A stream function for ${\bf F} = \langle P, Q \rangle$ is a function $g$ such that $\displaystyle P = \frac{\partial g}{\partial y}$ and $\displaystyle Q = -\frac{\partial g}{\partial x}.$ Stream functions are the source-free analog of potential functions for conservative fields.
4. $\displaystyle \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = 0$
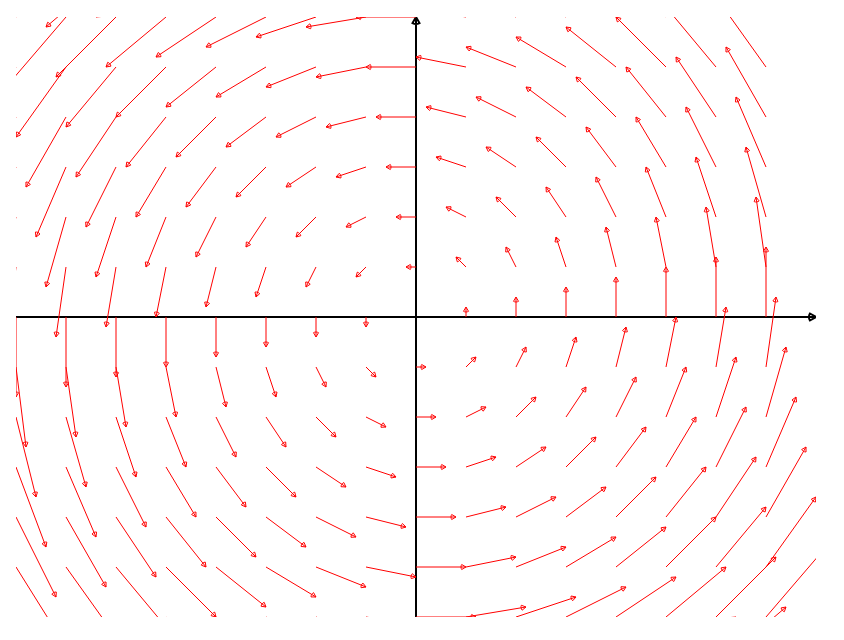
Example: Incompressible Fluid Flow Around a Cylinder
Consider a field modelling a steady-state, incompressible fluid flow around a cylinder.
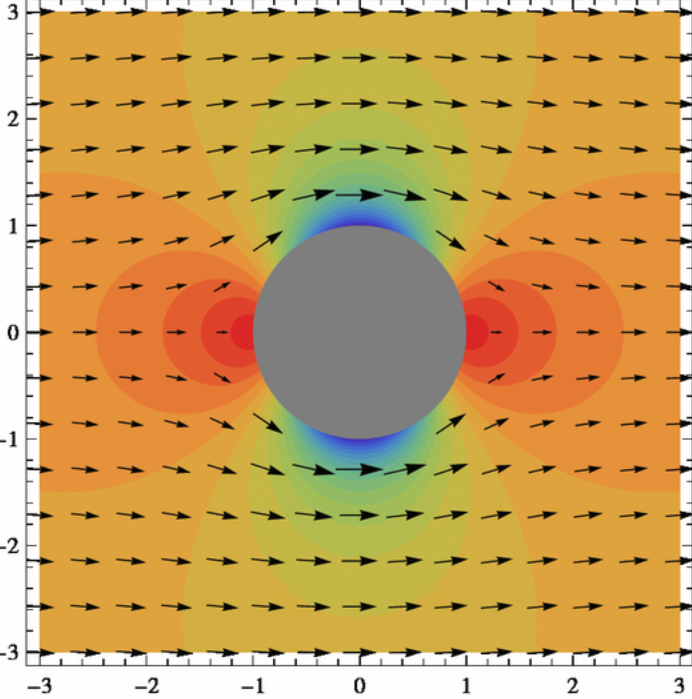 $\,$
$\,$
The stream lines of the field are on the right.
Summary of Properties of Conservative and Source-Free Fields
Let ${\bf F}=\langle P,Q\rangle$ be a vector field and $D$ be any open and simply connected domain. Also, let $C_1$ and $C_2$ be any simple, non-closed curves in $D$ with the same initial and final points. Finally, let $C$ be any simple, closed curve in $D.$ $$ \begin{array}{l|l} \mbox{Work Integrals}&\mbox{Incompressible Fluid-Flow Integrals}\\ \hline {\bf F} \mbox{ is Conservative (Irrotational) } & {\bf F} \mbox{ is Source-Free (Solenoidal)}\\ \displaystyle \iff \displaystyle \int_{C_1} {\bf F}\cdot {\bf T} \, ds=\int_{C_2} {\bf F}\cdot {\bf T} \, ds=0 &\iff \displaystyle \int_{C_1} {\bf F}\cdot {\bf N} \, ds=\int_{C_2} {\bf F}\cdot {\bf N} \, ds\\ \displaystyle \iff \mbox{ work is path independent }&\iff \mbox{ flux is path independent }\\ \displaystyle \iff \displaystyle \oint_{C} {\bf F} \cdot {\bf T} \, ds=0 & \iff\displaystyle \oint_{C} {\bf F} \cdot {\bf N} \, ds=0\\ \displaystyle \iff \mbox{ work over any closed curve is 0 }&\iff \displaystyle \mbox{ flux over any closed curve is 0 }\\ \displaystyle \iff \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 0 \mbox{ (CPP holds!)}&\iff \displaystyle \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = 0\\ \displaystyle \iff \mbox{for some $f,$ } P=\frac{\partial f}{\partial x} \mbox{ and } Q=\frac{\partial f}{\partial y}&\iff \displaystyle \mbox{For some $g,$ } P=\frac{\partial g}{\partial y} \mbox{ and } Q=-\frac{\partial g}{\partial x}\\ \displaystyle \iff {\bf F} \mbox{ has potential function $f$} &\iff {\bf F} \mbox{ has potential (stream) function $g$} \\ \end{array} $$
Fields which are Simultaneously Source-Free and Conservative
There are fields which have both properties of being conservative and source-free.
These kinds of fields occupy a very special place in both mathematics and physics.
Example
(a) Show that the field ${\bf F}(x,y)=\langle P,Q \rangle=\langle e^x\sin y,e^x\cos y \rangle$ is simultaneously source-free and conservative.
(b) Find a stream function $g$ for the field ${\bf F}.$
(c) Find a a potential function $f$ for the field ${\bf F}.$
(a) To show that the field is source-free, we observe that $$ \begin{array}{lll} \displaystyle \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y}&\displaystyle=\frac{\partial }{\partial x}e^x\sin y + \frac{\partial }{\partial y}e^x\cos y &\mbox{}\\ \displaystyle &\displaystyle =e^x\sin y+e^x(-\sin y) &\mbox{}\\ \displaystyle &\displaystyle =e^x\sin y-e^x\sin y &\mbox{}\\ \displaystyle &\displaystyle =0 &\mbox{}\\ \end{array} $$ and to show the field is conservative, we observe that $$ \begin{array}{lll} \displaystyle \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}&\displaystyle=\frac{\partial }{\partial x}e^x\cos y - \frac{\partial }{\partial y}e^x\sin y &\mbox{}\\ \displaystyle &\displaystyle =e^x\cos y -e^x\cos y &\mbox{}\\ \displaystyle &\displaystyle =0 &\mbox{}\\ \end{array} $$
(b) For ${\bf F} = \langle P, Q \rangle =\langle e^x\sin y,e^x\cos y \rangle,$ a stream function $g$ must satisfy $$\displaystyle P = \frac{\partial g}{\partial y}=e^x\sin y$$ and $$\displaystyle Q = -\frac{\partial g}{\partial x}=e^x\cos y$$
Performing a "partial" integration with respect to $y,$ we have $$ g(x,y)=-e^x\sin y+h(x) $$ Then $$ -e^x\cos y + h'(x)=\frac{\partial g}{\partial x}=-e^x\cos y $$ so that $$ h'(x)=0. $$ It follows that $$ h(x)=C $$ is a constant.
Thus $g(x,y)=-e^x\cos y + C$ is our stream function.
To verify, $$ \frac{\partial g}{\partial y}=\frac{\partial }{\partial y}(-e^x\cos y + C)=e^x\sin y=P $$ and $$ \frac{\partial g}{\partial x}=\frac{\partial }{\partial x}(-e^x\cos y + C)=-e^x\cos y=-Q $$ (c) A potential function $f$ satisfies ${\bf F}=\nabla f.$ That is, $$ \begin{array}{lll} \displaystyle &\displaystyle \frac{\partial f}{\partial x}=P=e^x\sin y &\mbox{}\\ \displaystyle &\displaystyle \frac{\partial f}{\partial y}=Q=e^x\cos y &\mbox{}\\ \end{array} $$ Partially integrating with respect to $x,$ $$ f(x,y)=e^x\sin y+h(y) $$ Then, $$ e^x\cos y+h'(y)=\frac{\partial f}{\partial y}=Q=e^x\cos y $$ so that $$ h'(y)=0 $$ Then $$ h(y)=C $$ is a constant, and our potential function is $$ f(x,y)=e^x\sin y+C. $$ To verify, $$ \frac{\partial f}{\partial x}=\frac{\partial }{\partial x}(e^x\sin y + C)=e^x\sin y=P $$ and $$ \frac{\partial f}{\partial y}=\frac{\partial }{\partial y}(e^x\sin y + C)=e^x\cos y=Q $$
In a moment we will say why fields which are simultaneously conservative and source-free are so special.
To understand why, we first need to define one more notion...
Harmonic Functions
A harmonic function $f$ is a function which satisfies Laplace's Equation. $$ \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}=0 $$
Some Fun Harmonic Function Facts
Laplace's Equation and its solutions (harmonic functions!) are hugely important in physics and the study of partial differential equations in general.
It is a partial differential equation which describes:
Steady-state Temperature Distributions
Steady States of Incompressible Fluid Flow
Static Electrical Potential
Gravitational Potential
Steady States of Reaction-Diffusion Processes
...to name only a few.
Also, harmonic functions are of central importance in complex analysis.
Big Facts
Suppose ${\bf F}(x,y)=\langle P,Q \rangle$ is a field that is simultaneously conservative and source-free in a simply connected domain $D.$
Then the following hold.
(a) The potential and stream functions of ${\bf F}$ are harmonic functions.
(b) If $P$ and $Q$ have continuous second partial derivatives, then $P$ and $Q$ are also harmonic
(a) Suppose ${\bf F}(x,y)=\langle P,Q \rangle.$
First we show that the potential function is harmonic.
Since ${\bf F}$ is conservative, it must have a potential function $f$ which satisfies $\displaystyle \frac{\partial f}{\partial x}=P$ and $\displaystyle \frac{\partial f}{\partial y}=Q,$ that is, ${\bf F}=\nabla f.$
But since ${\bf F}$ is also source-free, it must also satisfy $\displaystyle \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = 0.$
It follows that $$ \begin{array}{lll} &\displaystyle &\displaystyle \frac{\partial }{\partial x}P + \frac{\partial }{\partial y}Q = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle \frac{\partial }{\partial x} \left(\frac{\partial f}{\partial x}\right)+ \frac{\partial }{\partial y}\left(\frac{\partial f}{\partial y}\right) = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle \frac{\partial^2 f}{\partial x^2}+ \frac{\partial^2 f}{\partial y^2} = 0&\mbox{}\\ \end{array} $$
We now show the stream function is harmonic.
Since ${\bf F}$ is source-free, it must have a stream function $g$ which satisfies $\displaystyle \frac{\partial g}{\partial y}=P$ and $\displaystyle \frac{\partial g}{\partial x}=-Q.$
But since ${\bf F}$ is also conservative, it must also satisfy $\displaystyle \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 0.$ (By the $\mbox{CPP!}$)
It follows that $$ \begin{array}{lll} &\displaystyle &\displaystyle \frac{\partial }{\partial x}Q - \frac{\partial }{\partial y}P = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle \frac{\partial }{\partial x} \left(-\frac{\partial g}{\partial x}\right)- \frac{\partial }{\partial y}\left(\frac{\partial g}{\partial y}\right) = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle -\frac{\partial^2 g}{\partial x^2}- \frac{\partial^2 g}{\partial y^2} = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle \frac{\partial^2 g}{\partial x^2}+ \frac{\partial^2 g}{\partial y^2} = 0&\mbox{}\\ \end{array} $$
(b) Since ${\bf F}$ is conservative, we know that $\displaystyle \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0,$ and since ${\bf F}$ is also source-free, we know that $\displaystyle \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=0.$
Then $$ \begin{cases} \displaystyle \frac{\partial }{\partial x}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)=0\\ \displaystyle \frac{\partial }{\partial y}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)=0\\ \end{cases} \implies \begin{cases} \displaystyle \frac{\partial^2 P}{\partial x^2}+\frac{\partial^2 Q}{\partial x \partial y}=0\\ \displaystyle \frac{\partial^2 Q}{\partial y \partial x}-\frac{\partial^2 P}{\partial y^2}=0\\ \end{cases} \implies \begin{cases} \displaystyle \frac{\partial^2 P}{\partial x^2}+\color{magenta}{\frac{\partial^2 Q}{\partial x \partial y}}=0\\ \displaystyle \color{magenta}{\frac{\partial^2 Q}{\partial y \partial x}}=\frac{\partial^2 P}{\partial y^2}\\ \end{cases} $$ Since $P$ and $Q$ have continuous second partial derivatives, we know by Clairaut's Theorem that the mixed partials are equal.
Thus, $$ \frac{\partial^2 P}{\partial x^2}+\frac{\partial^2 P}{\partial y^2}=0 $$ so that $P$ is a harmonic function.
The argument demonstrating $\displaystyle \frac{\partial^2 Q}{\partial x^2}+\frac{\partial^2 Q}{\partial y^2}=0$ is similar to the above.
First we show that the potential function is harmonic.
Since ${\bf F}$ is conservative, it must have a potential function $f$ which satisfies $\displaystyle \frac{\partial f}{\partial x}=P$ and $\displaystyle \frac{\partial f}{\partial y}=Q,$ that is, ${\bf F}=\nabla f.$
But since ${\bf F}$ is also source-free, it must also satisfy $\displaystyle \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = 0.$
It follows that $$ \begin{array}{lll} &\displaystyle &\displaystyle \frac{\partial }{\partial x}P + \frac{\partial }{\partial y}Q = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle \frac{\partial }{\partial x} \left(\frac{\partial f}{\partial x}\right)+ \frac{\partial }{\partial y}\left(\frac{\partial f}{\partial y}\right) = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle \frac{\partial^2 f}{\partial x^2}+ \frac{\partial^2 f}{\partial y^2} = 0&\mbox{}\\ \end{array} $$
We now show the stream function is harmonic.
Since ${\bf F}$ is source-free, it must have a stream function $g$ which satisfies $\displaystyle \frac{\partial g}{\partial y}=P$ and $\displaystyle \frac{\partial g}{\partial x}=-Q.$
But since ${\bf F}$ is also conservative, it must also satisfy $\displaystyle \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 0.$ (By the $\mbox{CPP!}$)
It follows that $$ \begin{array}{lll} &\displaystyle &\displaystyle \frac{\partial }{\partial x}Q - \frac{\partial }{\partial y}P = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle \frac{\partial }{\partial x} \left(-\frac{\partial g}{\partial x}\right)- \frac{\partial }{\partial y}\left(\frac{\partial g}{\partial y}\right) = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle -\frac{\partial^2 g}{\partial x^2}- \frac{\partial^2 g}{\partial y^2} = 0&\mbox{}\\ \implies &\displaystyle &\displaystyle \frac{\partial^2 g}{\partial x^2}+ \frac{\partial^2 g}{\partial y^2} = 0&\mbox{}\\ \end{array} $$
(b) Since ${\bf F}$ is conservative, we know that $\displaystyle \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0,$ and since ${\bf F}$ is also source-free, we know that $\displaystyle \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=0.$
Then $$ \begin{cases} \displaystyle \frac{\partial }{\partial x}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)=0\\ \displaystyle \frac{\partial }{\partial y}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)=0\\ \end{cases} \implies \begin{cases} \displaystyle \frac{\partial^2 P}{\partial x^2}+\frac{\partial^2 Q}{\partial x \partial y}=0\\ \displaystyle \frac{\partial^2 Q}{\partial y \partial x}-\frac{\partial^2 P}{\partial y^2}=0\\ \end{cases} \implies \begin{cases} \displaystyle \frac{\partial^2 P}{\partial x^2}+\color{magenta}{\frac{\partial^2 Q}{\partial x \partial y}}=0\\ \displaystyle \color{magenta}{\frac{\partial^2 Q}{\partial y \partial x}}=\frac{\partial^2 P}{\partial y^2}\\ \end{cases} $$ Since $P$ and $Q$ have continuous second partial derivatives, we know by Clairaut's Theorem that the mixed partials are equal.
Thus, $$ \frac{\partial^2 P}{\partial x^2}+\frac{\partial^2 P}{\partial y^2}=0 $$ so that $P$ is a harmonic function.
The argument demonstrating $\displaystyle \frac{\partial^2 Q}{\partial x^2}+\frac{\partial^2 Q}{\partial y^2}=0$ is similar to the above.
Example
(a) Verify that the potential and stream functions of ${\bf F}(x,y)=\langle P,Q\rangle =\langle e^x\sin y,e^x\cos y \rangle$ are both harmonic.
(b) Verify that $P$ and $Q$ are both harmonic.
(a)
For the potential function $f(x,y)=e^x\sin y+C$ found in a previous example, we see that
$$
\begin{array}{lll}
\displaystyle \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}&\displaystyle=\frac{\partial^2 }{\partial x^2}(e^x\sin y+C)+\frac{\partial^2 }{\partial y^2}(e^x\sin y+C) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial }{\partial x}(e^x\sin y)+\frac{\partial }{\partial y}(e^x\cos y) &\mbox{}\\
\displaystyle &\displaystyle=e^x\sin y+e^x(-\sin y) &\mbox{}\\
\displaystyle &\displaystyle=e^x\sin y-e^x\sin y &\mbox{}\\
\displaystyle &\displaystyle=0 &\mbox{}\\
\end{array}
$$
For the stream function $g(x,y)=-e^x\cos y + C$ found in a previous example, we see that
$$
\begin{array}{lll}
\displaystyle \frac{\partial^2 g}{\partial x^2}+\frac{\partial^2 g}{\partial y^2}&\displaystyle=\frac{\partial^2 }{\partial x^2}(-e^x\cos y + C)+\frac{\partial^2 }{\partial y^2}(-e^x\cos y + C) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial }{\partial x}(-e^x\cos y)+\frac{\partial }{\partial y}(-e^x(-\sin y)) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial }{\partial x}(-e^x\cos y)+\frac{\partial }{\partial y}(e^x\sin y) &\mbox{}\\
\displaystyle &\displaystyle=-e^x\cos y+e^x\cos y &\mbox{}\\
\displaystyle &\displaystyle=0 &\mbox{}\\
\end{array}
$$
(b) Since $f$ and $g$ differ from $P$ and $Q$ by no more than a constant and constant multiple,
$P$ and $Q$ are also harmonic.
Applied Example of a Conservative and Source-Free Field
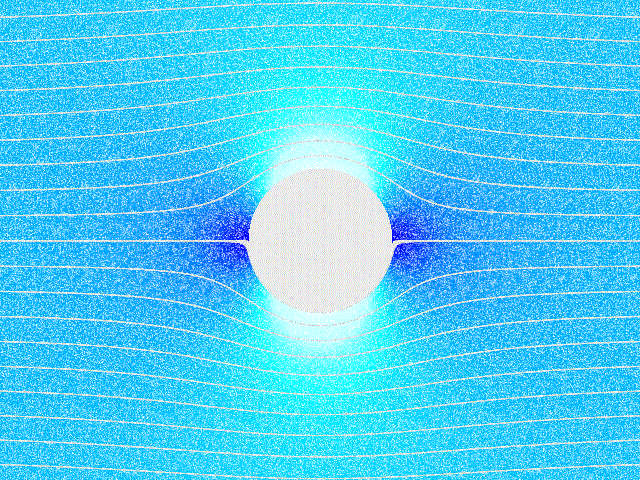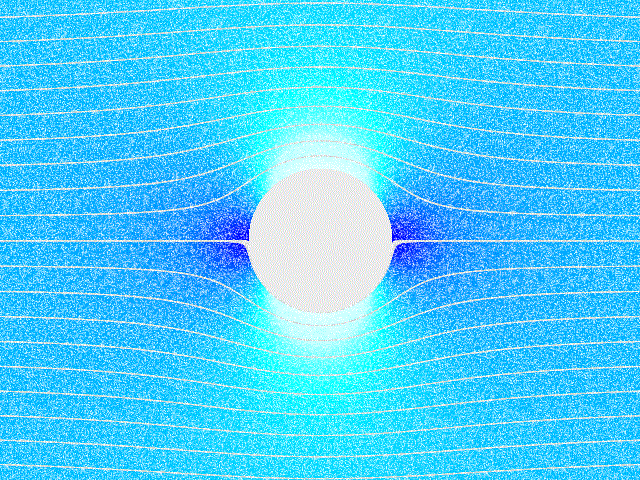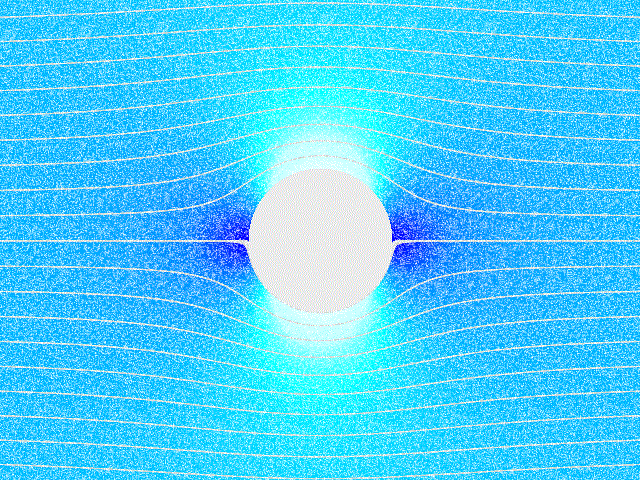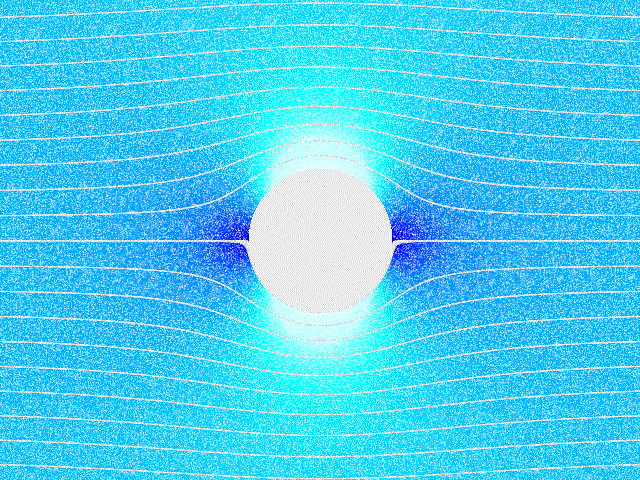
Consider a field modelling a steady-state, incompressible fluid flow around a cylinder.
 $\,$
$\,$
 $\,$
$\,$
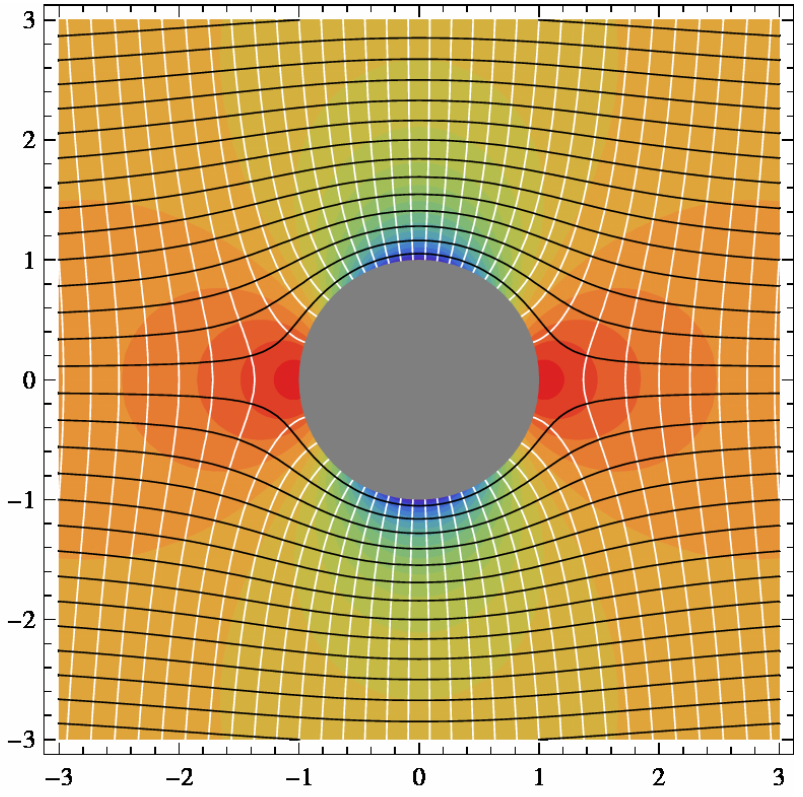
The stream lines of the source-free potential $g$ and level curves of the conservative potential $f$ of the field are on the far right.
Notice that solutions $f$ and $g$ intersect at right angles.