Conservative vector fields are named for the many situations in physics where a conservation principle is at work.
For example, conservation of energy, mass, momentum, etc.
Gravitational fields and electric fields are but two examples of conservative vector fields.
We'll soon see that the most notable and convenient property of conservative fields is that the path of integration is irrelevant.
Recall
A vector field ${\bf F}$ is conservative if for some two or three variable function $f,$ we have ${\bf F}=\nabla f.$
In this case, $f$ is called a potential function for ${\bf F}.$
Special Note: Conservative fields are also called irrotational.
We'll have more to say about this later, but for now, we'll just say that conservative fields don't have have any swirl to them.
The Fundamental Theorem for Line Integrals
Let $C$ be a piecewise smooth curve with parameterization ${\bf r}(t)$ for $a \leq t \leq b.$ Let $f$ be a function of two or three variables with first-order partial derivatives that exist and are continuous on $C.$ Then, $$\int_C \nabla f \cdot d{\bf r}=f({\bf r}(b))-f({\bf r}(a))$$
Example: Consider the potential function $f(x, y) = (x - 1)^2 y + (y + 1)^2 x$ for the vector field ${\bf F}=\nabla f = \langle 2xy - 2y + (y + 1)^2 , (x - 1)^2 + 2yx + 2x \rangle.$
(a) Directly calculate the integral $\displaystyle \int_{C} {\bf F} \cdot d{\bf r}$ where $C$ is the lower half of the unit circle oriented counterclockwise (positively).
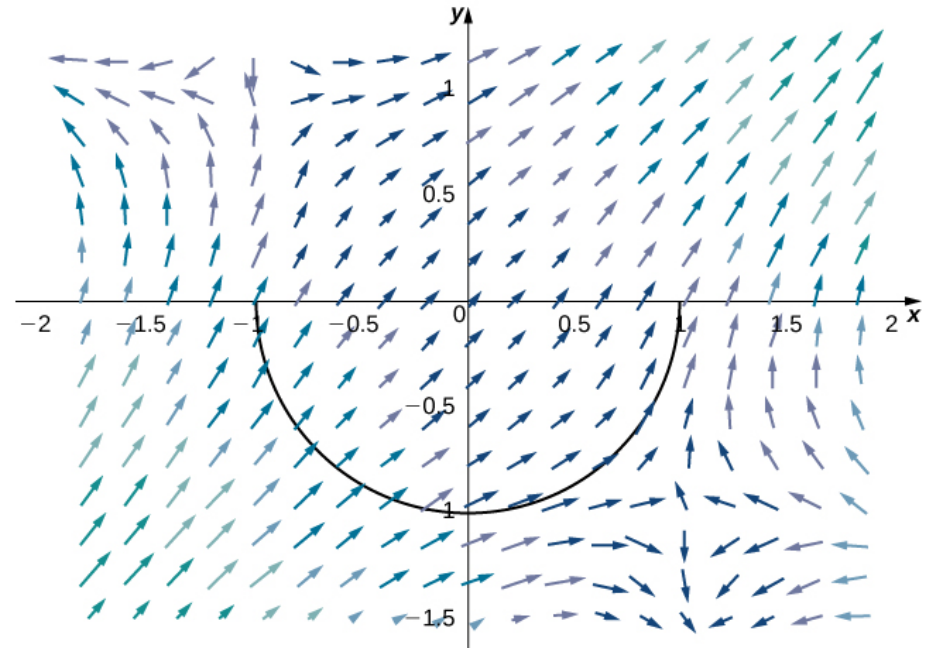
(b) Use the Fundamental Theorem of Line Integrals to calculate the integral $\displaystyle \int_{C} {\bf F} \cdot d{\bf r}.$
(a) First we parameterize $C$ as ${\bf r}(t)=\langle \cos t , \sin t \rangle$ over $\pi \leq t \leq 2\pi.$
Then ${\bf r}'(t)=\langle -\sin t , \cos t \rangle$ so that $$ \begin{array}{lll} \displaystyle \int_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_{\pi}^{2\pi} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} \langle 2x(t)y(t) - 2y(t) + (y(t) + 1)^2 , (x(t) - 1)^2 + 2y(t)x(t) + 2x(t) \rangle \cdot \langle -\sin t , \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} \langle 2\cos t \sin t - 2\sin t + (\sin t + 1)^2 , (\cos t - 1)^2 + 2\sin t \cos t + 2\cos t \rangle \cdot \langle -\sin t , \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} \langle 2\cos t \sin t - 2\sin t + \sin^2 t +2 \sin t + 1 , \cos^2 t-2\cos t + 1 + 2\sin t \cos t + 2\cos t \rangle \cdot \langle -\sin t , \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} \langle 2\cos t \sin t + \sin^2 t + 1 , \cos^2 t + 1 + 2\sin t \cos t \rangle \cdot \langle -\sin t , \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} (2\cos t \sin t + \sin^2 t + 1)(-\sin t)+(\cos^2 t + 1 + 2\sin t \cos t)(\cos t)\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} 2\cos t \sin^2 t - \sin^3 t -\sin t +\cos^3 t + \cos t + 2\sin t \cos^2 t\,dt &\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{2}{3}\sin^3 t +\frac{1}{3}(2+\sin^2 t)\cos t +\cos t +\frac{1}{3}(2+\cos^2 t)\sin t + \sin t - \frac{2}{3}\cos^3 t\right]_{\pi}^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\sin^3 (2\pi) +\frac{1}{3}(2+\sin^2 (2\pi))\cos (2\pi) +\cos (2\pi) +\frac{1}{3}(2+\cos^2 (2\pi))\sin (2\pi) + \sin (2\pi) - \frac{2}{3}\cos^3(2\pi) t-\left(\frac{2}{3}\sin^3(\pi) +\frac{1}{3}(2+\sin^2 (\pi))\cos (\pi) +\cos (\pi) +\frac{1}{3}(2+\cos^2 (\pi))\sin (\pi) + \sin (\pi) - \frac{2}{3}\cos^3 (\pi)\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}(0)^3 +\frac{1}{3}(2+0 )\cdot 1 +1 +\frac{1}{3}(2+1)\cdot 0 + 0 - \frac{2}{3}\cdot 1 -\left(\frac{2}{3}(0)^3 +\frac{1}{3}(2+0)(-1) +(-1) +\frac{1}{3}(2+(-1))\cdot 0 + 0 - \frac{2}{3}(-1)^3\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3} +1 - \frac{2}{3} -\left(-\frac{2}{3}-1 + \frac{2}{3}\right) &\mbox{}\\ \displaystyle &\displaystyle= 1-(-1) &\mbox{}\\ \displaystyle &\displaystyle= 2 &\mbox{}\\ \end{array} $$
(b) We first note that ${\bf r}(2\pi)=\langle \cos(2\pi),\sin(2\pi)\rangle=\langle 1,0 \rangle$ and ${\bf r}(\pi)=\langle \cos(\pi),\sin(\pi)\rangle=\langle -1,0 \rangle$
Then, by the FTLI, $$ \begin{array}{lll} \displaystyle \int_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_{C} \nabla f \cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=f({\bf r}(2\pi))-f({\bf r}(\pi)) &\mbox{}\\ \displaystyle &\displaystyle=f(1,0)-f(-1,0) &\mbox{}\\ \displaystyle &\displaystyle=(1 - 1)^2\cdot 0 + (0 + 1)^2\cdot 1-\left((-1 - 1)^2 \cdot 0 + (0 + 1)^2 (-1)\right) &\mbox{}\\ \displaystyle &\displaystyle=1-\left(-1\right) &\mbox{}\\ \displaystyle &\displaystyle=2 &\mbox{}\\ \end{array} $$
Which one do you prefer?
Then ${\bf r}'(t)=\langle -\sin t , \cos t \rangle$ so that $$ \begin{array}{lll} \displaystyle \int_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_{\pi}^{2\pi} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} \langle 2x(t)y(t) - 2y(t) + (y(t) + 1)^2 , (x(t) - 1)^2 + 2y(t)x(t) + 2x(t) \rangle \cdot \langle -\sin t , \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} \langle 2\cos t \sin t - 2\sin t + (\sin t + 1)^2 , (\cos t - 1)^2 + 2\sin t \cos t + 2\cos t \rangle \cdot \langle -\sin t , \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} \langle 2\cos t \sin t - 2\sin t + \sin^2 t +2 \sin t + 1 , \cos^2 t-2\cos t + 1 + 2\sin t \cos t + 2\cos t \rangle \cdot \langle -\sin t , \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} \langle 2\cos t \sin t + \sin^2 t + 1 , \cos^2 t + 1 + 2\sin t \cos t \rangle \cdot \langle -\sin t , \cos t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} (2\cos t \sin t + \sin^2 t + 1)(-\sin t)+(\cos^2 t + 1 + 2\sin t \cos t)(\cos t)\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi}^{2\pi} 2\cos t \sin^2 t - \sin^3 t -\sin t +\cos^3 t + \cos t + 2\sin t \cos^2 t\,dt &\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{2}{3}\sin^3 t +\frac{1}{3}(2+\sin^2 t)\cos t +\cos t +\frac{1}{3}(2+\cos^2 t)\sin t + \sin t - \frac{2}{3}\cos^3 t\right]_{\pi}^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\sin^3 (2\pi) +\frac{1}{3}(2+\sin^2 (2\pi))\cos (2\pi) +\cos (2\pi) +\frac{1}{3}(2+\cos^2 (2\pi))\sin (2\pi) + \sin (2\pi) - \frac{2}{3}\cos^3(2\pi) t-\left(\frac{2}{3}\sin^3(\pi) +\frac{1}{3}(2+\sin^2 (\pi))\cos (\pi) +\cos (\pi) +\frac{1}{3}(2+\cos^2 (\pi))\sin (\pi) + \sin (\pi) - \frac{2}{3}\cos^3 (\pi)\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}(0)^3 +\frac{1}{3}(2+0 )\cdot 1 +1 +\frac{1}{3}(2+1)\cdot 0 + 0 - \frac{2}{3}\cdot 1 -\left(\frac{2}{3}(0)^3 +\frac{1}{3}(2+0)(-1) +(-1) +\frac{1}{3}(2+(-1))\cdot 0 + 0 - \frac{2}{3}(-1)^3\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3} +1 - \frac{2}{3} -\left(-\frac{2}{3}-1 + \frac{2}{3}\right) &\mbox{}\\ \displaystyle &\displaystyle= 1-(-1) &\mbox{}\\ \displaystyle &\displaystyle= 2 &\mbox{}\\ \end{array} $$
(b) We first note that ${\bf r}(2\pi)=\langle \cos(2\pi),\sin(2\pi)\rangle=\langle 1,0 \rangle$ and ${\bf r}(\pi)=\langle \cos(\pi),\sin(\pi)\rangle=\langle -1,0 \rangle$
Then, by the FTLI, $$ \begin{array}{lll} \displaystyle \int_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_{C} \nabla f \cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=f({\bf r}(2\pi))-f({\bf r}(\pi)) &\mbox{}\\ \displaystyle &\displaystyle=f(1,0)-f(-1,0) &\mbox{}\\ \displaystyle &\displaystyle=(1 - 1)^2\cdot 0 + (0 + 1)^2\cdot 1-\left((-1 - 1)^2 \cdot 0 + (0 + 1)^2 (-1)\right) &\mbox{}\\ \displaystyle &\displaystyle=1-\left(-1\right) &\mbox{}\\ \displaystyle &\displaystyle=2 &\mbox{}\\ \end{array} $$
Which one do you prefer?
In Words
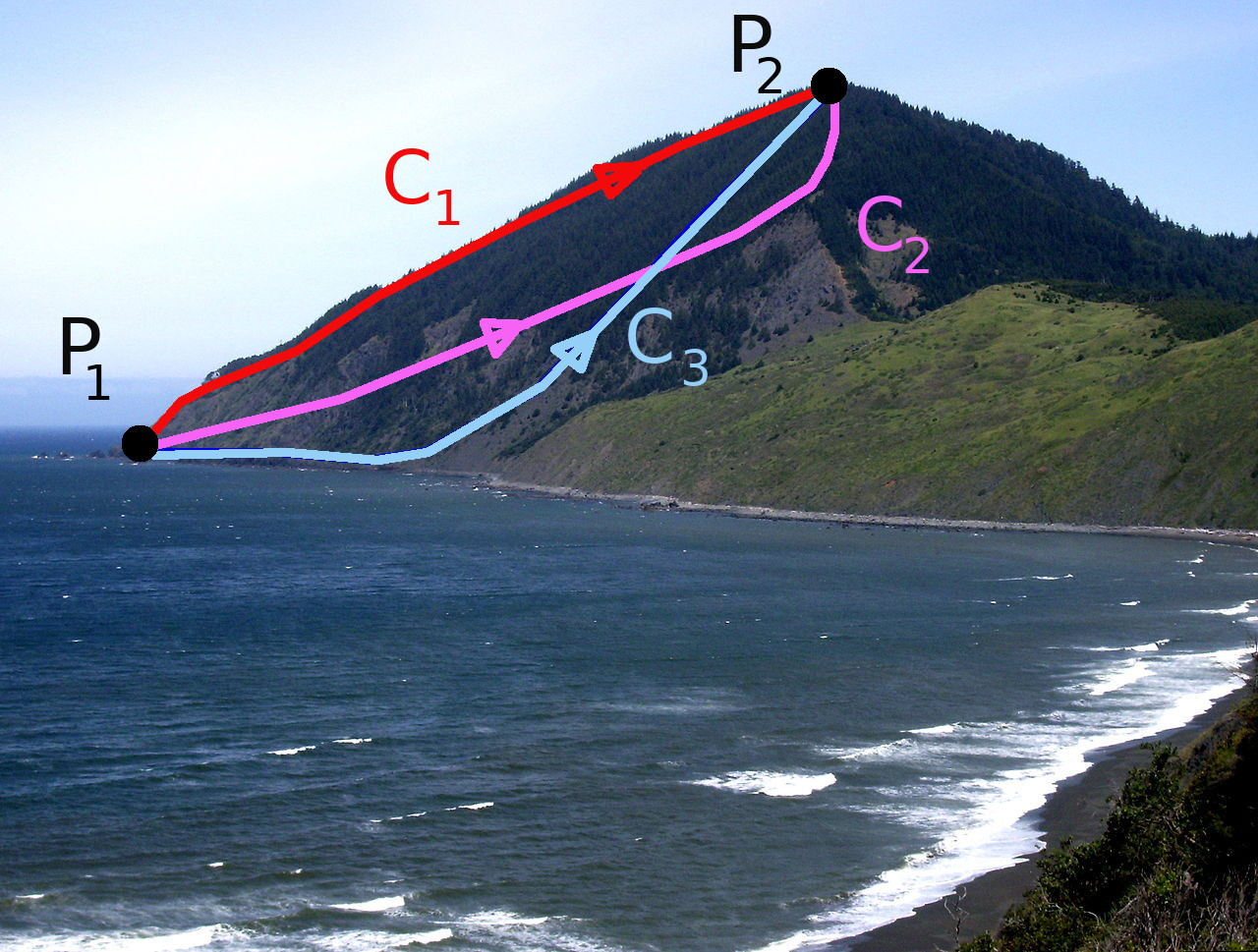
The Fundamental Theorem for Line Integrals tells us that the line integral of a conservative vector field (gradient field) is dependent only on the initial and final points on the path of integration.
That is, the line integral along any path from $P_1$ to $P_2$ will have the same value no matter the path.
This property is called path independence.
Formal Definition of Path Independence
Let ${\bf F}$ be a vector field with domain $D.$ The vector field ${\bf F}$ is independent of path (or path independent) if $$\displaystyle \int_{C_1} {\bf F} \cdot d{\bf r}= \int_{C_2} {\bf F} \cdot d{\bf r}$$ for any paths $C_1$ and $C_2$ in $D$ with the same initial and terminal points.

(Alternative) Formal Definition of Path Independence
Let ${\bf F}$ be a vector field with domain $D.$ The vector field ${\bf F}$ is independent of path (or path independent) if $$\displaystyle \oint_{C} {\bf F} \cdot d{\bf r}=0$$ for any closed curve $C$ in $D.$
Theorem: Path Independence of Conservative Fields
If ${\bf F}$ is a conservative vector field, then ${\bf F}$ is path independent.
Corollary
If ${\bf F}$ is a conservative field and $C$ is a closed curve, then the circulation of ${\bf F}$ along $C$ is zero. That is, $$\displaystyle \oint_{C} {\bf F} \cdot d{\bf r}=0$$
Example: Path Independence
$\mbox{Work Done Against Gravity}$
$=$
$\displaystyle \int_{C_1} {\bf F} \cdot d{\bf r}$
$=$
$\displaystyle \int_{C_2} {\bf F} \cdot d{\bf r}$
$=$
$\displaystyle \int_{C_3} {\bf F} \cdot d{\bf r}$
The Gist
Suppose we need to compute a line integral $\displaystyle \int_{C} {\bf F} \cdot d{\bf r}.$
If we can find a potential function $f,$ then the FTLI tells us that we're in business! $$\displaystyle \int_{C} {\bf F} \cdot d{\bf r}=\displaystyle \int_{C} \nabla f \cdot d{\bf r}=f({\bf r}(b))-f({\bf r}(a)).$$
Finding a Potential Function: Applied Example
Near the surface of the earth the strength of earth's gravitational field on an object of mass $m$ is approximately given by ${\bf F}=\langle 0,0,-mg \rangle=-mg\,{\bf k}$ where $g=9.8$ $\mbox{m}/\mbox{sec}^2$ is the gravitational constant.
Suppose a hiker and their pack weighs $90 \mbox{ kg}$ (about $200 \mbox{ lb}.$) Compute the amount of work the hiker performs against gravity from sea level to the top of Humbug Mountain which has an elevation of $538 \mbox{ m}$ $(1765 \mbox{ ft}).$
Let's find a potential function $f$ such that ${\bf F}=\nabla f.$
Now we know that $$\displaystyle \left \langle \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \right\rangle=\nabla f=\langle 0,0,-mg \rangle$$ so that $\displaystyle \frac{\partial f}{\partial x}=0$ and $\displaystyle \frac{\partial f}{\partial y}=0.$
That is, our potential function only needs to depend on $z.$
Furthermore, we know that $\displaystyle \frac{\partial f}{\partial z}=-mg$ which suggests $f(x,y,z)=-mgz$ as a potential function.
With our potential function, we may now compute the amount of work, $\displaystyle \int_{C} {\bf F} \cdot d{\bf r},$ the hiker performs against gravity.
Since we know the work depends only upon the change in elevation, and does not depend on any path, any starting point at sea level $(x_i,y_i,0)$ and the final point at the summit $(x_f,y_f,538)$ is all we need to compute the work. $$ \begin{array}{lll} \displaystyle \int_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_{C} \nabla f \cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=\displaystyle f(x_f,y_f,538)-f(x_i,y_i,0) &\mbox{}\\ \displaystyle &\displaystyle=-mg\cdot 538-(-mg\cdot 0) &\mbox{}\\ \displaystyle &\displaystyle=-90 \cdot 9.8\cdot 538 &\mbox{}\\ \displaystyle &\displaystyle=-474516 &\mbox{}\\ \end{array} $$ That is, the hiker did $474516$ joules of work against gravity.
For reference, not taking the efficiency of the human body into account, this is about $113.4$ calories.
Also, assuming $100\%$ efficiency, this amount of energy could power a $60$-watt for about $2.2$ hours.
Now we know that $$\displaystyle \left \langle \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \right\rangle=\nabla f=\langle 0,0,-mg \rangle$$ so that $\displaystyle \frac{\partial f}{\partial x}=0$ and $\displaystyle \frac{\partial f}{\partial y}=0.$
That is, our potential function only needs to depend on $z.$
Furthermore, we know that $\displaystyle \frac{\partial f}{\partial z}=-mg$ which suggests $f(x,y,z)=-mgz$ as a potential function.
With our potential function, we may now compute the amount of work, $\displaystyle \int_{C} {\bf F} \cdot d{\bf r},$ the hiker performs against gravity.
Since we know the work depends only upon the change in elevation, and does not depend on any path, any starting point at sea level $(x_i,y_i,0)$ and the final point at the summit $(x_f,y_f,538)$ is all we need to compute the work. $$ \begin{array}{lll} \displaystyle \int_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_{C} \nabla f \cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=\displaystyle f(x_f,y_f,538)-f(x_i,y_i,0) &\mbox{}\\ \displaystyle &\displaystyle=-mg\cdot 538-(-mg\cdot 0) &\mbox{}\\ \displaystyle &\displaystyle=-90 \cdot 9.8\cdot 538 &\mbox{}\\ \displaystyle &\displaystyle=-474516 &\mbox{}\\ \end{array} $$ That is, the hiker did $474516$ joules of work against gravity.
For reference, not taking the efficiency of the human body into account, this is about $113.4$ calories.
Also, assuming $100\%$ efficiency, this amount of energy could power a $60$-watt for about $2.2$ hours.
Finding a Potential Function: Nerdy Example
Find a potential function for ${\bf F}(x, y) = \langle e^x y^3 + y, 3e^x y^2 + x \rangle.$
We're looking for a function $f$ such that
$$
\left \langle \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right\rangle=\nabla f={\bf F}(x, y) = \langle e^x y^3 + y, 3e^x y^2 + x \rangle
$$
That is, we need $f$ to satisfy
$$
\frac{\partial f}{\partial x}=e^x y^3 + y
$$
and
$$
\frac{\partial f}{\partial y}=3e^x y^2 + x
$$
We'll begin by finding an "partial" antiderivative with respect to $x.$
$$
f(x,y)=e^x y^3 + yx+h(y)
$$
Notice that $h(y)$ doesn't depend on $x$ so that $\displaystyle \frac{\partial h}{\partial x}=0.$
We now take the partial of $f(x,y)$ with respect to $y$ of our potential function $f(x,y)$ above $$ \frac{\partial f}{\partial y}=3e^xy^2+x+h'(y) $$ and compare it to the known $\displaystyle \frac{\partial f}{\partial y}=3e^x y^2 + x.$
Both of these give $$ 3e^xy^2+x+h'(y)=\frac{\partial f}{\partial y}=3e^x y^2 + x $$ so that $$ h'(y)=0 $$ Then $h$ must be a constant function $$ h(y)=C. $$ Our potential function is then $$ f(x,y)=e^x y^3 + xy+C $$ where $C$ is any constant.
To verify we've found a potential function, we compute $\nabla f.$ $$ \begin{array}{lll} \displaystyle \nabla f&\displaystyle= \left \langle \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left \langle \frac{\partial }{\partial x}(e^x y^3 + xy+C),\frac{\partial }{\partial y}(e^x y^3 + xy+C) \right\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left \langle e^x y^3 + y,3e^x y^2 + x \right\rangle &\mbox{}\\ \displaystyle &\displaystyle={\bf F}(x,y)&\mbox{}\\ \end{array} $$
We now take the partial of $f(x,y)$ with respect to $y$ of our potential function $f(x,y)$ above $$ \frac{\partial f}{\partial y}=3e^xy^2+x+h'(y) $$ and compare it to the known $\displaystyle \frac{\partial f}{\partial y}=3e^x y^2 + x.$
Both of these give $$ 3e^xy^2+x+h'(y)=\frac{\partial f}{\partial y}=3e^x y^2 + x $$ so that $$ h'(y)=0 $$ Then $h$ must be a constant function $$ h(y)=C. $$ Our potential function is then $$ f(x,y)=e^x y^3 + xy+C $$ where $C$ is any constant.
To verify we've found a potential function, we compute $\nabla f.$ $$ \begin{array}{lll} \displaystyle \nabla f&\displaystyle= \left \langle \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left \langle \frac{\partial }{\partial x}(e^x y^3 + xy+C),\frac{\partial }{\partial y}(e^x y^3 + xy+C) \right\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left \langle e^x y^3 + y,3e^x y^2 + x \right\rangle &\mbox{}\\ \displaystyle &\displaystyle={\bf F}(x,y)&\mbox{}\\ \end{array} $$
Finding a Potential Function for a Conservative Vector Field
To find a potential function $f(x,y)$ of ${\bf F}(x, y) = \langle P(x, y), Q(x, y) \rangle:$
1. Integrate $P$ with respect to $x.$ This results in a function of the form $g(x, y) + h(y),$ where $h(y)$ is unknown.
2. Take the partial derivative of $g(x, y) + h(y)$ with respect to $y,$ which results in the function $g_y (x, y) + h'(y).$
3. Use the equation $g_y (x, y) + h'(y) = Q(x, y)$ to find $h'(y).$
4. Integrate $h'(y)$ to find $h(y).$
5. Any function of the form $f (x, y) = g(x, y) + h(y) + C,$ where $C$ is a constant, is a potential function for ${\bf F}.$
Finding a Potential Function: Gravitation: Find a potential function for the three-dimensional gravitational force $$ \begin{array}{ll} {\bf F}(x,y,z) &= \displaystyle \left \langle \frac{-Gm_1m_2x}{(x^2+y^2+z^2)^{3/2}},\frac{-Gm_1m_2y}{(x^2+y^2+z^2)^{3/2}},\frac{-Gm_1m_2z}{(x^2+y^2+z^2)^{3/2}} \right\rangle\\ &=\displaystyle \frac{-Gm_1m_2x}{(x^2+y^2+z^2)^{3/2}}\,{\bf i}+\frac{-Gm_1m_2y}{(x^2+y^2+z^2)^{3/2}}\,{\bf j}+\frac{-Gm_1m_2z}{(x^2+y^2+z^2)^{3/2}}\,{\bf k} \end{array} $$
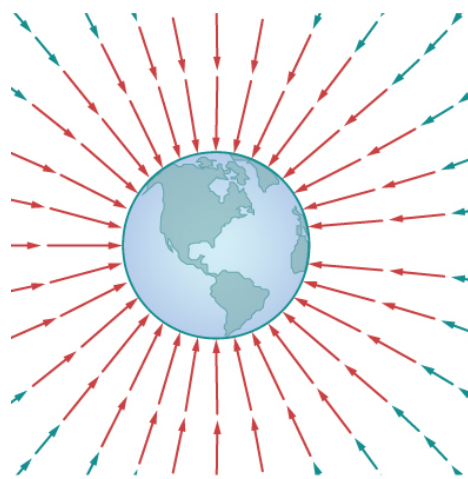
Recall that we showed earlier that $\displaystyle f(x,y,z)=\frac{Gm_1 m_2}{\sqrt{x^2+y^2+z^2}}$ is a potential function for ${\bf F}.$
What Do You Think?
Are there vector fields which are not conservative?
Answer: Yup.
Example
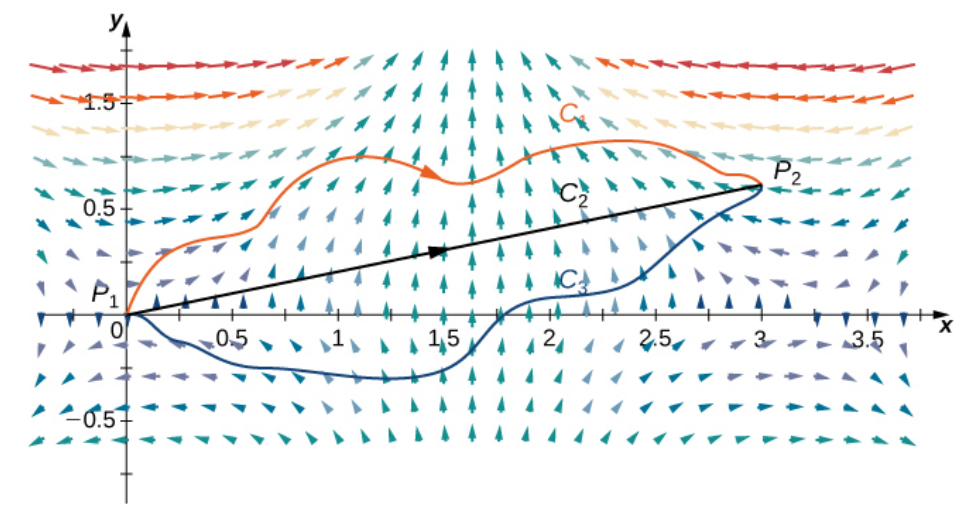
Show that ${\bf F}(x, y) = \langle xy, x^2 y^2 \rangle$ is not path independent by considering the line segment from $(0, 0)$ to $(2, 2)$ and the piece of the graph of $y =\displaystyle \frac{x^2}{2}$ that goes from $(0, 0)$ to $(2, 2).$
Note: Since $\mbox{Conservative}\implies \mbox{Path Independent},$ the above field ${\bf F}$ is also not conservative.
We will integrate over the paths shown below.
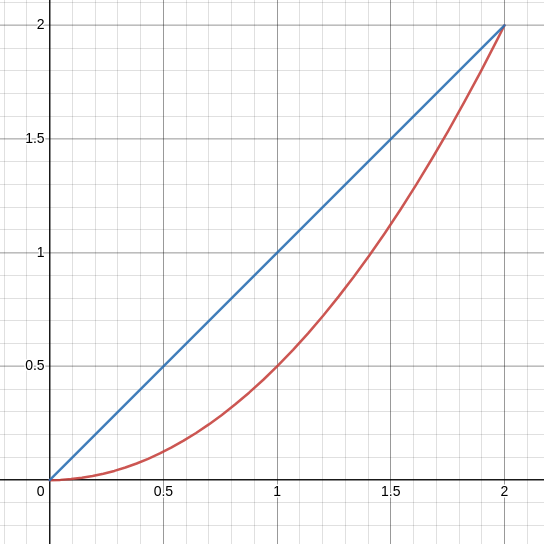
For the parabolic path $C_1,$ we will parameterize the curve as $${\bf r}_1(t)=\left \langle t,\frac{1}{2}t^2 \right\rangle$$ over $0\leq t\leq 2$ and for the straight-line path we will parameterize as $${\bf r}_2(t)=\left \langle t,t \right\rangle$$ over $0\leq t\leq 2.$
Then $$ \begin{array}{lll} \displaystyle \int_{C_1} {\bf F} \cdot d{\bf r}_1&\displaystyle=\int_{0}^{2} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}_1}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2} \left\langle x(t)y(t), x(t)^2 y(t)^2 \rangle \cdot \langle 1,t \right\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\left\langle t\cdot \frac{1}{2}t^2, t^2 \left(\frac{1}{2}t^2\right)^2 \right\rangle \cdot \langle 1,t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\left\langle \frac{1}{2}t^3, \frac{1}{4}t^6 \right\rangle \cdot \langle 1,t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\frac{1}{2}t^3+ \frac{1}{4}t^7 \,dt &\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{1}{8}t^4+ \frac{1}{32}t^8\right]_{0}^{2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{8}(2)^4+ \frac{1}{32}(2)^8 &\mbox{}\\ \displaystyle &\displaystyle= 10 &\mbox{}\\ \end{array} $$ and $$ \begin{array}{lll} \displaystyle \int_{C_2} {\bf F} \cdot d{\bf r}_2&\displaystyle=\int_{0}^{2} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}_2}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2} \langle x(t)y(t), x(t)^2 y(t)^2 \rangle \cdot \langle 1,1 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\left\langle t\cdot t, t^2 \cdot t^2 \right\rangle \cdot \langle 1,1 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\left\langle t^2, t^4\right\rangle \cdot \langle 1,1 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2} t^2+t^4 \,dt &\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{1}{3}t^3+ \frac{1}{5}t^5\right]_{0}^{2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}(2)^3+ \frac{1}{5}(2)^5 &\mbox{}\\ \displaystyle &\displaystyle= \frac{136}{15} &\mbox{}\\ \end{array} $$ Since both paths give different values, the field ${\bf F}(x, y) = \langle xy, x^2 y^2 \rangle$ is not path independent.

For the parabolic path $C_1,$ we will parameterize the curve as $${\bf r}_1(t)=\left \langle t,\frac{1}{2}t^2 \right\rangle$$ over $0\leq t\leq 2$ and for the straight-line path we will parameterize as $${\bf r}_2(t)=\left \langle t,t \right\rangle$$ over $0\leq t\leq 2.$
Then $$ \begin{array}{lll} \displaystyle \int_{C_1} {\bf F} \cdot d{\bf r}_1&\displaystyle=\int_{0}^{2} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}_1}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2} \left\langle x(t)y(t), x(t)^2 y(t)^2 \rangle \cdot \langle 1,t \right\rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\left\langle t\cdot \frac{1}{2}t^2, t^2 \left(\frac{1}{2}t^2\right)^2 \right\rangle \cdot \langle 1,t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\left\langle \frac{1}{2}t^3, \frac{1}{4}t^6 \right\rangle \cdot \langle 1,t \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\frac{1}{2}t^3+ \frac{1}{4}t^7 \,dt &\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{1}{8}t^4+ \frac{1}{32}t^8\right]_{0}^{2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{8}(2)^4+ \frac{1}{32}(2)^8 &\mbox{}\\ \displaystyle &\displaystyle= 10 &\mbox{}\\ \end{array} $$ and $$ \begin{array}{lll} \displaystyle \int_{C_2} {\bf F} \cdot d{\bf r}_2&\displaystyle=\int_{0}^{2} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}_2}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2} \langle x(t)y(t), x(t)^2 y(t)^2 \rangle \cdot \langle 1,1 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\left\langle t\cdot t, t^2 \cdot t^2 \right\rangle \cdot \langle 1,1 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\left\langle t^2, t^4\right\rangle \cdot \langle 1,1 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2} t^2+t^4 \,dt &\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{1}{3}t^3+ \frac{1}{5}t^5\right]_{0}^{2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}(2)^3+ \frac{1}{5}(2)^5 &\mbox{}\\ \displaystyle &\displaystyle= \frac{136}{15} &\mbox{}\\ \end{array} $$ Since both paths give different values, the field ${\bf F}(x, y) = \langle xy, x^2 y^2 \rangle$ is not path independent.
What Do You Think?
Is the property of being conservative equivalent to being path independent?
That is, is it also true that $$\mbox{Path Independent}\implies \mbox{Conservative}?$$
Answer: Not quite.
We must first introduce some topological restrictions to the domain of ${\bf F}$ before we can get a statement of logical equivalence.
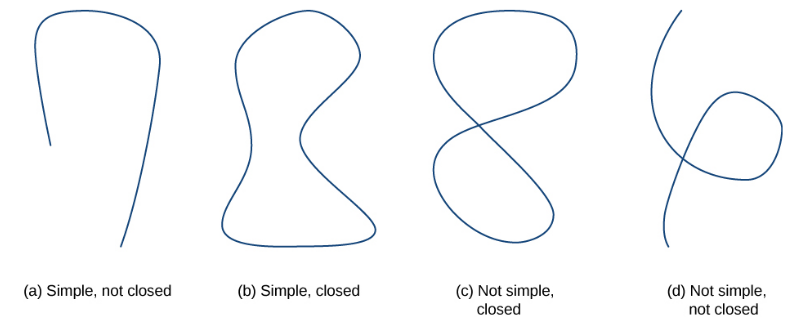
Closed Curves and Simple Curves
Curve $C$ is a closed curve if there is a parameterization ${\bf r}(t)$ for $a \leq t \leq b$ of $C$ such that the parameterization traverses the curve exactly once and ${\bf r}(a) = {\bf r}(b).$
Curve $C$ is a simple curve if $C$ does not cross itself. That is, $C$ is simple if there exists a parameterization ${\bf r}(t)$ for $a \leq t \leq b$ of $C$ such that ${\bf r}$ is one-to-one over $(a, b)$ allowing for the possibility that ${\bf r}(a) = {\bf r}(b),$ i.e., the simple curve is also closed.
Connected Regions and Simply Connected Regions
A region $D$ is a connected region if, for any two points $P_1$ and $P_2,$ there is a path from $P_1$ to $P_2$ with a trace contained entirely inside $D.$
A region $D$ is a simply connected region if $D$ is connected for any simple closed curve $C$ that lies inside $D,$ and curve $C$ can be shrunk continuously to a point while staying entirely inside $D.$
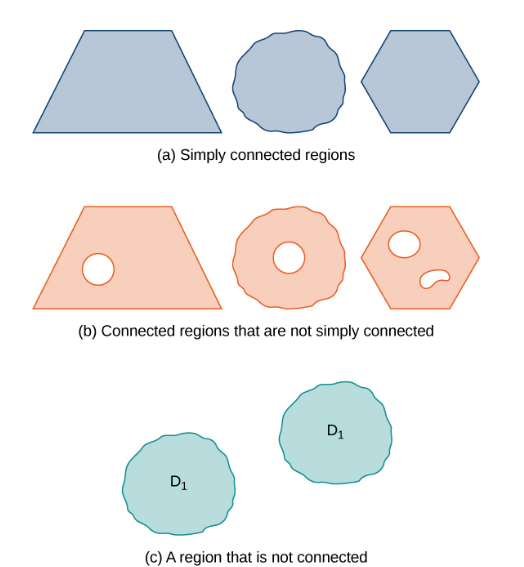
The Gist: In two dimensions, a region is simply connected if it is connected and has no holes.
Theorem
If ${\bf F}$ is a continuous vector field that is path independent and the domain $D$ of ${\bf F}$ is open and connected, then ${\bf F}$ is conservative.
Corollary
If ${\bf F}$ is a continuous vector field in an open and connected domain $D,$ then ${\bf F}$ is path independent if and only if ${\bf F}$ is conservative.
Conservative Tests
As we've seen, not all fields are conservative.
In other words, no matter how hard we try, we won't find a potential function which means the FTLI doesn't apply.
At this point, we must develop tools for understanding when a field is conservative or not.
If a field turns out not to be conservative, do not fear! We will develop further techniques!
The Cross-Partial Test for Conservative Fields: 2-Space
Let ${\bf F} = \langle P, Q \rangle$ be a vector field on an open, simply connected region $D.$
Then, $ \displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} $ (the $\mbox{CPP}$ holds!) throughout $D$ if and only if ${\bf F}$ is conservative.
Example
Determine whether ${\bf F}(x, y) = \langle P,Q \rangle=\langle \sin x \cos y, \cos x \sin y \rangle$ is conservative.
We see that
$$
\frac{\partial P}{\partial y}=-\sin x \sin y=\frac{\partial Q}{\partial x}
$$
(the $\mbox{CPP}$ holds!) on $\mathbb{R}^2.$
Since $\mathbb{R}^2$ is a simply connected region, we conclude by The Cross-Partial Test for Conservative Fields that ${\bf F}(x, y) = \langle \sin x \cos y, \cos x \sin y \rangle$ is a conservative field.
Since $\mathbb{R}^2$ is a simply connected region, we conclude by The Cross-Partial Test for Conservative Fields that ${\bf F}(x, y) = \langle \sin x \cos y, \cos x \sin y \rangle$ is a conservative field.
The Cross-Partial Test for Conservative Fields: 3-Space
Let ${\bf F} = \langle P, Q, R \rangle$ be a vector field on an open, simply connected region $D.$
Then, $$ \begin{array}{ll} \displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}, &\\ \displaystyle \frac{\partial P}{\partial z} = \frac{\partial R}{\partial x}, &\mbox{ and }\\ \displaystyle \frac{\partial Q}{\partial z} = \frac{\partial R}{\partial y} &\\ \end{array} $$ (the $\mbox{CPP}$ holds!) throughout $D$ if and only if ${\bf F}$ is conservative.
Example
Determine whether ${\bf F}(x, y, z)=\langle P,Q,R \rangle = \langle 2xy, x^2+2yz, y^2 \rangle$ is conservative.
If the field is conservative, find a potential function $f.$
We see that
$$
\begin{array}{ll}
\displaystyle \frac{\partial P}{\partial y}= 2x =\frac{\partial Q}{\partial x}, &\\
\displaystyle \frac{\partial P}{\partial z}= 0 =\frac{\partial R}{\partial x}, &\mbox{ and }\\
\displaystyle \frac{\partial Q}{\partial z}= 2y =\frac{\partial R}{\partial y} &\\
\end{array}
$$
(the $\mbox{CPP}$ holds!) on $\mathbb{R}^3.$
Since $\mathbb{R}^3$ is a simply connected region, we conclude by The Cross-Partial Test for Conservative Fields that ${\bf F}(x,y,z) = \langle 2xy, x^2+2yz, y^2 \rangle$ is a conservative field.
Now, we shall find a potential function $f$ which satisfies $$ \begin{array}{lll} \displaystyle &\displaystyle \frac{\partial f}{\partial x}=2xy &\mbox{}\\ \displaystyle &\displaystyle\frac{\partial f}{\partial y}=x^2+2yz &\mbox{}\\ \displaystyle &\displaystyle\frac{\partial f}{\partial z}=y^2 &\mbox{}\\ \end{array} $$ Computing a "partial" antiderivative with respect to $x,$ we have $$ f(x,y,z)=x^2y+h(y,z) $$ Then, using the above, we have that $$ \frac{\partial f}{\partial y}=x^2+\frac{\partial h}{\partial y} $$ Then from the original equation, $\displaystyle\frac{\partial f}{\partial y}=x^2+2yz,$ we have $$ x^2+\frac{\partial h}{\partial y}=\frac{\partial f}{\partial y}=x^2+2yz $$ so that $$ \frac{\partial h}{\partial y}=2yz $$ After another partial integration, $$ h(y,z)=y^2z+g(x,z) $$ Consequently, so far, we have that $$ f(x,y,z)=x^2y+y^2z+g(x,z) $$ We now compare the partials with respect to $z.$ $$ y^2+\frac{\partial g}{\partial z}=\frac{\partial f}{\partial z}=y^2 $$ That is, $$ \frac{\partial g}{\partial z}=0 $$ so that $g(x,z)=C$ is a constant.
We conclude that $f(x,y,z)=x^2y+y^2z+C.$
To verify that $f$ is indeed a potential function, we compute $\nabla f.$ $$ \begin{array}{lll} \displaystyle \nabla f&\displaystyle=\left\langle \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \right\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left\langle \frac{\partial }{\partial x}(x^2y+y^2z+C),\frac{\partial }{\partial y}(x^2y+y^2z+C),\frac{\partial }{\partial z}(x^2y+y^2z+C) \right\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left\langle 2xy,x^2+2yz,y^2 \right\rangle &\mbox{}\\ \displaystyle &\displaystyle={\bf F}(x,y,z) &\mbox{}\\ \end{array} $$
Since $\mathbb{R}^3$ is a simply connected region, we conclude by The Cross-Partial Test for Conservative Fields that ${\bf F}(x,y,z) = \langle 2xy, x^2+2yz, y^2 \rangle$ is a conservative field.
Now, we shall find a potential function $f$ which satisfies $$ \begin{array}{lll} \displaystyle &\displaystyle \frac{\partial f}{\partial x}=2xy &\mbox{}\\ \displaystyle &\displaystyle\frac{\partial f}{\partial y}=x^2+2yz &\mbox{}\\ \displaystyle &\displaystyle\frac{\partial f}{\partial z}=y^2 &\mbox{}\\ \end{array} $$ Computing a "partial" antiderivative with respect to $x,$ we have $$ f(x,y,z)=x^2y+h(y,z) $$ Then, using the above, we have that $$ \frac{\partial f}{\partial y}=x^2+\frac{\partial h}{\partial y} $$ Then from the original equation, $\displaystyle\frac{\partial f}{\partial y}=x^2+2yz,$ we have $$ x^2+\frac{\partial h}{\partial y}=\frac{\partial f}{\partial y}=x^2+2yz $$ so that $$ \frac{\partial h}{\partial y}=2yz $$ After another partial integration, $$ h(y,z)=y^2z+g(x,z) $$ Consequently, so far, we have that $$ f(x,y,z)=x^2y+y^2z+g(x,z) $$ We now compare the partials with respect to $z.$ $$ y^2+\frac{\partial g}{\partial z}=\frac{\partial f}{\partial z}=y^2 $$ That is, $$ \frac{\partial g}{\partial z}=0 $$ so that $g(x,z)=C$ is a constant.
We conclude that $f(x,y,z)=x^2y+y^2z+C.$
To verify that $f$ is indeed a potential function, we compute $\nabla f.$ $$ \begin{array}{lll} \displaystyle \nabla f&\displaystyle=\left\langle \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \right\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left\langle \frac{\partial }{\partial x}(x^2y+y^2z+C),\frac{\partial }{\partial y}(x^2y+y^2z+C),\frac{\partial }{\partial z}(x^2y+y^2z+C) \right\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left\langle 2xy,x^2+2yz,y^2 \right\rangle &\mbox{}\\ \displaystyle &\displaystyle={\bf F}(x,y,z) &\mbox{}\\ \end{array} $$
Recall These Examples
(a) Show that the field ${\bf F}(x,y)=\langle y,-x \rangle$ is not conservative.
(b) Show that the field ${\bf F}(x,y,z)=\langle x,y,xyz \rangle$ is not conservative.
(a) To show that ${\bf F}(x,y)=\langle y,-x \rangle=\langle P,Q \rangle$ is not conservative, we show that the $\mbox{CPP}$ fails.
That is, we will demonstrate that $$ \frac{\partial P}{\partial y}\neq \frac{\partial Q}{\partial x} $$ Computing both these derivatives, we have $$ \frac{\partial P}{\partial y}=\frac{\partial }{\partial y}y=1 $$ and $$ \frac{\partial Q}{\partial x}=\frac{\partial }{\partial x}(-x)=-1 $$ Thus, $$ \frac{\partial P}{\partial y}\neq \frac{\partial Q}{\partial x} $$ and the $\mbox{CPP}$ fails.
We conclude that the field ${\bf F}(x,y)=\langle y,-x \rangle$ is not conservative.
(b) To show that the the $\mbox{CPP}$ holds in three dimensions, ALL $3$ of the equations below must hold. $$ \begin{array}{l} \displaystyle \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\\ \displaystyle \frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}\\ \displaystyle \frac{\partial R}{\partial x}=\frac{\partial P}{\partial z} \end{array} $$ Thus, to show that the $\mbox{CPP}$ fails in $3$ dimensions, all we need to do is show that just $1$ is these equations doesn't hold for the field ${\bf F}(x,y,z)=\langle x,y,xyz \rangle=\langle P,Q,R \rangle.$
Here, it turns out that the first equation does hold since $$ \frac{\partial P}{\partial y}=0=\frac{\partial Q}{\partial x} $$ On the other hand, the second equation does not hold since $$ \frac{\partial Q}{\partial z}=0 $$ and $$ \frac{\partial R}{\partial y}=\frac{\partial }{\partial y}xyz=xz $$ Thus, $\displaystyle \frac{\partial Q}{\partial z}\neq \frac{\partial R}{\partial y}$ and the $\mbox{CPP}$ fails.
We conclude that the field ${\bf F}(x,y,z)=\langle x,y,xyz \rangle$ is not conservative.
Note: We could have also shown that the third equation of the $\mbox{CPP}$ doesn't hold.
That is, we will demonstrate that $$ \frac{\partial P}{\partial y}\neq \frac{\partial Q}{\partial x} $$ Computing both these derivatives, we have $$ \frac{\partial P}{\partial y}=\frac{\partial }{\partial y}y=1 $$ and $$ \frac{\partial Q}{\partial x}=\frac{\partial }{\partial x}(-x)=-1 $$ Thus, $$ \frac{\partial P}{\partial y}\neq \frac{\partial Q}{\partial x} $$ and the $\mbox{CPP}$ fails.
We conclude that the field ${\bf F}(x,y)=\langle y,-x \rangle$ is not conservative.
(b) To show that the the $\mbox{CPP}$ holds in three dimensions, ALL $3$ of the equations below must hold. $$ \begin{array}{l} \displaystyle \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\\ \displaystyle \frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}\\ \displaystyle \frac{\partial R}{\partial x}=\frac{\partial P}{\partial z} \end{array} $$ Thus, to show that the $\mbox{CPP}$ fails in $3$ dimensions, all we need to do is show that just $1$ is these equations doesn't hold for the field ${\bf F}(x,y,z)=\langle x,y,xyz \rangle=\langle P,Q,R \rangle.$
Here, it turns out that the first equation does hold since $$ \frac{\partial P}{\partial y}=0=\frac{\partial Q}{\partial x} $$ On the other hand, the second equation does not hold since $$ \frac{\partial Q}{\partial z}=0 $$ and $$ \frac{\partial R}{\partial y}=\frac{\partial }{\partial y}xyz=xz $$ Thus, $\displaystyle \frac{\partial Q}{\partial z}\neq \frac{\partial R}{\partial y}$ and the $\mbox{CPP}$ fails.
We conclude that the field ${\bf F}(x,y,z)=\langle x,y,xyz \rangle$ is not conservative.
Note: We could have also shown that the third equation of the $\mbox{CPP}$ doesn't hold.
Summary of Results
A field ${\bf F}$ is conservative means that ${\bf F}=\nabla f$ for some potential function $f.$
If $D$ is any domain, then $$ \begin{array}{lll} \displaystyle {\bf F} \mbox{ Conservative } \implies {\bf F} \mbox{ Path Independent}&\displaystyle &\mbox{}\\ \displaystyle {\bf F} \mbox{ Conservative } \implies \displaystyle \oint_{C} {\bf F} \cdot d{\bf r} =0 \mbox{ for any closed curve $C$ in $D$}&\displaystyle &\mbox{}\\ \displaystyle {\bf F} \mbox{ Conservative } \implies \mbox{The CPP holds in $D$}&\displaystyle &\mbox{}\\ {\bf F} \mbox{ Path Independent}\iff \displaystyle \oint_{C} {\bf F} \cdot d{\bf r} =0 \mbox{ for any closed curve $C$ in $D$}\\ \end{array} $$ If $D$ is any open and connected domain, then $$ \begin{array}{lll} \displaystyle {\bf F} \mbox{ Conservative } \iff {\bf F} \mbox{ Path Independent}&\displaystyle &\mbox{}\\ \displaystyle {\bf F} \mbox{ Conservative } \iff \displaystyle \oint_{C} {\bf F} \cdot d{\bf r} =0 \mbox{ for any closed curve $C$ in $D$}&\displaystyle &\mbox{}\\ \end{array} $$ If $D$ is any open and simply connected domain, then $$ \begin{array}{lll} \displaystyle {\bf F} \mbox{ Conservative } \iff \mbox{The CPP holds in $D$}&\displaystyle &\mbox{}\\ \end{array} $$
The Contrapositive
The contrapositive of the statement $P\implies Q$ is $\sim Q \implies \sim P.$
In other words, if you can show that $\sim Q \implies \sim P,$ then you've also shown that $P\implies Q.$
The way to use the results $$ \begin{array}{lll} \displaystyle {\bf F} \mbox{ Conservative } \implies {\bf F} \mbox{ Path Independent}&\displaystyle &\mbox{}\\ \displaystyle {\bf F} \mbox{ Conservative } \implies \displaystyle \oint_{C} {\bf F} \cdot d{\bf r} =0 \mbox{ for any closed curve $C$ in $D$}&\displaystyle &\mbox{}\\ \displaystyle {\bf F} \mbox{ Conservative } \implies \mbox{The CPP holds in $D$}&\displaystyle &\mbox{}\\ \end{array} $$ to show a field ${\bf F}$ is not conservative is to show the contrapositive. $$ \begin{array}{lll} {\bf F} \mbox{ Not Path Independent} \displaystyle \implies {\bf F} \mbox{ NOT Conservative }&\displaystyle &\mbox{}\\ \displaystyle \oint_{C} {\bf F} \cdot d{\bf r} \neq 0 \mbox{ for some closed curve $C$ in $D$}\implies \displaystyle {\bf F} \mbox{ NOT Conservative}&\displaystyle &\mbox{}\\ \mbox{The CPP DOES NOT hold in $D$} \implies \displaystyle {\bf F} \mbox{ NOT Conservative }&\displaystyle &\mbox{}\\ \end{array} $$
What Do You Think?
Is the field $\displaystyle {\bf F}(x, y)=\langle P,Q \rangle = \left\langle\frac{y}{x^2+y^2},\frac{-x}{x^2+y^2}\right \rangle$ conservative?
Whoa There, Tiger!
It's soooooooooooooooo easy to be overzealous with an awesome theorem.
For $\displaystyle {\bf F}(x, y)=\langle P,Q \rangle = \left\langle\frac{y}{x^2+y^2},\frac{-x}{x^2+y^2}\right \rangle,$ we can verify that $\displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}.$
Yet it's not difficult to show that ${\bf F}$ is not conservative!
What happened?
First we verify that $\displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$ by observing that
$$
\begin{array}{lll}
\displaystyle \frac{\partial P}{\partial y}&\displaystyle=\frac{\partial }{\partial y}\frac{y}{x^2+y^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{(x^2+y^2)\cdot 1-y\cdot 2y}{(x^2+y^2)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{x^2+y^2-2y^2}{(x^2+y^2)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{x^2-y^2}{(x^2+y^2)^2} &\mbox{}\\
\end{array}
$$
and
$$
\begin{array}{lll}
\displaystyle \frac{\partial Q}{\partial x}&\displaystyle=\frac{\partial }{\partial x}\frac{-x}{x^2+y^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{(x^2+y^2)\cdot (-1)-(-x)\cdot 2x}{(x^2+y^2)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-x^2-y^2+2x^2}{(x^2+y^2)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{x^2-y^2}{(x^2+y^2)^2} &\mbox{}\\
\end{array}
$$
are the same, so the $\mbox{CPP}$ holds.
BUT we also observe that $\displaystyle \oint_{C} {\bf F} \cdot d{\bf r}\neq 0$ around the unit circle oriented counterclockwise (positively).
Letting ${\bf r}(t)=\langle \cos t, \sin t\rangle$ over $0 \leq t \leq 2\pi,$ we have ${\bf r}'(t)=\langle -\sin t, \cos t\rangle$ so that $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_0^{2\pi} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\frac{y(t)}{x(t)^2+y(t)^2},\frac{-x(t)}{x(t)^2+y(t)^2}\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\frac{\sin t}{\cos^2 t+\sin^2 t},\frac{-\cos t}{\cos^2 t+\sin^2 t}\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\sin t,-\cos t\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -\sin^2 t-\cos^2 t \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -1 \,dt &\mbox{}\\ \displaystyle &\displaystyle=-2\pi &\mbox{}\\ \end{array} $$ We may now invoke the contrapositive statement $$ \displaystyle \oint_{C} {\bf F} \cdot d{\bf r} \neq 0 \mbox{ for some closed curve $C$ in $D$}\implies \displaystyle {\bf F} \mbox{ NOT Conservative} $$ Thus, the above calculation shows that ${\bf F}$ is not a conservative field.
So what happened?!
Well, I'm sooooooo glad you asked!
Notice that the curve $C$ is in a domain that is NOT simply connected since ${\bf F}$ is undefined at the origin.
Thus, there is a tiny pinhole at $(0,0)$ which makes the domain of ${\bf F}$ NOT simply connected.
In other words, we can't continuously shrink $C$ down to a point without the origin interfering.
This is why satisfying the $\mbox{CPP}$ was not enough to guarantee that ${\bf F}$ is conservative.
BUT we also observe that $\displaystyle \oint_{C} {\bf F} \cdot d{\bf r}\neq 0$ around the unit circle oriented counterclockwise (positively).
Letting ${\bf r}(t)=\langle \cos t, \sin t\rangle$ over $0 \leq t \leq 2\pi,$ we have ${\bf r}'(t)=\langle -\sin t, \cos t\rangle$ so that $$ \begin{array}{lll} \displaystyle \oint_{C} {\bf F} \cdot d{\bf r}&\displaystyle=\int_0^{2\pi} {\bf F}({\bf r}(t)) \cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\frac{y(t)}{x(t)^2+y(t)^2},\frac{-x(t)}{x(t)^2+y(t)^2}\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\frac{\sin t}{\cos^2 t+\sin^2 t},\frac{-\cos t}{\cos^2 t+\sin^2 t}\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} \left\langle\sin t,-\cos t\right \rangle \cdot \langle -\sin t, \cos t\rangle \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -\sin^2 t-\cos^2 t \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{2\pi} -1 \,dt &\mbox{}\\ \displaystyle &\displaystyle=-2\pi &\mbox{}\\ \end{array} $$ We may now invoke the contrapositive statement $$ \displaystyle \oint_{C} {\bf F} \cdot d{\bf r} \neq 0 \mbox{ for some closed curve $C$ in $D$}\implies \displaystyle {\bf F} \mbox{ NOT Conservative} $$ Thus, the above calculation shows that ${\bf F}$ is not a conservative field.
So what happened?!
Well, I'm sooooooo glad you asked!
Notice that the curve $C$ is in a domain that is NOT simply connected since ${\bf F}$ is undefined at the origin.
Thus, there is a tiny pinhole at $(0,0)$ which makes the domain of ${\bf F}$ NOT simply connected.
In other words, we can't continuously shrink $C$ down to a point without the origin interfering.
This is why satisfying the $\mbox{CPP}$ was not enough to guarantee that ${\bf F}$ is conservative.
Food for Thought
The gradient operator $\nabla$ is a generalized derivative. In fact, for any multivariable functions $f$ and $g,$ the following properties hold $$ \begin{array}{l} \nabla (f+g)=\nabla f + \nabla g\\\\ \nabla (cf)=c\nabla f\\\\ \nabla (fg)=g\nabla f+f\nabla g\\\\ \displaystyle \nabla\left(\frac{f}{g}\right)=\frac{g\nabla f-f\nabla g}{g^2}\\\\ \end{array} $$
Scenic Vista: The FTLI is a generalization of the Fundamental Theorem of Calculus. $$ \begin{array}{ll} \displaystyle \int_{(x_1,y_1,z_1)}^{(x_2,y_2,z_2)} \nabla f \cdot {\bf T} \,ds=\int_{(x_1,y_1,z_1)}^{(x_2,y_2,z_2)} \left(\frac{\partial f}{\partial x}\,dx+\frac{\partial f}{\partial y}\,dy+\frac{\partial f}{\partial z}\,dz\right) = f(x_2,y_2,z_2)-f(x_1,y_1,z_1)& \mbox{}\\ \displaystyle \int_{(x_1,y_1)}^{(x_2,y_2)} \nabla f \cdot {\bf T} \, ds=\int_{(x_1,y_1)}^{(x_2,y_2)} \left(\frac{\partial f}{\partial x}\,dx+\frac{\partial f}{\partial y}\,dy\right) = f(x_2,y_2)-f(x_1,y_1)& \mbox{}\\ \displaystyle \int_{x_1}^{x_2} \nabla f \cdot {\bf i} \, dx=\int_{x_1}^{x_2} \frac{df}{dx}\,dx= f(x_2)-f(x_1) & \mbox{}\\ \end{array} $$