Double an triple integrals are computed over regions of 2-space and 3-space.
Line integrals are calculated along curves.
As we'll soon see, line and flux integrals further generalize integrals of single-variable functions.
Opening Act
Scalar Line Integrals
Scalar Line Integrals
Scalar Line Integrals: Integrating Along a Curve
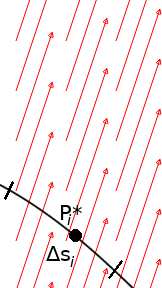
Scalar line integration takes place along a curve instead of being stuck to an axis. The generalized Riemann sum $\displaystyle \sum_{i=1}^{n}f(P_i^*)\,\Delta s_i$ estimates the line integral.
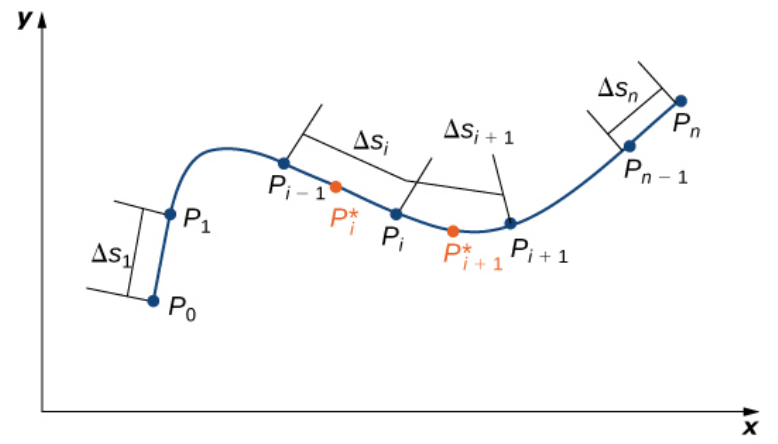
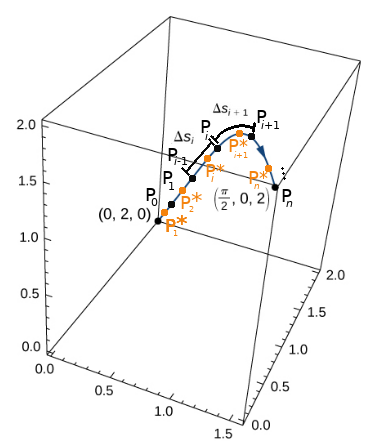
Scalar Line Integrals in 2-Space
For a two-variable function, $f(x,y),$ the scalar line integral is the area of the vertical sheet under the surface $z=f(x,y)$ which is approximately equal to $\displaystyle \sum_{i=1}^{n}f(P_i^*)\,\Delta s_i=\sum_{i=1}^{n}f(x_i^*,y_i^*)\,\Delta s_i.$
Scalar Line Integrals for Curves in 2-Space
Let $f(x,y)$ be a function with a domain that includes the smooth curve $C$ that is parameterized by ${\bf r}(t) = \langle x(t), y(t) \rangle$ for $a \leq t \leq b.$ The scalar line integral of $f$ along $C$ is $$\displaystyle \int_C f(x,y)\, ds=\lim_{n \rightarrow \infty}\sum_{i=1}^{n}f(P_i^*)\,\Delta s_i=\lim_{n \rightarrow \infty}\sum_{i=1}^{n}f(x_i^*,y_i^*)\,\Delta s_i.$$
Scalar Line Integrals for Curves in 3-Space
Let $f(x,y,z)$ be a function with a domain that includes the smooth curve $C$ that is parameterized by ${\bf r}(t) = \langle x(t), y(t), z(t) \rangle$ for $a \leq t \leq b.$ The scalar line integral of $f$ along $C$ is $$\displaystyle \int_C f(x,y,z)\, ds=\lim_{n \rightarrow \infty}\sum_{i=1}^{n}f(P_i^*)\,\Delta s_i=\lim_{n \rightarrow \infty}\sum_{i=1}^{n}f(x_i^*,y_i^*,z_i^*)\,\Delta s_i$$
Fact: The 3-D scalar line integral doesn't have as straightforward an interpretation as the 2-D version.
However, conceptually, all scalar line integrals are still quite similar to the single-variable definition of integration along an interval.
In fact...
Note how the definition of the scalar line integral reduces to the definition of a single-variable integral on an interval $[a,b]:$ letting $g(x,y,z)$ be a $3$ variable function, we can take $f(x)=g(x,0,0)$ with parameterization $x(t)=t,$ $y(t)=0,$ $z(t)=0,$ $a \leq t \leq b.$ Then, $$ \begin{array}{lll} \displaystyle \int_C g(x,y,z)\, ds&=\displaystyle \lim_{n \rightarrow \infty}\sum_{i=1}^{n}g(P_i^*)\,\Delta s_i&\\ &=\displaystyle \lim_{n \rightarrow \infty}\sum_{i=1}^{n}g(x_i^*,y_i^*,z_i^*)\,\Delta s_i&\\ &=\displaystyle \lim_{n \rightarrow \infty}\sum_{i=1}^{n}g(x_i^*,0,0)\,\Delta x_i&\mbox{since $C$ is the set of points in $[a,b]$}\\ &=\displaystyle \lim_{n \rightarrow \infty}\sum_{i=1}^{n}f(x_i^*)\,\Delta x_i&\mbox{since $f(x)=g(x,0,0).$}\\ &=\displaystyle \int_a^b f(x)\, dx. \end{array} $$
Evaluating Scalar Line Integrals
Using the definition can be quite cumbersome, so it would be nice to have a method for dealing with line integrals that is easier to use. We shall develop a method that involves a parameterization ${\bf r}(t)$ of of $C.$
We first recall that for a curve ${\bf r}(t),$ the arc length, $s,$ of a vector-valued function ${\bf r}(t)$ over the time interval $a \leq t \leq b$ is given by $$ s=\int_{a}^{b}\Vert{\bf r}'(t)\Vert\,dt $$ which allows us to define arc length as a function of $t$ $$ s(t)=\int_{a}^{t}\Vert{\bf r}'(\tau)\Vert\,d\tau $$ for $t\geq a.$
Evaluating Scalar Line Integrals
We note that $\displaystyle \Delta s_i = \int_{t_{i-1}}^{t_i}\Vert {\bf r}'(t)\Vert \,dt\approx\Vert {\bf r}'(t_i^*)\Vert\, (t_i-t_{i-1})= \Vert {\bf r}'(t_i^*)\Vert\, \Delta t_i$
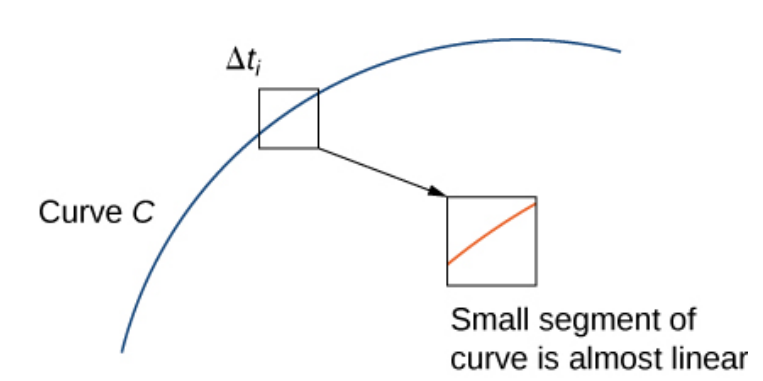
In the limit we have...
Evaluating Scalar Line Integrals
Let $f$ be a continuous function with a domain that includes the smooth curve $C$ with parameterization ${\bf r}(t)$ on $a \leq t \leq b.$ Then $$\displaystyle \int_C f\, ds=\int_a^b f({\bf r}(t))\, \Vert {\bf r}'(t)\Vert \,dt$$
Special Note
Since $$ s(t)=\int_{a}^{t}\Vert{\bf r}'(\tau)\Vert\,d\tau $$ we know that $$ \frac{ds}{dt}=\Vert{\bf r}'(t)\Vert $$ so that $$ds=\Vert{\bf r}'(t)\Vert \, dt$$ which gives $$\displaystyle \int_C f\, ds=\int_a^b f({\bf r}(t))\, \Vert {\bf r}'(t)\Vert \,dt$$
Since $\Vert {\bf r}'(t)\Vert=\sqrt{(x'(t))^2+(y'(t))^2}$ in 2-space and $\Vert {\bf r}'(t)\Vert=\sqrt{(x'(t))^2+(y'(t))^2+(z'(t))^2}$ in 3-space, we have the following formulas...
Evaluating Scalar Line Integrals
In 2-Space $$\displaystyle \int_C f(x,y)\, ds=\int_a^b f({\bf r}(t))\, \Vert {\bf r}'(t)\Vert \,dt=\int_a^b f(x(t),y(t))\,\sqrt{(x'(t))^2+(y'(t))^2} \,dt$$
In 3-Space $$\displaystyle \int_C f(x,y,z)\, ds=\int_a^b f({\bf r}(t))\, \Vert {\bf r}'(t)\Vert \,dt=\int_a^b f(x(t),y(t),z(t))\,\sqrt{(x'(t))^2+(y'(t))^2+(z'(t))^2} \,dt$$
Example
Find the value of $\displaystyle \int_C (x + y)\, ds,$ where $C$ is the curve parameterized by $x = t,$ $y = t,$ and $0 \leq t \leq 1.$
We first note that ${\bf r}(t)=\langle t,t\rangle$ so that ${\bf r}'(t)=\langle 1,1\rangle$
Then $\Vert {\bf r}'(t)=\sqrt{2}$ which gives $$ \begin{array}{lll} \displaystyle \int_C (x + y)\, ds&\displaystyle=\int_0^1 f({\bf r}(t))\, \Vert {\bf r}'(t)\Vert \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^1 (t+t) \, \sqrt{2} \,dt &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{2}\int_0^1 2t \, \,dt &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{2}[t^2]_0^1 &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{2}\cdot 1 &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{2} &\mbox{}\\ \end{array} $$
Then $\Vert {\bf r}'(t)=\sqrt{2}$ which gives $$ \begin{array}{lll} \displaystyle \int_C (x + y)\, ds&\displaystyle=\int_0^1 f({\bf r}(t))\, \Vert {\bf r}'(t)\Vert \,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^1 (t+t) \, \sqrt{2} \,dt &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{2}\int_0^1 2t \, \,dt &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{2}[t^2]_0^1 &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{2}\cdot 1 &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{2} &\mbox{}\\ \end{array} $$
Application: Mass from Density
Calculate the mass of a wire in the shape of a curve $C$ parameterized by ${\bf r}(t)=\langle t, 2 \cos t, 2 \sin t \rangle$ for $\displaystyle 0 \leq t \leq \frac{\pi}{2}$ with a density function given by $\rho(x, y, z) = e^x + yz$ $\mbox{kg/m}$
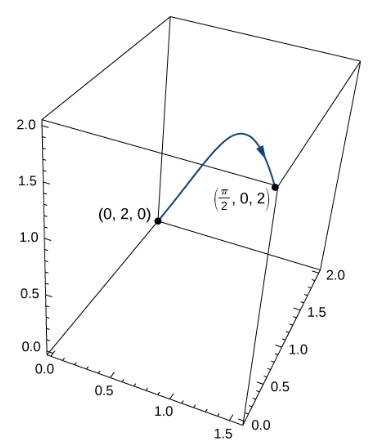
We break up the wire into $n$ small arcs of length $\Delta s_i.$
The mass of the piece $\Delta s_i$ is approximately given by $$ \rho(P_i^*) \Delta s_i $$ Summing over all the arcs, the approximate mass of the wire is $$ \sum_{i=1}^{n}\rho(P_i^*)\,\Delta s_i $$
In the limit, the mass of the wire is given by the line integral
$$
\int_C \rho(x,y,z)\, ds
$$
Thus, to find the mass of the wire in question, we must evaluate the line integral
$$
\int_C e^x +yz \, ds
$$
With ${\bf r}(t)=\langle t, 2 \cos t, 2 \sin t \rangle$ we have ${\bf r}'(t)=\langle 1, -2 \sin t, 2 \cos t \rangle$ so that
$$\Vert {\bf r}'(t)\Vert=\sqrt{ 1^2+(-2 \sin t)^2+ (2 \cos t)^2}=\sqrt{ 1+4\sin^2 t+4\cos^2 t}=\sqrt{1+4}=\sqrt{5}$$
Then
$$
\begin{array}{lll}
\displaystyle \mbox{mass}&\displaystyle= \int_C \rho(x,y,z)\, ds &\mbox{}\\
\displaystyle &\displaystyle= \int_C e^x +yz \, ds &\mbox{}\\
\displaystyle &\displaystyle= \int_a^b \rho({\bf r}(t)) \Vert {\bf r}'(t)\Vert \, dt &\mbox{}\\
\displaystyle &\displaystyle=\int_0^{\pi/2} (e^t +(2\cos t)(2\sin t)) \Vert {\bf r}'(t)\Vert \, dt &\mbox{}\\
\displaystyle &\displaystyle=\int_0^{\pi/2} (e^t +4\cos t \sin t) \sqrt{5} \, dt &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{5}\int_0^{\pi/2} e^t +2\sin (2t) \, dt &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{5}\left[ e^t -\cos (2t) \right]_0^{\pi/2} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{5}\left[ e^{\pi/2} -\cos (\pi)-(e^0 -\cos (2\cdot 0)) \right] &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{5}\left[ e^{\pi/2} -(-1)-(1 -1) \right] &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{5}\left( e^{\pi/2}+1 \right) &\mbox{}\\
\displaystyle &\displaystyle\approx 12.99262241 &\mbox{}\\
\end{array}
$$
The mass of the wire is about $13$ $\mbox{kg}.$
The mass of the piece $\Delta s_i$ is approximately given by $$ \rho(P_i^*) \Delta s_i $$ Summing over all the arcs, the approximate mass of the wire is $$ \sum_{i=1}^{n}\rho(P_i^*)\,\Delta s_i $$
Main Act
Vector Line Integrals
Vector Line Integrals
Recall: The Notion of Work
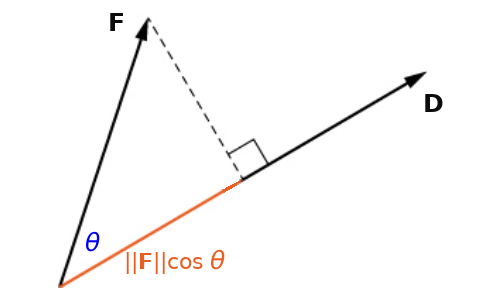
The work $W$ done on an object experiencing a constant force ${\bf F}$ over a displacement ${\bf D}$ is $$ \begin{array}{ll} W&=(\mbox{Magnitude of Force ${\bf F}$ in Direction of ${\bf D}$})(\mbox{Magnitude of ${\bf D}$})\\ &=(\Vert {\bf F} \Vert \cos \theta)\Vert {\bf D} \Vert\\ &=\Vert {\bf F} \Vert \Vert {\bf D} \Vert \cos \theta\\ &={\bf F}\cdot {\bf D}\\ \end{array} $$
Big Question: How do we calculate work when if the force is always changing and motion isn't in a straight line?
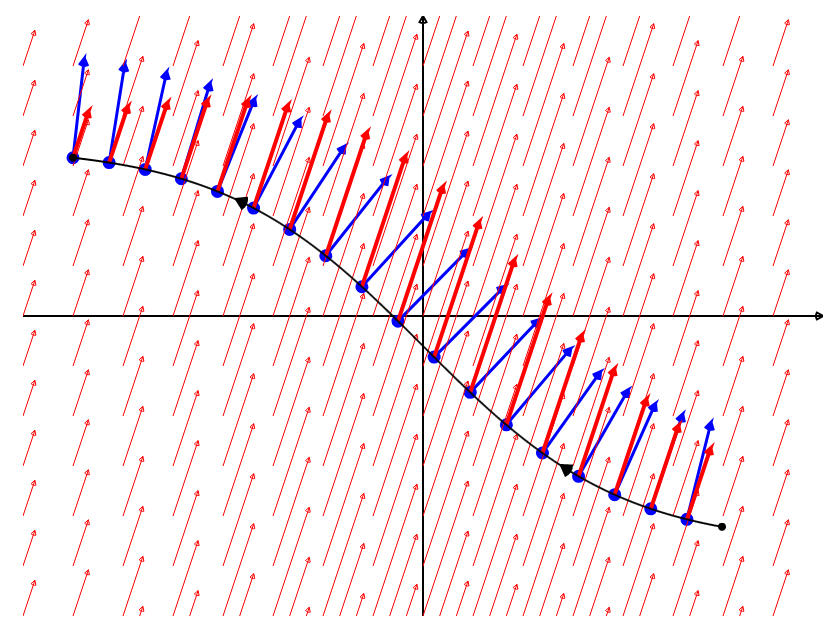
Consider an object moving through a vector field of forces along a curved path like the one below.
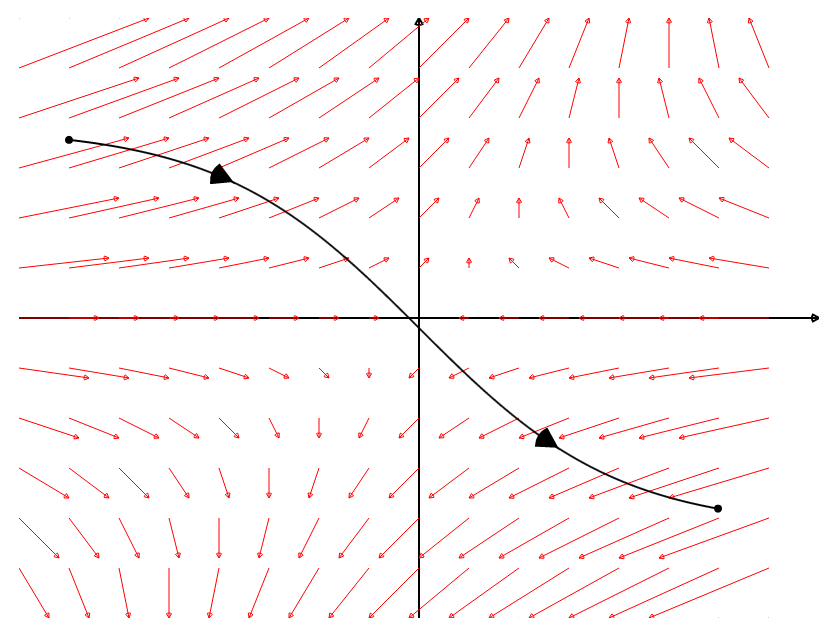
Calculating Work Along a Curve
We break up our curve into a series of sub-arcs small enough so that
1) each sub-arc is approximately linear, and
2) the field ${\bf F}$ is roughly uniform.
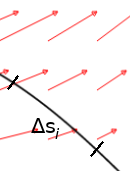
Calculating Work Along a Curve
Choose a point $P_i^*$ on the $i$th sub-arc.
Calculating Work Along a Curve
Let ${\bf T}(P_i^*)$ is the unit tangent vector at the point $P_i^*$ and let ${\bf F}(P_i^*)$ be the force.
Calculating Work Along a Curve
The work required to move a "tiny length" $\Delta s_i$ along the curve is approximately ${\bf F}(P_i^*)\cdot {\bf T}(P_i^*)\, \Delta s_i$
Calculating Work Along a Curve $$\displaystyle \mbox{Work}\approx \sum_{i=1}^{n} {\bf F}(P_i^*)\cdot {\bf T}(P_i^*)\, \Delta s_i$$
Definition: Work Along a Curve
Let ${\bf F}$ be vector field of forces along oriented smooth oriented curve $C.$ Then the work required to traverse $C$ is $$\displaystyle \mbox{Work}=\int_C {\bf F}\cdot{\bf T}\,ds=\lim_{n \rightarrow \infty} \sum_{i=1}^{n} {\bf F}(P_i^*)\cdot {\bf T}(P_i^*)\, \Delta s_i$$
Definition: Vector Line Integral
The vector line integral of vector field ${\bf F}$ along oriented smooth curve $C$ is $$\displaystyle \int_C {\bf F}\cdot{\bf T}\,ds =\lim_{n \rightarrow \infty} \sum_{i=1}^{n} {\bf F}(P_i^*)\cdot {\bf T}(P_i^*)\, \Delta s_i$$ provided the limit exists.
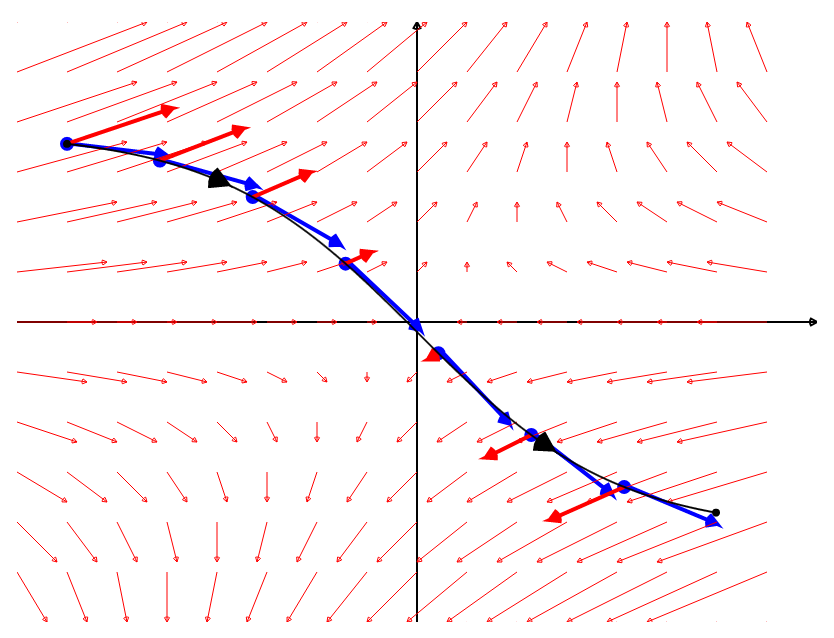
In Words
The line integral is the the limit of the sum of tangential components of a vector field along a curve.
In Three Dimensions: The line-integral definition carries over perfectly to three dimensions. $$\displaystyle \int_C {\bf F}\cdot{\bf T}\,ds =\lim_{n \rightarrow \infty} \sum_{i=1}^{n} {\bf F}(P_i^*)\cdot {\bf T}(P_i^*)\, \Delta s_i$$
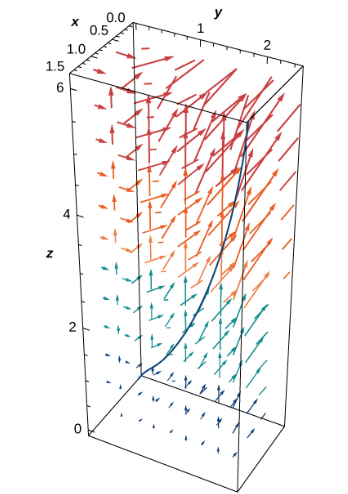
Evaluating Line Integrals
Here we recall two facts about a a curve ${\bf r}(t):$
1) The unit tangent vector ${\bf T}$ is given by $\displaystyle \frac{{\bf r}'(t)}{\Vert{\bf r}'(t)\Vert}.$
2) $ds=\Vert{\bf r}'(t)\Vert \, dt. $
Together, these two facts give: $$\int_C {\bf F}\cdot{\bf T}\,ds=\int_C {\bf F}\cdot \frac{{\bf r}'(t)}{\Vert{\bf r}'(t)\Vert}\Vert{\bf r}'(t)\Vert \, dt=\int_C {\bf F}({\bf r}(t))\cdot{\bf r}'(t)\,dt$$ We now have a much easier way to evaluate line integrals than the definition!
Evaluating Line Integrals
2-Space: Let ${\bf F}=\langle P(x,y),Q(x,y)\rangle$ be a vector field and let $C$ be a smooth curve with parameterization ${\bf r}(t) = \langle x(t), y(t) \rangle$ for $a \leq t \leq b.$ Then, the line integral of ${\bf F}$ along $C$ is $$\int_C {\bf F}\cdot{\bf T}\,ds=\int_C {\bf F}({\bf r}(t))\cdot{\bf r}'(t)\,dt$$
3-Space: Let ${\bf F}=\langle P(x,y,z),Q(x,y,z),R(x,y,z)\rangle$ be a vector field and let $C$ be a smooth curve with parameterization ${\bf r}(t) = \langle x(t), y(t),z(t) \rangle$ for $a \leq t \leq b.$ Then, the line integral of ${\bf F}$ along $C$ is $$\int_C {\bf F}\cdot{\bf T}\,ds=\int_C {\bf F}({\bf r}(t))\cdot{\bf r}'(t)\,dt$$
Example: Let ${\bf F}(x, y) = \langle P(x, y), Q(x, y) \rangle = \langle x^2, -xy \rangle=x^2\,{\bf i}-xy\,{\bf j}$ and let $C$ the quarter unit circle in quadrant $1$ oriented counterclockwise (positively). Calculate the line integral $\displaystyle \int_C {\bf F}\cdot{\bf T}\,ds.$
We parameterize $C$ as ${\bf r}(t)=\langle \cos t, \sin t \rangle$ over $\displaystyle 0 \leq t \leq \frac{\pi}{2}.$
Then ${\bf r}'(t)=\langle -\sin t, \cos t \rangle$ so that $$ \begin{array}{lll} \displaystyle \int_C {\bf F}\cdot{\bf T}\,ds&\displaystyle= \int_a^b {\bf F}({\bf r}(t))\cdot{\bf r}'(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} \langle x(t)^2, -x(t)y(t) \rangle \cdot \langle -\sin t, \cos t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} \langle \cos^2 t, -\cos t \sin t \rangle \cdot \langle -\sin t, \cos t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} (\cos^2 t)(-\sin t)+(-\cos t \sin t)(\cos t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} -2\cos^2 t \sin t \,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} 2\cos^2 t (-\sin t )\,dt&\mbox{set up phantom $u$-substitution}\\ \displaystyle &\displaystyle= \left[ \frac{2}{3}\cos^3 t\right]_0^{\pi/2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\cos^3 \left(\frac{\pi}{2}\right)-\frac{2}{3}\cos^3 (0) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\cdot 0^3-\frac{2}{3}\cdot 1^3 &\mbox{}\\ \displaystyle &\displaystyle= -\frac{2}{3} &\mbox{}\\ \end{array} $$
Then ${\bf r}'(t)=\langle -\sin t, \cos t \rangle$ so that $$ \begin{array}{lll} \displaystyle \int_C {\bf F}\cdot{\bf T}\,ds&\displaystyle= \int_a^b {\bf F}({\bf r}(t))\cdot{\bf r}'(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} \langle x(t)^2, -x(t)y(t) \rangle \cdot \langle -\sin t, \cos t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} \langle \cos^2 t, -\cos t \sin t \rangle \cdot \langle -\sin t, \cos t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} (\cos^2 t)(-\sin t)+(-\cos t \sin t)(\cos t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} -2\cos^2 t \sin t \,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} 2\cos^2 t (-\sin t )\,dt&\mbox{set up phantom $u$-substitution}\\ \displaystyle &\displaystyle= \left[ \frac{2}{3}\cos^3 t\right]_0^{\pi/2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\cos^3 \left(\frac{\pi}{2}\right)-\frac{2}{3}\cos^3 (0) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\cdot 0^3-\frac{2}{3}\cdot 1^3 &\mbox{}\\ \displaystyle &\displaystyle= -\frac{2}{3} &\mbox{}\\ \end{array} $$
A Note About Notation
Since $\displaystyle \int_C {\bf F}\cdot{\bf T}\,ds=\int_C {\bf F}({\bf r}(t))\cdot{\bf r}'(t)\,dt=\int_C {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt,$ we will often use the notation $$\int_C {\bf F}\cdot d{\bf r}$$ for the line integral $\displaystyle \int_C {\bf F}\cdot{\bf T}\,ds.$
Line Integral (Displacement Vector Definition): $\displaystyle \int_C {\bf F}\cdot d{\bf r}=\lim_{n \rightarrow \infty} \sum_{i=1}^{n} {\bf F}(P_i^*)\cdot \Delta {\bf r}_i$
Example (Reverse Orientation): Let ${\bf F}(x, y) = \langle P(x, y), Q(x, y) \rangle = \langle x^2, -xy \rangle=x^2\,{\bf i}-xy\,{\bf j}$ and let $C$ the unit quarter circle in quadrant $1$ oriented clockwise (negatively). Calculate the line integral $\displaystyle \int_{C} {\bf F}\cdot d{\bf r}.$
We parameterize $C$ as ${\bf r}(t)=\left \langle \cos \left(\frac{\pi}{2}-t\right), \sin \left(\frac{\pi}{2}-t\right) \right \rangle=\langle \sin t, \cos t \rangle$
over $\displaystyle 0 \leq t \leq \frac{\pi}{2}.$
Then $\displaystyle \frac{d{\bf r}}{dt} = {\bf r}'(t)=\langle \cos t, -\sin t \rangle$ so that $$ \begin{array}{lll} \displaystyle \int_C {\bf F}\cdot d{\bf r}&\displaystyle= \int_a^b {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} \langle x(t)^2, -x(t)y(t) \rangle \cdot \langle \cos t, -\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} \langle \sin^2 t, -\sin t \cos t \rangle \cdot \langle \cos t, -\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} (\sin^2 t)(\cos t)+(-\sin t \cos t)(-\sin t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} 2\sin^2 t \cos t \,dt&\mbox{}\\ \displaystyle &\displaystyle= \left[ \frac{2}{3}\sin^3 t\right]_0^{\pi/2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\sin^3 \left(\frac{\pi}{2}\right)-\frac{2}{3}\sin^3 (0) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\cdot 1^3-\frac{2}{3}\cdot 0^3 &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3} &\mbox{}\\ \end{array} $$
Then $\displaystyle \frac{d{\bf r}}{dt} = {\bf r}'(t)=\langle \cos t, -\sin t \rangle$ so that $$ \begin{array}{lll} \displaystyle \int_C {\bf F}\cdot d{\bf r}&\displaystyle= \int_a^b {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} \langle x(t)^2, -x(t)y(t) \rangle \cdot \langle \cos t, -\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} \langle \sin^2 t, -\sin t \cos t \rangle \cdot \langle \cos t, -\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} (\sin^2 t)(\cos t)+(-\sin t \cos t)(-\sin t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{\pi/2} 2\sin^2 t \cos t \,dt&\mbox{}\\ \displaystyle &\displaystyle= \left[ \frac{2}{3}\sin^3 t\right]_0^{\pi/2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\sin^3 \left(\frac{\pi}{2}\right)-\frac{2}{3}\sin^3 (0) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3}\cdot 1^3-\frac{2}{3}\cdot 0^3 &\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{3} &\mbox{}\\ \end{array} $$
Reverse Orientation in General
Let $C$ be an oriented curve and let $-C$ denote the same curve but with the orientation reversed. Then, $$\int_{-C} {\bf F}\cdot d{\bf r}=-\int_C {\bf F}\cdot d{\bf r}$$
|  |
| $C$ | $-C$ |
Remark
When thinking of the notion of work, the fact $\displaystyle \int_{-C} {\bf F}\cdot d{\bf r}=-\int_C {\bf F}\cdot d{\bf r}$ makes sense.
Suppose you hike up humbug mountain. The amount of work you do against gravity on the way up is the amount of work gravity does on you on the way back down.
Linearity Properties of Line Integrals
Let ${\bf F}$ and ${\bf G}$ be continuous vector fields with domains that include the oriented smooth curve $C.$ Then, $$ \begin{array}{l} \displaystyle \int_{C} ({\bf F}+{\bf G})\cdot d{\bf r}=\int_{C} {\bf F}\cdot d{\bf r}+\int_{C} {\bf G}\cdot d{\bf r}\\ \displaystyle \int_{C} k{\bf F}\cdot d{\bf r}=k\int_{C} {\bf F}\cdot d{\bf r}\\ \end{array} $$
Yet Another Notation: Scalar Differential Form
Since $\displaystyle \frac{d{\bf r}}{dt}=\frac{dx}{dt}\,{\bf i}+\frac{dy}{dt}\,{\bf j}$ we often use the notation $$ d{\bf r}=dx\,{\bf i}+dy\,{\bf j}=\langle dx,dy \rangle $$ For the field ${\bf F}(x,y)=P(x,y)\,{\bf i}+Q(x,y)\,{\bf j}=\langle P(x,y),Q(x,y) \rangle,$ the above leads us to write $$ \begin{array}{ll} \displaystyle \int_{C} {\bf F}\cdot d{\bf r}&=\displaystyle \int_{C} \left(P(x,y)\,{\bf i}+Q(x,y)\,{\bf j}\right)\cdot\left(dx\,{\bf i}+dy\,{\bf j}\right)\\ &=\displaystyle \int_{C} \langle P(x,y),Q(x,y) \rangle \cdot \langle dx,dy\rangle \\ &=\displaystyle \int_{C} P(x,y)\,dx+Q(x,y)\,dy \\ \end{array} $$ We will also see the last of the above written simply as $\displaystyle \int_{C} P\,dx+Q\,dy.$
In Three Dimensions...
Since $\displaystyle \frac{d{\bf r}}{dt}=\frac{dx}{dt}\,{\bf i}+\frac{dy}{dt}\,{\bf j}+\frac{dz}{dt}\,{\bf k}$ we often use the notation $$ d{\bf r}=dx\,{\bf i}+dy\,{\bf j}+dz\,{\bf k}=\langle dx,dy,dz \rangle $$ For the field ${\bf F}(x,y)=P(x,y,z)\,{\bf i}+Q(x,y,z)\,{\bf j}+R(x,y,z)\,{\bf k}=\langle P(x,y,z),Q(x,y,z),R(x,y,z) \rangle,$ the above leads us to write $$ \begin{array}{ll} \displaystyle \int_{C} {\bf F}\cdot d{\bf r}&=\displaystyle \int_{C} \left(P(x,y,z){\bf i}+Q(x,y,z){\bf j}+R(x,y,z){\bf k}\right)\cdot\left(dx\,{\bf i}+dy\,{\bf j}+dz\,{\bf k}\right)\\ &=\displaystyle \int_{C} \langle P(x,y,z),Q(x,y,z),R(x,y,z) \rangle \cdot \langle dx,dy,dz \rangle \\ &=\displaystyle \int_{C} P(x,y,z)dx+Q(x,y,z)\,dy+R(x,y,z)\,dz \\ \end{array} $$ We will also see the last of the above written simply as $\displaystyle \int_{C} P\,dx+Q\,dy+R\,dz.$
Example
Find the value of the line integral $$\displaystyle \int_{C} 4x\,dx + z\,dy + 4y^2\,dz$$ where $C$ is the curve parameterized by ${\bf r}(t) = \langle 4 \cos(2t), 2 \sin(2t), 3 \rangle$ for $\displaystyle 0 \leq t \leq \frac{\pi}{4}.$
Here ${\bf r}(t) = \langle 4 \cos(2t), 2 \sin(2t), 3 \rangle$ so that ${\bf r}'(t) = \langle -8 \sin(2t), 4 \cos(2t), 0 \rangle.$
Then $$ \begin{array}{lll} \displaystyle \int_{C} 4x\,dx + z\,dy + 4y^2\,dz&\displaystyle=\int_{C} \langle 4x , z , 4y^2 \rangle \cdot \langle dx,dy,dz \rangle&\mbox{}\\ \displaystyle &\displaystyle=\int_{C} {\bf F} \cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=\int_a^b {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} \langle 4x(t) , z(t) , 4y(t)^2 \rangle \cdot \langle -8 \sin(2t), 4 \cos(2t), 0 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} \langle 4\cdot 4\cos(2t) , 3 ,4\cdot 4 \sin^2(2t) \rangle \cdot \langle -8 \sin(2t), 4 \cos(2t), 0 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} \langle 16\cos(2t) , 3 ,16 \sin^2(2t) \rangle \cdot \langle -8 \sin(2t), 4 \cos(2t), 0 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} -128\cos(2t)\sin(2t)+12\cos(2t)+0\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} -64\sin(4t)+12\cos(2t)\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[16\cos(4t)+6\sin(2t)\right]_0^{\pi/4} &\mbox{}\\ \displaystyle &\displaystyle=\left(16\cos(\pi)+6\sin\left(\frac{\pi}{2}\right)\right)-\left(16\cos(0)+6\sin(0)\right) &\mbox{}\\ \displaystyle &\displaystyle=16(-1)+6(1)-16-6(0)&\mbox{}\\ \displaystyle &\displaystyle=-26 &\mbox{}\\ \end{array} $$ Scenic Alternative: We could have simply worked directly with the scalar differential notation by noting that $$ \begin{array}{lllll} &\displaystyle x=4\cos(2t) &\displaystyle y=2\sin(2t) &\displaystyle z=3&\mbox{}\\ \implies &\displaystyle \frac{dx}{dt}-8\sin(2t)&\displaystyle \frac{dy}{dt}=4\cos(2t)&\displaystyle \frac{dz}{dt}=0&\mbox{}\\ \implies &\displaystyle dx=-8\sin(2t)\,dt&\displaystyle dy=4\cos(2t)\,dt&\displaystyle dz=0\,dt&\mbox{}\\ \end{array} $$ so that $$ \begin{array}{lll} \displaystyle \int_{C} 4x\,dx + z\,dy + 4y^2\,dz&\displaystyle=\int_0^{\pi/4} 4\cdot \underbrace{4\cos(2t)}_{x}\cdot \underbrace{(-8\sin(2t))\,dt}_{dx}+\underbrace{3}_{z}\cdot \underbrace{4\cos(2t)\, dt}_{dy}+4\cdot \underbrace{4\sin^2(2t)}_{y^2} \cdot \underbrace{0 \, dt}_{dz}&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} -128 \cos(2t)\sin(2t)\,dt+12\cos(2t)\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} (-128 \cos(2t)\sin(2t)+12\cos(2t)) \,dt\,\,\,\,\,\,\,\,\,\,\mbox{ undistribute $dt$}&\mbox{}\\ \displaystyle &\displaystyle=\left[16\cos(4t)+6\sin(2t)\right]_0^{\pi/4} &\mbox{}\\ \displaystyle &\displaystyle=\left(16\cos(\pi)+6\sin\left(\frac{\pi}{2}\right)\right)-\left(16\cos(0)+6\sin(0)\right) &\mbox{}\\ \displaystyle &\displaystyle=16(-1)+6(1)-16-6(0)&\mbox{}\\ \displaystyle &\displaystyle=-26 &\mbox{}\\ \end{array} $$
Then $$ \begin{array}{lll} \displaystyle \int_{C} 4x\,dx + z\,dy + 4y^2\,dz&\displaystyle=\int_{C} \langle 4x , z , 4y^2 \rangle \cdot \langle dx,dy,dz \rangle&\mbox{}\\ \displaystyle &\displaystyle=\int_{C} {\bf F} \cdot d{\bf r} &\mbox{}\\ \displaystyle &\displaystyle=\int_a^b {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} \langle 4x(t) , z(t) , 4y(t)^2 \rangle \cdot \langle -8 \sin(2t), 4 \cos(2t), 0 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} \langle 4\cdot 4\cos(2t) , 3 ,4\cdot 4 \sin^2(2t) \rangle \cdot \langle -8 \sin(2t), 4 \cos(2t), 0 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} \langle 16\cos(2t) , 3 ,16 \sin^2(2t) \rangle \cdot \langle -8 \sin(2t), 4 \cos(2t), 0 \rangle\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} -128\cos(2t)\sin(2t)+12\cos(2t)+0\,dt &\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} -64\sin(4t)+12\cos(2t)\,dt &\mbox{}\\ \displaystyle &\displaystyle=\left[16\cos(4t)+6\sin(2t)\right]_0^{\pi/4} &\mbox{}\\ \displaystyle &\displaystyle=\left(16\cos(\pi)+6\sin\left(\frac{\pi}{2}\right)\right)-\left(16\cos(0)+6\sin(0)\right) &\mbox{}\\ \displaystyle &\displaystyle=16(-1)+6(1)-16-6(0)&\mbox{}\\ \displaystyle &\displaystyle=-26 &\mbox{}\\ \end{array} $$ Scenic Alternative: We could have simply worked directly with the scalar differential notation by noting that $$ \begin{array}{lllll} &\displaystyle x=4\cos(2t) &\displaystyle y=2\sin(2t) &\displaystyle z=3&\mbox{}\\ \implies &\displaystyle \frac{dx}{dt}-8\sin(2t)&\displaystyle \frac{dy}{dt}=4\cos(2t)&\displaystyle \frac{dz}{dt}=0&\mbox{}\\ \implies &\displaystyle dx=-8\sin(2t)\,dt&\displaystyle dy=4\cos(2t)\,dt&\displaystyle dz=0\,dt&\mbox{}\\ \end{array} $$ so that $$ \begin{array}{lll} \displaystyle \int_{C} 4x\,dx + z\,dy + 4y^2\,dz&\displaystyle=\int_0^{\pi/4} 4\cdot \underbrace{4\cos(2t)}_{x}\cdot \underbrace{(-8\sin(2t))\,dt}_{dx}+\underbrace{3}_{z}\cdot \underbrace{4\cos(2t)\, dt}_{dy}+4\cdot \underbrace{4\sin^2(2t)}_{y^2} \cdot \underbrace{0 \, dt}_{dz}&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} -128 \cos(2t)\sin(2t)\,dt+12\cos(2t)\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_0^{\pi/4} (-128 \cos(2t)\sin(2t)+12\cos(2t)) \,dt\,\,\,\,\,\,\,\,\,\,\mbox{ undistribute $dt$}&\mbox{}\\ \displaystyle &\displaystyle=\left[16\cos(4t)+6\sin(2t)\right]_0^{\pi/4} &\mbox{}\\ \displaystyle &\displaystyle=\left(16\cos(\pi)+6\sin\left(\frac{\pi}{2}\right)\right)-\left(16\cos(0)+6\sin(0)\right) &\mbox{}\\ \displaystyle &\displaystyle=16(-1)+6(1)-16-6(0)&\mbox{}\\ \displaystyle &\displaystyle=-26 &\mbox{}\\ \end{array} $$
Remark
Scalar differential notation is used often since the field ${\bf F}$ we're working with is embedded in the notation.
In the last example, the notation $$\displaystyle \int_{C} 4x\,dx + z\,dy + 4y^2\,dz$$ tells us that the field we're integrating over is ${\bf F}(x,y,z)=\langle 4x,z,4y^2\rangle=4x\,{\bf i}+z\,{\bf j}+4y^2\,{\bf k}.$
Integrating on Piecewise-Smooth Paths
Let $C$ be an oriented curve made out of smooth curves joined end to end. To find the line integral, we may simply evaluate the integral on each piece and add them together.
For example, $$\int_{C} {\bf F}\cdot d{\bf r}=\int_{C_1+C_2+C_3} {\bf F}\cdot d{\bf r}=\int_{C_1} {\bf F}\cdot d{\bf r}_1+\int_{C_2} {\bf F}\cdot d{\bf r}_2+\int_{C_3} {\bf F}\cdot d{\bf r}_3$$
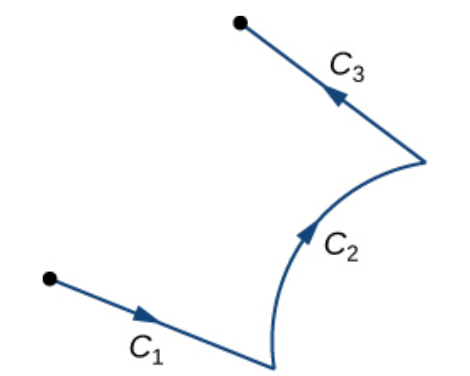
Example: Let ${\bf F}(x, y) = \langle P(x, y), Q(x, y) \rangle = \langle x-2y, y-x \rangle=(x-2y){\bf i}+(y-x)\,{\bf j}$ and let $C$ is be a rectangle with vertices $(0, 0),$ $(2, 0),$ $(2, 1),$ and $(0, 1)$ oriented counterclockwise (positively). Calculate the line integral $\displaystyle \int_{C} {\bf F}\cdot d{\bf r}.$
We shall break up our curve into $4$ pieces and parameterize each curve separately.
$$
\begin{array}{lll}
\displaystyle C_1:&\displaystyle {\bf r}_1(t)=\langle t,0\rangle &\mbox{over $0\leq t\leq 2$}\\
\displaystyle C_2:&\displaystyle {\bf r}_2(t)=\langle 2,t\rangle &\mbox{over $0\leq t\leq 1$}\\
\displaystyle C_3:&\displaystyle {\bf r}_3(t)=\langle 2-t,1\rangle &\mbox{over $0\leq t\leq 2$}\\
\displaystyle C_4:&\displaystyle {\bf r}_4(t)=\langle 0,1-t \rangle &\mbox{over $0\leq t\leq 1$}\\
\end{array}
$$
Then
$$
\begin{array}{lll}
\displaystyle \int_{C} {\bf F}\cdot d{\bf r}&\displaystyle= \int_{C_1+C_2+C_3+C_4} {\bf F}\cdot d{\bf r}&\mbox{}\\
\displaystyle &\displaystyle= \int_{C_1} {\bf F}\cdot d{\bf r}_1+\int_{C_2} {\bf F}\cdot d{\bf r}_2+\int_{C_3} {\bf F}\cdot d{\bf r}_3+\int_{C_4} {\bf F}\cdot d{\bf r}_4&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{2} {\bf F}({\bf r}_1)\cdot \frac{d{\bf r}_1}{dt}\,dt+\int_{0}^{1} {\bf F}({\bf r}_2)\cdot \frac{d{\bf r}_2}{dt}\,dt+\int_{0}^{2} {\bf F}({\bf r}_3)\cdot \frac{d{\bf r}_3}{dt}\,dt+\int_{0}^{1} {\bf F}({\bf r}_4)\cdot \frac{d{\bf r}_4}{dt}\,dt&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2} \langle x_1(t)-2y_1(t),y_1(t)-x_1(t) \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle x_2(t)-2y_2(t),y_2(t)-x_2(t) \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle x_3(t)-2y_3(t),y_3(t)-x_3(t) \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle x_4(t)-2y_4(t),y_4(t)-x_4(t) \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2} \langle t-2\cdot 0,0-t \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle 2-2t,t-2 \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle 2-t-2\cdot 1,1-(2-t) \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle 0-2(1-t),1-t-0 \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2} \langle t,-t \rangle \cdot \langle 1,0\rangle \,dt+\int_{0}^{1} \langle 2-2t,t-2 \rangle \cdot \langle 0,2\rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle \,\,\,\,\,\,\,\,+\int_{0}^{2} \langle -t,t-1 \rangle \cdot \langle -1,0\rangle\,dt+\int_{0}^{1} \langle 2t-2,1-t \rangle \cdot \langle 0,-1\rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{2} t \,dt+\int_{0}^{1} t-2 \,dt+\int_{0}^{2} t\,dt+\int_{0}^{1} t-1\,dt&\mbox{}\\
\displaystyle &\displaystyle= \left[\frac{1}{2}t^2\right]_{0}^{2} + \left[\frac{1}{2}t^2-2t\right]_{0}^{1}+\left[\frac{1}{2}t^2\right]_{0}^{2}+\left[\frac{1}{2}t^2-t\right]_{0}^{1}&\mbox{}\\
\displaystyle &\displaystyle= (2)+\left(\frac{1}{2}-2\right)+(2)+\left(\frac{1}{2}-1\right)&\mbox{}\\
\displaystyle &\displaystyle= 2+\left(-\frac{3}{2}\right)+2+\left(-\frac{1}{2}\right)&\mbox{}\\
\displaystyle &\displaystyle= 2&\mbox{}\\
\end{array}
$$
Example: Work in $3$ Dimensions
How much work is done on an object moving in a vector force field ${\bf F} = \langle yz, xy, xz \rangle$ along the path ${\bf r}(t) = \langle t^2 , t, t^4 \rangle,$ for $0 \leq t \leq 1 ?$
The work is given by the line integral $\displaystyle \int_C {\bf F}\cdot d{\bf r}=\int_C {\bf F}\cdot {\bf T} \, ds.$
Since ${\bf r}'(t) = \langle 2t , 1, 4t^3 \rangle,$ we have $$ \begin{array}{lll} \displaystyle \int_C {\bf F}\cdot d{\bf r}&\displaystyle= \int_a^b {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{1} \langle y(t)z(t), x(t)y(t), x(t)z(t) \rangle \cdot \langle 2t,1,4t^3 \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{1} \langle t\cdot t^4, t^2\cdot t, t^2\cdot t^4 \rangle \cdot \langle 2t,1,4t^3 \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{1} 2t^6+t^3+4t^9\,dt&\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{2}{7}t^7+\frac{1}{4}t^4+\frac{4}{10}t^{10}\right]_0^{1}&\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{7}+\frac{1}{4}+\frac{4}{10}&\mbox{}\\ \displaystyle &\displaystyle= \frac{131}{140}&\mbox{}\\ \end{array} $$
Since ${\bf r}'(t) = \langle 2t , 1, 4t^3 \rangle,$ we have $$ \begin{array}{lll} \displaystyle \int_C {\bf F}\cdot d{\bf r}&\displaystyle= \int_a^b {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{1} \langle y(t)z(t), x(t)y(t), x(t)z(t) \rangle \cdot \langle 2t,1,4t^3 \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{1} \langle t\cdot t^4, t^2\cdot t, t^2\cdot t^4 \rangle \cdot \langle 2t,1,4t^3 \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{1} 2t^6+t^3+4t^9\,dt&\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{2}{7}t^7+\frac{1}{4}t^4+\frac{4}{10}t^{10}\right]_0^{1}&\mbox{}\\ \displaystyle &\displaystyle= \frac{2}{7}+\frac{1}{4}+\frac{4}{10}&\mbox{}\\ \displaystyle &\displaystyle= \frac{131}{140}&\mbox{}\\ \end{array} $$
Flux Integrals: A Motivating Example
Imagine a fluid flowing through some boundary.
If the velocity of the fluid is described by a vector field, the flux is the rate at which the fluid is flowing through the boundary.
Calculating Flux Across a Curve: We break up our curve into a series of sub-arcs small enough so that
1) each sub-arc is approximately linear, and
2) the field ${\bf F}$ is roughly uniform.
Calculating Flux Across a Curve
Choose a point $P_i^*$ on the $i$th sub-arc.
Calculating Flux Across a Curve
Let ${\bf N}(P_i^*)$ is the unit normal vector at the point $P_i^*$ and let ${\bf F}(P_i^*)$ be the fluid velocity.
Calculating Flux Across a Curve
The rate of of fluid flow across a "tiny length" $\Delta s_i$ is approximately ${\bf F}(P_i^*)\cdot {\bf N}(P_i^*)\, \Delta s_i$
Flux Across a Curve $$\displaystyle \mbox{Flux}\approx \sum_{i=1}^{n} {\bf F}(P_i^*)\cdot {\bf N}(P_i^*)\, \Delta s_i$$
|
|
|
Definition: Flux Integral
The flux integral of vector field ${\bf F}$ across an oriented smooth curve $C$ is $$\displaystyle \int_C {\bf F}\cdot{\bf N}\,ds =\lim_{n \rightarrow \infty} \sum_{i=1}^{n} {\bf F}(P_i^*)\cdot {\bf N}(P_i^*)\, \Delta s_i$$ provided the limit exists.
In Words
The flux integral is the the limit of the sum of normal components of a vector field along a curve.
Fun Flux Fact
Flux integrals are important not just in describing fluid flows, but are also indispensable in the mathematics which describe electricity and magnetism.
Evaluating Flux Integrals: Here we observe four facts about a curve ${\bf r}(t)$ and its normal vector ${\bf n}(t):$
1) The unit normal vector ${\bf N}$ is given by $\displaystyle \frac{{\bf n}(t)}{\Vert{\bf n}(t)\Vert}.$
2) ${\bf n}(t)$ $=$ ${\bf r}'(t)$ $\times$ ${\bf k}$ $=$ $\langle x'(t),y'(t),0 \rangle$ $\times$ ${\bf k}$ $=$ $\langle y'(t),-x'(t),0 \rangle$
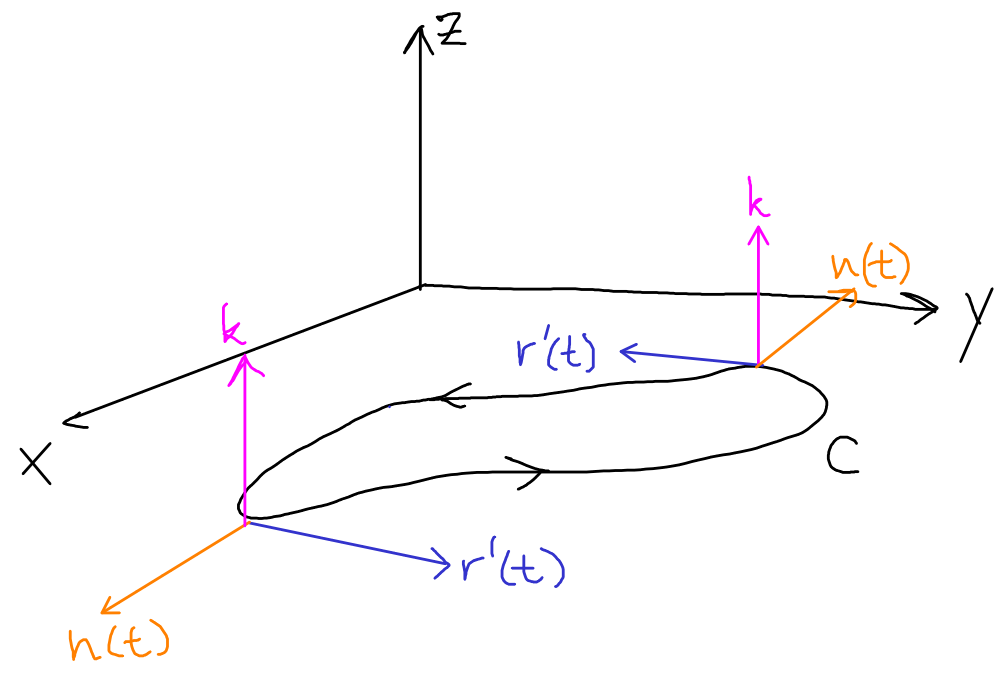
3) From 2) we have $\Vert{\bf r}'(t)\Vert$ $=$ $\sqrt{(x'(t))^2+(y'(t))^2}$ $=$ $\sqrt{(y'(t))^2+(-x'(t))^2}$ $=$ $\Vert{\bf n}(t)\Vert$
4) $ds=\Vert{\bf r}'(t)\Vert \, dt$ (just as we noted previously)
Together, these four facts give: $$\int_C {\bf F}\cdot{\bf N}\,ds =\int_C {\bf F}\cdot \frac{{\bf n}(t)}{\Vert{\bf n}(t)\Vert}\Vert{\bf r}'(t)\Vert \, dt =\int_C {\bf F}\cdot \frac{{\bf n}(t)}{\Vert{\bf r}'(t)\Vert}\Vert{\bf r}'(t)\Vert \, dt =\int_C {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt$$ We now have a much easier way to evaluate flux integrals than the definition!
Calculating Flux Across a Curve
Let ${\bf F}$ be a vector field and let $C$ be a smooth curve with parameterization ${\bf r}(t) = \langle x(t), y(t) \rangle,$ for $a \leq t \leq b.$ Moreover, let ${\bf n}(t) = \langle y'(t), -x'(t) \rangle.$ Then, the flux of ${\bf F}$ across $C$ is $$\int_C {\bf F}\cdot{\bf N}\,ds =\int_C {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt$$
Important Note
The orientation of the curve determines which direction the normal vectors point.
Example: Calculate the flux of ${\bf F} = \langle x + y, 2y \rangle$ across the line segment from $(0, 1)$ to $(1, 0),$ where the curve is oriented from left to right.
We first parameterize the curve as ${\bf r}(t)=\langle t,1-t \rangle$ over $0\leq t \leq 1.$
Then ${\bf r}'(t)=\langle 1,-1 \rangle.$
It follows that ${\bf n}(t)=\langle y'(t), -x'(t) \rangle=\langle -1,-1\rangle.$
Thus the flux of ${\bf F}$ across the curve ${\bf r}$ is $$ \begin{array}{lll} \displaystyle \int_C {\bf F}\cdot{\bf N}\,ds&\displaystyle= \int_C {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} \langle x(t)+y(t),2y(t) \rangle \cdot \langle -1,-1\rangle \,dt & \mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} \langle t+1-t,2(1-t) \rangle \cdot \langle -1,-1\rangle \,dt & \mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} \langle 1,2-2t \rangle \cdot \langle -1,-1\rangle \,dt & \mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} -1+2t-2 \,dt & \mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} 2t-3 \,dt & \mbox{}\\ \displaystyle &\displaystyle=\left[t^2-3t\right]_{0}^{1} & \mbox{}\\ \displaystyle &\displaystyle= 1-3 & \mbox{}\\ \displaystyle &\displaystyle= -2 & \mbox{}\\ \end{array} $$
Then ${\bf r}'(t)=\langle 1,-1 \rangle.$
It follows that ${\bf n}(t)=\langle y'(t), -x'(t) \rangle=\langle -1,-1\rangle.$
Thus the flux of ${\bf F}$ across the curve ${\bf r}$ is $$ \begin{array}{lll} \displaystyle \int_C {\bf F}\cdot{\bf N}\,ds&\displaystyle= \int_C {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} \langle x(t)+y(t),2y(t) \rangle \cdot \langle -1,-1\rangle \,dt & \mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} \langle t+1-t,2(1-t) \rangle \cdot \langle -1,-1\rangle \,dt & \mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} \langle 1,2-2t \rangle \cdot \langle -1,-1\rangle \,dt & \mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} -1+2t-2 \,dt & \mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{1} 2t-3 \,dt & \mbox{}\\ \displaystyle &\displaystyle=\left[t^2-3t\right]_{0}^{1} & \mbox{}\\ \displaystyle &\displaystyle= 1-3 & \mbox{}\\ \displaystyle &\displaystyle= -2 & \mbox{}\\ \end{array} $$
Flux Integrals in Scalar Differential Form
From the result $$\int_C {\bf F}\cdot{\bf N}\,ds =\int_C {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt$$ as well as the fact we observed that ${\bf n}(t)=\langle y'(t),-x'(t) \rangle=\langle \frac{dy}{dt},-\frac{dx}{dt} \rangle,$ we have that ${\bf n}(t)\, dt=\langle dy,-dx \rangle.$ Then, $$\int_C {\bf F}\cdot{\bf N}\,ds =\int_C {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt =\int_C \langle P(x,y),Q(x,y) \rangle \cdot \langle dy,-dx \rangle =\int_C -Q(x,y)\, dx + P(x,y) \,dy $$ The last of the above integrals can be written more simply as $\displaystyle \int_C -Q\, dx + P \,dy.$ This is the scalar differential form of a flux integral in two dimensions.
Line and Flux Integrals on Closed Curves
 |  |
| An Oriented Curve (Not Closed) | A Closed Curve |
| (Oriented Counterclockwise) |
Line and Flux Integrals on Closed Curves
Line and flux integrals on closed curves have a special notation: $\displaystyle \oint.$
Circulation
The line integral $\displaystyle \oint_C {\bf F}\cdot d{\bf r}=\oint_C {\bf F}\cdot{\bf T}\,ds$ on a closed curve $C$ is called the circulation of ${\bf F}$ on $C.$
Example: Let ${\bf F}(x, y) = \langle -y, x-y \rangle=-y\,{\bf i}+(x-y)\,{\bf j}$ and let $C$ the unit circle oriented counterclockwise (positively).
Calculate: (a) the circulation of ${\bf F}$ along $C:$ $\displaystyle \oint_C {\bf F}\cdot d{\bf r}$ and (b) the outward flux $\displaystyle \oint_C {\bf F}\cdot {\bf N} \,ds.$
(a)
Our curve is parameterized by ${\bf r}(t)=\langle \cos t,\sin t \rangle$ over $0 \leq t \leq 2\pi$ so that ${\bf r}'(t)=\langle -\sin t, \cos t \rangle.$
$$
\begin{array}{lll}
\displaystyle \oint_C {\bf F}\cdot d{\bf r}&\displaystyle= \int_a^b {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_0^{2\pi} \langle -y(t),x(t)-y(t) \rangle \cdot \langle -\sin t, \cos t \rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_0^{2\pi} \langle -\sin t,\cos t-\sin t \rangle \cdot \langle -\sin t, \cos t \rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_0^{2\pi} \sin^2 t +\cos^2 t -\sin t\cos t \,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_0^{2\pi} 1 -\frac{1}{2}\sin (2t) \,dt&\mbox{trig identities!}\\
\displaystyle &\displaystyle= \left[t +\frac{1}{4}\cos (2t)\right]_0^{2\pi}&\mbox{}\\
\displaystyle &\displaystyle= 2\pi +\frac{1}{4}\cos (4\pi)-\left(0 +\frac{1}{4}\cos (0)\right)&\mbox{}\\
\displaystyle &\displaystyle= 2\pi +\frac{1}{4}-\frac{1}{4}&\mbox{}\\
\displaystyle &\displaystyle= 2\pi &\mbox{}\\
\end{array}
$$
(b) From the above ${\bf n}(t)=\langle y'(t), -x'(t) \rangle=\langle \cos t,\sin t \rangle.$
Then $$ \begin{array}{lll} \displaystyle \oint_C {\bf F}\cdot{\bf N}\,ds&\displaystyle= \int_0^{2\pi} {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle -y(t),x(t)-y(t) \rangle\cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle -\sin t,\cos t-\sin t \rangle \cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} -\sin t \cos t +\cos t \sin t -\sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\int_0^{2\pi} \sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\int_0^{2\pi} \frac{1-\cos(2t)}{2}\,dt&\mbox{trig identity!}\\ \displaystyle &\displaystyle= -\frac{1}{2}\int_0^{2\pi} 1-\cos(2t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\frac{1}{2}\left[t-\frac{1}{2}\sin(2t)\right]_0^{2\pi}&\mbox{}\\ \displaystyle &\displaystyle= -\pi&\mbox{}\\ \end{array} $$
(b) From the above ${\bf n}(t)=\langle y'(t), -x'(t) \rangle=\langle \cos t,\sin t \rangle.$
Then $$ \begin{array}{lll} \displaystyle \oint_C {\bf F}\cdot{\bf N}\,ds&\displaystyle= \int_0^{2\pi} {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle -y(t),x(t)-y(t) \rangle\cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle -\sin t,\cos t-\sin t \rangle \cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} -\sin t \cos t +\cos t \sin t -\sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\int_0^{2\pi} \sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\int_0^{2\pi} \frac{1-\cos(2t)}{2}\,dt&\mbox{trig identity!}\\ \displaystyle &\displaystyle= -\frac{1}{2}\int_0^{2\pi} 1-\cos(2t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= -\frac{1}{2}\left[t-\frac{1}{2}\sin(2t)\right]_0^{2\pi}&\mbox{}\\ \displaystyle &\displaystyle= -\pi&\mbox{}\\ \end{array} $$
Example: Let ${\bf F}(x, y) = \langle x, y \rangle=x\,{\bf i}+y\,{\bf j}$ and let $C$ the unit circle oriented counterclockwise (positively).
Calculate: (a) the circulation of ${\bf F}$ along $C:$ $\displaystyle \oint_C {\bf F}\cdot d{\bf r}$ and (b) the outward flux $\displaystyle \oint_C {\bf F}\cdot {\bf N} \,ds.$
(a)
Our curve is parameterized by ${\bf r}(t)=\langle \cos t,\sin t \rangle$ over $0 \leq t \leq 2\pi$ so that ${\bf r}'(t)=\langle -\sin t, \cos t \rangle.$
$$
\begin{array}{lll}
\displaystyle \oint_C {\bf F}\cdot d{\bf r}&\displaystyle= \int_a^b {\bf F}({\bf r}(t))\cdot \frac{d{\bf r}}{dt}\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_0^{2\pi} \langle x(t),y(t) \rangle \cdot \langle -\sin t, \cos t \rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_0^{2\pi} \langle \cos t,\sin t \rangle \cdot \langle -\sin t, \cos t \rangle\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_0^{2\pi} -\cos t \sin t +\sin t \cos t\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_0^{2\pi} 0\,dt&\mbox{}\\
\displaystyle &\displaystyle= 0 &\mbox{}\\
\end{array}
$$
(b) From the above ${\bf n}(t)=\langle y'(t), -x'(t) \rangle=\langle \cos t,\sin t \rangle.$
Then $$ \begin{array}{lll} \displaystyle \oint_C {\bf F}\cdot{\bf N}\,ds&\displaystyle= \int_0^{2\pi} {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle x(t),y(t) \rangle\cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle \cos t,\sin t \rangle \cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \cos^2 t +\sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} 1\,dt&\mbox{}\\ \displaystyle &\displaystyle= 2\pi&\mbox{}\\ \end{array} $$
(b) From the above ${\bf n}(t)=\langle y'(t), -x'(t) \rangle=\langle \cos t,\sin t \rangle.$
Then $$ \begin{array}{lll} \displaystyle \oint_C {\bf F}\cdot{\bf N}\,ds&\displaystyle= \int_0^{2\pi} {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle x(t),y(t) \rangle\cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \langle \cos t,\sin t \rangle \cdot \langle \cos t,\sin t \rangle\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} \cos^2 t +\sin^2 t\,dt&\mbox{}\\ \displaystyle &\displaystyle= \int_0^{2\pi} 1\,dt&\mbox{}\\ \displaystyle &\displaystyle= 2\pi&\mbox{}\\ \end{array} $$
Summary of Notations for Line and Flux Integrals
| Line Integral | Flux Integral | |
| Definition | $\displaystyle \int_C {\bf F}\cdot {\bf T}\, ds$ | $\displaystyle \int_C {\bf F}\cdot {\bf N}\, ds$ |
| Vector Differential | $\displaystyle \int_C {\bf F}\cdot d{\bf r}$ | |
| Scalar Differential | $\displaystyle \int_{C} P\,dx+Q\,dy$ or $\displaystyle \int_{C} P\,dx+Q\,dy+R\,dz$ | $\displaystyle \int_{C} -Q\,dx+P\,dy$ |
| Parameterized Form | $\displaystyle \int_C {\bf F}({\bf r}(t))\cdot{\bf r}'(t)\,dt$ | $\displaystyle \int_C {\bf F}({\bf r}(t))\cdot{\bf n}(t)\,dt$ where ${\bf n}(t)=\langle y'(t),-x'(t)\rangle$ |
For closed curves we may write $\displaystyle \oint.$
Applications of Line and Flux Integrals
Finding Mass from Density
Calculating Work in a Force Field
Electricity and Magnetism