Holt.Blue

Vector Fields

Recall that a vector-valued function is a function which maps a single real number to a vector in either two or three-dimensional space.

These functions gave us curves in two and three dimensions.

Today we begin studying vector fields which map a point in either $\mathbb{R}^2$ or $\mathbb{R}^3$ to a vector in two or three-dimensional space.

























Vector Fields in $\mathbb{R}^2$

A vector field in $\mathbb{R}^2$ is a function ${\bf F}$ of the form $$ {\bf F}(x,y)=\langle P(x,y),Q(x,y)\rangle=P(x,y)\,{\bf i}+Q(x,y)\,{\bf j} $$ where $P(x,y)$ and $Q(x,y)$ are two-variable, real-valued functions.



























Examples

For the vector field ${\bf F}(x, y) = \langle -y, x \rangle=-y\,{\bf i}+x\,{\bf j},$ find ${\bf F}(0, 1)$ and ${\bf F}(2, 1).$ Show/Hide Answer!



For the vector field ${\bf F}(x, y) = \langle x, y \rangle=x\,{\bf i}+y\,{\bf j},$ find ${\bf F}(1, 2).$ Show/Hide Answer!



For the vector field ${\bf F}(x, y) = \langle y, 0 \rangle=y\,{\bf i},$ find ${\bf F}(1, 2).$ Show/Hide Answer!



























Visually Representing Vector Fields

Consider a vector field ${\bf F}(x, y)=\langle P(x,y),Q(x,y)\rangle.$

We may represent this field by plotting the vector $\langle P(x,y),Q(x,y)\rangle$ with the location $(x,y)$ as its initial point.





















Example

Plot the vector field ${\bf F}(x, y) = \langle -y, x \rangle$ by making a table of values for $\langle -y, x \rangle$ for various values of $x$ and $y.$





















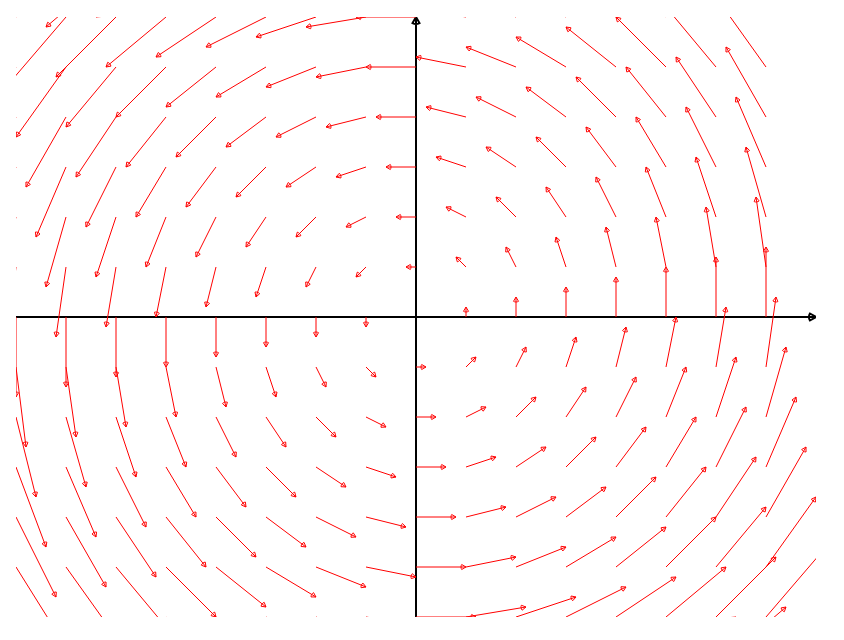
Other Examples

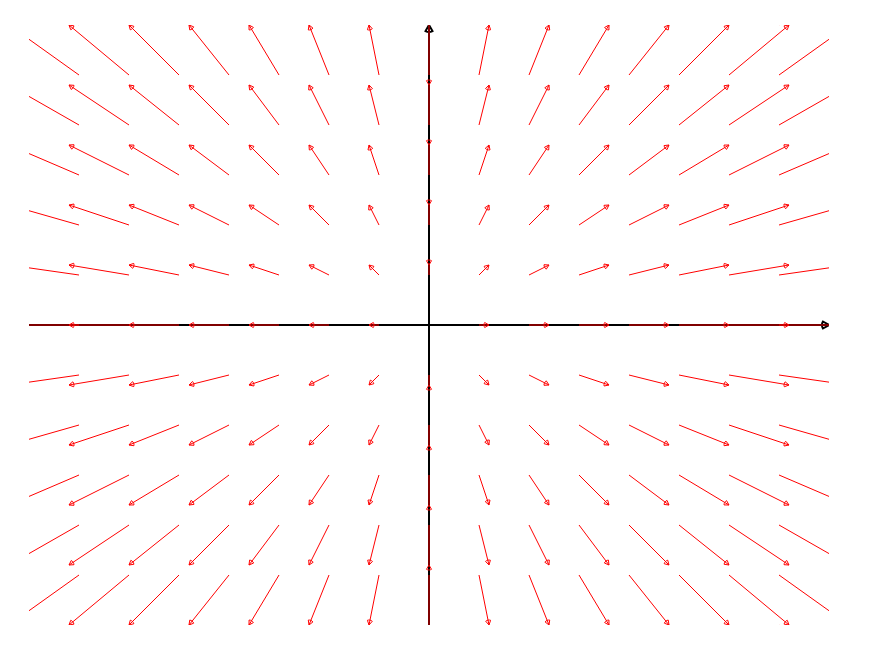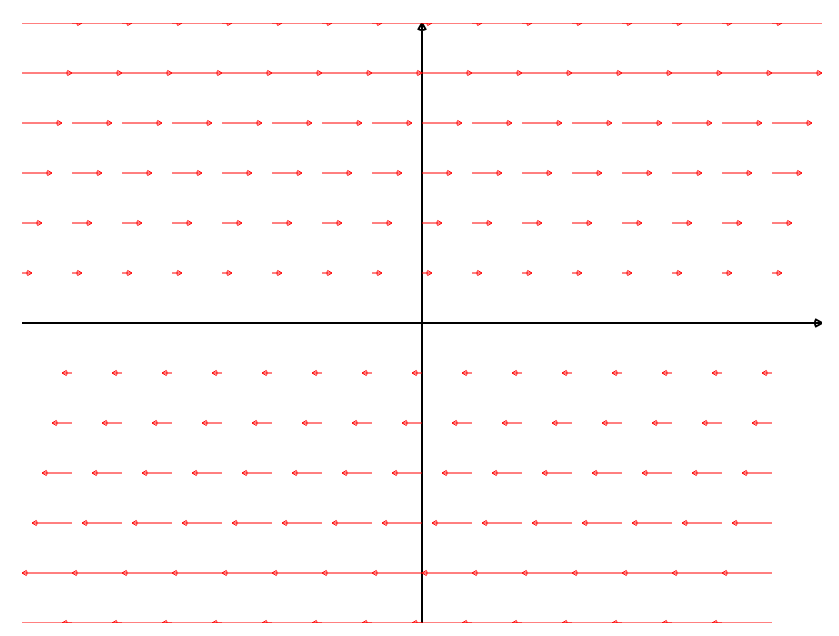${\bf F}(x, y) = \langle -y, x \rangle=-y\,{\bf i}+x\,{\bf j}$	${\bf F}(x, y) = \langle x, y \rangle=x\,{\bf i}+y\,{\bf j}$	${\bf F}(x, y) = \langle y, 0 \rangle=y\,{\bf i}$

Applications of Vector Fields in $\mathbb{R}^2$

Vector fields in $\mathbb{R}^2$ model lots of different phenomena.

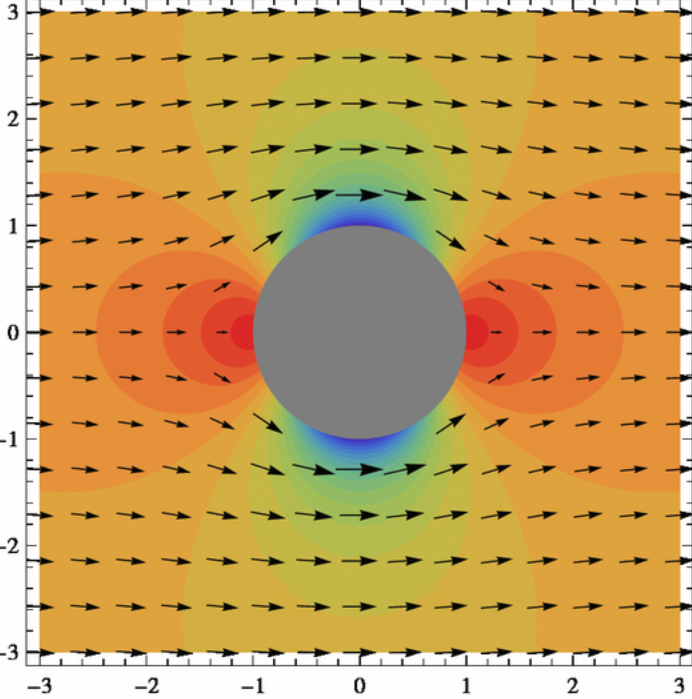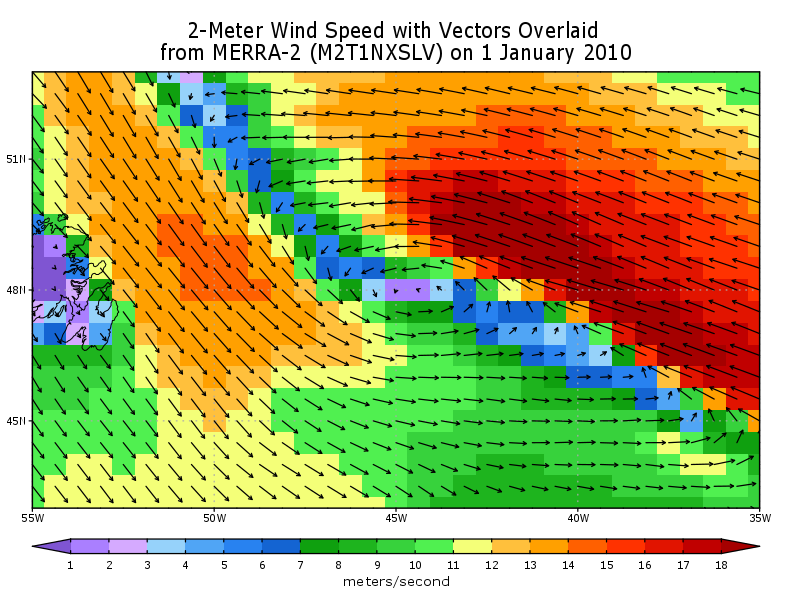Fluid Flow	Wind Speed	Unchanging Electric Fields

Radial Fields

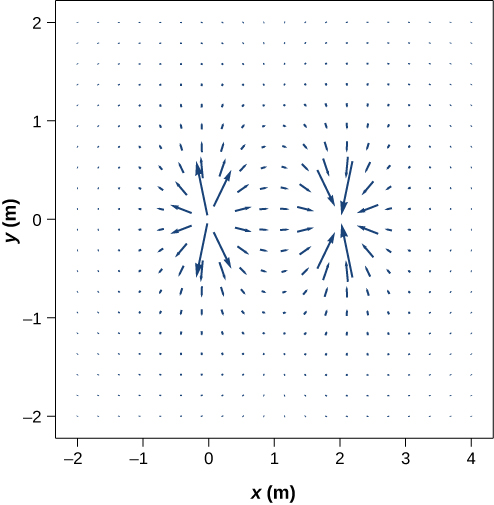
Radial fields are those which "point outward or inward" from an origin. An unchanging electric field with a single charged particle is an example of a radial field.































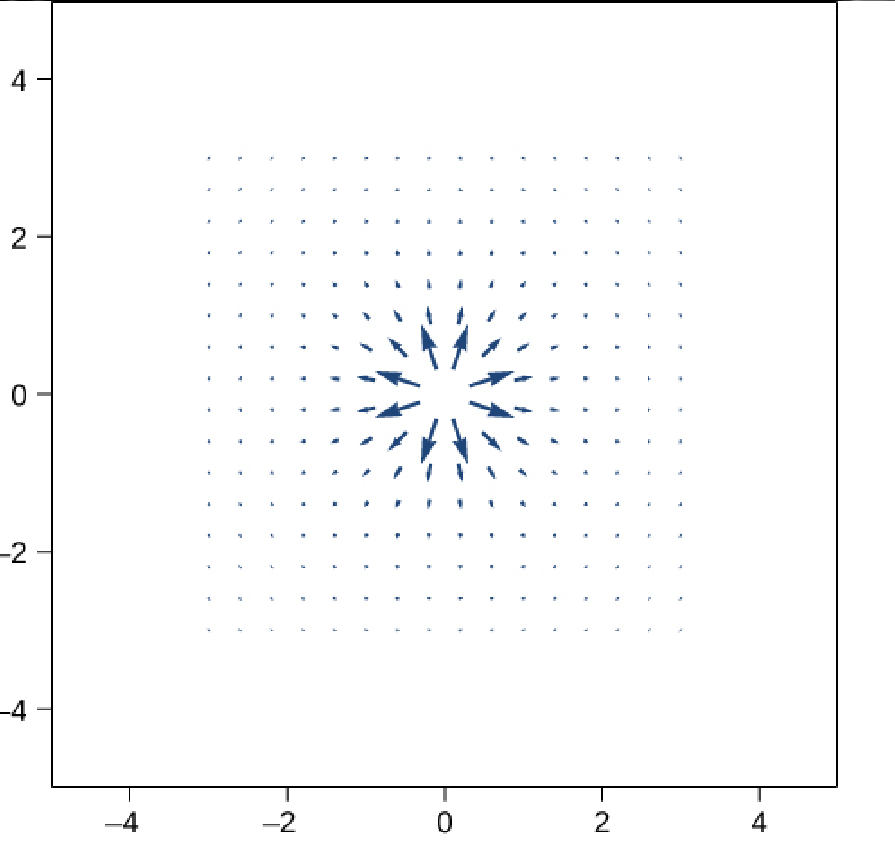
Rotational Fields

Rotational fields are the kind which model "curling" or "circling" around an origin. Examples include some magnetic fields, as well as vortices like whirlpools, hurricanes, and tornadoes.





























Other Fields

Some vector fields are a little harder to classify, but come back to this one later.


We will have more to say about this later as we proceed, but the germ of the idea is worth discussing now.

Generally all fields can be expressed as some combination of fields with "radial" and "rotational" characteristics.































Example

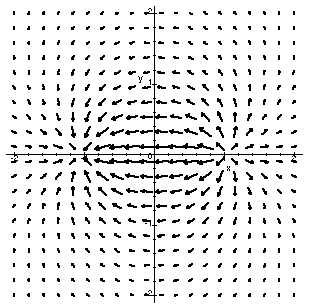
Sketch a graph of the vector field ${\bf F}$ given by $$ {\bf F}(x, y) = \frac{y}{x^2+y^2}\,{\bf i}-\frac{x}{x^2+y^2}\,{\bf j} $$ What kind of phenomenon could this vector field potentially model?

Is this a radial or rotational field? Show/Hide Answer!

































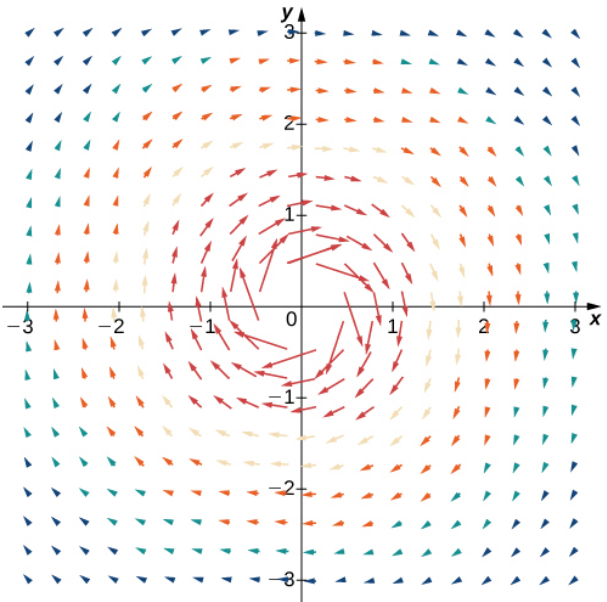
Field Lines

When we look at curves that "go with the flow" of a vector field, we get field lines.

More precisely, field lines are curves for which the field vector is tangent to the curve.

Field lines can reveal the nature of a field. For example, if a field is radial or rotational.



























Example

Consider the field $ {\bf F}(x, y) = y\,{\bf i}-x\,{\bf j} $

What do the field lines look like?

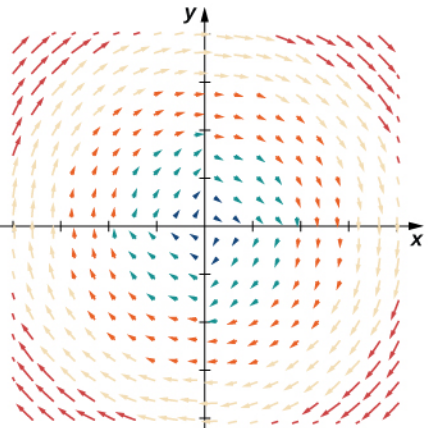
Is this a radial or rotational field? Show/Hide Answer!





























Example

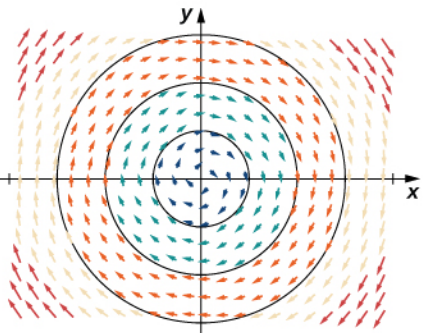
Consider the field $ {\bf F}(x, y) = x\,{\bf i}+y\,{\bf j} $

What do the field lines look like?

Is this a radial or rotational field? Show/Hide Answer!

































Fields Lines in Physics

The electric field for two oppositely charged objects.





























Fields Lines in Physics

The electric field for a single charged object.





























Fields Lines in Physics

The magnetic field surrounding a bar magnet.

The field lines are traced out by the iron filings under the influence of the magnetic field.




























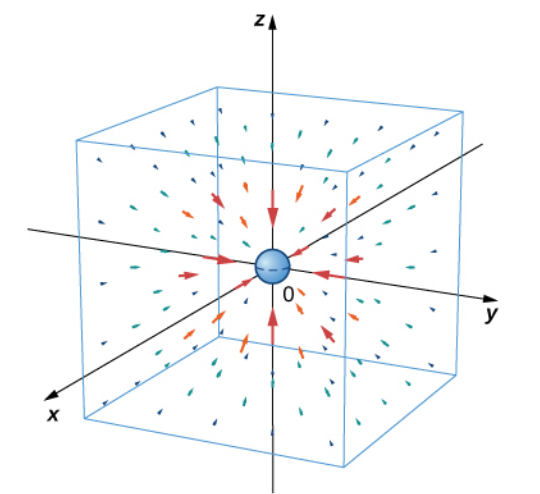
The above concept can also be applied to three dimensions.

To every point in three-dimensional space, we can assign a three-dimensional vector.



























Vector Fields in $\mathbb{R}^3$

A vector field in $\mathbb{R}^3$ is a function ${\bf F}$ of the form $$ {\bf F}(x,y,z)=\langle P(x,y,z),Q(x,y,z),R(x,y,z)\rangle=P(x,y,z)\,{\bf i}+Q(x,y,z)\,{\bf j}+R(x,y,z)\,{\bf k} $$ where $P(x,y,z),$ $Q(x,y,z),$ and $R(x,y,z)$ are three-variable, real-valued functions.



























Example

Consider the vector field ${\bf F}$ given by $$ {\bf F}(x,y,z) = \langle 1,1,z\rangle = \,{\bf i}+\,{\bf j}+z\,{\bf k} $$





























Application

Newton's Law of Gravitation in vector form is $${\bf F}(x,y,z)=-Gm_1 m_2\left \langle\frac{x}{r^3},\frac{y}{r^3},\frac{z}{r^3}\right \rangle$$ where $r=\Vert \langle x,y,z \rangle \Vert=\sqrt{x^2+y^2+z^2}.$

${\bf F}$ describes the force a mass $m_1$ located at $(0,0,0)$ exerts on a second mass $m_2$ located at $(x,y,z).$



























Application

From the above, we may model the gravitational force earth exerts on a mass $m$ at any point in space on or above earth's surface. $$ {\bf F}(x,y,z)=-Gm_e m\left \langle\frac{x}{(x^2+y^2+z^2)^{3/2}},\frac{y}{(x^2+y^2+z^2)^{3/2}},\frac{z}{(x^2+y^2+z^2)^{3/2}}\right \rangle $$ where $G=6.67384 \times 10^{-11}$ $\mbox{m}^3\mbox{kg}^{-1}\mbox{s}^{-2}$ is the universal gravitational constant and $m_e=5.972\times 10^{24}$ $\mbox{kg}$ is the mass of earth.



























Application

The moon orbits earth at an average distance of $\mbox{385,000.6}$ $\mbox{km}$ and has a mass of $m=7.342\times 10^{22}$ $\mbox{kg}.$

For a particular moment in time, set up a coordinate system with earth's center located at $(0,0,0)$ and the moon's center located at $(\mbox{385 000 600},0,0).$

Find the force vector on the moon at $(\mbox{385 000 600},0,0).$


Show/Hide Answer!


























What Do You Think?

Is earth's gravitational field radial or rotational?































Recall

Recall that the gradient of a two and three variable function is given by $$ \nabla f(x,y)=\frac{\partial f}{\partial x}\,{\bf i}+\frac{\partial f}{\partial y}\,{\bf j} $$ in two dimensions and $$ \nabla f(x,y,z)=\frac{\partial f}{\partial x}\,{\bf i}+\frac{\partial f}{\partial y}\,{\bf j}+\frac{\partial f}{\partial z}\,{\bf k} $$ in three dimensions.

Also recall that the vector $\nabla f$ is perpendicular to the level curves or level surfaces of $f.$





































The thing to notice here is that $\nabla f$ is a vector field!

























Gradient Fields

We call a field ${\bf F}$ a gradient field if $$ {\bf F}=\nabla f $$ for some scalar function $f.$

























Example

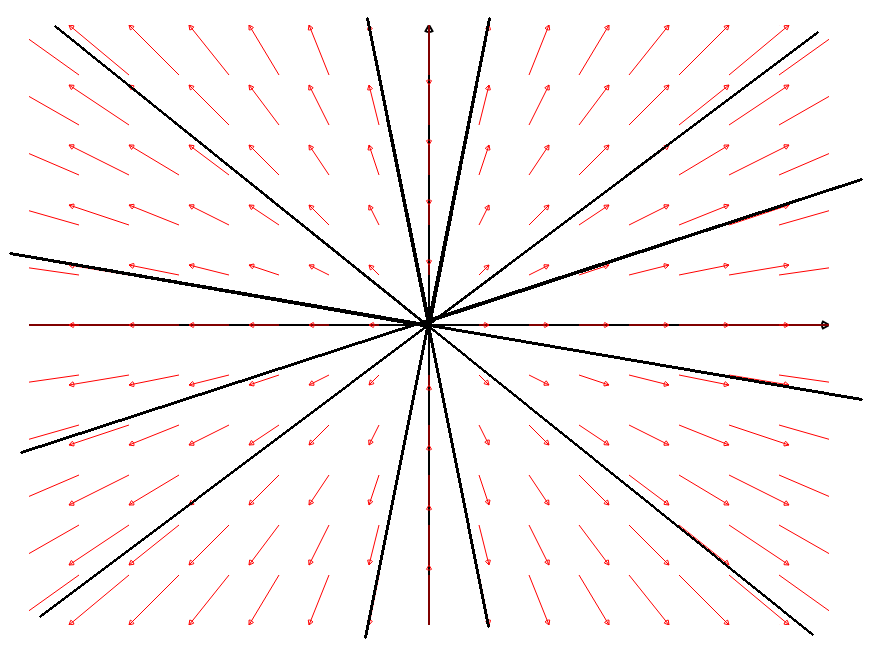
Consider the function $f(x,y)=x^2y^2.$ Then $\nabla f(x,y)=\left\langle 2xy^2,2x^2y \right\rangle.$

The level curves of $f$ and the gradient field $\nabla f$ are plotted on the same axes below.



























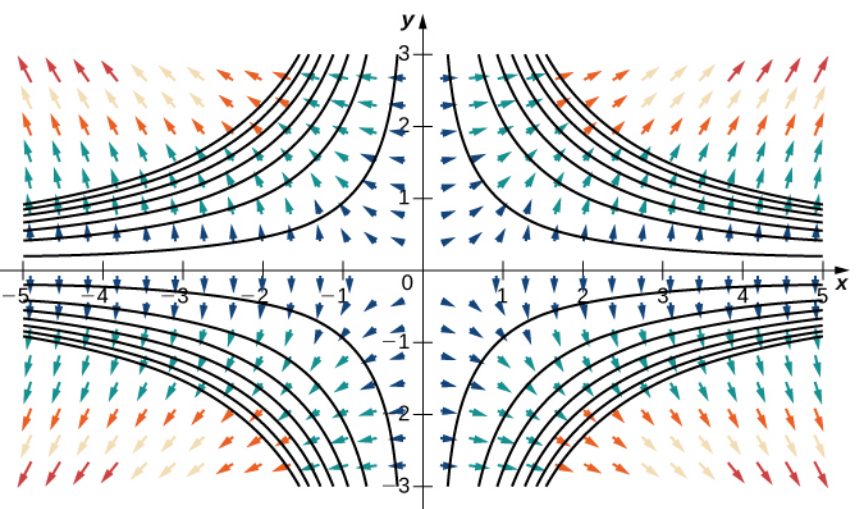
As we shall learn quite well by the end of the course, gradient fields are a special kind of vector field.

That is, not all vector fields are gradient fields.

Because they're so special, gradient fields have a second, more descriptive name: conservative vector fields.























Conservative Vector Fields

Conservative vector fields have a special place in physics because where there's a conservation law, there's a conservative field.

For example, if you hike up a mountain, the work you do against gravity (a conservative field!) to get to the top is the same no matter what path you take. There's a conservation of energy principle at work here.





















Potential Functions

Suppose ${\bf F}$ is a conservative (gradient!) vector field such that $$ {\bf F}=\nabla f $$ for some scalar function $f.$

Then we say that $f$ is a potential function for ${\bf F}.$





























Example

$f(x,y)=x^2y^2$ is a potential function for ${\bf F}(x,y)=\langle 2xy^2,2y^2x\rangle$ since $\nabla f=\langle 2xy^2,2y^2x\rangle= {\bf F}$























Example

Verify that $f (x, y, z) = x^2 yz -\sin(xy)$ is a potential function for $${\bf F}(x,y,z)=\langle 2xyz-y\cos(xy),x^2z-x\cos(xy),x^2y\rangle$$ Show/Hide Answer!

























Example

Verify that gravitational potential $\displaystyle f(x,y,z)=\frac{Gm_1 m_2}{\sqrt{x^2+y^2+z^2}}$ is the potential function of the gravitational force $$ {\bf F}(x,y,z)=-Gm_1 m_2\left \langle\frac{x}{(x^2+y^2+z^2)^{3/2}},\frac{y}{(x^2+y^2+z^2)^{3/2}},\frac{z}{(x^2+y^2+z^2)^{3/2}}\right \rangle $$ That is, verify that ${\bf F}=\nabla f.$ Show/Hide Answer!































Special Note

In certain situations, especially in physics, the potential function is defined to be the opposite of the gradient vector to agree with how a physical law is stated.

























Application

The electric field is the opposite of the gradient of the voltage. $${\bf E} = -\nabla V$$ That is $V$ is a "potential" function of the electric field ${\bf E}.$ This essentially says that the electric field points "downhill on voltage mountain."































Application

Suppose that $Q$ is a point charge located at the origin.

Verify that the electric potential $\displaystyle V(x, y) = \frac{Q}{4\pi\varepsilon_0}\frac{1}{\sqrt{x^2+y^2}}$ is a potential function for the electric field $${\bf E}(x,y) = \frac{Q}{4\pi\varepsilon_0} \left \langle \frac{x}{(x^2+y^2)^{3/2}},\frac{y}{(x^2+y^2)^{3/2}}\right\rangle$$ That is, show that ${\bf E}=-\nabla V$

Show/Hide Answer!































Do you notice any similarities with electric and gravitational potential?





























Uniqueness of Potential Functions

For a conservative vector field ${\bf F},$ a potential function is not unique.

For a silly example, $f(x,y)=x^2y^2$ and $g(x,y)=x^2y^2+5$ are both potential functions for $${\bf F}(x,y)=\langle 2xy^2,2y^2x\rangle.$$ The question is are there other possibilities?

What do you think?





























Uniqueness of Potential Functions

Let ${\bf F}$ be a conservative vector field on an open and connected domain and let $f$ and $g$ be functions such that $\nabla f = {\bf F}$ and $\nabla g = {\bf F}.$

Then, there is a constant $C$ such that $f = g + C.$

Another way of saying this is that potential functions are unique up to a constant.

























Big Question

Are all vector fields conservative?





























Big Answer

Nope.





























Another Big Question

If we can't find or don't have a potential function $f,$ how do we know if a vector field is conservative or not?























Incomplete Answer

It's kind of complicated.

But that's something we'll get deeper into later once we've developed the right machinery.

In the meantime we have...

























The Cross-Partial Property of Conservative Vector Fields

Let ${\bf F}$ be a vector field in two or three dimensions such that the component functions of ${\bf F}$ have continuous second- order mixed-partial derivatives on the domain of ${\bf F}.$

If ${\bf F}(x,y)=\langle P(x,y),Q(x,y)\rangle$ is a conservative vector field in $\mathbb{R}^2,$ then $\displaystyle \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}.$

If ${\bf F}(x,y,z)=\langle P(x,y,z),Q(x,y,z),R(x,y,z)\rangle$ is a conservative vector field in $\mathbb{R}^3,$ then

$$ \begin{array}{l} \displaystyle \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\\ \displaystyle \frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}\\ \displaystyle \frac{\partial R}{\partial x}=\frac{\partial P}{\partial z} \end{array} $$























How to Use the Above Result

The Cross-Partial Property of Conservative Vector Fields, which we'll abbreviate as $\mbox{CPP},$ can be represented in the following way. $$ \mbox{Conservative}\implies\mbox{CPP Holds} $$ The contrapositve of the above is generally how the statement is used to show a field is not conservative: $$ \mbox{CPP Fails}\implies\mbox{Not Conservative} $$





















Examples

(a) Show that the field ${\bf F}(x,y)=\langle y,-x \rangle$ is not conservative.

(b) Show that the field ${\bf F}(x,y,z)=\langle x,y,xyz \rangle$ is not conservative. Show/Hide Answer!

























For now, to show that a field ${\bf F}$ is conservative still requires finding an $f$ such that ${\bf F}=\nabla f.$































Dire Warning

When you say $$ \mbox{CPP Holds}\implies\mbox{Conservative} $$

YOU MAKE KITTY ANGRY!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

The Big Picture

Speaking very loosely here:

"Purely radial" ("expansive/contractive") fields are conservative.

Fields which have rotational ("swirly") characteristics are not conservative.

Later, we will make precise the notion of how "radial" and how "rotational" a field is.

Radial	Rotational