When a situation exhibits circular symmetry, using coordinate system in which the phenomenon is more naturally described can greatly reduce the complexity of the problem.
For example, we saw how converting a double integral from rectangular to polar coordinates (or vice versa!) can greatly reduce the amount of work required to evaluate the integral.
Here, we describe two circularly symmetric coordinate systems in three dimensions: cylindrical and spherical coordinates.
Cylindrical Coordinates
In cylindrical coordinates, a point in space is described as $(r,\theta,z).$
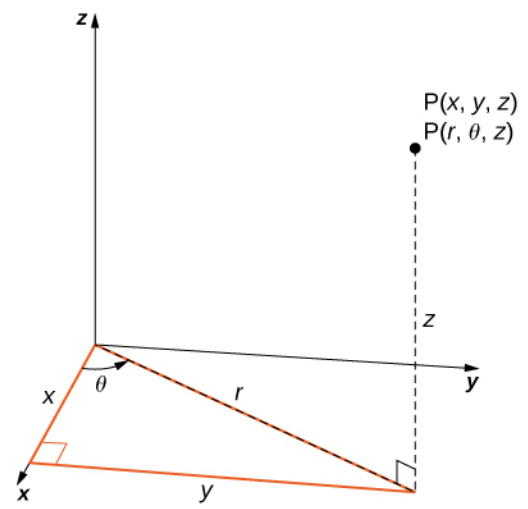
Relating Rectangular and Cylindrical Coordinates
We can express a location in cylindrical coordinates $(r,\theta,z)$ in terms of rectangular coordinates, $(x,y,z)=(r\cos \theta, r\sin \theta,z),$ that is $$ \begin{array}{l} x=r\cos \theta\\ y=r\sin\theta\\ z=z \end{array} $$

Relating Rectangular and Cylindrical Coordinates
Since $x=r\cos \theta$ and $y=r\sin\theta,$ we have that $x^2+y^2=r^2.$
That is, cylindrical coordinates are useful for describing situations which have circular symmetry around a vertical axis.

Example
The point in cylindrical coordinates $\displaystyle \left(4,\frac{2\pi}{3},-2\right)$ is graphed below.
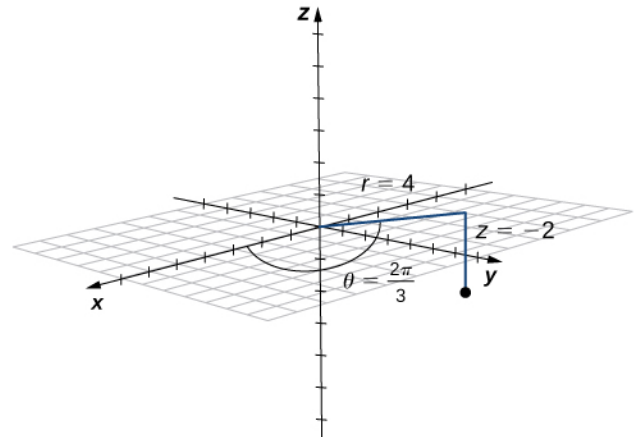
In rectangular coordinates this point is expressed as $(-2,2\sqrt{3},-2).$
Surfaces in Cylindrical Coordinates
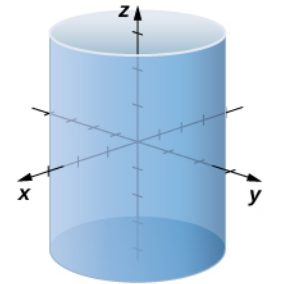 | 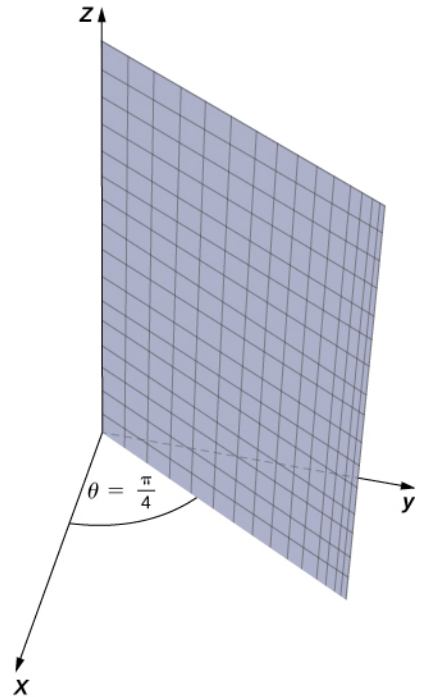 |  |
| $r=3$ | $\displaystyle \theta=\frac{\pi}{4}$ | $z=2$ |
Other Examples of Surfaces in Cylindrical Coordinates
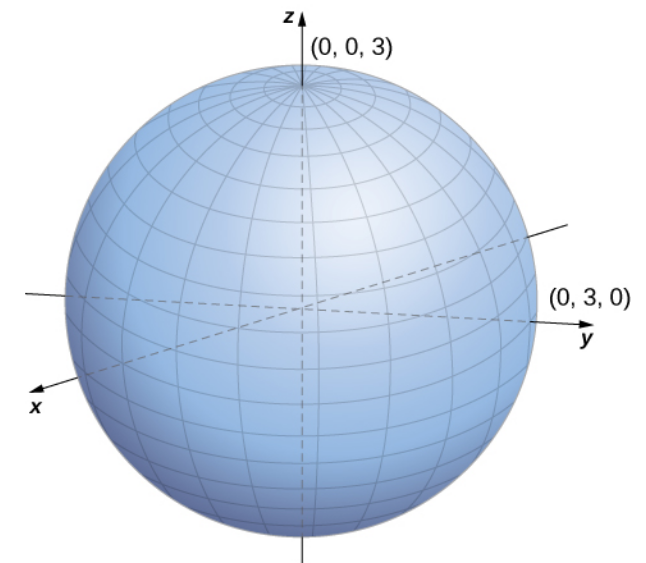 | 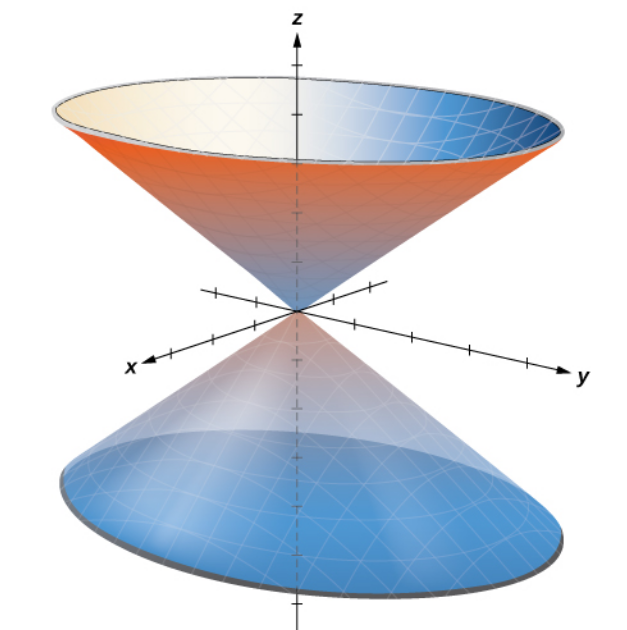 |
| $r^2+z^2=9$ | $\displaystyle z=r$ |
Triple Integrals in Cylindrical Coordinates
Just as we began computing double integrals over rectangular regions, we begin estimating the triple integral of $f(x,y,z)$ over a "cylindrical box" region $B.$
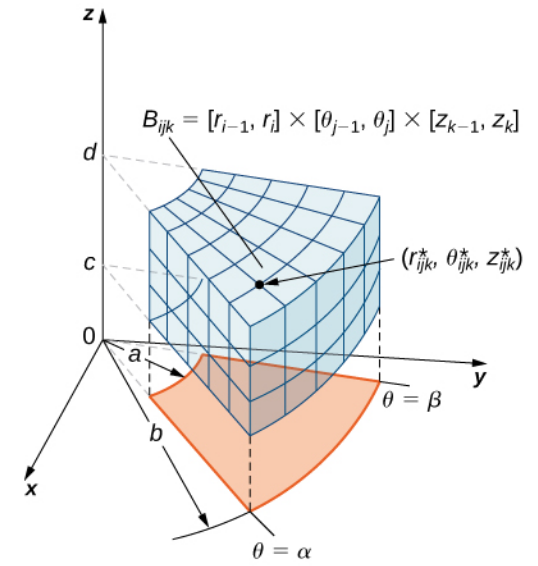
Triple Integrals in Cylindrical Coordinates
We construct our cylindrical box region as $B$ as $[a,b]\times [\alpha,\beta]\times [c,d].$

Triple Integrals in Cylindrical Coordinates
We then break up $[a,b]$ into $\ell$ intervals of size $\Delta r,$ $[\alpha,\beta]$ into $m$ intervals of size $\Delta \theta,$ and $[c,d]$ into $n$ intervals of size $\Delta z$ so that the $ijk$th cylindrical sub-box, $B_{ijk}$ is given by $[r_{i-1},r_{i}]\times [\theta_{j-1},\theta_{j}]\times [z_{k-1},z_{k}].$

Triple Integrals in Cylindrical Coordinates
In each subinterval $[r_{i-1},r_{i}]$ we choose a point $r_i^*,$ and in each subinterval $[\theta_{j-1},\theta_{j}]$ choose a point $\theta_j^*,$ and in each subinterval $[z_{k-1},z_{k}]$ choose a point $z_k^*.$

Triple Integrals in Cylindrical Coordinates
Since the arguments of $f(x,y,z)$ are in rectangular coordinates, to approximate the integral, we need to evaluate $f$ at the rectangular equivalent of the point $(r_i^*,\theta_j^*,z_k)$ which is given by $$(x_i^*,y_i^*,z_k^*)=(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*,z_k^*).$$ The function value at the $ijk$th cylindrical sub-box is $ f(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*,z_k^*) $

Triple Integrals in Cylindrical Coordinates
The volume of the $ijk$th box is $r_i^*\Delta \,\theta \, \Delta r \, \Delta z, $ and its function value is $f(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*,z_k^*)$ so that the "hyper-volume" at the $ijk$th box is $$ f(x_i^*,y_j^*,z_k^*)\,\Delta V=f(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*,z_k^*)\,r_i^*\, \Delta \, \theta \, \Delta r \, \Delta z $$

Triple Integrals in Cylindrical Coordinates
Adding up all of volumes of all the cylindrical boxes gives us an approximation of the integral. $$ \mbox{Integral over $B$} \displaystyle\approx\sum_{k=1}^{n}\sum_{j=1}^{m}\sum_{i=1}^{\ell}f(x_i^*,y_j^*,z_k^*)\,\Delta V =\displaystyle\sum_{k=1}^{n}\sum_{j=1}^{m}\sum_{i=1}^{\ell} f(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*,z_k^*)\,r_i^*\, \Delta \, \theta \, \Delta r \, \Delta z $$

Triple Integrals in Cylindrical Coordinates
In the limit, we get the triple integral in cylindrical coordinates...
Triple Integrals in Cylindrical Coordinates
The triple integral of the function $f (x, y,z)$ over the cylindrical box $B=[a,b]\times[\alpha,\beta]\times[c,d]$ is $$ \iiint_{B} f(x,y,z) \,dV = \iiint_B f(r\cos \theta, r\sin \theta,z)\,r\,dr\,d\theta\,dz = \int_{c}^{d} \int_{\alpha}^{\beta} \int_{a}^{b} f(r\cos \theta, r\sin \theta,z)\,r\,dr\,d\theta\,dz $$

Example
Find $ \displaystyle \iiint_{B} xy \,dV $ where $B=\left\{(x,y,z)\in \mathbb{R}^3\Bigr| x^2+y^2\leq 1, x \geq 0, x \geq y, -1 \leq z \leq 1 \right\}$ is the solid shown below.
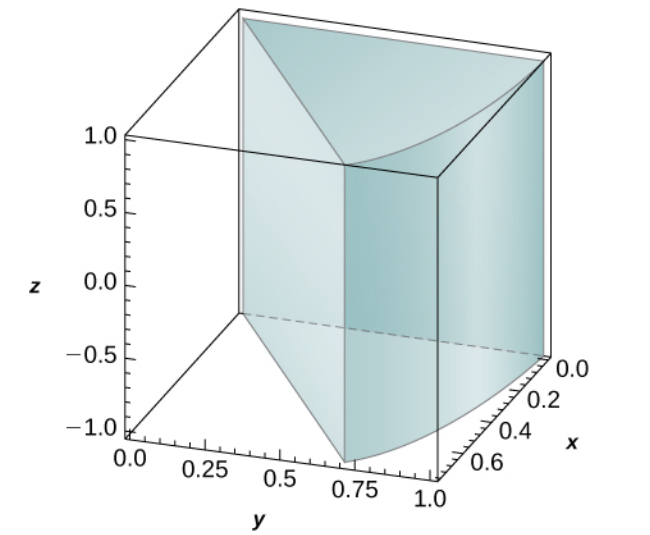
In cylindrical coordinates, we may describe the region as
$$
\displaystyle B=\left\{(r,\theta, z)\in \mathbb{R}^3\Bigr| 0 \leq r \leq 1, \frac{\pi}{4} \leq \theta \leq \frac{\pi}{2}, -1 \leq z \leq 1 \right\}
$$
Thus
$$
\begin{array}{lll}
\displaystyle \iiint_{B} xy \,dV&\displaystyle=\int_{-1}^{1}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\int_{0}^{1} (r\cos \theta) (r\sin \theta) r\, dr \, d\theta \, dz &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\int_{0}^{1} r^3 \cos \theta \sin \theta \, dr \, d\theta \, dz &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \left[\frac{1}{4}r^4 \cos \theta \sin \theta\right]_{0}^{1} \, d\theta \, dz &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \frac{1}{4} \cos \theta \sin \theta \, d\theta \, dz &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \frac{1}{8} \sin 2\theta \, d\theta \, dz &\mbox{trig identity}\\
\displaystyle &\displaystyle=\frac{1}{8}\int_{-1}^{1}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \sin 2\theta \, d\theta \, dz &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{8}\int_{-1}^{1} \left[-\frac{1}{2}\cos 2\theta\right]_{\frac{\pi}{4}}^{\frac{\pi}{2}}\, dz &\mbox{}\\
\displaystyle &\displaystyle=-\frac{1}{16}\int_{-1}^{1} \left[\cos 2\theta\right]_{\frac{\pi}{4}}^{\frac{\pi}{2}}\, dz &\mbox{}\\
\displaystyle &\displaystyle=-\frac{1}{16}\int_{-1}^{1} \left[\cos \left(2\cdot \frac{\pi}{2}\right)-\cos \left(2\cdot \frac{\pi}{4}\right)\right]\, dz &\mbox{}\\
\displaystyle &\displaystyle=-\frac{1}{16}\int_{-1}^{1} \left[-1-0\right]\, dz &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{16}\int_{-1}^{1} \, dz &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{16}[z]_{-1}^{1} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{16}\cdot 2&\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{8}&\mbox{}\\
\end{array}
$$
Triple Integral in Cylindrical Coordinates Over General Regions
For a general solid region $E$ projected onto a region $D$ in the $r\theta$-plane, $$ \begin{array}{ll} \displaystyle\iiint_E f(r\cos \theta, r\sin \theta,z)\,r\,dr\,d\theta\,dz &\displaystyle=\iint_{D} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,dA\\ &\displaystyle=\int_{\alpha}^{\beta} \int_{v_1(\theta)}^{v_2(\theta)} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,dr\,d\theta\\ &\displaystyle=\int_{a}^{b} \int_{v_1(r)}^{v_2(r)} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,d\theta \, dr \end{array} $$
Example
Consider the region $E$ inside the right circular cylinder with equation $r = 2 \sin \theta,$ bounded below by the $r\theta$-plane and bounded above by the sphere with radius $4$ centered at the origin. Set up a triple integral over this region with a function $f (x, y, z)$ in cylindrical coordinates.
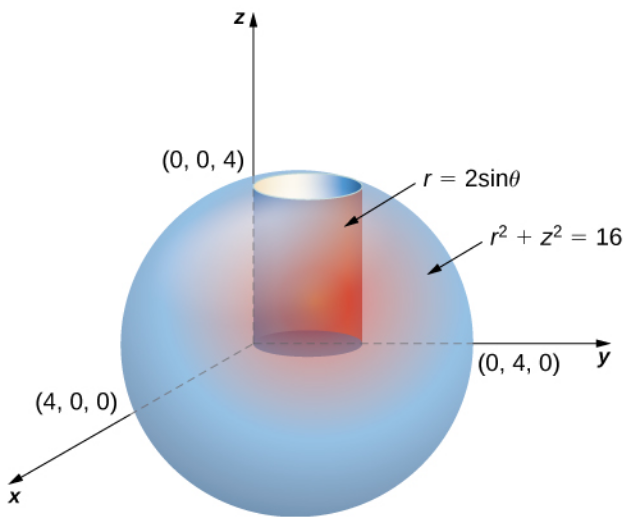
In cylindrical coordinates, we may describe the region as
$$
\displaystyle E=\left\{(r,\theta, z)\in \mathbb{R}^3\Bigr| 0 \leq \theta \leq \pi, 0 \leq r \leq 2\sin \theta, 0 \leq z \leq \sqrt{16-r^2} \right\}
$$
The projection onto the $r\theta$-plane is
$$\
\displaystyle D=\left\{(r,\theta)\in \mathbb{R}^2\Bigr| 0 \leq \theta \leq \pi, 0 \leq r \leq 2\sin \theta\right\}
$$
Thus
$$
\begin{array}{lll}
\displaystyle \iiint_{E} f (x, y, z) \,dV&\displaystyle=\iint_{D} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,dA &\mbox{}\\
\displaystyle &\displaystyle=\int_{\alpha}^{\beta} \int_{v_1(\theta)}^{v_2(\theta)} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,dr\,d\theta &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{\pi} \int_{0}^{2\sin \theta} \int_{0}^{\sqrt{16-r^2}} f (r\cos \theta, r\sin \theta, z) \, r \,dz\, dr \, d\theta &\mbox{}\\
\end{array}
$$
Other Orders of Integration
For a general solid region $E$ projected onto a region $D$ in the $\theta z$-plane, $$ \begin{array}{ll} \displaystyle\iiint_E f(r\cos \theta, r\sin \theta,z)\,r\,dr\,d\theta\,dz &\displaystyle=\int_{c}^{d} \int_{v_1(z)}^{v_2(z)} \left[\int_{u_1(\theta,z)}^{u_2(\theta,z)} f(r\cos \theta, r\sin \theta,z)\,r\,dr\right]\,d\theta\,dz\\ &\displaystyle=\int_{\alpha}^{\beta} \int_{v_1(\theta)}^{v_2(\theta)} \left[\int_{u_1(\theta,z)}^{u_2(\theta,z)} f(r\cos \theta, r\sin \theta,z)\,r\,dr\right]\,dz \,d\theta \end{array} $$ For a general solid region $E$ projected onto a region $D$ in the $rz$-plane, $$ \begin{array}{ll} \displaystyle\iiint_E f(r\cos \theta, r\sin \theta,z)\,r\,dr\,d\theta\,dz &\displaystyle=\int_{\alpha}^{\beta} \int_{v_1(z)}^{v_2(z)} \left[\int_{u_1(r,z)}^{u_2(r,z)} f(r\cos \theta, r\sin \theta,z)\,r \,d\theta\right]\,dr\,\,dz\\ &\displaystyle=\int_{c}^{d} \int_{v_1(r)}^{v_2(r)} \left[\int_{u_1(r,z)}^{u_2(r,z)} f(r\cos \theta, r\sin \theta,z)\,r \,d\theta\right]\,dz\,\,dr \end{array} $$
Example
Let $E$ be the region bounded below by the cone $z = \sqrt{x^2 + y^2}$ and above by the paraboloid $z = 2 - x^2 - y^2.$ Set up the triple integral $\displaystyle \iiint_{E} f (x, y, z) \,dV$ in cylindrical coordinates of the region, using the following orders of integration:
(a) $dz\, dr \, d\theta$
(b) $dr\, dz \,d\theta.$
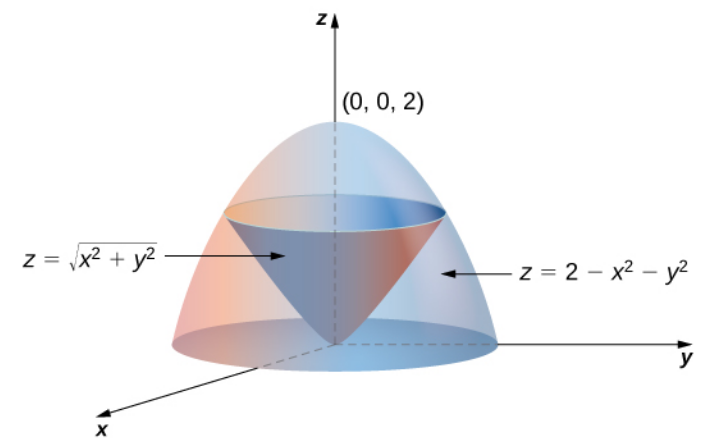
(a) For the order $dz\, dr \, d\theta,$ we must express the vertical $z$ as lying between two surfaces, both of which are functions $r$ and $\theta.$
For the lower cone surface, $z = \sqrt{x^2 + y^2}=r,$ and for the upper paraboloid surface, $z = 2 - x^2 - y^2=2-r^2.$ That is, $$ r\leq z \leq 2-r^2 $$ We now describe the projection $D$ onto the $r\theta$-plane. The boundary of $D$ is precisely where the two surfaces $z =r$ and $z=2-z^2$ intersect. That is, $$ \begin{array}{lll} &\displaystyle r=2-r^2 &\mbox{}\\ \implies &\displaystyle r^2+r-2=0&\mbox{}\\ \implies &\displaystyle (r+2)(r-1)=0&\mbox{}\\ \implies &\displaystyle r=-2 \mbox{ OR } r=1.&\mbox{}\\ \end{array} $$ Since we consider $r$ to be positive, we reject the negative root so that $r=1,$ which we interpret as the circle of radius $1$ in polar coordinates.
This is the boundary of $D.$
If follows that $D$ can be described as $D=\left\{(r,\theta)\in \mathbb{R}^2 \Bigr| 0 \leq r \leq 1, 0 \leq \theta \leq 2\pi\right\}$
The region $E$ is then $$ E=\left\{(r,\theta, z)\in \mathbb{R}^3 \Bigr| 0 \leq \theta \leq 2\pi, 0 \leq r \leq 1, r\leq z \leq 2-r^2 \right\} $$ We may then set up our integral as $$ \begin{array}{lll} %\displaystyle \iiint_{E} f (x, y, z) \,dV&\displaystyle=\iint_{D} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,dA &\mbox{}\\ %\displaystyle &\displaystyle=\int_{\alpha}^{\beta} \int_{v_1(\theta)}^{v_2(\theta)} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,dr\,d\theta &\mbox{}\\ \displaystyle \iiint_{E} f (x, y, z) \,dV &\displaystyle=\int_{0}^{2\pi} \int_{0}^{1} \int_{r}^{2-r^2} f (r\cos \theta, r\sin \theta, z) \, r \,dz\, dr \, d\theta &\mbox{}\\ \end{array} $$ (b) For the order $dr\, dz \, d\theta,$ we must express $r$ as a function of $z$ and $\theta.$
Since the reqion $E$ has cylindrical symmetery, $r$ does not depend on $\theta.$ However, $r$ certainly depends on $z.$
For the lower cone surface, $r = \sqrt{x^2 + y^2}=z$ when $0\leq z \leq 1.$
The upper paraboloid surface $z = 2 - x^2 - y^2=2-r^2$ gives us $r=\pm\sqrt{2-z}.$ Again, since $r\geq 0,$ we take the positive root so that $r=\sqrt{2-z}.$ This occurs when $1 \leq z \leq 2.$
In summary, we have $$ r= \begin{cases} z, & 0 \leq z \leq 1\\ \sqrt{2-z}, & 1 \leq z \leq 2\\ \end{cases} $$ We now consider the domain $D$ in the $\theta z$-plane. Since the region has cylindrical symmetry, every $(r,\theta,z)$ in the region can occur at any angle $0\leq \theta \leq 2\pi.$ That is, $z$ does not depend on $r.$ The limits of integration on $z$ are therefore constants.
If follows that $E$ can be described in two pieces: the lower, cone-shaped part $$E_L=\left\{(r,\theta, z)\in \mathbb{R}^3\Bigr| 0 \leq \theta \leq 2\pi, 0 \leq z \leq 1, 0 \leq r \leq z \right\}$$ and the upper, gum-drop shaped part $$E_U=\left\{(r,\theta, z)\in \mathbb{R}^3\Bigr| 0 \leq \theta \leq 2\pi, 1 \leq z \leq 2, 0 \leq r \leq \sqrt{2-z} \right\}$$ We may then set up our integral as $$ \begin{array}{lll} \displaystyle \iiint_{E} f (x, y, z) \,dV& \displaystyle \iiint_{E_L\cup E_U} f (x, y, z) \,dV &\mbox{}\\ \displaystyle & \displaystyle \iiint_{E_L} f (x, y, z) \,dV+\iiint_{E_U} f (x, y, z) \,dV &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{1} \int_{0}^{z} f (r\cos \theta, r\sin \theta, z) \, r \,dr\, dz \, d\theta+\int_{0}^{2\pi} \int_{1}^{2} \int_{0}^{\sqrt{2-z}} f (r\cos \theta, r\sin \theta, z) \, r \,dr\, dz \, d\theta &\mbox{}\\ \end{array} $$
For the lower cone surface, $z = \sqrt{x^2 + y^2}=r,$ and for the upper paraboloid surface, $z = 2 - x^2 - y^2=2-r^2.$ That is, $$ r\leq z \leq 2-r^2 $$ We now describe the projection $D$ onto the $r\theta$-plane. The boundary of $D$ is precisely where the two surfaces $z =r$ and $z=2-z^2$ intersect. That is, $$ \begin{array}{lll} &\displaystyle r=2-r^2 &\mbox{}\\ \implies &\displaystyle r^2+r-2=0&\mbox{}\\ \implies &\displaystyle (r+2)(r-1)=0&\mbox{}\\ \implies &\displaystyle r=-2 \mbox{ OR } r=1.&\mbox{}\\ \end{array} $$ Since we consider $r$ to be positive, we reject the negative root so that $r=1,$ which we interpret as the circle of radius $1$ in polar coordinates.
This is the boundary of $D.$
If follows that $D$ can be described as $D=\left\{(r,\theta)\in \mathbb{R}^2 \Bigr| 0 \leq r \leq 1, 0 \leq \theta \leq 2\pi\right\}$
The region $E$ is then $$ E=\left\{(r,\theta, z)\in \mathbb{R}^3 \Bigr| 0 \leq \theta \leq 2\pi, 0 \leq r \leq 1, r\leq z \leq 2-r^2 \right\} $$ We may then set up our integral as $$ \begin{array}{lll} %\displaystyle \iiint_{E} f (x, y, z) \,dV&\displaystyle=\iint_{D} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,dA &\mbox{}\\ %\displaystyle &\displaystyle=\int_{\alpha}^{\beta} \int_{v_1(\theta)}^{v_2(\theta)} \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r\cos \theta, r\sin \theta,z)\,r \,dz\right]\,dr\,d\theta &\mbox{}\\ \displaystyle \iiint_{E} f (x, y, z) \,dV &\displaystyle=\int_{0}^{2\pi} \int_{0}^{1} \int_{r}^{2-r^2} f (r\cos \theta, r\sin \theta, z) \, r \,dz\, dr \, d\theta &\mbox{}\\ \end{array} $$ (b) For the order $dr\, dz \, d\theta,$ we must express $r$ as a function of $z$ and $\theta.$
Since the reqion $E$ has cylindrical symmetery, $r$ does not depend on $\theta.$ However, $r$ certainly depends on $z.$
For the lower cone surface, $r = \sqrt{x^2 + y^2}=z$ when $0\leq z \leq 1.$
The upper paraboloid surface $z = 2 - x^2 - y^2=2-r^2$ gives us $r=\pm\sqrt{2-z}.$ Again, since $r\geq 0,$ we take the positive root so that $r=\sqrt{2-z}.$ This occurs when $1 \leq z \leq 2.$
In summary, we have $$ r= \begin{cases} z, & 0 \leq z \leq 1\\ \sqrt{2-z}, & 1 \leq z \leq 2\\ \end{cases} $$ We now consider the domain $D$ in the $\theta z$-plane. Since the region has cylindrical symmetry, every $(r,\theta,z)$ in the region can occur at any angle $0\leq \theta \leq 2\pi.$ That is, $z$ does not depend on $r.$ The limits of integration on $z$ are therefore constants.
If follows that $E$ can be described in two pieces: the lower, cone-shaped part $$E_L=\left\{(r,\theta, z)\in \mathbb{R}^3\Bigr| 0 \leq \theta \leq 2\pi, 0 \leq z \leq 1, 0 \leq r \leq z \right\}$$ and the upper, gum-drop shaped part $$E_U=\left\{(r,\theta, z)\in \mathbb{R}^3\Bigr| 0 \leq \theta \leq 2\pi, 1 \leq z \leq 2, 0 \leq r \leq \sqrt{2-z} \right\}$$ We may then set up our integral as $$ \begin{array}{lll} \displaystyle \iiint_{E} f (x, y, z) \,dV& \displaystyle \iiint_{E_L\cup E_U} f (x, y, z) \,dV &\mbox{}\\ \displaystyle & \displaystyle \iiint_{E_L} f (x, y, z) \,dV+\iiint_{E_U} f (x, y, z) \,dV &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{1} \int_{0}^{z} f (r\cos \theta, r\sin \theta, z) \, r \,dr\, dz \, d\theta+\int_{0}^{2\pi} \int_{1}^{2} \int_{0}^{\sqrt{2-z}} f (r\cos \theta, r\sin \theta, z) \, r \,dr\, dz \, d\theta &\mbox{}\\ \end{array} $$
Spherical Coordinates
In spherical coordinates, a point in space is described as $(\rho,\theta,\varphi).$
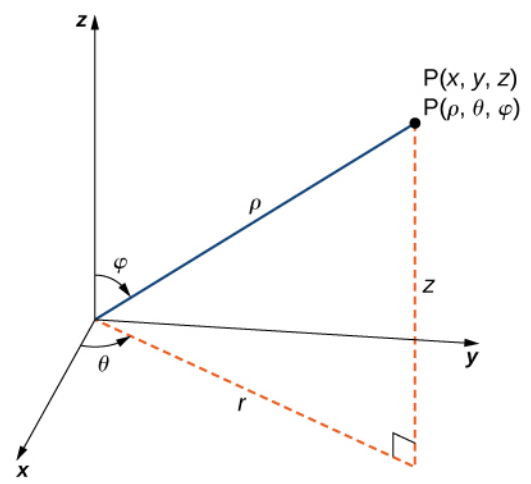
Relating Rectangular and Spherical Coordinates
We can express a location in spherical coordinates $(\rho,\theta,\varphi)$ in rectangular coordinates, $(x,y,z)=(r\cos \theta, r\sin \theta,\rho \cos \varphi)=(\rho \sin \varphi \cos \theta,\rho \sin \varphi \sin \theta,\rho \cos \varphi),$ that is $$ \begin{array}{l} x=\rho \sin \varphi \cos \theta\\ y=\rho \sin \varphi \sin \theta\\ z=\rho \cos \varphi \end{array} $$

Relating Rectangular and Spherical Coordinates
Since $(x,y,z)$ is on a sphere of radius $\rho,$ $x^2+y^2+z^2=\rho^2.$
That is, spherical coordinates are useful for describing situations which have circular symmetry around the origin.

A Note on Notation
Please be aware that there are two different ways of denoting the Greek letter "phi" (pronounced "fee").
The two notations are $\varphi$ and $\phi.$
Please be aware that our textbook uses both.
Example
The point in spherical coordinates $\displaystyle \left(8,\frac{\pi}{3},\frac{\pi}{6}\right)$ is graphed below.

In rectangular coordinates this point is expressed as $(2,2\sqrt{3},4\sqrt{3}).$
Surfaces in Spherical Coordinates
 |  | 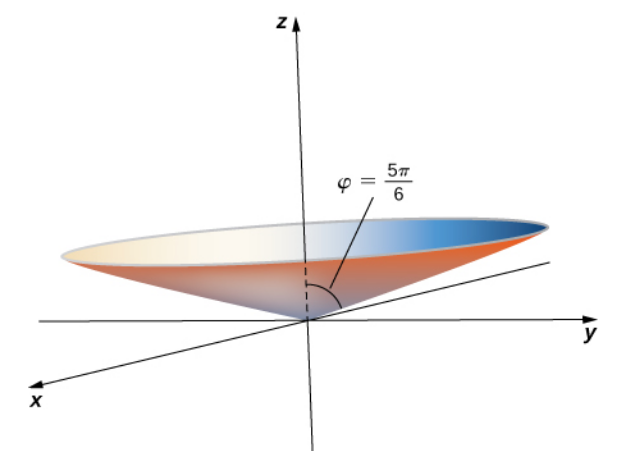 |
| $\rho=3$ | $\displaystyle \theta=\frac{\pi}{4}$ | $\displaystyle \varphi=\frac{5\pi}{6}$ |
Triple Integrals in Spherical Coordinates
From the figure we see that $\Delta V=\color{#f30b0b}{\Delta \theta \rho \sin \phi}\cdot \color{magenta}{\Delta \rho}\cdot \color{#ff7e27}{\rho \Delta \phi}=\rho^2\sin\phi\,\Delta \rho \, \Delta \phi \,\Delta \theta$
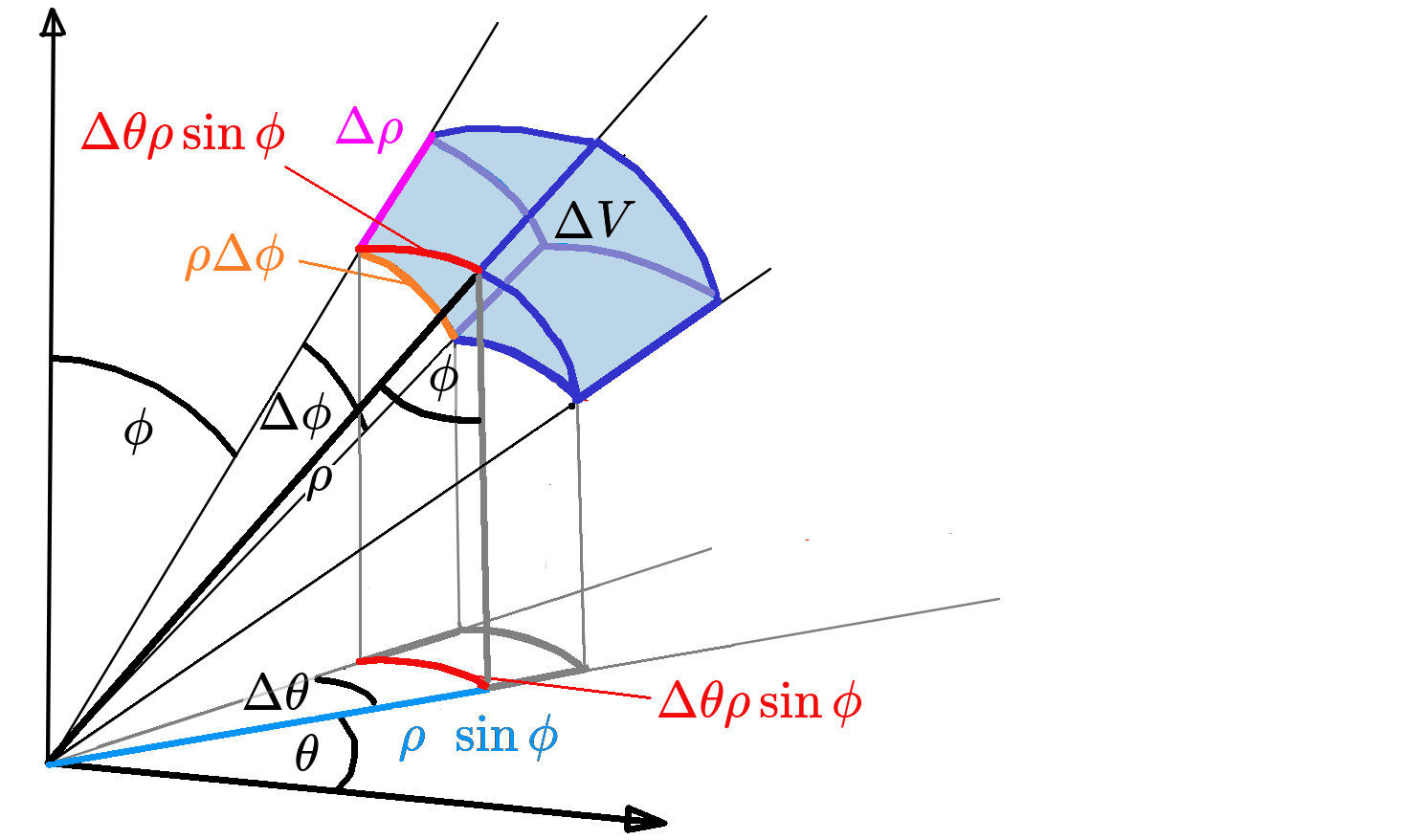
Triple Integrals in Spherical Coordinates
Taking it to the limit...
Triple Integrals in Spherical Coordinates
If $f(x,y,z)$ is continuous on a spherical solid box $B = [a, b] \times [\alpha, \beta] \times [\gamma, \delta],$ then $$ \begin{array}{ll} \displaystyle \iiint_B f(x,y,z)\, dV &\displaystyle =\iiint_B f(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2 \sin \phi \, d\rho \, d\phi \, d\theta\\ &\displaystyle= \int_{\alpha}^{\beta} \int_{\gamma}^{\delta} \int_{a}^{b} f(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta \end{array} $$
Example
Use spherical coordinates to set up an iterated triple integral to find $$ \iiint_{E} \sqrt{x^2+y^2+z^2} \,dV $$ the region bounded by the cone $z = \sqrt{3(x^2 + y^2)}$ and the hemisphere $z =\sqrt{4 - x^2 - y^2}.$
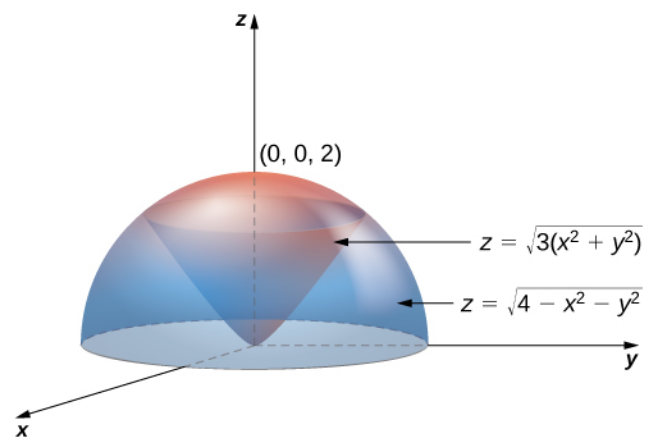
The region of integration $E$ can be described as
$$
\displaystyle E=\left\{(\rho,\phi,\theta)\in \mathbb{R}^3\Bigr| 0 \leq \rho \leq 2, 0 \leq \theta \leq 2\pi, 0\leq \phi \leq \phi_0 \right\}
$$
where $\phi_0$ is the angle between the cone's surface and the $z$-axis.
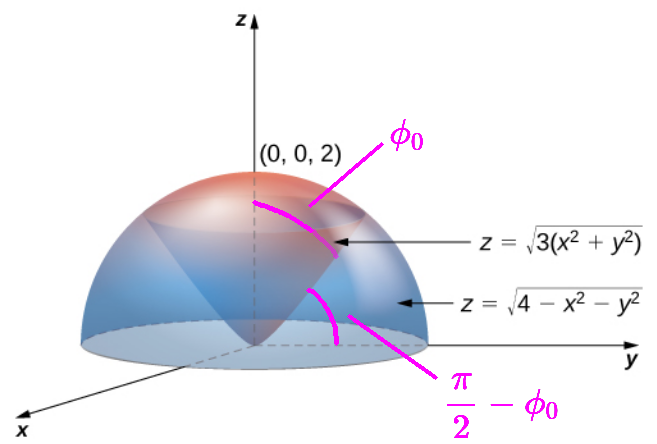
At any point $(x,y,z),$ the vertical distance $z$ is $\sqrt{3(x^2 + y^2)}$ and the horizontal distance in the $xy$-plane is $\sqrt{x^2 + y^2}.$
Then, the angle of elevation $\displaystyle \frac{\pi}{2}-\phi_0$ the cone's surface makes with the $xy$-plane satisfies $$ \begin{array}{lll} &\displaystyle \tan \left(\frac{\pi}{2}-\phi \right)=\frac{\sqrt{3(x^2 + y^2)}}{\sqrt{x^2 + y^2}}&\mbox{}\\ \implies &\displaystyle \tan \left(\frac{\pi}{2}-\phi \right) =\sqrt{3} &\mbox{}\\ \implies &\displaystyle \frac{\pi}{2}-\phi = \frac{\pi}{3}&\mbox{}\\ \implies &\displaystyle \phi =\frac{\pi}{2}- \frac{\pi}{3}&\mbox{}\\ \implies &\displaystyle \phi =\frac{\pi}{6}&\mbox{}\\ \end{array} $$ Thus the region of integration $E$ can be described as $$ \displaystyle E=\left\{(\rho,\phi,\theta)\in \mathbb{R}^3\Bigr| 0 \leq \rho \leq 2, 0 \leq \theta \leq 2\pi, 0\leq \phi \leq \frac{\pi}{6}\right\} $$ Thus, since $\sqrt{x^2+y^2+z^2}=\rho,$ our integral becomes $$ \begin{array}{lll} \displaystyle \iiint_{E} \sqrt{x^2+y^2+z^2} \,dV&\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/6} \int_{0}^{2} \rho \cdot \rho^2\sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/6} \int_{0}^{2} \rho^3\sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \end{array} $$
Special Note: To appreciate what we have just done, consider the same integral in rectangular coordinates. $$ \iiint_{E} \sqrt{x^2+y^2+z^2} \,dV=\int_{-1}^{1} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{\sqrt{3(x^2 + y^2)}}^{\sqrt{4-x^2-y^2}} \sqrt{x^2+y^2+z^2} \, dz \, dy \,dx $$

At any point $(x,y,z),$ the vertical distance $z$ is $\sqrt{3(x^2 + y^2)}$ and the horizontal distance in the $xy$-plane is $\sqrt{x^2 + y^2}.$
Then, the angle of elevation $\displaystyle \frac{\pi}{2}-\phi_0$ the cone's surface makes with the $xy$-plane satisfies $$ \begin{array}{lll} &\displaystyle \tan \left(\frac{\pi}{2}-\phi \right)=\frac{\sqrt{3(x^2 + y^2)}}{\sqrt{x^2 + y^2}}&\mbox{}\\ \implies &\displaystyle \tan \left(\frac{\pi}{2}-\phi \right) =\sqrt{3} &\mbox{}\\ \implies &\displaystyle \frac{\pi}{2}-\phi = \frac{\pi}{3}&\mbox{}\\ \implies &\displaystyle \phi =\frac{\pi}{2}- \frac{\pi}{3}&\mbox{}\\ \implies &\displaystyle \phi =\frac{\pi}{6}&\mbox{}\\ \end{array} $$ Thus the region of integration $E$ can be described as $$ \displaystyle E=\left\{(\rho,\phi,\theta)\in \mathbb{R}^3\Bigr| 0 \leq \rho \leq 2, 0 \leq \theta \leq 2\pi, 0\leq \phi \leq \frac{\pi}{6}\right\} $$ Thus, since $\sqrt{x^2+y^2+z^2}=\rho,$ our integral becomes $$ \begin{array}{lll} \displaystyle \iiint_{E} \sqrt{x^2+y^2+z^2} \,dV&\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/6} \int_{0}^{2} \rho \cdot \rho^2\sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/6} \int_{0}^{2} \rho^3\sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \end{array} $$
Special Note: To appreciate what we have just done, consider the same integral in rectangular coordinates. $$ \iiint_{E} \sqrt{x^2+y^2+z^2} \,dV=\int_{-1}^{1} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{\sqrt{3(x^2 + y^2)}}^{\sqrt{4-x^2-y^2}} \sqrt{x^2+y^2+z^2} \, dz \, dy \,dx $$
Triple Integrals in Spherical Coordinates Over General Regions
For a general region $E$ in space, $$ \begin{array}{lll} &\displaystyle \iiint_E f(x,y,z)\, dV\\ &\displaystyle =\iiint_E f(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2 \sin \phi \, d\rho \, d\phi \, d\theta&\mbox{}\\ &\displaystyle= \iint_{D_1} \left[\int_{u_1(\theta,\phi)}^{u_2(\theta,\phi)} f(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2\sin \phi \, d\rho \right]\, d\phi \, d\theta&\mbox{$D_1$ is $E$ projected onto the $\theta\phi$-plane}\\ &\displaystyle= \iint_{D_2} \left[\int_{v_1(\rho,\theta)}^{v_2(\rho,\theta)} f(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2\sin \phi \, d\phi \right] \, d\rho \, d\theta&\mbox{$D_2$ is $E$ projected onto the $\rho\theta$-plane}\\ &\displaystyle= \iint_{D_3} \left[\int_{w_1(\rho,\phi)}^{w_2(\rho,\phi)} f(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2\sin \phi \, d\theta \right] \, d\rho \, d\phi &\mbox{$D_3$ is $E$ projected onto the $\rho\phi$-plane} \end{array} $$
Example
Let $E$ be the region bounded below by the cone $z = \sqrt{x^2 + y^2}$ and above by the sphere $z = x^2 + y^2 + z^2.$
Set up a triple integral in spherical coordinates and find the volume of the region using the following two orders of integration
(a) $d\rho \, d\phi \, d\theta$
(b) $d\phi \, d\rho \, d\theta$
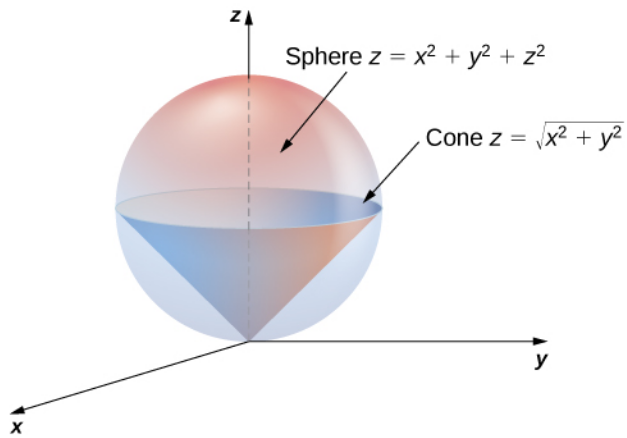
(a) $d\rho \, d\phi \, d\theta$
The sphere is given by $z=x^2+y^2+z^2=\rho^2,$ and in general $z=\rho\cos \phi$ when transforming to spherical coordinates. Thus $$ \begin{array}{lll} &\displaystyle \rho^2=\rho \cos \phi&\mbox{}\\ \implies &\displaystyle \rho=\cos \phi &\mbox{}\\ \end{array} $$ So, in spherical coordinates, we may describe the entire sphere in the figure as $\rho=\cos \phi$ where $0 \leq \phi \leq \displaystyle \frac{\pi}{2}.$ (Remember that shifted circles in polar coordinates have the form $r=a\cos \theta$ and $r=a\sin \theta.$)
To get the region of integration, we merely need to stop at $\phi=\displaystyle \frac{\pi}{4}$ since this is the angle the surface of the cone makes with the $z$ axis.
We may then describe this region $E$ as $$ \displaystyle E=\left\{(\rho,\phi,\theta)\in \mathbb{R}^3\Bigr| 0 \leq \theta \leq \pi, 0\leq \phi \leq \frac{\pi}{4},0 \leq \rho \leq \cos \phi \right\} $$ Our volume integral is therefore $$ \begin{array}{lll} \displaystyle \iiint_{E} \,dV&\displaystyle= \iint_{D} \left[\int_{u_1(\theta,\phi)}^{u_2(\theta,\phi)} \,\rho^2\sin \phi \, d\rho \right]\, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{\alpha}^{\beta} \int_{v_1(\theta)}^{v_2(\theta)}\int_{u_1(\theta,\phi)}^{u_2(\theta,\phi)} \,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/4} \int_{0}^{\cos \phi} \rho^2 \sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \end{array} $$ Computing the volume of $E,$ $$ \begin{array}{lll} \displaystyle \iiint_{E} \,dV& \displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/4} \int_{0}^{\cos \phi} \rho^2 \sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/4} \left[ \frac{1}{3}\rho^3 \sin \phi \right]_{0}^{\cos \phi} \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/4} \frac{1}{3}\cos^3 \phi \sin \phi \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \int_{0}^{\pi/4} \cos^3 \phi \sin \phi \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ -\frac{1}{4}\cos^4 \phi \right]_{0}^{\pi/4} \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ -\frac{1}{4}\cos^4\left(\frac{\pi}{4}\right) -\left(-\frac{1}{4}\cos^4(0)\right) \right] \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ -\frac{1}{4}\left(\frac{1}{\sqrt{2}}\right)^4+\frac{1}{4}\right] \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ \frac{1}{4}-\frac{1}{4}\left(\frac{1}{4}\right)\right] \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ \frac{4}{16}-\frac{1}{16}\right] \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi}\frac{3}{16} \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\cdot \frac{3}{16}\int_{0}^{2\pi} \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{16}\cdot 2\pi &\mbox{}\\ \displaystyle &\displaystyle= \frac{\pi}{8} &\mbox{}\\ \end{array} $$ (b) $d\phi \, d\rho \, d\theta$
We want to set up our integral as $$ \begin{array}{lll} \displaystyle \iiint_{E} \,dV&\displaystyle= \iint_{D_2} \left[\int_{v_1(\rho,\theta)}^{v_2(\rho,\theta)}\, \rho^2\sin \phi \, d\phi \right] \, d\rho \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{\theta=0}^{\theta=2\pi} \int_{\rho=v_1(\theta)}^{\rho=v_2(\theta)} \int_{\phi=v_1(\rho,\theta)}^{\phi=v_2(\rho,\theta)} \,\rho^2\sin \phi \, d\phi \, d\rho \, d\theta &\mbox{}\\ \end{array} $$ Now, since the region $E$ has circular symmetry about the $z$ axis, neither $\phi$ nor $\rho$ depend on $\theta.$
So, the integral will have the form $$ \int_{\theta=0}^{\theta=2\pi} \int_{\rho=\mbox{constant}_1}^{\rho=\mbox{constant}_2} \int_{\phi=u_1(\rho)}^{\phi=u_2(\rho)} \rho^2\sin \phi \, d\phi \, d\rho \, d\theta $$ Now, from both the figure and part (a), we know that $\rho=\cos \phi$ on the interval $\displaystyle 0 \leq \phi \leq \frac{\pi}{4}.$
To understand how $\phi$ varies in terms of $\rho,$ we draw a picture of the situation.
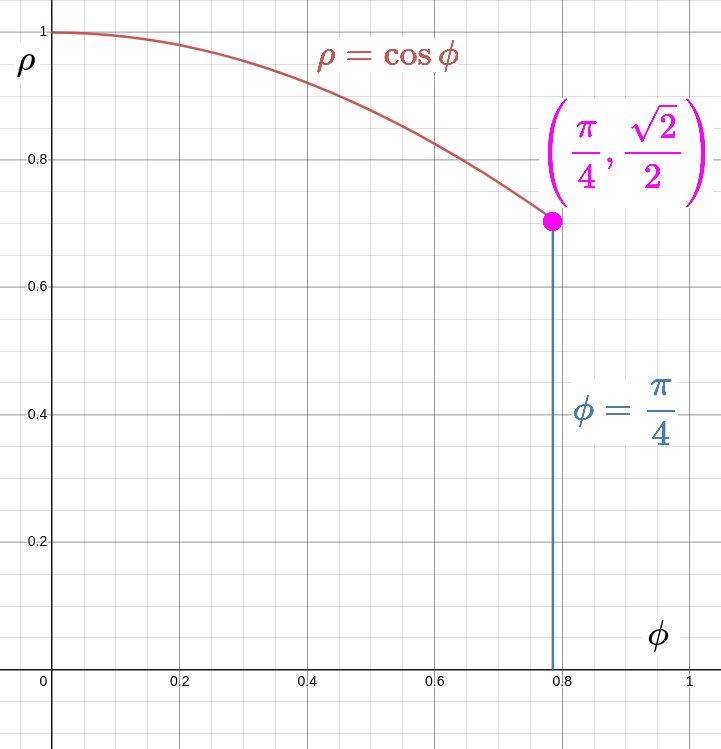
From our graph, it's plain to see that $\phi$ as a function of $\rho$ must be expressed piecewise as $$ \phi= \begin{cases} \displaystyle \frac{\pi}{4} & \displaystyle 0 \leq \rho \leq \frac{\sqrt{2}}{2}\\ \displaystyle \cos^{-1} \rho & \displaystyle \frac{\sqrt{2}}{2} \leq \rho \leq 1 \end{cases} $$ Thus, our integral must be broken up into two parts: $$ \iiint_{E} \,dV = \int_{\theta=0}^{\theta=2\pi} \int_{\rho=0}^{\rho=\sqrt{2}/2} \int_{\phi=0}^{\phi=\pi/4} \,\rho^2\sin \phi \, d\phi \, d\rho \, d\theta +\int_{\theta=0}^{\theta=2\pi} \int_{\rho=\sqrt{2}/2}^{\rho=1} \int_{\phi=0}^{\phi=\cos^{-1} \rho} \,\rho^2\sin \phi \, d\phi \, d\rho \, d\theta $$ Clearly, this integral is not as warm and fuzzy as the one we obtained in part (a).
The sphere is given by $z=x^2+y^2+z^2=\rho^2,$ and in general $z=\rho\cos \phi$ when transforming to spherical coordinates. Thus $$ \begin{array}{lll} &\displaystyle \rho^2=\rho \cos \phi&\mbox{}\\ \implies &\displaystyle \rho=\cos \phi &\mbox{}\\ \end{array} $$ So, in spherical coordinates, we may describe the entire sphere in the figure as $\rho=\cos \phi$ where $0 \leq \phi \leq \displaystyle \frac{\pi}{2}.$ (Remember that shifted circles in polar coordinates have the form $r=a\cos \theta$ and $r=a\sin \theta.$)
To get the region of integration, we merely need to stop at $\phi=\displaystyle \frac{\pi}{4}$ since this is the angle the surface of the cone makes with the $z$ axis.
We may then describe this region $E$ as $$ \displaystyle E=\left\{(\rho,\phi,\theta)\in \mathbb{R}^3\Bigr| 0 \leq \theta \leq \pi, 0\leq \phi \leq \frac{\pi}{4},0 \leq \rho \leq \cos \phi \right\} $$ Our volume integral is therefore $$ \begin{array}{lll} \displaystyle \iiint_{E} \,dV&\displaystyle= \iint_{D} \left[\int_{u_1(\theta,\phi)}^{u_2(\theta,\phi)} \,\rho^2\sin \phi \, d\rho \right]\, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{\alpha}^{\beta} \int_{v_1(\theta)}^{v_2(\theta)}\int_{u_1(\theta,\phi)}^{u_2(\theta,\phi)} \,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/4} \int_{0}^{\cos \phi} \rho^2 \sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \end{array} $$ Computing the volume of $E,$ $$ \begin{array}{lll} \displaystyle \iiint_{E} \,dV& \displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/4} \int_{0}^{\cos \phi} \rho^2 \sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/4} \left[ \frac{1}{3}\rho^3 \sin \phi \right]_{0}^{\cos \phi} \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi} \int_{0}^{\pi/4} \frac{1}{3}\cos^3 \phi \sin \phi \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \int_{0}^{\pi/4} \cos^3 \phi \sin \phi \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ -\frac{1}{4}\cos^4 \phi \right]_{0}^{\pi/4} \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ -\frac{1}{4}\cos^4\left(\frac{\pi}{4}\right) -\left(-\frac{1}{4}\cos^4(0)\right) \right] \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ -\frac{1}{4}\left(\frac{1}{\sqrt{2}}\right)^4+\frac{1}{4}\right] \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ \frac{1}{4}-\frac{1}{4}\left(\frac{1}{4}\right)\right] \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi} \left[ \frac{4}{16}-\frac{1}{16}\right] \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\int_{0}^{2\pi}\frac{3}{16} \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{3}\cdot \frac{3}{16}\int_{0}^{2\pi} \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{16}\cdot 2\pi &\mbox{}\\ \displaystyle &\displaystyle= \frac{\pi}{8} &\mbox{}\\ \end{array} $$ (b) $d\phi \, d\rho \, d\theta$
We want to set up our integral as $$ \begin{array}{lll} \displaystyle \iiint_{E} \,dV&\displaystyle= \iint_{D_2} \left[\int_{v_1(\rho,\theta)}^{v_2(\rho,\theta)}\, \rho^2\sin \phi \, d\phi \right] \, d\rho \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{\theta=0}^{\theta=2\pi} \int_{\rho=v_1(\theta)}^{\rho=v_2(\theta)} \int_{\phi=v_1(\rho,\theta)}^{\phi=v_2(\rho,\theta)} \,\rho^2\sin \phi \, d\phi \, d\rho \, d\theta &\mbox{}\\ \end{array} $$ Now, since the region $E$ has circular symmetry about the $z$ axis, neither $\phi$ nor $\rho$ depend on $\theta.$
So, the integral will have the form $$ \int_{\theta=0}^{\theta=2\pi} \int_{\rho=\mbox{constant}_1}^{\rho=\mbox{constant}_2} \int_{\phi=u_1(\rho)}^{\phi=u_2(\rho)} \rho^2\sin \phi \, d\phi \, d\rho \, d\theta $$ Now, from both the figure and part (a), we know that $\rho=\cos \phi$ on the interval $\displaystyle 0 \leq \phi \leq \frac{\pi}{4}.$
To understand how $\phi$ varies in terms of $\rho,$ we draw a picture of the situation.

From our graph, it's plain to see that $\phi$ as a function of $\rho$ must be expressed piecewise as $$ \phi= \begin{cases} \displaystyle \frac{\pi}{4} & \displaystyle 0 \leq \rho \leq \frac{\sqrt{2}}{2}\\ \displaystyle \cos^{-1} \rho & \displaystyle \frac{\sqrt{2}}{2} \leq \rho \leq 1 \end{cases} $$ Thus, our integral must be broken up into two parts: $$ \iiint_{E} \,dV = \int_{\theta=0}^{\theta=2\pi} \int_{\rho=0}^{\rho=\sqrt{2}/2} \int_{\phi=0}^{\phi=\pi/4} \,\rho^2\sin \phi \, d\phi \, d\rho \, d\theta +\int_{\theta=0}^{\theta=2\pi} \int_{\rho=\sqrt{2}/2}^{\rho=1} \int_{\phi=0}^{\phi=\cos^{-1} \rho} \,\rho^2\sin \phi \, d\phi \, d\rho \, d\theta $$ Clearly, this integral is not as warm and fuzzy as the one we obtained in part (a).
Example
Use rectangular, cylindrical, and spherical coordinates to set up triple integrals for finding the volume of the region inside the sphere $x^2 + y^2 + z^2 = 4$ but outside the cylinder $x^2 + y^2 = 1.$
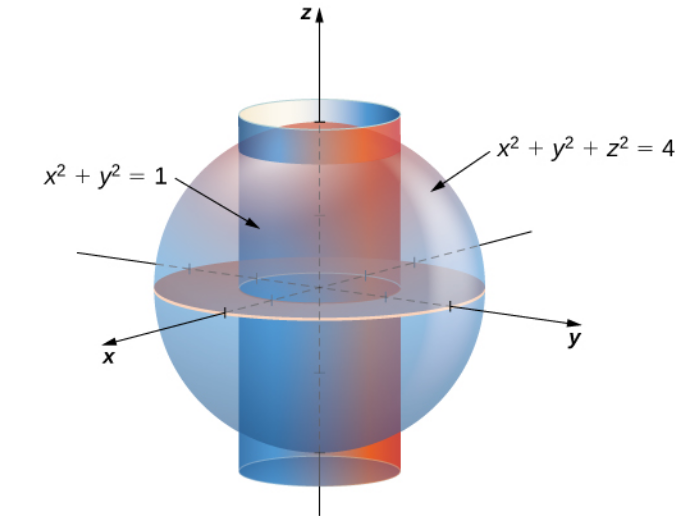
Rectangular Coordinates: The region $E$ may be expressed as $$ \displaystyle E=\mbox{Sphere}\backslash\mbox{Middle Piece} $$ where $$ \mbox{Sphere}=\left\{(x,y,z)\in \mathbb{R}^3\Bigr| -2\leq x \leq 2, -\sqrt{4-x^2}\leq y\leq\sqrt{4-x^2} , -\sqrt{4-x^2-y^2}\leq z \leq \sqrt{4-x^2-y^2}\right\} $$ and $$ \mbox{Middle Piece}=\left\{(x,y,z)\in \mathbb{R}^3\Bigr| -1\leq x \leq 1, -\sqrt{1-x^2}\leq y\leq\sqrt{1-x^2} , -\sqrt{4-x^2-y^2}\leq z \leq \sqrt{4-x^2-y^2}\right\} $$ The volume as an integral is then expressed as $$ \begin{array}{lll} \displaystyle V(E)&\displaystyle=\iiint_E \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{\mbox{Sphere}\backslash\mbox{Middle Piece}} \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{\mbox{Sphere}} \, dV-\iiint_{\mbox{Middle Piece}} \, dV &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{2} \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{-\sqrt{4-x^2-y^2}}^{\sqrt{4-x^2-y^2}} \, dz \, dy \, dx -\int_{-1}^{1} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{-\sqrt{4-x^2-y^2}}^{\sqrt{4-x^2-y^2}} \, dz \, dy \, dx &\mbox{}\\ \end{array} $$
Cylindrical Coordinates: Since $x^2+y^2+z^2=4,$ we may write $z=\pm\sqrt{4-x^2-y^2}=\pm\sqrt{4-r^2}.$
Thus the region $E$ may be expressed as $$ \displaystyle E=\left\{(r,\theta,z)\in \mathbb{R}^3\Bigr| 1\leq r \leq 2, 0 \leq \theta \leq 2\pi, -\sqrt{4-r^2}\leq z \leq \sqrt{4-r^2}\right\} $$ The volume as an integral is then expressed as $$ \begin{array}{lll} \displaystyle V(E)&\displaystyle=\iiint_E \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{E} \, r \, dz \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{1}^{2} \int_{-\sqrt{4-r^2}}^{\sqrt{4-r^2}} \, r \, dz \, dr \, d\theta &\mbox{}\\ \end{array} $$
Spherical Coordinates: We will set up our volume integral as
$$ \begin{array}{lll} \displaystyle \iiint_E \, dV &\displaystyle= \iint_{D} \left[\int_{u_1(\theta,\phi)}^{u_2(\theta,\phi)} \,\rho^2\sin \phi \, d\rho \right]\, d\phi \, d\theta&\mbox{}\\ \displaystyle &\displaystyle= \int_{\theta=0}^{2\pi}\int_{\phi=v_1(\theta)}^{\phi=v_2(\theta)}\int_{\rho=u_1(\theta,\phi)}^{\rho=u_2(\theta,\phi)}\,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta&\mbox{}\\ \end{array} $$ First, we note that since the region has circular symmetry about the $z$-axis, neither $\rho$ nor $\phi$ vary with $\theta.$
Thus, our integral will have the form $$ \begin{array}{lll} \displaystyle \iiint_E \, dV &\displaystyle= \int_{\theta=0}^{2\pi}\int_{\phi=\mbox{constant}_1}^{\phi=\mbox{constant}_2}\int_{\rho=u_1(\phi)}^{\rho=u_2(\phi)}\,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta&\mbox{}\\ \end{array} $$ To further pin down the limits of integration, we look at a cross-section of the region $E.$
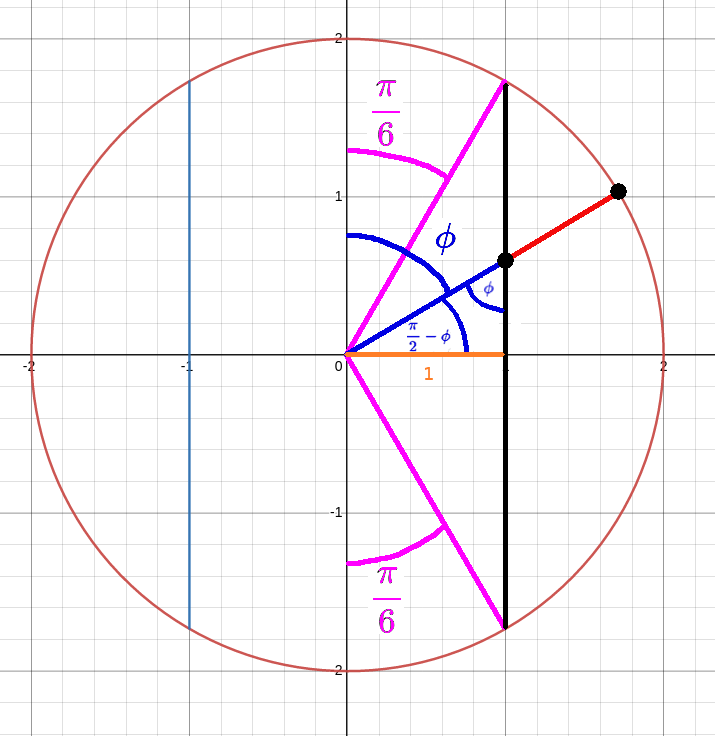
From the figure we see that $ \displaystyle \sin \phi=\frac{\color{darkorange}{1}}{\color{blue}{\mbox{hypotenuse}}} $ so that $$ \rho=\color{blue}{\mbox{hypotenuse}}=\csc \phi $$ is the lower limit of integration on the inner integral.
Since the outer sphere has radius $\rho=2,$ this is the upper limit on the inner integral.
Then, so far, we have $$ \begin{array}{lll} \displaystyle \iiint_E \, dV &\displaystyle= \int_{\theta=0}^{\theta=2\pi}\int_{\phi=\mbox{constant}_1}^{\phi=\mbox{constant}_2}\int_{\rho=\csc \phi}^{\rho=2} f(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta&\mbox{}\\ \end{array} $$ Now, the figure also shows that $\displaystyle \color{magenta}{\frac{\pi}{6}} \leq \phi \leq \color{magenta}{\frac{5\pi}{6}},$
Thus the volume as a triple integral is expressed as $$ \begin{array}{lll} \displaystyle V(E)&\displaystyle=\iiint_E \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{E} \, \rho^2 \sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{\pi/6}^{5\pi/6} \int_{\csc \phi}^{2} \rho^2 \sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\ \end{array} $$
Application
Using data from here, we fitted a model which predicts the density of the atmosphere in terms of an altitude in meters.
At a distance $\rho$ kilometers from the center of the earth, a model which approximates the density $\delta$ of air is $$\delta = 1.4477 e^{-0.1414(\rho-6370)}, \,\,\,\mbox{ in kg}/\mbox{m}^3$$

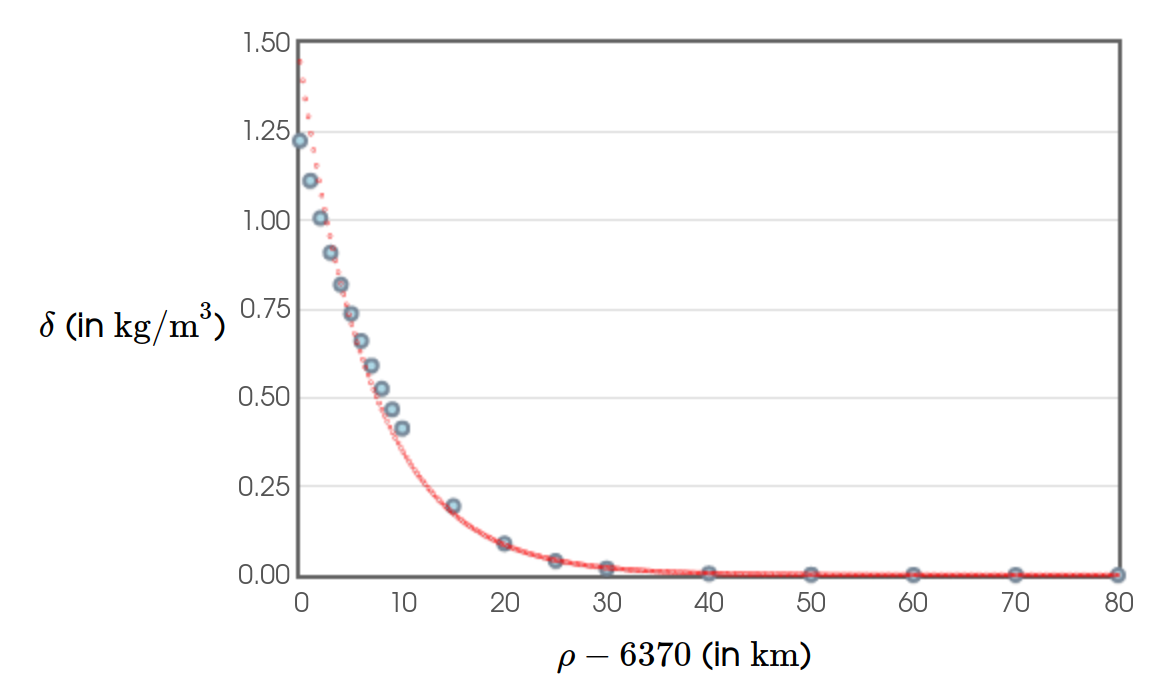
Use this model to estimate the mass of earth's atmosphere up to $80$ km above the surface.
Our region of integration $A$ is a larger sphere of radius $6450$ (the top of the stratosphere) with a smaller inner sphere of radius $6370$ (earth's surface)
is removed. That is, in spherical coordinates,
$$
\displaystyle A=\left\{(\rho,\phi,\theta)\in \mathbb{R}^3\Bigr| 0 \leq \theta \leq 2\pi, 0\leq \phi \leq \pi, 6370 \leq \rho \leq 6450 \right\}
$$
Now, we note that in order to integrate, we must make the units of $\delta,$ $\mbox{kg/m}^3,$ consistent with the units of $\rho,$ $\mbox{km}.$
We shall convert $\delta$ from $\mbox{kg/m}^3$ to $\mbox{kg/km}^3$ by multiplying by $10^9$ since there are $10^9$ cubic meters in $1$ cubic
kilometer. That is, we restate our model as
$$\delta = 1.4477\times 10^9 \cdot e^{-0.1414(\rho-6370)}, \,\,\,\mbox{ in kg}/\mbox{km}^3$$
Then the mass is
$$
\begin{array}{lll}
\displaystyle \iiint_A \delta(x,y,z)\, dV&\displaystyle=\iiint_A \delta(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{\pi} \int_{6370}^{6450} \delta(\rho \sin \phi \cos \theta,\rho \sin \phi \sin \theta,\rho \cos \phi)\,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2\pi} \int_{0}^{\pi} \int_{6370}^{6450} 1.4477\times 10^9 \cdot e^{-0.1414(\rho-6370)}\,\rho^2\sin \phi \, d\rho \, d\phi \, d\theta&\mbox{}\\
\displaystyle &\displaystyle=1.4477\times 10^9\int_{0}^{2\pi} \int_{0}^{\pi} \sin \phi \left(\int_{6370}^{6450} \rho^2 e^{-0.1452(\rho-6370)} \, d\rho\right) \, d\phi \, d\theta&\mbox{}\\
\displaystyle &\displaystyle=1.4477\times 10^9 \left(\int_{6370}^{6450} \rho^2 e^{-0.1452(\rho-6370)} \, d\rho\right) \left(\int_{0}^{2\pi} \int_{0}^{\pi} \sin \phi \, d\phi \, d\theta \right)&\mbox{}\\
\displaystyle &\displaystyle=1.4477\times 10^9 \left(\int_{6370}^{6450} \rho^2 e^{-0.1452(\rho-6370)} \, d\rho\right)\left(\int_{0}^{\pi} \sin \phi \, d\phi\right) \left(\int_{0}^{2\pi} \, d\theta \right)&\mbox{}\\
\displaystyle &\displaystyle\approx 1.4477\times 10^9 \left(2.80058\times 10^8\right)\cdot 2 \cdot 2 \pi&\mbox{}\\
\displaystyle &\displaystyle\approx 5.09\times 10^{18}&\mbox{}\\
\end{array}
$$
That is, the mass of earth's atmosphere to an altitude of $80$ km is about $5.09\times 10^{18}$ kilograms.
Special Note: According to the Handbook of Chemistry and Physics, the mass of earth's total atmosphere is about $5.15 \times 10^{18}$ kilograms.
Special Note: According to the Handbook of Chemistry and Physics, the mass of earth's total atmosphere is about $5.15 \times 10^{18}$ kilograms.