Today we integrate functions of three variables over regions in space!
The geometrical interpretation is less straightforward too, but nonetheless, triple integrals are VERY useful!
Triple Integrals Over Rectangular Regions
Triple integrals are computed with three-variable functions $f(x,y,z).$

The geometrical interpretation is not as straightforward as double integrals since the result is a hyper-volume (more than $3$-D volume).
Triple Integrals Over Rectangular Regions
Just as we began computing double integrals over rectangular regions, we begin estimating the triple integral of $f(x,y,z)$ over a rectangular "box" region $B.$

Triple Integrals Over Rectangular Regions
We construct our box region as $B$ as $[a,b]\times [c,d]\times [r,s].$

Triple Integrals Over Rectangular Regions
We then break up $[a,b]$ into $\ell$ intervals of size $\Delta x,$ $[c,d]$ into $m$ intervals of size $\Delta y,$ and $[r,s]$ into $n$ intervals of size $\Delta z,$

Triple Integrals Over Rectangular Regions
In each subinterval $[x_{i-1},x_{i}]$ we choose a point $x_i^*,$ and in each subinterval $[y_{j-1},y_{j}]$ choose a point $y_j^*,$ and in each subinterval $[z_{k-1},z_{k}]$ choose a point $z_k^*.$
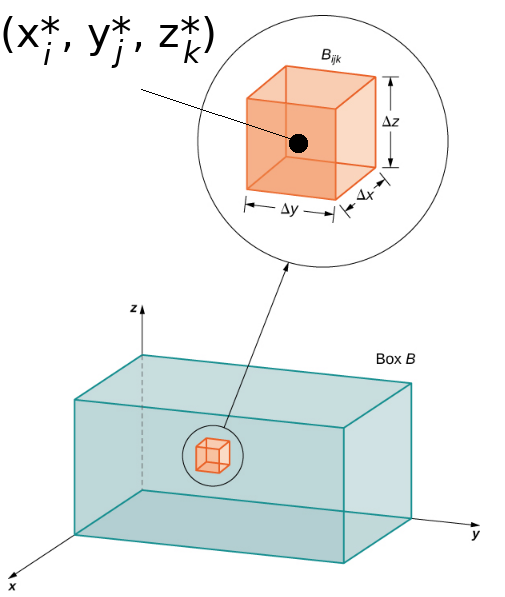
Triple Integrals Over Rectangular Regions
The function value at the $ijk$th rectangular box is $f(x_i^*,y_j^*,z_k)$ so that the "volume" of the $ijk$th box is $$ f(x_i^*,y_j^*,z_k)\,\Delta x\, \Delta y \, \Delta z=f(x_i^*,y_j^*,z_k)\,\Delta V $$

Triple Integrals Over Rectangular Regions
Adding up all of volumes of all the boxes gives us an approximation of the volume under the surface. $$ \mbox{Integral over $B$}\approx\sum_{k=1}^{n}\sum_{j=1}^{m}\sum_{i=1}^{\ell}f(x_i^*,y_j^*,z_k^*)\,\Delta V $$

Triple Integrals Over Rectangular Regions
In the limit, we get the triple integral...
Triple Integrals Over Rectangular Regions
The triple integral of the function $f (x, y,z)$ over the rectangular region $R=[a,b]\times[c,d]\times[r,s]$ in $\mathbb{R}^3$ is defined as $$ \iiint_{B} f(x,y,z) \,dV=\lim_{\ell,m,n \rightarrow \infty}\sum_{k=1}^{n}\sum_{j=1}^{m}\sum_{i=1}^{\ell}f(x_i^*,y_j^*,z_k^*)\,\Delta V $$ When this limit exists, we say that $f(x,y,z)$ is integrable over $B.$
Fubini’s Theorem for Triple Integrals
If $f (x, y, z)$ is continuous on a rectangular box $B = [a, b] \times [c, d] \times [r, s],$ then $$ \iiint_{B} f(x,y,z) \,dV= \int_{r}^{s} \int_{c}^{d}\int_{a}^{b} f(x,y,z) \,dx \,dy \, dz $$ This integral is also equal to any of the other five possible orderings for the iterated triple integral.
Example
Evaluate the triple integral $$ \iiint_{B} x^2 yz \,dV $$ over $B = \left\{(x, y, z)\in \mathbb{R}^3| -2 \leq x \leq 1, 0 \leq y \leq 3, 1 \leq z \leq 5 \right\}$ as shown in the following figure.
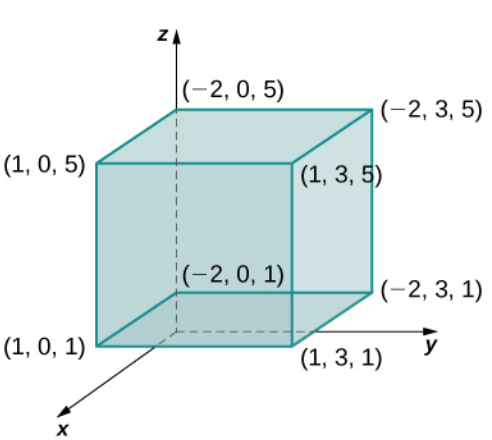
$$
\begin{array}{lll}
\displaystyle \iiint_{B} x^2 yz \,dV&\displaystyle= \int_{-2}^{1}\int_{0}^{3}\int_{1}^{5} x^2 yz \, dz \, dy \, dx&\mbox{}\\
\displaystyle &\displaystyle=\int_{-2}^{1}\int_{0}^{3} x^2 y \cdot \left[\frac{1}{2}z^2\right]_{1}^{5} \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{-2}^{1}\int_{0}^{3} x^2 y \cdot 12 \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle=12\int_{-2}^{1}\int_{0}^{3} x^2 y \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle=12\int_{-2}^{1} x^2 \cdot \left[\frac{1}{2}y^2\right]_{0}^{3} \, dx &\mbox{}\\
\displaystyle &\displaystyle=12\cdot\frac{9}{2}\int_{-2}^{1} x^2 \, dx &\mbox{}\\
\displaystyle &\displaystyle=54\int_{-2}^{1} x^2 \, dx &\mbox{}\\
\displaystyle &\displaystyle=54\cdot \left[\frac{1}{3}x^3\right]_{-2}^{1} \, dx &\mbox{}\\
\displaystyle &\displaystyle=54\cdot 3 &\mbox{}\\
\displaystyle &\displaystyle=162 &\mbox{}\\
\end{array}
$$
Scenic Alternative
Since $f(x,y,z)=x^2yz$ is a product of single-variable functions of $x,$ $y,$ and $z,$ we may do the following. $$ \begin{array}{lll} \displaystyle \iiint_{B} x^2 yz \,dV&\displaystyle= \int_{-2}^{1}\int_{0}^{3}\int_{1}^{5} x^2 yz \, dz \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{1}\int_{0}^{3}x^2 y\left(\int_{1}^{5} z \, dz\right) \, dy \, dx &\mbox{since $x$ and $y$ are constant wrt to $z$}\\ \displaystyle &\displaystyle=\left(\int_{-2}^{1}\int_{0}^{3}x^2 y \, dy \, dx\right) \left(\int_{1}^{5} z \, dz\right)&\mbox{pull out constant}\\ \displaystyle &\displaystyle=\left(\int_{-2}^{1}x^2 \left(\int_{0}^{3} y \, dy\right) \, dx\right) \left(\int_{1}^{5} z \, dz\right)&\mbox{since $x$ is constant wrt to $y$}\\ \displaystyle &\displaystyle=\left(\int_{-2}^{1}x^2 \, dx\right)\left(\int_{0}^{3} y \, dy\right) \left(\int_{1}^{5} z \, dz\right)&\mbox{pull out constant}\\ \displaystyle &\displaystyle=\left[\frac{1}{3}x^3 \right]_{-2}^{1}\left[ \frac{1}{2}y^2\right]_{0}^{3} \left[ \frac{1}{2}z^2 \right]_{1}^{5}&\mbox{}\\ \displaystyle &\displaystyle=162 &\mbox{}\\ \end{array} $$
Since $f(x,y,z)=x^2yz$ is a product of single-variable functions of $x,$ $y,$ and $z,$ we may do the following. $$ \begin{array}{lll} \displaystyle \iiint_{B} x^2 yz \,dV&\displaystyle= \int_{-2}^{1}\int_{0}^{3}\int_{1}^{5} x^2 yz \, dz \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{1}\int_{0}^{3}x^2 y\left(\int_{1}^{5} z \, dz\right) \, dy \, dx &\mbox{since $x$ and $y$ are constant wrt to $z$}\\ \displaystyle &\displaystyle=\left(\int_{-2}^{1}\int_{0}^{3}x^2 y \, dy \, dx\right) \left(\int_{1}^{5} z \, dz\right)&\mbox{pull out constant}\\ \displaystyle &\displaystyle=\left(\int_{-2}^{1}x^2 \left(\int_{0}^{3} y \, dy\right) \, dx\right) \left(\int_{1}^{5} z \, dz\right)&\mbox{since $x$ is constant wrt to $y$}\\ \displaystyle &\displaystyle=\left(\int_{-2}^{1}x^2 \, dx\right)\left(\int_{0}^{3} y \, dy\right) \left(\int_{1}^{5} z \, dz\right)&\mbox{pull out constant}\\ \displaystyle &\displaystyle=\left[\frac{1}{3}x^3 \right]_{-2}^{1}\left[ \frac{1}{2}y^2\right]_{0}^{3} \left[ \frac{1}{2}z^2 \right]_{1}^{5}&\mbox{}\\ \displaystyle &\displaystyle=162 &\mbox{}\\ \end{array} $$
Triple Integrals Over General Regions
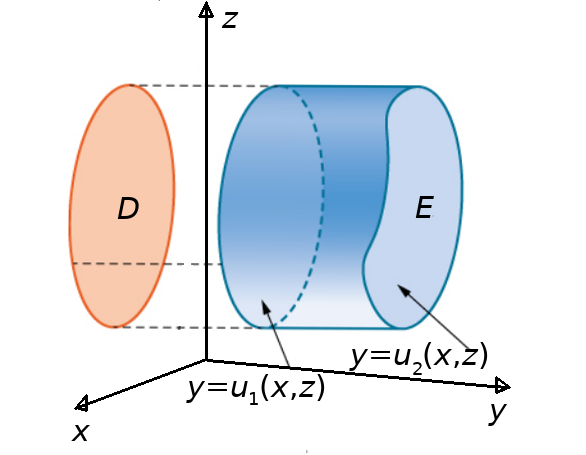
The triple integral of a continuous function $f (x, y, z)$ over a general three-dimensional region $E = \left\{(x, y, z) \in \mathbb{R}^3|(x, y) \in D, u_1(x, y) \leq z \leq u_2(x, y)\right\},$ where $D$ is the projection of $E$ onto the $xy$ -plane, is $$ \iiint_{E} f(x,y,z) \,dV= \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz\right] \,dA $$

Triple Integrals Over General Regions: Part 2
The triple integral of a continuous function $f (x, y, z)$ over a general three-dimensional region $E = \left\{(x, y, z) \in \mathbb{R}^3|(x, z) \in D, u_1(x, z) \leq y \leq u_2(x, z)\right\},$ where $D$ is the projection of $E$ onto the $xz$ -plane, is $$ \iiint_{E} f(x,y,z) \,dV= \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} f(x,y,z) \,dy\right] \,dA $$
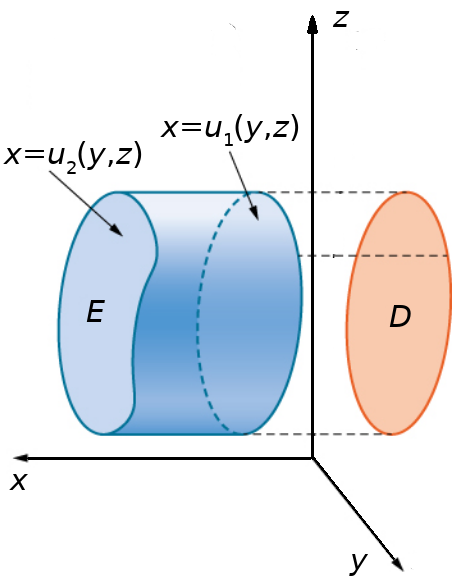
Triple Integrals Over General Regions: Part 3
The triple integral of a continuous function $f (x, y, z)$ over a general three-dimensional region $E = \left\{(x, y, z) \in \mathbb{R}^3|(y, z) \in D, u_1(y, z) \leq x \leq u_2(y, z)\right\},$ where $D$ is the projection of $E$ onto the $yz$ -plane, is $$ \iiint_{E} f(x,y,z) \,dV= \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} f(x,y,z) \,dx\right] \,dA $$
Big Note
Expressing a triple integral as an iterated integral,
1) the inner-most integral can have limits which are functions of the two outer variables
2) the middle integral can have limits which are functions of the outer-most variable
3) the limits on the outer integral are always constants.
Example
Evaluate the intergal $$ \iiint_{E} x+2yz \,dV $$ over the solid $E=\{(x,y,z)\in\mathbb{R}^3| 0 \leq x \leq 2, 0 \leq y \leq x, 0 \leq z \leq 4 - x - y\}$ as seen in the following figure.
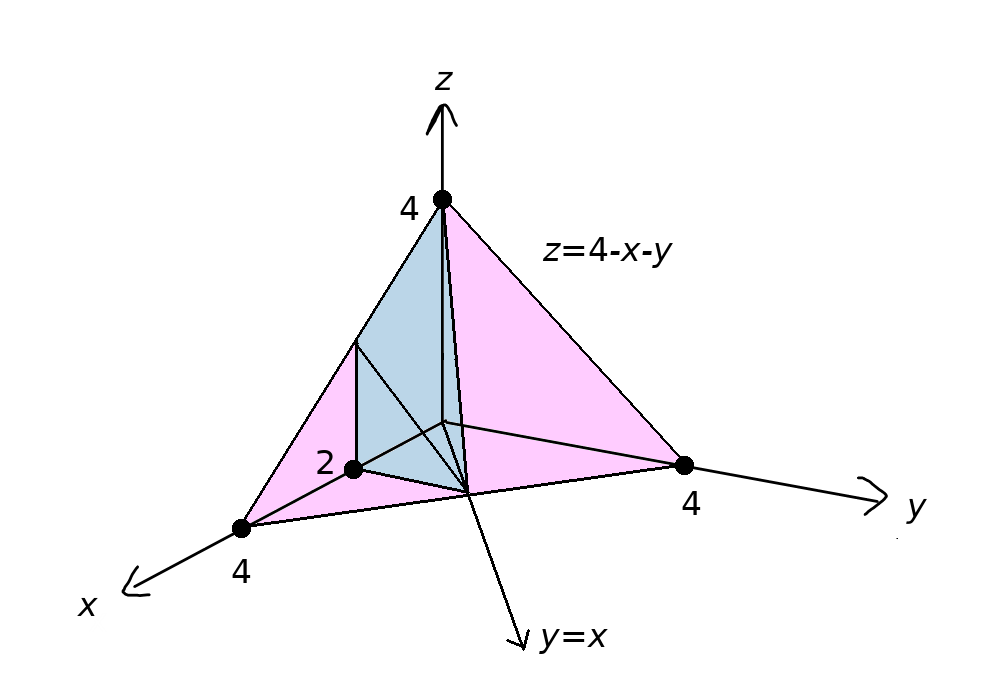
We shall then set this integral up as
$$
\begin{array}{lll}
\displaystyle \iiint_{E} x + 2yz \,dV&\displaystyle=\int_{0}^{2}\int_{0}^{x}\int_{0}^{4-x-y} x + 2yz\, dz \, dy \, dx&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\int_{0}^{x} \left[xz + yz^2\right]_{0}^{4-x-y} \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\int_{0}^{x} \left[x(4-x-y) + y(4-x-y)^2-0\right] \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\int_{0}^{x} 4x-x^2-xy + y(16-8x-8y+2xy+x^2+y^2) \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\int_{0}^{x} 4x-x^2\color{magenta}{-xy} + 16y\color{magenta}{-8xy}-8y^2+2xy^2+x^2y+y^3 \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\int_{0}^{x} 4x-x^2 + 16y-9xy-8y^2+2xy^2+x^2y+y^3 \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\left[ 4xy-x^2y + 8y^2-\frac{9}{2}xy^2-\frac{8}{3}y^3+\frac{2}{3}xy^3+\frac{1}{2}x^2y^2+\frac{1}{4}y^4\right]_{0}^{x} \, dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\color{magenta}{4x^2}\color{blue}{-x^3} + \color{magenta}{8x^2}\color{blue}{-\frac{9}{2}x^3-\frac{8}{3}x^3}+\frac{2}{3} x^4+\frac{1}{2}x^4+\frac{1}{4}x^4 \, dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}12x^2-\frac{49}{6}x^3+\frac{17}{12}x^4 \, dx &\mbox{}\\
\displaystyle &\displaystyle=\left[4x^3-\frac{49}{24}x^4+\frac{17}{60}x^5 \right]_{0}^{2} &\mbox{}\\
\displaystyle &\displaystyle= 4(2)^3-\frac{49}{24}(2)^4+\frac{17}{60}(2)^5 -0 &\mbox{}\\
\displaystyle &\displaystyle= \frac{42}{5} &\mbox{}\\
\displaystyle &\displaystyle= 8.4 &\mbox{}\\
\end{array}
$$
Volumes of Regions
We can express the volume of a region $E$ as $$ V(E)=\iiint_E \, dV $$ $\star$ Note the similarities to the one and two-dimensional case. $\star$
Example
Find the volume of the solid $E=\{(x,y,z)\in\mathbb{R}^3| 0 \leq x \leq 2, 0 \leq y \leq x, 0 \leq z \leq 4 - x - y\}$ as seen in the following figure.

$$
\begin{array}{lll}
\displaystyle V(E)&\displaystyle =\iiint_{E} \,dV&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\int_{0}^{x}\int_{0}^{4-x-y} \, dz \, dy \, dx&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\int_{0}^{x}\left[z\right]_{0}^{4-x-y}\, dy \, dx&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\int_{0}^{x}4-x-y \, dy \, dx&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}\left[4y-xy-\frac{1}{2}y^2\right]_{0}^{x} \, dx&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}4x-x^2-\frac{1}{2}x^2 \, dx&\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{2}4x-\frac{3}{2}x^2 \, dx&\mbox{}\\
\displaystyle &\displaystyle=\left[2x^2-\frac{1}{2}x^3 \right]_{0}^{2}&\mbox{}\\
\displaystyle &\displaystyle=2(2)^2-\frac{1}{2}(2)^3&\mbox{}\\
\displaystyle &\displaystyle=8-4&\mbox{}\\
\displaystyle &\displaystyle=4&\mbox{}\\
\end{array}
$$
The Average Value of a Three-Variable Function
If $f (x, y, z)$ is integrable over a solid bounded region $E$ with positive volume $V(E),$ then the average value of the function is $$ f_{avg}=\frac{1}{V(E)}\iiint_E f(x,y,z)\,dV $$
Example
Find the average value of $f(x,y,z) = x + 2yz$ over the solid $E=\{(x,y,z)\in\mathbb{R}^3| 0 \leq x \leq 2, 0 \leq y \leq x, 0 \leq z \leq 4 - x - y\}$ pictured below.

From the above examples we know that $\displaystyle \iiint_{E} x + 2yz \,dV=8.4$ and $V(E)=4.$
Thus, $$ f_{avg}=\frac{1}{V(E)}\iiint_E f(x,y,z)\,dV=\frac{1}{V(E)}\iiint_E x + 2yz\,dV=\frac{1}{4}\cdot 8.4=2.1 $$
Thus, $$ f_{avg}=\frac{1}{V(E)}\iiint_E f(x,y,z)\,dV=\frac{1}{V(E)}\iiint_E x + 2yz\,dV=\frac{1}{4}\cdot 8.4=2.1 $$
Changing the Order of Integration
For an iterated triple integral, there are $6$ possible orders of integration. $$ \int_{r}^{s}\int_{v_1(z)}^{v_2(z)}\int_{u_1(y,z)}^{u_2(y,z)}f(x,y,z)\, dx \, dy \, dz\\ \int_{c}^{d}\int_{v_1(y)}^{v_2(y)}\int_{u_1(y,z)}^{u_2(y,z)}f(x,y,z)\, dx \, dz \, dy\\ \int_{r}^{s}\int_{v_1(z)}^{v_2(z)}\int_{u_1(x,z)}^{u_2(x,z)}f(x,y,z)\, dy \, dx \, dz\\ \int_{a}^{b}\int_{v_1(x)}^{v_2(x)}\int_{u_1(x,z)}^{u_2(x,z)}f(x,y,z)\, dy \, dz \, dx\\ \int_{c}^{d}\int_{v_1(y)}^{v_2(y)}\int_{u_1(x,y)}^{u_2(x,y)}f(x,y,z)\, dz \, dx \, dy\\ \int_{a}^{b}\int_{v_1(x)}^{v_2(x)}\int_{u_1(x,y)}^{u_2(x,y)}f(x,y,z)\, dz \, dy \, dx $$ Natrually, some will likely be easier than others.
Example: Changing the Order of Integration
Calculate the volume of the region $E=\{(x,y,z)\in\mathbb{R}^3|-2\leq x \leq 2, x^2 \leq y \leq 4, 0 \leq z \leq 4-y \}$ by doing the following:
(a) Set up the volume integral using all six orders of integration.
(b) Evaluate two of these integrals to calculate the volume and confirm the result.
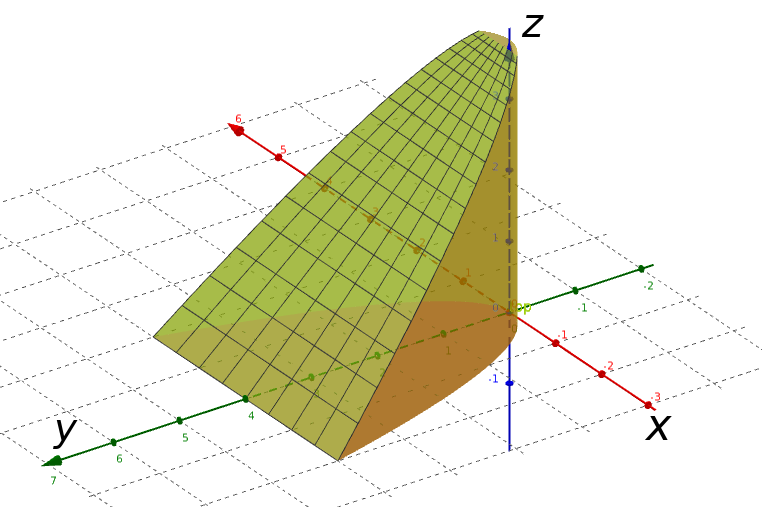
(a)
Integrating First with Respect to $z$:
Projecting the region $E$ onto the $xy$ plane gives us a two-dimensional region $D$ as seen below.

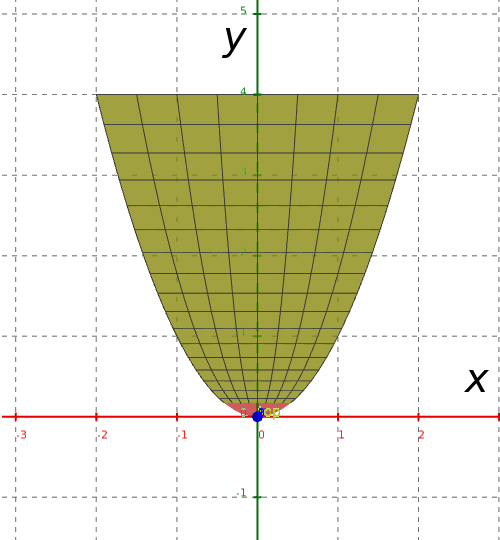
As a Type I region, $D$ can be described as $D=\{(x,y)\in\mathbb{R}^2|-2\leq x \leq 2, x^2 \leq y \leq 4 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} \,dz\right] \,dA =\int_{a}^{b}\int_{v_1(x)}^{v_2(x)}\int_{u_1(x,y)}^{u_2(x,y)}\, dz \, dy \, dx =\int_{x=-2}^{x=2}\int_{y=x^2}^{y=4}\int_{z=0}^{z=4-y}\, dz \, dy \, dx $$ As a Type II region, $D$ can be described as $D=\{(x,y)\in\mathbb{R}^2|-\sqrt{y} \leq x \leq \sqrt{y}, 0\leq y \leq 4 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} \,dz\right] \,dA =\int_{c}^{d}\int_{v_1(y)}^{v_2(y)}\int_{u_1(x,y)}^{u_2(x,y)}\, dz \, dx \, dy =\int_{y=0}^{y=4}\int_{x=-\sqrt{y}}^{x=\sqrt{y}}\int_{z=0}^{z=4-y}\, dz \, dx \, dy $$ Integrating First with Respect to $y$:
We note that $y$ is bounded above by the plane $z=4-y,$ (i.e., $y=4-z,$) and below by the parabolic cylinder $y=x^2.$ Thus $x^2 \leq y \leq 4-z.$
Projecting the region onto the $xz$-plane, we need to express $z$ as function of $x.$ Intersecting the plane $z=4-y$ with the cylinder $y=x^2,$ we get $z=4-x^2$ bounded below by $0.$
The projection, which we shall again call $D,$ is seen below.

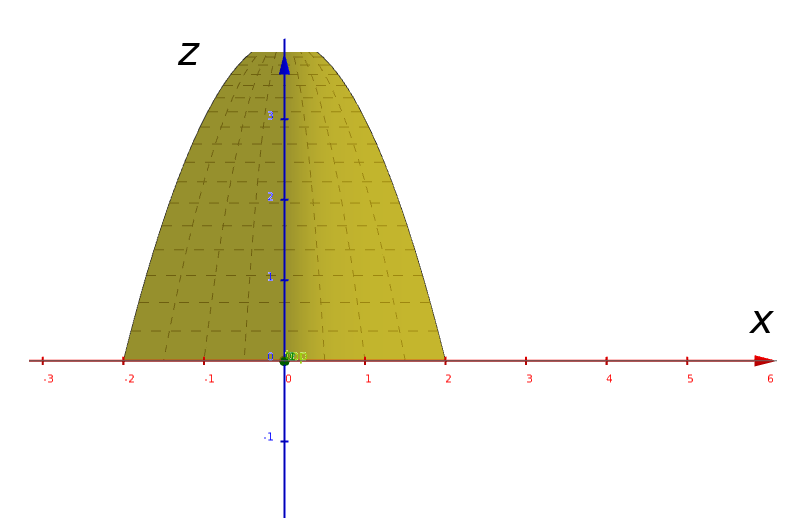
As a Type I region, $D$ can be described as $D=\{(x,z)\in\mathbb{R}^2|-2\leq x \leq 2, 0 \leq z \leq 4-x^2 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} \,dy\right] \,dA =\int_{a}^{b}\int_{v_1(x)}^{v_2(x)}\int_{u_1(x,z)}^{u_2(x,z)}\, dy \, dz \, dx =\int_{x=-2}^{x=2}\int_{z=0}^{z=4-x^2}\int_{y=x^2}^{y=4-z}\, dy \, dz \, dx $$ As a Type II region, $D$ can be described as $D=\{(x,z)\in\mathbb{R}^2|-\sqrt{4-z} \leq x \leq \sqrt{4-z}, 0\leq z \leq 4 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} \,dy\right] \,dA =\int_{r}^{s}\int_{v_1(z)}^{v_2(z)}\int_{u_1(x,z)}^{u_2(x,z)}\, dy \, dx \, dz =\int_{z=0}^{z=4}\int_{x=-\sqrt{4-z}}^{x=\sqrt{4-z}}\int_{y=x^2}^{y=4-z}\, dy \, dx \, dz $$
Integrating First with Respect to $x$:
We note that $y$ is bounded above by $x=\sqrt{y},$ and below by $x=-\sqrt{y},$ Thus, $-\sqrt{y} \leq x \leq \sqrt{y}.$
Projecting the region onto the $yz$-plane, we need to express $z$ as function of $y.$ The bounding plane $z=4-y,$ gives us $z$ as a function of $y$ in the $yz$-plane. Also, the region is bounded below by the plane $z=0.$ Thus $0 \leq z \leq 4-y.$
The projection, which we shall (yet) again call $D,$ is seen below.


As a Type I region, $D$ can be described as $D=\{(y,z)\in\mathbb{R}^2| 0\leq y \leq 4, 0 \leq z \leq 4-y \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} \,dx\right] \,dA =\int_{c}^{d}\int_{v_1(y)}^{v_2(y)}\int_{u_1(y,z)}^{u_2(y,z)}\, dx \, dz \, dy =\int_{y=0}^{y=4}\int_{z=0}^{z=4-y}\int_{x=-\sqrt{y}}^{x=\sqrt{y}}\, dx \, dz \, dy $$ As a Type II region, $D$ can be described as $D=\{(x,z)\in\mathbb{R}^2|-\sqrt{4-z} \leq x \leq \sqrt{4-z}, 0\leq z \leq 4 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} \,dx\right] \,dA =\int_{r}^{s}\int_{v_1(z)}^{v_2(z)}\int_{u_1(y,z)}^{u_2(y,z)}\, dx \, dy \, dz =\int_{z=0}^{z=4}\int_{y=0}^{y=4-z}\int_{x=-\sqrt{y}}^{x=\sqrt{y}}\, dx \, dy \, dz $$
(b)
We now evaluate two of these integrals. $$ \begin{array}{lll} \displaystyle \int_{x=-2}^{x=2}\int_{y=x^2}^{y=4}\int_{z=0}^{z=4-y}\, dz \, dy \, dx&\displaystyle= \int_{-2}^{2}\int_{x^2}^{4}\int_{0}^{4-y}\, dz \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}\int_{x^2}^{4}[z]_{0}^{4-y} \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}\int_{x^2}^{4} 4-y \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}\left[4y-\frac{1}{2}y^2\right]_{x^2}^{4} \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}\left[4\cdot 4-\frac{1}{2}(4)^2-\left(4x^2-\frac{1}{2}x^4\right)\right] \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}8-4x^2+\frac{1}{2}x^4 \, dx&\mbox{}\\ \displaystyle &\displaystyle= \left[8x-\frac{4}{3}x^3+\frac{1}{10}x^5\right]_{-2}^{2}&\mbox{}\\ \displaystyle &\displaystyle= \left(8(2)-\frac{4}{3}(2)^3+\frac{1}{10}(2)^5\right)-\left(8(-2)-\frac{4}{3}(-2)^3+\frac{1}{10}(-2)^5\right)&\mbox{}\\ \displaystyle &\displaystyle= \frac{256}{15}&\mbox{}\\ \end{array} $$ $$ \begin{array}{lll} \displaystyle \int_{z=0}^{z=4}\int_{x=-\sqrt{4-z}}^{x=\sqrt{4-z}}\int_{y=x^2}^{y=4-z}\, dy \, dx \, dz&\displaystyle=\int_{0}^{4}\int_{-\sqrt{4-z}}^{\sqrt{4-z}}\int_{x^2}^{4-z}\, dy \, dx \, dz &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\int_{-\sqrt{4-z}}^{\sqrt{4-z}}[y]_{x^2}^{4-z} \, dx \, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\int_{-\sqrt{4-z}}^{\sqrt{4-z}}4-z-x^2 \, dx \, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\left[(4-z)x-\frac{1}{3}x^3\right]_{-\sqrt{4-z}}^{\sqrt{4-z}} \, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\left[(4-z)\sqrt{4-z}-\frac{1}{3}\left(\sqrt{4-z}\right)^3\right]-\left[(4-z)(-\sqrt{4-z})-\frac{1}{3}\left(-\sqrt{4-z}\right)^3\right]\, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}(\sqrt{4-z})^3-\frac{1}{3}\left(\sqrt{4-z}\right)^3+(\sqrt{4-z})^3-\frac{1}{3}\left(\sqrt{4-z}\right)^3\, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\frac{4}{3}\left(\sqrt{4-z}\right)^3 dz&\mbox{}\\ \displaystyle &\displaystyle= \frac{4}{3}\int_{0}^{4}\left(4-z\right)^{3/2} dz&\mbox{}\\ \displaystyle &\displaystyle= \frac{4}{3}\left[-\frac{2}{5}\left(4-z\right)^{5/2}\right]_{0}^{4}&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[\left(4-z\right)^{5/2}\right]_{0}^{4}&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[\left(4-4\right)^{5/2}-\left(4-0\right)^{5/2}\right]&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[-4^{5/2}\right]&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[-2^5\right]&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[-32\right]&\mbox{}\\ \displaystyle &\displaystyle= \frac{256}{15}&\mbox{}\\ \end{array} $$
Integrating First with Respect to $z$:
Projecting the region $E$ onto the $xy$ plane gives us a two-dimensional region $D$ as seen below.


As a Type I region, $D$ can be described as $D=\{(x,y)\in\mathbb{R}^2|-2\leq x \leq 2, x^2 \leq y \leq 4 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} \,dz\right] \,dA =\int_{a}^{b}\int_{v_1(x)}^{v_2(x)}\int_{u_1(x,y)}^{u_2(x,y)}\, dz \, dy \, dx =\int_{x=-2}^{x=2}\int_{y=x^2}^{y=4}\int_{z=0}^{z=4-y}\, dz \, dy \, dx $$ As a Type II region, $D$ can be described as $D=\{(x,y)\in\mathbb{R}^2|-\sqrt{y} \leq x \leq \sqrt{y}, 0\leq y \leq 4 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} \,dz\right] \,dA =\int_{c}^{d}\int_{v_1(y)}^{v_2(y)}\int_{u_1(x,y)}^{u_2(x,y)}\, dz \, dx \, dy =\int_{y=0}^{y=4}\int_{x=-\sqrt{y}}^{x=\sqrt{y}}\int_{z=0}^{z=4-y}\, dz \, dx \, dy $$ Integrating First with Respect to $y$:
We note that $y$ is bounded above by the plane $z=4-y,$ (i.e., $y=4-z,$) and below by the parabolic cylinder $y=x^2.$ Thus $x^2 \leq y \leq 4-z.$
Projecting the region onto the $xz$-plane, we need to express $z$ as function of $x.$ Intersecting the plane $z=4-y$ with the cylinder $y=x^2,$ we get $z=4-x^2$ bounded below by $0.$
The projection, which we shall again call $D,$ is seen below.


As a Type I region, $D$ can be described as $D=\{(x,z)\in\mathbb{R}^2|-2\leq x \leq 2, 0 \leq z \leq 4-x^2 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} \,dy\right] \,dA =\int_{a}^{b}\int_{v_1(x)}^{v_2(x)}\int_{u_1(x,z)}^{u_2(x,z)}\, dy \, dz \, dx =\int_{x=-2}^{x=2}\int_{z=0}^{z=4-x^2}\int_{y=x^2}^{y=4-z}\, dy \, dz \, dx $$ As a Type II region, $D$ can be described as $D=\{(x,z)\in\mathbb{R}^2|-\sqrt{4-z} \leq x \leq \sqrt{4-z}, 0\leq z \leq 4 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} \,dy\right] \,dA =\int_{r}^{s}\int_{v_1(z)}^{v_2(z)}\int_{u_1(x,z)}^{u_2(x,z)}\, dy \, dx \, dz =\int_{z=0}^{z=4}\int_{x=-\sqrt{4-z}}^{x=\sqrt{4-z}}\int_{y=x^2}^{y=4-z}\, dy \, dx \, dz $$
Integrating First with Respect to $x$:
We note that $y$ is bounded above by $x=\sqrt{y},$ and below by $x=-\sqrt{y},$ Thus, $-\sqrt{y} \leq x \leq \sqrt{y}.$
Projecting the region onto the $yz$-plane, we need to express $z$ as function of $y.$ The bounding plane $z=4-y,$ gives us $z$ as a function of $y$ in the $yz$-plane. Also, the region is bounded below by the plane $z=0.$ Thus $0 \leq z \leq 4-y.$
The projection, which we shall (yet) again call $D,$ is seen below.


As a Type I region, $D$ can be described as $D=\{(y,z)\in\mathbb{R}^2| 0\leq y \leq 4, 0 \leq z \leq 4-y \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} \,dx\right] \,dA =\int_{c}^{d}\int_{v_1(y)}^{v_2(y)}\int_{u_1(y,z)}^{u_2(y,z)}\, dx \, dz \, dy =\int_{y=0}^{y=4}\int_{z=0}^{z=4-y}\int_{x=-\sqrt{y}}^{x=\sqrt{y}}\, dx \, dz \, dy $$ As a Type II region, $D$ can be described as $D=\{(x,z)\in\mathbb{R}^2|-\sqrt{4-z} \leq x \leq \sqrt{4-z}, 0\leq z \leq 4 \}.$ $$ \iiint_{E} \,dV= \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} \,dx\right] \,dA =\int_{r}^{s}\int_{v_1(z)}^{v_2(z)}\int_{u_1(y,z)}^{u_2(y,z)}\, dx \, dy \, dz =\int_{z=0}^{z=4}\int_{y=0}^{y=4-z}\int_{x=-\sqrt{y}}^{x=\sqrt{y}}\, dx \, dy \, dz $$
(b)
We now evaluate two of these integrals. $$ \begin{array}{lll} \displaystyle \int_{x=-2}^{x=2}\int_{y=x^2}^{y=4}\int_{z=0}^{z=4-y}\, dz \, dy \, dx&\displaystyle= \int_{-2}^{2}\int_{x^2}^{4}\int_{0}^{4-y}\, dz \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}\int_{x^2}^{4}[z]_{0}^{4-y} \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}\int_{x^2}^{4} 4-y \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}\left[4y-\frac{1}{2}y^2\right]_{x^2}^{4} \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}\left[4\cdot 4-\frac{1}{2}(4)^2-\left(4x^2-\frac{1}{2}x^4\right)\right] \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{-2}^{2}8-4x^2+\frac{1}{2}x^4 \, dx&\mbox{}\\ \displaystyle &\displaystyle= \left[8x-\frac{4}{3}x^3+\frac{1}{10}x^5\right]_{-2}^{2}&\mbox{}\\ \displaystyle &\displaystyle= \left(8(2)-\frac{4}{3}(2)^3+\frac{1}{10}(2)^5\right)-\left(8(-2)-\frac{4}{3}(-2)^3+\frac{1}{10}(-2)^5\right)&\mbox{}\\ \displaystyle &\displaystyle= \frac{256}{15}&\mbox{}\\ \end{array} $$ $$ \begin{array}{lll} \displaystyle \int_{z=0}^{z=4}\int_{x=-\sqrt{4-z}}^{x=\sqrt{4-z}}\int_{y=x^2}^{y=4-z}\, dy \, dx \, dz&\displaystyle=\int_{0}^{4}\int_{-\sqrt{4-z}}^{\sqrt{4-z}}\int_{x^2}^{4-z}\, dy \, dx \, dz &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\int_{-\sqrt{4-z}}^{\sqrt{4-z}}[y]_{x^2}^{4-z} \, dx \, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\int_{-\sqrt{4-z}}^{\sqrt{4-z}}4-z-x^2 \, dx \, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\left[(4-z)x-\frac{1}{3}x^3\right]_{-\sqrt{4-z}}^{\sqrt{4-z}} \, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\left[(4-z)\sqrt{4-z}-\frac{1}{3}\left(\sqrt{4-z}\right)^3\right]-\left[(4-z)(-\sqrt{4-z})-\frac{1}{3}\left(-\sqrt{4-z}\right)^3\right]\, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}(\sqrt{4-z})^3-\frac{1}{3}\left(\sqrt{4-z}\right)^3+(\sqrt{4-z})^3-\frac{1}{3}\left(\sqrt{4-z}\right)^3\, dz&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{4}\frac{4}{3}\left(\sqrt{4-z}\right)^3 dz&\mbox{}\\ \displaystyle &\displaystyle= \frac{4}{3}\int_{0}^{4}\left(4-z\right)^{3/2} dz&\mbox{}\\ \displaystyle &\displaystyle= \frac{4}{3}\left[-\frac{2}{5}\left(4-z\right)^{5/2}\right]_{0}^{4}&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[\left(4-z\right)^{5/2}\right]_{0}^{4}&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[\left(4-4\right)^{5/2}-\left(4-0\right)^{5/2}\right]&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[-4^{5/2}\right]&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[-2^5\right]&\mbox{}\\ \displaystyle &\displaystyle= -\frac{8}{15}\left[-32\right]&\mbox{}\\ \displaystyle &\displaystyle= \frac{256}{15}&\mbox{}\\ \end{array} $$
Changing the Order of Integration
As with double integrals, and as the previous example hints at, the order of integration when evaluating triple integrals can be the difference between a snarling dog and an adorable kitten.
Example: Changing the Order of Integration
Evaluate the triple integral $$\iiint_E \sqrt{x^2 + z^2} \, dV$$ where $E$ is the region bounded by the paraboloid $y = x^2 + z^2$ and the plane $y = 4.$
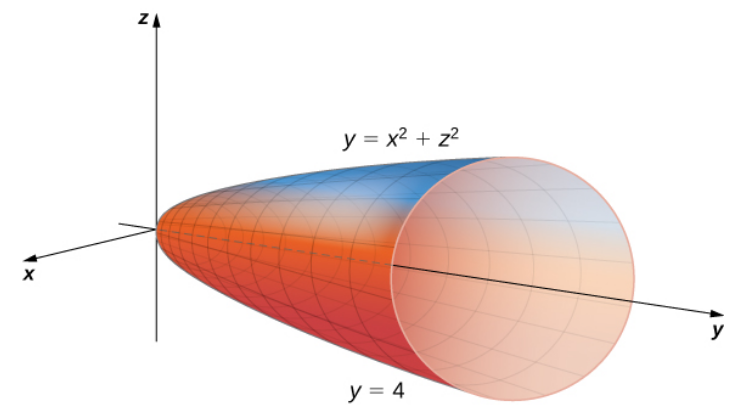
The most expedient way to deal with this integral is to integrate with respect to $y$ first
since $y$ can be expressed as a single function of $x$ and $z.$
Then we may say that $x^2+z^2 \leq y \leq 4.$
Projecting the region onto the $xz$-plane, we have a disk of radius $2,$ that is $-\sqrt{4-x^2} \leq z \leq \sqrt{4-x^2}$ with $-2 \leq x \leq 2.$
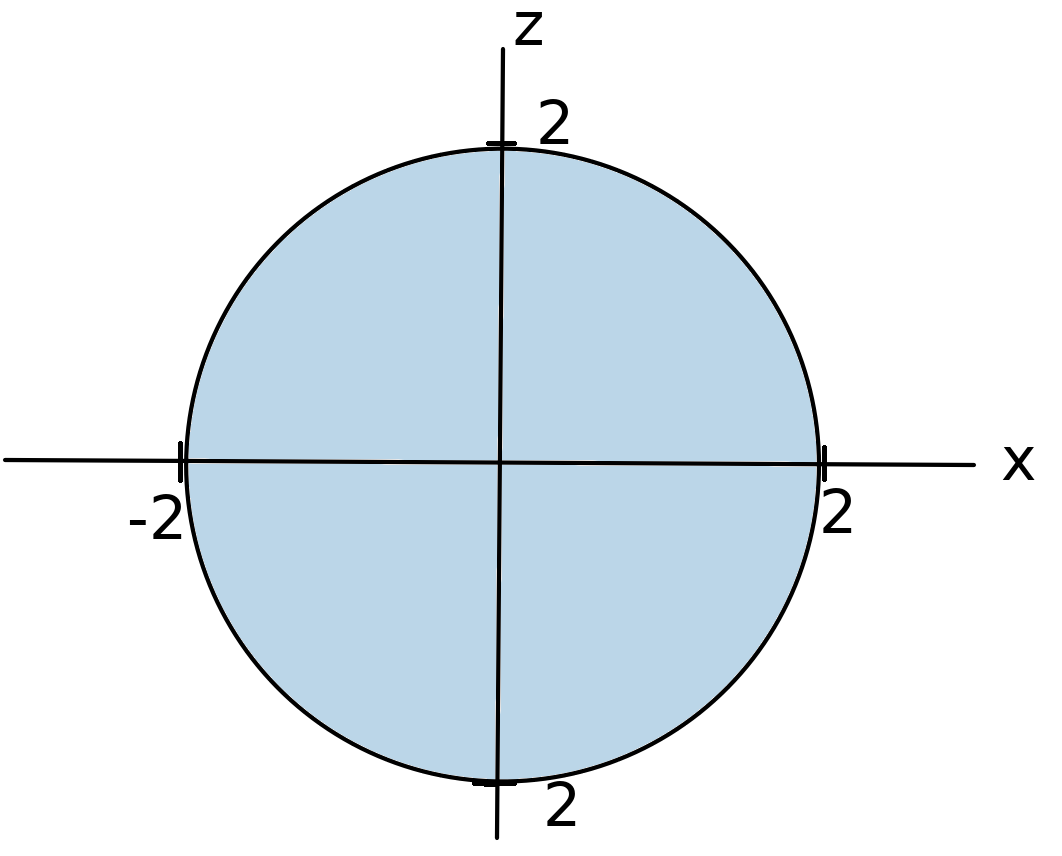
Our region of integration may then be described as $$ E=\left\{(x,y,z)\in\mathbb{R}^3|-2\leq x \leq 2, -\sqrt{4-x^2} \leq z \leq \sqrt{4-x^2}, 0 \leq y \leq x^2+z^2 \right\} $$ The integral may then be computed as $$ \begin{array}{lll} \displaystyle \iiint_E \sqrt{x^2 + z^2} \, dV&\displaystyle=\int_{x=-2}^{x=2}\int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2 + z^2}^{y=4}\sqrt{x^2 + z^2} \, dy \, dz \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{x^2 + z^2}^{4}\sqrt{x^2 + z^2} \, dy \, dz \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}\left[y\sqrt{x^2 + z^2}\right]_{x^2 + z^2}^{4} \, dz \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}(4-x^2-z^2)\sqrt{x^2 + z^2} \, dz \, dx &\mbox{}\\ \end{array} $$ Before proceeding any further, we notice that the region in the $xz$-plane is circular, which suggests that polar coordinates might be a nice choice for transforming the integral into an adorable kitten.
Letting $x=r \cos \theta$ and $z=r\sin \theta,$ we have $dz\,dx=r\,dr\,d\theta$ and $r^2=x^2+z^2.$
The integral may therefore be re-expressed as $$ \begin{array}{lll} \displaystyle \iiint_E \sqrt{x^2 + z^2} \, dV&\displaystyle=\int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}(4-x^2-z^2)\sqrt{x^2 + z^2} \, dz \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2}(4-r^2)r \cdot r\, dr \, d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2} 4r^2-r^4\, dr \, d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \left[\frac{4}{3}r^3-\frac{1}{5}r^5\right]_{0}^{2}\, d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \frac{4}{3}(2)^3-\frac{1}{5}(2)^5\, d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \frac{64}{15} d\theta&\mbox{}\\ \displaystyle &\displaystyle=\frac{64}{15}\int_{0}^{2\pi} d\theta&\mbox{}\\ \displaystyle &\displaystyle=\frac{64}{15}\cdot 2\pi &\mbox{}\\ \displaystyle &\displaystyle=\frac{128\pi}{15} &\mbox{}\\ \end{array} $$
Note: Setting the above integral up in the order $dz\, dy\, dx$ would result in the integral $$ \int_{x=-2}^{x=2}\int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}}\sqrt{x^2 + z^2} \, dy \, dz \, dx $$ which doesn't admit any nice transformations into polar coordinates.
So take your pick: $$ \begin{array}{ccc} \displaystyle \int_{-2}^{2}\int_{x^2}^{4} \int_{-\sqrt{y-x^2}}^{\sqrt{y-x^2}}\sqrt{x^2 + z^2} \, dy \, dz \, dx & \displaystyle \int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{x^2 + z^2}^{4}\sqrt{x^2 + z^2} \, dy \, dz \, dx=\int_{0}^{2\pi}\int_{0}^{2}(4-r^2)r \cdot r\, dr \, d\theta &\mbox{}\\ \displaystyle \mbox{snarling dog} &\displaystyle\mbox{adorable kitten (in disguise)} &\mbox{}\\ \end{array} $$
Then we may say that $x^2+z^2 \leq y \leq 4.$
Projecting the region onto the $xz$-plane, we have a disk of radius $2,$ that is $-\sqrt{4-x^2} \leq z \leq \sqrt{4-x^2}$ with $-2 \leq x \leq 2.$

Our region of integration may then be described as $$ E=\left\{(x,y,z)\in\mathbb{R}^3|-2\leq x \leq 2, -\sqrt{4-x^2} \leq z \leq \sqrt{4-x^2}, 0 \leq y \leq x^2+z^2 \right\} $$ The integral may then be computed as $$ \begin{array}{lll} \displaystyle \iiint_E \sqrt{x^2 + z^2} \, dV&\displaystyle=\int_{x=-2}^{x=2}\int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2 + z^2}^{y=4}\sqrt{x^2 + z^2} \, dy \, dz \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{x^2 + z^2}^{4}\sqrt{x^2 + z^2} \, dy \, dz \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}\left[y\sqrt{x^2 + z^2}\right]_{x^2 + z^2}^{4} \, dz \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}(4-x^2-z^2)\sqrt{x^2 + z^2} \, dz \, dx &\mbox{}\\ \end{array} $$ Before proceeding any further, we notice that the region in the $xz$-plane is circular, which suggests that polar coordinates might be a nice choice for transforming the integral into an adorable kitten.
Letting $x=r \cos \theta$ and $z=r\sin \theta,$ we have $dz\,dx=r\,dr\,d\theta$ and $r^2=x^2+z^2.$
The integral may therefore be re-expressed as $$ \begin{array}{lll} \displaystyle \iiint_E \sqrt{x^2 + z^2} \, dV&\displaystyle=\int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}(4-x^2-z^2)\sqrt{x^2 + z^2} \, dz \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2}(4-r^2)r \cdot r\, dr \, d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2} 4r^2-r^4\, dr \, d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \left[\frac{4}{3}r^3-\frac{1}{5}r^5\right]_{0}^{2}\, d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \frac{4}{3}(2)^3-\frac{1}{5}(2)^5\, d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi} \frac{64}{15} d\theta&\mbox{}\\ \displaystyle &\displaystyle=\frac{64}{15}\int_{0}^{2\pi} d\theta&\mbox{}\\ \displaystyle &\displaystyle=\frac{64}{15}\cdot 2\pi &\mbox{}\\ \displaystyle &\displaystyle=\frac{128\pi}{15} &\mbox{}\\ \end{array} $$
Note: Setting the above integral up in the order $dz\, dy\, dx$ would result in the integral $$ \int_{x=-2}^{x=2}\int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}}\sqrt{x^2 + z^2} \, dy \, dz \, dx $$ which doesn't admit any nice transformations into polar coordinates.
So take your pick: $$ \begin{array}{ccc} \displaystyle \int_{-2}^{2}\int_{x^2}^{4} \int_{-\sqrt{y-x^2}}^{\sqrt{y-x^2}}\sqrt{x^2 + z^2} \, dy \, dz \, dx & \displaystyle \int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{x^2 + z^2}^{4}\sqrt{x^2 + z^2} \, dy \, dz \, dx=\int_{0}^{2\pi}\int_{0}^{2}(4-r^2)r \cdot r\, dr \, d\theta &\mbox{}\\ \displaystyle \mbox{snarling dog} &\displaystyle\mbox{adorable kitten (in disguise)} &\mbox{}\\ \end{array} $$
Application: Mass from Density
If we have a solid object $Q$ with a density function $\rho(x, y, z)$ at any point $(x, y, z)$ in space, then its mass is $$ \iiint_Q \rho(x,y,z)\, dV $$
Example
Suppose that $Q$ is a solid region bounded by $x + 2y + 3z = 6$ and the coordinate planes and has density $\rho(x, y, z) = x^2yz.$
Set up a triple integral which gives the total mass of $Q.$
Do not evaluate the integral.
The region $Q$ is graphed in a straightforward way.
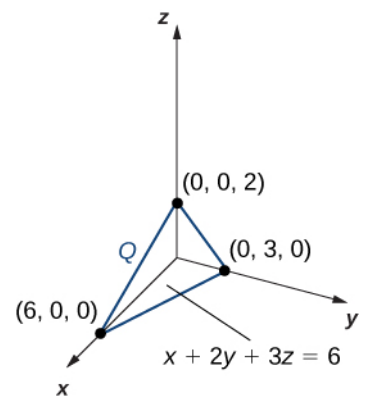
From the figure, we may write the region as $$E=\displaystyle \left \{(x,y,z)\in\mathbb{R}^3 \Bigr|0\leq x \leq 6, 0 \leq y \leq \frac{6-x}{2}, 0 \leq z \leq \frac{6-x-2y}{3} \right \}.$$ Thus, the mass of $Q$ is given by $$ \begin{array}{lll} \displaystyle \iiint_Q \rho(x,y,z) \, dV& \displaystyle \iiint_Q x^2yz \, dV &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{6}\int_{0}^{\frac{6-x}{2}}\int_{0}^{\frac{6-x-2y}{3}} x^2yz \, dz \, dy \, dx&\mbox{}\\ %\displaystyle &\displaystyle=\frac{108}{35} &\mbox{}\\ %\displaystyle &\displaystyle\approx 3.086 &\mbox{}\\ \end{array} $$

From the figure, we may write the region as $$E=\displaystyle \left \{(x,y,z)\in\mathbb{R}^3 \Bigr|0\leq x \leq 6, 0 \leq y \leq \frac{6-x}{2}, 0 \leq z \leq \frac{6-x-2y}{3} \right \}.$$ Thus, the mass of $Q$ is given by $$ \begin{array}{lll} \displaystyle \iiint_Q \rho(x,y,z) \, dV& \displaystyle \iiint_Q x^2yz \, dV &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{6}\int_{0}^{\frac{6-x}{2}}\int_{0}^{\frac{6-x-2y}{3}} x^2yz \, dz \, dy \, dx&\mbox{}\\ %\displaystyle &\displaystyle=\frac{108}{35} &\mbox{}\\ %\displaystyle &\displaystyle\approx 3.086 &\mbox{}\\ \end{array} $$
Example
A rectangularly-shaped soil sample has a roughly vertical density gradient since the deeper soil is more densely packed than soil nearer to the surface.
Suppose our sample has a length and width of $30$ $\mbox{cm}$ and a depth of $10$ $\mbox{cm}.$ (Notice that density only depends on depth.)
Furthermore, suppose the density at the point $(x,y,z)$ is modelled by $\rho(x, y, z) = 1.7e^{-0.1 z}$ $\mbox{g}/\mbox{cm}^3.$
Find the mass of the soil sample.
Let $S$ be the box-shaped region of our soil sample. Then the mass is $$ \begin{array}{lll} \displaystyle \iiint_S \rho(x,y,z) \, dV&\displaystyle= \int_{0}^{30}\int_{0}^{30}\int_{0}^{10}1.7e^{-0.1 z}\, dz \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{30}\int_{0}^{30}\left[-\frac{1.7e^{-0.1 z}}{0.1}\right]_{0}^{10} \, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{30}\int_{0}^{30}\left[-17e^{-0.1 z}\right]_{0}^{10} \, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{30}\int_{0}^{30}\left[-17e^{-0.1 \cdot 10}-(-17e^{-0.1 \cdot 0})\right] \, dy \, dx &\mbox{}\\ %\displaystyle &\displaystyle=\int_{0}^{30}\int_{0}^{30}-17e^{-1}+17 \, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{30}\int_{0}^{30}17-17e^{-1} \, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=(17-17e^{-1})\int_{0}^{30}\int_{0}^{30} \, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=(17-17e^{-1})\cdot 900 &\mbox{}\\ \displaystyle &\displaystyle\approx 9671.44455 &\mbox{}\\ \end{array} $$ The mass of the soil sample is about $9671.4$ grams.