As we have discussed in previous courses, some situations are best understood in a "circular" environment.
For example, modelling the virbration of a circular drum head is more conveniently described using a "circular," or polar coordinate system.
In the same way, certain integrals are much more conveniently evaluated in a different coordinate system.
In polar coordinates, we will see how certain nasty integrals can be transformed into lovable teddy bears!
Recall: Polar Coordinates
The relationship between polar coordinates $(r,\theta)$ and rectangular coordinates $(x,y)$ is $$x=r\cos \theta \,\,\mbox{ and }\,\, y=r\sin \theta.$$
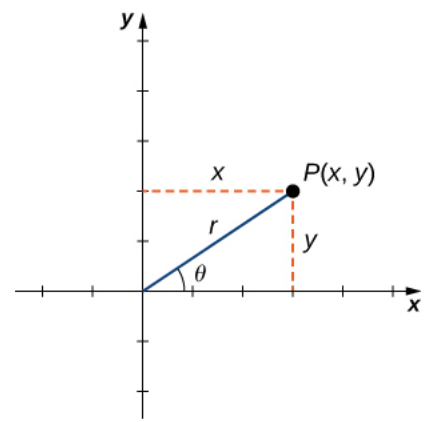
Double Integrals in Polar Coordinates
We begin by considering the area of a "polar rectangle."
We describe our polar rectangle as $$R=\left\{(r,\theta)| a\leq r\leq b, \alpha \leq \theta \leq \beta\right\}=[a,b]\times[\alpha,\beta]$$
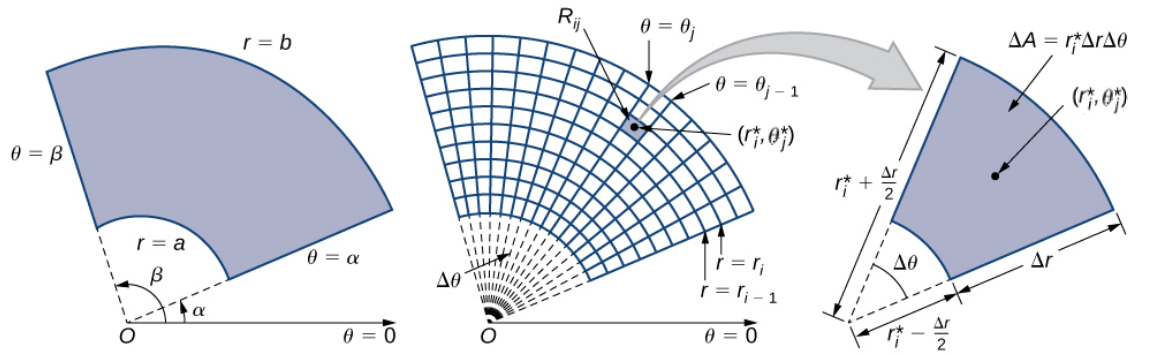
Double Integrals in Polar Coordinates
We then break up $[a,b]$ into $m$ intervals of size $\Delta r$ and $[\alpha,\beta]$ into $n$ intervals of size $\Delta \theta.$

Double Integrals in Polar Coordinates
In each radial subinterval $[r_{i-1},r_{i}]$ we choose a point $r_i^*$ and in each angular subinterval $[\theta_{j-1},\theta_{j}]$ we choose a point $\theta_j^*.$

For our purposes, we shall choose $r_i^*$ and $\theta_j^*$ to be the midpoints of their respective subintervals.
Double Integrals in Polar Coordinates
The area $\Delta A$ of the polar subrectangle is then $$ \begin{array}{ll} \Delta A &=\mbox{Outer Sector}-\mbox{Inner Sector}\\ &=\displaystyle\frac{1}{2}r_i^2 \, \Delta \theta-\frac{1}{2}r_{i-1}^2 \, \Delta \theta\\ &=\displaystyle \frac{1}{2}\left(r_i^*+\frac{\Delta r}{2}\right)^2\,\Delta \theta- \frac{1}{2}\left(r_i^*-\frac{\Delta r}{2}\right)^2\,\Delta \theta\\ &=r_i^*\,\Delta r \,\Delta \theta \end{array} $$

Double Integrals in Polar Coordinates
Since the arguments of $f(x,y)$ are in rectangular coordinates, to approximate the volume under the surface we need to evaluate $f$ at the rectangular equivalent of the point $(r_i^*,\theta_j^*)$ which is given by $$(x_i^*,y_i^*)=(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*).$$
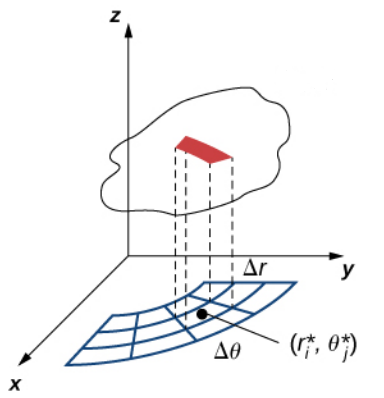
Double Integrals in Polar Coordinates
The volume under the surface (a "polar box") over the polar sub-rectangle of area $r_i^*\,\Delta r \,\Delta \theta$ is $$f(x_i^*,y_j^*)\,\Delta A=f(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*)r_i^*\,\Delta r \,\Delta \,\theta.$$

Double Integrals in Polar Coordinates
Adding up all of volumes of all the "polar boxes" gives us an approximation of the volume under the surface. $$ \mbox{Volume}\approx\sum_{j=1}^{n}\sum_{i=1}^{m}f(x_i^*,y_j^*)\,\Delta A=\sum_{j=1}^{n}\sum_{i=1}^{m}f(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*)\,r_i^*\,\Delta r \,\Delta \,\theta $$
In the limit we have...
Double Integrals in Polar Coordinates
$$ \iint_R f(x,y)\,dA=\lim_{m,n\rightarrow \infty}\sum_{j=1}^{n}\sum_{i=1}^{m}f(r_i^*\cos\theta_j^*,r_i^*\sin\theta_j^*)\,r_i^* \, \Delta r \, \Delta \, \theta =\iint_{R}f(r\cos \theta,r\sin \theta)\,r\,dr\,d\theta $$
Example
Evaluate the integral $\displaystyle \iint_R 4 - x^2 - y^2\,dA$ where $R$ is the circle of radius $2$ on the $xy$-plane.
As a polar region, the region $R$ is given by $0 \leq r \leq 2,$ $\displaystyle 0 \leq \theta \leq 2\pi.$
Then $$ \begin{array}{lll} \displaystyle \iint_R 4 - x^2 - y^2\,dA&\displaystyle= \iint_{R}f(r\cos \theta,r\sin \theta)\,r\,dr\,d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2}(4-(r\cos \theta)^2-(r\sin \theta)^2)\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2}(4-r^2(\cos^2 \theta+\sin^2 \theta))\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2}(4-r^2)\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\left(\int_{0}^{2}(4-r^2)\,r\,dr\right)\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\left(\int_{0}^{2\pi}\,d\theta\right) \left(\int_{0}^{2}(4-r^2)\,r\,dr\right) &\mbox{$\displaystyle \int_{0}^{2}(4-r^2)\,r\,dr$ is a constant we can pull out}\\ \displaystyle &\displaystyle=2\pi\int_{0}^{2}4r-r^3\,dr &\mbox{}\\ \displaystyle &\displaystyle=2\pi\left[2r^2-\frac{1}{4}r^4\right]_{0}^{2} &\mbox{}\\ \displaystyle &\displaystyle=2\pi\left[2\cdot 2^2-\frac{1}{4}(2)^4\right] &\mbox{}\\ \displaystyle &\displaystyle=2\pi\left[8-4\right] &\mbox{}\\ \displaystyle &\displaystyle=8\pi &\mbox{}\\ \end{array} $$
To appreciate what we have just done, consider the integral $\displaystyle\int_{0}^{2\pi}\int_{0}^{2}(4-r^2)\,r\,dr\,d\theta$ written in rectangular coordinates: $$ \int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}4-x^2-y^2\,dy\,dx $$
Then $$ \begin{array}{lll} \displaystyle \iint_R 4 - x^2 - y^2\,dA&\displaystyle= \iint_{R}f(r\cos \theta,r\sin \theta)\,r\,dr\,d\theta&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2}(4-(r\cos \theta)^2-(r\sin \theta)^2)\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2}(4-r^2(\cos^2 \theta+\sin^2 \theta))\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{2}(4-r^2)\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\left(\int_{0}^{2}(4-r^2)\,r\,dr\right)\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\left(\int_{0}^{2\pi}\,d\theta\right) \left(\int_{0}^{2}(4-r^2)\,r\,dr\right) &\mbox{$\displaystyle \int_{0}^{2}(4-r^2)\,r\,dr$ is a constant we can pull out}\\ \displaystyle &\displaystyle=2\pi\int_{0}^{2}4r-r^3\,dr &\mbox{}\\ \displaystyle &\displaystyle=2\pi\left[2r^2-\frac{1}{4}r^4\right]_{0}^{2} &\mbox{}\\ \displaystyle &\displaystyle=2\pi\left[2\cdot 2^2-\frac{1}{4}(2)^4\right] &\mbox{}\\ \displaystyle &\displaystyle=2\pi\left[8-4\right] &\mbox{}\\ \displaystyle &\displaystyle=8\pi &\mbox{}\\ \end{array} $$
To appreciate what we have just done, consider the integral $\displaystyle\int_{0}^{2\pi}\int_{0}^{2}(4-r^2)\,r\,dr\,d\theta$ written in rectangular coordinates: $$ \int_{-2}^{2}\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}4-x^2-y^2\,dy\,dx $$
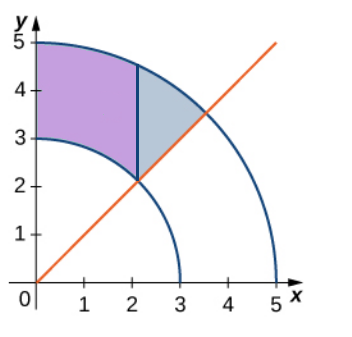
Example
Find $\displaystyle \iint_D xy^2 \, dA$ over the region $D$ pictured below.
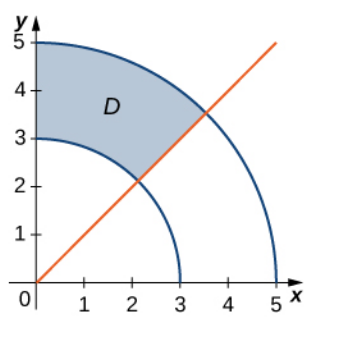
As a polar region, $D$ is given by $3 \leq r \leq 5,$ $\displaystyle \frac{\pi}{4} \leq \theta \leq \frac{\pi}{2}.$
Then $$ \begin{array}{lll} \displaystyle \iint_D xy^2 \, dA&\displaystyle=\iint_{D}f(r\cos \theta,r\sin \theta)\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{\pi/4}^{\pi/2}\int_{3}^{5} (r\cos \theta)(r\sin \theta)^2\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi/4}^{\pi/2} \int_{3}^{5} \,r^4\sin^2 \theta \cos \theta\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi/4}^{\pi/2}\sin^2 \theta \cos \theta \left(\int_{3}^{5} \,r^4\,dr\right)\,d\theta &\mbox{}\\ \displaystyle &\displaystyle= \left(\int_{3}^{5} \,r^4\,dr\right)\left(\int_{\pi/4}^{\pi/2}\sin^2 \theta \cos \theta \,d\theta\right) &\mbox{pulling out $\displaystyle \int_{3}^{5} \,r^4\,dr$}\\ \displaystyle &\displaystyle= \left[ \frac{1}{5}r^5\right]_{3}^{5}\left[\frac{1}{3}\sin^3 \theta\right]_{\pi/4}^{\pi/2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{5}\cdot\frac{1}{3}\left[ r^5\right]_{3}^{5}\left[\sin^3 \theta\right]_{\pi/4}^{\pi/2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{15}\left(5^5-3^5\right)\left(\sin^3 \frac{\pi}{2}-\sin^3 \frac{\pi}{4}\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{15}\cdot 2882 \left(1^3-\left(\frac{\sqrt{2}}{2}\right)^3\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2882}{15}\cdot \left(1-\frac{\sqrt{2}}{4}\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2882}{15}\cdot\frac{4-\sqrt{2}}{4}&\mbox{}\\ \displaystyle &\displaystyle= \frac{1441}{15}\cdot\frac{4-\sqrt{2}}{2}&\mbox{}\\ \displaystyle &\displaystyle= \frac{1441(4-\sqrt{2})}{30}&\mbox{}\\ \displaystyle &\displaystyle\approx 124.2039419\mbox{}\\ \end{array} $$
Again, we point out how much more cuddly the polar version $\displaystyle \int_{\pi/4}^{\pi/2} \int_{3}^{5} \,r^4\sin^2 \theta \cos \theta\,dr\,d\theta$ is compared to a rectangular version. $$ \int_{0}^{\frac{3\sqrt{2}}{2}}\int_{\sqrt{9-x^2}}^{\sqrt{25-x^2}} xy^2 \, dy \, dx+\int_{\frac{3\sqrt{2}}{2}}^{\frac{5\sqrt{2}}{2}}\int_{x}^{\sqrt{25-x^2}} xy^2 \, dy \, dx $$
Then $$ \begin{array}{lll} \displaystyle \iint_D xy^2 \, dA&\displaystyle=\iint_{D}f(r\cos \theta,r\sin \theta)\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{\pi/4}^{\pi/2}\int_{3}^{5} (r\cos \theta)(r\sin \theta)^2\,r\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi/4}^{\pi/2} \int_{3}^{5} \,r^4\sin^2 \theta \cos \theta\,dr\,d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{\pi/4}^{\pi/2}\sin^2 \theta \cos \theta \left(\int_{3}^{5} \,r^4\,dr\right)\,d\theta &\mbox{}\\ \displaystyle &\displaystyle= \left(\int_{3}^{5} \,r^4\,dr\right)\left(\int_{\pi/4}^{\pi/2}\sin^2 \theta \cos \theta \,d\theta\right) &\mbox{pulling out $\displaystyle \int_{3}^{5} \,r^4\,dr$}\\ \displaystyle &\displaystyle= \left[ \frac{1}{5}r^5\right]_{3}^{5}\left[\frac{1}{3}\sin^3 \theta\right]_{\pi/4}^{\pi/2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{5}\cdot\frac{1}{3}\left[ r^5\right]_{3}^{5}\left[\sin^3 \theta\right]_{\pi/4}^{\pi/2} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{15}\left(5^5-3^5\right)\left(\sin^3 \frac{\pi}{2}-\sin^3 \frac{\pi}{4}\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{15}\cdot 2882 \left(1^3-\left(\frac{\sqrt{2}}{2}\right)^3\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2882}{15}\cdot \left(1-\frac{\sqrt{2}}{4}\right) &\mbox{}\\ \displaystyle &\displaystyle= \frac{2882}{15}\cdot\frac{4-\sqrt{2}}{4}&\mbox{}\\ \displaystyle &\displaystyle= \frac{1441}{15}\cdot\frac{4-\sqrt{2}}{2}&\mbox{}\\ \displaystyle &\displaystyle= \frac{1441(4-\sqrt{2})}{30}&\mbox{}\\ \displaystyle &\displaystyle\approx 124.2039419\mbox{}\\ \end{array} $$
Again, we point out how much more cuddly the polar version $\displaystyle \int_{\pi/4}^{\pi/2} \int_{3}^{5} \,r^4\sin^2 \theta \cos \theta\,dr\,d\theta$ is compared to a rectangular version. $$ \int_{0}^{\frac{3\sqrt{2}}{2}}\int_{\sqrt{9-x^2}}^{\sqrt{25-x^2}} xy^2 \, dy \, dx+\int_{\frac{3\sqrt{2}}{2}}^{\frac{5\sqrt{2}}{2}}\int_{x}^{\sqrt{25-x^2}} xy^2 \, dy \, dx $$

Double Integrals over General Polar Regions
If $f (x,y)$ is continuous on a general polar region $D$ as described above, then $$ \iint_D f(x,y)\, dA=\int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} f(r\cos \theta,r\sin \theta)\, r \, dr \, d\theta $$

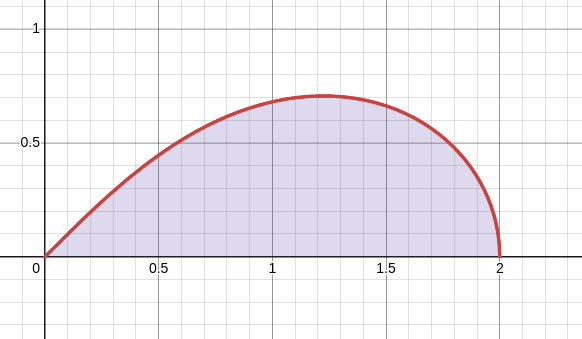
Example
Evaluate the integral $$\iint_{D} r^2 \sin^2(2\theta)\, r \, dr \, d\theta$$ where $\displaystyle D =\left\{(r,\theta)|0 \leq \theta \leq \frac{\pi}{4}, 0 \leq r \leq 2 \sqrt{\cos(2\theta)}\right\}$
$$
\begin{array}{lll}
\displaystyle \iint_{D} r^2 \sin^2(2\theta)\, r \, dr \, d\theta&\displaystyle=\int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} f(r\cos \theta,r\sin \theta)\, r \, dr \, d\theta &\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{\pi/4} \int_{0}^{2\sqrt{\cos(2\theta)}} r^2 \sin^2(2\theta)\, r \, dr \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{\pi/4} \int_{0}^{2\sqrt{\cos(2\theta)}} \sin^2(2\theta)\, r^3 \, dr \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{\pi/4} \sin^2(2\theta) \left(\int_{0}^{2\sqrt{\cos(2\theta)}} \, r^3 \, dr \right)\, d\theta&\mbox{Can't pull out integral this time!}\\
\displaystyle &\displaystyle= \int_{0}^{\pi/4} \sin^2(2\theta) \left[\frac{1}{4}r^4\right]_{0}^{2\sqrt{\cos(2\theta)}}\, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{\pi/4} \sin^2(2\theta) \left[\frac{1}{4}\left(2\sqrt{\cos(2\theta)}\right)^4\right]\, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{\pi/4} \sin^2(2\theta) \left[4\cos^2(2\theta)\right]\, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{\pi/4} \left[2\sin(2\theta)\cos(2\theta)\right]^2\, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{\pi/4} \sin^2(4\theta)\, d\theta&\mbox{trig identity!}\\
\displaystyle &\displaystyle= \int_{0}^{\pi} \sin^2(u)\, \frac{1}{4}du&\mbox{}\\
\displaystyle &\displaystyle= \frac{1}{4}\int_{0}^{\pi} \sin^2(u)\, du&\mbox{}\\
\displaystyle &\displaystyle= \frac{1}{4}\left[\frac{1}{2}u-\frac{1}{4}\sin(2u)\right]_{0}^{\pi}&\mbox{integral table}\\
\displaystyle &\displaystyle= \frac{1}{4}\left[\frac{1}{2}\cdot \pi-\frac{1}{4}\sin\left(2\cdot \pi\right)\right]&\mbox{}\\
\displaystyle &\displaystyle= \frac{\pi}{8}&\mbox{}\\
\end{array}
$$
Example: Finding a Volume Using a Double Integral
A cylindrical hole of diameter $6$ cm is bored through a sphere of radius $5$ cm such that the axis of the cylinder passes through the center of the sphere. Find the volume of the resulting spherical ring.

To find the volume, $V,$ of the ring, we'll find the volume under the radius-$5$ hemisphere $z=\sqrt{25-x^2-y^2}$ over the region
$\displaystyle D =\left\{(r,\theta)|0 \leq \theta \leq 2\pi, 3 \leq r \leq 5\right\}.$
under

The result will give us $\displaystyle \frac{1}{2}V.$
Thus, $$ \begin{array}{lll} \displaystyle V&\displaystyle=2\iint_{D} \sqrt{25-x^2-y^2} \, dA&\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{3}^{5} \sqrt{25-(r\cos\theta)^2-(r\sin\theta)^2} \, r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{3}^{5} \sqrt{25-(r\cos\theta)^2-(r\sin\theta)^2} \, r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{3}^{5} \sqrt{25-r^2} \, r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{16}^{0} \sqrt{u} \left(-\frac{1}{2} \, du\right) \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{0}^{16} \sqrt{u} \cdot \frac{1}{2} \, du \, d\theta &\mbox{integral property}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\left(\int_{0}^{16} \sqrt{u} \, du \right)\, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\, d\theta \left(\int_{0}^{16} \sqrt{u} \, du \right) &\mbox{}\\ \displaystyle &\displaystyle=2\pi \left[\frac{2}{3}u^{3/2}\right]_{0}^{16} &\mbox{}\\ \displaystyle &\displaystyle=2\pi \left[\frac{2}{3}(16)^{3/2}\right] &\mbox{}\\ \displaystyle &\displaystyle=2\pi \cdot \frac{2}{3}\cdot 64 &\mbox{}\\ \displaystyle &\displaystyle=\frac{256\pi}{3} &\mbox{}\\ \end{array} $$ The volume of the ring is $\displaystyle=\frac{256\pi}{3},$ or about $268.08,$ $\mbox{cm}^3$

The result will give us $\displaystyle \frac{1}{2}V.$
Thus, $$ \begin{array}{lll} \displaystyle V&\displaystyle=2\iint_{D} \sqrt{25-x^2-y^2} \, dA&\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{3}^{5} \sqrt{25-(r\cos\theta)^2-(r\sin\theta)^2} \, r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{3}^{5} \sqrt{25-(r\cos\theta)^2-(r\sin\theta)^2} \, r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{3}^{5} \sqrt{25-r^2} \, r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{16}^{0} \sqrt{u} \left(-\frac{1}{2} \, du\right) \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=2\int_{0}^{2\pi}\int_{0}^{16} \sqrt{u} \cdot \frac{1}{2} \, du \, d\theta &\mbox{integral property}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\left(\int_{0}^{16} \sqrt{u} \, du \right)\, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\, d\theta \left(\int_{0}^{16} \sqrt{u} \, du \right) &\mbox{}\\ \displaystyle &\displaystyle=2\pi \left[\frac{2}{3}u^{3/2}\right]_{0}^{16} &\mbox{}\\ \displaystyle &\displaystyle=2\pi \left[\frac{2}{3}(16)^{3/2}\right] &\mbox{}\\ \displaystyle &\displaystyle=2\pi \cdot \frac{2}{3}\cdot 64 &\mbox{}\\ \displaystyle &\displaystyle=\frac{256\pi}{3} &\mbox{}\\ \end{array} $$ The volume of the ring is $\displaystyle=\frac{256\pi}{3},$ or about $268.08,$ $\mbox{cm}^3$
Finding Areas of Polar Regions
The area of a polar region $D$ can be found as $$ A(D)=\iint_{D} \,dA=\iint_D r \, dr \, d\theta $$

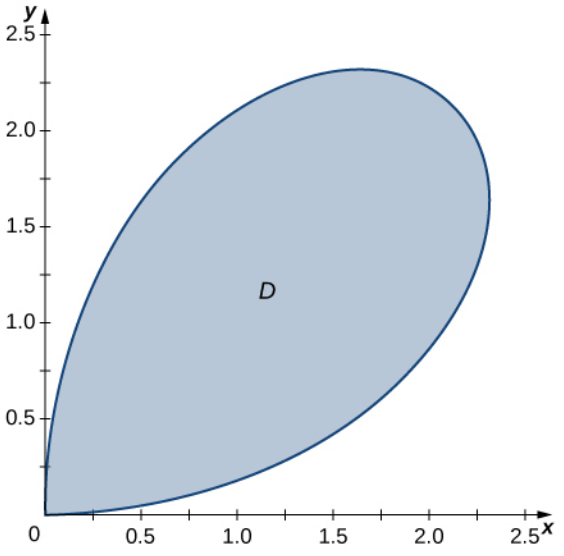
Example
Find the area of the region $D$ bounded by the polar curve $r=3\sin(2\theta)$ where $\displaystyle 0 \leq \theta \leq \frac{\pi}{2}.$
$$
\begin{array}{lll}
\displaystyle A(D)&\displaystyle=\iint_{D} \,dA &\mbox{}\\
\displaystyle &\displaystyle=\iint_D r \, dr \, d\theta &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{\pi/2}\int_{0}^{3\sin(2\theta)} r \, dr \, d\theta &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{\pi/2}\left[\frac{1}{2}r^2\right]_{0}^{3\sin(2\theta)} \, d\theta &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{\pi/2}\frac{1}{2}(3\sin(2\theta))^2 \, d\theta &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{\pi/2}\frac{1}{2}\cdot 9\sin^2(2\theta) \, d\theta &\mbox{}\\
\displaystyle &\displaystyle=\frac{9}{2}\int_{0}^{\pi/2}\sin^2(2\theta) \, d\theta &\mbox{}\\
\displaystyle &\displaystyle=\frac{9}{2}\int_{0}^{\pi}\sin^2(u)\, \frac{1}{2}\, du &\mbox{}\\
\displaystyle &\displaystyle=\frac{9}{4}\int_{0}^{\pi}\sin^2(u)\, du &\mbox{}\\
\displaystyle &\displaystyle= \frac{9}{4}\left[\frac{1}{2}u-\frac{1}{4}\sin(2u)\right]_{0}^{\pi}&\mbox{integral table}\\
\displaystyle &\displaystyle= \frac{9}{4}\left[\frac{1}{2}\cdot \pi-\frac{1}{4}\sin\left(2\cdot \pi\right)\right]&\mbox{}\\
\displaystyle &\displaystyle= \frac{9\pi}{8}&\mbox{}\\
\end{array}
$$
Example
Determine the average value of the function $f (x, y) = \sqrt{x^2 + y^2}$ over the region $D$ bounded by the polar curve $r=3\sin(2\theta)$ where $\displaystyle 0 \leq \theta \leq \frac{\pi}{2}.$

$$
\begin{array}{lll}
\displaystyle f_{avg}&\displaystyle= \frac{1}{A(D)}\iint_D f(x,y)\, dA&\mbox{}\\
\displaystyle &\displaystyle= \frac{1}{\frac{9\pi}{8}}\iint_D f(x,y)\, dA&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\iint_D f(x,y)\, dA&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\iint_D f(r\cos \theta,r\sin \theta)\, r \, dr \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\int_{0}^{\pi/2}\int_{0}^{3\sin(2\theta)} \sqrt{(r\cos \theta)^2+(r\sin \theta)^2} \, r \, dr \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\int_{0}^{\pi/2}\int_{0}^{3\sin(2\theta)}\sqrt{r^2} \, r \, dr \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\int_{0}^{\pi/2}\int_{0}^{3\sin(2\theta)} |r| \, r \, dr \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\int_{0}^{\pi/2}\int_{0}^{3\sin(2\theta)} r \cdot \, r \, dr \, d\theta&\mbox{since $r\geq 0$}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\int_{0}^{\pi/2}\int_{0}^{3\sin(2\theta)} r^2 \, dr \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\int_{0}^{\pi/2}\left[\frac{1}{3}r^3\right]_{0}^{3\sin(2\theta)} \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\int_{0}^{\pi/2}\left[\frac{1}{3}(3\sin(2\theta))^3\right] \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{9\pi}\int_{0}^{\pi/2}9\sin^3(2\theta))^3 \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{\pi}\int_{0}^{\pi/2}\sin^3(2\theta) \, d\theta&\mbox{}\\
\displaystyle &\displaystyle= \frac{8}{\pi}\int_{0}^{\pi}\sin^3(u) \cdot \frac{1}{2} \, du&\mbox{}\\
\displaystyle &\displaystyle= \frac{4}{\pi}\int_{0}^{\pi}\sin^3(u) \, du&\mbox{}\\
\displaystyle &\displaystyle= \frac{4}{\pi}\left[-\frac{1}{3}(2+\sin^2(u))\cos u\right]_{0}^{\pi}&\mbox{using integral table}\\
\displaystyle &\displaystyle= \frac{4}{\pi}\left[-\frac{1}{3}(2+\sin^2(\pi))\cos \pi-\left(-\frac{1}{3}(2+\sin^2(0))\cos 0\right)\right]&\mbox{}\\
\displaystyle &\displaystyle= \frac{4}{\pi}\left[-\frac{1}{3}(2+0)(-1)-\left(-\frac{1}{3}(2+0)\cdot 1\right)\right]&\mbox{}\\
\displaystyle &\displaystyle= \frac{4}{\pi}\left[\frac{2}{3}-\left(-\frac{2}{3}\right)\right]&\mbox{}\\
\displaystyle &\displaystyle= \frac{4}{\pi}\cdot \frac{4}{3}&\mbox{}\\
\displaystyle &\displaystyle= \frac{16}{3\pi}&\mbox{}\\
\end{array}
$$
Example: Finding Area Between Two Polar Curves
Find the area enclosed by the circle $r = 3 \cos \theta$ and the cardioid $r = 1 + \cos \theta.$
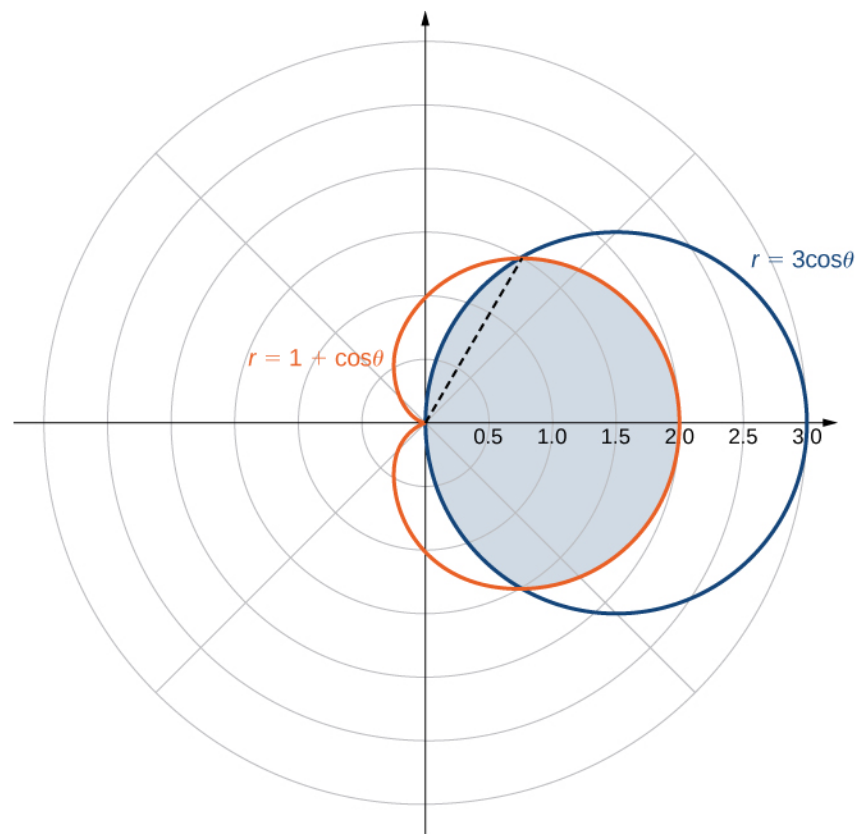
Instead of integrating over $\displaystyle -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2},$
we will intergrate over $\displaystyle 0 \leq \theta \leq \frac{\pi}{2}$ and then double the resulting area.
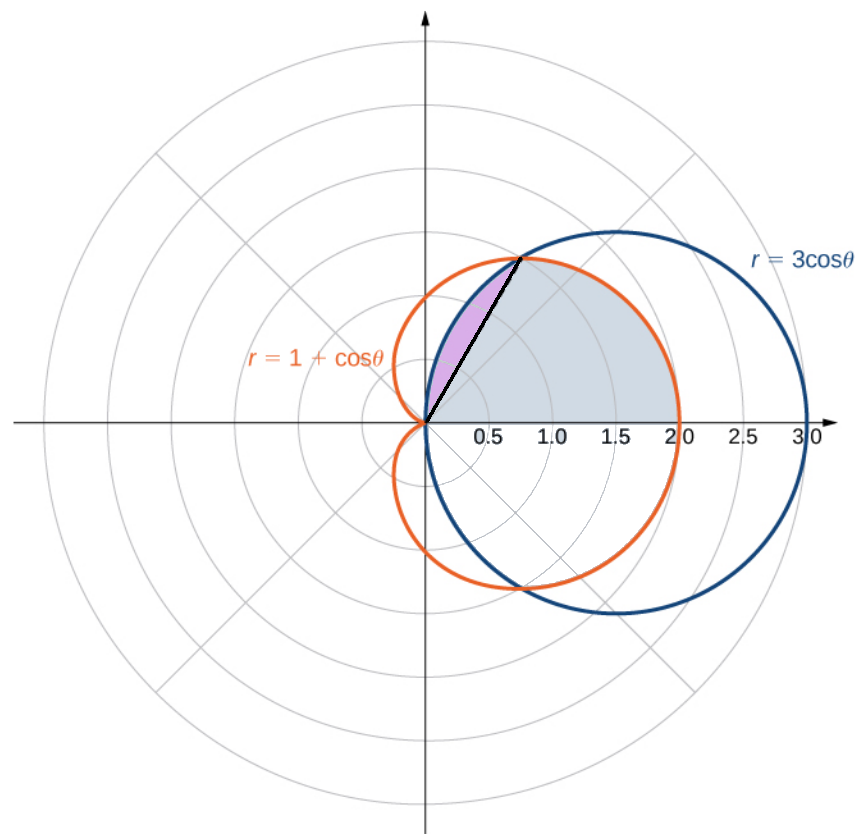
Now, at the angle shown, the polar curve changes from $\color{#ea5f23}{r=1+\cos \theta}$ to $\color{#124378}{r=3\cos \theta}.$
So, we must break this upper region $U$ into two regions $S$ and $T$ separated by this angle.
To do this, we must first find this angle by determining where the two curves intersect by solving the equation $$ 1+\cos\theta =3\cos \theta $$ which gives $$ \begin{array}{lll} &\displaystyle 1 =2\cos \theta &\mbox{}\\ \implies &\displaystyle \cos \theta =\frac{1}{2}&\mbox{}\\ \implies &\displaystyle \theta =\cos^{-1}\left(\frac{1}{2}\right)&\mbox{}\\ \implies &\displaystyle \theta =\frac{\pi}{3}&\mbox{ since $\theta$ is in the firtst quadrant}\\ \end{array} $$ Calling the entire region $D,$ we we may find the area of $D$ as $$ \begin{array}{lll} \displaystyle A(D)&\displaystyle=2A(U)\,\mbox{ the region is twice the area of the upper region} &\\ \displaystyle &\displaystyle=2A(S\cup T) &\mbox{}\\ \displaystyle &\displaystyle=2\iint_{S \cup T}\, dA &\mbox{}\\ \displaystyle &\displaystyle=2\left(\iint_{S}\, dA + \iint_{T}\, dA \right)\, \mbox{ integral property}&\\ \displaystyle &\displaystyle=2\left(\iint_{S}\, r \, dr \, d\theta + \iint_{T}\, r \, dr \, d\theta \right)\,\mbox{ switching to polar coordinates}&\\ \displaystyle &\displaystyle=2\left(\int_{0}^{\pi/3}\int_{0}^{1+\cos \theta}\, r \, dr \, d\theta + \int_{\pi/3}^{\pi/2}\int_{0}^{3\cos \theta}\, r \, dr \, d\theta \right)&\mbox{}\\ \displaystyle &\displaystyle=2\left(\int_{0}^{\pi/3}\left[\frac{1}{2}r^2\right]_{0}^{1+\cos \theta} \, d\theta + \int_{\pi/3}^{\pi/2}\left[\frac{1}{2}r^2\right]_{0}^{3\cos \theta} \, d\theta \right)&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{\pi/3}\left[r^2\right]_{0}^{1+\cos \theta} \, d\theta + \int_{\pi/3}^{\pi/2}\left[r^2\right]_{0}^{3\cos \theta} \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{\pi/3}(1+\cos \theta)^2 \, d\theta + \int_{\pi/3}^{\pi/2}(3\cos \theta)^2 \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{\pi/3}1+2\cos \theta+\cos^2\theta \, d\theta + 9\int_{\pi/3}^{\pi/2}\cos^2 \theta \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\left[\theta+2\sin \theta+\frac{1}{2}\theta+\frac{1}{4}\sin(2\theta)\right]_{0}^{\pi/3} + 9\left[\frac{1}{2}\theta+\frac{1}{4}\sin(2\theta) \right]_{\pi/3}^{\pi/2}\,\mbox{ using integral table} &\\ \displaystyle &\displaystyle=\left[\frac{\pi}{3}+2\sin \frac{\pi}{3}+\frac{1}{2}\cdot \frac{\pi}{3}+\frac{1}{4}\sin\frac{2\pi}{3}-0\right] + 9\left[\frac{1}{2}\cdot \frac{\pi}{2}+\frac{1}{4}\sin(\pi)-\left(\frac{1}{2}\cdot \frac{\pi}{3}+\frac{1}{4}\sin \frac{2\pi}{3}\right) \right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{3}+2\cdot \frac{\sqrt{3}}{2}+\frac{\pi}{6}+\frac{1}{4}\cdot\frac{\sqrt{3}}{2} + 9\left[\frac{\pi}{4}+0-\frac{\pi}{6}-\frac{1}{4}\cdot\frac{\sqrt{3}}{2} \right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{2}+\frac{9\sqrt{3}}{8} + 9\left[\frac{\pi}{12}-\frac{\sqrt{3}}{8} \right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{2}+\frac{9\sqrt{3}}{8} +\frac{3\pi}{4}-\frac{9\sqrt{3}}{8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{5\pi}{4} &\mbox{}\\ \end{array} $$

Now, at the angle shown, the polar curve changes from $\color{#ea5f23}{r=1+\cos \theta}$ to $\color{#124378}{r=3\cos \theta}.$
So, we must break this upper region $U$ into two regions $S$ and $T$ separated by this angle.
To do this, we must first find this angle by determining where the two curves intersect by solving the equation $$ 1+\cos\theta =3\cos \theta $$ which gives $$ \begin{array}{lll} &\displaystyle 1 =2\cos \theta &\mbox{}\\ \implies &\displaystyle \cos \theta =\frac{1}{2}&\mbox{}\\ \implies &\displaystyle \theta =\cos^{-1}\left(\frac{1}{2}\right)&\mbox{}\\ \implies &\displaystyle \theta =\frac{\pi}{3}&\mbox{ since $\theta$ is in the firtst quadrant}\\ \end{array} $$ Calling the entire region $D,$ we we may find the area of $D$ as $$ \begin{array}{lll} \displaystyle A(D)&\displaystyle=2A(U)\,\mbox{ the region is twice the area of the upper region} &\\ \displaystyle &\displaystyle=2A(S\cup T) &\mbox{}\\ \displaystyle &\displaystyle=2\iint_{S \cup T}\, dA &\mbox{}\\ \displaystyle &\displaystyle=2\left(\iint_{S}\, dA + \iint_{T}\, dA \right)\, \mbox{ integral property}&\\ \displaystyle &\displaystyle=2\left(\iint_{S}\, r \, dr \, d\theta + \iint_{T}\, r \, dr \, d\theta \right)\,\mbox{ switching to polar coordinates}&\\ \displaystyle &\displaystyle=2\left(\int_{0}^{\pi/3}\int_{0}^{1+\cos \theta}\, r \, dr \, d\theta + \int_{\pi/3}^{\pi/2}\int_{0}^{3\cos \theta}\, r \, dr \, d\theta \right)&\mbox{}\\ \displaystyle &\displaystyle=2\left(\int_{0}^{\pi/3}\left[\frac{1}{2}r^2\right]_{0}^{1+\cos \theta} \, d\theta + \int_{\pi/3}^{\pi/2}\left[\frac{1}{2}r^2\right]_{0}^{3\cos \theta} \, d\theta \right)&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{\pi/3}\left[r^2\right]_{0}^{1+\cos \theta} \, d\theta + \int_{\pi/3}^{\pi/2}\left[r^2\right]_{0}^{3\cos \theta} \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{\pi/3}(1+\cos \theta)^2 \, d\theta + \int_{\pi/3}^{\pi/2}(3\cos \theta)^2 \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{\pi/3}1+2\cos \theta+\cos^2\theta \, d\theta + 9\int_{\pi/3}^{\pi/2}\cos^2 \theta \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\left[\theta+2\sin \theta+\frac{1}{2}\theta+\frac{1}{4}\sin(2\theta)\right]_{0}^{\pi/3} + 9\left[\frac{1}{2}\theta+\frac{1}{4}\sin(2\theta) \right]_{\pi/3}^{\pi/2}\,\mbox{ using integral table} &\\ \displaystyle &\displaystyle=\left[\frac{\pi}{3}+2\sin \frac{\pi}{3}+\frac{1}{2}\cdot \frac{\pi}{3}+\frac{1}{4}\sin\frac{2\pi}{3}-0\right] + 9\left[\frac{1}{2}\cdot \frac{\pi}{2}+\frac{1}{4}\sin(\pi)-\left(\frac{1}{2}\cdot \frac{\pi}{3}+\frac{1}{4}\sin \frac{2\pi}{3}\right) \right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{3}+2\cdot \frac{\sqrt{3}}{2}+\frac{\pi}{6}+\frac{1}{4}\cdot\frac{\sqrt{3}}{2} + 9\left[\frac{\pi}{4}+0-\frac{\pi}{6}-\frac{1}{4}\cdot\frac{\sqrt{3}}{2} \right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{2}+\frac{9\sqrt{3}}{8} + 9\left[\frac{\pi}{12}-\frac{\sqrt{3}}{8} \right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{2}+\frac{9\sqrt{3}}{8} +\frac{3\pi}{4}-\frac{9\sqrt{3}}{8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{5\pi}{4} &\mbox{}\\ \end{array} $$
Bonus Problem
Use your newly-acquired knowledge of double integrals in polar coordinates to evaluate the following. $$ \int_{-\infty}^{\infty}e^{-x^2}\, dx $$
$$
\begin{array}{lll}
\displaystyle \int_{-\infty}^{\infty}e^{-x^2}\, dx &\displaystyle=\sqrt{\left(\int_{-\infty}^{\infty}e^{-x^2}\, dx\right)^2} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{\left(\int_{-\infty}^{\infty}e^{-x^2}\, dx\right)\left(\int_{-\infty}^{\infty}e^{-x^2}\, dx\right)} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{\left(\int_{-\infty}^{\infty}e^{-x^2}\, dx\right)\left(\int_{-\infty}^{\infty}e^{-y^2}\, dy\right)} &\mbox{change variable of integration}\\
\displaystyle &\displaystyle=\sqrt{\int_{-\infty}^{\infty}e^{-x^2}\left(\int_{-\infty}^{\infty}e^{-y^2}\, dy\right)\, dx} &\mbox{$\displaystyle \int_{-\infty}^{\infty}e^{-y^2}\, dy$ is a constant}\\
\displaystyle &\displaystyle=\sqrt{\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-x^2} e^{-y^2}\, dy \, dx} &\mbox{$e^{-x^2}$ is a constant wrt to $y$}\\
\displaystyle &\displaystyle=\sqrt{\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-x^2-y^2} \, dy \, dx} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{\int_{0}^{2\pi}\int_{0}^{\infty}e^{-r^2} r \, dr \, d\theta} &\mbox{switching to polar coordinates}\\
\displaystyle &\displaystyle=\sqrt{\left(\int_{0}^{2\pi} \, d\theta\right) \left(\int_{0}^{\infty}e^{-r^2} r \, dr\right)} &\mbox{$\displaystyle \int_{0}^{\infty}e^{-r^2} r \, dr$ is a constant}\\
\displaystyle &\displaystyle=\sqrt{2\pi \int_{0}^{-\infty}e^{u} \left(-\frac{1}{2} \, du\right)} &\mbox{letting $u=-r^2$ so that $\displaystyle r\,dr =-\frac{1}{2}du$}\\
\displaystyle &\displaystyle=\sqrt{2\pi \cdot \frac{1}{2}\int_{-\infty}^{0}e^{u} \, du} &\mbox{using properties of integrals}\\
\displaystyle &\displaystyle=\sqrt{\pi \left[e^{u}\right]_{-\infty}^{0}} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{\pi \lim_{a\rightarrow -\infty}\left[e^{u}\right]_{a}^{0}} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{\pi \lim_{a\rightarrow -\infty}\left[1-e^a\right]} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{\pi \cdot 1} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{\pi} &\mbox{}\\
\end{array}
$$
Quote of the Day
"A mathematician is one to whom that $ \displaystyle \int_{-\infty}^{\infty}e^{-x^2}\, dx=\sqrt{\pi} $ is as obvious as that twice two makes four is to you."
– Sir William Thomson, (Lord Kelvin).

Quote of the Day Redux
"Heavier-than-air flying machines are impossible."
– Sir William Thomson, (Lord Kelvin).
