We continue from last time by learning how to integrate two-variable functions over non-rectangular regions.
Double Integrals Over General Regions
We begin by considering double integrals over a non-rectangular region $D.$
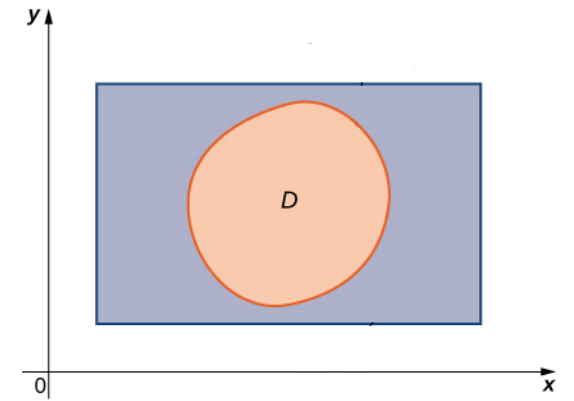
Regions Bounded by Functions of $x$ or $y$
The non-rectangular regions we discuss today are those whose boundary can be described by functions of either $x$ or $y.$
There are two types which we shall discuss...

Type I: Between Two Functions of $x$
A region $D$ in the $(x, y)$-plane is of Type I if it lies between two vertical lines and the graphs of two continuous functions $g_1 (x)$ and $g_2 (x).$ That is $$ D = \left\{(x, y) \in \mathbb{R}^2|a \leq x \leq b, g_1 (x) \leq y \leq g_2 (x)\right \} $$

Type II: Between Two Functions of $y$
A region $D$ in the $(x, y)$-plane is of Type II if it lies between two horizontal lines and the graphs of two continuous functions $h_1 (y)$ and $h_2 (y).$ That is $$ D = \left\{(x, y) \in \mathbb{R}^2|h_1(y) \leq x \leq h_2(y), c \leq y \leq d\right \} $$
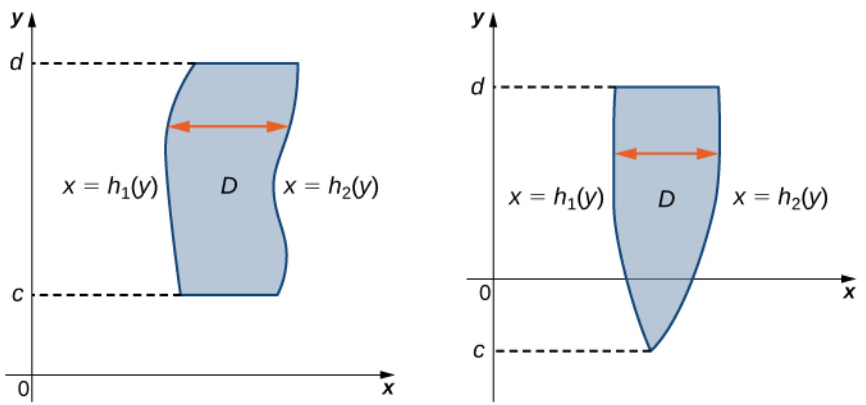
Fact
Many of the kinds of regions we will be dealing with can be classified as as both Type I and Type II.
Example
Describe the region below as a Type I region and as a Type II region.
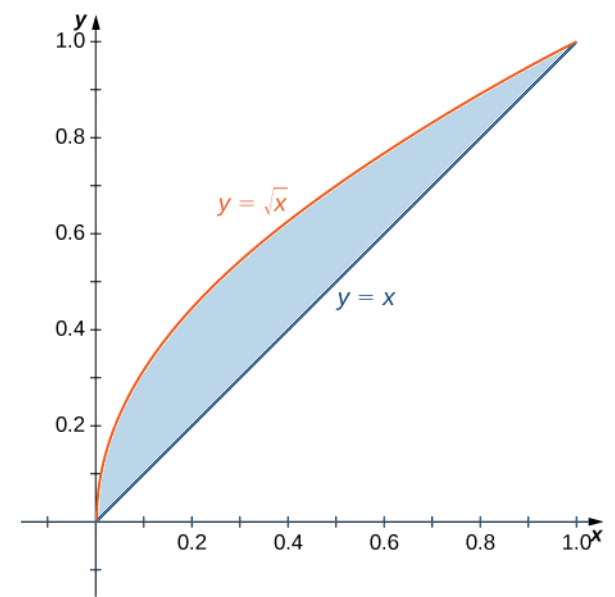
As a Type I region, we describe it as
$$
\color{#426a94}{x}\leq y \leq \color{#e96026}{\sqrt{x}}, \,\,\, \color{magenta}{0}\leq x \leq \color{#0594f8}{1}
$$
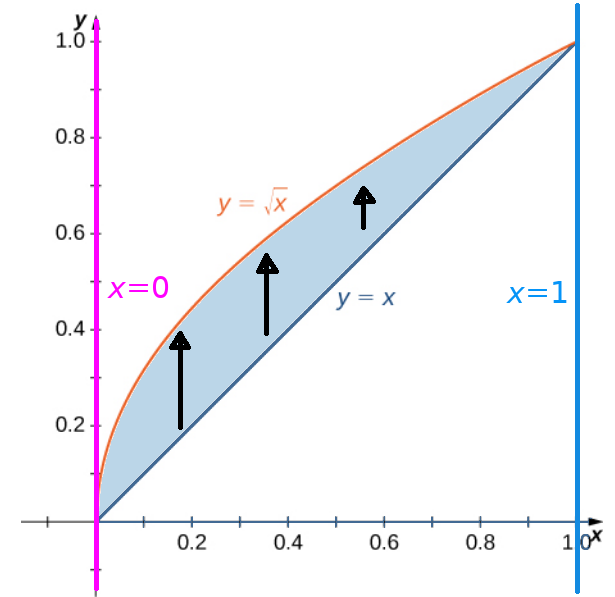
As a Type II region, we describe it as $$ \color{#e96026}{y^2}\leq x \leq \color{#426a94}{y}, \,\,\, \color{magenta}{0} \leq y \leq \color{#0594f8}{1} $$


As a Type II region, we describe it as $$ \color{#e96026}{y^2}\leq x \leq \color{#426a94}{y}, \,\,\, \color{magenta}{0} \leq y \leq \color{#0594f8}{1} $$

Okay! So how do we find double integrals then?!
Well, I'm glad you asked! The answer is....
Fubini's Theorem: The Strong Form
For a function $f (x, y)$ that is continuous on a region $D$ of Type I, we have $$ \iint_D f(x,y) \, dA=\iint_D f(x,y) \, dy \, dx =\int_{a}^{b} \left[\int_{g_1(x)}^{g_2(x)} f(x,y) \,dy\right]\,dx $$
For a function $f (x, y)$ that is continuous on a region $D$ of Type II, we have $$ \iint_D f(x,y) \, dA=\iint_D f(x,y) \, dx \, dy =\int_{c}^{d} \left[\int_{h_1(y)}^{h_2(y)} f(x,y) \,dx\right]\,dy $$
Big Note
Expressing a double integral as an iterated integral,
1) the inner integral can have limits which are be functions of the outer variable
2) the limits on the outer integral are always constants.
Example
Find $ \displaystyle \iint_{D} x+y^2 \, dA $ where $D$ is the shaded region shown below.

We can view this region as being both Type I and Type II. We shall do both and see that the value of the integral is the same.
As a Type I Region: We express both curves as functions of $x.$
 $$
\begin{array}{lll}
\displaystyle \iint_{D} x+y^2 \, dA&\displaystyle=\color{black}{\int_{\color{magenta}{x=0}}^{\color{#0594f8}{x=1}}}\color{black}{\int_{\color{#426a94}{y=x}}^{\color{#e96026}{y=\sqrt{x}}}} x+y^2 \, \color{black}{dy} \, \color{black}{dx} &\mbox{by the Great (and strong!) Fubini!}\\
\displaystyle &\displaystyle=\int_{0}^{1}\int_{x}^{\sqrt{x}} x+y^2 \, dy \,dx &\mbox{a more common notation}\\
\displaystyle &\displaystyle=\int_{0}^{1}\left[ xy+\frac{1}{3}y^3 \right]_{x}^{\sqrt{x}} \,dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}\left[ x\sqrt{x}+\frac{1}{3}(\sqrt{x})^3 \right]-\left[ x\cdot x+\frac{1}{3}x^3 \right] \,dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}\left[ x^{3/2}+\frac{1}{3}x^{3/2} \right]-\left[ x^2+\frac{1}{3}x^3 \right] \,dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}\frac{4}{3}x^{3/2}-x^2-\frac{1}{3}x^3 \,dx &\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{4}{3}\cdot \frac{2}{5}x^{5/2}-\frac{1}{3}x^3-\frac{1}{3}\cdot \frac{1}{4}x^4\right]_{0}^{1} &\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{8}{15}x^{5/2}-\frac{1}{3}x^3-\frac{1}{12}x^4\right]_{0}^{1} &\mbox{}\\
\displaystyle &\displaystyle=\frac{8}{15}-\frac{1}{3}-\frac{1}{12} &\mbox{}\\
\displaystyle &\displaystyle=\frac{7}{60} &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \iint_{D} x+y^2 \, dA&\displaystyle=\color{black}{\int_{\color{magenta}{x=0}}^{\color{#0594f8}{x=1}}}\color{black}{\int_{\color{#426a94}{y=x}}^{\color{#e96026}{y=\sqrt{x}}}} x+y^2 \, \color{black}{dy} \, \color{black}{dx} &\mbox{by the Great (and strong!) Fubini!}\\
\displaystyle &\displaystyle=\int_{0}^{1}\int_{x}^{\sqrt{x}} x+y^2 \, dy \,dx &\mbox{a more common notation}\\
\displaystyle &\displaystyle=\int_{0}^{1}\left[ xy+\frac{1}{3}y^3 \right]_{x}^{\sqrt{x}} \,dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}\left[ x\sqrt{x}+\frac{1}{3}(\sqrt{x})^3 \right]-\left[ x\cdot x+\frac{1}{3}x^3 \right] \,dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}\left[ x^{3/2}+\frac{1}{3}x^{3/2} \right]-\left[ x^2+\frac{1}{3}x^3 \right] \,dx &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}\frac{4}{3}x^{3/2}-x^2-\frac{1}{3}x^3 \,dx &\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{4}{3}\cdot \frac{2}{5}x^{5/2}-\frac{1}{3}x^3-\frac{1}{3}\cdot \frac{1}{4}x^4\right]_{0}^{1} &\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{8}{15}x^{5/2}-\frac{1}{3}x^3-\frac{1}{12}x^4\right]_{0}^{1} &\mbox{}\\
\displaystyle &\displaystyle=\frac{8}{15}-\frac{1}{3}-\frac{1}{12} &\mbox{}\\
\displaystyle &\displaystyle=\frac{7}{60} &\mbox{}\\
\end{array}
$$
As a Type II Region: We now express both curves as functions of $y.$
 $$
\begin{array}{lll}
\displaystyle \iint_{D} x+y^2 \, dA&\displaystyle=\color{black}{\int_{\color{magenta}{y=0}}^{\color{#0594f8}{y=1}}}\color{black}{\int_{\color{#e96026}{x=y^2}}^{\color{#426a94}{x=y}}} x+y^2 \, \color{black}{dx} \, \color{black}{dy}&\mbox{by the Great (and strong!) Fubini!}\\
\displaystyle &\displaystyle=\int_{0}^{1}\int_{y^2}^{y} x+y^2 \, dx \,dy &\mbox{a more common notation}\\
\displaystyle &\displaystyle=\int_{0}^{1} \left[\frac{1}{2}x^2+y^2x\right]_{y^2}^{y} \,dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1} \left[\frac{1}{2}y^2+y^2\cdot y\right]-\left[\frac{1}{2}(y^2)^2+y^2\cdot y^2\right] \,dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1} \frac{1}{2}y^2+y^3-\frac{3}{2}y^4 \,dy &\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{1}{2}\cdot \frac{1}{3}y^3+\frac{1}{4}y^4 -\frac{3}{2}\cdot \frac{1}{5}y^5\right]_{0}^{1}&\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{1}{6}y^4+\frac{1}{4}y^4- \frac{3}{10}y^5\right]_{0}^{1}&\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{6}+\frac{1}{4}-\frac{3}{10}&\mbox{}\\
\displaystyle &\displaystyle=\frac{7}{60}&\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \iint_{D} x+y^2 \, dA&\displaystyle=\color{black}{\int_{\color{magenta}{y=0}}^{\color{#0594f8}{y=1}}}\color{black}{\int_{\color{#e96026}{x=y^2}}^{\color{#426a94}{x=y}}} x+y^2 \, \color{black}{dx} \, \color{black}{dy}&\mbox{by the Great (and strong!) Fubini!}\\
\displaystyle &\displaystyle=\int_{0}^{1}\int_{y^2}^{y} x+y^2 \, dx \,dy &\mbox{a more common notation}\\
\displaystyle &\displaystyle=\int_{0}^{1} \left[\frac{1}{2}x^2+y^2x\right]_{y^2}^{y} \,dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1} \left[\frac{1}{2}y^2+y^2\cdot y\right]-\left[\frac{1}{2}(y^2)^2+y^2\cdot y^2\right] \,dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1} \frac{1}{2}y^2+y^3-\frac{3}{2}y^4 \,dy &\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{1}{2}\cdot \frac{1}{3}y^3+\frac{1}{4}y^4 -\frac{3}{2}\cdot \frac{1}{5}y^5\right]_{0}^{1}&\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{1}{6}y^4+\frac{1}{4}y^4- \frac{3}{10}y^5\right]_{0}^{1}&\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{6}+\frac{1}{4}-\frac{3}{10}&\mbox{}\\
\displaystyle &\displaystyle=\frac{7}{60}&\mbox{}\\
\end{array}
$$
For comparison, we place the setup of the two integrals side by side.

 $$
\displaystyle\color{black}{\int_{\color{magenta}{x=0}}^{\color{#0594f8}{x=1}}}\color{black}{\int_{\color{#426a94}{y=x}}^{\color{#e96026}{y=\sqrt{x}}}} x+y^2 \, \color{black}{dy} \, \color{black}{dx}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\displaystyle\color{black}{\int_{\color{magenta}{y=0}}^{\color{#0594f8}{y=1}}}\color{black}{\int_{\color{#e96026}{x=y^2}}^{\color{#426a94}{x=y}}} x+y^2 \, \color{black}{dx} \, \color{black}{dy}
$$
$$
\displaystyle\color{black}{\int_{\color{magenta}{x=0}}^{\color{#0594f8}{x=1}}}\color{black}{\int_{\color{#426a94}{y=x}}^{\color{#e96026}{y=\sqrt{x}}}} x+y^2 \, \color{black}{dy} \, \color{black}{dx}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\displaystyle\color{black}{\int_{\color{magenta}{y=0}}^{\color{#0594f8}{y=1}}}\color{black}{\int_{\color{#e96026}{x=y^2}}^{\color{#426a94}{x=y}}} x+y^2 \, \color{black}{dx} \, \color{black}{dy}
$$
As a Type I Region: We express both curves as functions of $x.$

As a Type II Region: We now express both curves as functions of $y.$

For comparison, we place the setup of the two integrals side by side.

 $$
\displaystyle\color{black}{\int_{\color{magenta}{x=0}}^{\color{#0594f8}{x=1}}}\color{black}{\int_{\color{#426a94}{y=x}}^{\color{#e96026}{y=\sqrt{x}}}} x+y^2 \, \color{black}{dy} \, \color{black}{dx}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\displaystyle\color{black}{\int_{\color{magenta}{y=0}}^{\color{#0594f8}{y=1}}}\color{black}{\int_{\color{#e96026}{x=y^2}}^{\color{#426a94}{x=y}}} x+y^2 \, \color{black}{dx} \, \color{black}{dy}
$$
$$
\displaystyle\color{black}{\int_{\color{magenta}{x=0}}^{\color{#0594f8}{x=1}}}\color{black}{\int_{\color{#426a94}{y=x}}^{\color{#e96026}{y=\sqrt{x}}}} x+y^2 \, \color{black}{dy} \, \color{black}{dx}
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\displaystyle\color{black}{\int_{\color{magenta}{y=0}}^{\color{#0594f8}{y=1}}}\color{black}{\int_{\color{#e96026}{x=y^2}}^{\color{#426a94}{x=y}}} x+y^2 \, \color{black}{dx} \, \color{black}{dy}
$$
Fact
Some regions are expressible only as a single Type I or Type II region.
Example
Find $ \displaystyle \iint_D xy+1 \, dA $ over the region below.
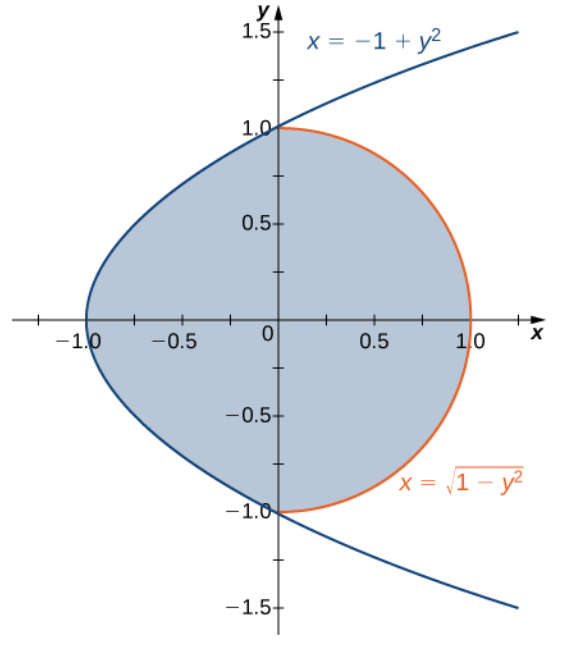
This region is expressible as a Type II region.
$$
\begin{array}{lll}
\displaystyle \iint_D xy+1 \, dA&\displaystyle=\int_{y=-1}^{y=1}\int_{\color{#426a94}{x=y^2-1}}^{\color{#e96026}{x=\sqrt{1-y^2}}} xy+1 \, dx \, dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1}\int_{y^2-1}^{\sqrt{1-y^2}} xy+1 \, dx \, dy &\mbox{a more common notation}\\
\displaystyle &\displaystyle=\int_{-1}^{1} \left[\frac{1}{2}x^2y+x\right]_{y^2-1}^{\sqrt{1-y^2}} \, dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1} \left[\frac{1}{2}\left(\sqrt{1-y^2}\right)^2y+\sqrt{1-y^2}\right]-\left[\frac{1}{2}(y^2-1)^2y+y^2-1\right] \, dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1} \left[\frac{1}{2}(1-y^2)y+\sqrt{1-y^2}\right]-\left[\frac{1}{2}(y^4-2y^2+1)y+y^2-1\right] \, dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1} \left[\frac{1}{2}(1-y^2)y+\sqrt{1-y^2}\right]-\left[\frac{1}{2}y^5-y^3+\frac{1}{2}y+y^2-1\right] \, dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1} \frac{1}{2}y-\frac{1}{2}y^3+\sqrt{1-y^2}-\frac{1}{2}y^5+y^3-\frac{1}{2}y-y^2+1 \, dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{-1}^{1} \frac{1}{2}y^3+\sqrt{1-y^2}-\frac{1}{2}y^5-y^2+1 \, dy &\mbox{combine like terms}\\
\displaystyle &\displaystyle=\int_{-1}^{1} -\frac{1}{2}y^5+\frac{1}{2}y^3-y^2+1 +\sqrt{1-y^2}\, dy &\mbox{rearrange terms}\\
\displaystyle &\displaystyle=\left[ -\frac{1}{2}\cdot \frac{1}{6}y^6+\frac{1}{2}\cdot \frac{1}{4}y^4-\frac{1}{3}y^3+y +\frac{1}{2}y\sqrt{1-y^2}+\frac{1}{2}\sin^{-1}y\right]_{-1}^{1} &\mbox{integral table}\\
\displaystyle &\displaystyle=\left[ -\frac{1}{12}y^6+\frac{1}{8}y^4-\frac{1}{3}y^3+y +\frac{1}{2}y\sqrt{1-y^2}+\frac{1}{2}\sin^{-1}y\right]_{-1}^{1} &\mbox{simplify}\\
\displaystyle &\displaystyle=\left[ -\frac{1}{12}y^6+\frac{1}{8}y^4\right]_{-1}^{1}+\left[-\frac{1}{3}y^3+y\right]_{-1}^{1} +\left[\frac{1}{2}y\sqrt{1-y^2}\right]_{-1}^{1}+\left[\frac{1}{2}\sin^{-1}y\right]_{-1}^{1} &\mbox{}\\
\displaystyle &\displaystyle=0+\left[\frac{2}{3}\right]-\left[-\frac{2}{3}\right]+0+\left[\frac{1}{2}\sin^{-1}y\right]-\left[\frac{1}{2}\sin^{-1}y\right] &\mbox{}\\
\displaystyle &\displaystyle=\frac{4}{3}+\left[\frac{1}{2}\sin^{-1}(1)\right]-\left[\frac{1}{2}\sin^{-1}(-1)\right] &\mbox{}\\
\displaystyle &\displaystyle=\frac{4}{3}+\left[\frac{1}{2}\cdot\frac{\pi}{2}\right]-\left[\frac{1}{2}\cdot \left(-\frac{\pi}{2}\right)\right] &\mbox{}\\
\displaystyle &\displaystyle=\frac{4}{3}+\frac{\pi}{2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{8+3\pi}{6} &\mbox{}\\
\end{array}
$$
Properties of Double Integrals
Great news! All the properties of double integrals for rectangular regions $R$ hold for more general regions $D!$
Assume that the functions $f (x, y)$ and $g(x, y)$ are integrable over the rectangular region $D$ and that $S$ and $T$ are subregions of $R.$ Also assume that $c,$ $m,$ and $M$ are real numbers. Then, $$ \begin{array}{ll} \displaystyle \iint_{D} f(x,y)+g(x,y) \,dA=\iint_{D} f(x,y) \,dA+\iint_{D} g(x,y) \,dA&\mbox{}\\ \displaystyle \iint_{D} cf(x,y)\,dA=c\iint_{D} f(x,y) \,dA&\mbox{}\\ \displaystyle S \cap T=\varnothing \implies \iint_{S \cup T} f(x,y) \,dA=\iint_{S} f(x,y) \,dA+\iint_{T} f(x,y) \,dA&\mbox{}\\ \displaystyle f(x,y)\geq g(x,y)\implies \iint_{D} f(x,y) \,dA\geq \iint_{D} g(x,y) \,dA&\mbox{}\\ \displaystyle m \leq f (x, y) \leq M\implies mA(R)\leq \iint_{D} f(x,y) \,dA\leq MA(R) \end{array} $$
Properties of Double Integrals
For stranger regions, the following property is exceedingly useful.
$$\displaystyle S \cap T=\varnothing \implies \iint_{S \cup T} f(x,y) \,dA=\iint_{S} f(x,y) \,dA+\iint_{T} f(x,y) \,dA$$ This property tells us that if our region $D=S\cup T$ is made up of two disjoint (non-overlapping) regions $S$ and $T,$ we may simply add the two integrals taken over $S$ and $T$ individually.
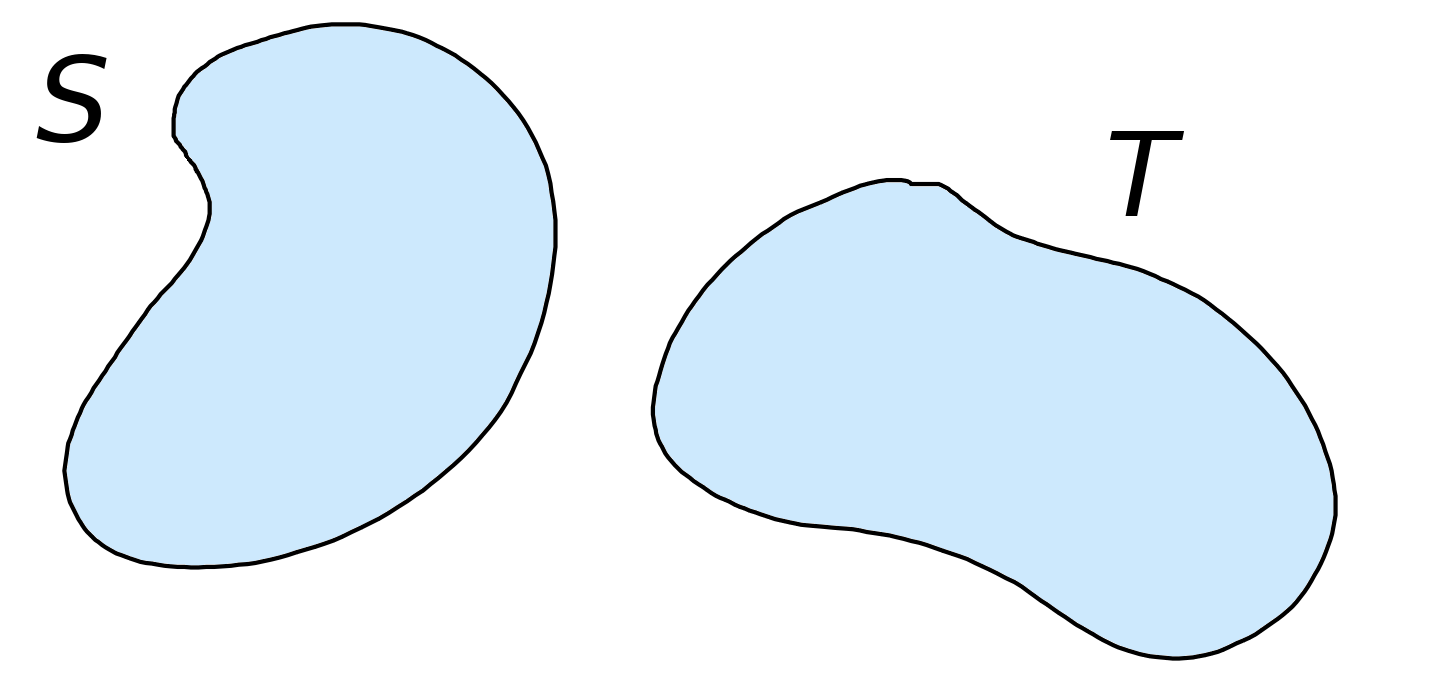
Special Note: The result $$\iint_{S \cup T} f(x,y) \,dA=\iint_{S} f(x,y) \,dA+\iint_{T} f(x,y) \,dA$$ still holds if the boundaries of $S$ and $T$ overlap.

Example
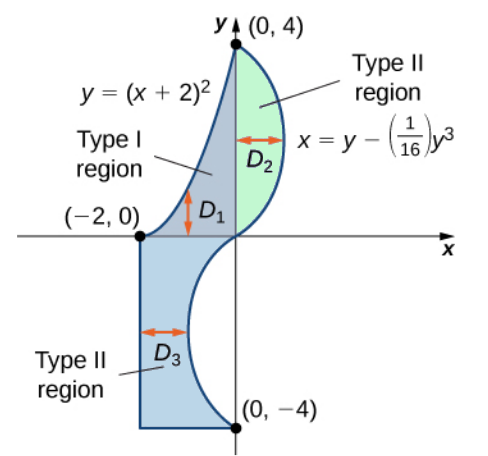
Consider the oddly-shaped region $D$ below. It has no particular type (unless we resort to piecewise-defined functions), but it can be decomposed into $3$ regions $D_1,$ $D_2,$ and $D_3$ which do fall into the Type I or Type II category. We then see that $$ \iint_{D} f(x,y) \,dA=\iint_{D_1} f(x,y) \,dA+\iint_{D_2} f(x,y) \,dA+\iint_{D_3} f(x,y) \,dA $$
Bonus Property: When Two Regions Overlap by More than Their Boundaries
If $f$ is an integrable function, then for any two regions $S$ and $T,$ $$\iint_{S \cup T} f(x,y) \,dA=\iint_{S} f(x,y) \,dA+\iint_{T} f(x,y) \,dA-\iint_{S \cap T} f(x,y)\,dA$$
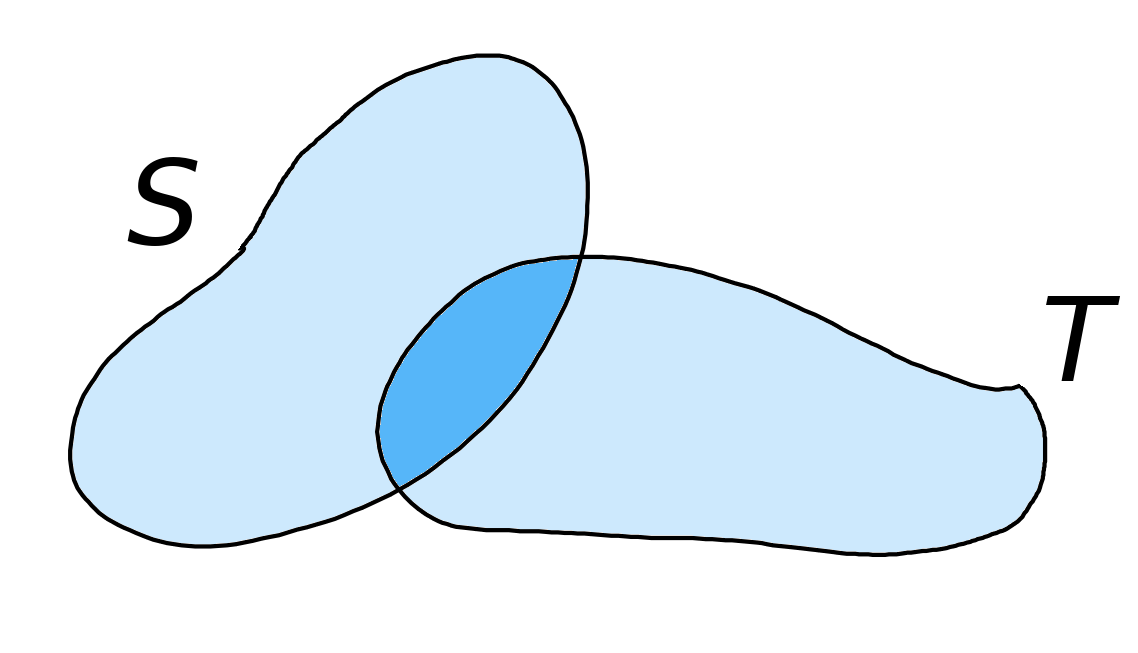
Example
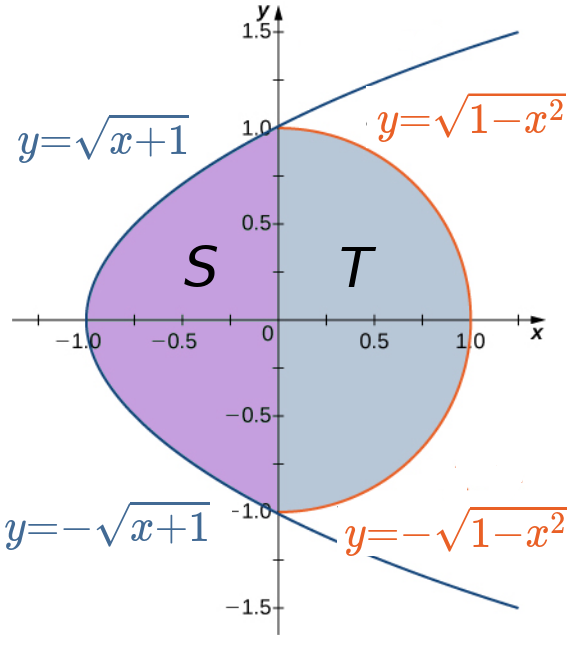
Set up the integral $ \displaystyle \iint_D xy+1 \, dA $ over a union of two Type I regions.

The region $D$ can be expressed as the union of two Type I regions $S$ and $T$ as seen below.
 $$
\begin{array}{lll}
\displaystyle \iint_D xy+1 \, dA &\displaystyle=\iint_{S \cup T} xy+1 \, dA &\mbox{}\\
\displaystyle &\displaystyle=\iint_{S} xy+1 \, dA+\iint_{T} xy+1 \, dA &\mbox{by integral properties}\\
\displaystyle &\displaystyle=\int_{-1}^{0} \int_{\color{#426a94}{y=-\sqrt{x+1}}}^{\color{#426a94}{y=\sqrt{x+1}}} xy+1 \, dy \, dx +\int_{0}^{1} \int_{\color{#e96026}{y=-\sqrt{1-x^2}}}^{\color{#e96026}{y=\sqrt{1-x^2}}} xy+1 \, dy \, dx &\mbox{by the Great Fubini!}\\
\displaystyle &\displaystyle=\int_{-1}^{0} \int_{-\sqrt{x+1}}^{\sqrt{x+1}} xy+1 \, dy \, dx +\int_{0}^{1} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} xy+1 \, dy \, dx &\mbox{a more standard notation}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \iint_D xy+1 \, dA &\displaystyle=\iint_{S \cup T} xy+1 \, dA &\mbox{}\\
\displaystyle &\displaystyle=\iint_{S} xy+1 \, dA+\iint_{T} xy+1 \, dA &\mbox{by integral properties}\\
\displaystyle &\displaystyle=\int_{-1}^{0} \int_{\color{#426a94}{y=-\sqrt{x+1}}}^{\color{#426a94}{y=\sqrt{x+1}}} xy+1 \, dy \, dx +\int_{0}^{1} \int_{\color{#e96026}{y=-\sqrt{1-x^2}}}^{\color{#e96026}{y=\sqrt{1-x^2}}} xy+1 \, dy \, dx &\mbox{by the Great Fubini!}\\
\displaystyle &\displaystyle=\int_{-1}^{0} \int_{-\sqrt{x+1}}^{\sqrt{x+1}} xy+1 \, dy \, dx +\int_{0}^{1} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} xy+1 \, dy \, dx &\mbox{a more standard notation}\\
\end{array}
$$

The Order of Integration Sometimes Matters
As we saw with rectangular regions, it is also true for more general regions that sometimes one order of integration is easier than another.
Areas of Planar Regions
One bonus application of double integrals is that expressing areas of area of planar regions becomes a lot simpler.
We know that $\displaystyle \iint_{D} f(x,y) \,dA$ is the (signed) volume under the surface on the region $D.$
If follows that $A(D)=\displaystyle \iint_{D} 1\,dA,$ or even more simply, $$A(D)=\iint_{D} \,dA$$ is the area of the region $D.$
Note: This is a two-dimensional analogue to the statement $\displaystyle \int_{a}^{b}\,dx=b-a,$ the length of the interval $[a,b].$
Example
Find the area of the region $D$ below by stating it as a double integral.

$$
\begin{array}{lll}
\displaystyle A(D)& =\displaystyle \iint_D \, dA &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}\int_{y^2}^{y} \, dx \,dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}\int_{y^2}^{y} 1 \, dx \,dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}[x]_{y^2}^{y} \,dy &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{1}y-y^2 \,dy &\mbox{}\\
\displaystyle &\displaystyle=\left[\frac{1}{2}y^2-\frac{1}{3}y^3\right]_{0}^{1} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{2}-\frac{1}{3} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{6} &\mbox{}\\
\end{array}
$$
The Average Value of a Function Over a General Region $D$
Finding the average value of a two-variable function over a general region hasn't changed much
The Average Value of a Function $f(x,y)$ over a General Region $D$
The average value of a two-variable function $f(x,y)$ on a region $D$ is defined to be $$ \displaystyle f_{avg}=\frac{1}{A(D)}\iint_D f(x,y)\, dA $$
Example
Find the average value of $f(x,y)=x+y^2$ over the region $D$ below.

From the above examples, we know that
$$
\iint_D f(x,y)\, dA =\iint_D x+y^2\, dA=\frac{7}{60}
$$
and
$$
A(D)=\iint_D\, dA=\frac{1}{6}
$$
Thus,
$$
\begin{array}{lll}
\displaystyle f_{avg}&\displaystyle=\frac{1}{A(D)}\iint_D f(x,y)\, dA &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{\frac{1}{6}}\cdot \frac{7}{60} &\mbox{}\\
\displaystyle &\displaystyle=\frac{6}{1}\cdot \frac{7}{60} &\mbox{}\\
\displaystyle &\displaystyle=\frac{7}{10}&\mbox{}\\
\end{array}
$$
Double Improper Integrals
Recall that in single-variable calculus an improper integral is one for which either the interval of integration is infinite, or the integrand is infinite.
In the two-variable case, this definition is very similar:
A double improper integral is one for which either the region of integration is infinite, or the integrand is infinite.
Double Improper Integrals Over Infinite Regions
If $R$ is an unbounded rectangle $R = \left \{(x, y)\in \mathbb{R}^2: a \leq x \leq \infty, c \leq y \leq \infty \right \},$ then when the limit exists, we have $$ \iint_R f(x,y) \, dA=\int_{a}^{\infty} \int_{c}^{\infty} f(x,y)\,dy\,dx=\lim_{b,d\rightarrow \infty}\int_{a}^{b} \int_{c}^{d} f(x,y)\,dy\,dx $$ and $$ \iint_R f(x,y) \, dA=\int_{c}^{\infty} \int_{a}^{\infty} f(x,y)\,dx\,dy=\lim_{b,d\rightarrow \infty}\int_{c}^{d} \int_{a}^{b} f(x,y)\,dx\,dy $$
Example
Find $$ \int_{0}^{\infty}\int_{0}^{\infty} xy e^{-x^2-y^2} \, dy \, dx $$
$$
\begin{array}{lll}
\displaystyle \int_{0}^{\infty}\int_{0}^{\infty} xy e^{-x^2-y^2} \, dy \, dx &\displaystyle=\lim_{b,d\rightarrow \infty} \int_{0}^{b}\int_{0}^{d} xy e^{-x^2-y^2} \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle= \lim_{b,d\rightarrow \infty} \int_{0}^{b}\int_{0}^{d} x e^{-x^2} ye^{-y^2} \, dy \, dx &\mbox{}\\
\displaystyle &\displaystyle= \lim_{b,d\rightarrow \infty} \int_{0}^{b} x e^{-x^2} \left(\int_{0}^{d} ye^{-y^2} \, dy\right) \, dx &\mbox{treating $x$ as a constant wrt $y$}\\
\displaystyle &\displaystyle= \lim_{b,d\rightarrow \infty} \int_{0}^{b} x e^{-x^2} \left[-\frac{1}{2}e^{-y^2}\right]_{0}^{d} \, dx &\mbox{}\\
\displaystyle &\displaystyle= \lim_{b,d\rightarrow \infty} \int_{0}^{b} x e^{-x^2} \left(-\frac{1}{2}e^{-d^2}+\frac{1}{2}\right) \, dx &\mbox{}\\
\displaystyle &\displaystyle= \lim_{b,d\rightarrow \infty} \left(-\frac{1}{2}e^{-d^2}+\frac{1}{2}\right)\int_{0}^{b} x e^{-x^2} \, dx &\mbox{treating expression as constant wrt $x$}\\
\displaystyle &\displaystyle= \lim_{b,d\rightarrow \infty} \left(-\frac{1}{2}e^{-d^2}+\frac{1}{2}\right)\left(-\frac{1}{2}e^{-b^2}+\frac{1}{2}\right)&\mbox{by the same process above}\\
\displaystyle &\displaystyle= \frac{1}{4}&\mbox{}\\
\end{array}
$$
Probability Theory in a Nutshell
A continuous random variable is a quantity that occurs over a spectrum of decimal values.
For example, a randomly chosen person's height or weight be considered a considered a continuous random variable.
Probability Theory in a Nutshell
For a continuous random variable $X,$ some outcomes will be more likely than others.
For example, if we take a the height in inches of a randomly chosen woman in her $20$'s, we're more likely to measure a height that is close to the average than one that is really far above or below average.
We model the probability of the occurrence of such random variables with a probability density function, or PDF.
Probability Theory in a Nutshell
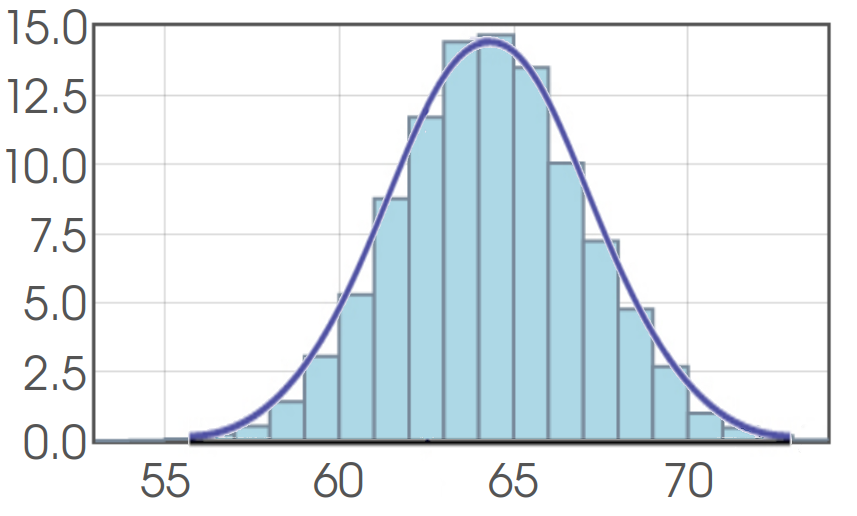
In the case of a randomly-chosen, young woman's height, the PDF looks something like the purple curve below which models the data gathered in blue.
Probability Theory in a Nutshell
The probability is not the height of the curve, but the area.

Probability Theory in a Nutshell
For example, the probability that a young woman's height is between $68$ and $70$ inches tall is the area under the curve.

Probability Theory in a Nutshell
For the PDF curve below, the probability of that a randomly chosen young woman's height is between $68$ and $70$ inches is $0.0679.$
That is, the height of a randomly chosen young woman will fall between $68$ and $70$ inches about $6.79\%$ of the time.

$P(68 \lt X \lt 70)=\mbox{Area under the Curve}=0.0679$
Probability Theory in a Nutshell
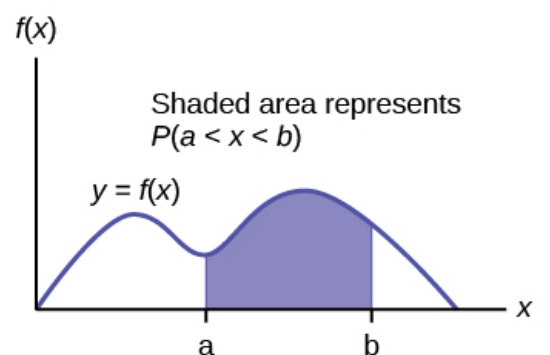
For a generic PDF, $y=f(x),$ the probability that a continuous random variable $X$ will land between $a$ and $b$ is the area under the curve from $a$ to $b,$ or $$ P(a\leq X \leq b)=\int_{a}^{b}f(x)\,dx $$
Probability Theory in a Nutshell
The probability that $X$ lands somewhere in its domain is $1,$ that with $100\%$ certainty. This means the area under the entire PDF curve must be $1.$ Thus, a PDF must satisfy $$ P(-\infty \leq X \leq \infty)=\int_{-\infty}^{\infty}f(x)\,dx=1 $$
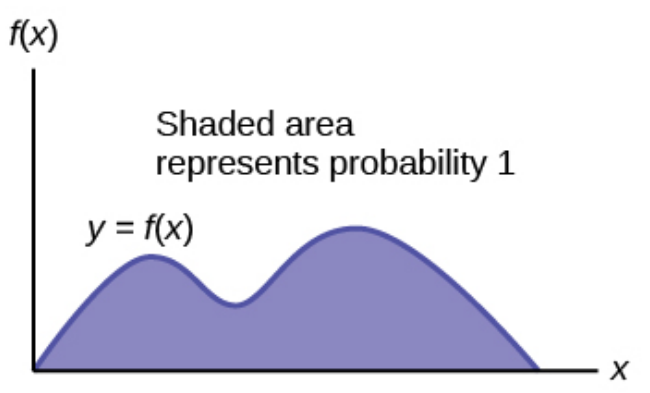
Probability Theory in a Nutshell
The expected value, $E(X),$ of a continuous random variable $X$ is $$ E(X)=\int_{-\infty}^{\infty}xf(x)\,dx $$

This is nothing more than a mean, or average value for the random variable. For the PDF of young womens' heights above, $E(X)=64.3$ inches.
Multiple Continuous Random Variables
Consider a pair of continuous random variables $X$ and $Y,$ such as height or weight. The joint density function $f$ of $X$ and $Y$ satisfies the probability that $(X, Y)$ lies in a certain region $D$ $$ P\left((x,y)\in D\right)=\iint_D f(x,y)\, dA $$ Since the probabilities can never be negative and must lie between $0$ and $1,$ the joint density function satisfies the the condition that $f(x,y)\geq 0$ on $\mathbb{R}^2$ and $$ \iint_{\mathbb{R}^2}f(x,y)\,dA=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\,dA=1 $$
Independent Random Variables
The variables $X$ and $Y$ are said to be independent random variables if their joint density function is the product of their individual density functions: $$f (x, y) = f_X (x) f_Y (y)$$ Practically independence simply means knowing information about one random variable gives us no additional information about the other.
For example, flip a coin and roll a die. Knowing that the coin came up heads tells us nothing about the probability that the die came up $6.$
Another example: randomly choose two young women from the U.S. population. Knowing the height of one woman tells us nothing about the height of the other.
Example
At a drive-thru restaurant, customers spend, on average, $3$ minutes placing their orders and an additional $5$ minutes paying for and picking up their meals. Assume that placing the order and paying for/picking up the meal are two independent events $X$ and $Y.$
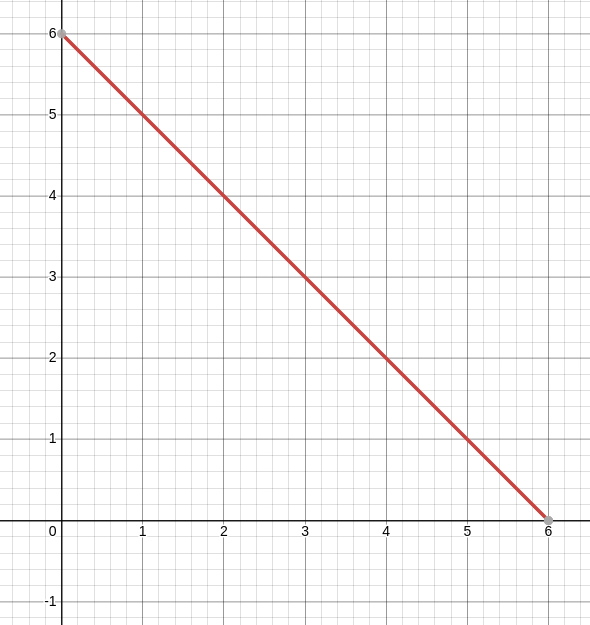
If the waiting times are modelled by the exponential probability densities $\displaystyle f_X(x)=\frac{1}{3}e^{-x/3}$ where $x\in [0,\infty)$ and $\displaystyle f_Y(y)=\frac{1}{5}e^{-y/5}$ where $y\in [0,\infty),$ the probability that a customer will spend less than $6$ minutes in the drive-thru line is given by $$P(X+Y\lt 6)=\iint_D f(x,y)\,dA$$ where $D=\left\{(x, y)|x \geq 0, y \geq 0, x + y \leq 6\right\}.$
Find $P(X+Y\lt 6)$ and interpret the result.
The region of integration $D=\left\{(x, y)|x \geq 0, y \geq 0, x + y \leq 6\right\}.$ is shown below.
Then, $$ \begin{array}{lll} \displaystyle P(X+Y<6)&\displaystyle=\iint_D f(x,y)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D f_X(x)f_Y(y)\, dA &\mbox{since $X$ and $Y$ are independent}\\ \displaystyle &\displaystyle=\int_{0}^{6} \int_{0}^{6-x} \left(\frac{1}{3}e^{-x/3}\right)\left(\frac{1}{5}e^{-y/5}\right)\, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{6} \left(\frac{1}{3}e^{-x/3}\right) \int_{0}^{6-x} \left(\frac{1}{5}e^{-y/5}\right)\, dy \, dx &\mbox{$x$ is constant wrt $y$}\\ \displaystyle &\displaystyle=\int_{0}^{6} \left(\frac{1}{3}e^{-x/3}\right) \left[-e^{-y/5}\right]_{0}^{6-x} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{6} \left(\frac{1}{3}e^{-x/3}\right) \left(-e^{-(6-x)/5}+1\right) \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{6} -e^{-x/3}e^{-(6-x)/5}+e^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{6} -e^{-2x/15-6/5}+e^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{6} -e^{-2x/15}e^{-6/5}+e^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{6} -e^{-6/5}e^{-2x/15}+e^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left[-e^{-6/5}\left(-\frac{15}{2}e^{-2x/15}\right)-3e^{-x/3}\right]_{0}^{6} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left[\frac{15}{2}e^{-6/5}e^{-2x/15}-3e^{-x/3}\right]_{0}^{6} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[\frac{15}{2}e^{-6/5}e^{-2\cdot 6/15}-3e^{-6/3}\right]-\left[\frac{15}{2}e^{-6/5}e^{-2\cdot 0/15}-3e^{-0/3}\right]\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[\frac{15}{2}e^{-6/5}e^{-4/5}-3e^{-2}\right]-\left[\frac{15}{2}e^{-6/5}-3\right]\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[\frac{15}{2}e^{-2}-3e^{-2}\right]-\left[\frac{15}{2}e^{-6/5}-3\right]\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\frac{9}{2}e^{-2}+3-\frac{15}{2}e^{-6/5}\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{3}{2}e^{-2}+1-\frac{5}{2}e^{-6/5} &\mbox{}\\ \displaystyle &\displaystyle\approx 0.4500173951 &\mbox{}\\ \end{array} $$ Interpretation: There is about a $45\%$ chance that a randomly chosen customer will spend less than $6$ minutes in the drive-thru line.

Then, $$ \begin{array}{lll} \displaystyle P(X+Y<6)&\displaystyle=\iint_D f(x,y)\, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D f_X(x)f_Y(y)\, dA &\mbox{since $X$ and $Y$ are independent}\\ \displaystyle &\displaystyle=\int_{0}^{6} \int_{0}^{6-x} \left(\frac{1}{3}e^{-x/3}\right)\left(\frac{1}{5}e^{-y/5}\right)\, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{6} \left(\frac{1}{3}e^{-x/3}\right) \int_{0}^{6-x} \left(\frac{1}{5}e^{-y/5}\right)\, dy \, dx &\mbox{$x$ is constant wrt $y$}\\ \displaystyle &\displaystyle=\int_{0}^{6} \left(\frac{1}{3}e^{-x/3}\right) \left[-e^{-y/5}\right]_{0}^{6-x} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{6} \left(\frac{1}{3}e^{-x/3}\right) \left(-e^{-(6-x)/5}+1\right) \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{6} -e^{-x/3}e^{-(6-x)/5}+e^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{6} -e^{-2x/15-6/5}+e^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{6} -e^{-2x/15}e^{-6/5}+e^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{6} -e^{-6/5}e^{-2x/15}+e^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left[-e^{-6/5}\left(-\frac{15}{2}e^{-2x/15}\right)-3e^{-x/3}\right]_{0}^{6} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left[\frac{15}{2}e^{-6/5}e^{-2x/15}-3e^{-x/3}\right]_{0}^{6} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[\frac{15}{2}e^{-6/5}e^{-2\cdot 6/15}-3e^{-6/3}\right]-\left[\frac{15}{2}e^{-6/5}e^{-2\cdot 0/15}-3e^{-0/3}\right]\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[\frac{15}{2}e^{-6/5}e^{-4/5}-3e^{-2}\right]-\left[\frac{15}{2}e^{-6/5}-3\right]\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[\frac{15}{2}e^{-2}-3e^{-2}\right]-\left[\frac{15}{2}e^{-6/5}-3\right]\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\frac{9}{2}e^{-2}+3-\frac{15}{2}e^{-6/5}\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{3}{2}e^{-2}+1-\frac{5}{2}e^{-6/5} &\mbox{}\\ \displaystyle &\displaystyle\approx 0.4500173951 &\mbox{}\\ \end{array} $$ Interpretation: There is about a $45\%$ chance that a randomly chosen customer will spend less than $6$ minutes in the drive-thru line.
Expected Value Redux
Let $f(x,y)$ be the joint density function of $X$ and $Y.$
Then, the expected values $E(X)$ and $E(Y)$ are given by $$ E(X)=\iint_{S} xf(x,y)\, dA \,\,\,\,\,\,\,\, \mbox{ and } \,\,\,\,\,\,\,\, E(Y)=\iint_{S} yf(x,y)\, dA $$ where $S$ is the sample space of both $X$ and $Y,$ that is, all possible outcomes $(X,Y).$
Bonus Example
At a drive-thru restaurant, customers spend, on average, $3$ minutes placing their orders and an additional $5$ minutes paying for and picking up their meals. Assume that placing the order and paying for/picking up the meal are two independent events $X$ and $Y.$
If the waiting times are modelled by the exponential probability densities $\displaystyle f_X(x)=\frac{1}{3}e^{-x/3}$ where $x\in [0,\infty)$ and $\displaystyle f_Y(y)=\frac{1}{5}e^{-y/5}$ where $y\in [0,\infty),$ show that $E(X)=3$ and $E(Y)=5.$
Since the sample space of both $X$ and $Y$ individually are $[0,\infty),$ the sample space of
$S$ of all possible outcomes $(X,Y)$ is $S=[0,\infty)\times [0,\infty),$ or, the first quadrant.
It follows that $$ \begin{array}{lll} \displaystyle E(X)&\displaystyle= \iint_{S} xf(x,y)\, dA&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{\infty}\int_{0}^{\infty} xf_X(x)f_Y(y)\, dy \, dx &\mbox{since $X$ and $Y$ are independent}\\ \displaystyle &\displaystyle=\int_{0}^{\infty}\int_{0}^{\infty} x\left(\frac{1}{3}e^{-x/3}\right)\left(\frac{1}{5}e^{-y/5}\right)\, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} xe^{-x/3} \int_{0}^{\infty} \left(\frac{1}{5}e^{-y/5}\right)\, dy \, dx &\mbox{since $x$ is constant wrt $y$}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} xe^{-x/3} \left[-e^{-y/5}\right]_{0}^{\infty} \, dx &\mbox{this is really loosey-goosey notation!}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} xe^{-x/3} \cdot [-0-(-1)] \, dx &\mbox{not advised unless you really know what you're doing!}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} xe^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} uv' \, dx &\mbox{letting $u=x,$ and $v'=e^{-x/3}$}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[uv\right]_{0}^{\infty}-\int_{0}^{\infty} u'v \, dx\right) &\mbox{integration by parts with more lazy notation}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[x\cdot \left(-3e^{-x/3}\right)\right]_{0}^{\infty}-\int_{0}^{\infty} 1 \cdot \left(-3e^{-x/3}\right) \, dx\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[-3xe^{-x/3}\right]_{0}^{\infty}+3\int_{0}^{\infty}e^{-x/3} \, dx\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(0+3\left[-3e^{-x/3}\right]_{0}^{\infty}\right) &\mbox{use L'Hospital to show $\displaystyle \lim_{x\rightarrow\infty}\left[-3xe^{-x/3}\right]=0$}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(3\cdot 3\right) &\mbox{}\\ \displaystyle &\displaystyle=3 &\mbox{}\\ \end{array} $$ We're done. We leave showing $E(Y)=5$ as an exercise.
It follows that $$ \begin{array}{lll} \displaystyle E(X)&\displaystyle= \iint_{S} xf(x,y)\, dA&\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{\infty}\int_{0}^{\infty} xf_X(x)f_Y(y)\, dy \, dx &\mbox{since $X$ and $Y$ are independent}\\ \displaystyle &\displaystyle=\int_{0}^{\infty}\int_{0}^{\infty} x\left(\frac{1}{3}e^{-x/3}\right)\left(\frac{1}{5}e^{-y/5}\right)\, dy \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} xe^{-x/3} \int_{0}^{\infty} \left(\frac{1}{5}e^{-y/5}\right)\, dy \, dx &\mbox{since $x$ is constant wrt $y$}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} xe^{-x/3} \left[-e^{-y/5}\right]_{0}^{\infty} \, dx &\mbox{this is really loosey-goosey notation!}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} xe^{-x/3} \cdot [-0-(-1)] \, dx &\mbox{not advised unless you really know what you're doing!}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} xe^{-x/3} \, dx &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\int_{0}^{\infty} uv' \, dx &\mbox{letting $u=x,$ and $v'=e^{-x/3}$}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[uv\right]_{0}^{\infty}-\int_{0}^{\infty} u'v \, dx\right) &\mbox{integration by parts with more lazy notation}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[x\cdot \left(-3e^{-x/3}\right)\right]_{0}^{\infty}-\int_{0}^{\infty} 1 \cdot \left(-3e^{-x/3}\right) \, dx\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(\left[-3xe^{-x/3}\right]_{0}^{\infty}+3\int_{0}^{\infty}e^{-x/3} \, dx\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(0+3\left[-3e^{-x/3}\right]_{0}^{\infty}\right) &\mbox{use L'Hospital to show $\displaystyle \lim_{x\rightarrow\infty}\left[-3xe^{-x/3}\right]=0$}\\ \displaystyle &\displaystyle=\frac{1}{3}\left(3\cdot 3\right) &\mbox{}\\ \displaystyle &\displaystyle=3 &\mbox{}\\ \end{array} $$ We're done. We leave showing $E(Y)=5$ as an exercise.