We begin learning how to optimize in the multivariable setting.
Recall
Does anyone here remember the definition of a critical point for a single-variable function?
Critical Points
Let $z = f (x, y)$ be a function of two variables that is defined on an open set containing the point $(x_0, y_0).$ The point $(x_0, y_0)$ is called a critical point of a function of two variables $f$ if either of the following occur:
1) $f_x(x_0, y_0)=0$ and $f_y(x_0, y_0)=0$
2) $f_x(x_0, y_0)$ or $f_y(x_0, y_0)$ are undefined
Critical Points (Alternative Definition)
Let $z = f (x, y)$ be a function of two variables that is defined on an open set containing the point $(x_0, y_0).$ The point $(x_0, y_0)$ is called a critical point of a function of two variables $f$ if either $$ \nabla f(x_0,y_0)={\bf 0} \\\mbox{ or }\\ \nabla f(x_0,y_0) \mbox{ is undefined} $$
Example
Find the critical points of the functions.
$f (x, y) = x^3 + 2xy - 2x - 4y$
Since $f_x(x,y)=3x^2+2y-2$ and $f_y(x,y)=2x-4,$ the derivatives are defined everywhere.
So, the critical points are those which satisfy the following system of equations. $$ \begin{cases} 3x^2+2y-2=0\\ 2x-4=0 \end{cases} $$ The second equation gives $x=2.$
Thus, from the first equation we have $3(2)^2+2y-2=0,$ or $2y+10=0,$ so that $y=-5.$
The above gives us a single critical point $(2,-5).$
So, the critical points are those which satisfy the following system of equations. $$ \begin{cases} 3x^2+2y-2=0\\ 2x-4=0 \end{cases} $$ The second equation gives $x=2.$
Thus, from the first equation we have $3(2)^2+2y-2=0,$ or $2y+10=0,$ so that $y=-5.$
The above gives us a single critical point $(2,-5).$
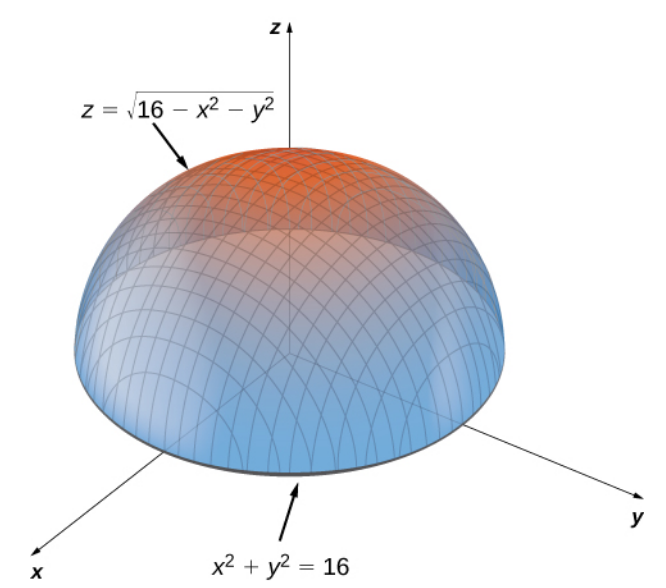
$f(x,y)=\sqrt{16-x^2-y^2}$
We begin by finding $f_x(x,y)$ and $f_y(x,y).$
$$
\begin{array}{lll}
\displaystyle f_x(x,y)&\displaystyle= \frac{\partial}{\partial x} \sqrt{16-x^2-y^2}&\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{2\sqrt{16-x^2-y^2}}\frac{\partial}{\partial x}(16-x^2-y^2) &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{2\sqrt{16-x^2-y^2}}(-2x) &\mbox{}\\
\displaystyle &\displaystyle=-\frac{x}{\sqrt{16-x^2-y^2}} &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle f_y(x,y)&\displaystyle= \frac{\partial}{\partial y} \sqrt{16-x^2-y^2}&\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{2\sqrt{16-x^2-y^2}}\frac{\partial}{\partial y}(16-x^2-y^2) &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{2\sqrt{16-x^2-y^2}}(-2y) &\mbox{}\\
\displaystyle &\displaystyle=-\frac{y}{\sqrt{16-x^2-y^2}} &\mbox{}\\
\end{array}
$$
We first find the critical points which make both derivatives $0.$
Setting $f_x(x,y)=0$ and $f_y(x,y)=0,$ we get the system $$ \begin{cases} \displaystyle -\frac{x}{\sqrt{16-x^2-y^2}}=0\\ \displaystyle -\frac{y}{\sqrt{16-x^2-y^2}}=0 \end{cases} $$ whose only solution is $(x,y)=(0,0).$
Thus, $(0,0)$ is a critical point.
We now consider critical points which make the derivatives undefined.
From the above calculations we see that both $f_x(x,y)$ and $f_y(x,y)$ are undefined precisely when $\sqrt{16-x^2-y^2}=0.$
That is, when $x^2+y^2=16.$
Thus, the critical points which make the derivative undefined are those which lie on the circle of radius $4.$
Note: This set is the boundary of the domain of $f(x,y).$
In summary, the critical points of $f$ are $(0,0)$ and any $(x,y)$ which lie on the circle of radius $4,$ that is, where $x^2+y^2=16.$
Setting $f_x(x,y)=0$ and $f_y(x,y)=0,$ we get the system $$ \begin{cases} \displaystyle -\frac{x}{\sqrt{16-x^2-y^2}}=0\\ \displaystyle -\frac{y}{\sqrt{16-x^2-y^2}}=0 \end{cases} $$ whose only solution is $(x,y)=(0,0).$
Thus, $(0,0)$ is a critical point.
We now consider critical points which make the derivatives undefined.
From the above calculations we see that both $f_x(x,y)$ and $f_y(x,y)$ are undefined precisely when $\sqrt{16-x^2-y^2}=0.$
That is, when $x^2+y^2=16.$
Thus, the critical points which make the derivative undefined are those which lie on the circle of radius $4.$
Note: This set is the boundary of the domain of $f(x,y).$
In summary, the critical points of $f$ are $(0,0)$ and any $(x,y)$ which lie on the circle of radius $4,$ that is, where $x^2+y^2=16.$

Local and Global Maxima
Let $z = f (x, y)$ be a function of two variables that is defined and continuous on an open set containing the point $(x_0, y_0).$
Then $f$ has a local maximum at $(x_0, y_0)$ if $f (x_0, y_0) \geq f (x, y)$ for all points $(x, y)$ within some disk centered at $(x_0, y_0).$
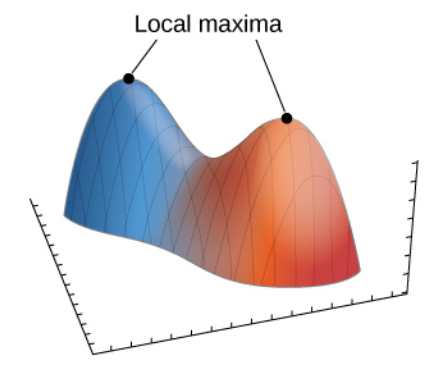
If the preceding inequality holds for every point $(x, y)$ in the domain of $f ,$ then $f$ has a global maximum (also called an absolute maximum) at $(x_0, y_0).$
Local and Global Minima
Let $z = f (x, y)$ be a function of two variables that is defined and continuous on an open set containing the point $(x_0, y_0).$
Then $f$ has a local minimum at $(x_0, y_0)$ if $f (x_0, y_0) \leq f (x, y)$ for all points $(x, y)$ within some disk centered at $(x_0, y_0).$
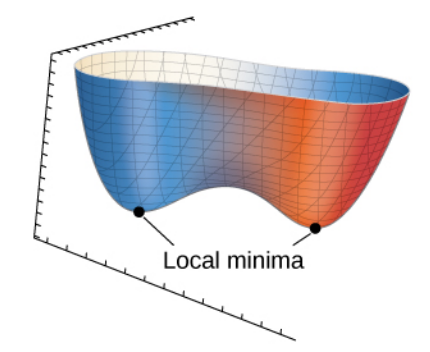
If the preceding inequality holds for every point $(x, y)$ in the domain of $f ,$ then $f$ has a global minimum (also called an absolute minimum) at $(x_0, y_0).$
Local and Global Extrema
If $(x_0, y_0)$ is either a local maximum or local minimum value, then it is called a local extremum.
Fermat's Theorem in Two Dimensions
Let $z = f (x, y)$ be a function of two variables that is defined and continuous on an open set containing the point $(x_0, y_0).$
Suppose $f_x$ and $f_y$ each exists at $(x_0, y_0).$
If $f$ has a local extremum at $(x_0, y_0),$ then $(x_0, y_0)$ is a critical point of $f.$
How to Use Fermat's Theorem
Fermat's Theorem essentially says $$ \mbox{extremum}\implies\mbox{critical point}. $$
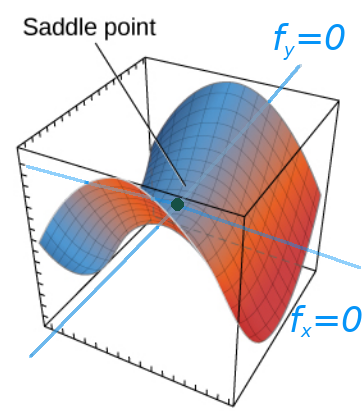
Dire Warning
The converse of Fermat's Theorem does not hold in general That is, the following statement is in general false. $$ \mbox{critical point}\implies\mbox{extremum} $$ The following situation provides a counterexample to the above statement.
How to Use Fermat's Theorem
Fermat's Theorem, $$ \mbox{extremum}\implies\mbox{critical point}, $$ tells us that by finding all the critical points of a function, we are merely generating a list of candidates $(x_0,y_0)$ of possible extrema.
Saddle Points
Given the function $z = f (x, y),$ the point $(x_0, y_0, f (x_0, y_0))$ is a saddle point if both $f_x (x_0, y_0) = 0$ and $f_y (x_0, y_0) = 0,$ but $f$ does not have a local extremum at $(x_0, y_0).$

Example
In the case of $f(x,y)=\sqrt{16-x^2-y^2},$ the critical points coincide with the extrema.
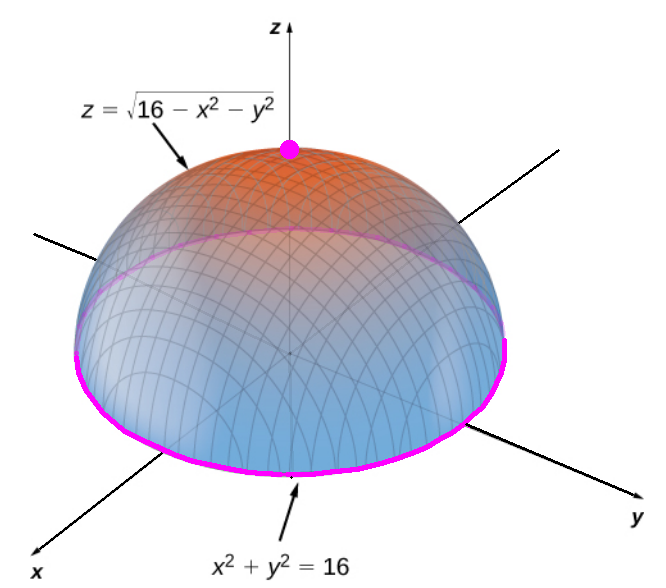
The critical point $(0,0)$ is a maximum, and the points on the circle $x^2+y^2=16$ are all minima.
The next result is the two-dimensional equivalent of the Second-Derivative Test from first-term calculus.
This is the tool we will use to determine if a critical point is a maximum or a minimum.
The Second-Derivatives Test
Let $z = f (x, y)$ be a function of two variables for which the first and second-order partial derivatives are continuous on some disk containing the point $(x_0, y_0).$ Suppose $f_x (x_0, y_0) = 0$ and $f_y (x_0, y_0) = 0.$ Define the quantity $$ D = f_{xx} (x_0, y_0) f_{yy} (x_0, y_0) -(f_{xy} (x_0, y_0))^2 = \left| \begin{array}{cc} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \\ \end{array}\right| $$ (i) If $D \gt 0$ and $f_{xx} (x_0, y_0) \gt 0,$ then $f$ has a local minimum at $(x_0, y_0).$
(ii) If $D \gt 0$ and $f_{xx} (x_0, y_0) \lt 0,$ then $f$ has a local maximum at $(x_0, y_0).$
(iii) If $D \lt 0,$ then $f$ has a saddle point at $(x_0, y_0).$
(iv) If $D = 0,$ then the test is inconclusive.
Example
Use the second derivative to find the local extrema of the function $f (x, y) = x^3 + 2xy - 6x - 4y^2.$
First, we find the critical points.
Now, $f_x(x, y) = 3x^2 + 2y - 6,$ and $f_y (x, y) = 2x-8y.$
The derivatives are defined for all $(x,y),$ thus, our only critical points are those which solve the system $$ \begin{cases} 3x^2 + 2y - 6&=0\\ 2x-8y&=0 \end{cases} $$ From the second equation, we have that $x=4y.$
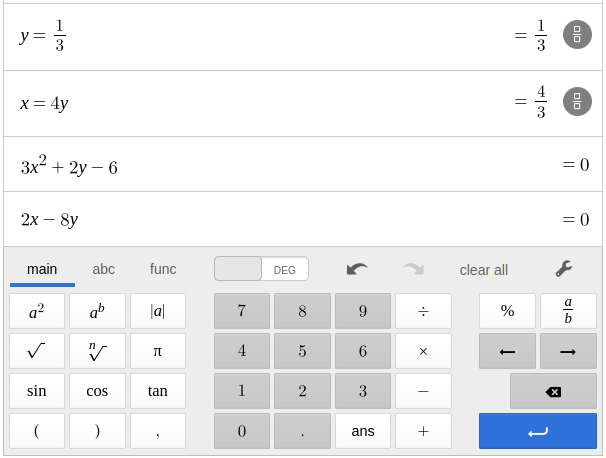
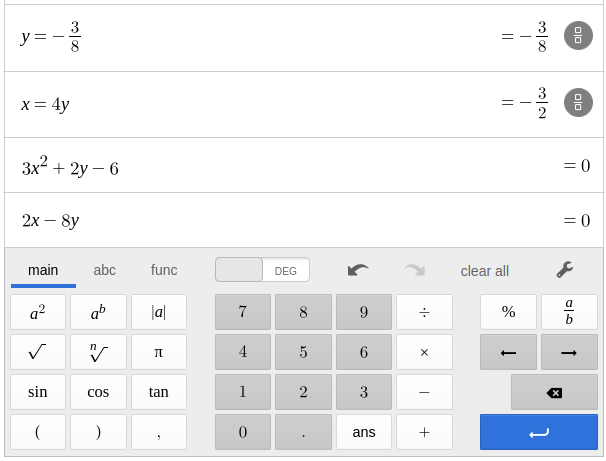
Then, by the first equation $3(4y)^2+2y-6=0,$ which gives $$ \begin{array}{lll} &\displaystyle 48y^2+2y-6=0 &\mbox{}\\ \implies &\displaystyle 24y^2+y-3=0&\mbox{}\\ \implies &\displaystyle (3y-1)(8y+3)=0&\mbox{}\\ \implies &\displaystyle 3y-1=0 \,\,\mbox{OR}\,\, 8y+3=0&\mbox{}\\ \implies &\displaystyle y=\frac{1}{3} \,\,\mbox{OR}\,\,y=-\frac{3}{8}&\mbox{}\\ \end{array} $$ Then, $\displaystyle x=4y=4\cdot \frac{1}{3}=\frac{4}{3}$ OR $\displaystyle x=4y=4\cdot \left(-\frac{3}{8}\right)=-\frac{3}{2}.$
Thus, our two critical points are $\displaystyle\left(\frac{4}{3},\frac{1}{3}\right)$ and $\displaystyle\left(-\frac{3}{2},-\frac{3}{8}\right).$
We check both solutions to be sure we've nailed it.
Since the partial derivatives are continuous everywhere, we may now use the Second Derivatives Test on our critical points.
Computing our second derivatives, $$ f_{xx}(x,y)=6x\\ f_{yy}(x,y)=-8\\ f_{xy}(x,y)=2\\ $$ Thus, $$ \begin{array}{lll} \displaystyle D&\displaystyle=f_{xx} (x, y) f_{yy} (x, y) -(f_{xy} (x, y))^2 &\mbox{}\\ \displaystyle &\displaystyle= \left| \begin{array}{cc} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \\ \end{array}\right|&\mbox{}\\ \displaystyle &\displaystyle= (6x)\cdot (-8) -2^2&\mbox{}\\ \displaystyle &\displaystyle= -48x-4&\mbox{}\\ \end{array} $$ At $\displaystyle\left(\frac{4}{3},\frac{1}{3}\right),$ $$ D=-48\cdot \left(\frac{4}{3}\right)-4=-68 \lt 0. $$ Thus, $\displaystyle\left(\frac{4}{3},\frac{1}{3}\right)$ is a saddle point by the Second Derivatives Test.
At $\displaystyle\left(-\frac{3}{2},-\frac{3}{8}\right),$ $$ D=-48\cdot \left(-\frac{3}{2}\right)-4=68 \gt 0. $$ Thus, since $\displaystyle f_{xx}\left(-\frac{3}{2},-\frac{3}{8}\right)=6\cdot \left(-\frac{3}{2}\right)=-9 \lt 0,$ we have by the Second Derivatives Test that $\displaystyle\left(-\frac{3}{2},-\frac{3}{8}\right)$ is a local maximum.
Now, $f_x(x, y) = 3x^2 + 2y - 6,$ and $f_y (x, y) = 2x-8y.$
The derivatives are defined for all $(x,y),$ thus, our only critical points are those which solve the system $$ \begin{cases} 3x^2 + 2y - 6&=0\\ 2x-8y&=0 \end{cases} $$ From the second equation, we have that $x=4y.$
Then, by the first equation $3(4y)^2+2y-6=0,$ which gives $$ \begin{array}{lll} &\displaystyle 48y^2+2y-6=0 &\mbox{}\\ \implies &\displaystyle 24y^2+y-3=0&\mbox{}\\ \implies &\displaystyle (3y-1)(8y+3)=0&\mbox{}\\ \implies &\displaystyle 3y-1=0 \,\,\mbox{OR}\,\, 8y+3=0&\mbox{}\\ \implies &\displaystyle y=\frac{1}{3} \,\,\mbox{OR}\,\,y=-\frac{3}{8}&\mbox{}\\ \end{array} $$ Then, $\displaystyle x=4y=4\cdot \frac{1}{3}=\frac{4}{3}$ OR $\displaystyle x=4y=4\cdot \left(-\frac{3}{8}\right)=-\frac{3}{2}.$
Thus, our two critical points are $\displaystyle\left(\frac{4}{3},\frac{1}{3}\right)$ and $\displaystyle\left(-\frac{3}{2},-\frac{3}{8}\right).$
We check both solutions to be sure we've nailed it.


Since the partial derivatives are continuous everywhere, we may now use the Second Derivatives Test on our critical points.
Computing our second derivatives, $$ f_{xx}(x,y)=6x\\ f_{yy}(x,y)=-8\\ f_{xy}(x,y)=2\\ $$ Thus, $$ \begin{array}{lll} \displaystyle D&\displaystyle=f_{xx} (x, y) f_{yy} (x, y) -(f_{xy} (x, y))^2 &\mbox{}\\ \displaystyle &\displaystyle= \left| \begin{array}{cc} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \\ \end{array}\right|&\mbox{}\\ \displaystyle &\displaystyle= (6x)\cdot (-8) -2^2&\mbox{}\\ \displaystyle &\displaystyle= -48x-4&\mbox{}\\ \end{array} $$ At $\displaystyle\left(\frac{4}{3},\frac{1}{3}\right),$ $$ D=-48\cdot \left(\frac{4}{3}\right)-4=-68 \lt 0. $$ Thus, $\displaystyle\left(\frac{4}{3},\frac{1}{3}\right)$ is a saddle point by the Second Derivatives Test.
At $\displaystyle\left(-\frac{3}{2},-\frac{3}{8}\right),$ $$ D=-48\cdot \left(-\frac{3}{2}\right)-4=68 \gt 0. $$ Thus, since $\displaystyle f_{xx}\left(-\frac{3}{2},-\frac{3}{8}\right)=6\cdot \left(-\frac{3}{2}\right)=-9 \lt 0,$ we have by the Second Derivatives Test that $\displaystyle\left(-\frac{3}{2},-\frac{3}{8}\right)$ is a local maximum.
Application
A cardboard box without a lid is to be made with a volume of $4$ $\mbox{ft}^3.$
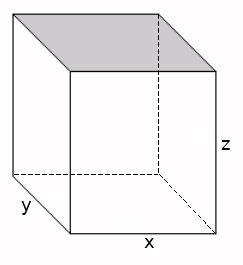
We must first find an expression for the surface area of the box.

From the picture, we see that each of the four sides: two sides with area $xz,$ and two sides with area $yz.$ The bottom has an area of $xy.$
Thus, the surface area $S$ is given by $$ S=2xz+2yz+xy. $$ The problem situation requires that we restrict the domain of $S$ to $x \gt 0$ and $y \gt 0$ and we will only be considering these values.
Now, the volume of the box is $xyz,$ and since the box must be $4$ cubic feet, we have $xyz=4.$
Then, $\displaystyle z=\frac{4}{xy}.$ Substituting this equation into the above surface-area equation we have $$ S(x,y)=2x\cdot \frac{4}{xy}+2y\cdot \frac{4}{xy}+xy=\frac{8}{y}+\frac{8}{x}+xy $$ We shall now find the dimensions of the base $x$ and $y$ which minimize $S.$
Now, $\displaystyle S_x(x,y)=-\frac{8}{x^2}+y$ and $\displaystyle S_y(x,y)=-\frac{8}{y^2}+x.$
We shall first find the critical points which solve the system $$ \begin{cases} \displaystyle -\frac{8}{x^2}+y=0\\ \displaystyle -\frac{8}{y^2}+x=0 \end{cases} $$ These equations can rewritten as $$ \begin{cases} \displaystyle y=\frac{8}{x^2}\\ \displaystyle x=\frac{8}{y^2} \end{cases} $$ Then $x^2y=8=y^2x$ from which it follows that $x=y.$
Thus, $\displaystyle x=\frac{8}{x^2}$ and $\displaystyle y=\frac{8}{y^2}$ from which we have $x^3=8$ and $y^3=8.$
Therefore, we have a single critical point $(x,y)=(\sqrt[3]{8},\sqrt[3]{8})=(2,2)$ which makes both partial derivatives $0.$
In the domain of the problem situation, there are no critical points which make $S_x$ and $S_y$ undefined.
Thus, the only critical we need to consider is then $(2,2).$
We will now show using the Second Derivatives Test that $(2,2)$ is a local minimum.
Computing the second derivatives, $$ S_{xx}(x,y)=\frac{16}{x^3}\\ S_{yy}(x,y)=\frac{16}{y^3}\\ S_{xy}(x,y)=1 $$ we may then compute $D.$ $$ \begin{array}{lll} \displaystyle D &\displaystyle= S_{xx}S_{yy}-S_{xy}^2 &\mbox{}\\ \displaystyle &\displaystyle=\frac{16}{x^3}\cdot \frac{16}{y^3}-1^2 &\mbox{}\\ \displaystyle &\displaystyle=\frac{256}{x^3y^3} -1 &\mbox{}\\ \end{array} $$ At $(2,2),$ $D\gt 0$ since $$ \begin{array}{lll} \displaystyle D &\displaystyle=\frac{256}{x^3y^3} -1 &\mbox{}\\ \displaystyle &\displaystyle=\frac{256}{2^3 \cdot 2^3} -1 &\mbox{}\\ \displaystyle &\displaystyle=\frac{256}{8\cdot 8} -1 &\mbox{}\\ \displaystyle &\displaystyle= 3&\mbox{}\\ \end{array} $$ Also, $\displaystyle S_{xx}(2,2)=\frac{16}{2^3}=2\gt 0.$
Finally, we note that the first and second-order partial derivatives are continuous on the domain of the problem situation.
The the above facts along with the Second Derivatives Test give us that $(2,2)$ is a local minimum on the domain of the problem situation.
The height of the box at this point is $\displaystyle z=\frac{4}{xy}=\frac{4}{2\cdot 2}=1.$
Since $S$ is positive on the entire domain of the problem situation, $(2,2)$ must be an absolute minimum.
Thus, the dimensions which minimize the surface area $S$ while maintaining a volume of $4$ cubic feet is a box with a $2$ feet by $2$ feet base and a height of $1$ foot.

From the picture, we see that each of the four sides: two sides with area $xz,$ and two sides with area $yz.$ The bottom has an area of $xy.$
Thus, the surface area $S$ is given by $$ S=2xz+2yz+xy. $$ The problem situation requires that we restrict the domain of $S$ to $x \gt 0$ and $y \gt 0$ and we will only be considering these values.
Now, the volume of the box is $xyz,$ and since the box must be $4$ cubic feet, we have $xyz=4.$
Then, $\displaystyle z=\frac{4}{xy}.$ Substituting this equation into the above surface-area equation we have $$ S(x,y)=2x\cdot \frac{4}{xy}+2y\cdot \frac{4}{xy}+xy=\frac{8}{y}+\frac{8}{x}+xy $$ We shall now find the dimensions of the base $x$ and $y$ which minimize $S.$
Now, $\displaystyle S_x(x,y)=-\frac{8}{x^2}+y$ and $\displaystyle S_y(x,y)=-\frac{8}{y^2}+x.$
We shall first find the critical points which solve the system $$ \begin{cases} \displaystyle -\frac{8}{x^2}+y=0\\ \displaystyle -\frac{8}{y^2}+x=0 \end{cases} $$ These equations can rewritten as $$ \begin{cases} \displaystyle y=\frac{8}{x^2}\\ \displaystyle x=\frac{8}{y^2} \end{cases} $$ Then $x^2y=8=y^2x$ from which it follows that $x=y.$
Thus, $\displaystyle x=\frac{8}{x^2}$ and $\displaystyle y=\frac{8}{y^2}$ from which we have $x^3=8$ and $y^3=8.$
Therefore, we have a single critical point $(x,y)=(\sqrt[3]{8},\sqrt[3]{8})=(2,2)$ which makes both partial derivatives $0.$
In the domain of the problem situation, there are no critical points which make $S_x$ and $S_y$ undefined.
Thus, the only critical we need to consider is then $(2,2).$
We will now show using the Second Derivatives Test that $(2,2)$ is a local minimum.
Computing the second derivatives, $$ S_{xx}(x,y)=\frac{16}{x^3}\\ S_{yy}(x,y)=\frac{16}{y^3}\\ S_{xy}(x,y)=1 $$ we may then compute $D.$ $$ \begin{array}{lll} \displaystyle D &\displaystyle= S_{xx}S_{yy}-S_{xy}^2 &\mbox{}\\ \displaystyle &\displaystyle=\frac{16}{x^3}\cdot \frac{16}{y^3}-1^2 &\mbox{}\\ \displaystyle &\displaystyle=\frac{256}{x^3y^3} -1 &\mbox{}\\ \end{array} $$ At $(2,2),$ $D\gt 0$ since $$ \begin{array}{lll} \displaystyle D &\displaystyle=\frac{256}{x^3y^3} -1 &\mbox{}\\ \displaystyle &\displaystyle=\frac{256}{2^3 \cdot 2^3} -1 &\mbox{}\\ \displaystyle &\displaystyle=\frac{256}{8\cdot 8} -1 &\mbox{}\\ \displaystyle &\displaystyle= 3&\mbox{}\\ \end{array} $$ Also, $\displaystyle S_{xx}(2,2)=\frac{16}{2^3}=2\gt 0.$
Finally, we note that the first and second-order partial derivatives are continuous on the domain of the problem situation.
The the above facts along with the Second Derivatives Test give us that $(2,2)$ is a local minimum on the domain of the problem situation.
The height of the box at this point is $\displaystyle z=\frac{4}{xy}=\frac{4}{2\cdot 2}=1.$
Since $S$ is positive on the entire domain of the problem situation, $(2,2)$ must be an absolute minimum.
Thus, the dimensions which minimize the surface area $S$ while maintaining a volume of $4$ cubic feet is a box with a $2$ feet by $2$ feet base and a height of $1$ foot.

Finding Absolute Extrema on a Closed and Bounded Domain
Recall that finding the extreme for a single-variable function $f(x)$ on a closed and bounded interval $[a,b]$ amounted evaluating $f$ at the critical points in the interior of the interval, $(a,b),$ and the endpoints (boundary) of the interval $a$ and $b.$
We can do the same for a closed and bounded region in the $xy$-plane.
However, just like the previous case, we need to know that extreme values actually exist...
Closed and Bounded Sets in the Plane
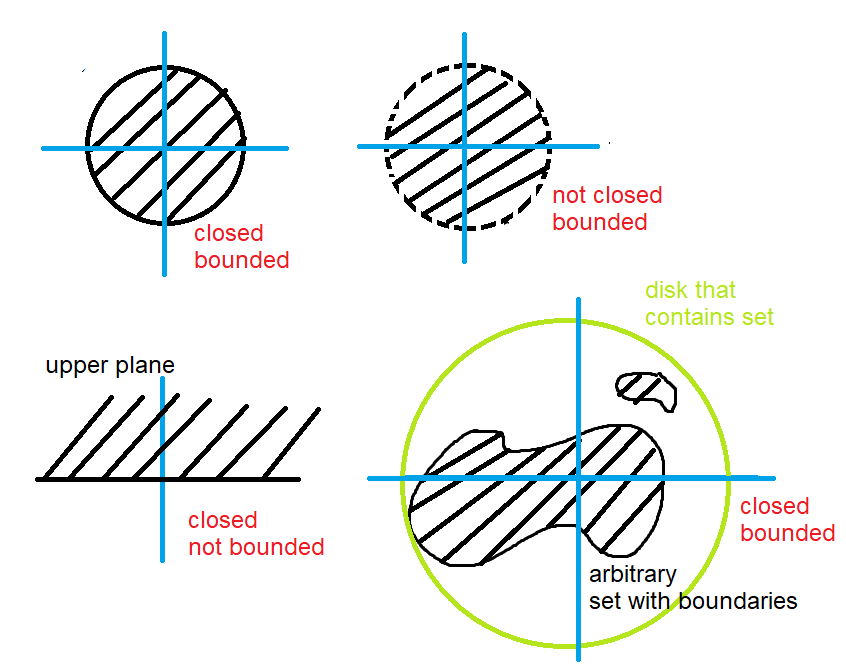
The Extreme-Value Theorem
A continuous function $f (x, y)$ on a closed and bounded set $D$ in the plane attains an absolute maximum value at some point of $D$ and an absolute minimum value at some point of $D.$
Finding Absolute Extrema on a Closed and Bounded Domain
Assume $z = f (x, y)$ is a differentiable function of two variables defined on a closed, bounded set $D.$ Then $f$ will attain the absolute maximum value and the absolute minimum value, which are, respectively, the largest and smallest values found among the following:
(i) The values of $f$ at the critical points of $f$ in the interior of $D.$
(ii) The maximum and minimum values of $f$ on the boundary of $D.$
That is, the only possible values for the global extrema of $f$ on $D$ are the extreme values of $f$ on the interior or boundary of $D.$
Finding Absolute Extrema on a Closed and Bounded Domain
Let $z = f (x, y)$ be a continuous function of two variables defined on a closed, bounded set $D,$ and assume $f$ is differentiable on $D.$ To find the absolute maximum and minimum values of $f$ on $D,$ do the following:
1. Determine the critical points of $f$ in the interior of $D.$
2. Determine the maximum and minimum values of $f$ on the boundary $D.$
3. The absolute maximum and minimum values of $f$ will occur at one of the values obtained above.
Example
Use the problem-solving strategy for finding absolute extrema of a function to determine the absolute extrema of $$f(x, y) = x^2 + y^2 + 4x - 6y$$ on the domain $D$ defined by all $(x,y)$ such that $x^2 + y^2 \leq 16.$
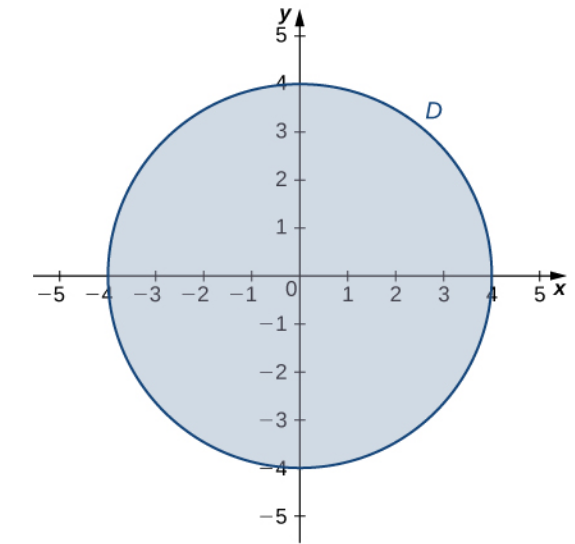
We first find all critical points in the restricted domain $D=\{(x,y)\in \mathbb{R}^2|x^2+y^2\leq 16\}.$
That is, we consider the collection of all points $(x,y)$ such that $x^2+y^2\leq 16.$
Now, $f_x(x,y)=2x+4$ and $f_y(x,y)=2y-6.$
Since these derivatives are defined for all $(x,y),$ we only need to consider points where the first partial derivatives are $0.$ $$ \begin{cases} 2x+4=0\\ 2y-6=0 \end{cases} $$ We see that $(x,y)=(-2,3)$ is the only point which satisfies the system. Since the point is in $D,$ we shall consider this point a critical point and is a candidate for an absolute extremum.
We now consider the function values along the boundary.
We shall parameterize the boundary and find the extrema of $f$ on this curve.
A parameterization for the boundary (a circle of radius $4$) is $$ x=4\cos t\\ y=4\sin t $$ Then, the value of $f$ at any point $t$ on the parameterization is $$ \begin{array}{lll} \displaystyle F(t)&\displaystyle=f(x(t),y(t)) &\mbox{}\\ \displaystyle &\displaystyle=f(4\cos t,4\sin t) &\mbox{}\\ \displaystyle &\displaystyle= (4\cos t)^2 + (4\sin t)^2 + 4(4\cos t) - 6(4\sin t)&\mbox{}\\ \displaystyle &\displaystyle= 4(\cos^2 t +\sin^2 t) + 16\cos t - 24\sin t&\mbox{}\\ \displaystyle &\displaystyle= 4 + 16\cos t - 24\sin t&\mbox{}\\ \end{array} $$
Thus, we must find the extrema of the single-variable function $F(t).$
We seek values of $t$ such that $$F'(t)=-16 \sin t-24 \cos t =0$$ Using identities we shall write $\sin t=\sqrt{1-\cos^2 t}$ so that $$ -16 \sqrt{1-\cos^2 t}-24 \cos t =0 $$ which simplifies to $$ -2 \sqrt{1-\cos^2 t}=3 \cos t $$ Then $$ \begin{array}{lll} &\displaystyle 4(1-\cos^2 t)=9\cos^2 t&\mbox{}\\ \implies &\displaystyle 4-4\cos^2 t=9\cos^2 t&\mbox{}\\ \implies &\displaystyle 4=13\cos^2 t&\mbox{}\\ \implies &\displaystyle \cos^2 t=\frac{4}{13}&\mbox{}\\ \implies &\displaystyle \cos t=\pm\frac{2}{\sqrt{13}}&\mbox{}\\ \end{array} $$ Thus, we may say that a candidate point for an extremum occurs on points such that $$ x=4\cos t=4\cdot\left(\pm\frac{2}{\sqrt{13}}\right)=\pm \frac{8}{\sqrt{13}} $$ Since a boundary point $(x,y)$ must satisfy $x^2+y^2=16$, we may determine candidates for $y.$ $$ \begin{array}{lll} &\displaystyle \left(\pm \frac{8}{\sqrt{13}}\right)^2+y^2 =16&\mbox{}\\ \implies &\displaystyle \frac{64}{13}+y^2=16 &\mbox{}\\ \implies &\displaystyle y^2=16-\frac{64}{13} &\mbox{}\\ \implies &\displaystyle y^2=\frac{144}{13} &\mbox{}\\ \implies &\displaystyle y=\pm\frac{12}{\sqrt{13}} &\mbox{}\\ \end{array} $$ Thus, we have four candidates on the boundary: $$ \left(\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right), \left(-\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right) $$ Revisiting our derivative, $$ F'(t)=-16 \sin t-24 \cos t=-4y(t)-6x(t). $$ we see that only two of the above candidates actually satisfy $F'(t)=0,$ and they are $$ \left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right) $$ since $$ F'(t)=-16 \sin t-24 \cos t=-4y(t)-6x(t)=-4\left(-\frac{12}{\sqrt{13}}\right)-6\left(\frac{8}{\sqrt{13}}\right)=0 $$ and $$ F'(t)=-16 \sin t-24 \cos t=-4y(t)-6x(t)=-4\left(\frac{12}{\sqrt{13}}\right)-6\left(-\frac{8}{\sqrt{13}}\right)=0. $$ The critical points on the boundary are therefore $$ \left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right) $$
In summary, the critical points on $D$ are $$ (-2,3), \left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right) $$ Since, $$ f(-2,3)=(-2)^2 + (3)^2 + 4(-2) - 6(3)=-13\\ f\left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right)=\left(-\frac{8}{\sqrt{13}}\right)^2 + \left(\frac{12}{\sqrt{13}}\right)^2 + \left(-\frac{8}{\sqrt{13}}\right) - 6\left(\frac{12}{\sqrt{13}}\right)\approx -12.8444102\\ f\left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right)=\left(\frac{8}{\sqrt{13}}\right)^2 + \left(-\frac{12}{\sqrt{13}}\right)^2 + \left(\frac{8}{\sqrt{13}}\right) - 6\left(-\frac{12}{\sqrt{13}}\right)\approx 44.8444102 $$
Thus, $(-2,3)$ is the absolute minimum and $\displaystyle \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right)$ is the absolute maximum on $D.$
That is, we consider the collection of all points $(x,y)$ such that $x^2+y^2\leq 16.$
Now, $f_x(x,y)=2x+4$ and $f_y(x,y)=2y-6.$
Since these derivatives are defined for all $(x,y),$ we only need to consider points where the first partial derivatives are $0.$ $$ \begin{cases} 2x+4=0\\ 2y-6=0 \end{cases} $$ We see that $(x,y)=(-2,3)$ is the only point which satisfies the system. Since the point is in $D,$ we shall consider this point a critical point and is a candidate for an absolute extremum.
We now consider the function values along the boundary.
We shall parameterize the boundary and find the extrema of $f$ on this curve.
A parameterization for the boundary (a circle of radius $4$) is $$ x=4\cos t\\ y=4\sin t $$ Then, the value of $f$ at any point $t$ on the parameterization is $$ \begin{array}{lll} \displaystyle F(t)&\displaystyle=f(x(t),y(t)) &\mbox{}\\ \displaystyle &\displaystyle=f(4\cos t,4\sin t) &\mbox{}\\ \displaystyle &\displaystyle= (4\cos t)^2 + (4\sin t)^2 + 4(4\cos t) - 6(4\sin t)&\mbox{}\\ \displaystyle &\displaystyle= 4(\cos^2 t +\sin^2 t) + 16\cos t - 24\sin t&\mbox{}\\ \displaystyle &\displaystyle= 4 + 16\cos t - 24\sin t&\mbox{}\\ \end{array} $$
Thus, we must find the extrema of the single-variable function $F(t).$
We seek values of $t$ such that $$F'(t)=-16 \sin t-24 \cos t =0$$ Using identities we shall write $\sin t=\sqrt{1-\cos^2 t}$ so that $$ -16 \sqrt{1-\cos^2 t}-24 \cos t =0 $$ which simplifies to $$ -2 \sqrt{1-\cos^2 t}=3 \cos t $$ Then $$ \begin{array}{lll} &\displaystyle 4(1-\cos^2 t)=9\cos^2 t&\mbox{}\\ \implies &\displaystyle 4-4\cos^2 t=9\cos^2 t&\mbox{}\\ \implies &\displaystyle 4=13\cos^2 t&\mbox{}\\ \implies &\displaystyle \cos^2 t=\frac{4}{13}&\mbox{}\\ \implies &\displaystyle \cos t=\pm\frac{2}{\sqrt{13}}&\mbox{}\\ \end{array} $$ Thus, we may say that a candidate point for an extremum occurs on points such that $$ x=4\cos t=4\cdot\left(\pm\frac{2}{\sqrt{13}}\right)=\pm \frac{8}{\sqrt{13}} $$ Since a boundary point $(x,y)$ must satisfy $x^2+y^2=16$, we may determine candidates for $y.$ $$ \begin{array}{lll} &\displaystyle \left(\pm \frac{8}{\sqrt{13}}\right)^2+y^2 =16&\mbox{}\\ \implies &\displaystyle \frac{64}{13}+y^2=16 &\mbox{}\\ \implies &\displaystyle y^2=16-\frac{64}{13} &\mbox{}\\ \implies &\displaystyle y^2=\frac{144}{13} &\mbox{}\\ \implies &\displaystyle y=\pm\frac{12}{\sqrt{13}} &\mbox{}\\ \end{array} $$ Thus, we have four candidates on the boundary: $$ \left(\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right), \left(-\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right) $$ Revisiting our derivative, $$ F'(t)=-16 \sin t-24 \cos t=-4y(t)-6x(t). $$ we see that only two of the above candidates actually satisfy $F'(t)=0,$ and they are $$ \left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right) $$ since $$ F'(t)=-16 \sin t-24 \cos t=-4y(t)-6x(t)=-4\left(-\frac{12}{\sqrt{13}}\right)-6\left(\frac{8}{\sqrt{13}}\right)=0 $$ and $$ F'(t)=-16 \sin t-24 \cos t=-4y(t)-6x(t)=-4\left(\frac{12}{\sqrt{13}}\right)-6\left(-\frac{8}{\sqrt{13}}\right)=0. $$ The critical points on the boundary are therefore $$ \left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right) $$
In summary, the critical points on $D$ are $$ (-2,3), \left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right), \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right) $$ Since, $$ f(-2,3)=(-2)^2 + (3)^2 + 4(-2) - 6(3)=-13\\ f\left(-\frac{8}{\sqrt{13}},\frac{12}{\sqrt{13}}\right)=\left(-\frac{8}{\sqrt{13}}\right)^2 + \left(\frac{12}{\sqrt{13}}\right)^2 + \left(-\frac{8}{\sqrt{13}}\right) - 6\left(\frac{12}{\sqrt{13}}\right)\approx -12.8444102\\ f\left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right)=\left(\frac{8}{\sqrt{13}}\right)^2 + \left(-\frac{12}{\sqrt{13}}\right)^2 + \left(\frac{8}{\sqrt{13}}\right) - 6\left(-\frac{12}{\sqrt{13}}\right)\approx 44.8444102 $$
Thus, $(-2,3)$ is the absolute minimum and $\displaystyle \left(\frac{8}{\sqrt{13}},-\frac{12}{\sqrt{13}}\right)$ is the absolute maximum on $D.$

Application
When data follow an approximately linear trend, it is common to model the trend with a line as in the graph below. Our goal is the find the slope $m$ and $y$-intercept $b$ of the "line of best fit."
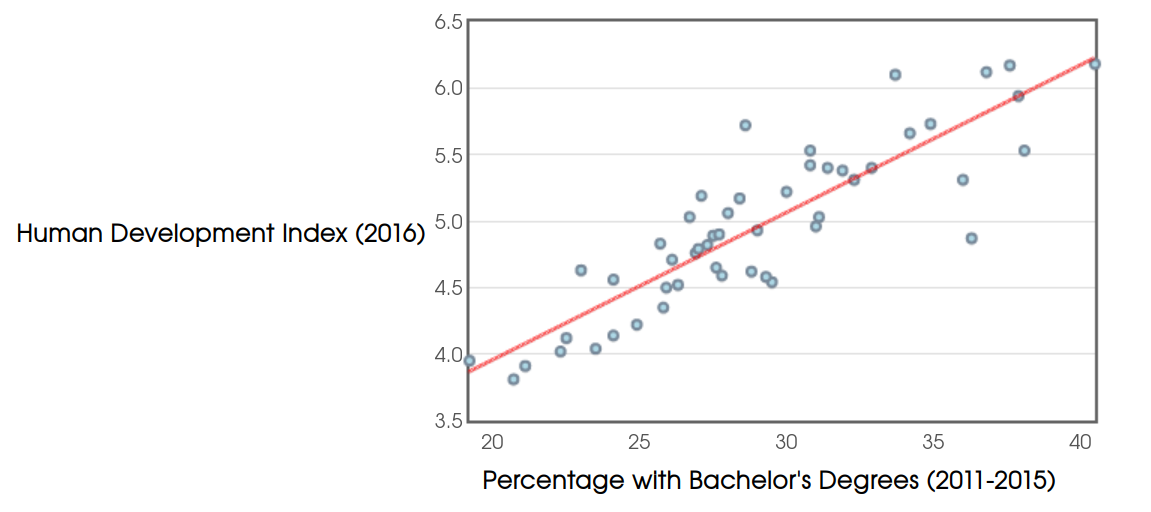
Application
We shall label the $xy$ pairs in the data set $(x_1,y_1),$ $(x_2,y_2),$...,$(x_n,y_n)$ and write our line of best fit as $y=mx+b$.
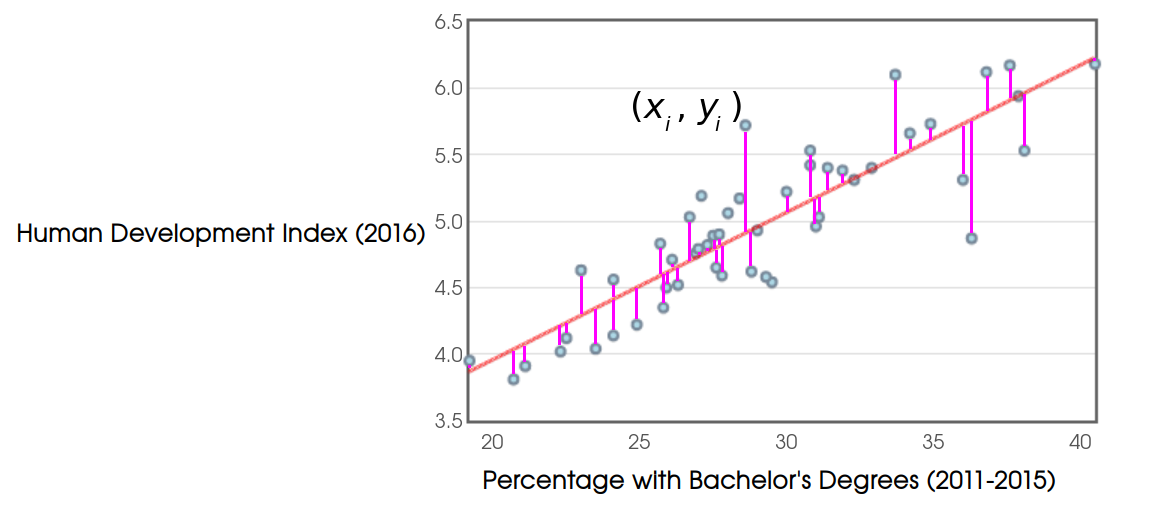
Application
The squares of the pink distances of each data point on the line are called the squared deviations, $(mx_i+b-y_i)^2$

Application
We now add up all the squared deviations and note that this is a function of $m$ and $b.$ $$S(m,b)=\sum_{i=1}^{n}(mx_i+b-y_i)^2$$ The line of best fit $y=mx+b$ is the one which minimizes the sum of squared deviations $S(m,b)$ over all possible values of $m$ and $b!$

Finding a formulas for $m$ and $b$ for the line of best fit is your next FYE Problem.