Holt.Blue

The Gradient and Directional Derivatives

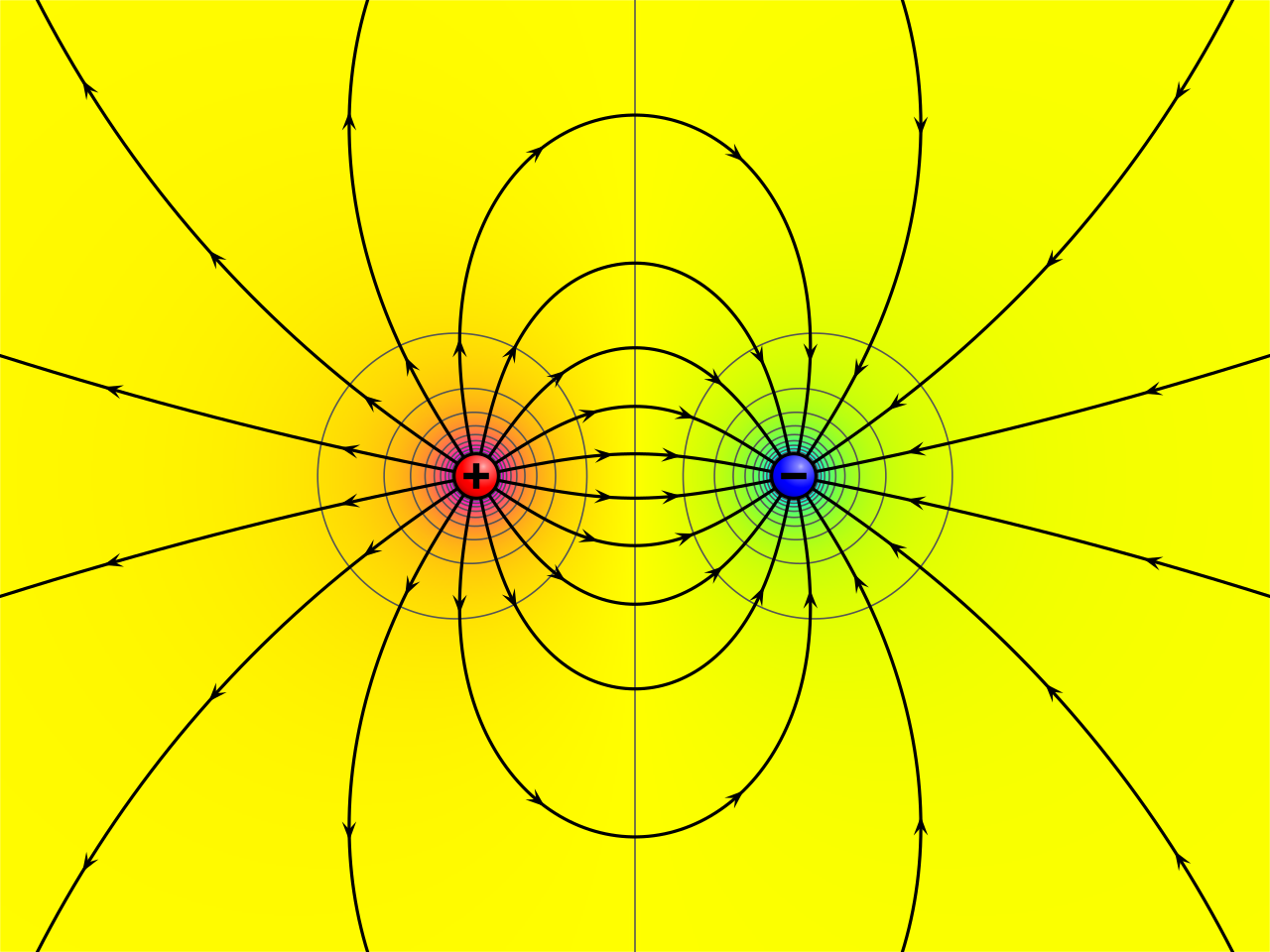
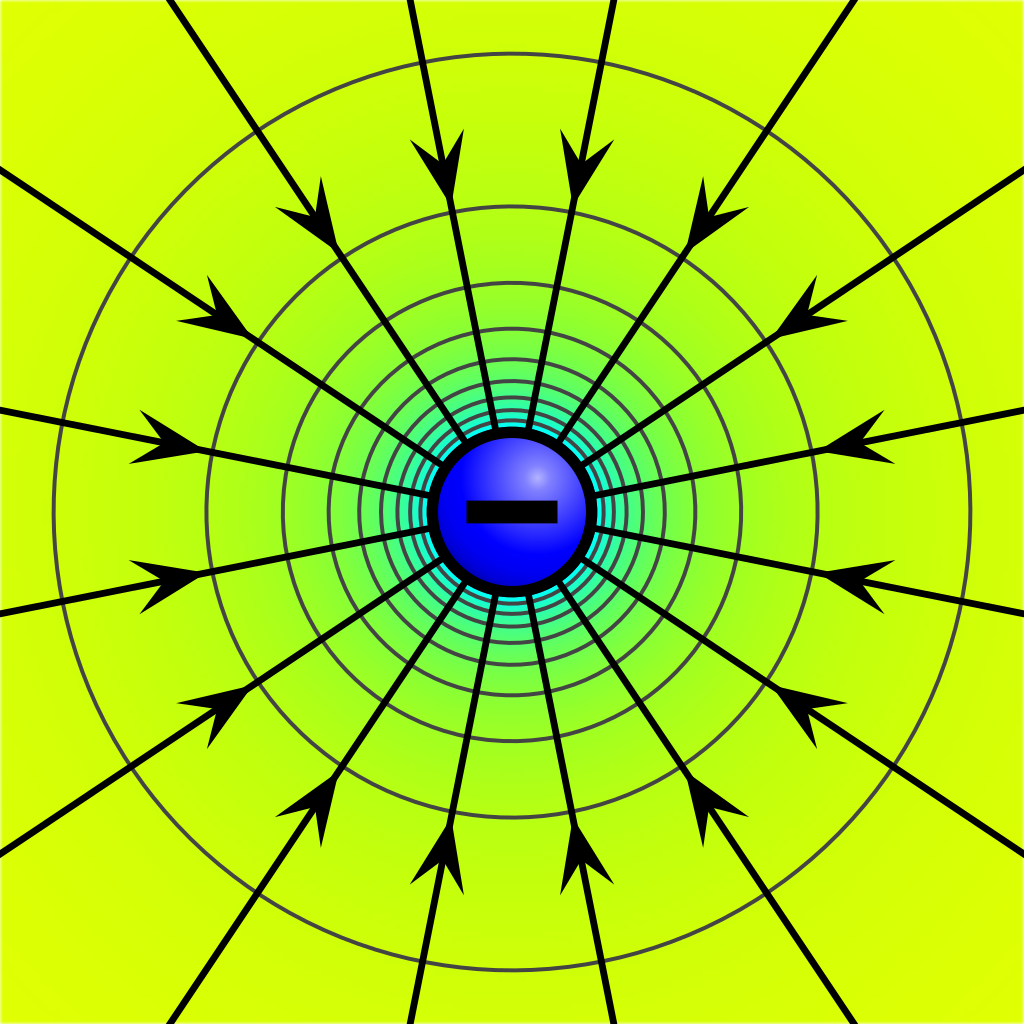
Today, we will further generalize the notion of derivatives.



























The Gradient

We're going to look at another way to understand the rate of change of a multivariable function $f$ called the gradient of $f.$

























The Gradient in Two Dimensions

Let $z=f(x,y)$ be a differentiable function. Then the gradient of $f,$ denoted $\nabla f$ or $\nabla f(x,y)$ is the vector $$ \nabla f=\frac{\partial f}{\partial x}\,{\bf i}+\frac{\partial f}{\partial y}\,{\bf j} $$



























Properties of the Gradient

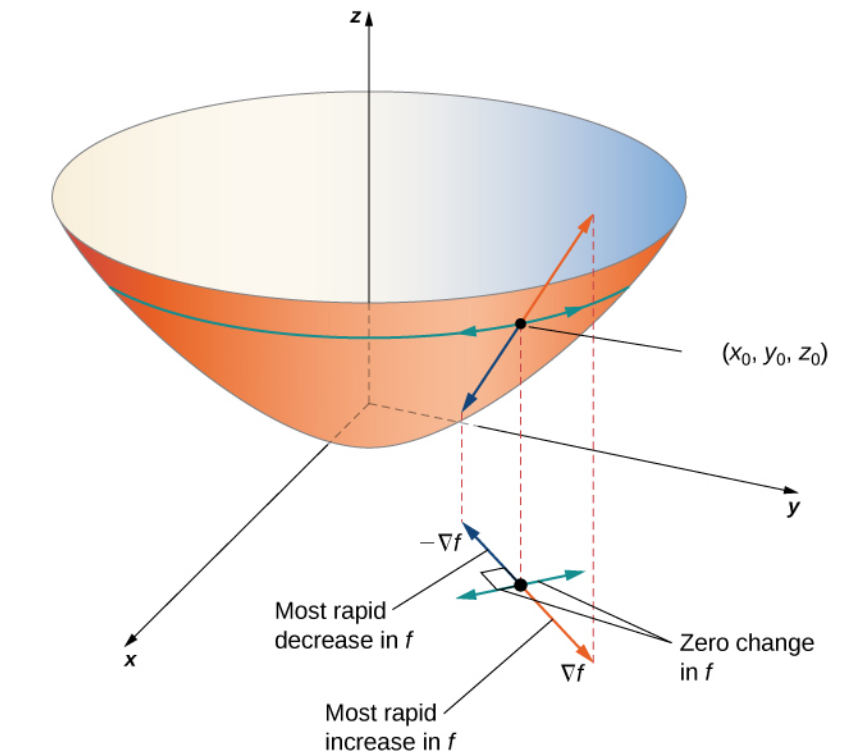
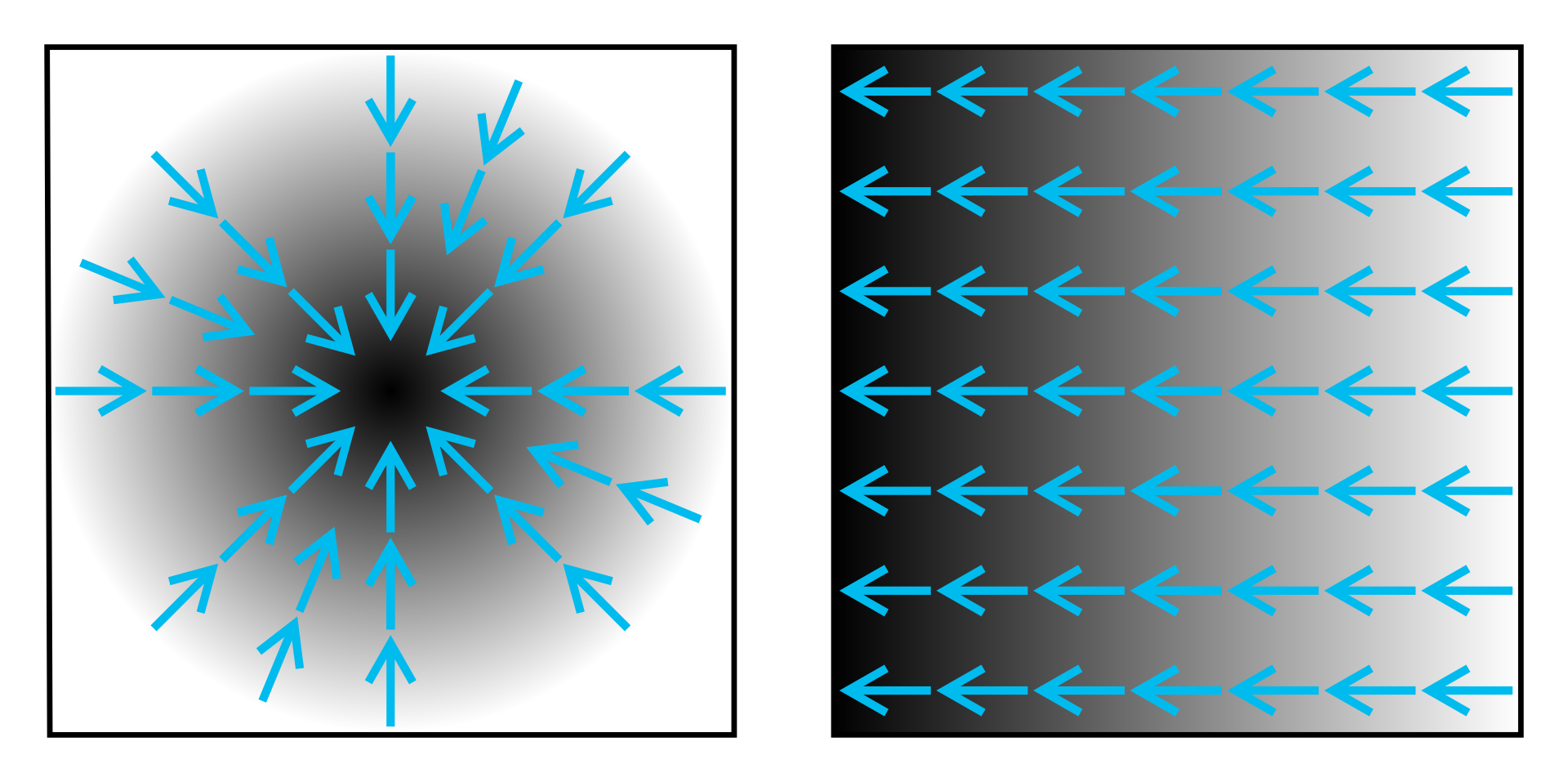
1. $\nabla f(x,y)$ points in the direction of the greatest non-negative rate of change of $f(x,y).$
2. $\Vert \nabla f(x,y)\Vert$ is equal to the greatest non-negative rate of change of $f(x,y)$ of all possible directions.
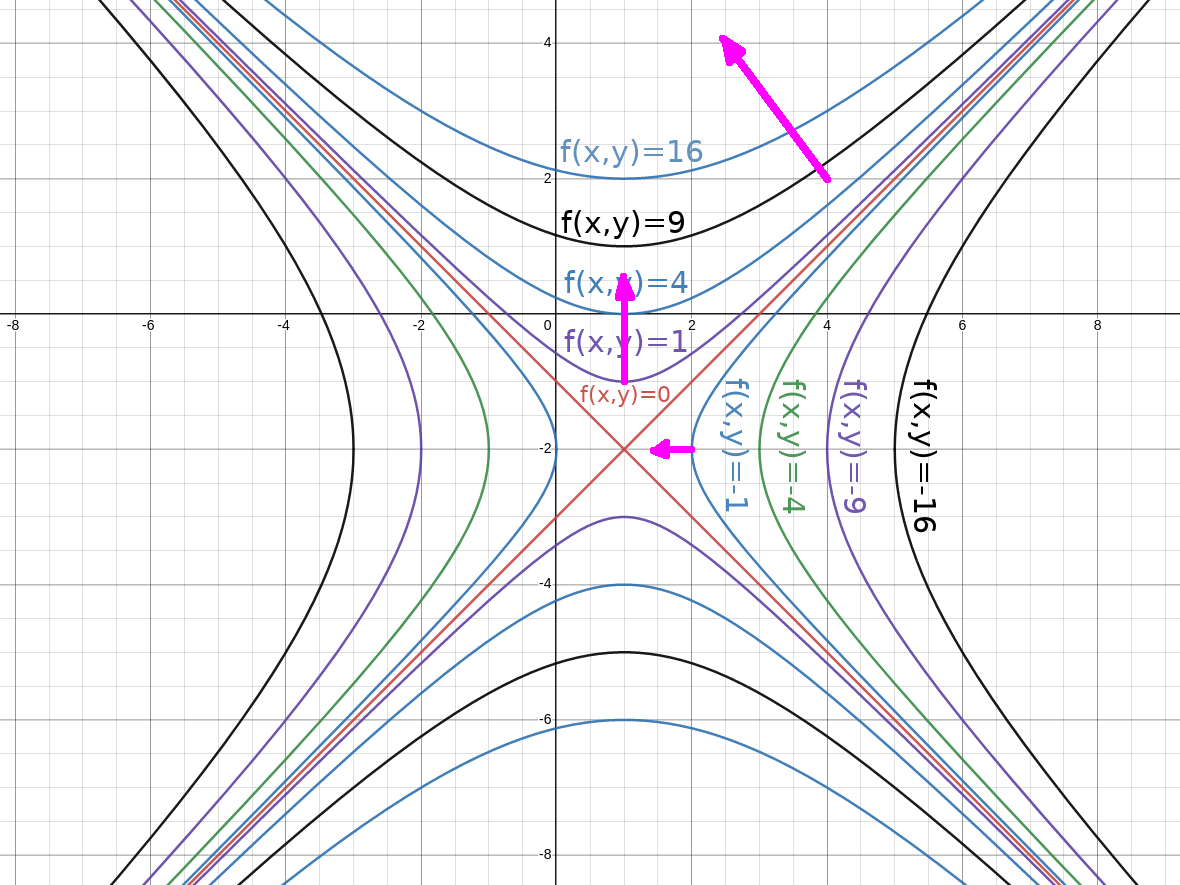
3. $\nabla f(x,y)$ is normal to the level curves of $f(x,y).$

What the Gradient Tells Us




































Argument for $\nabla f$ Perpendicular to Level Curves $f(x,y)=c$

Recall from the previous section that the slope of the tangent line to the level curve $f(x,y)=c$ is given by $\displaystyle \frac{dy}{dx}=-\frac{f_x}{f_y}.$

Then a tangent vector to the level curve is $\left \langle 1,-\frac{f_x}{f_y}\right \rangle.$

It follows that $$ \begin{array}{lll} \displaystyle \nabla f\cdot \left \langle 1,-\frac{f_x}{f_y}\right \rangle &\displaystyle= \left\langle f_x,f_y\right \rangle \cdot \left \langle 1,-\frac{f_x}{f_y}\right \rangle &\mbox{}\\ \displaystyle &\displaystyle= f_x\cdot 1+f_y\cdot\left(-\frac{f_x}{f_y}\right)&\mbox{}\\ \displaystyle &\displaystyle= 0&\mbox{}\\ \end{array} $$ Thus, $\nabla f$ is perpendicular to the level curves $f(x,y)=c$

























Understanding the Gradient Intuitively

Imagine yourself as a runner on a smooth, curved surface, and you're looking for the best workout by running in the direction of steepest ascent. This is the direction of the gradient. The rate of elevation gain per unit length is the magnitude of the gradient.





























Understanding the Gradient Intuitively

Again, imagine yourself on a smooth, curved surface and you let a bouncy ball roll down from rest, the initial direction it travels at the point of release is the opposite direction which the gradient vector points. The magnitude of the gradient is the rate at which the ball loses elevation per unit length.





























The Gradient in Practice

If you've ever heard the terms "gradient," "temperature gradient," "color gradient," etcetera, the gradient vector is intimately related to these ideas.

































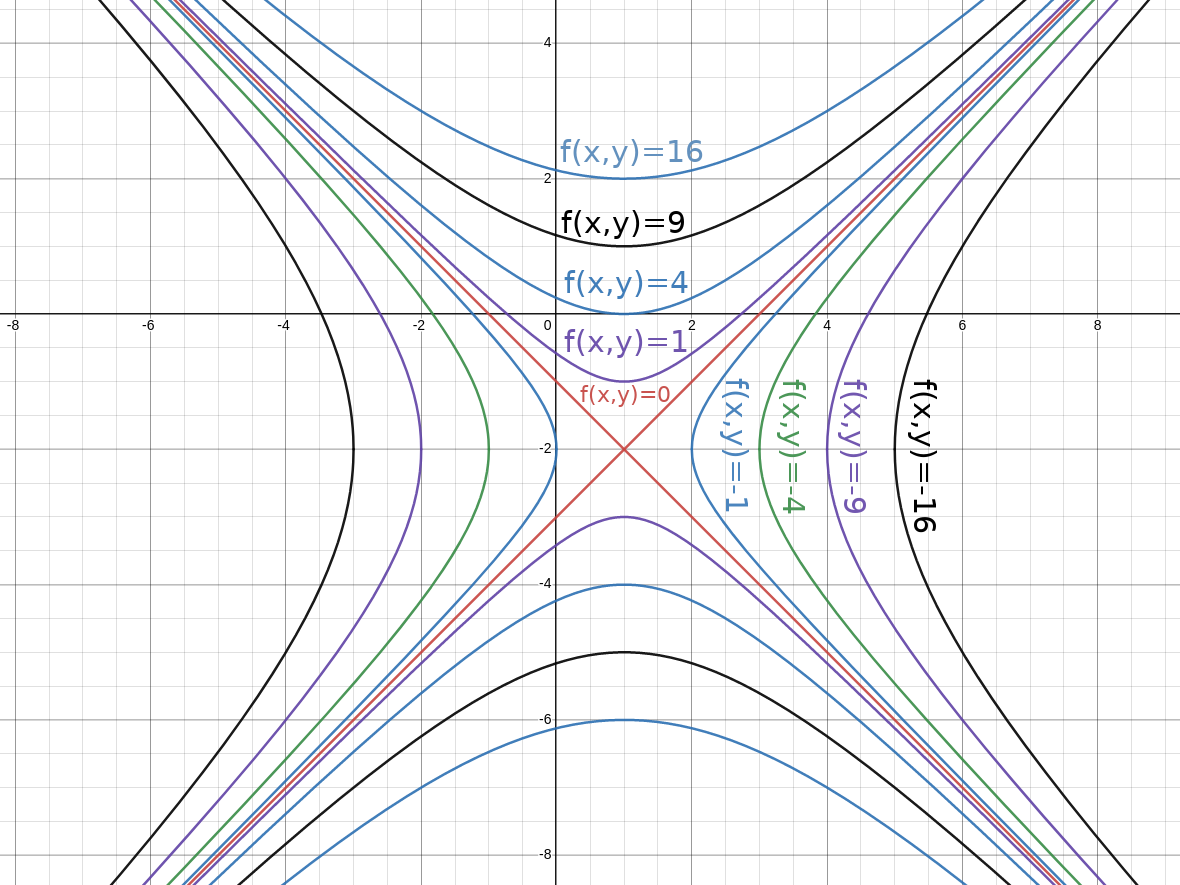
Example

For $f (x, y) = y^{2}-x^{2}+4y+2x+3$ for $f(x,y)=0$, find $\nabla f.$

Also find $\nabla f(1,1),$ $\nabla f(2,-2),$ and $\nabla f(4,2).$

Show/Hide Answer!





























Application

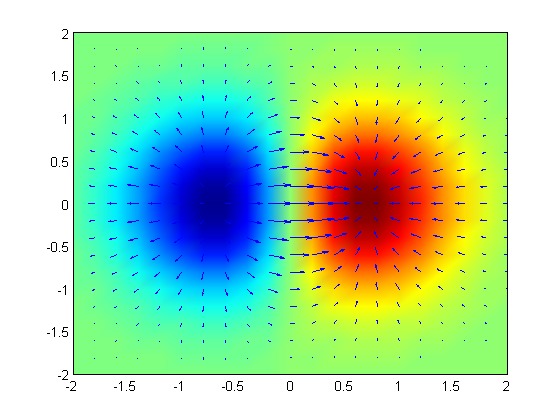
If we have a function $V$ which describes the electric potential (voltage) at a point $(x, y),$ then the electric field vector at $(x, y)$ is $${\bf E} = -\nabla V(x, y).$$ This says that the electric field points in the opposite direction of the greatest rate of change. ("Charged particles roll down Voltage Mountain.")































Application

For a point charge $Q$ located at the origin, the electric potential (voltage) at the point $(x, y)$ is modelled by $\displaystyle V(x, y) = \frac{1}{4\pi\varepsilon_0}\frac{Q}{\sqrt{x^2+y^2}}$ where $\varepsilon_0 \approx 8.854 \times 10^{-12}$ farads per meter.

Taking $Q=1.602 \times 10^{-19}$ coulombs (the charge of a single proton), find the electric field vector ${\bf E} = -\nabla V(x, y)$ at $(3,4).$

Show/Hide Answer!































The Gradient in Three Dimensions

Let $w=f(x,y,z)$ be a differentiable function. Then the gradient of $f,$ denoted $\nabla f$ or $\nabla f(x,y,z)$ is the vector $$ \nabla f=\frac{\partial f}{\partial x}\,{\bf i}+\frac{\partial f}{\partial y}\,{\bf j}+\frac{\partial f}{\partial z}\,{\bf k} $$



























Properties of the Gradient

1. $\nabla f(x,y,z)$ points in the direction of the greatest non-negative rate of change of $f(x,y,z).$
2. $\Vert \nabla f(x,y,z)\Vert$ is equal to the greatest non-negative rate of change of $f(x,y,z)$ of all possible directions.
3. $\nabla f(x,y,z)$ is normal to the level surfaces of $f(x,y,z).$

Example

Find $\nabla f$ for $f (x, y, z) = e^{-2z} \sin 2x \cos 2y.$ Show/Hide Answer!

































Directional Derivatives

When we compute the partial derivatives $\displaystyle \frac{\partial f}{\partial x},$ $\displaystyle \frac{\partial f}{\partial y},$ $\displaystyle \frac{\partial f}{\partial z},...$ of a function $f,$ we are finding the derivative in the $x,$ $y,$ and $z,...$ directions.

It is possible to find the rate of change (the slope of the tangent line) in any possible direction by finding a unit vector ${\bf u}$ pointing in the direction of interest.



























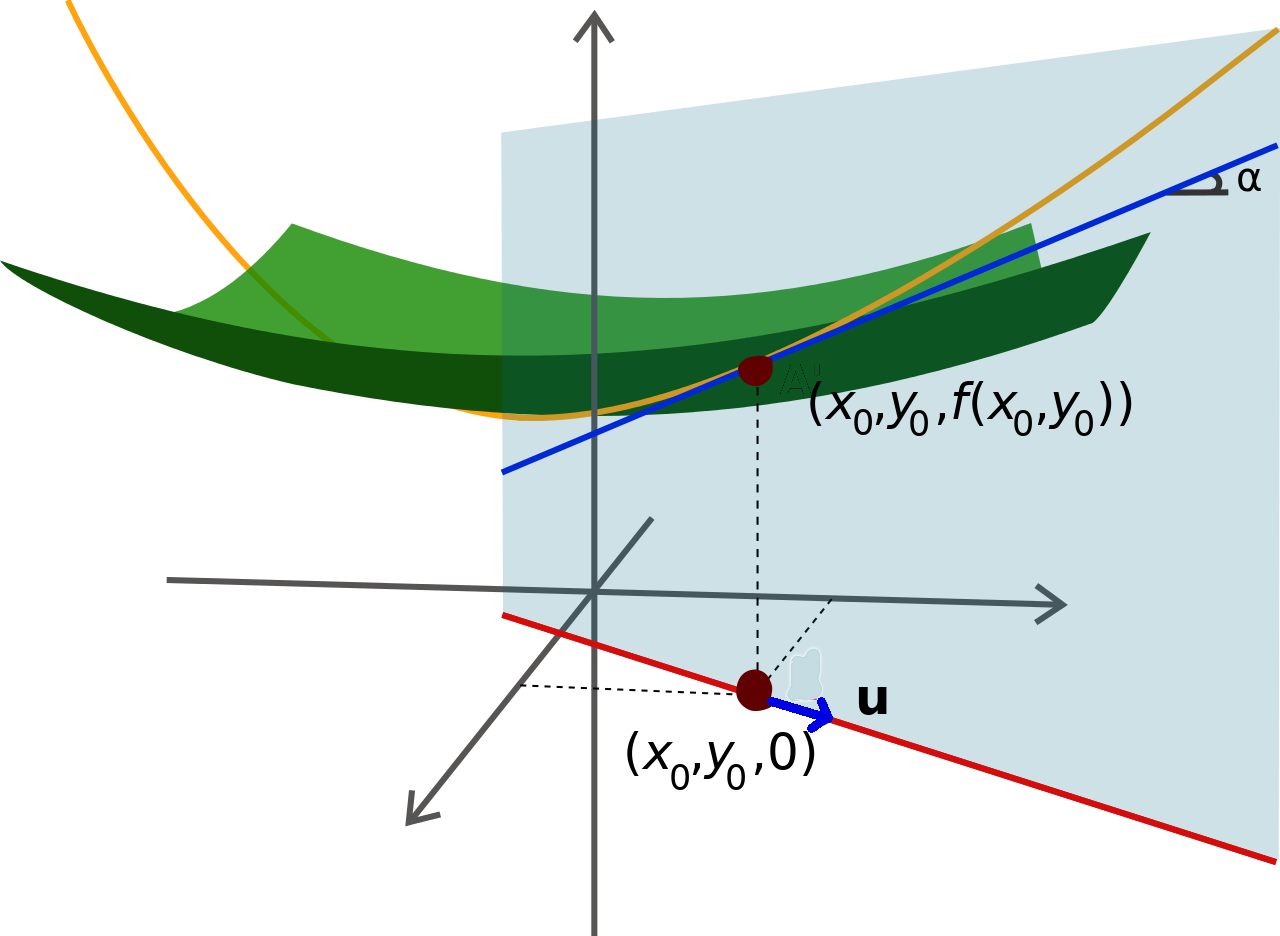
The Directional Derivative in Two Dimensions

If ${\bf u}=u_1\,{\bf i}+u_2\,{\bf j}$ is a unit vector, then the directional derivative, denoted $D_{{\bf u}}f(x_0,y_0),$ is defined to be $$ D_{{\bf u}}f(x_0,y_0)=\lim_{h \rightarrow 0}\frac{f(x_0+hu_1,y_0+hu_2)-f(x_0,y_0)}{h} $$


$D_{{\bf u}}f(x_0,y_0)$ is the slope of the tangent line of $f$ at $(x_0,y_0)$ in the direction of ${\bf u}.$






















An Equivalent Definition

If ${\bf u}=\cos \theta\,{\bf i}+\sin \theta \,{\bf j}$ (a unit vector), then the directional derivative, denoted $D_{{\bf u}}f(a,b),$ is defined to be $$ D_{{\bf u}}f(a,b)=\lim_{h \rightarrow 0}\frac{f(a+h\cos \theta,b+h\sin \theta)-f(a,b)}{h} $$
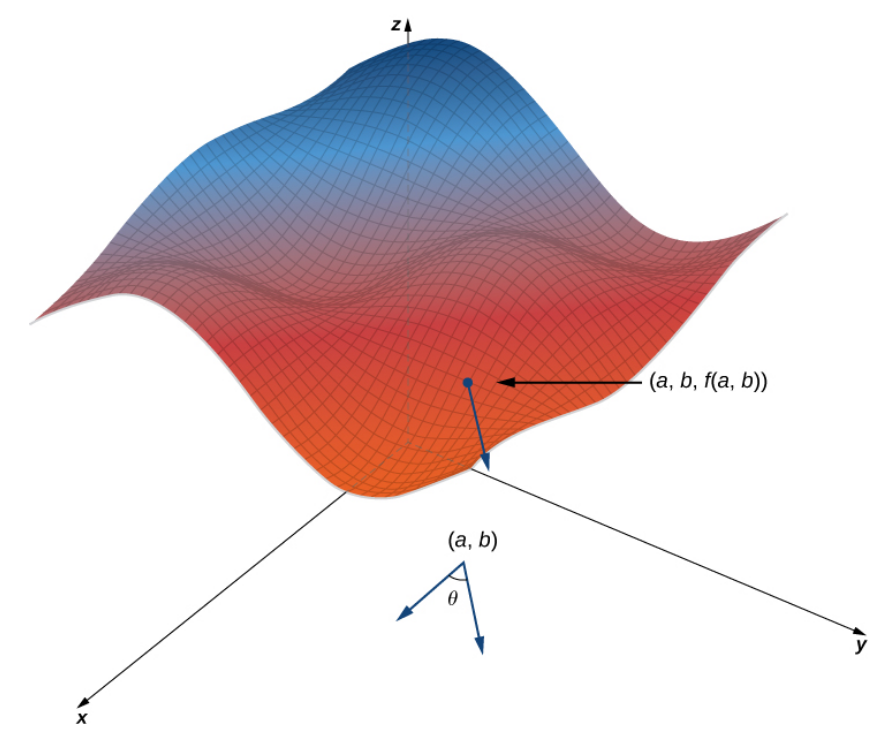
$D_{{\bf u}}f(a,b)$ is the slope of the tangent line of $f$ at $(a,b)$ in the direction of ${\bf u}.$






















Example

Find the directional derivative $D_{{\bf u}}f(x,y)$ of $f (x, y) = x^2 - xy + 3y^2$ in the direction ${\bf u}=\frac{3}{5}\,{\bf i}+\frac{4}{5}\,{\bf j}$ at the point $(-1,2).$

Show/Hide Answer!































A Nice Fact

Let ${\bf u}$ be a unit vector and let $f(x,y)$ be a differentiable function at the point $(x_0,y_0)$. Then $$ D_{{\bf u}}f(x_0,y_0)=\nabla f(x_0,y_0)\cdot {\bf u} $$





























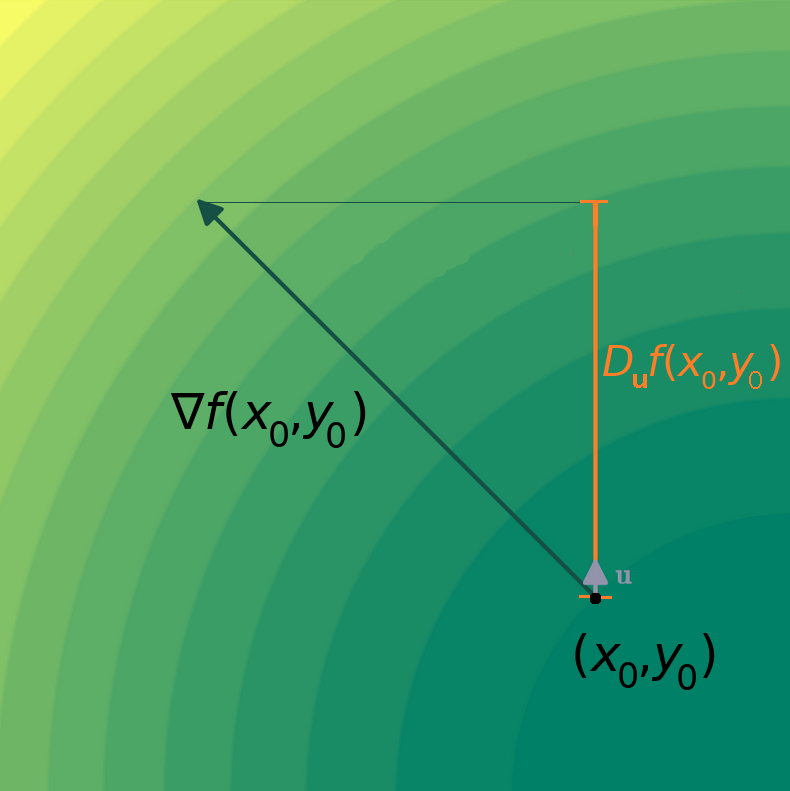
A Little Sump'm' Sump'm' to Notice

The directional derivatives in the directions of the unit vectors $\bf{i}$ and $\bf{j}$ are $$ D_{\bf{i}}(x,y)=\lim_{h \rightarrow 0}\frac{f(x+h\cdot 1,y+h\cdot 0)-f(x,y)}{h}=\lim_{h \rightarrow 0}\frac{f(x+h,y)-f(x,y)}{h}=\frac{\partial f}{\partial x} $$ and $$ D_{\bf{j}}(x,y)=\lim_{h \rightarrow 0}\frac{f(x+h\cdot 0,y+h\cdot 1)-f(x,y)}{h}=\lim_{h \rightarrow 0}\frac{f(x,y+h)-f(x,y)}{h}=\frac{\partial f}{\partial y} $$ Makes sense, right? :D



























Example

Find the directional derivative $D_{{\bf u}}f(x,y)$ of $f (x, y) = x^2 - xy + 3y^2$ in the direction ${\bf u}=\frac{3}{5}\,{\bf i}+\frac{4}{5}\,{\bf j}$ at the point $(-1,2).$

Show/Hide Answer!































The Directional Derivative in Three Dimensions

If ${\bf u}=u_1\,{\bf i}+u_2\,{\bf j}+u_3\,{\bf k}$ is a unit vector, then the directional derivative, denoted $D_{{\bf u}}f(x_0,y_0,z_0),$ is defined to be $$ D_{{\bf u}}f(x_0,y_0,z_0)=\lim_{h \rightarrow 0}\frac{f(x_0+hu_1,y_0+hu_2,z_0+hu_3)-f(x_0,y_0,z_0)}{h} $$

































Of course, we could simply use the three-dimensional equivalent of our nice fact...





























A Nice Fact

Let ${\bf u}$ be a unit vector in $\mathbb{R}^3$ and let $f(x,y,z)$ be a differentiable function at the point $(x_0,y_0,z_0)$. Then $$ D_{{\bf u}}f(x_0,y_0,z_0)=\nabla f(x_0,y_0,z_0)\cdot {\bf u} $$





























Application

If we have a function $V$ which describes the electric potential (voltage) at a point in space $(x, y, z),$ then the electric field vector at $(x, y, z)$ is $${\bf E} = -\nabla V(x, y, z).$$ This says that the electric field points in the opposite direction of the greatest rate of change.































Example

The electrical potential (voltage) in a certain region of space is given by the function $$V(x, y, z) = 5x^2 - 3xy + xyz.$$ (a) In which direction does the voltage change most rapidly at point $(3, 4, 5) ?$

(b) What is the electric field vector at $(3, 4, 5) ?$

(c) What is the maximum rate of change of the voltage at point $(3, 4, 5) ?$

(d) Find the rate of change of the voltage at point $(3, 4, 5)$ in the direction of the vector $\langle 1, 1, -1 \rangle.$ Show/Hide Answer!

































The Chain Rule in Vector Form Redux

Recall that by letting ${\bf r}(t_1,t_2,\ldots,t_n)=\langle x_1(t_1,t_2,\ldots,t_n),x_2(t_1,t_2,\ldots,t_n),\ldots,x_m(t_1,t_2,\ldots,t_n)\rangle$ be a multivariable vector-valued function and writing $f(x_1,x_2,\ldots,x_m)$ as $f({\bf r}),$ we may write the general chain rule in vector form as $$ \frac{\partial f}{\partial t_j}=\langle f_{x_1}({\bf r}),f_{x_2}({\bf r}),\ldots,f_{x_m}({\bf r})\rangle \cdot \frac{\partial {\bf r}}{\partial t_j} $$ Since the gradient of a function of a multivariable function $f(x_1,x_2,\ldots,x_m)$ is defined to be $\langle f_{x_1}({\bf r}),f_{x_2}({\bf r}),\ldots,f_{x_m}({\bf r})\rangle,$ we may state the general chain rule in an even more compact form. $$ \frac{\partial f}{\partial t_j}=\nabla f({\bf r}) \cdot \frac{\partial {\bf r}}{\partial t_j} $$