For multivariable functions, the chain rule still applies.
However, the chain rule takes on a more generalized form in a multivariate setting.
Recall: The Single Variable Chain Rule
Recall the single variable chain rule using Leibniz notation.
Suppose $y=f(x)$ and $x=g(t).$ Then $y=f(g(t))$ is a differentiable function and $$ \frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt} $$
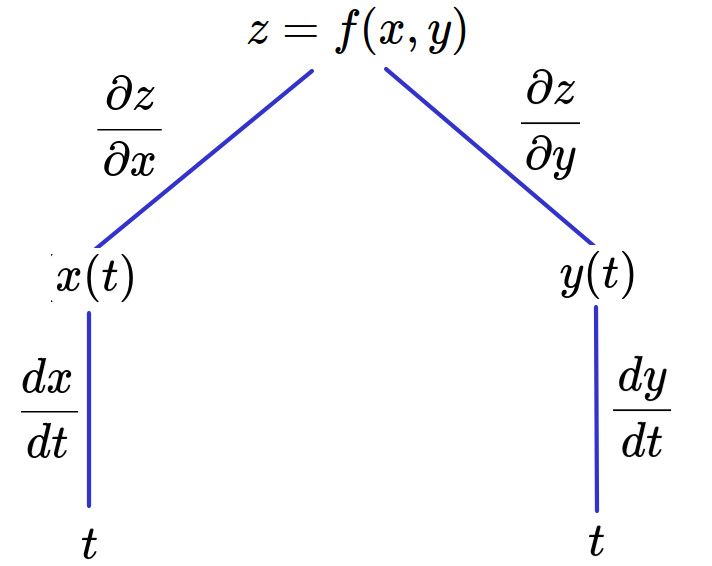
The Chain Rule for and Two Intermediate Variables and One Independent Variable
Suppose that $x = g(t)$ and $y = h(t)$ are differentiable functions of $t$ and $z = f (x, y)$ is a differentiable function of $x$ and $y.$
Then $z = f(x(t), y(t))$ is a differentiable function of $t$ and $$ \frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} $$
Example
Calculate $\displaystyle \frac{dz}{dt}$ given that $z = f (x, y) = x^2 - 3xy + 2y^2,$ $x = x(t) = 3 \sin 2t,$ and $y = y(t) = 4 \cos 2t.$
Express the final answer in terms of $t.$
$$
\begin{array}{lll}
\displaystyle \frac{dz}{dt}&\displaystyle=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} &\mbox{}\\
\displaystyle &\displaystyle=(2x-3y)(6\cos 2t)+(-3x+4y)(-8\sin 2t) &\mbox{}\\
\displaystyle &\displaystyle=(12x-18y)(\cos 2t)+(24x-32y)(\sin 2t) &\mbox{}\\
\displaystyle &\displaystyle=(12[3 \sin 2t]-18[4 \cos 2t])(\cos 2t)+(24[3 \sin 2t]-32[4 \cos 2t])(\sin 2t) &\mbox{$x =3 \sin 2t,\, y = 4 \cos 2t$}\\
\displaystyle &\displaystyle=36 \sin 2t\cos 2t-72\cos^2 2t+72\sin^2 2t-128\sin 2t \cos 2t &\mbox{}\\
\displaystyle &\displaystyle=-92\sin 2t \cos 2t-72(\cos^2 2t-\sin^2 2t) &\mbox{}\\
\displaystyle &\displaystyle=-92\sin 2t \cos 2t-72(\cos^2 2t-\sin^2 2t) &\mbox{}\\
\displaystyle &\displaystyle=-46\sin 4t-72\cos 4t &\mbox{}\\
\end{array}
$$
Visualizing the Chain Rule: $ \displaystyle \frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} $
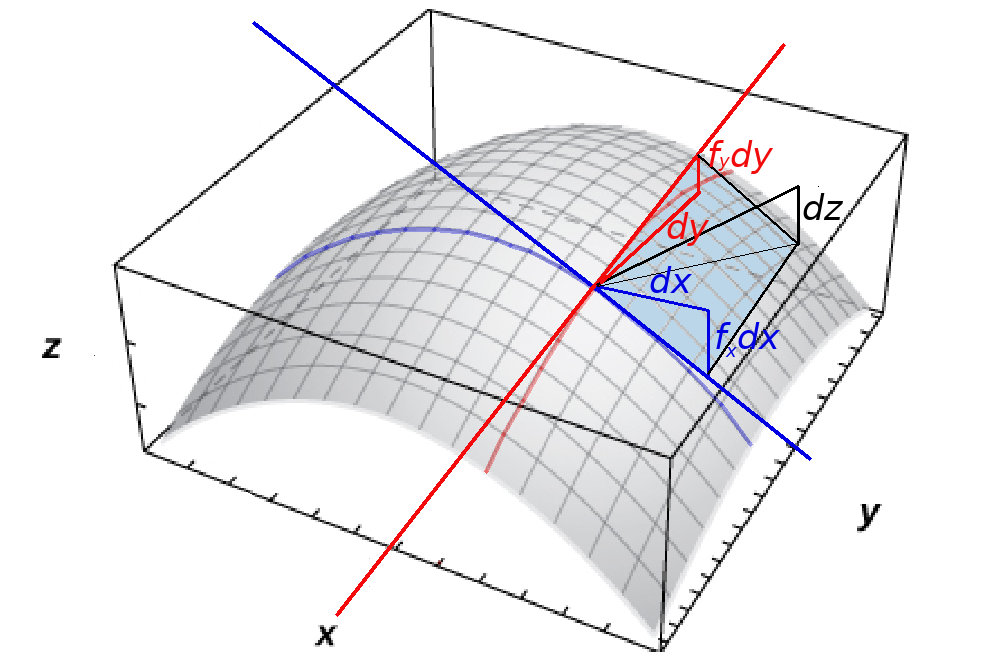
A Fun Note on Differentials
Recall that the total differential of $z = f (x, y)$ is defined as $dz = f_x (x_0, y_0)\,dx + f_y (x_0, y_0)\,dy.$ We may also express this as $$ dz = \frac{\partial z}{\partial x}\,dx + \frac{\partial z}{\partial y}\,dy $$
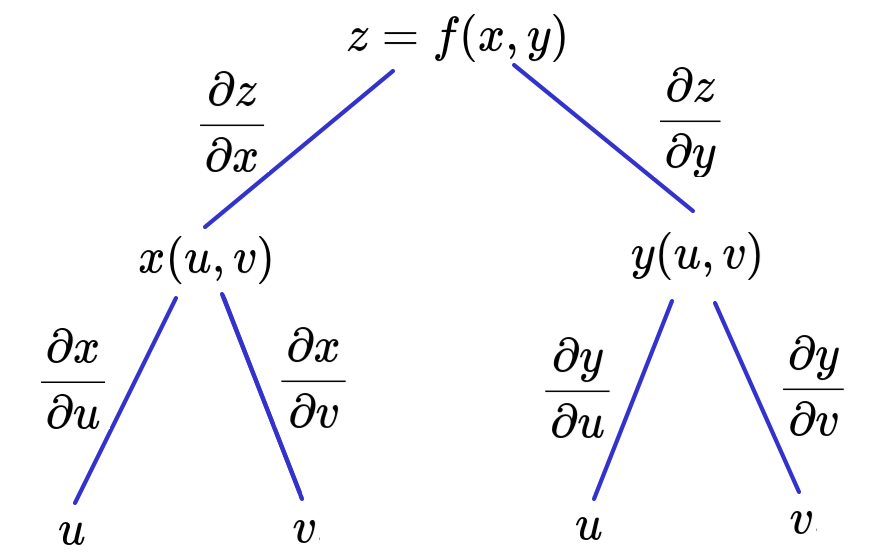
The Chain Rule for Two Intermediate Variables and Two Independent Variables
Suppose $x = g(u, v)$ and $y = h(u, v)$ are differentiable functions of $u$ and $v,$ and $z = f (x, y)$ is a differentiable function of $x$ and $y.$ Then, $z = f (x(u, v), y(u, v))$ is a differentiable function of $u$ and $v,$ and $$ \frac{\partial z}{\partial u}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial u} \,\,\,\,\,\,\,\mbox{ and }\,\,\,\,\,\,\, \frac{\partial z}{\partial v}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial v} $$
The Chain Rule for Two Independent Variables $$ \displaystyle \frac{\partial z}{\partial u}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial u} \,\,\,\,\,\,\,\mbox{ and }\,\,\,\,\,\,\, \frac{\partial z}{\partial v}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial v} $$
Example
Calculate $\displaystyle \frac{\partial z}{\partial u}$ and $\displaystyle \frac{\partial z}{\partial v}$ given that $$ z=f(x,y)=\frac{2x-y}{x+3y}, $$ $x(u,v)=e^{2u}\cos 3v,$ and $y(u,v)=e^{2u}\sin 3v$
Before we begin, we calculate $\displaystyle \frac{\partial z}{\partial x}$ and $\displaystyle \frac{\partial z}{\partial y}.$
$$
\begin{array}{lll}
\displaystyle \frac{\partial z}{\partial x}&\displaystyle=\frac{\partial}{\partial x}\left(\frac{2x-y}{x+3y}\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{(x+3y)\frac{\partial}{\partial x}(2x-y)-(2x-y)\frac{\partial}{\partial x}(x+3y)}{(x+3y)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{(x+3y)\cdot 2-(2x-y)\cdot 1}{(x+3y)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{2x+6y-2x+y}{(x+3y)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{7y}{(x+3y)^2} &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial z}{\partial y}&\displaystyle=\frac{\partial}{\partial y}\left(\frac{2x-y}{x+3y}\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{(x+3y)\frac{\partial}{\partial y}(2x-y)-(2x-y)\frac{\partial}{\partial y}(x+3y)}{(x+3y)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{(x+3y)\cdot(-1)-(2x-y)\cdot 3}{(x+3y)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-x-3y-6x+3y}{(x+3y)^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-7x}{(x+3y)^2} &\mbox{}\\
\end{array}
$$
We may now calculate $\displaystyle \frac{\partial z}{\partial u}$ and $\displaystyle \frac{\partial z}{\partial v}.$
$$
\begin{array}{lll}
\displaystyle \frac{\partial z}{\partial u}&\displaystyle=\frac{\partial z}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial u} &\mbox{}\\
\displaystyle &\displaystyle= \frac{7y}{(x+3y)^2}(2e^{2u}\cos 3v)-\frac{7x}{(x+3y)^2}(2e^{2u}\sin 3v)&\mbox{}\\
\displaystyle &\displaystyle= \frac{7e^{2u}\sin 3v}{(e^{2u}\cos 3v+3e^{2u}\sin 3v)^2}(2e^{2u}\cos 3v)-\frac{7e^{2u}\cos 3v}{(e^{2u}\cos 3v+3e^{2u}\sin 3v)^2}(2e^{2u}\sin 3v)&\mbox{}\\
\displaystyle &\displaystyle= \frac{14e^{4u}\sin 3v \cos 3v}{(e^{2u}\cos 3v+3e^{2u}\sin 3v)^2}-\frac{14e^{4u}\sin 3v \cos 3v}{(e^{2u}\cos 3v+3e^{2u}\sin 3v)^2}&\mbox{}\\
\displaystyle &\displaystyle= 0&\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial z}{\partial v}&\displaystyle=\frac{\partial z}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial v} &\mbox{}\\
\displaystyle &\displaystyle= \frac{7y}{(x+3y)^2}(-3e^{2u}\sin 3v)-\frac{7x}{(x+3y)^2}(3e^{2u}\cos 3v)&\mbox{}\\
\displaystyle &\displaystyle= \frac{7e^{2u}\sin 3v}{(e^{2u}\cos 3v+3e^{2u}\sin 3v)^2}(-3e^{2u}\sin 3v)-\frac{7e^{2u}\cos 3v}{(e^{2u}\cos 3v+3e^{2u}\sin 3v)^2}(3e^{2u}\cos 3v)&\mbox{}\\
\displaystyle &\displaystyle= -\frac{21e^{4u}\sin^2 3v}{(e^{2u}\cos 3v+3e^{2u}\sin 3v)^2}-\frac{21e^{4u}\cos^2 3v}{(e^{2u}\cos 3v+3e^{2u}\sin 3v)^2}&\mbox{}\\
\displaystyle &\displaystyle= -\frac{21e^{4u}\sin^2 3v}{(e^{2u}(\cos 3v+3\sin 3v))^2}-\frac{21e^{4u}\cos^2 3v}{(e^{2u}(\cos 3v+3\sin 3v))^2}&\mbox{}\\
\displaystyle &\displaystyle= -\frac{21e^{4u}\sin^2 3v}{e^{4u}(\cos 3v+3\sin 3v)^2}-\frac{21e^{4u}\cos^2 3v}{e^{4u}(\cos 3v+3\sin 3v)^2}&\mbox{}\\
\displaystyle &\displaystyle= -\frac{21\sin^2 3v}{(\cos 3v+3\sin 3v)^2}-\frac{21\cos^2 3v}{(\cos 3v+3\sin 3v)^2}&\mbox{}\\
\displaystyle &\displaystyle= \frac{-21(\sin^2 3v+\cos^2 3v)}{(\cos 3v+3\sin 3v)^2}&\mbox{}\\
\displaystyle &\displaystyle= \frac{-21}{(\cos 3v+3\sin 3v)^2}&\mbox{}\\
\displaystyle &\displaystyle&\mbox{}\\
\end{array}
$$
We will now experience the POWAH!! of the general chain rule.
The General Chain Rule: $m$ Intermediate Variables and $n$ Independent Variables
Let $w = f (x_1, x_2 ,..., x_m)$ be a differentiable function of $m$ independent variables, and for each $i \in \{1,..., m\},$ let $x_i = x_i(t_1, t_2 ,..., t_n)$ be a differentiable function of $n$ independent variables. Then $$ \frac{\partial w}{\partial t_j}=\frac{\partial w}{\partial x_1}\frac{\partial x_1}{\partial t_j}+\frac{\partial w}{\partial x_2}\frac{\partial x_2}{\partial t_j}+\cdots+\frac{\partial w}{\partial x_m}\frac{\partial x_m}{\partial t_j} $$
The General Chain Rule $$ \frac{\partial w}{\partial t_j}=\frac{\partial w}{\partial x_1}\frac{\partial x_1}{\partial t_j}+\frac{\partial w}{\partial x_2}\frac{\partial x_2}{\partial t_j}+\cdots+\frac{\partial w}{\partial x_i}\frac{\partial x_i}{\partial t_j}+\cdots+\frac{\partial w}{\partial x_m}\frac{\partial x_m}{\partial t_j} $$
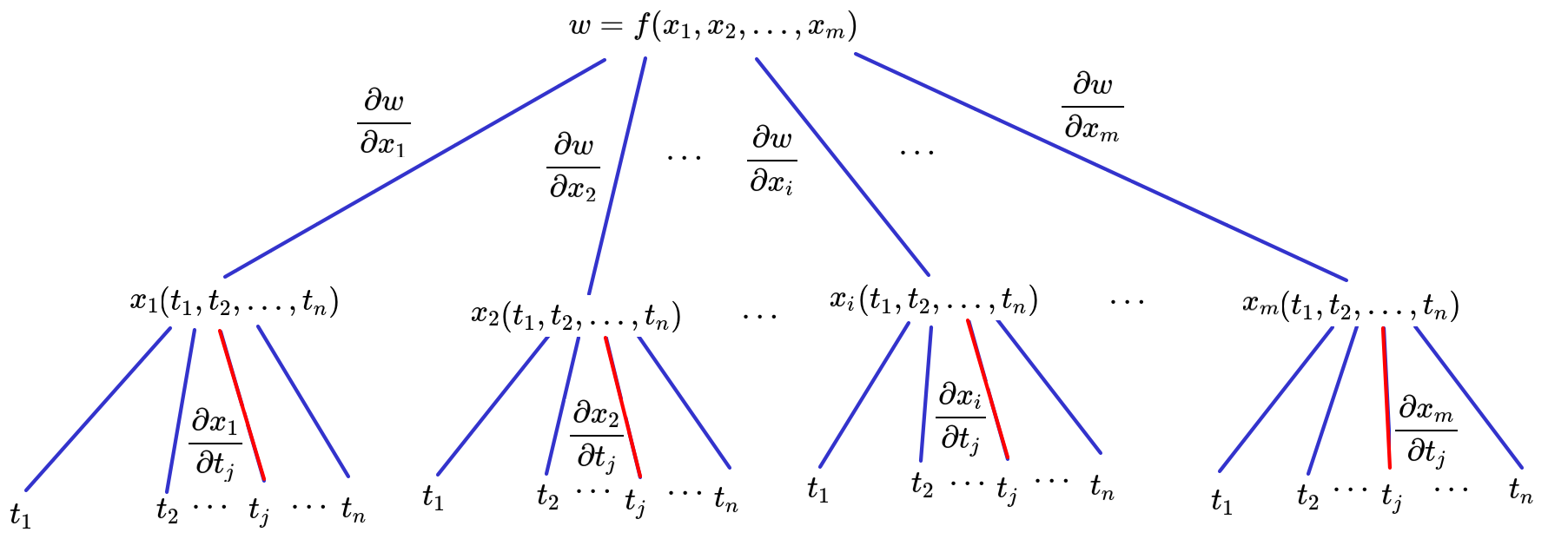
For Those Who Like Sigma Notation
If you like, you may write out the general chain rule in sigma notation. $$ \frac{\partial w}{\partial t_j}=\sum_{i=1}^{m}\frac{\partial w}{\partial x_i}\frac{\partial x_i}{\partial t_j} $$
Example
Calculate $\displaystyle \frac{\partial w}{\partial u}$ and $\displaystyle \frac{\partial w}{\partial v}$ if $$ w=f(x,y,z)=3x^2-2xy+4z^2 $$ where $x=x(u,v)=e^u\sin v,$ $y=y(u,v)=e^u\cos v,$ and $z=z(u,v)=e^u.$
The chain rule in this case is
$$
\frac{\partial w}{\partial u}=\frac{\partial w}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial u}
\,\,\,\,\,\,\,\mbox{ and }\,\,\,\,\,\,\,
\frac{\partial w}{\partial v}=\frac{\partial w}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial v}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial v}
$$
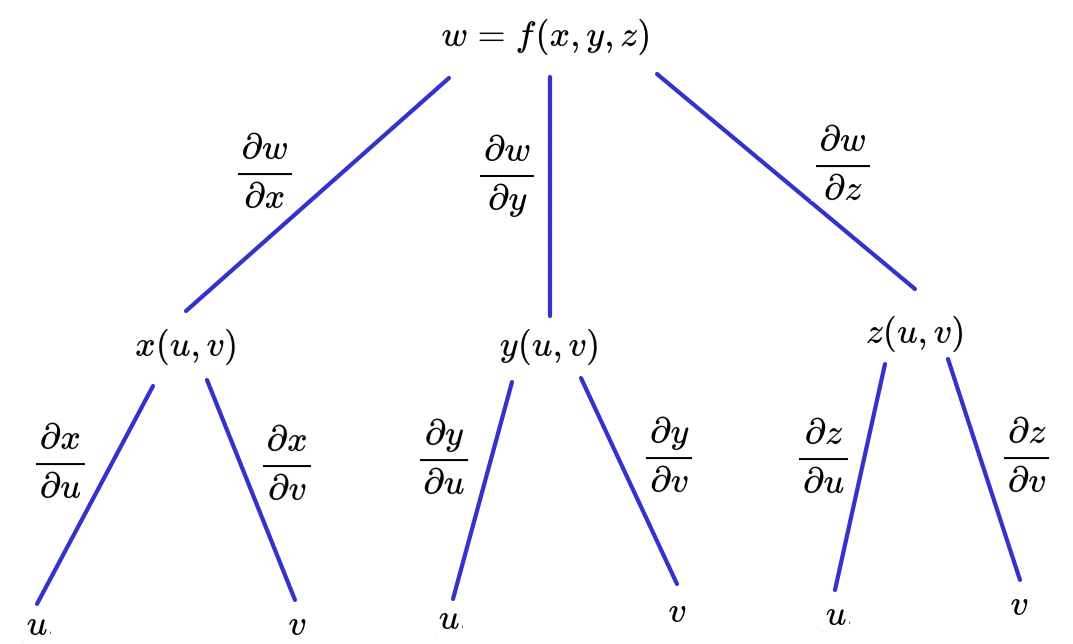 First,
$$
\begin{array}{lll}
\displaystyle \frac{\partial w}{\partial x}&\displaystyle= 6x-2y&\mbox{}\\
\displaystyle \frac{\partial w}{\partial y}&\displaystyle= -2x&\mbox{}\\
\displaystyle \frac{\partial w}{\partial z}&\displaystyle=8z &\mbox{}\\
\end{array}
$$
Then,
$$
\begin{array}{lll}
\displaystyle \frac{\partial w}{\partial u}&\displaystyle=\frac{\partial w}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial u} &\mbox{}\\
\displaystyle &\displaystyle=(6x-2y)e^u \sin v+(-2x)e^u \cos v+(8z)e^u &\mbox{}\\
\displaystyle &\displaystyle=(6e^u\sin v-2e^u\cos v)e^u \sin v+(-2e^u\sin v)e^u \cos v+(8e^u)e^u &\mbox{}\\
\displaystyle &\displaystyle=6e^{2u}\sin^2 v-2e^{2u}\sin v\cos v-2e^{2u}\sin v \cos v+8e^{2u} &\mbox{}\\
\displaystyle &\displaystyle=6e^{2u}\sin^2 v-4e^{2u}\sin v\cos v+8e^{2u} &\mbox{}\\
\displaystyle &\displaystyle=2e^{2u}\left(3\sin^2 v-2\sin v\cos v+4\right) &\mbox{}\\
\end{array}
$$
and
$$
\begin{array}{lll}
\displaystyle \frac{\partial w}{\partial v}&\displaystyle= \frac{\partial w}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial v}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial v}&\mbox{}\\
\displaystyle &\displaystyle= (6x-2y)e^u \cos v+(-2x)(-e^u \sin v)+(8z)\cdot 0&\mbox{}\\
\displaystyle &\displaystyle= (6e^u\sin v-2e^u\cos v)e^u \cos v+(-2e^u\sin v)(-e^u \sin v)&\mbox{}\\
\displaystyle &\displaystyle= 6e^{2u}\sin v\cos v-2e^{2u}\cos^2 v+2e^{2u}\sin^2 v&\mbox{}\\
\displaystyle &\displaystyle= e^{2u}(3\cdot 2\sin v\cos v-2(\cos^2 v-\sin^2 v))&\mbox{}\\
\displaystyle &\displaystyle= e^{2u}(3\sin 2v-2\cos 2v)&\mbox{}\\
\end{array}
$$
First,
$$
\begin{array}{lll}
\displaystyle \frac{\partial w}{\partial x}&\displaystyle= 6x-2y&\mbox{}\\
\displaystyle \frac{\partial w}{\partial y}&\displaystyle= -2x&\mbox{}\\
\displaystyle \frac{\partial w}{\partial z}&\displaystyle=8z &\mbox{}\\
\end{array}
$$
Then,
$$
\begin{array}{lll}
\displaystyle \frac{\partial w}{\partial u}&\displaystyle=\frac{\partial w}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial u} &\mbox{}\\
\displaystyle &\displaystyle=(6x-2y)e^u \sin v+(-2x)e^u \cos v+(8z)e^u &\mbox{}\\
\displaystyle &\displaystyle=(6e^u\sin v-2e^u\cos v)e^u \sin v+(-2e^u\sin v)e^u \cos v+(8e^u)e^u &\mbox{}\\
\displaystyle &\displaystyle=6e^{2u}\sin^2 v-2e^{2u}\sin v\cos v-2e^{2u}\sin v \cos v+8e^{2u} &\mbox{}\\
\displaystyle &\displaystyle=6e^{2u}\sin^2 v-4e^{2u}\sin v\cos v+8e^{2u} &\mbox{}\\
\displaystyle &\displaystyle=2e^{2u}\left(3\sin^2 v-2\sin v\cos v+4\right) &\mbox{}\\
\end{array}
$$
and
$$
\begin{array}{lll}
\displaystyle \frac{\partial w}{\partial v}&\displaystyle= \frac{\partial w}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial v}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial v}&\mbox{}\\
\displaystyle &\displaystyle= (6x-2y)e^u \cos v+(-2x)(-e^u \sin v)+(8z)\cdot 0&\mbox{}\\
\displaystyle &\displaystyle= (6e^u\sin v-2e^u\cos v)e^u \cos v+(-2e^u\sin v)(-e^u \sin v)&\mbox{}\\
\displaystyle &\displaystyle= 6e^{2u}\sin v\cos v-2e^{2u}\cos^2 v+2e^{2u}\sin^2 v&\mbox{}\\
\displaystyle &\displaystyle= e^{2u}(3\cdot 2\sin v\cos v-2(\cos^2 v-\sin^2 v))&\mbox{}\\
\displaystyle &\displaystyle= e^{2u}(3\sin 2v-2\cos 2v)&\mbox{}\\
\end{array}
$$

Example
Use the general chain rule to create a tree diagram for the case when $w = f (x, y),$ $x = x(t, u, v),$ and $y = y(t, u, v),$ and write out the formulas for the three partial derivatives of $w.$
Here we have two intermediate variables, $x$ and $y,$ and three independent variables, $t,$ $u,$ and $v.$
So, the tree diagram is as follows.
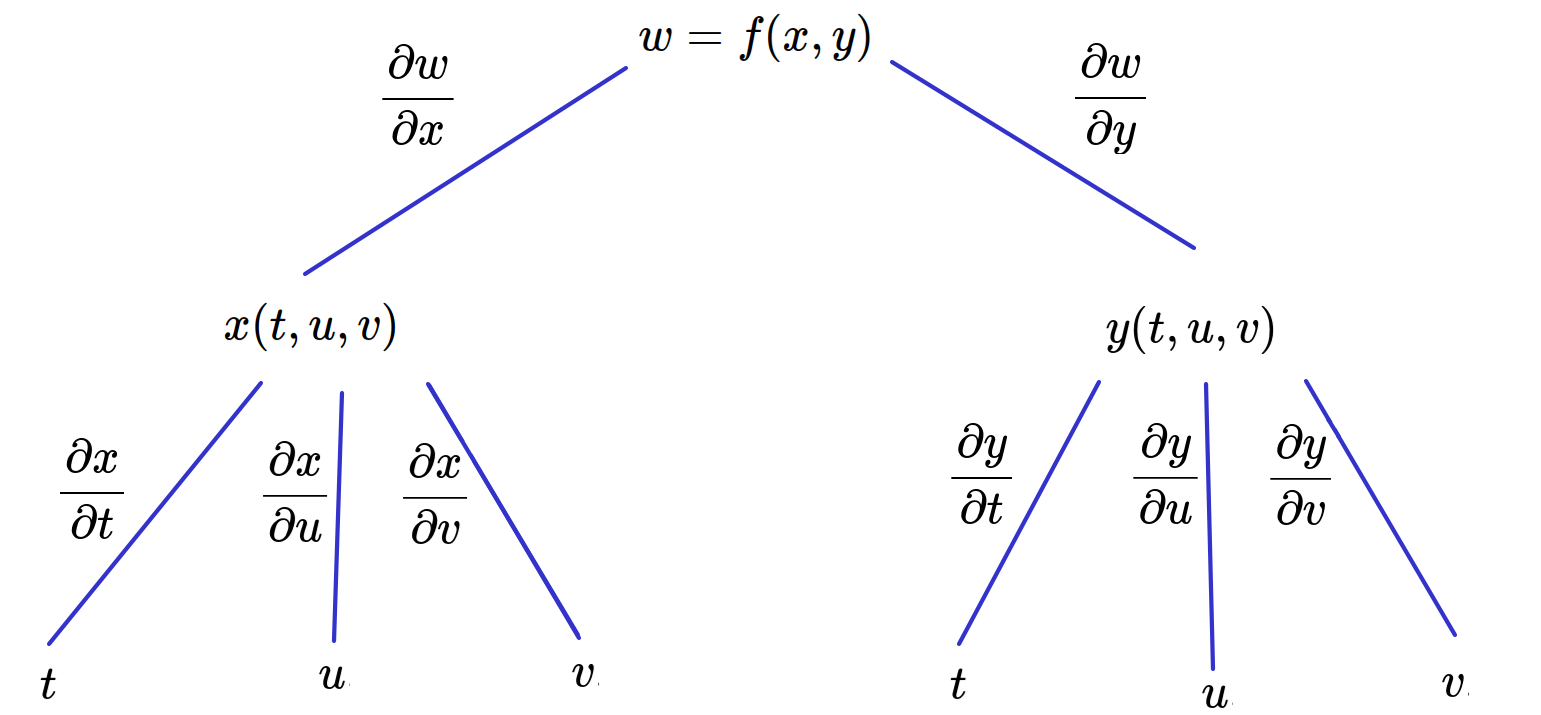
Thus, the three formulas are $$ \begin{array}{lll} \displaystyle \frac{\partial w}{\partial t}&\displaystyle=\frac{\partial w}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial t} &\mbox{}\\ \displaystyle \frac{\partial w}{\partial u}&\displaystyle= \frac{\partial w}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial u}&\mbox{}\\ \displaystyle \frac{\partial w}{\partial v}&\displaystyle= \frac{\partial w}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial v}&\mbox{}\\ \end{array} $$
So, the tree diagram is as follows.

Thus, the three formulas are $$ \begin{array}{lll} \displaystyle \frac{\partial w}{\partial t}&\displaystyle=\frac{\partial w}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial t} &\mbox{}\\ \displaystyle \frac{\partial w}{\partial u}&\displaystyle= \frac{\partial w}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial u}&\mbox{}\\ \displaystyle \frac{\partial w}{\partial v}&\displaystyle= \frac{\partial w}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial v}&\mbox{}\\ \end{array} $$
The Chain Rule in Vector Form
We may write the equation $$ \frac{\partial f}{\partial t_j}=\frac{\partial f}{\partial x_1}\frac{\partial x_1}{\partial t_j}+\frac{\partial f}{\partial x_2}\frac{\partial x_2}{\partial t_j}+\cdots+\frac{\partial f}{\partial x_m}\frac{\partial x_m}{\partial t_j} $$ as a dot product of vectors in $\mathbb{R}^m.$ $$ \frac{\partial f}{\partial t_j}= \left\langle\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\ldots,\frac{\partial f}{\partial x_m}\right\rangle \cdot \left\langle\frac{\partial x_1}{\partial t_j},\frac{\partial x_2}{\partial t_j},\ldots,\frac{\partial x_m}{\partial t_j}\right\rangle $$ If we let ${\bf r}(t_1,t_2,\ldots,t_n)=\langle x_1(t_1,t_2,\ldots,t_n),x_2(t_1,t_2,\ldots,t_n),\ldots,x_m(t_1,t_2,\ldots,t_n)\rangle$ be a multivariable vector-valued function, we may write $$ \frac{\partial {\bf r}}{\partial t_j}=\left\langle\frac{\partial x_1}{\partial t_j},\frac{\partial x_2}{\partial t_j},\ldots,\frac{\partial x_m}{\partial t_j}\right\rangle $$ Then, writing $f(x_1,x_2,\ldots,x_m)$ as $f({\bf r}),$ we may write the general chain rule in vector form as $$ \frac{\partial f}{\partial t_j}=\langle f_{x_1}({\bf r}),f_{x_2}({\bf r}),\ldots,f_{x_m}({\bf r})\rangle \cdot \frac{\partial {\bf r}}{\partial t_j} $$
Implicit Differentiation
Recall the notion of implicit differentiation.
A classic example is to find $\displaystyle \frac{dy}{dx}$ for $$x^2+y^2=25.$$ Thinking of $y$ defined implicitly as a function of $x,$ we differentiate both sides with respect to $x,$ $$ \begin{array}{lll} &x^2+y^2=25&\\ \implies & \displaystyle \frac{d}{dx}(x^2+y^2)=\frac{d}{dx}25&\mbox{differentiate both sides with respect to $x$}\\ \implies & \displaystyle \frac{d}{dx}x^2+\frac{d}{dx}y^2=0&\mbox{}\\ \implies & \displaystyle 2x+2y\frac{dy}{dx}=0&\mbox{by the Chain Rule ($y$ is a function of $x$)}\\ \implies & \displaystyle \frac{dy}{dx}=-\frac{x}{y}&\mbox{solving for $\displaystyle \frac{dy}{dx}$}\\ \end{array} $$
Implicit Differentiation
With the formula $ \displaystyle \frac{dy}{dx}=-\frac{x}{y} $ we may now determine the slope of the tangent line at at any point $(x,y)$ on $x^2+y^2=25.$ For example, at $(x,y)=(3,4)$ we have $\displaystyle \frac{dy}{dx}=-\frac{x}{y}=-\frac{3}{4}.$

Implicit Differentiation
We shall now use the general chain rule to perform implicit differentiation from the perspective of partial derivatives. The advantage of this new perspective is that it will give us a closed-form expression for $\displaystyle \frac{dy}{dx}$ from an implicitly defined curve $f(x,y)=c$ (a level curve).
We write $z=f(x,y)=f(x,y(x))=c$ and treat $x$ as the independent variable.
Taking the derivative with respect to $x$ on both sides and applying the Chain Rule for Two Intermediate Variables and One Independent Variable, $$ \frac{dz}{dx}=\frac{\partial z}{\partial x}\frac{dx}{dx}+\frac{\partial z}{\partial y}\frac{dy}{dx}=\frac{d}{dx}c $$ Since $\displaystyle \frac{d}{dx}c=0$ and $\displaystyle \frac{dx}{dx}=1,$ the above becomes $$ \frac{\partial z}{\partial x}+\frac{\partial z}{\partial y}\frac{dy}{dx}=0 $$ Solving for $\displaystyle \frac{dy}{dx}$ we get...
Implicit Differentiation
For a curve implicitly defined by $z=f(x,y)=c,$ $$ \frac{dy}{dx}=-\frac{\displaystyle \frac{\partial z}{\partial x}}{\displaystyle \frac{\partial z}{\partial y}}=-\frac{f_x}{f_y} $$
Example
For the example $z=f(x,y)=x^2+y^2=25,$ use the above techniques to find $\displaystyle \frac{dy}{dx}$
$$
\frac{dy}{dx}=-\frac{f_x}{f_y}=-\frac{2x}{2y}=-\frac{x}{y}
$$
Example
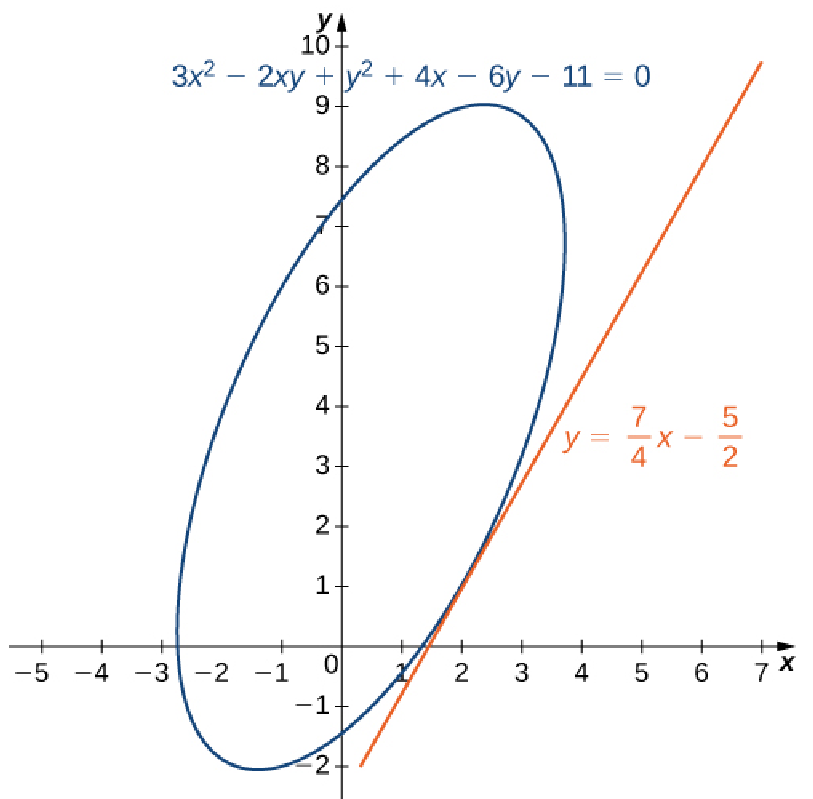
Calculate $\displaystyle \frac{dy}{dx}$ if $y$ is defined implicitly as a function of $x$ via the equation $$3x^2 - 2xy + y^2 + 4x - 6y - 11 = 0.$$ Find the equation of the tangent line to the graph of this curve at point $(2, 1).$
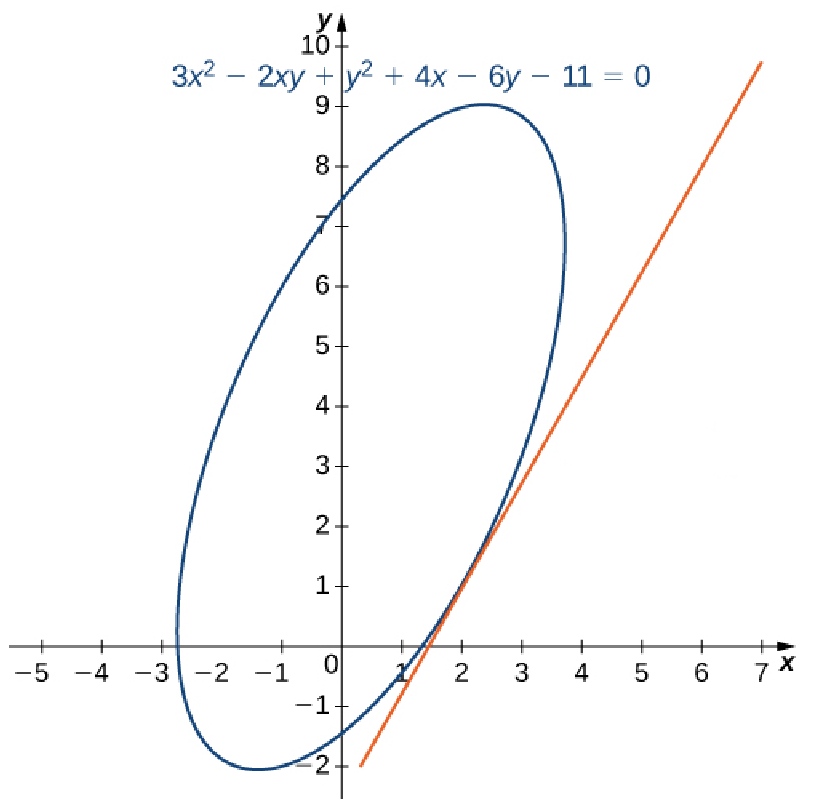
We first find the slope of the tangent line at $(2,1).$
$$
\frac{dy}{dx}=-\frac{f_x}{f_y}=-\frac{6x-2y+4}{-2x+2y-6}
$$
So, the slope of the tangent line at $(2,1)$ is
$$
\frac{dy}{dx}\Bigr|_{(x,y)=(2,1)}=-\frac{6(2)-2(1)+4}{-2(2)+2(1)-6}=\frac{7}{4}
$$
The tangent line in point slope form is then
$$
y-1=\frac{7}{4}(x-2)
$$
so that
$$
y=\frac{7}{4}x-\frac{10}{4}=\frac{7}{4}x-\frac{5}{2}
$$

Implicit Differentiation
The above technique applies to functions of more than two variables. For example, for (level!) surfaces implicitly defined by $w=f(x,y,z)=c,$ we may assume that $z$ is implicitly a function of $x$ and $y.$ That is, $$ w=f(x,y,z(x,y))=c $$ Taking the partial derivative with respect to $x$ and $y$ to both sides and applying the chain rule for two independent variables (and three intermediate variables), $$ \frac{\partial w}{\partial x}=\frac{\partial w}{\partial x}\frac{\partial x}{\partial x}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial x}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial x}=\frac{\partial}{\partial x}c \,\,\,\,\,\,\,\mbox{ and }\,\,\,\,\,\,\, \frac{\partial w}{\partial y}=\frac{\partial w}{\partial x}\frac{\partial x}{\partial y}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial y}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial y}=\frac{\partial}{\partial y}c $$ Now $\displaystyle \frac{\partial x}{\partial x}=1,$ $\displaystyle \frac{\partial y}{\partial y}=1,$ $\displaystyle \frac{\partial}{\partial x}y=0,$ and $\displaystyle \frac{\partial}{\partial y}x=0,$ thus the above gives us $$ \frac{\partial w}{\partial x}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial x}=0 \,\,\,\,\,\,\,\mbox{ and }\,\,\,\,\,\,\, \frac{\partial w}{\partial y}+\frac{\partial w}{\partial z}\frac{\partial z}{\partial y}=0 $$ We may now solve for $\displaystyle \frac{\partial z}{\partial x}$ and $\displaystyle \frac{\partial z}{\partial y}$...
Implicit Differentiation
For a surface implicitly defined by $w=f(x,y,z)=c,$ $$ \frac{\partial z}{\partial x}=-\frac{\displaystyle \frac{\partial w}{\partial x}}{\displaystyle \frac{\partial w}{\partial z}}=-\frac{f_x}{f_z} \,\,\,\,\,\,\,\mbox{ and }\,\,\,\,\,\,\, \frac{\partial z}{\partial y}=-\frac{\displaystyle \frac{\partial w}{\partial y}}{\displaystyle \frac{\partial w}{\partial z}}=-\frac{f_y}{f_z} $$
Example
Find $\displaystyle \frac{\partial z}{\partial x}$ and $\displaystyle \frac{\partial z}{\partial y}$ given $x^2 e^y - yze^x = 0.$
$$
\begin{array}{lll}
\displaystyle \frac{\partial z}{\partial x}&\displaystyle= -\frac{f_x}{f_z} &\mbox{}\\
\displaystyle &\displaystyle= -\frac{2xe^y-yze^x}{-ye^x}&\mbox{}\\
\displaystyle &\displaystyle= \frac{2xe^y-yze^x}{ye^x}&\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial z}{\partial y}&\displaystyle= -\frac{f_y}{f_z} &\mbox{}\\
\displaystyle &\displaystyle= -\frac{x^2e^y-ze^x}{-ye^x} &\mbox{}\\
\displaystyle &\displaystyle= \frac{x^2e^y-ze^x}{ye^x} &\mbox{}\\
\end{array}
$$