We know how to compute the rate of change of a function of a single variable.
For functions of multiple variables, the idea of a function's rate of change depends a great deal more upon context.
A function $f$'s rate of change at a point $(x,y)$ or $(x,y,z)$ isn't clear on its since the rate of change depends on the direction of change in either the plane or space.
Partial derivatives help us to simplify the problem by considering a multivariate function's rate of change in a single direction.
Partial Derivatives with Two Variables
Let $f (x, y)$ be a function of two variables.
Then the partial derivative of $f$ with respect to $x,$ written as $\displaystyle \frac{\partial f}{\partial x}$ or $f_x,$ is defined as $$ \frac{\partial f}{\partial x}=\lim_{h \rightarrow 0}\frac{f(x+h,y)-f(x,y)}{h} $$ and the partial derivative of $f$ with respect to $y,$ written as $\displaystyle \frac{\partial f}{\partial y}$ or $f_y,$ is defined as $$ \frac{\partial f}{\partial y}=\lim_{h \rightarrow 0}\frac{f(x,y+h)-f(x,y)}{h} $$
Partial Derivatives with Two Variables
$\displaystyle \frac{\partial f}{\partial x}=f_x(x,y)$ is the derivative of $f$ with respect to $x$ holding $y$ constant.
$\displaystyle \frac{\partial f}{\partial y}=f_y(x,y)$ is the derivative of $f$ with respect to $y$ holding $x$ constant.
Partial Derivatives with Two Variables
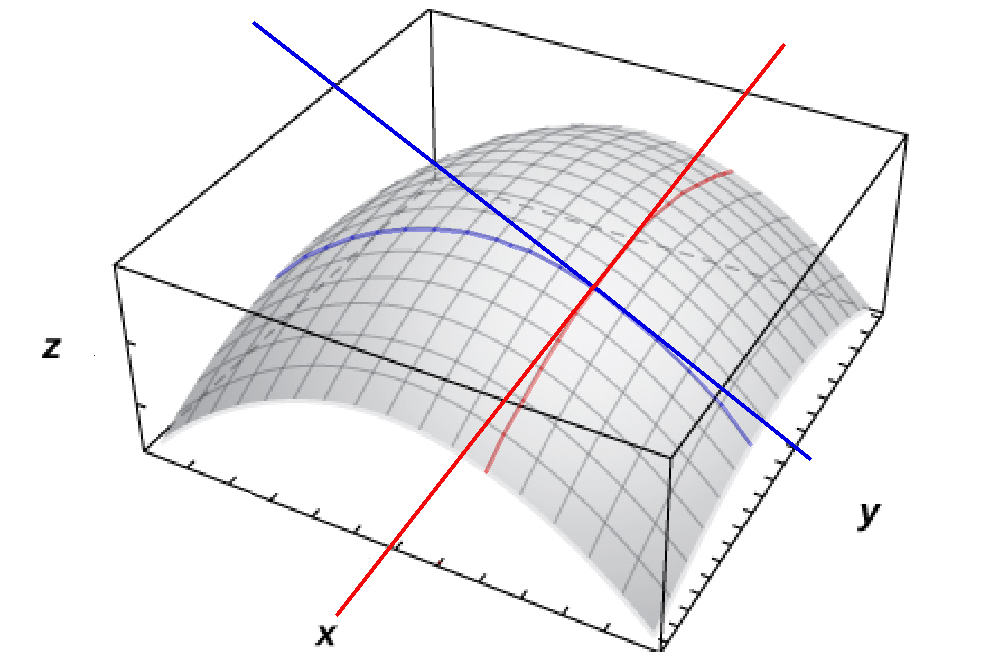
$\displaystyle \frac{\partial f}{\partial x}=f_x(x,y)$ is the slope of the tangent line in the positive $x$ direction.
$\displaystyle \frac{\partial f}{\partial y}=f_y(x,y)$ is the slope of the tangent line in the positive $y$ direction.
Partial Derivatives with Two Variables

At the point $(x_0,y_0)$ in the plane,
$\displaystyle \frac{\partial f}{\partial x}(x_0,y_0)=f_x(x_0,y_0)=\frac{d}{dx}f(x,y_0)\Bigr\rvert_{x=x_0}$
$\displaystyle \frac{\partial f}{\partial y}(x_0,y_0)=f_y(x_0,y_0)=\frac{d}{dy}f(x_0,y)\Bigr\rvert_{y=y_0}$
We can think of partial derivatives as ordinary derivatives along the vertical traces.
Example
Use the definition of the partial derivative as a limit to calculate $\displaystyle \frac{\partial f}{\partial x}$ and $\displaystyle \frac{\partial f}{\partial y}$ for $$f (x, y) = 4x^2 + 2xy - y^2 + 3x - 2y + 5$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial x}&\displaystyle=\lim_{h \rightarrow 0}\frac{f(x+h,y)-f(x,y)}{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{4(x+h)^2 + 2(x+h)y - y^2 + 3(x+h) - 2y + 5-(4x^2 + 2xy - y^2 + 3x - 2y + 5)}{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{4(x^2+2xh+h^2) + 2xy+2hy - y^2 + 3x+3h - 2y + 5-4x^2 - 2xy + y^2 - 3x + 2y - 5}{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{4x^2+8xh+4h^2 +2hy +3h -4x^2 }{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{8xh+4h^2 +2hy +3h}{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}(8x+4h +2y +3) &\mbox{}\\
\displaystyle &\displaystyle=8x +2y +3 &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial y}&\displaystyle=\lim_{h \rightarrow 0}\frac{f(x,y+h)-f(x,y)}{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{4x^2 + 2x(y+h) - (y+h)^2 + 3x - 2(y+h) + 5-(4x^2 + 2xy - y^2 + 3x - 2y + 5)}{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{4x^2 + 2xy+2xh - (y^2+2yh+h^2) + 3x - 2y-2h + 5-4x^2 - 2xy + y^2 - 3x + 2y - 5}{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{2xh - (y^2+2yh+h^2) -2h + y^2 }{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{2xh - y^2-2yh-h^2 -2h + y^2 }{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}\frac{2xh -2yh-h^2 -2h }{h} &\mbox{}\\
\displaystyle &\displaystyle=\lim_{h \rightarrow 0}(2x -2y-h +2 ) &\mbox{}\\
\displaystyle &\displaystyle=2x -2y -2 &\mbox{}\\
\end{array}
$$
Partial Derivatives with Two Variables
For $f (x, y) = 4x^2 + 2xy - y^2 + 3x - 2y + 5,$ we saw that $$ \frac{\partial f}{\partial x}=f_x(x,y)= 8x + 2y + 3\,\,\,\, \mbox{ and }\,\,\,\, \frac{\partial f}{\partial y}=f_y(x,y) = 2x -2y- 2$$ From this example, it is clear that computing partial derivatives is essentially the same process as computing ordinary derivatives.
When differentiating with respect to a particular variable, we treat all other variables as constants.
Example
Calculate $\displaystyle \frac{\partial f}{\partial x}$ and $\displaystyle \frac{\partial f}{\partial y}$ for the function $f (x, y) = \tan(x^3 - 3x^2 y^2 + 2y^4)$ by holding the opposite variable constant, then differentiating.
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial x}&\displaystyle= \frac{\partial }{\partial x}\left(\tan(x^3 - 3x^2 y^2 + 2y^4)\right)&\mbox{}\\
\displaystyle &\displaystyle= \sec^2(x^3 - 3x^2 y^2 + 2y^4)\frac{\partial }{\partial x}\left(x^3 - 3x^2 y^2 + 2y^4\right)&\mbox{Chain Rule}\\
\displaystyle &\displaystyle= \sec^2(x^3 - 3x^2 y^2 + 2y^4)\left(3x^2 - 6x y^2\right)&\mbox{}\\
\displaystyle &\displaystyle= \left(3x^2 - 6x y^2\right)\sec^2(x^3 - 3x^2 y^2 + 2y^4)&\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial y}&\displaystyle= \frac{\partial }{\partial y}\left(\tan(x^3 - 3x^2 y^2 + 2y^4)\right)&\mbox{}\\
\displaystyle &\displaystyle= \sec^2(x^3 - 3x^2 y^2 + 2y^4)\frac{\partial }{\partial y}\left(x^3 - 3x^2 y^2 + 2y^4\right)&\mbox{Chain Rule}\\
\displaystyle &\displaystyle= \sec^2(x^3 - 3x^2 y^2 + 2y^4)\left(-6x^2y+8y^3\right)&\mbox{}\\
\displaystyle &\displaystyle= \left(-6x^2y+8y^3\right)\sec^2(x^3 - 3x^2 y^2 + 2y^4)&\mbox{}\\
\end{array}
$$
Example
For $f(x,y)=2-x^2-y^2,$ use shortcut rules to compute $\displaystyle \frac{\partial f}{\partial x}$ and $\displaystyle \frac{\partial f}{\partial y}.$
Then, compute $\displaystyle \frac{\partial f}{\partial x}(1,-1)$ and $\displaystyle \frac{\partial f}{\partial y}(1,-1)$ and interpret the meaning of these values.
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial x}&\displaystyle= \frac{\partial }{\partial x}(2-x^2-y^2)&\mbox{}\\
\displaystyle &\displaystyle=-2x &\mbox{}\\
\end{array}
$$
and
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial x}&\displaystyle= \frac{\partial }{\partial y}(2-x^2-y^2)&\mbox{}\\
\displaystyle &\displaystyle=-2y &\mbox{}\\
\end{array}
$$
Thus $$\displaystyle \frac{\partial f}{\partial x}(1,-1)=-2(1)=-2$$
and
$$\displaystyle \frac{\partial f}{\partial y}(1,-1)=-2(-1)=2$$
We interpret $f_x(1,-1)=-2$ to mean that when travelling in the positive $x$ direction at $(1,-1),$ the function
values are decreasing at a rate of $2.$
We interpret $f_y(1,-1)=2$ to mean that when travelling in the positive $y$ direction at $(1,-1),$ the function values are increasing at a rate of $2.$
We interpret $f_y(1,-1)=2$ to mean that when travelling in the positive $y$ direction at $(1,-1),$ the function values are increasing at a rate of $2.$
Partial Derivatives with Two Variables
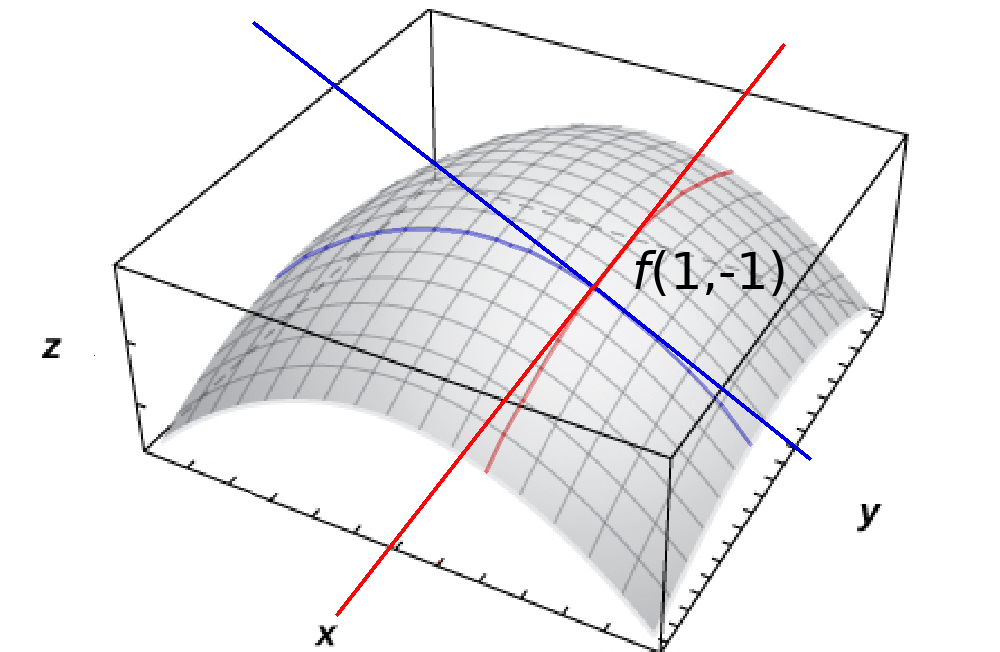
For $f(x,y)=2-x^2-y^2$ below,
$\displaystyle \frac{\partial f}{\partial x}(1,-1)=f_x(1,-1)=-2(1)=-2$
$\displaystyle \frac{\partial f}{\partial y}(1,-1)=f_y(1,-1)=-2(-1)=2$
Partial Derivatives with Two Variables

For $f(x,y)=2-x^2-y^2$ below,
$\displaystyle \frac{\partial f}{\partial x}(1,-1)=\frac{d}{dx}f(x,-1)\Bigr\rvert_{x=1}=-2$
$\displaystyle \frac{\partial f}{\partial y}(1,-1)=\frac{d}{dy}f(1,y)\Bigr\rvert_{y=-1}=2$
We can think of partial derivatives as ordinary derivatives along the vertical traces.
Example
Use the contour diagram for $f (x, y) = y^{2}-x^{2}+4y+2x+3$ for $f(x,y)=0$, $\pm 1,$ $\pm 4,$ $\pm 9,$ and $\pm 16$ to estimate $\displaystyle \frac{\partial f}{\partial x}(1,1)$ and $f_y(1,1).$ Then, compare your estimate with the exact values.
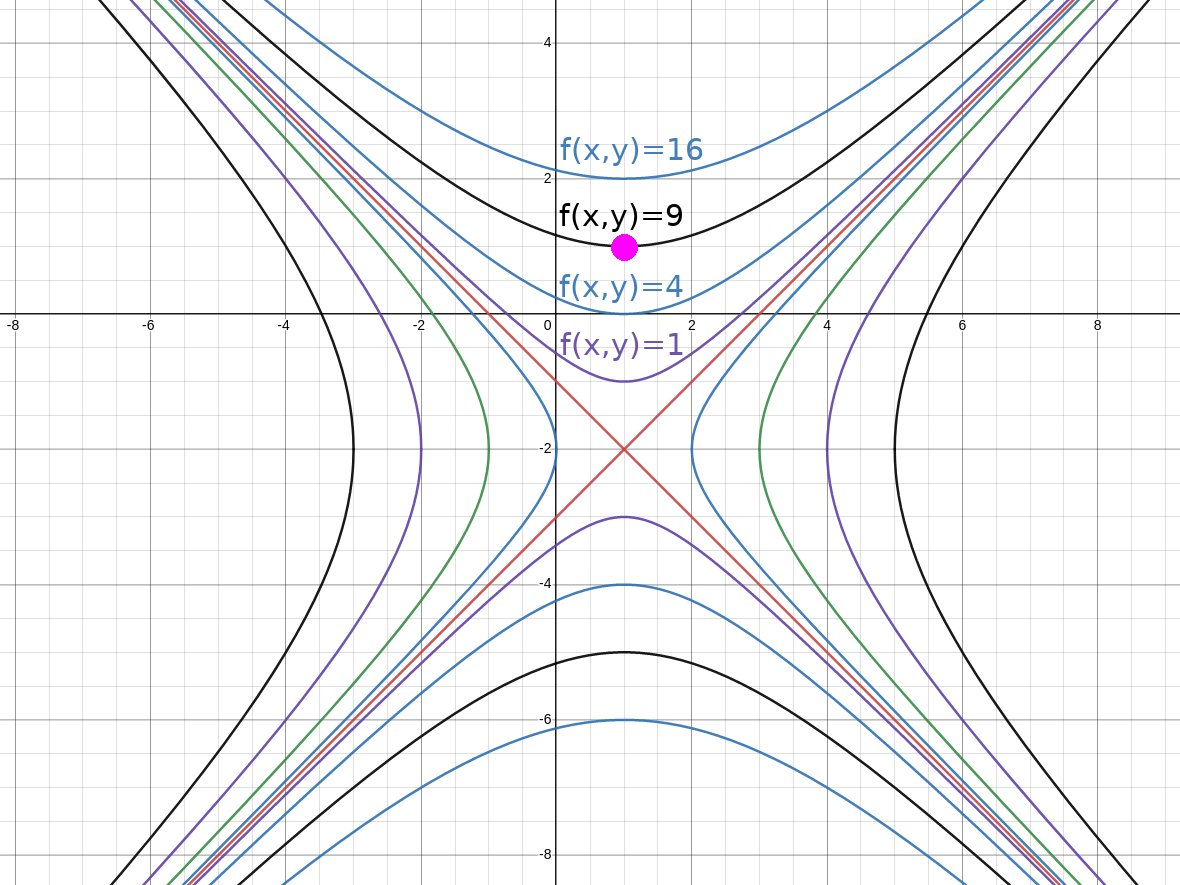

We first approximate $\displaystyle \frac{\partial f}{\partial x}(1,1),$
From the contour diagram, the "forward difference" is $$ \begin{array}{lll} \displaystyle \frac{\partial f}{\partial x}(1,1) &\displaystyle\approx \frac{f(1+\color{blue}{\Delta x},1)-f(1,1)}{\color{blue}{\Delta x}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{f(1+\color{blue}{2.25},1)-f(1,1)}{\color{blue}{2.25}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{f(3.25,1)-f(1,1)}{\color{blue}{2.25}}&\mbox{}\\ \displaystyle &\displaystyle\approx \frac{4-9}{\color{blue}{2.25}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{-5}{2.25}&\mbox{}\\ \displaystyle &\displaystyle= -2.\overline{2}&\mbox{}\\ \end{array} $$ and the "backward difference" is $$ \begin{array}{lll} \displaystyle \frac{\partial f}{\partial x}(1,1) &\displaystyle\approx \frac{f(1+\color{darkorange}{\Delta x},1)-f(1,1)}{\color{darkorange}{\Delta x}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{f(1+(\color{darkorange}{-2.25}),1)-f(1,1)}{\color{darkorange}{-2.25}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{f(-1.25,1)-f(1,1)}{\color{darkorange}{-2.25}}&\mbox{}\\ \displaystyle &\displaystyle\approx \frac{4-9}{\color{darkorange}{-2.25}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{-5}{-2.25}&\mbox{}\\ \displaystyle &\displaystyle= 2.\overline{2}&\mbox{}\\ \end{array} $$ The "centered difference" is the average of the forward and backward differences for a better approximation. Thus, $$ \displaystyle \frac{\partial f}{\partial x}(1,1)\approx\frac{-2.\overline{2}+2.\overline{2}}{2}=0 $$
We compare the above approximation to the exact value: $\displaystyle \frac{\partial f}{\partial x}=-2x+2$ so that $\displaystyle \frac{\partial f}{\partial x}(1,1)=0.$
In this case, the approximation matches the exact value.
Now, we approximate $\displaystyle \frac{\partial f}{\partial y}(1,1).$
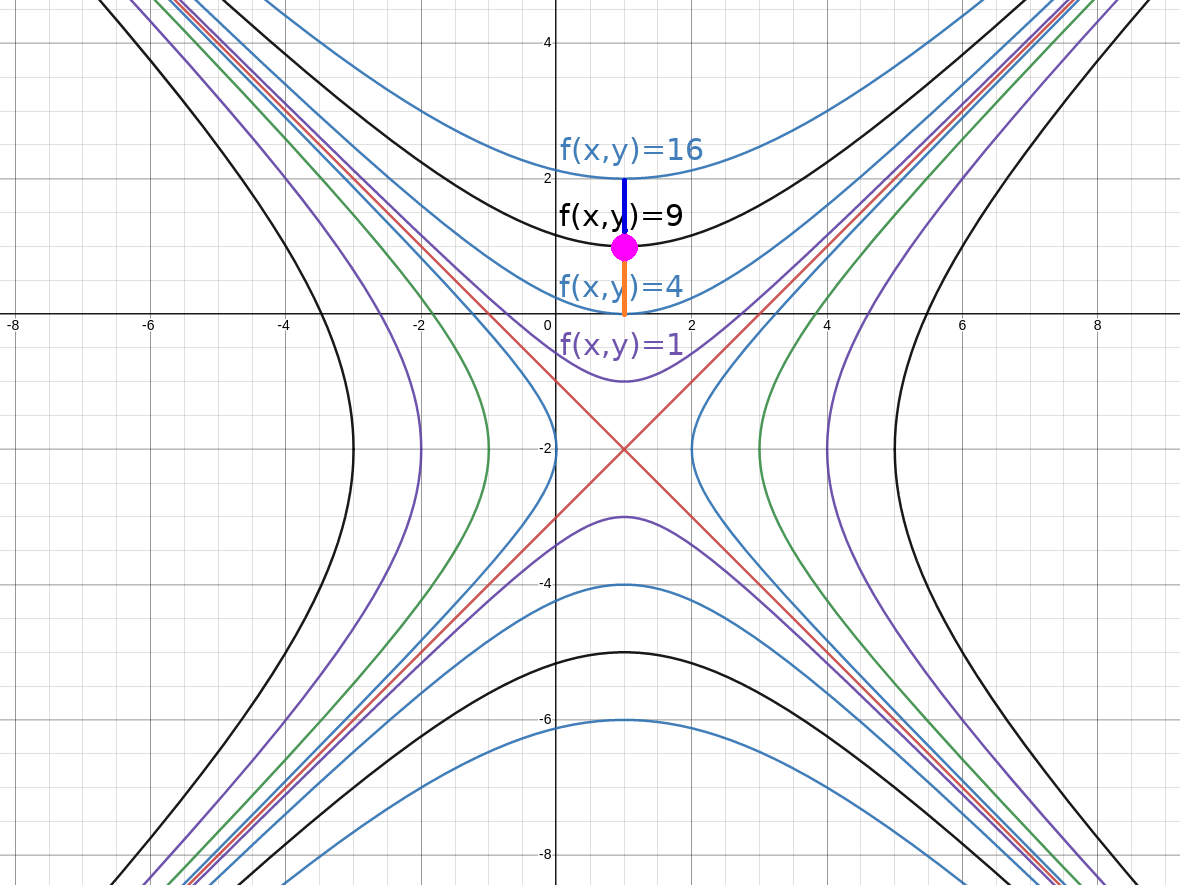
From the contour diagram, the "forward difference" is $$ \begin{array}{lll} \displaystyle \frac{\partial f}{\partial y}(1,1) &\displaystyle\approx \frac{f(1,1+\color{blue}{\Delta y})-f(1,1)}{\color{blue}{\Delta y}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{f(1,1+\color{blue}{1})-f(1,1)}{\color{blue}{1}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{f(1,2)-f(1,1)}{\color{blue}{1}}&\mbox{}\\ \displaystyle &\displaystyle = \frac{16-9}{\color{blue}{1}}&\mbox{}\\ \displaystyle &\displaystyle= 7&\mbox{}\\ \end{array} $$ and the "backward difference" is $$ \begin{array}{lll} \displaystyle \frac{\partial f}{\partial y}(1,1) &\displaystyle\approx \frac{f(1,1+\color{darkorange}{\Delta y})-f(1,1)}{\color{darkorange}{\Delta y}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{f(1,1+(\color{darkorange}{-1}))-f(1,1)}{\color{darkorange}{-1}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{f(1,0)-f(1,1)}{\color{darkorange}{-1}}&\mbox{}\\ \displaystyle &\displaystyle\approx \frac{4-9}{\color{darkorange}{-1}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{-5}{-1}&\mbox{}\\ \displaystyle &\displaystyle= 5&\mbox{}\\ \end{array} $$ The "centered difference" is the average of the forward and backward differences for a better approximation. Thus, $$ \displaystyle \frac{\partial f}{\partial x}(1,1)\approx\frac{5+7}{2}=6. $$ We compare the above approximation to the exact value $\displaystyle \frac{\partial f}{\partial y}=2y+4$ so that $\displaystyle \frac{\partial f}{\partial x}(1,1)=6.$
Partial Derivatives with Three Variables
Let $f (x, y,z)$ be a function of three variables.
Then the partial derivative of $f$ with respect to $x,$ written as $\displaystyle \frac{\partial f}{\partial x}$ or $f_x,$ is defined as $$ \frac{\partial f}{\partial x}=\lim_{h \rightarrow 0}\frac{f(x+h,y,z)-f(x,y,z)}{h}, $$ the partial derivative of $f$ with respect to $y,$ written as $\displaystyle \frac{\partial f}{\partial y}$ or $f_y,$ is defined as $$ \frac{\partial f}{\partial y}=\lim_{h \rightarrow 0}\frac{f(x,y+h,z)-f(x,y,z)}{h}, $$ and the partial derivative of $f$ with respect to $z,$ written as $\displaystyle \frac{\partial f}{\partial z}$ or $f_z,$ is defined as $$ \frac{\partial f}{\partial z}=\lim_{h \rightarrow 0}\frac{f(x,y,z+h)-f(x,y,z)}{h} $$
Partial Derivatives with Two Variables
$\displaystyle \frac{\partial f}{\partial x}=f_x(x,y,z)$ is the derivative of $f$ with respect to $x$ holding $y$ and $z$ constant.
$\displaystyle \frac{\partial f}{\partial y}=f_y(x,y,z)$ is the derivative of $f$ with respect to $y$ holding $x$ and $z$ constant.
$\displaystyle \frac{\partial f}{\partial z}=f_z(x,y,z)$ is the derivative of $f$ with respect to $y$ holding $x$ and $y$ constant.
Partial Derivatives with Three Variables
Just as the two-variable case, computing partial derivatives for a function of three variables is essentially the same process as computing ordinary derivatives.
When differentiating with respect to a particular variable, we treat all other variables as constants.
Partial Derivatives with Three Variables
Calculate $\displaystyle \frac{\partial f}{\partial x},$ $\displaystyle \frac{\partial f}{\partial y},$ and $\displaystyle \frac{\partial f}{\partial z}$ for the function $$f(x, y, z) = \sin(x^2 y - z)+ \cos(x^2 - yz)$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial x}&\displaystyle=\frac{\partial }{\partial x}(\sin(x^2 y - z)+ \cos(x^2 - yz)) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial }{\partial x}\sin(x^2 y - z)+ \frac{\partial }{\partial x}\cos(x^2 - yz) &\mbox{}\\
\displaystyle &\displaystyle=\cos(x^2 y - z)\frac{\partial }{\partial x}(x^2 y - z)- \sin(x^2 - yz)\frac{\partial }{\partial x}(x^2-yz) &\mbox{}\\
\displaystyle &\displaystyle=\cos(x^2 y - z)(2x y)- \sin(x^2 - yz)(2x) &\mbox{}\\
\displaystyle &\displaystyle=2x[y\cos(x^2 y - z)- \sin(x^2 - yz)] &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial y}&\displaystyle=\frac{\partial }{\partial y}(\sin(x^2 y - z)+ \cos(x^2 - yz)) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial }{\partial y}\sin(x^2 y - z)+ \frac{\partial }{\partial y}\cos(x^2 - yz) &\mbox{}\\
\displaystyle &\displaystyle=\cos(x^2 y - z)\frac{\partial }{\partial y}(x^2 y - z)- \sin(x^2 - yz)\frac{\partial }{\partial y}(x^2-yz) &\mbox{}\\
\displaystyle &\displaystyle=\cos(x^2 y - z)(x^2)- \sin(x^2 - yz)(-z) &\mbox{}\\
\displaystyle &\displaystyle=x^2\cos(x^2 y - z)+z \sin(x^2 - yz) &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial f}{\partial z}&\displaystyle=\frac{\partial }{\partial z}(\sin(x^2 y - z)+ \cos(x^2 - yz)) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial }{\partial z}\sin(x^2 y - z)+ \frac{\partial }{\partial z}\cos(x^2 - yz) &\mbox{}\\
\displaystyle &\displaystyle=\cos(x^2 y - z)\frac{\partial }{\partial z}(x^2 y - z)- \sin(x^2 - yz)\frac{\partial }{\partial z}(x^2-yz) &\mbox{}\\
\displaystyle &\displaystyle=\cos(x^2 y - z)(-1)- \sin(x^2 - yz)(-y) &\mbox{}\\
\displaystyle &\displaystyle=-\cos(x^2 y - z)+y \sin(x^2 - yz) &\mbox{}\\
\end{array}
$$
Higher-Order Partial Derivatives
Just as we can take higher order derivatives of a function $y=f(x),$ $$ \frac{d^2f}{dx^2}=\frac{d}{dx}\left(\frac{df}{dx}\right)\\ \frac{d^3f}{dx^3}=\frac{d}{dx}\left(\frac{d^2f}{dx^2}\right)\\ \frac{d^4f}{dx^4}=\frac{d}{dx}\left(\frac{d^3f}{dx^3}\right)\\ \frac{d^5f}{dx^5}=\frac{d}{dx}\left(\frac{d^4f}{dx^4}\right)\\ \vdots $$ we can do the same thing for partial derivatives...
Higher-Order Partial Derivatives
For a two-variable function $f(x,y),$ $$ \begin{array}{cc} \displaystyle\frac{\partial^2f}{\partial x^2}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)\,\,\,\,\,\,&\displaystyle\frac{\partial^2f}{\partial y^2}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)\\ \displaystyle\frac{\partial^3f}{\partial x^3}=\frac{\partial}{\partial x}\left(\frac{\partial^2 f}{\partial x^2}\right)&\displaystyle\frac{\partial^3f}{\partial y^3}=\frac{\partial}{\partial y}\left(\frac{\partial^2 f}{\partial y^2}\right)\\ \displaystyle\frac{\partial^4f}{\partial x^4}=\frac{\partial}{\partial x}\left(\frac{\partial^3 f}{\partial x^3}\right)&\displaystyle\frac{\partial^4f}{\partial y^4}=\frac{\partial}{\partial y}\left(\frac{\partial^3 f}{\partial y^3}\right)\\ \displaystyle\frac{\partial^5f}{\partial x^5}=\frac{\partial}{\partial x}\left(\frac{\partial^4 f}{\partial x^4}\right)&\displaystyle\frac{\partial^4f}{\partial y^4}=\frac{\partial}{\partial y}\left(\frac{\partial^4 f}{\partial y^4}\right)\\ \vdots & \vdots\\ \end{array} $$
For a three-variable function $f(x,y,z),$ $$ \begin{array}{ccc} \displaystyle \frac{\partial^2f}{\partial x^2}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)\,\,\,\,\,\,&\displaystyle\frac{\partial^2f}{\partial y^2}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)\,\,\,\,\,&\displaystyle\frac{\partial^2f}{\partial z^2}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial z}\right)\\ \displaystyle\frac{\partial^3f}{\partial x^3}=\frac{\partial}{\partial x}\left(\frac{\partial^2 f}{\partial x^2}\right)&\displaystyle\frac{\partial^3f}{\partial y^3}=\frac{\partial}{\partial y}\left(\frac{\partial^2 f}{\partial y^2}\right)&\displaystyle\frac{\partial^3f}{\partial z^3}=\frac{\partial}{\partial z}\left(\frac{\partial^2 f}{\partial z^2}\right)\\ \displaystyle\frac{\partial^4f}{\partial x^4}=\frac{\partial}{\partial x}\left(\frac{\partial^3 f}{\partial x^3}\right)&\displaystyle\frac{\partial^4f}{\partial y^4}=\frac{\partial}{\partial y}\left(\frac{\partial^3 f}{\partial y^3}\right)&\displaystyle\frac{\partial^4f}{\partial z^4}=\frac{\partial}{\partial z}\left(\frac{\partial^3 f}{\partial z^3}\right)\\ \displaystyle\frac{\partial^5f}{\partial x^5}=\frac{\partial}{\partial x}\left(\frac{\partial^4 f}{\partial x^4}\right)&\displaystyle\frac{\partial^4f}{\partial y^4}=\frac{\partial}{\partial y}\left(\frac{\partial^4 f}{\partial y^4}\right)&\displaystyle\frac{\partial^4f}{\partial z^4}=\frac{\partial}{\partial z}\left(\frac{\partial^4 f}{\partial z^4}\right)\\ \vdots & \vdots & \vdots\\ \end{array} $$
Other Notations
$$\displaystyle \frac{\partial^2f}{\partial x^2}=f_{xx}$$ $$\displaystyle \frac{\partial^2f}{\partial y^2}=f_{yy}$$ $$\displaystyle \frac{\partial^2f}{\partial z^2}=f_{zz}$$ $$\displaystyle \frac{\partial^3f}{\partial x^3}=f_{xxx}$$ $$\displaystyle \frac{\partial^3f}{\partial y^3}=f_{yyy}$$ $$\displaystyle \frac{\partial^3f}{\partial z^3}=f_{zzz}$$
Example
For $$f (x, y) = \sin(3x - 2y) + \cos(x + 4y)$$ compute $\displaystyle \frac{\partial^2f}{\partial x^2}=f_{xx}$ and $\displaystyle \frac{\partial^2f}{\partial y^2}=f_{yy}.$
$$
\begin{array}{lll}
\displaystyle \frac{\partial^2 f}{\partial x^2}&\displaystyle=\frac{\partial}{\partial x}\left(\frac{\partial}{\partial x}(\sin(3x - 2y) + \cos(x + 4y))\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}\left(\frac{\partial}{\partial x}\sin(3x - 2y) + \frac{\partial}{\partial x}\cos(x + 4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}\left(\cos(3x - 2y)\frac{\partial}{\partial x}(3x-2y) - \sin(x + 4y)\frac{\partial}{\partial x}(x+4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}\left(\cos(3x - 2y)\cdot 3 - \sin(x + 4y)\cdot 1\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}\left(3\cos(3x - 2y) - \sin(x + 4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}(-2\cos(3x - 2y)) - \frac{\partial}{\partial x}(4\sin(x + 4y)) &\mbox{}\\
\displaystyle &\displaystyle=-2\sin(3x - 2y)\frac{\partial}{\partial x}(3x-2y) - 4\cos(x + 4y)\frac{\partial}{\partial x}(x+4y) &\mbox{}\\
\displaystyle &\displaystyle=-2\sin(3x - 2y)\cdot 3 - \cos(x + 4y)\cdot 1 &\mbox{}\\
\displaystyle &\displaystyle=-9\sin(3x - 2y) - \cos(x + 4y) &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial^2 f}{\partial y^2}&\displaystyle=\frac{\partial}{\partial y}\left(\frac{\partial}{\partial y}(\sin(3x - 2y) + \cos(x + 4y))\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}\left(\frac{\partial}{\partial y}\sin(3x - 2y) + \frac{\partial}{\partial y}\cos(x + 4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}\left(\cos(3x - 2y)\frac{\partial}{\partial y}(3x-2y) - \sin(x + 4y)\frac{\partial}{\partial y}(x+4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}\left(\cos(3x - 2y)\cdot (-2) - \sin(x + 4y)\cdot 4\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}\left(-2\cos(3x - 2y) - 4\sin(x + 4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}(-2\cos(3x - 2y)) - \frac{\partial}{\partial y}(4\sin(x + 4y)) &\mbox{}\\
\displaystyle &\displaystyle=2\sin(3x - 2y)\frac{\partial}{\partial y}(3x-2y) - 4\cos(x + 4y)\frac{\partial}{\partial y}(x+4y) &\mbox{}\\
\displaystyle &\displaystyle=2\sin(3x - 2y)\cdot (-2) - 4\cos(x + 4y)\cdot 4 &\mbox{}\\
\displaystyle &\displaystyle=-4\sin(3x - 2y) - 16\cos(x + 4y) &\mbox{}\\
\end{array}
$$
Mixed Partial Derivatives
When we take partial derivatives, there's nothing that says we need to stick to a single variable.
That is, for a function $f(x,y),$ we can take the partial with respect to $x,$ and then take the partial with respect to $y.$
For example, $$ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right), $$ which has the special notation $$ \frac{\partial^2f}{\partial y \, \partial x}=f_{xy} $$
Mixed Partial Derivatives
For a two-variable function $f(x,y),$ $$ \frac{\partial^2f}{\partial x \, \partial y}=f_{yx} $$ $$ \frac{\partial^2f}{\partial y \, \partial x}=f_{xy} $$ Note that for the expression $f_{xy},$ the order is first $x$ and then $y,$ and for the expression $f_{yx},$ the order is first $y$ and then $x.$
Example
For $$f (x, y) = \sin(3x - 2y) + \cos(x + 4y)$$ compute $\displaystyle \frac{\partial^2f}{\partial y \, \partial x}=f_{xy}$ and $\displaystyle \frac{\partial^2f}{\partial x \,\partial y}=f_{yx}.$
$$
\begin{array}{lll}
\displaystyle \frac{\partial^2f}{\partial x \, \partial y}&\displaystyle=\frac{\partial}{\partial x}\left(\frac{\partial}{\partial y}(\sin(3x - 2y) + \cos(x + 4y))\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}\left(\frac{\partial}{\partial y}\sin(3x - 2y) + \frac{\partial}{\partial y}\cos(x + 4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}\left(\cos(3x - 2y)\frac{\partial}{\partial y}(3x-2y) -\sin(x + 4y)\frac{\partial}{\partial y}(x+4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}\left(\cos(3x - 2y)\cdot(-2) -\sin(x + 4y)\cdot 4\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}\left(-2\cos(3x - 2y) -4\sin(x + 4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial x}(-2\cos(3x - 2y)) -\frac{\partial}{\partial x}(4\sin(x + 4y)) &\mbox{}\\
\displaystyle &\displaystyle=2\sin(3x - 2y)\frac{\partial}{\partial x}(3x-2y) -4\cos(x + 4y)\frac{\partial}{\partial x}(x+4y) &\mbox{}\\
\displaystyle &\displaystyle=2\sin(3x - 2y)\cdot 3 -4\cos(x + 4y)\cdot 1 &\mbox{}\\
\displaystyle &\displaystyle=6\sin(3x - 2y) -4\cos(x + 4y) &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{\partial^2f}{\partial y \, \partial x}&\displaystyle=\frac{\partial}{\partial y}\left(\frac{\partial}{\partial x}(\sin(3x - 2y) + \cos(x + 4y))\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}\left(\frac{\partial}{\partial x}\sin(3x - 2y) + \frac{\partial}{\partial x}\cos(x + 4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}\left(\cos(3x - 2y)\frac{\partial}{\partial x}(3x-2y) -\sin(x + 4y)\frac{\partial}{\partial x}(x+4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}\left(\cos(3x - 2y)\cdot 3 -\sin(x + 4y)\cdot 1\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}\left(3\cos(3x - 2y) -\sin(x + 4y)\right) &\mbox{}\\
\displaystyle &\displaystyle=\frac{\partial}{\partial y}(3\cos(3x - 2y)) -\frac{\partial}{\partial x}(\sin(x + 4y)) &\mbox{}\\
\displaystyle &\displaystyle=-3\sin(3x - 2y)\frac{\partial}{\partial y}(3x-2y) -\cos(x + 4y)\frac{\partial}{\partial y}(x+4y) &\mbox{}\\
\displaystyle &\displaystyle=-3\sin(3x - 2y)\cdot (-2) -\cos(x + 4y)\cdot 4 &\mbox{}\\
\displaystyle &\displaystyle=6\sin(3x - 2y) -4\cos(x + 4y) &\mbox{}\\
\end{array}
$$
Do you notice anything interesting?
You May Have Noticed...
For the above example, the mixed partials $f_{xy}$ and $f_{yx}$ are equal.
Question: Does this always happen????????? What do you think?
Equality of Mixed Partial Derivatives: Clairaut’s Theorem
Suppose that $f (x, y)$ is defined on an open disk $D$ that contains the point $(a, b).$
If the functions $f_{xy}$ and $f_{yx}$ are continuous on $D,$ then $f_{xy}(a,b) = f_{yx}(a,b).$
Partial Differential Equations
Some of the most useful equations in the physical sciences are partial differential equations. Just as regular (ordinary) differential equation is one that involves a function and its derivatives, a partial differential equation is an equation involving a multivariable function and its derivatives. These include $$ \begin{array}{ll} \displaystyle \frac{\partial T}{\partial t}=k\frac{\partial^2 T}{\partial x^2}&\mbox{the heat equation in one dimension}\\ \displaystyle \frac{\partial T}{\partial t}=k\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right)&\mbox{the heat equation in two dimensions}\\ \displaystyle \frac{\partial T}{\partial t}=k\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}+\frac{\partial^2 T}{\partial z^2}\right)&\mbox{the heat equation in three dimensions}\\\\ \displaystyle \frac{\partial u^2}{\partial t^2}=c^2\left(\frac{\partial^2 u}{\partial x^2}\right)&\mbox{the wave equation in one dimension}\\ \displaystyle \frac{\partial u^2}{\partial t^2}=c^2\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right)&\mbox{the wave equation in two dimensions}\\ \displaystyle \frac{\partial u^2}{\partial t^2}=c^2\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2}\right)&\mbox{the heat equation in three dimensions}\\ \end{array} $$
Example
Verify that $u(x,t)=e^{-\pi^2m^2kt}\sin(m\pi x)$ is a solution to the one-dimensional heat equation $\displaystyle \frac{\partial u}{\partial t}=k\frac{\partial^2 u}{\partial x^2}.$
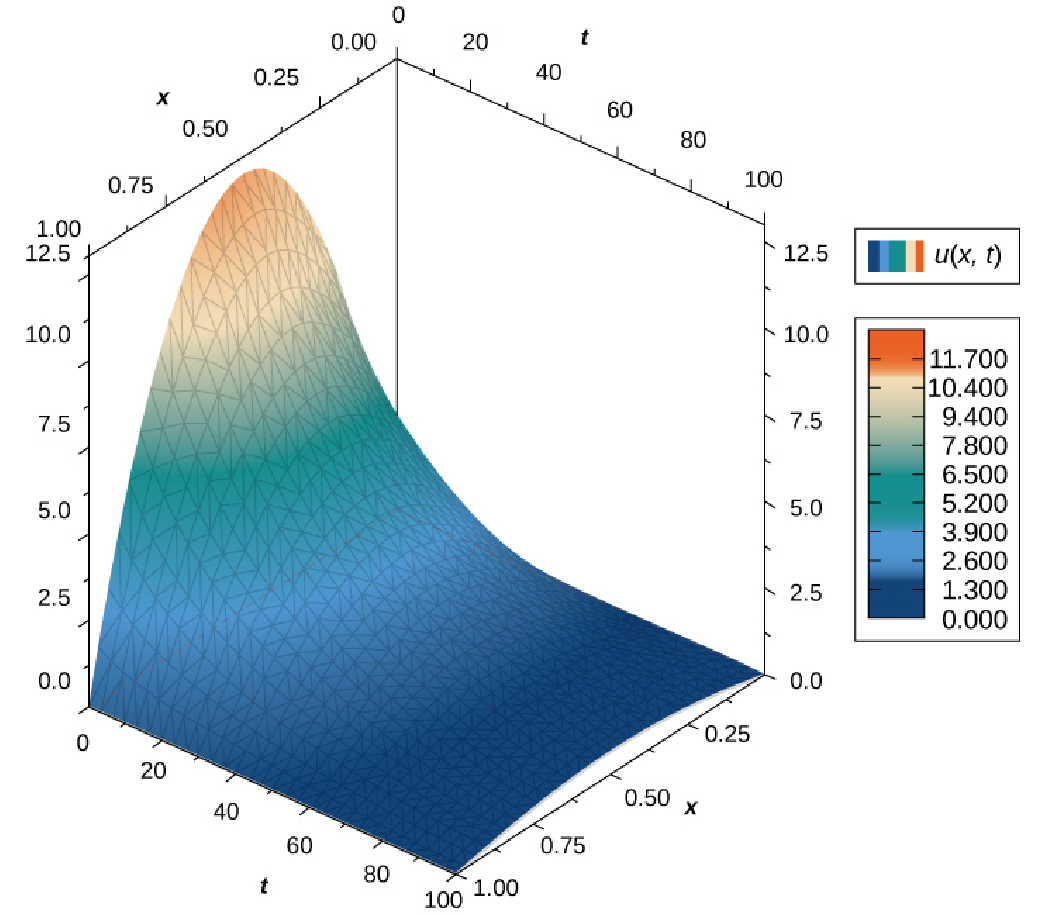
On the left-hand side we have
$$
\begin{array}{lll}
\displaystyle \frac{\partial u}{\partial t}&\displaystyle=\frac{\partial }{\partial t}\left(e^{-\pi^2m^2kt}\sin(m\pi x)\right) &\mbox{}\\
\displaystyle &\displaystyle=e^{-\pi^2m^2kt}\sin(m\pi x)\frac{\partial }{\partial t}(-\pi^2m^2kt) &\mbox{}\\
\displaystyle &\displaystyle=e^{-\pi^2m^2kt}\sin(m\pi x)(-\pi^2m^2k) &\mbox{}\\
\displaystyle &\displaystyle=-\pi^2m^2ke^{-\pi^2m^2kt}\sin(m\pi x) &\mbox{}\\
\end{array}
$$
and on the right-hand side we have
$$
\begin{array}{lll}
\displaystyle k\frac{\partial^2 u}{\partial x^2}&\displaystyle=k\frac{\partial^2 }{\partial x^2}\left(e^{-\pi^2m^2kt}\sin(m\pi x)\right) &\mbox{}\\
\displaystyle &\displaystyle=k\frac{\partial }{\partial x}\left(\frac{\partial }{\partial x}e^{-\pi^2m^2kt}\sin(m\pi x)\right)&\mbox{}\\
\displaystyle &\displaystyle=k\frac{\partial }{\partial x}\left(e^{-\pi^2m^2kt}\cos(m\pi x)\frac{\partial }{\partial x}(m\pi x)\right)&\mbox{}\\
\displaystyle &\displaystyle=k\frac{\partial }{\partial x}\left(e^{-\pi^2m^2kt}\cos(m\pi x)(m\pi)\right)&\mbox{}\\
\displaystyle &\displaystyle=m\pi k\frac{\partial }{\partial x}\left(e^{-\pi^2m^2kt}\cos(m\pi x)\right)&\mbox{}\\
\displaystyle &\displaystyle=m\pi k e^{-\pi^2m^2kt}(-\sin(m\pi x))\frac{\partial }{\partial x}(m\pi x)&\mbox{}\\
\displaystyle &\displaystyle=-m\pi k e^{-\pi^2m^2kt}\sin(m\pi x)(m\pi)&\mbox{}\\
\displaystyle &\displaystyle=-m^2\pi^2 k e^{-\pi^2m^2kt}\sin(m\pi x)&\mbox{}\\
\end{array}
$$
Therefore,
$\displaystyle \frac{\partial u}{\partial t}=-m^2\pi^2 k e^{-\pi^2m^2kt}\sin(m\pi x)=k\frac{\partial^2 u}{\partial x^2}.$
Thus, $u(x,t)=e^{-\pi^2m^2kt}\sin(m\pi x)$ satisfies the heat equation.
Thus, $u(x,t)=e^{-\pi^2m^2kt}\sin(m\pi x)$ satisfies the heat equation.
The Heat Equation in Action $\displaystyle \frac{\partial u}{\partial t}=k\frac{\partial^2 u}{\partial x^2}$
The solution $u(x,t)=e^{-\pi^2m^2kt}\sin(m\pi x)$ with $m=$ and $k=$
$u(x,$$t$$)$