Today, it's all about modelling motion in space with vector-valued functions!
Kinematics in $2$ and $3$-Dimensional Space
Let ${\bf s}(t)$ be the position of an object either in the the plane ${\bf s}(t)=x(t)\,{\bf i}+y(t)\,{\bf j}$ or in space ${\bf s}(t)=x(t)\,{\bf i}+y(t)\,{\bf j}+z(t)\,{\bf k}.$
The velocity vector is ${\bf v}(t)={\bf s}'(t).$
The acceleration vector is ${\bf a}(t)={\bf s}''(t).$
The speed of the object is the length of the velocity vector $v(t)=\Vert{\bf v}(t)\Vert.$
Position, Velocity, and Acceleration Vectors
${\bf s}(t)$$, \,\,$
${\bf v}(t)$
$, \,\,$
${\bf a}(t)$
Example:
${\bf s}(t)=3\cos t\,{\bf i}+\sin (2t)\,{\bf j}$$, \,\,$
${\bf v}(t)=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$$, \,\,$
${\bf a}(t)=-3\cos t\,{\bf i}-4\sin (2t)\,{\bf j}$
Example
A particle moves in a path defined by the vector-valued function $${\bf s}(t)=t^2\,{\bf i}+(2t-3)\,{\bf j}+(3t^2-3t)\,{\bf k}$$ where $t$ measures time in seconds and distance is measured in feet.
Find ${\bf v}(t)$ and ${\bf a}(t).$
$${\bf v}(t)={\bf s}'(t)=2t\,{\bf i}+2\,{\bf j}+(6t-3)\,{\bf k}$$
$${\bf a}(t)={\bf v}'(t)={\bf s}''(t)=2\,{\bf i}+6\,{\bf k}$$
Components of Acceleration
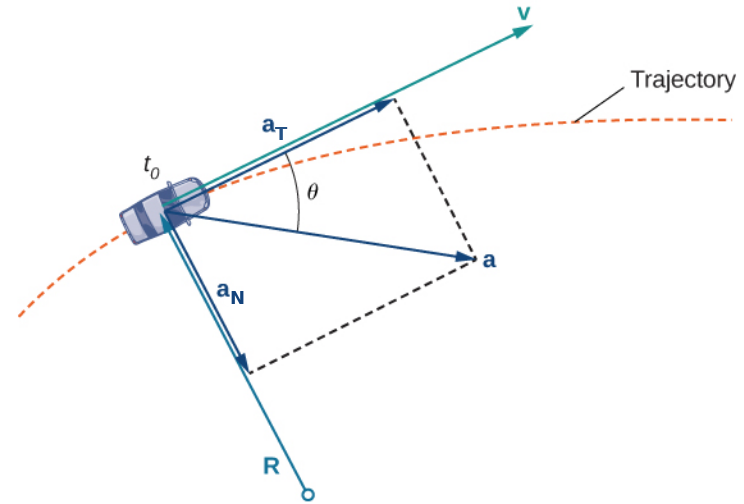
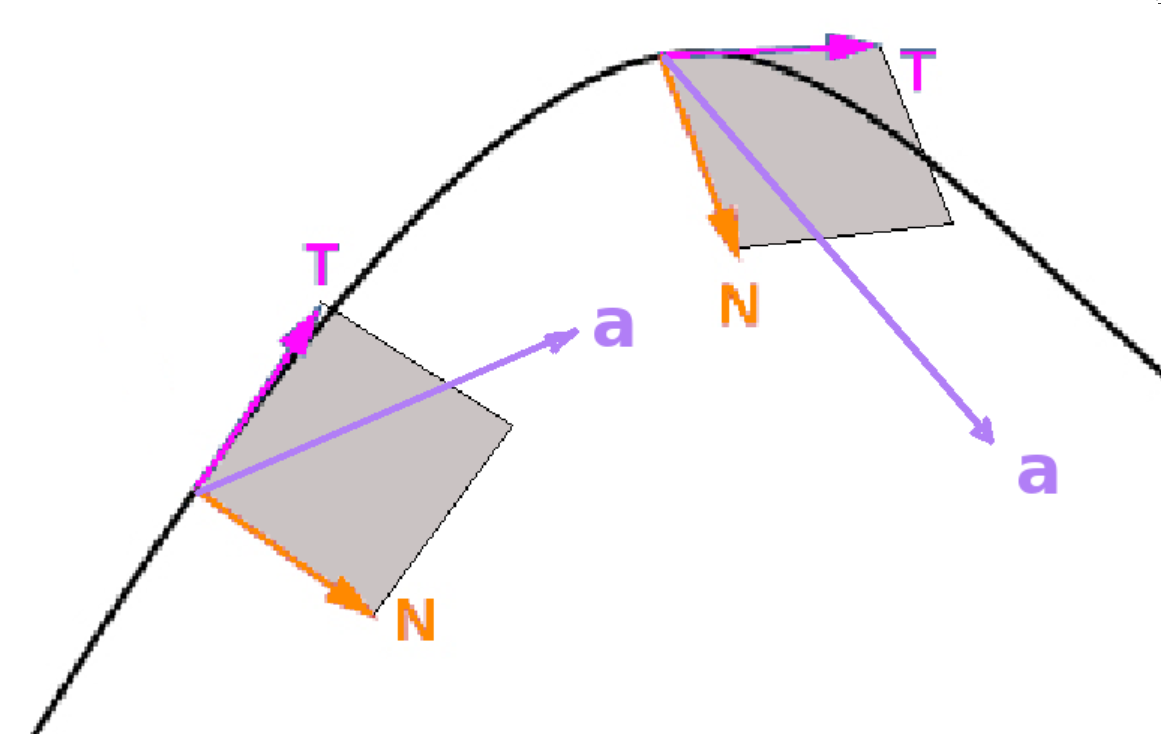
When an object moves along a trajectory, the unit tangent vector ${\bf T}$ and the principal unit normal vector ${\bf N}$ provide a useful frame of reference for describing acceleration. One reason for this is that for any curve in $2$ or $3$-dimensional space, the acceleration vector, ${\bf a}(t),$ always lies in the plane formed by ${\bf T}(t)$ and ${\bf N}(t).$
That is, we may always express ${\bf a}(t)$ as a linear combination of just ${\bf T}(t)$ and ${\bf N}(t),$ $$ {\bf a}(t)=a_{{\bf T}}{\bf T}(t)+a_{{\bf N}}{\bf N}(t) $$ where $a_{{\bf T}}$ and $a_{{\bf N}}$ are the tangential and normal components of ${\bf a}(t).$
Components of Acceleration
${\bf a}($$t$$)=$$x''(t)$ $\,{\bf i}$$+y''(t)$$\,{\bf j}$
$=$$a_{{\bf T}}$ ${\bf T}($$t$$)%=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$
$+$$a_{{\bf N}}$ ${\bf N}($$t$$)%=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$
Components of Acceleration
You might wonder why we would go to all this trouble to make a new coordinate system centered round a particle at every instant in time. However, if we imagine ourselves as the particle, we begin to see how useful this concept is.
Consider the situation of driving. If you are interested in acceleration (and forces), an ${\bf i}$-${\bf j}$-${\bf k}$ vector is not as useful as a vector stated in simple terms of a "forward" vector and a "side" vector.

The "forward" vector is ${\bf T}(t)$ and the "side" vector is ${\bf N}(t).$ The amount of "forward" acceleration is $a_{{\bf T}}$ and the amount of "side" acceleration is $a_{{\bf N}}.$
Components of Acceleration
With the notion of curvature, we may explicitly state the formulas for the scalar components acceleration ${\bf a}(t)$ as a linear combination of ${\bf T}(t)$ and ${\bf N}(t).$


The next result summarizes everything above while giving explicit formulas for $a_{{\bf T}}$ and $a_{{\bf N}}.$
Components of Acceleration
The acceleration vector ${\bf a}(t)$ of an object moving along a curve traced out by a twice-differentiable function ${\bf s}(t)$ lies in the (osculating) plane formed by the unit tangent vector ${\bf T}(t)$ and the principal unit normal vector ${\bf N}(t).$
Furthermore, $$ {\bf a}(t)=v'(t){\bf T}(t)+\kappa[v(t)]^2{\bf N}(t) $$ where $v(t)=\Vert{\bf v}(t)\Vert$ and $\kappa$ is the curvature at $t.$


We know that
$$
\displaystyle \kappa(t)=\frac{\Vert{\bf T}'(t)\Vert}{\Vert{\bf r}'(t)\Vert}=\frac{\Vert{\bf T}'(t)\Vert}{v(t)}
$$
Then
$$
\color{magenta}{\Vert{\bf T}'(t)\Vert=\kappa(t)v(t)}
$$
We also know that
$$
\displaystyle {\bf T}(t)=\frac{{\bf r}'(t)}{\Vert{\bf r}'(t)\Vert}=\frac{{\bf r}'(t)}{v(t)}
$$
so that
$$
\color{blue}{{\bf r}'(t)=v(t){\bf T}(t)}
$$
Then
$$
\begin{array}{lll}
\displaystyle {\bf a}(t)&\displaystyle= {\bf r}''(t)&\mbox{}\\
\displaystyle &\displaystyle=\frac{d}{dt}\color{blue}{{\bf r}'(t)}&\mbox{}\\
\displaystyle &\displaystyle=\frac{d}{dt}\left[\color{blue}{v(t){\bf T}(t)}\right]&\mbox{by the above}\\
\displaystyle &\displaystyle=v'(t){\bf T}(t)+v(t){\bf T}'(t) &\mbox{by product rules for vector-valued functions}\\
\displaystyle &\displaystyle=v'(t){\bf T}(t)+v(t)\color{magenta}{\Vert{\bf T}'(t)\Vert} {\bf N}(t) &\mbox{by definition, $\displaystyle {\bf N}(t)=\frac{{\bf T}'(t)}{\Vert{\bf T}'(t)\Vert}$}\\
\displaystyle &\displaystyle=v'(t){\bf T}(t)+v(t)\color{magenta}{\kappa(t)v(t)} {\bf N}(t) &\mbox{by the above}\\
\displaystyle &\displaystyle=v'(t){\bf T}(t)+\kappa(t)\left[v(t)\right]^2 {\bf N}(t) &\mbox{}\\
\end{array}
$$
Components of Acceleration
Let's think about the equation $$ {\bf a}(t)=v'(t){\bf T}(t)+\kappa[v(t)]^2{\bf N}(t) $$ for a moment. In particular, let's look the normal component of acceleration.
Again, we imagine ourselves driving on a curvy road. If we move at a constant speed, the sharper the curve (as measured by $\kappa$), the greater the "side" acceleration, and therefore, the greater the force we feel as the door pushes up against us.
Moreover, notice that doubling the speed when rounding a curve increases the "side" acceleration (and force) by $4$ times!

Example: For ${\bf s}(t)$ below, find the components of acceleration $a_{{\bf T}}$ and $a_{{\bf N}}.$
${\bf s}(t)=3\cos t\,{\bf i}+2\sin t\,{\bf j}$$, \,\,$
${\bf v}(t)=-3\sin t\,{\bf i}+2\cos t\,{\bf j}$$, \,\,$
${\bf a}(t)=-3\cos t\,{\bf i}-2\sin t\,{\bf j}$$, \,\,$
From the last section we know that
$$
v(t)=\Vert {\bf v}(t)\Vert=\Vert {\bf s}'(t)\Vert=\sqrt{5\sin^2 t+4}
$$
Thus,
$$a_{{\bf T}}=v'(t)=\frac{d}{dt}\Vert {\bf v}(t)\Vert=\frac{d}{dt}\sqrt{5\sin^2 t+4}=\frac{5\sin t \cos t}{\sqrt{5\sin^2 t+4}}$$
Also, from the last section,
$$
\kappa(t)=\displaystyle \frac{6}{\left(\sqrt{5\sin^2 t+4}\right)^3}
$$
We then have
$$
a_{{\bf N}}=\kappa[v(t)]^2
=\frac{6}{\left(\sqrt{5\sin^2 t+4}\right)^3}\left[\sqrt{5\sin^2 t+4}\right]^2
=\frac{6}{\sqrt{5\sin^2 t+4}}
$$
Thus, we may now describe acceleration entirely in terms of ${\bf T}(t)$ and ${\bf N}(t).$
$$
a_{{\bf T}}=\frac{5\sin t \cos t}{\sqrt{5\sin^2 t+4}}, \,\,\,\,
a_{{\bf N}}=\frac{6}{\sqrt{5\sin^2 t+4}}
$$
${\bf a}($$t$$)=$$-3\cos t$ $\,{\bf i}$$-2\sin t$$\,{\bf j}$
$=$$a_{{\bf T}}$ ${\bf T}($$t$$)%=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$
$+$$a_{{\bf N}}$ ${\bf N}($$t$$)%=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$
The next result allows us to express the tangential and normal components of acceleration without having to calculate the curvature.
Components of Acceleration
Let ${\bf r}(t)$ be a vector-valued function that denotes the position of an object as a function of time. Then ${\bf a}(t)={\bf r}''(t)$ is the acceleration vector. The tangential and normal components of acceleration $a_{{\bf T}}$ and $a_{{\bf N}}$ are given by the formulas $$ a_{{\bf T}}={\bf a}\cdot {\bf T}=\frac{{\bf v}\cdot {\bf a}}{\Vert {\bf v} \Vert} \,\,\,\,\,\,\,\mbox{ and }\,\,\,\,\,\,\, a_{{\bf N}}={\bf a}\cdot {\bf N}=\frac{\Vert{\bf v}\times {\bf a}\Vert}{\Vert {\bf v} \Vert}=\sqrt{\Vert{\bf a}\Vert^2-a_{{\bf T}}^2} $$

Example: For ${\bf s}(t)$ below, find the components of acceleration $a_{{\bf T}}$ and $a_{{\bf N}}.$
${\bf s}(t)=3\cos t\,{\bf i}+\sin (2t)\,{\bf j}$$, \,\,$
${\bf v}(t)=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$$, \,\,$
${\bf a}($$t$$)=$$-3\cos t$ $\,{\bf i}$$-4\sin (2t)$$\,{\bf j}$ $=$$a_{{\bf T}}$ ${\bf T}($$t$$)%=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$ $+$$a_{{\bf N}}$ ${\bf N}($$t$$)%=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$
${\bf a}($$t$$)=$$-3\cos t$ $\,{\bf i}$$-4\sin (2t)$$\,{\bf j}$ $=$$a_{{\bf T}}$ ${\bf T}($$t$$)%=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$ $+$$a_{{\bf N}}$ ${\bf N}($$t$$)%=-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}$
Using the above results, we have for the tangential component
$$
\begin{array}{lll}
\displaystyle a_{{\bf T}}&\displaystyle= \frac{{\bf v}\cdot {\bf a}}{\Vert {\bf v} \Vert}&\mbox{}\\
\displaystyle &\displaystyle= \frac{(-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j})\cdot (-3\cos t\,{\bf i}-4\sin (2t)\,{\bf j})}{\Vert -3\sin t\,{\bf i}+2\cos (2t)\,{\bf j} \Vert}&\mbox{}\\
\displaystyle &\displaystyle=\frac{9\sin t\cos t-8 \sin(2t)\cos(2t)}{\sqrt{9\sin^2 t+4\cos^2(2t)}}&\mbox{}\\
%\displaystyle &\displaystyle=\frac{\frac{9}{2}\sin(2t)-8 \sin(2t)\cos(2t)}{\sqrt{9\sin^2 t+4\cos^2(2t)}}&\mbox{}\\
\end{array}
$$
For the normal component, we use the formula
$\displaystyle a_{{\bf N}}=\frac{\Vert{\bf v}\times {\bf a}\Vert}{\Vert {\bf v} \Vert}.$
First, we note that $$ \begin{array}{lll} \displaystyle {\bf v}\times {\bf a}&=(-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}) \times (-3\cos t\,{\bf i}-4\sin (2t)\,{\bf j})&\mbox{}\\ \displaystyle &\displaystyle=\left|\begin{array}{ccc} {\bf i}&{\bf j}&{\bf k} \\ -3\sin t&2\cos (2t)&0 \\ -3\cos t&-4\sin (2t)&0 \\ \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(12\sin t \sin (2t)+6\cos t\cos (2t)){\bf k} &\mbox{}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle a_{{\bf N}} &\displaystyle= \frac{\Vert{\bf v}\times {\bf a}\Vert}{\Vert {\bf v} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\Vert (12\sin t \sin (2t)+6\cos t\cos (2t)){\bf k} \Vert}{\sqrt{9\sin^2 t+4\cos^2(2t)}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{(12\sin t \sin (2t)+6\cos t\cos (2t))^2}}{\sqrt{9\sin^2 t+4\cos^2(2t)}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{|12\sin t \sin (2t)+6\cos t\cos (2t)|}{\sqrt{9\sin^2 t+4\cos^2(2t)}}&\mbox{}\\ \end{array} $$ Not-So-Scenic Alternative
We may alternatively compute the normal component as $$ \begin{array}{lll} \displaystyle a_{{\bf N}}&\displaystyle= \sqrt{\Vert{\bf a}\Vert^2-a_{{\bf T}}^2}&\mbox{}\\ \displaystyle &\displaystyle= \sqrt{{\bf a}\cdot {\bf a}-\left(\frac{9\sin t\cos t-8 \sin(2t)\cos(2t)}{\sqrt{9\sin^2 t+4\cos^2(2t)}}\right)^2} &\mbox{}\\ \displaystyle &\displaystyle= \sqrt{(-3\cos t\,{\bf i}-4\sin (2t)\,{\bf j})\cdot(-3\cos t\,{\bf i}-4\sin (2t)\,{\bf j})-\frac{(9\sin t\cos t-8 \sin(2t)\cos(2t))^2}{9\sin^2 t+4\cos^2(2t)}} &\mbox{}\\ \displaystyle &\displaystyle= \sqrt{9\cos^2 t+16\sin^2 (2t)-\frac{(9\sin t\cos t-8 \sin(2t)\cos(2t))^2}{9\sin^2 t+4\cos^2(2t)}} &\mbox{}\\ \end{array} $$
First, we note that $$ \begin{array}{lll} \displaystyle {\bf v}\times {\bf a}&=(-3\sin t\,{\bf i}+2\cos (2t)\,{\bf j}) \times (-3\cos t\,{\bf i}-4\sin (2t)\,{\bf j})&\mbox{}\\ \displaystyle &\displaystyle=\left|\begin{array}{ccc} {\bf i}&{\bf j}&{\bf k} \\ -3\sin t&2\cos (2t)&0 \\ -3\cos t&-4\sin (2t)&0 \\ \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(12\sin t \sin (2t)+6\cos t\cos (2t)){\bf k} &\mbox{}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle a_{{\bf N}} &\displaystyle= \frac{\Vert{\bf v}\times {\bf a}\Vert}{\Vert {\bf v} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\Vert (12\sin t \sin (2t)+6\cos t\cos (2t)){\bf k} \Vert}{\sqrt{9\sin^2 t+4\cos^2(2t)}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{(12\sin t \sin (2t)+6\cos t\cos (2t))^2}}{\sqrt{9\sin^2 t+4\cos^2(2t)}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{|12\sin t \sin (2t)+6\cos t\cos (2t)|}{\sqrt{9\sin^2 t+4\cos^2(2t)}}&\mbox{}\\ \end{array} $$ Not-So-Scenic Alternative
We may alternatively compute the normal component as $$ \begin{array}{lll} \displaystyle a_{{\bf N}}&\displaystyle= \sqrt{\Vert{\bf a}\Vert^2-a_{{\bf T}}^2}&\mbox{}\\ \displaystyle &\displaystyle= \sqrt{{\bf a}\cdot {\bf a}-\left(\frac{9\sin t\cos t-8 \sin(2t)\cos(2t)}{\sqrt{9\sin^2 t+4\cos^2(2t)}}\right)^2} &\mbox{}\\ \displaystyle &\displaystyle= \sqrt{(-3\cos t\,{\bf i}-4\sin (2t)\,{\bf j})\cdot(-3\cos t\,{\bf i}-4\sin (2t)\,{\bf j})-\frac{(9\sin t\cos t-8 \sin(2t)\cos(2t))^2}{9\sin^2 t+4\cos^2(2t)}} &\mbox{}\\ \displaystyle &\displaystyle= \sqrt{9\cos^2 t+16\sin^2 (2t)-\frac{(9\sin t\cos t-8 \sin(2t)\cos(2t))^2}{9\sin^2 t+4\cos^2(2t)}} &\mbox{}\\ \end{array} $$
Example
A particle moves in a path defined by the vector-valued function $${\bf s}(t)=t^2\,{\bf i}+(2t-3)\,{\bf j}+(3t^2-3t)\,{\bf k}$$ where $t$ measures time in seconds and distance is measured in feet.
Find the components of acceleration $a_{{\bf T}}$ and $a_{{\bf N}}$ at time $t.$
From a previous example, ${\bf v}(t)=2t\,{\bf i}+2\,{\bf j}+(6t-3)\,{\bf k}$ and ${\bf a}(t)=2\,{\bf i}+6\,{\bf k}.$
Then $$ \begin{array}{lll} \displaystyle a_{{\bf T}}&\displaystyle= \frac{{\bf v}\cdot {\bf a}}{\Vert {\bf v} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{(2t\,{\bf i}+2\,{\bf j}+(6t-3)\,{\bf k})\cdot (2\,{\bf i}+6\,{\bf k})}{\Vert 2t\,{\bf i}+2\,{\bf j}+(6t-3)\,{\bf k} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{4t+36t-18}{\sqrt{4t^2+4+(6t-3)^2}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{40t-18}{\sqrt{4t^2+4+36t^2-36t+9}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{40t-18}{\sqrt{40t^2-36t+13}}&\mbox{}\\ \end{array} $$ To find $a_{{\bf N}},$ we note that $$ \begin{array}{lll} \displaystyle {\bf v}\times {\bf a}&=(2t\,{\bf i}+2\,{\bf j}+(6t-3)\,{\bf k})\times (2\,{\bf i}+6\,{\bf k}))&\mbox{}\\ \displaystyle &\displaystyle=\left|\begin{array}{ccc} {\bf i}&{\bf j}&{\bf k} \\ 2t&2&6t-3 \\ 2&0&6 \\ \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle= (12-0){\bf i}-(12t-(12t-6)){\bf j}+4{\bf k}&\mbox{}\\ \displaystyle &\displaystyle= 12{\bf i}-6{\bf j}+4{\bf k}&\mbox{}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle a_{{\bf N}} &\displaystyle= \frac{\Vert{\bf v}\times {\bf a}\Vert}{\Vert {\bf v} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\Vert12{\bf i}-6{\bf j}+4{\bf k}\Vert}{\sqrt{40t^2-36t+13}}&\mbox{from above calculation}\\ \displaystyle &\displaystyle= \frac{\sqrt{144+36+16}}{\sqrt{40t^2-36t+13}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{196}}{\sqrt{40t^2-36t+13}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{14}{\sqrt{40t^2-36t+13}}&\mbox{}\\ \end{array} $$
Then $$ \begin{array}{lll} \displaystyle a_{{\bf T}}&\displaystyle= \frac{{\bf v}\cdot {\bf a}}{\Vert {\bf v} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{(2t\,{\bf i}+2\,{\bf j}+(6t-3)\,{\bf k})\cdot (2\,{\bf i}+6\,{\bf k})}{\Vert 2t\,{\bf i}+2\,{\bf j}+(6t-3)\,{\bf k} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{4t+36t-18}{\sqrt{4t^2+4+(6t-3)^2}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{40t-18}{\sqrt{4t^2+4+36t^2-36t+9}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{40t-18}{\sqrt{40t^2-36t+13}}&\mbox{}\\ \end{array} $$ To find $a_{{\bf N}},$ we note that $$ \begin{array}{lll} \displaystyle {\bf v}\times {\bf a}&=(2t\,{\bf i}+2\,{\bf j}+(6t-3)\,{\bf k})\times (2\,{\bf i}+6\,{\bf k}))&\mbox{}\\ \displaystyle &\displaystyle=\left|\begin{array}{ccc} {\bf i}&{\bf j}&{\bf k} \\ 2t&2&6t-3 \\ 2&0&6 \\ \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle= (12-0){\bf i}-(12t-(12t-6)){\bf j}+4{\bf k}&\mbox{}\\ \displaystyle &\displaystyle= 12{\bf i}-6{\bf j}+4{\bf k}&\mbox{}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle a_{{\bf N}} &\displaystyle= \frac{\Vert{\bf v}\times {\bf a}\Vert}{\Vert {\bf v} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\Vert12{\bf i}-6{\bf j}+4{\bf k}\Vert}{\sqrt{40t^2-36t+13}}&\mbox{from above calculation}\\ \displaystyle &\displaystyle= \frac{\sqrt{144+36+16}}{\sqrt{40t^2-36t+13}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{196}}{\sqrt{40t^2-36t+13}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{14}{\sqrt{40t^2-36t+13}}&\mbox{}\\ \end{array} $$
Projectile Motion
We shall now apply what we've learned about motion to modelling trajectories of objects hurled into the air at phenomenal speed.
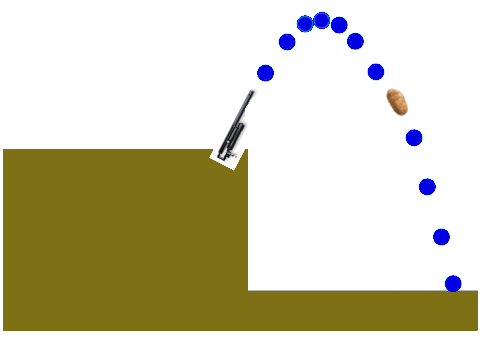
Example
Using propane, ethanol, methanol and butane, a potato cannon produce muzzle velocities of between $28$ and $48$ meters per second. (Source: U.S. Air Force Measures Potato Cannon Muzzle Velocities).
Suppose the muzzle velocity of a potato cannon is $48$ meters per second and that it is fired at a $60^{\circ}$ angle from a the top of a $100$-meter cliff. Assuming the downward acceleration due to gravity is $9.8$ $\mbox{m/s}^2,$ and ignoring air resistance, use a vector valued function to model its trajectory.

Projectile Motion
Before we solve this particular problem, let's look at projectile motion in general.
When a projectile is in the air, it is subject only to the influence of gravity (ignoring air resistance).
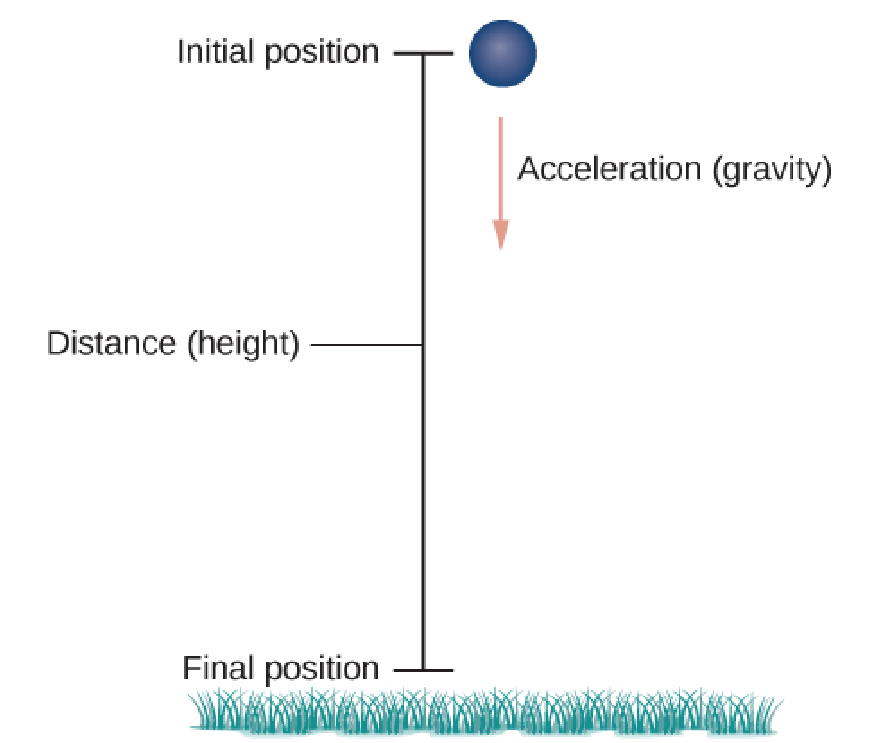
Projectile Motion
The acceleration vector in the diagram is ${\bf a}(t)=-g\,{\bf j}.$

Projectile Motion
Since ${\bf v}'(t)={\bf a}(t)=-g\,{\bf j},$ we may recover ${\bf v}(t)$ by integration. $$ {\bf v}(t)=\int {\bf v}'(t)\, dt=\int -g\,{\bf j} \, dt=-gt\,{\bf j}+{\bf v}_0 $$ where the constant of integration is ${\bf v}_0,$ an initial velocity vector.
Projectile Motion
Since ${\bf s}'(t)=-9.8t\,{\bf j}+{\bf v}_0,$ we may recover position ${\bf s}(t)$ by integrating again. $$ {\bf s}(t)=\int {\bf s}'(t)\, dt=\int -gt\,{\bf j}+{\bf v}_0 \, dt=-\frac{1}{2}gt^2\,{\bf j}+{\bf v}_0 t+{\bf s}_0 $$ where ${\bf s}_0$ is an initial velocity vector.
Projectile Motion
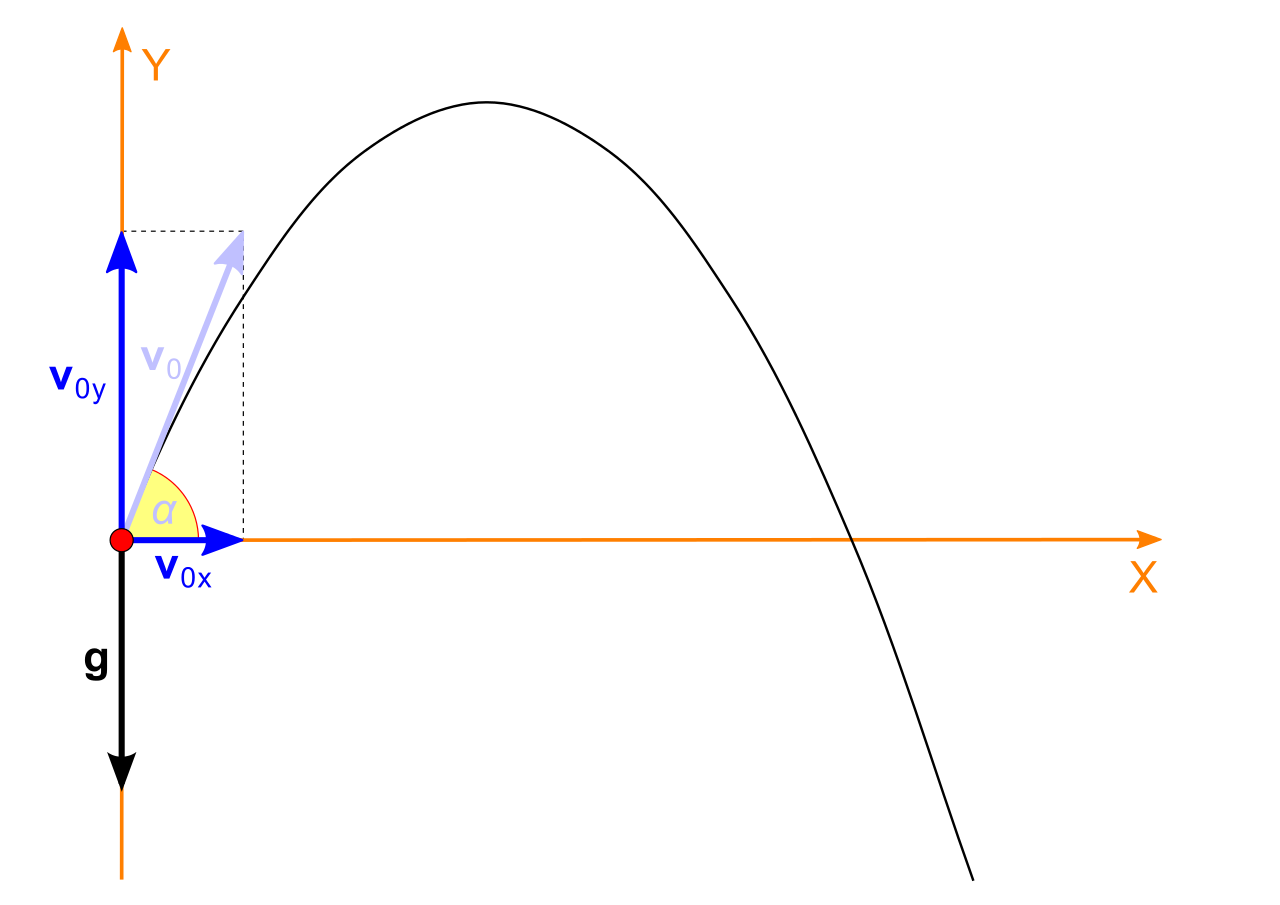
If a projectile is fired at an angle $\alpha,$ we can determine the vertical and horizontal components of velocity.
Taking the muzzle velocity $v_0$ to be $\Vert{\bf v}_0\Vert,$ we have $ {\bf v}_0=v_0\cos \alpha \,{\bf i}+v_0\sin \alpha \,{\bf j}. $
Projectile Motion
So far we have that $$ {\bf s}(t)=-\frac{1}{2}gt^2\,{\bf j}+{\bf v}_0 t+{\bf s}_0 $$ and $$ {\bf v}_0=v_0\cos \alpha \,{\bf i}+v_0\sin \alpha \,{\bf j}. $$ Putting these together we have $$ \begin{array}{ll} {\bf s}(t)&=\displaystyle -\frac{1}{2}gt^2\,{\bf j}+(v_0\cos \alpha \,{\bf i}+v_0\sin \alpha \,{\bf j}) t+{\bf s}_0\\ &=\displaystyle v_0 t\cos \alpha \,{\bf i}+\left(v_0 t\sin \alpha-\frac{1}{2}gt^2\right)\,{\bf j}+{\bf s}_0\\ \end{array} $$ We are now ready to model the flight of our potato!
Flight of the Potato
Suppose the muzzle velocity of a potato cannon is $48$ meters per second and that it is fired at a $60^{\circ}$ angle from a the top of a $100$-meter cliff. Assuming the downward acceleration due to gravity is $9.8$ $\mbox{m/s}^2,$ and ignoring air resistance, use a vector valued function to model its trajectory.

The problem gives us $g=9.8$ $\mbox{m/s}^2,$ $\alpha=60^{\circ},$ $v_0=48$ meters per second, and ${\bf s}_0=100\,{\bf j}$ meters.
Flight of the Potato $$ \begin{array}{ll} {\bf s}(t)&=\displaystyle v_0 t \cos \alpha \,{\bf i}+\left(v_0 t\sin \alpha-\frac{1}{2}gt^2\right)\,{\bf j}+{\bf s}_0\\ &=\displaystyle 48 t \cos 60^{\circ} \,{\bf i}+\left(48 t \sin 60^{\circ}-\frac{1}{2}\cdot 9.8t^2\right)\,{\bf j}+100\,{\bf j}\\ &=\displaystyle 24 t \,{\bf i}+\left(100+24 \sqrt{3} t -4.9 t^2\right)\,{\bf j}\\ \end{array} $$
Flight of the Potato
${\bf s}($$t$$)=$$24t$$\,{\bf i}$$+(100+24\sqrt{3}t-4.9t^2)$$\,{\bf j}$
$, \,\,$
${\bf v}($$t$$)=$$24$$\,{\bf i}$$+(24\sqrt{3}-9.8t)$$\,{\bf j}$
$, \,\,$
${\bf a}($$t$$)=$$0$$\,{\bf i}$$-9.8$$\,{\bf j}$
Some Fun Questions
1) How long will the potato stay in flight before hitting the ground?
2) How far will it go?
3) How high will it go?
More Potato Shenanigans
We're now going to consider the model when firing from the ground. That is, when ${\bf s}_0={\bf 0}.$ $$ {\bf s}(t)=\displaystyle v_0 t\cos \alpha \,{\bf i}+\left(v_0 t\sin \alpha-\frac{1}{2}gt^2\right)\,{\bf j} $$ Let's answer the same fun questions as last time, but this time in general. For the above model:
1) How long will the potato stay in flight before hitting the ground?
The potato is on the ground when the vertical component of ${\bf s}(t)$ is $0.$ That is, when
$$
v_0 t\sin \alpha-\frac{1}{2}gt^2=0.
$$
Since $t=0$ is trivial, we assume that $t\neq 0$ and divide it out of the above expression to get
$$
v_0 \sin \alpha-\frac{1}{2}gt=0.
$$
Then,
$$
t=t_{splat}=\frac{2v_0\sin \alpha}{g}.
$$
2) How far will it go?
The horizontal component of ${\bf s}(t)$ is $v_0 t\cos \alpha.$
At $\displaystyle t=t_{splat}=\frac{2v_0\sin \alpha}{g},$ the horizontal component is $$ v_0 \frac{2v_0\sin \alpha}{g}\cos \alpha =\frac{v_0^2\cdot 2\sin \alpha \cos \alpha}{g} =\frac{v_0^2\sin(2\alpha)}{g} $$ Thus, the potato will land $\displaystyle \frac{v_0^2\sin(2\alpha)}{g}$ meters away.
Note: This distance is called the range.
At $\displaystyle t=t_{splat}=\frac{2v_0\sin \alpha}{g},$ the horizontal component is $$ v_0 \frac{2v_0\sin \alpha}{g}\cos \alpha =\frac{v_0^2\cdot 2\sin \alpha \cos \alpha}{g} =\frac{v_0^2\sin(2\alpha)}{g} $$ Thus, the potato will land $\displaystyle \frac{v_0^2\sin(2\alpha)}{g}$ meters away.
Note: This distance is called the range.
3) How high will it go?
The potato reaches its maximum height when the vertical component of
${\bf v}(t)=\displaystyle v_0 \cos \alpha \,{\bf i}+\left(v_0 \sin \alpha-gt\right)\,{\bf j}$ is $0.$
That is, when $v_0 \sin \alpha-gt=0,$ or
$$
t=t_{max}=\frac{v_0\sin \alpha}{g}
$$
Plugging $t_{max}$ into the height component gives the maximum height, $h_{max}.$
$$
\begin{array}{lll}
\displaystyle h_{max}&\displaystyle= v_0 t_{max}\sin \alpha-\frac{1}{2}gt_{max}^2&\mbox{}\\
\displaystyle &\displaystyle=v_0\left(\frac{v_0\sin \alpha}{g}\right)\sin \alpha-\frac{1}{2}g\left(\frac{v_0\sin \alpha}{g}\right)^2 &\mbox{}\\
\displaystyle &\displaystyle=\frac{v_0^2\sin^2 \alpha}{g}-\frac{v_0^2\sin^2 \alpha}{2g} &\mbox{}\\
\displaystyle &\displaystyle=\frac{v_0^2\sin^2 \alpha}{2g} &\mbox{}\\
\end{array}
$$
Bonus Question: What angle $\alpha$ maximizes the range?
Above, we saw that the range $R$ is given by $\displaystyle R=\frac{v_0^2\sin(2\alpha)}{g}.$
To find the value of $\alpha$ which maximizes the range, we set $\displaystyle \frac{dR}{d\alpha}=0.$ $$ \begin{array}{lrll} &\displaystyle \frac{dR}{d\alpha}&\displaystyle=\frac{2v_0^2\cos (2\alpha)}{g} &=0\mbox{}\\ \implies&\displaystyle \cos (2\alpha)&\displaystyle=0 &\mbox{}\\ \implies&\displaystyle 2\alpha &\displaystyle=\frac{\pi}{2} &\mbox{assuming $0\leq\alpha\leq \frac{\pi}{2}$}\\ \implies&\displaystyle \alpha &\displaystyle=\frac{\pi}{4} &\mbox{}\\ \end{array} $$ Thus, $\displaystyle \frac{\pi}{2} \mbox{ rad}=45^{\circ}$ maximizes the range.
Special Note: This number changes a bit when the model takes into account air resistance.
To find the value of $\alpha$ which maximizes the range, we set $\displaystyle \frac{dR}{d\alpha}=0.$ $$ \begin{array}{lrll} &\displaystyle \frac{dR}{d\alpha}&\displaystyle=\frac{2v_0^2\cos (2\alpha)}{g} &=0\mbox{}\\ \implies&\displaystyle \cos (2\alpha)&\displaystyle=0 &\mbox{}\\ \implies&\displaystyle 2\alpha &\displaystyle=\frac{\pi}{2} &\mbox{assuming $0\leq\alpha\leq \frac{\pi}{2}$}\\ \implies&\displaystyle \alpha &\displaystyle=\frac{\pi}{4} &\mbox{}\\ \end{array} $$ Thus, $\displaystyle \frac{\pi}{2} \mbox{ rad}=45^{\circ}$ maximizes the range.
Special Note: This number changes a bit when the model takes into account air resistance.
Flight of the Potato
Muzzle Velocity $v_0=$ $\mbox{m/sec}$ Angle $\alpha=$$\mbox{}^{\circ}$
Muzzle Velocity $v_0=$ $\mbox{m/sec}$ Angle $\alpha=$$\mbox{}^{\circ}$
${\bf s}($$t$$)=$$v_0 t\cos \alpha$$\,{\bf i}$$+(v_0t\sin \alpha t-4.9t^2)$$\,{\bf j}$
$, \,\,$
${\bf v}($$t$$)=$$v_0 t\cos \alpha$$\,{\bf i}$$+(v_0\sin \alpha-9.8t)$$\,{\bf j}$
$, \,\,$
${\bf a}($$t$$)=$$0$$\,{\bf i}$$-9.8$$\,{\bf j}$
Celestial Mechanics
We shall conclude with one of the greatest achievements of the human intellect: understanding the motion of celestial bodies.
We shall first state Kepler's Laws of Planetary Motion.

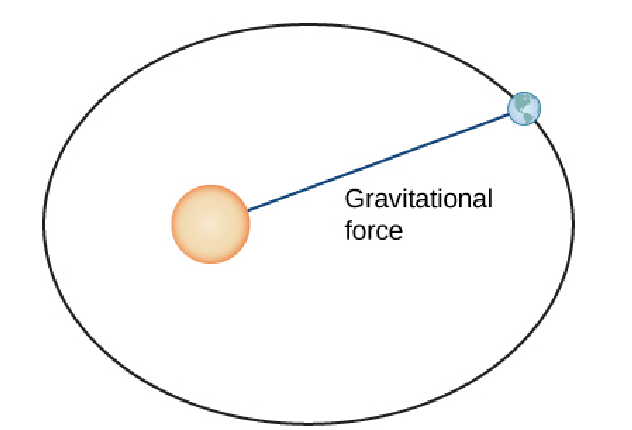
Kepler's First of Law Planetary Motion
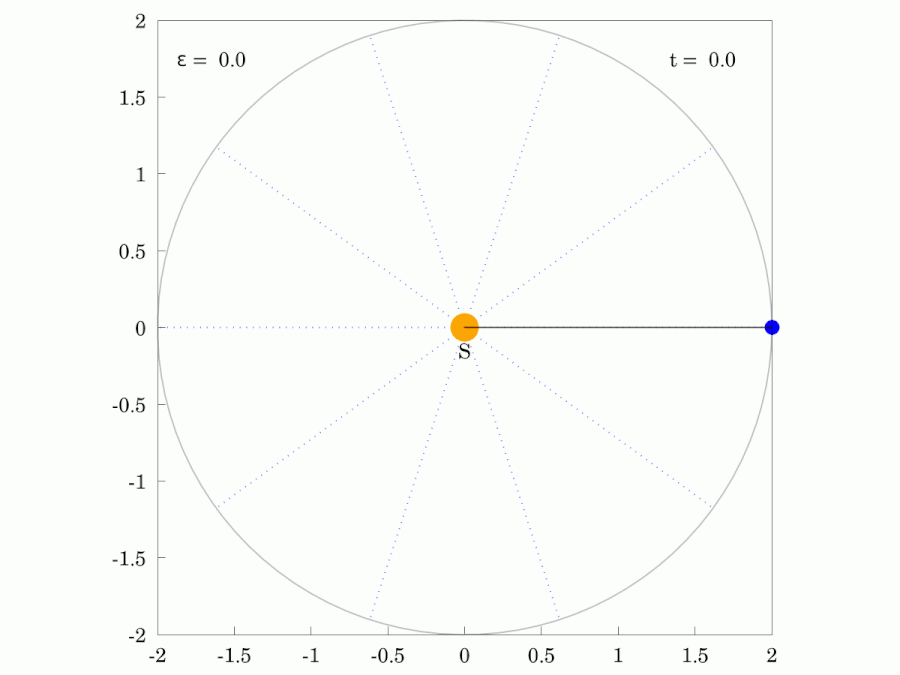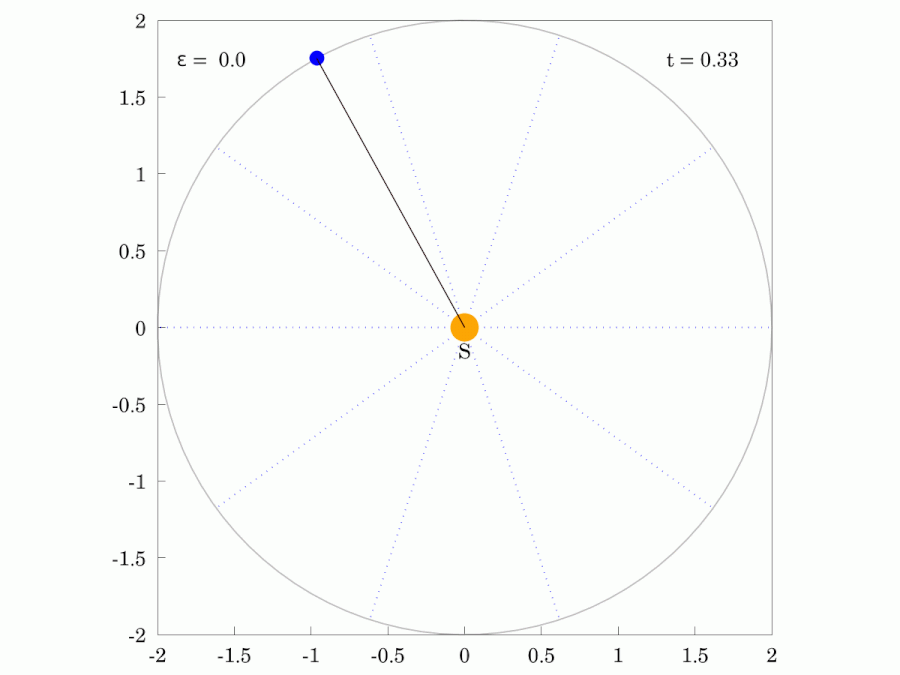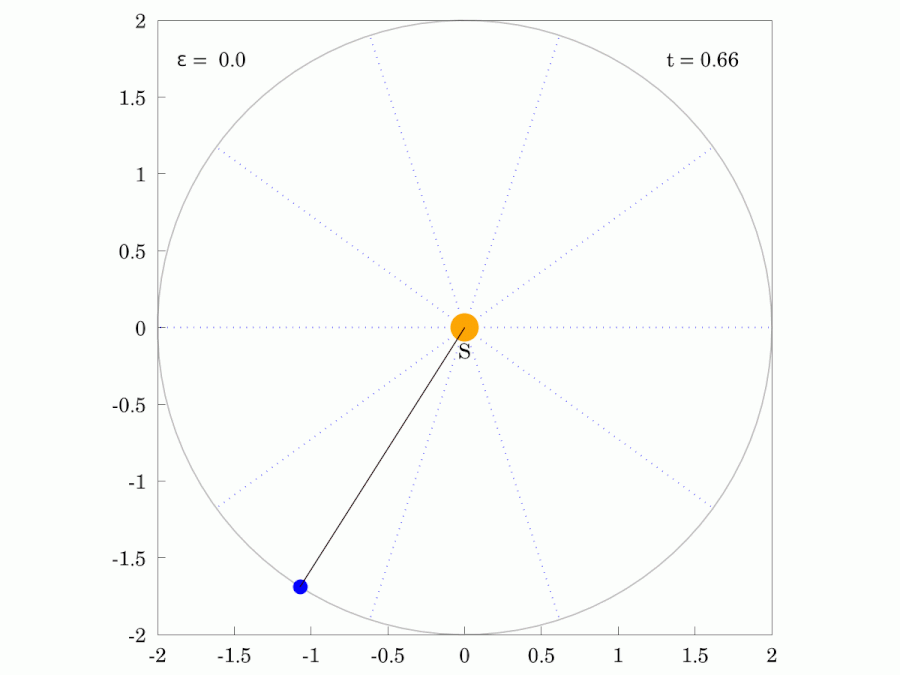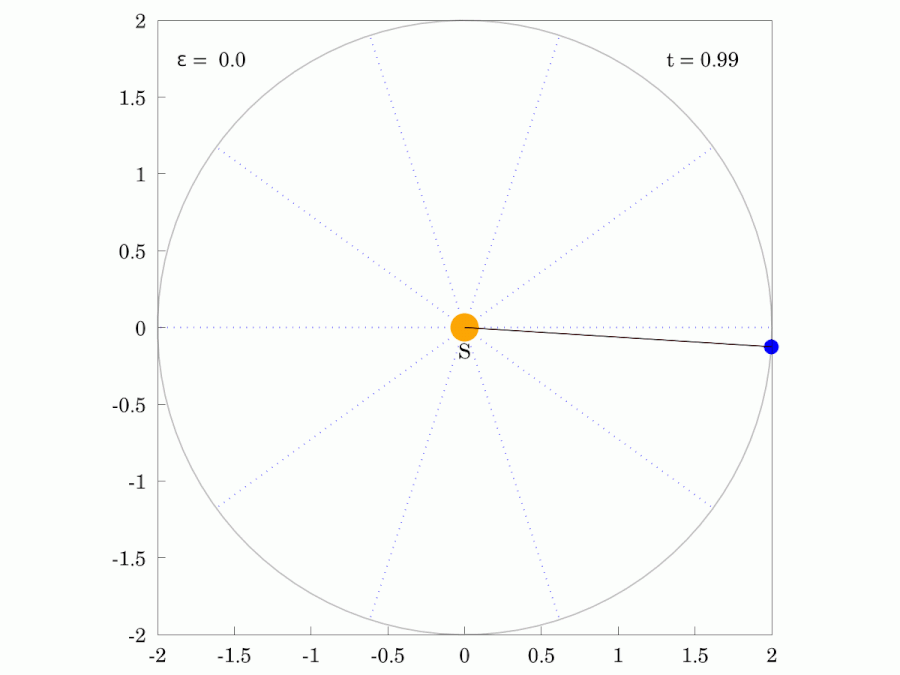
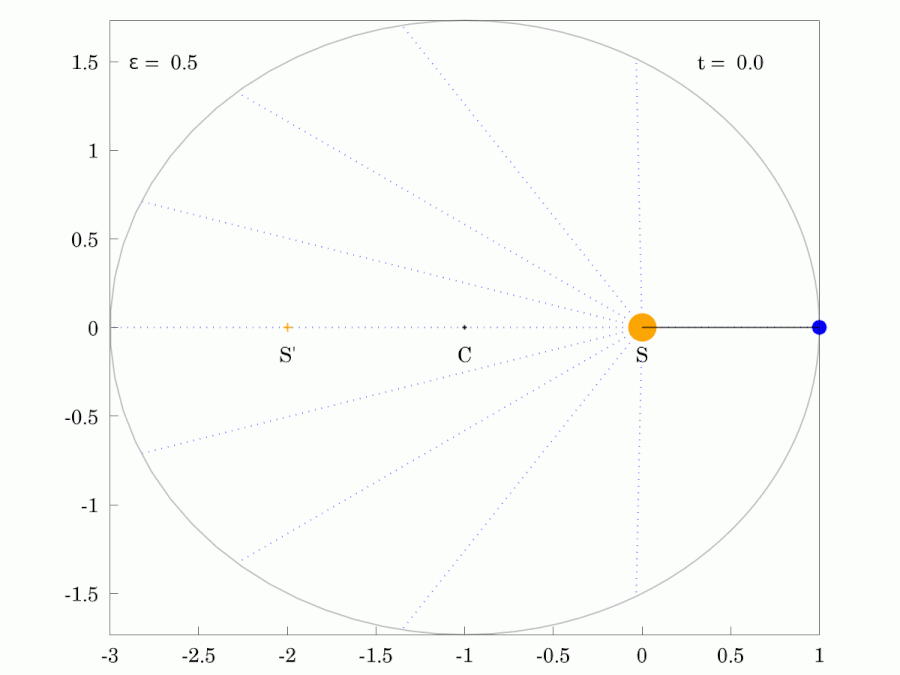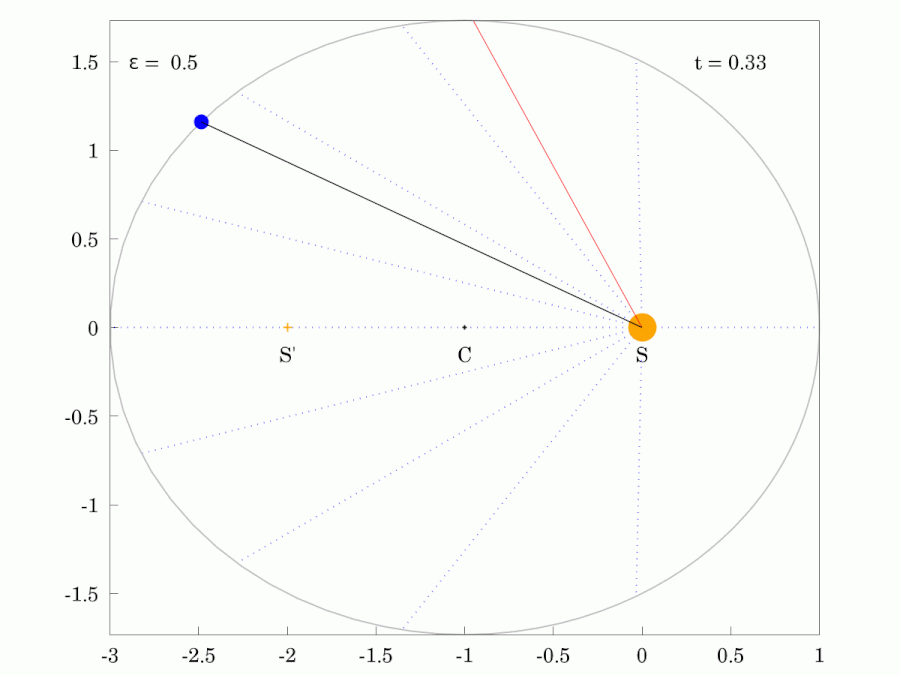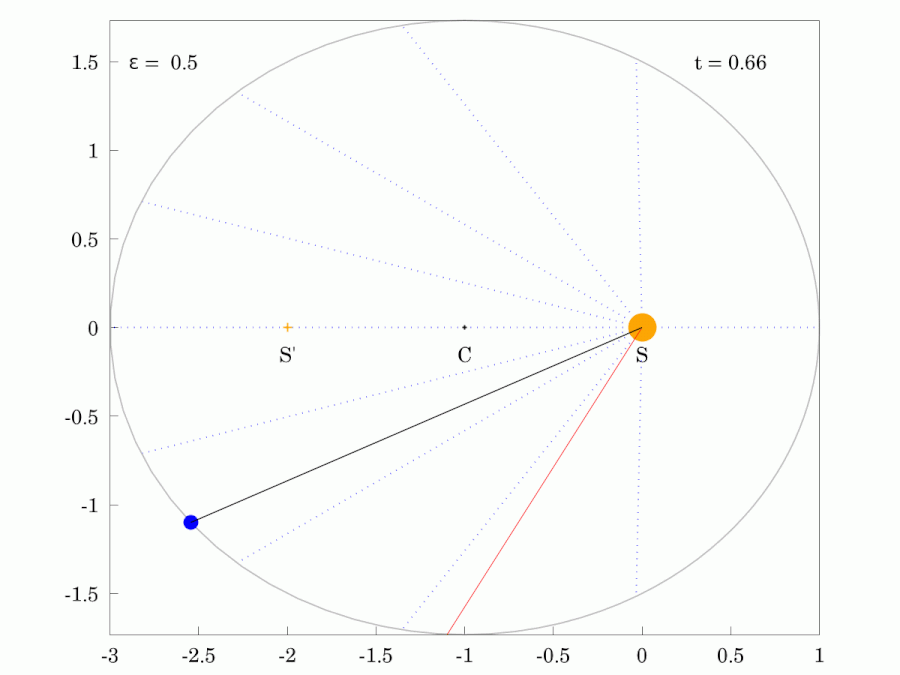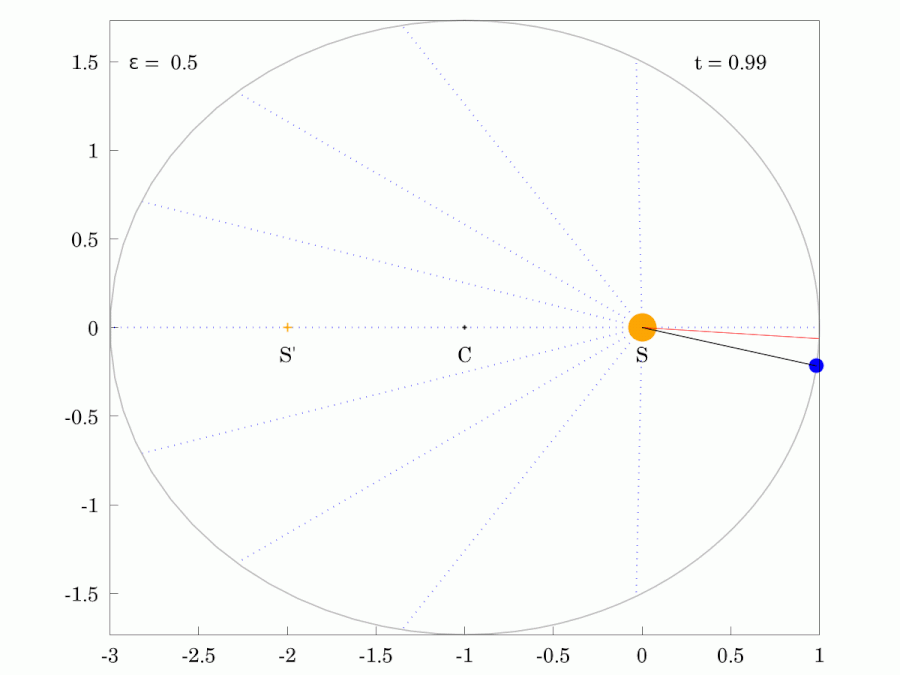
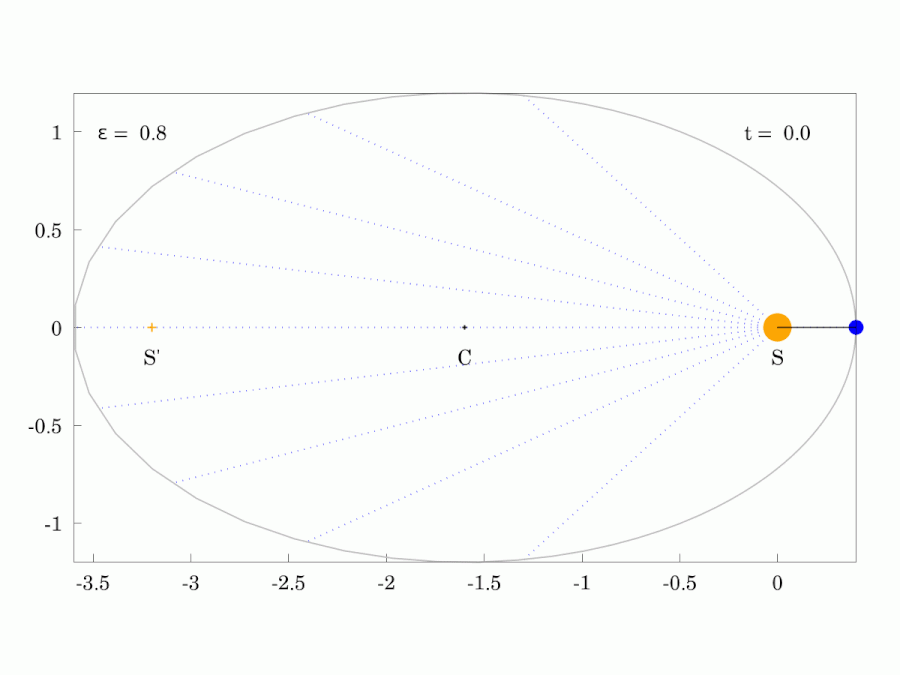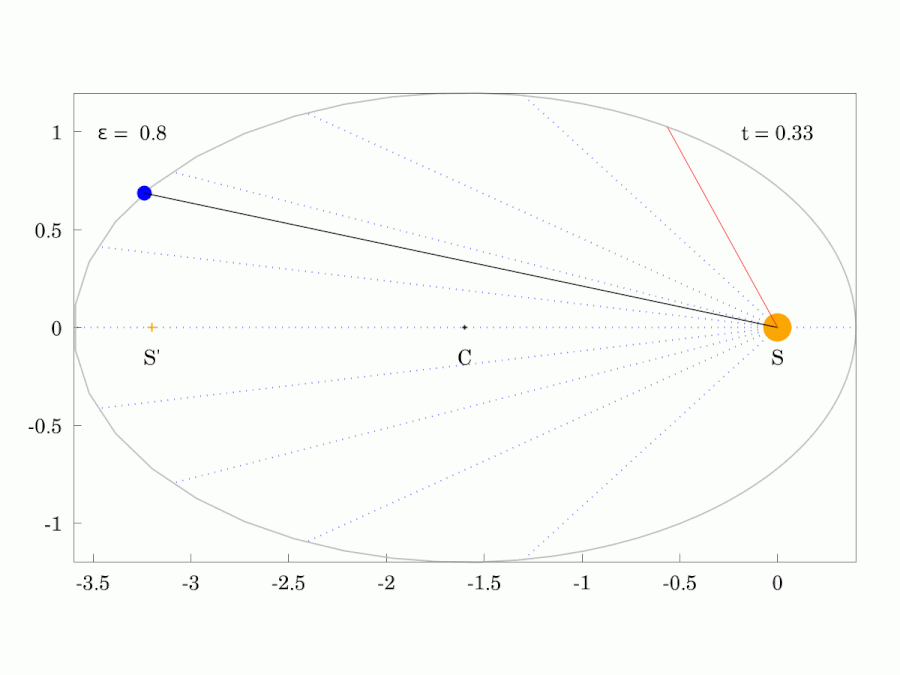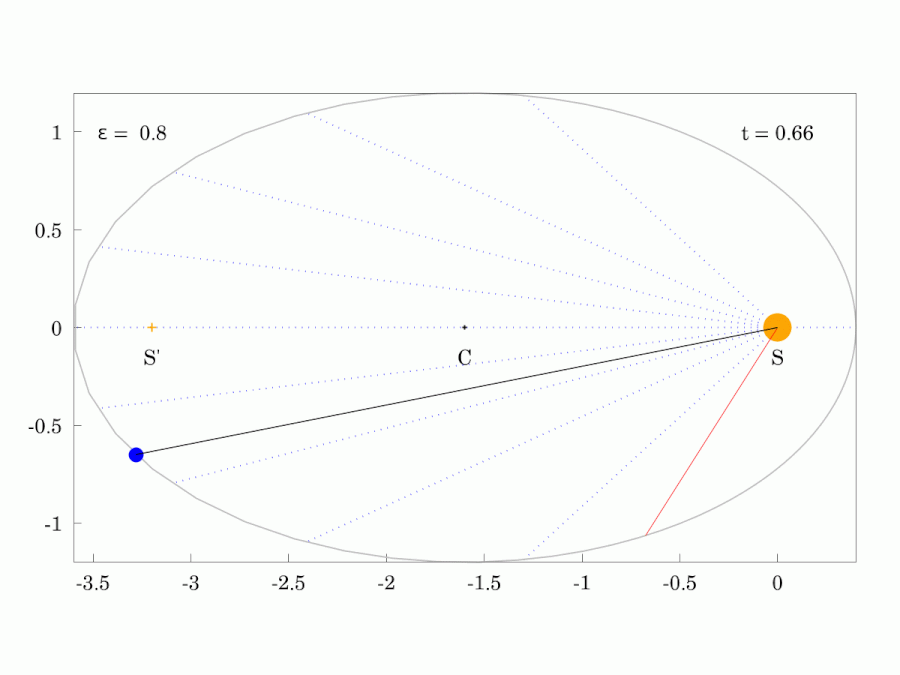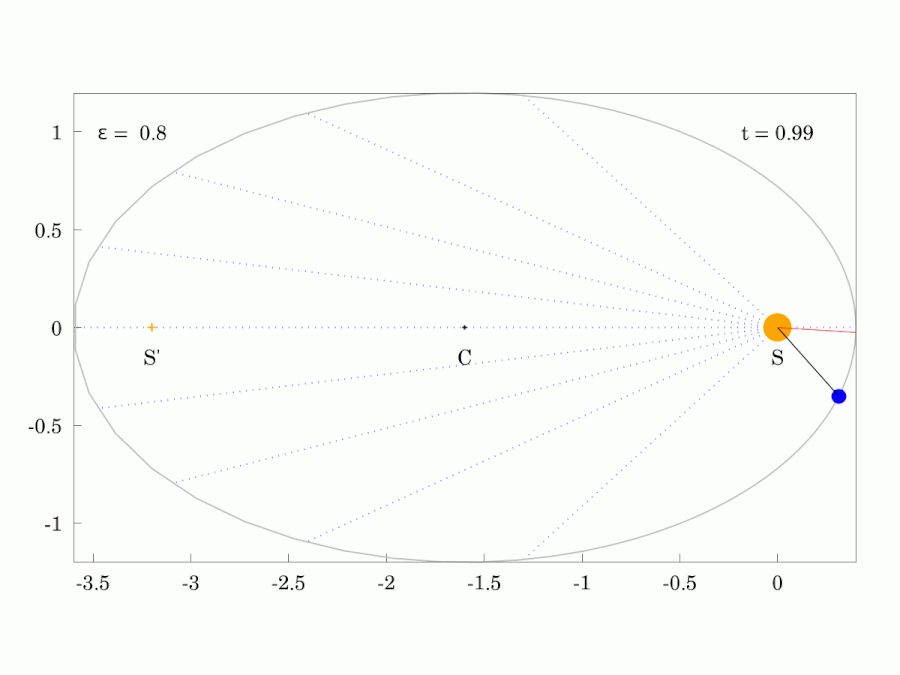
The path of any planet about the Sun is elliptical in shape, with the center of the Sun located at one focus of the ellipse.
Kepler's Second of Law Planetary Motion
A line drawn from the center of the Sun to the center of a planet sweeps out equal areas in equal time intervals.
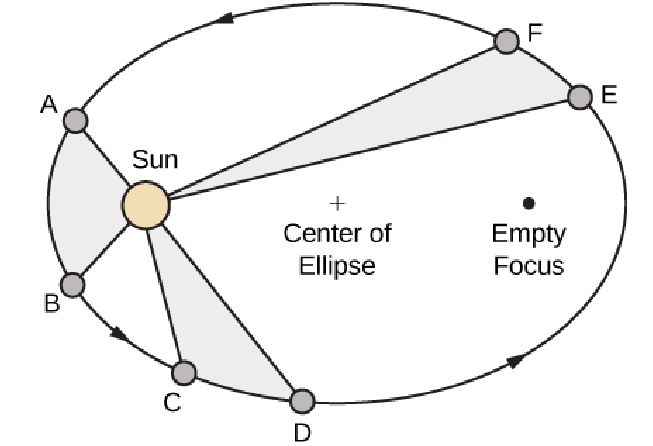
Kepler's Second of Law Planetary Motion
A line drawn from the center of the Sun to the center of a planet sweeps out equal areas in equal time intervals.
Kepler's Third of Law Planetary Motion
The ratio of the squares of the periods of any two planets is equal to the ratio of the cubes of the lengths of their semimajor orbital axes.
Planetary Motion
Orbits with increasing eccentricity from left to right.
The Newtonian Synthesis
Isaac Newton is quoted as saying, "if I have seen further, it is by standing on the shoulders of giants."
There are various interpretations of this remark, but my favorite is the idea that Newton was acknowledging the the colossal contributions of his predecessors.
Kepler's laws were derived from astronomical data, so, before Newton, there was no known underlying mechanism for why they should be true. They were simply laws that described what was visibly true.
Newton showed that Kepler's Laws are a consequence of the more general physical laws formulated in his monumental work "Principia Mathematica."


A Big Moment in this Course and Your Scientific Education
Using the vector techniques we have developed in this course, we will now use Newton's second law and the law of gravitation (stated here in vector form) to prove Kepler's First Law: the ellipse law.

The Derivation
In vector form, the two fundamental laws we use are
1) Newton's Second Law: $\displaystyle {\bf F}=m{\bf a}=m\frac{d{\bf v}}{dt}$
2) Newton's Universal Law of Gravitation: $\displaystyle {\bf F}=-\frac{GmM}{\Vert {\bf r} \Vert^3}{\bf r}.$
Note #1: In 2) the negative is there so that the force vector points toward the sun instead of the planet.
Note #2: The position vector is denoted here as ${\bf r}$ instead of ${\bf s}.$
The Derivation
From both equations above, we have $\displaystyle m\frac{d{\bf v}}{dt}=-\frac{GmM}{\Vert {\bf r} \Vert^3}{\bf r}$ which, cancelling $m,$ gives $$ \displaystyle \frac{d{\bf v}}{dt}=-\frac{GM}{\Vert {\bf r} \Vert^3}{\bf r} $$ The above tells that at any time $t,$ $\displaystyle \frac{d{\bf v}}{dt}$ and ${\bf r}$ are scalar multiples of one another.
We may deduce that these two vectors are parallel.
Question: What is the cross product of two parallel vectors? Conclusions?
The Derivation
It follows that $\displaystyle {\bf r}\times\frac{d{\bf v}}{dt}={\bf 0}.$
Thus, $$ \begin{array}{lll} \displaystyle \frac{d}{dt}({\bf r}\times {\bf v})&\displaystyle=\frac{d{\bf r}}{dt}\times {\bf v} + {\bf r}\times\frac{d{\bf v}}{dt} &\mbox{Derivative of Cross Product}\\ \displaystyle &\displaystyle=\frac{d{\bf r}}{dt}\times {\bf v} &\mbox{by the above}\\ \displaystyle &\displaystyle={\bf v}\times{\bf v} &\mbox{since $\displaystyle \frac{d{\bf r}}{dt}={\bf v}$}\\ \displaystyle &\displaystyle={\bf 0} &\mbox{vector crossed with itself is ${\bf 0}$}\\ \end{array} $$ Integrating, this gives...?????
The Derivation
It follows that $\displaystyle {\bf r}\times{\bf v}={\bf C}$ where ${\bf C}$ is a constant vector.
So, at every instant $t,$ the vectors ${\bf r}$ and ${\bf v}$ are always perpendicular to ${\bf C}.$
Question: What does this mean????????????????????
The Derivation
It means that the vectors ${\bf r}$ and ${\bf v}$ lie in a plane perpendicular to ${\bf C}.$
We now consider the vector $\displaystyle\frac{d{\bf v}}{dt}\times {\bf C}.$ $$ \begin{array}{lll} \displaystyle \frac{d{\bf v}}{dt}\times {\bf C}&\displaystyle=\frac{d{\bf v}}{dt}\times {\bf C} &\mbox{}\\ \displaystyle &\displaystyle= \color{darkorange}{\frac{d{\bf v}}{dt}}\times({\bf r}\times{\bf v})&\mbox{}\\ \displaystyle &\displaystyle= \color{darkorange}{-\frac{GM}{\Vert {\bf r} \Vert^3}}\color{magenta}{{\bf r}\times({\bf r}\times{\bf v})}&\color{darkorange}{\mbox{by Newton's Laws}}\\ \displaystyle &\displaystyle= -\frac{GM}{\Vert {\bf r} \Vert^3}[\color{magenta}{({\bf r}\cdot {\bf v}){\bf r}-({\bf r}\cdot {\bf r}){\bf v}}]&\color{magenta}{\mbox{by a FYE Problem}}\\ \end{array} $$ We will now derive a more handy way to express ${\bf r}\cdot {\bf v}.$
The Derivation
Using more properties of vector-valued derivatives, $$ \begin{array}{lll} \displaystyle \frac{d}{dt}( {\bf r}\cdot {\bf r})&\displaystyle=\frac{d{\bf r}}{dt}\cdot{\bf r}+{\bf r}\cdot\frac{d{\bf r}}{dt} &\mbox{Derivative of Dot Product}\\ \displaystyle &\displaystyle= {\bf r}\cdot \frac{d{\bf r}}{dt}+ {\bf r}\cdot \frac{d{\bf r}}{dt}&\mbox{by commutativity of dot product}\\ \displaystyle &\displaystyle= 2 {\bf r}\cdot \frac{d{\bf r}}{dt}&\mbox{}\\ \displaystyle &\displaystyle= 2 {\bf r}\cdot{\bf v}&\mbox{}\\ \end{array} $$ Also, since $\displaystyle {\bf r}\cdot {\bf r}=\Vert {\bf r} \Vert^2,$ we have $$ \begin{array}{lll} \displaystyle \frac{d}{dt}( {\bf r}\cdot {\bf r})&\displaystyle=\frac{d}{dt}\Vert {\bf r} \Vert^2 &\mbox{}\\ \displaystyle &\displaystyle= 2 \Vert{\bf r}\Vert \frac{d}{dt}\Vert{\bf r}\Vert&\mbox{by the Chain Rule}\\ \end{array} $$ From the above we conclude that $\displaystyle {\bf r}\cdot{\bf v}=\Vert{\bf r}\Vert \frac{d}{dt}\Vert{\bf r}\Vert.$
The Derivation
From what we have established so far, $$ \begin{array}{lll} \displaystyle \frac{d{\bf v}}{dt}\times {\bf C}&\displaystyle= -\frac{GM}{\Vert {\bf r} \Vert^3}[({\bf r}\cdot {\bf v}){\bf r}-({\bf r}\cdot {\bf r}){\bf v}]&\mbox{}\\ \displaystyle &\displaystyle= -\frac{GM}{\Vert {\bf r} \Vert^3}\left[\left(\Vert{\bf r}\Vert \frac{d}{dt}\Vert{\bf r}\Vert\right){\bf r}-\Vert {\bf r} \Vert^2{\bf v}\right]&\mbox{}\\ \displaystyle &\displaystyle= -GM\left[\frac{1}{\Vert{\bf r}\Vert^2}\left(\frac{d}{dt}\Vert{\bf r}\Vert\right){\bf r}-\frac{1}{\Vert{\bf r}\Vert}{\bf v}\right]&\mbox{}\\ \displaystyle &\displaystyle= GM\left[\frac{{\bf v}}{\Vert{\bf r}\Vert}-\frac{1}{\Vert{\bf r}\Vert^2}\left(\frac{d}{dt}\Vert{\bf r}\Vert\right){\bf r}\right]&\mbox{}\\ \displaystyle &\displaystyle= GM\left[\frac{\Vert{\bf r}\Vert{\bf v}}{\Vert{\bf r}\Vert^2}-\frac{\left(\frac{d}{dt}\Vert{\bf r}\Vert\right){\bf r}}{\Vert{\bf r}\Vert^2}\right]&\mbox{}\\ \displaystyle &\displaystyle= GM\left[\frac{\Vert{\bf r}\Vert\frac{d{\bf r}}{dt}}{\Vert{\bf r}\Vert^2}-\frac{{\bf r}\left(\frac{d}{dt}\Vert{\bf r}\Vert\right)}{\Vert{\bf r}\Vert^2}\right]&\mbox{}\\ \end{array} $$ Does this last expression look familiar?
The Derivation
Thus, we have shown that $$ \begin{array}{lll} \displaystyle \frac{d{\bf v}}{dt}\times {\bf C}&\displaystyle= GM\frac{d}{dt}\left(\frac{{\bf r}}{\Vert{\bf r}\Vert}\right)&\mbox{}\\ \end{array} $$
The Derivation
We now integrate both sides. $$ \begin{array}{lrll} &\displaystyle \int \frac{d{\bf v}}{dt}\times {\bf C} \, dt=&\displaystyle \int \left(GM\frac{d}{dt}\left(\frac{{\bf r}}{\Vert{\bf r}\Vert}\right)\right) \,dt &\\ \implies &\displaystyle \int \left(\color{black}{\frac{d{\bf v}}{dt}\times {\bf C}+ \frac{d{\bf C}}{dt}\times {\bf v}}\right)\, dt=&\displaystyle GM\frac{{\bf r}}{\Vert{\bf r}\Vert}+{\bf D}_1&\mbox{since $\displaystyle\frac{d{\bf C}}{dt}={\bf 0}$}\\ \implies &\displaystyle \int \frac{d}{dt}(\color{black}{{\bf v}\times {\bf C}})\, dt=&\displaystyle GM\frac{{\bf r}}{\Vert{\bf r}\Vert}+{\bf D}_1&\mbox{Derivative of Cross Product}\\ \implies &\displaystyle ({\bf v}\times {\bf C})+{\bf D}_2=&\displaystyle GM\frac{{\bf r}}{\Vert{\bf r}\Vert}+{\bf D}_1&\\ \implies &\displaystyle {\bf v}\times {\bf C}=&\displaystyle GM\frac{{\bf r}}{\Vert{\bf r}\Vert}+{\bf D}_1-{\bf D}_2&\\ \implies &\displaystyle {\bf v}\times {\bf C}=&\displaystyle GM\frac{{\bf r}}{\Vert{\bf r}\Vert}+{\bf D}&\\ \end{array} $$ where ${\bf D}$ is another constant vector of integration.
From this last equation, we may now solve for ${\bf r}.$
The Derivation
From $ \displaystyle {\bf v}\times {\bf C}= GM\frac{{\bf r}}{\Vert{\bf r}\Vert}+{\bf D} $ we have $$ \begin{array}{lll} \displaystyle \displaystyle {\bf r}\cdot({\bf v}\times {\bf C})&\displaystyle={\bf r}\cdot \left(GM\frac{{\bf r}}{\Vert{\bf r}\Vert}+{\bf D}\right) &\mbox{}\\ \displaystyle &\displaystyle= GM\frac{{\bf r}\cdot{\bf r}}{\Vert{\bf r}\Vert}+{\bf r}\cdot{\bf D} &\mbox{}\\ \displaystyle &\displaystyle= GM\Vert{\bf r}\Vert+{\bf r}\cdot{\bf D} &\mbox{}\\ \end{array} $$ But by a FYE Problem we know that ${\bf r}\cdot({\bf v}\times {\bf C})=({\bf r}\times{\bf v})\cdot {\bf C}.$
We then have $$\displaystyle ({\bf r}\times{\bf v})\cdot {\bf C}= GM\Vert{\bf r}\Vert+{\bf r}\cdot{\bf D}.$$ But what's ${\bf r}\times{\bf v}$?!?!?
The Derivation
Since ${\bf r}\times{\bf v}={\bf C},$ the above gives $$ \displaystyle {\bf C}\cdot {\bf C}= GM\Vert{\bf r}\Vert+{\bf r}\cdot{\bf D} $$ We re-express this as $$ \displaystyle \Vert{\bf C}\Vert^2= GM\Vert{\bf r}\Vert+\Vert{\bf r}\Vert \Vert{\bf D}\Vert\cos \theta $$ We may now solve for $\Vert{\bf r}\Vert!$
The Derivation
The above gives $$ \displaystyle \Vert{\bf r}\Vert=\frac{\Vert{\bf C}\Vert^2}{( GM+ \Vert{\bf D}\Vert\cos \theta)} $$ which we may rewrite as $$ \displaystyle \Vert{\bf r}\Vert=\frac{\Vert{\bf C}\Vert^2}{GM}\frac{1}{(1 + e\cos \theta)} $$ where $\displaystyle e=\frac{\Vert{\bf D}\Vert}{GM}.$
The Derivation
Since $\displaystyle e=\frac{\Vert{\bf D}\Vert}{GM},$ $$ \displaystyle \Vert{\bf r}\Vert =\frac{\Vert{\bf C}\Vert^2}{GM}\frac{1}{(1 + e\cos \theta)} =\frac{\Vert{\bf D}\Vert}{\Vert{\bf D}\Vert}\frac{\Vert{\bf C}\Vert^2}{GM}\frac{1}{(1 + e\cos \theta)} =\frac{\Vert{\bf C}\Vert^2}{\Vert{\bf D}\Vert}\frac{\Vert{\bf D}\Vert}{GM}\frac{1}{(1 + e\cos \theta)} $$ Thus, $$ \displaystyle \Vert{\bf r}\Vert =\frac{\Vert{\bf C}\Vert^2}{\Vert{\bf D}\Vert}\frac{e}{(1 + e\cos \theta)} $$ which is the polar representation of a general conic section with eccentricity $\displaystyle e=\frac{\Vert{\bf D}\Vert}{GM}$ and focal parameter $\displaystyle \frac{\Vert{\bf C}\Vert^2}{\Vert{\bf D}\Vert}.$
Thus, any closed orbit must be an ellipse! And we have proved Kepler's First Law! :D