Today, we cover the nitty gritty details which describe the behavior of curves in both $2$ and $3$-dimensional space.
Arc Length of a Vector-Valued Function
Suppose the location of an object is given by the vector-valued function $\Vert{\bf r}(t)\Vert.$
Since the rate at which an object's distance is changing is $\Vert{\bf r}'(t)\Vert,$ the net change theorem says that the distance travelled by the object over the time interval $a \leq t \leq b$ is given by $$ \int_{a}^{b}\Vert{\bf r}'(t)\Vert\,dt $$ Special Note: This is nothing more than a special case of the Net Change Theorem; an integral of a rate of change of distance gives total change in distance.
Arc Length of a Vector-Valued Function
The arc length, $s,$ of a vector-valued function ${\bf r}(t)$ over the time interval $a \leq t \leq b$ is given by $$ s=\int_{a}^{b}\Vert{\bf r}'(t)\Vert\,dt $$ In $\mathbb{R}^2,$ $$ s=\int_{a}^{b}\Vert{\bf r}'(t)\Vert\,dt=\int_{a}^{b}\sqrt{\left(f'(t)\right)^2+\left(g'(t)\right)^2}\,dt $$ and in $\mathbb{R}^3,$ $$ s=\int_{a}^{b}\Vert{\bf r}'(t)\Vert\,dt=\int_{a}^{b}\sqrt{\left(f'(t)\right)^2+\left(g'(t)\right)^2+\left(h'(t)\right)^2}\,dt $$
Example
Find the arc length of the curve $${\bf r}(t)=\langle 2t^2 + 1, 2t^2-1, t^3\rangle$$ over $0 \leq t \leq 3.$
Since ${\bf r}(t)=\langle 2t^2 + 1, 2t^2-1, t^3\rangle,$ we have
${\bf r}'(t)=\langle 4t, 4t, 3t^2\rangle$
$$
\begin{array}{lll}
\displaystyle s &\displaystyle= \int_{a}^{b}\Vert{\bf r}'(t)\Vert\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{3}\sqrt{(4t)^2+(4t)^2+(3t^2)^2}\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{3}\sqrt{16t^2+16t^2+9t^4}\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{3}\sqrt{9t^4+32t^2}\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{3}\sqrt{t^2(9t^2+32)}\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{3}|t|\sqrt{9t^2+32}\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{3}t\sqrt{9t^2+32}\,dt&\mbox{ since $0 \leq t \leq 3$}\\
\displaystyle &\displaystyle= \int_{0}^{3}\sqrt{9t^2+32}\,t\,dt&\mbox{}\\
\displaystyle &\displaystyle= \int_{32}^{113}\sqrt{u}\,\frac{du}{18}&\mbox{letting $u=9t^2+32$ so that $\displaystyle \frac{du}{18}=t\,dt$}\\
\displaystyle &\displaystyle= \frac{1}{18}\int_{32}^{113}\sqrt{u}\, du&\mbox{}\\
\displaystyle &\displaystyle= \frac{1}{18}\left[\frac{2}{3}u^{3/2}\right]_{32}^{113}&\mbox{}\\
\displaystyle &\displaystyle= \frac{1}{18}\cdot \frac{2}{3}\left[u^{3/2}\right]_{32}^{113}&\mbox{}\\
\displaystyle &\displaystyle= \frac{1}{27}\left[113^{3/2}-32^{3/2}\right]&\mbox{}\\
\displaystyle &\displaystyle \approx 37.78470892&\mbox{}\\
\end{array}
$$
Arc-Length Parameterization
Recall that the parameterization of a curve is not unique.
In fact, some parameterizations can be more useful than others.
Here, we shall discuss parameterizations which involve using arc length as the parameter instead of "just some number" $t.$
Arc-Length Parameterization
An arc-length function for ${\bf r}(t)$ is given by $$ s(t)=\int_{a}^{t}\Vert{\bf r}'(\tau)\Vert\,d\tau $$ for $t\geq a.$
That is, we may express the arc length, $s,$ as a function of a parameter $t.$
If this function has an inverse, we can do something nice...
Arc-Length Parameterization
Consider a circle of radius $4$ given by ${\bf r}(t)=4\cos t\,{\bf i}+4\sin t\,{\bf j}$ for $t \geq 0.$
The arc-length function is given by $$ \begin{array}{ll} s&=\displaystyle \int_{0}^{t}\Vert{\bf r}'(\tau)\Vert\,d\tau\\ &=\displaystyle \int_{0}^{t}\Vert -4\sin \tau\,{\bf i}+4\cos \tau\,{\bf j}\Vert\,d\tau\\ &=\displaystyle \int_{0}^{t}\sqrt{ (-4\sin \tau)^2+(4\cos \tau)^2}\,d\tau\\ &=\displaystyle \int_{0}^{t}4\,d\tau\\ &=\displaystyle 4t.\\ \end{array} $$ Notice that we may solve $s=4t$ for $t$ to get $\displaystyle t=\frac{s}{4}.$
Arc-Length Parameterization
Since $t$ is a function of $s,$ that is, $\displaystyle t(s)=\frac{s}{4},$ we may now reparameterize the circle ${\bf r}(t)=4\cos t\,{\bf i}+4\sin t\,{\bf j}$ for $t \geq 0$ in terms of arc length as, $\displaystyle {\bf r}(t(s))=4\cos (t(s)) \,{\bf i}+4\sin (t(s))\,{\bf j}.$
Then the arc-length parameterization is $$ {\bf r}(s)=4\cos \left(\frac{s}{4}\right) \,{\bf i}+4\sin \left(\frac{s}{4}\right)\,{\bf j} $$ for $s\geq 0.$
Example
Find the arc-length parameterization for $${\bf r}(t) = \langle 3\cos t, 3\sin t , 4t \rangle$$ on $t \geq 0.$
Since ${\bf r}(t) = \langle -3\sin t, 3\cos t , 4 \rangle$
$$
\begin{array}{lll}
\displaystyle s(t)&\displaystyle= \int_{0}^{t}\Vert{\bf r}'(\tau)\Vert\,d\tau&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{t}\sqrt{(-3\sin \tau)^2+(3\cos \tau)^2+4^2}\,d\tau&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{t}\sqrt{9\sin^2 \tau+9\cos^2 \tau+16}\,d\tau&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{t}\sqrt{9+16}\,d\tau&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{t}\sqrt{25}\,d\tau&\mbox{}\\
\displaystyle &\displaystyle= \int_{0}^{t}5\,d\tau&\mbox{}\\
\displaystyle &\displaystyle= [5\tau]_{0}^{t}&\mbox{}\\
\displaystyle &\displaystyle= 5t&\mbox{}\\
\end{array}
$$
Therefore, $\displaystyle t=\frac{1}{5}s.$
We then have that $${\bf r}(s) = \left\langle 3\cos\left(\frac{1}{5}s\right), 3\sin\left(\frac{1}{5}s\right) , \frac{4}{5}s\right\rangle$$
We then have that $${\bf r}(s) = \left\langle 3\cos\left(\frac{1}{5}s\right), 3\sin\left(\frac{1}{5}s\right) , \frac{4}{5}s\right\rangle$$
The Big Deal
An arc-length parameterization isn't just any old parameterization.
We can now understand how measure how "sharply" a curve bends and twists.
This notion is formalized as the curvature at a point.
The Definition of Curvature
Let ${\bf r}(s)$ be the arc-length parameterization of a smooth curve.
The curvature, $\kappa,$ is $$ \kappa=\left\Vert\frac{d{\bf T}}{ds}\right\Vert=\Vert{\bf T}'(s)\Vert $$ The curvature measures the rate at which the unit tangent vector varies with respect to arc length as we move along the curve.
In other words, curvature is the rate at which our direction is changing with respect to distance travelled along the curve.
Curvature
Intuitively, we can think of curvature as how "sharp" a curve is.
If we drive along a curve, the harder we have to turn the steering wheel, the sharper the curve, the larger the curvature. Most of the time the curvature is changing.
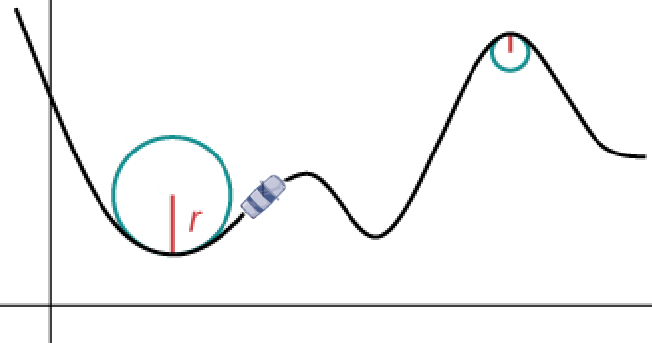
Curvature
Notice that how much we need to turn the steering wheel doesn't depend on velocity or time, but on where we are on the curve.
This is the reason we needed to define curvature using the arc-length parameterization.

Example
Use the definition of curvature to find the curvature of the circle $$ {\bf r}(s)=4\cos \left(\frac{s}{4}\right) \,{\bf i}+4\sin \left(\frac{s}{4}\right)\,{\bf j} $$ Before we do any calculations: using the driving analogy above, any guesses about the curvature of a circle?
We first compute the unit tangent vector ${\bf T}(s).$
$$
\begin{array}{lll}
\displaystyle {\bf T}(s)&\displaystyle= \frac{{\bf r}'(s)}{\Vert{\bf r}'(s)\Vert}&\mbox{}\\
\displaystyle &\displaystyle= \frac{-\sin \left(\frac{s}{4}\right) \,{\bf i}+\cos \left(\frac{s}{4}\right)\,{\bf j}}{\sqrt{\left(-\sin \left(\frac{s}{4}\right)\right)^2+\left(\cos \left(\frac{s}{4}\right)\right)^2}}&\mbox{}\\
\displaystyle &\displaystyle= \frac{-\sin \left(\frac{s}{4}\right) \,{\bf i}+\cos \left(\frac{s}{4}\right)\,{\bf j}}{\sqrt{\sin^2 \left(\frac{s}{4}\right)+\cos^2 \left(\frac{s}{4}\right)}}&\mbox{}\\
\displaystyle &\displaystyle= -\sin \left(\frac{s}{4}\right) \,{\bf i}+\cos \left(\frac{s}{4}\right)\,{\bf j}&\mbox{}\\
\end{array}
$$
Thus $\displaystyle {\bf T}'(s)=-\frac{1}{4}\cos \left(\frac{s}{4}\right) \,{\bf i}-\frac{1}{4}\sin \left(\frac{s}{4}\right)\,{\bf j}.$
We may now compute the curvature. $$ \begin{array}{lll} \displaystyle \kappa &\displaystyle=\left\Vert\frac{d{\bf T}}{ds}\right\Vert=\Vert{\bf T}'(s)\Vert &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\left(-\frac{1}{4}\cos \left(\frac{s}{4}\right)\right)^2+\left(-\frac{1}{4}\sin \left(\frac{s}{4}\right)\right)^2} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\frac{1}{16}\cos^2 \left(\frac{s}{4}\right)+\frac{1}{16}\sin^2 \left(\frac{s}{4}\right)} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\frac{1}{16}} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{4} &\mbox{}\\ \end{array} $$
We may now compute the curvature. $$ \begin{array}{lll} \displaystyle \kappa &\displaystyle=\left\Vert\frac{d{\bf T}}{ds}\right\Vert=\Vert{\bf T}'(s)\Vert &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\left(-\frac{1}{4}\cos \left(\frac{s}{4}\right)\right)^2+\left(-\frac{1}{4}\sin \left(\frac{s}{4}\right)\right)^2} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\frac{1}{16}\cos^2 \left(\frac{s}{4}\right)+\frac{1}{16}\sin^2 \left(\frac{s}{4}\right)} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\frac{1}{16}} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{4} &\mbox{}\\ \end{array} $$
Fact of Life: The definition of curvature is difficult to use.
Never fear though, help is on the way!
It turns out that calculating curvature is easy with any parameterization!
Chain Rule to the Rescue
Recall that in our arc-length parameterization, we expressed arc length $s$ as a function of $t.$ That is $s=s(t).$ We then solved for $t$ as a function of $s$ so that $t=t(s).$
The Chain Rule coupled with the Inverse Function Theorem allows us to write $$ \frac{d{\bf T}}{ds}=\frac{d{\bf T}}{dt}\frac{dt}{ds}=\frac{\frac{d{\bf T}}{dt}}{\frac{ds}{dt}}. $$ But since $\displaystyle s(t)=\int_{a}^{t}\Vert{\bf r}'(\tau)\Vert\,d\tau,$ we have that $\displaystyle \frac{ds}{dt}=\Vert{\bf r}'(t)\Vert.$
Thus, $$ \frac{d{\bf T}}{ds}=\frac{{\bf T}'(t)}{\Vert{\bf r}'(t)\Vert} $$ From the above we have...
Theorem
Let ${\bf r}(t)$ be any parameterization of a smooth curve $C.$ Then, the curvature, $\kappa,$ at $t$ is given by $$ \kappa(t)=\frac{\Vert{\bf T}'(t)\Vert}{\Vert{\bf r}'(t)\Vert} $$ provided $\Vert{\bf r}'(t)\Vert\neq 0.$
Example
Find the curvature of a circle of radius $r,$ $${\bf r}(t)=r\cos t \, {\bf i}+r\sin t \, {\bf j}$$
We shall use the formula $\displaystyle \kappa(t)=\frac{\Vert{\bf T}'(t)\Vert}{\Vert{\bf r}'(t)\Vert}$ to find the curvature.
We first note that ${\bf r}'(t)=-r\sin t \, {\bf i}+r\cos t \, {\bf j}.$ Thus, $$ \begin{array}{lll} \displaystyle {\bf T}(t)&\displaystyle=\frac{{\bf r}'(t)}{\Vert {\bf r}'(t) \Vert}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{\sqrt{(-r\sin t)^2+(r\cos t)^2}}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{\sqrt{r^2\sin^2 t+r^2\cos^2 t}}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{\sqrt{r^2}}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{|r|}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{r}&\mbox{since $r\gt 0$}\\ \displaystyle &\displaystyle=-\sin t \, {\bf i}+\cos t \, {\bf j}&\mbox{}\\ \end{array} $$ Then ${\bf T}'(t)=-\cos t \, {\bf i}-\sin t \, {\bf j}$ so that the curvature is $$ \begin{array}{lll} \displaystyle \kappa(t)&\displaystyle= \frac{\Vert{\bf T}'(t)\Vert}{\Vert{\bf r}'(t)\Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\Vert-\cos t \, {\bf i}-\sin t \, {\bf j}\Vert}{\Vert-r\sin t \, {\bf i}+r\cos t \, {\bf j}\Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{(-\cos t)^2+(-\sin t)^2}}{r}&\mbox{from above, $\Vert{\bf r}'(t)\Vert=r$}\\ \displaystyle &\displaystyle= \frac{\sqrt{\cos^2 t+ \sin^2 t}}{r}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{1}}{r}&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{r}&\mbox{}\\ \end{array} $$
We first note that ${\bf r}'(t)=-r\sin t \, {\bf i}+r\cos t \, {\bf j}.$ Thus, $$ \begin{array}{lll} \displaystyle {\bf T}(t)&\displaystyle=\frac{{\bf r}'(t)}{\Vert {\bf r}'(t) \Vert}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{\sqrt{(-r\sin t)^2+(r\cos t)^2}}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{\sqrt{r^2\sin^2 t+r^2\cos^2 t}}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{\sqrt{r^2}}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{|r|}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-r\sin t \, {\bf i}+r\cos t \, {\bf j}}{r}&\mbox{since $r\gt 0$}\\ \displaystyle &\displaystyle=-\sin t \, {\bf i}+\cos t \, {\bf j}&\mbox{}\\ \end{array} $$ Then ${\bf T}'(t)=-\cos t \, {\bf i}-\sin t \, {\bf j}$ so that the curvature is $$ \begin{array}{lll} \displaystyle \kappa(t)&\displaystyle= \frac{\Vert{\bf T}'(t)\Vert}{\Vert{\bf r}'(t)\Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\Vert-\cos t \, {\bf i}-\sin t \, {\bf j}\Vert}{\Vert-r\sin t \, {\bf i}+r\cos t \, {\bf j}\Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{(-\cos t)^2+(-\sin t)^2}}{r}&\mbox{from above, $\Vert{\bf r}'(t)\Vert=r$}\\ \displaystyle &\displaystyle= \frac{\sqrt{\cos^2 t+ \sin^2 t}}{r}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{1}}{r}&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{r}&\mbox{}\\ \end{array} $$
When is comes to calculating curvature, the above theorem is a lifeline, indeed.
But is there a way to calculate the curvature based upon ${\bf r}(t)$ alone without having to go through the extra calculation to find ${\bf T}'(t)?$
Theorem
Let ${\bf r}(t)$ be any parameterization of a smooth curve $C.$ Then, the curvature, $\kappa,$ at $t$ is given by $$ \kappa(t)=\frac{\Vert{\bf r}'(t)\times{\bf r}''(t)\Vert}{\Vert{\bf r}'(t)\Vert^3} $$ provided $\Vert{\bf r}'(t)\Vert\neq 0.$
Example
Find the curvature of the helix $${\bf r}(t)=4\cos t \, {\bf i}+4\sin t \, {\bf j}+3t\,{\bf k}$$ at $\displaystyle t=\frac{4\pi}{3}.$
For ${\bf r}(t)=4\cos t \, {\bf i}+4\sin t \, {\bf j}+3t\,{\bf k},$ we have $${\bf r}'(t)=-4\sin t \, {\bf i}+4\cos t \, {\bf j}+3\,{\bf k}$$
and $${\bf r}''(t)=-4\cos t \, {\bf i}-4\sin t \, {\bf j}.$$
Then
$$
\begin{array}{lll}
\displaystyle {\bf r}'(t)\times{\bf r}''(t)&\displaystyle= (-4\sin t \, {\bf i}+4\cos t \, {\bf j}+3\,{\bf k})\times(-4\cos t \, {\bf i}-4\sin t \, {\bf j})&\mbox{}\\
\displaystyle &\displaystyle=\left|\begin{array}{ccc} {\bf i}&{\bf j}&{\bf k} \\ -4\sin t&4\cos t&3 \\ -4\cos t&-4\sin t& 0 \\ \end{array}\right| &\mbox{}\\
\displaystyle &\displaystyle= (0-(-12\sin t)) {\bf i}-(0-(-12\cos t)){\bf j}+(16\sin^2 t+16\cos^2 t){\bf k}&\mbox{}\\
\displaystyle &\displaystyle= 12\sin t \, {\bf i}-12\cos t\,{\bf j}+16\,{\bf k}&\mbox{}\\
\end{array}
$$
Finally,
$$
\begin{array}{lll}
\displaystyle \kappa(t)&\displaystyle= \frac{\Vert{\bf r}'(t)\times{\bf r}''(t)\Vert}{\Vert{\bf r}'(t)\Vert^3}&\mbox{}\\
\displaystyle &\displaystyle= \frac{\Vert 12\sin t \, {\bf i}-12\cos t\,{\bf j}+16\,{\bf k} \Vert}{\Vert -4\sin t \, {\bf i}+4\cos t \, {\bf j}+3\,{\bf k} \Vert^3}&\mbox{}\\
\displaystyle &\displaystyle= \frac{ \sqrt{144\sin^2 t+144\cos^2 t+256} }{\left(\sqrt{16\sin^2 t+16\cos^2 t+9}\right)^3}&\mbox{}\\
\displaystyle &\displaystyle= \frac{\sqrt{144+256}}{\left(\sqrt{16+9}\right)^3}&\mbox{}\\
\displaystyle &\displaystyle= \frac{\sqrt{400}}{\sqrt{25}^3}&\mbox{}\\
\displaystyle &\displaystyle= \frac{20}{5^3}&\mbox{}\\
\displaystyle &\displaystyle= \frac{4}{25}&\mbox{}\\
\end{array}
$$
Thus, the curvature at every point in the helix (including $\displaystyle t=\frac{4\pi}{3}$) is $\displaystyle \frac{4}{25}.$
Example
Even though the last theorem involves a cross product, we can still apply the formula to a curve in the plane.
Find the curvature of the ellipse $${\bf r}(t)=3\cos t \, {\bf i}+2\sin t \, {\bf j}$$ at $t=0$ and $\displaystyle t=\frac{\pi}{2}.$
We will find the curvature for an arbitrary value of $t.$ First,
$$
{\bf r}(t)=3\cos t \, {\bf i}+2\sin t \, {\bf j}\\
{\bf r}'(t)=-3\sin t \, {\bf i}+2\cos t \, {\bf j}\\
{\bf r}''(t)=-3\cos t \, {\bf i}-2\sin t \, {\bf j}\\
$$
and
$$
{\bf r}'(t)\times{\bf r}''(t)
=\left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k}\\ -3\sin t & 2\cos t & 0 \\ -3\cos t & -2\sin t & 0\\ \end{array}\right|
=0\,{\bf i}-0\,{\bf j}+(6\sin^2 t+6\cos t){\bf k}=6{\bf k}.
$$
Also, from the last section we have,
$$
\Vert {\bf r}'(t)\Vert=\sqrt{5\sin^2 t+4}
$$
Then,
$$
\begin{array}{ll}
\kappa(t)
&=\displaystyle \frac{\Vert{\bf r}'(t)\times{\bf r}''(t)\Vert}{\Vert{\bf r}'(t)\Vert^3}\\
&=\displaystyle \frac{1}{\Vert{\bf r}'(t)\Vert^3}\Vert {\bf r}'(t)\times{\bf r}''(t)\Vert\\
&=\displaystyle \frac{1}{\left(\sqrt{5\sin^2 t+4}\right)^3}\left\Vert 6{\bf k} \right\Vert\\
&=\displaystyle \frac{6}{\left(\sqrt{5\sin^2 t+4}\right)^3}\\
\end{array}
$$
Thus, the curvature at $t=0$ is
$$
\kappa(0)=\frac{6}{\left(\sqrt{5\sin^2 (0)+4}\right)^3}=\frac{6}{8}=\frac{3}{4}
$$
and at $\displaystyle t=\frac{\pi}{2}$ is
$$
\kappa\left(\frac{\pi}{2}\right)=\frac{6}{\left(\sqrt{5\sin^2 \left(\frac{\pi}{2}\right)+4}\right)^3}=\frac{6}{27}=\frac{2}{9}
$$
Curvature of Functions $y=f(x)$
If we parameterize a plane curve given by $y=f(x),$ as $${\bf r}(t)=t \, {\bf i}+f(t) \, {\bf j},$$ we may use the above theorem and the idea of the above example to get the following result...
Curvature of Functions $y=f(x)$
For a plane curve determined by $y=f(x),$ the curvature is given by $$ \kappa(x)=\frac{|f''(x)|}{\left(1+[f'(x)]^2\right)^{3/2}} $$
Example
Find the curvature function, $\kappa(x)$ of the curve $y=x^2-2$.
For $f(x)=x^2,$
$$
\begin{array}{lll}
\displaystyle \kappa(x)&\displaystyle= \frac{|f''(x)|}{\left(1+[f'(x)]^2\right)^{3/2}}&\mbox{}\\
\displaystyle &\displaystyle=\frac{|2|}{\left(1+[2x]^2\right)^{3/2}} &\mbox{}\\
\displaystyle &\displaystyle=\frac{2}{\left(1+4x^2\right)^{3/2}} &\mbox{}\\
\end{array}
$$
Normal Vectors
Recall that a vector perpendicular to a plane is is called a normal vector.
For a curve in the plane or in space, a vector perpendicular to the curve is also called a normal vector.
If this vector has length $1,$ then it is called a unit normal vector.
At any point on the curve, there are infinitely many unit normal vectors.
We uniquely define a unit normal vector to a curve in the following way...
The Principal Unit Normal Vector
The principal unit normal vector denoted as ${\bf N}(t)$ is defined to be $$ {\bf N}(t)=\frac{{\bf T}'(t)}{\Vert{\bf T}'(t)\Vert} $$ provided $\Vert{\bf T}'(t)\Vert\neq 0$
The Principal Unit Normal Vector in the Plane
${\bf T}(t)$$, \,\,$
${\bf N}(t)$
Example
Calculate the principal unit normal vector ${\bf N}(t)$ for $$ {\bf r}(t)=3\cos t\,{\bf i}+2\sin t\,{\bf j} $$
From the previous section we know that
$$
\displaystyle {\bf T}(t)=\frac{-3\sin t}{\sqrt{5\sin^2 t+4}}\,{\bf i}+\frac{2\cos t}{\sqrt{5\sin^2 t+4}}\,{\bf j}
$$
Polishing off our first-term-calculus chops, we compute ${\bf T}'(t).$
$$
\begin{array}{ll}
{\bf T}'(t)&=\displaystyle \frac{d}{dt}\left(\frac{-3\sin t}{\sqrt{5\sin^2 t+4}}\right)\,{\bf i}+\frac{d}{dt}\left(\frac{2\cos t}{\sqrt{5\sin^2 t+4}}\right)\,{\bf j}\\
&=\displaystyle \frac{(\sqrt{5\sin^2 t+4})(-3\cos t)+(3\sin t)\frac{1}{2\sqrt{5\sin^2 t+4}}10\sin t \cos t }{5\sin^2 t+4}\,{\bf i}+\frac{\sqrt{5\sin^2 t+4}(-2\sin t)-(2\cos t) \frac{1}{2\sqrt{5\sin^2 t+4}}10\sin t \cos t }{5\sin^2 t+4}\,{\bf j}\\
&=\displaystyle \frac{(5\sin^2 t+4)(-3\cos t)+(3\sin t)5\sin t \cos t }{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf i}+\frac{(5\sin^2 t+4)(-2\sin t)-(2\cos t) 5\sin t \cos t }{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf j}\\
&=\displaystyle \frac{-15\sin^2 t \cos t -12\cos t+15\sin^2 t \cos t }{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf i}+\frac{-10\sin^3 t -8 \sin t-10\cos^2 t \sin t }{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf j}\\
&=\displaystyle \frac{-12\cos t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf i}+\frac{(-10\sin^2 t -10\cos^2 t) \sin t -8 \sin t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf j}\\
&=\displaystyle \frac{-12\cos t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf i}+\frac{-10\sin t -8 \sin t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf j}\\
&=\displaystyle \frac{-12\cos t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf i}+\frac{-18 \sin t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf j}\\
\end{array}
$$
Then,
$$
\begin{array}{ll}
\Vert{\bf T}'(t)\Vert
&=\displaystyle \sqrt{\left(\frac{-12\cos t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\right)^2+\left(\frac{-18 \sin t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\right)^2}\\
&=\displaystyle \sqrt{ \frac{144\cos^2 t}{\left(5\sin^2 t+4\right)^3}+ \frac{324\sin^2 t}{\left(5\sin^2 t+4\right)^3} }\\
&=\displaystyle \sqrt{ \frac{144\cos^2 t+144\sin^2 t +180 \sin^2 t}{(5\sin^2 t+4)^3} }\\
&=\displaystyle \sqrt{ \frac{144 +180 \sin^2 t}{(5\sin^2 t+4)^3} }\\
&=\displaystyle \sqrt{ \frac{36(4 + 5\sin^2 t)}{(5\sin^2 t+4)^3} }\\
&=\displaystyle \sqrt{ \frac{36}{(5\sin^2 t+4)^2} }\\
&=\displaystyle \frac{6}{|5\sin^2 t+4|}\\
&=\displaystyle \frac{6}{5\sin^2 t+4}\\
\end{array}
$$
Finally, we have
$$
\begin{array}{ll}
{\bf N}(t)
&=\displaystyle \frac{{\bf T}'(t)}{\Vert {\bf T}'(t) \Vert}\\
&=\displaystyle \frac{1}{\Vert {\bf T}'(t) \Vert}\left(\frac{-12\cos t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf i}+\frac{-18 \sin t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf j}\right)\\
&=\displaystyle \frac{5\sin^2 t+4}{6}\left(\frac{-12\cos t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf i}+\frac{-18 \sin t}{\left(\sqrt{5\sin^2 t+4}\right)^3}\,{\bf j}\right)\\
&=\displaystyle \frac{-2\cos t}{\sqrt{5\sin^2 t+4}}\,{\bf i}+\frac{-3 \sin t}{\sqrt{5\sin^2 t+4}}\,{\bf j}\\
&=\displaystyle -\frac{2\cos t}{\sqrt{5\sin^2 t+4}}\,{\bf i}-\frac{3 \sin t}{\sqrt{5\sin^2 t+4}}\,{\bf j}\\
\end{array}
$$
Example:
${\bf r}($$t$$)=$$3\cos t$$\,{\bf i}$$+2\sin t$$\,{\bf j}$$, \,\,$
${\bf T}($$t$$)=$$\displaystyle \frac{-3\sin t}{\sqrt{5\sin^2 t+4}}$$\,{\bf i}$$\displaystyle +\frac{2\cos t}{\sqrt{5\sin^2 t+4}}$$\,{\bf j}$ $, \,\,$ ${\bf N}($$t$$)=$$\displaystyle \frac{-2\cos t}{\sqrt{5\sin^2 t+4}}$$\,{\bf i}$$+\displaystyle \frac{-3 \sin t}{\sqrt{5\sin^2 t+4}}$$\,{\bf j}$
${\bf T}($$t$$)=$$\displaystyle \frac{-3\sin t}{\sqrt{5\sin^2 t+4}}$$\,{\bf i}$$\displaystyle +\frac{2\cos t}{\sqrt{5\sin^2 t+4}}$$\,{\bf j}$ $, \,\,$ ${\bf N}($$t$$)=$$\displaystyle \frac{-2\cos t}{\sqrt{5\sin^2 t+4}}$$\,{\bf i}$$+\displaystyle \frac{-3 \sin t}{\sqrt{5\sin^2 t+4}}$$\,{\bf j}$
The Principal Unit Normal and Tangent Vectors in Space
In space, ${\bf T}(t)$ and ${\bf N}(t)$ are defined in the same way as they are in the plane.
However, the third dimension allows for more complex behavior.
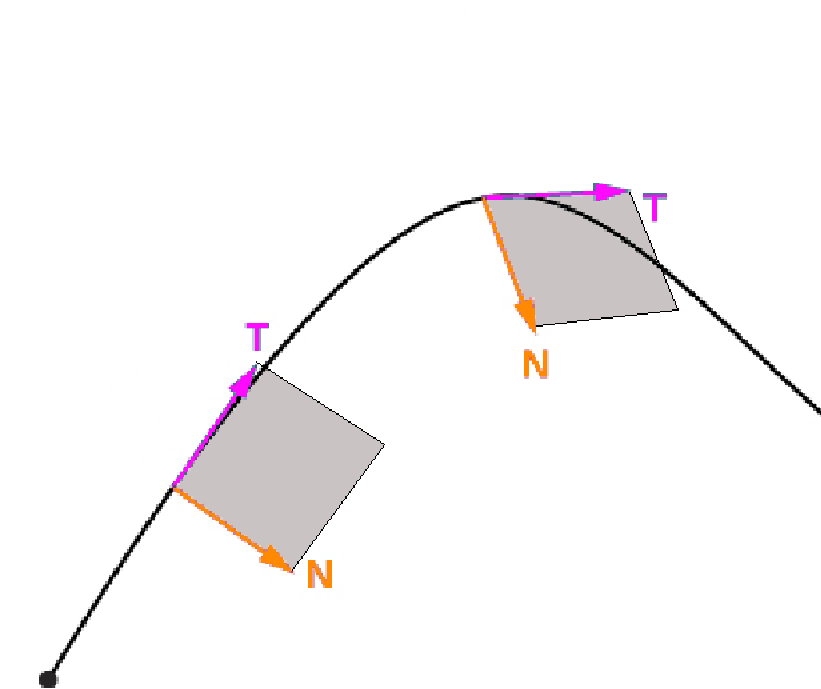
At each point along the curve, the two orthogonal tangent an normal vectors form a not-necessarily-level plane called the osculating plane.
Example
Find the principal unit normal vector, ${\bf N}(t),$ at an arbitrary point $t$ on the helix $${\bf r}(t)=4\cos t \, {\bf i}+4\sin t \, {\bf j}+3t\,{\bf k}$$
We must first calculate the unit tangent.
$$
\begin{array}{lll}
\displaystyle {\bf T}(t) &\displaystyle= \frac{{\bf r}'(t)}{\Vert {\bf r}'(t) \Vert}&\mbox{}\\
\displaystyle &\displaystyle=\frac{-4\sin t \, {\bf i}+4\cos t \, {\bf j}+3\,{\bf k}}{\Vert-4\sin t \, {\bf i}+4\cos t \, {\bf j}+3\,{\bf k}\Vert} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-4\sin t \, {\bf i}+4\cos t \, {\bf j}+3\,{\bf k}}{5} &\mbox{from our previous curvature calculation}\\
\displaystyle &\displaystyle=-\frac{4}{5}\sin t \, {\bf i}+\frac{4}{5}\cos t \, {\bf j}+\frac{3}{5}\,{\bf k} &\mbox{}\\
\end{array}
$$
Then $\displaystyle {\bf T}'(t)=-\frac{4}{5}\cos t \, {\bf i}-\frac{4}{5}\sin t \, {\bf j}$ so that
$$
\begin{array}{lll}
\displaystyle {\bf N}(t) &\displaystyle= \frac{{\bf T}'(t)}{\Vert {\bf T}'(t) \Vert}&\mbox{}\\
\displaystyle &\displaystyle= \frac{-\frac{4}{5}\cos t \, {\bf i}-\frac{4}{5}\sin t \, {\bf j}}{\Vert -\frac{4}{5}\cos t \, {\bf i}-\frac{4}{5}\sin t \, {\bf j} \Vert} &\mbox{}\\
\displaystyle &\displaystyle= \frac{-\frac{4}{5}\cos t \, {\bf i}-\frac{4}{5}\sin t \, {\bf j}}{\frac{4}{5}} &\mbox{}\\
\displaystyle &\displaystyle=-\cos t \, {\bf i}-\sin t \, {\bf j} &\mbox{}\\
\end{array}
$$
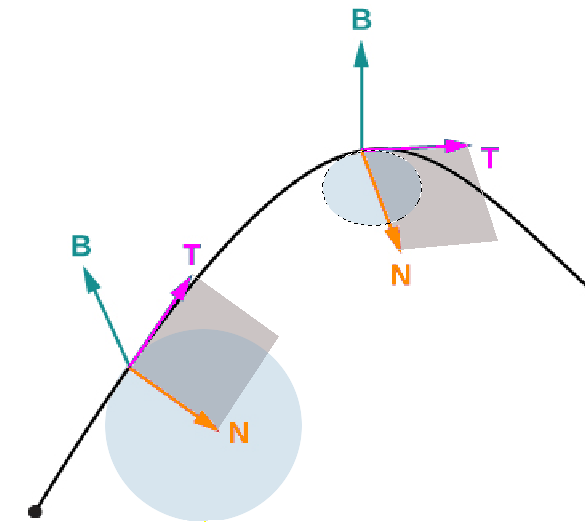
The Binormal Vector for Curves in Space
When we take the cross product of ${\bf T}(t)$ and ${\bf N}(t),$ we get another unit normal vector called the binormal vector denoted ${\bf B}(t)$ .
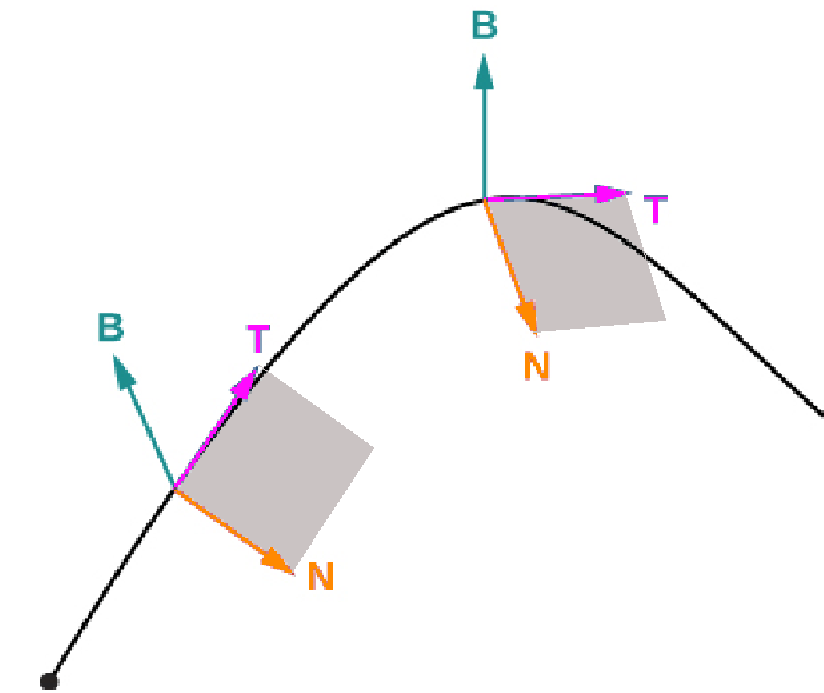
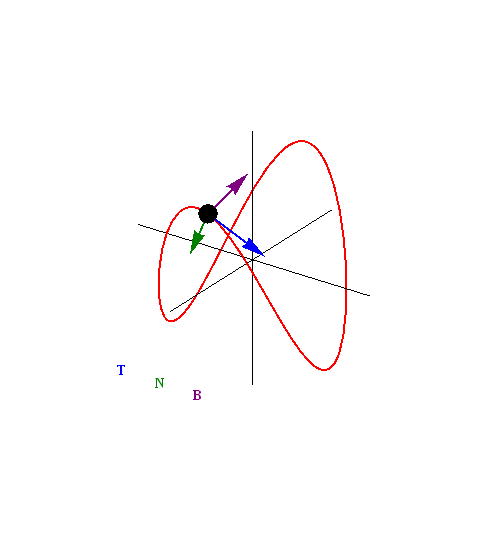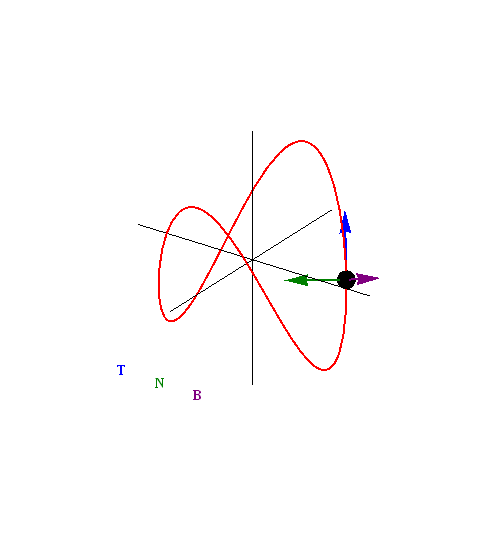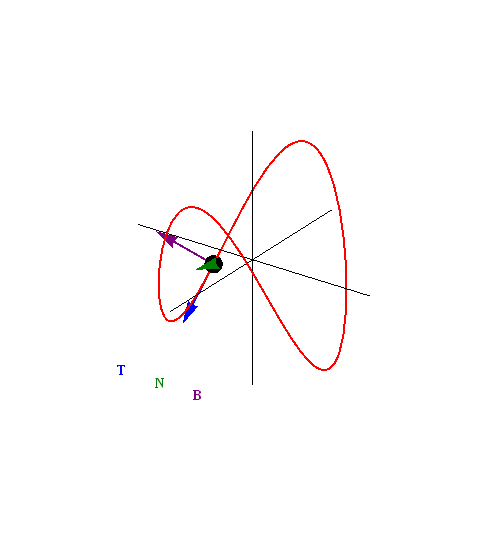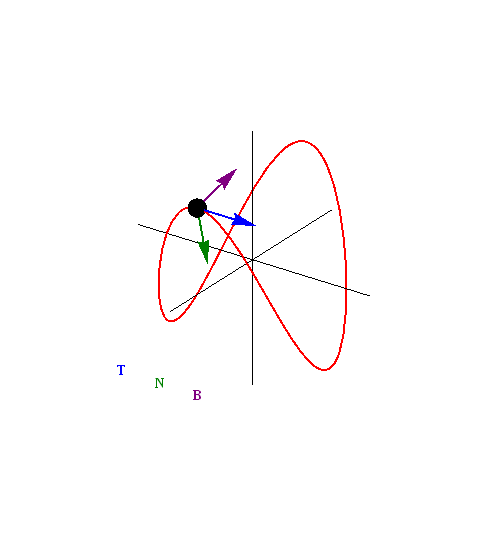
These three vectors have a special name: the Frenet* Frame of Reference, which is also known as a ${\bf TNB}$ frame.
*Pronounced "fre-nay"
The ${\bf TNB}$ Frame
${\bf B}(t)$
$=$
${\bf T}(t)$
$\times$
${\bf N}(t)$

The ${\bf TNB}$ frame is a set of three mutually orthogonal unit vectors which describe the motion of a curve defined by a vector-valued function ${\bf r}(t).$
Example of ${\bf TNB}$ Frame
Example
Find the ${\bf TNB}$ frame at an arbitrary point $t$ on the helix $${\bf r}(t)=4\cos t \, {\bf i}+4\sin t \, {\bf j}+3t\,{\bf k}$$
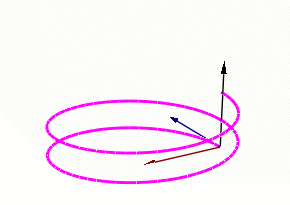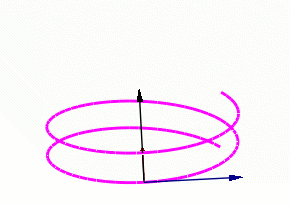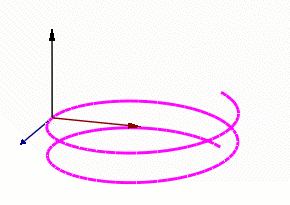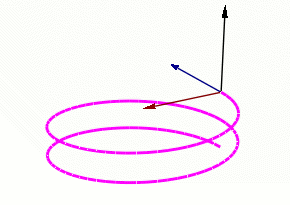
From the previous example we have already found ${\bf T}$ and ${\bf N}:$
$$\displaystyle {\bf T}(t)=-\frac{4}{5}\sin t \, {\bf i}+\frac{4}{5}\cos t \, {\bf j}+\frac{3}{5}\,{\bf k}$$
and $$\displaystyle {\bf N}(t)=-\cos t \, {\bf i}-\sin t \, {\bf j}$$
We now find the binormal vector ${\bf B}.$
$$
\begin{array}{lll}
\displaystyle {\bf B}(t)&\displaystyle= {\bf T}(t)\times{\bf N}(t)&\mbox{}\\
\displaystyle &\displaystyle= \left(-\frac{4}{5}\sin t \, {\bf i}+\frac{4}{5}\cos t \, {\bf j}+\frac{3}{5}\,{\bf k}\right)\times(-\cos t \, {\bf i}-\sin t \, {\bf j}) &\mbox{}\\
\displaystyle &\displaystyle= \left|\begin{array}{ccc} {\bf i}&{\bf j}&{\bf k} \\ -\frac{4}{5}\sin t&\frac{4}{5}\cos t&\frac{3}{5} \\ -\cos t&-\sin t&0 \\ \end{array}\right| &\mbox{}\\
\displaystyle &\displaystyle= \frac{3}{5}\sin t \, {\bf i}-\frac{3}{5}\cos t \, {\bf j}+\frac{4}{5}{\bf k}&\mbox{}\\
\end{array}
$$
In summary, the ${\bf TNB}$-frame at any point $t$ is
$$
\begin{array}{rl}
{\bf T}(t)&=-\frac{4}{5}\sin t \, {\bf i}+\frac{4}{5}\cos t \, {\bf j}+\frac{3}{5}\,{\bf k}\\
{\bf N}(t)&=-\cos t \, {\bf i}-\sin t \, {\bf j}\\
{\bf B}(t)&=\frac{3}{5}\sin t \, {\bf i}-\frac{3}{5}\cos t \, {\bf j}+\frac{4}{5}{\bf k}\\
\end{array}
$$


The Circle of Curvature
Recall the driving analogy for curvature.
Suppose we're in the middle of a turn when suddenly, the steering wheel gets stuck!
Assuming we could continue our path without any interruption of motion, our path would be a circle.
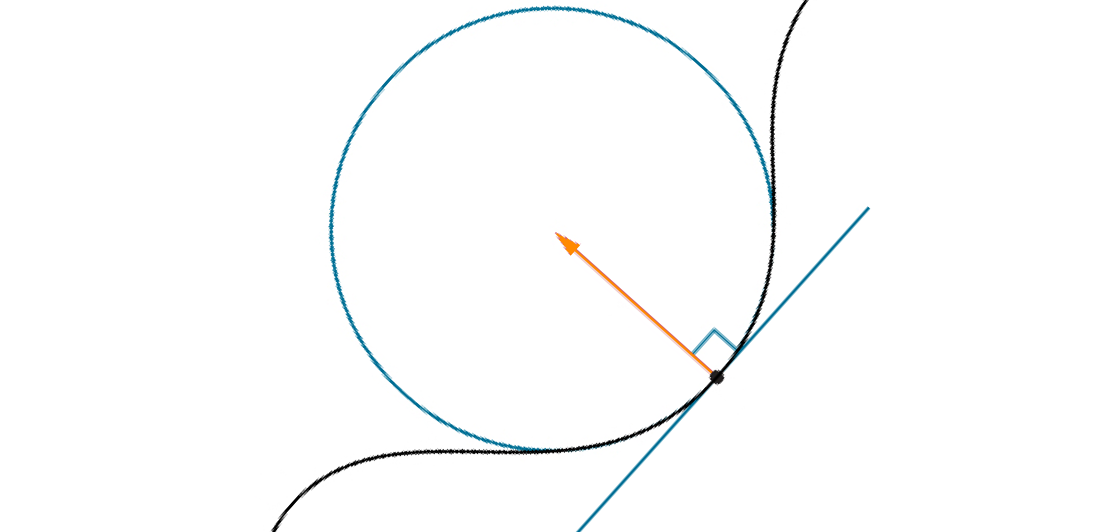
This is the idea of the circle of curvature.
The Circle of Curvature
Notice that at the point the steering wheel gets stuck:
- The curvature of the circle and the curve are the same.
- The tangent line of the circle and the curve are the same.

This idea leads to the following definition...
The Circle of Curvature in the Plane
At a point on a curve, the circle of curvature, also known as the osculating circle, the circle with the same point, tangent, line, and curvature, and lies on the concave side of the curve.

Special Note: A circle with curvature $\kappa$ has radius $\displaystyle\frac{1}{\kappa}.$ So, the smaller the circle of curvature, the sharper the curve.
Question: Has anyone heard the phrase "to turn on a dime"?
The Circle of Curvature
Example
Find the circle of curvature at $t=0$ and $\displaystyle t=\frac{\pi}{2}$ on the ellipse ${\bf r}(t)=3\cos t \, {\bf i}+2\sin t \, {\bf j}.$
Find the circle of curvature at $t=0$ and $\displaystyle t=\frac{\pi}{2}$ on the ellipse ${\bf r}(t)=3\cos t \, {\bf i}+2\sin t \, {\bf j}.$
From a previous example we know that $\displaystyle \kappa(0)=\frac{3}{4}$ and
$\displaystyle \kappa\left(\frac{\pi}{2}\right)=\frac{2}{9}.$
Using this information we will find the circle of curvature at both points.
At $t=0:$ The circle of curvature at $t=0$ has radius $\displaystyle \frac{1}{\kappa}=\frac{4}{3}.$
Also, since ${\bf r}(0)=3\cos 0 \, {\bf i}+2\sin 0 \, {\bf j}=3{\bf i}=\langle 3,0 \rangle,$ the point $(3,0)$ is on the graph of the ellipse and is on the edge circle as seen in the figure below.

We see that the circle is centered at $\displaystyle \left(\frac{5}{3},0\right)$ so that the equation of our circle of curvature is $$ \left(x-\frac{5}{3}\right)^2+y^2=\frac{16}{9} $$ At $\displaystyle t=\frac{\pi}{2}:$ The circle of curvature at $\displaystyle t=\frac{\pi}{2}$ has radius $\displaystyle \frac{1}{\kappa}=\frac{9}{2}.$
Also, since ${\bf r}\left(\frac{\pi}{2}\right)=3\cos \left(\frac{\pi}{2}\right) \, {\bf i}+2\sin \left(\frac{\pi}{2}\right) \, {\bf j}=2{\bf j}=\langle 0,2 \rangle,$ the point $(0,2)$ is on the graph of the ellipse and is on the edge circle as seen in the figure below.
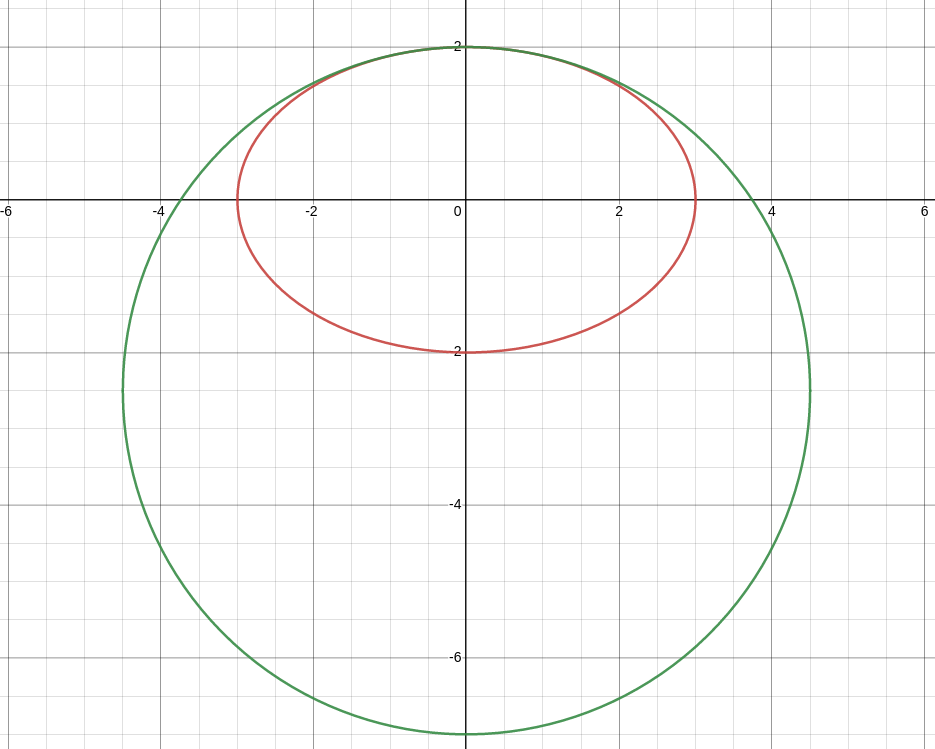
We see that the circle is centered at $\displaystyle \left(0,-\frac{5}{2}\right)$ so that the equation of our circle of curvature is $$ x^2+\left(y+\frac{5}{2}\right)^2=\frac{81}{4} $$
Using this information we will find the circle of curvature at both points.
At $t=0:$ The circle of curvature at $t=0$ has radius $\displaystyle \frac{1}{\kappa}=\frac{4}{3}.$
Also, since ${\bf r}(0)=3\cos 0 \, {\bf i}+2\sin 0 \, {\bf j}=3{\bf i}=\langle 3,0 \rangle,$ the point $(3,0)$ is on the graph of the ellipse and is on the edge circle as seen in the figure below.

We see that the circle is centered at $\displaystyle \left(\frac{5}{3},0\right)$ so that the equation of our circle of curvature is $$ \left(x-\frac{5}{3}\right)^2+y^2=\frac{16}{9} $$ At $\displaystyle t=\frac{\pi}{2}:$ The circle of curvature at $\displaystyle t=\frac{\pi}{2}$ has radius $\displaystyle \frac{1}{\kappa}=\frac{9}{2}.$
Also, since ${\bf r}\left(\frac{\pi}{2}\right)=3\cos \left(\frac{\pi}{2}\right) \, {\bf i}+2\sin \left(\frac{\pi}{2}\right) \, {\bf j}=2{\bf j}=\langle 0,2 \rangle,$ the point $(0,2)$ is on the graph of the ellipse and is on the edge circle as seen in the figure below.

We see that the circle is centered at $\displaystyle \left(0,-\frac{5}{2}\right)$ so that the equation of our circle of curvature is $$ x^2+\left(y+\frac{5}{2}\right)^2=\frac{81}{4} $$
Example
Find the circle of curvature for $y=x^2-2$ at $x=0.$
Find the circle of curvature for $y=x^2-2$ at $x=0.$
From a previous example, we know that
$$
\displaystyle \kappa(x)=\frac{2}{\left(1+4x^2\right)^{3/2}}
$$
Thus, at $x=0$ th curvature is $\displaystyle \kappa(0)=\frac{2}{\left(1+4\cdot 0^2\right)^{3/2}}=2.$
The radius of curvature is then $\displaystyle \frac{1}{\kappa}=\frac{1}{2}.$
We also know that $(0,-2)$ is a point on the graph of $y=x^2-2.$
It follows from the above two facts that the center of the circle is $\displaystyle \left(0,-\frac{3}{2}\right).$
To see this more clearly, we draw the figure using the information we have.
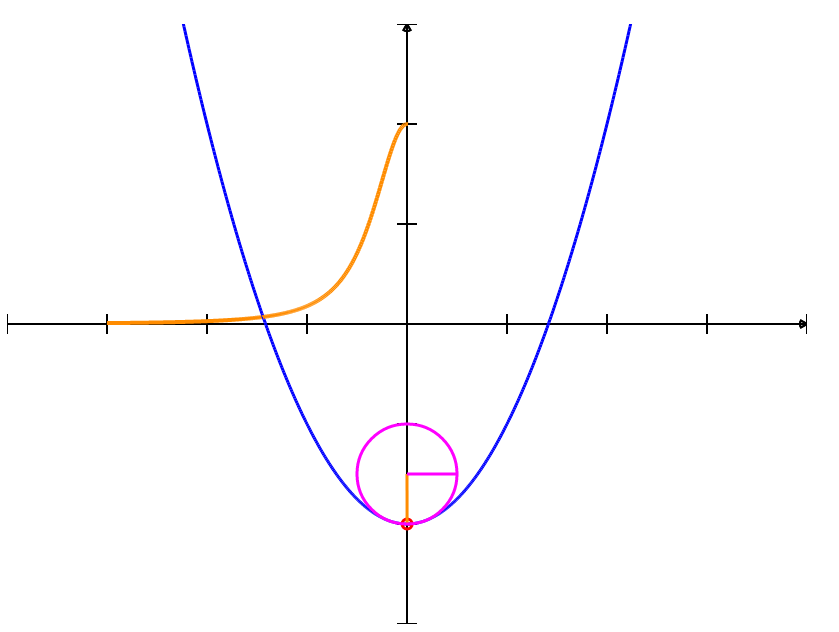
Since our circle of curvature has radius $\displaystyle \frac{1}{2}$ and is centered at $\displaystyle \left(0,-\frac{3}{2}\right),$ it is described by the equation $$ x^2+\left(y+\frac{3}{2}\right)^2=\frac{1}{4} $$
The radius of curvature is then $\displaystyle \frac{1}{\kappa}=\frac{1}{2}.$
We also know that $(0,-2)$ is a point on the graph of $y=x^2-2.$
It follows from the above two facts that the center of the circle is $\displaystyle \left(0,-\frac{3}{2}\right).$
To see this more clearly, we draw the figure using the information we have.

Since our circle of curvature has radius $\displaystyle \frac{1}{2}$ and is centered at $\displaystyle \left(0,-\frac{3}{2}\right),$ it is described by the equation $$ x^2+\left(y+\frac{3}{2}\right)^2=\frac{1}{4} $$
The Circle of Curvature for Curves in Space
At a point on a curve, the circle of curvature, also known as the osculating circle, the circle which lies in the osculating plane with the same point, tangent, line, and curvature, and lies on the concave side of the curve.
Applications
In the next section, we'll discuss some applications of the above ideas to physics.
However, the next example shows how curvature can be applied to understanding the self propulsion of certain kinds of microorganisms.
Application
The video below uses a "signed" curvature to illustrate how an aggregate of amoebae of the species Dictyostelium discoideum use peristalsis for self propulsion.
Summary of Formulas
${\bf TNB}$ Frame $$ \begin{array}{lr} \displaystyle {\bf T}(t)=\frac{{\bf r}'(t)}{\Vert {\bf r}'(t)\Vert} & \mbox{principal unit tangent vector}\\ \displaystyle {\bf N}(t)=\frac{{\bf T}'(t)}{\Vert {\bf T}'(t)\Vert} & \mbox{principal unit normal vector}\\ \displaystyle {\bf B}(t)={\bf T}(t)\times {\bf N}(t) & \mbox{binormal vector}\\ \end{array} $$ Curvature $$ \begin{array}{lr} \displaystyle \kappa=\left\Vert\frac{d{\bf T}}{ds}\right\Vert=\frac{\Vert{\bf T}'(t)\Vert}{\Vert {\bf r}'(t)\Vert}=\frac{\Vert{\bf r}'(t)\times{\bf r}''(t)\Vert}{\Vert{\bf r}'(t)\Vert^3} & \mbox{curvature of ${\bf r}(t)$ at $t$}\\ \displaystyle \kappa(x)=\frac{|f''(x)|}{\left(1+[f'(x)]^2\right)^{3/2}} & \mbox{curvature of $f(x)$ at $x$}\\ \end{array} $$