Just as a single-variable function maps a number to a number, a vector-valued function maps a number to a vector.
Vector-Valued functions describe curves either in the plane or in space
Vector-Valued Functions in the Plane
A vector-valued function in $\mathbb{R}^2$ has the form $${\bf r}(t)=f(t)\,{\bf i}+g(t)\,{\bf j}=\langle f(t),g(t)\rangle$$ where $f(t)$ and $g(t)$ are real valued functions of a single variable (or parameter) $t.$
Example
For the vector-valued function ${\bf r}(t)=3\cos t\,{\bf i}+2\sin t\,{\bf j}$ find
$\displaystyle {\bf r}\left(0\right)$
$$
\begin{array}{lll}
\displaystyle {\bf r}\left(0\right)&\displaystyle= 3\cos\left(0\right)\,{\bf i}+2\sin\left(0\right)\,{\bf j}&\mbox{}\\
\displaystyle &\displaystyle= 3{\bf i}+0{\bf j}&\mbox{}\\
\displaystyle &\displaystyle= 3{\bf i}&\mbox{}\\
\displaystyle &\displaystyle=\langle 3,0\rangle &\mbox{}\\
\end{array}
$$
$\displaystyle {\bf r}\left(\frac{3\pi}{4}\right)$
$$
\begin{array}{lll}
\displaystyle {\bf r}\left(\frac{3\pi}{4}\right)&\displaystyle= 3\cos\left(\frac{3\pi}{4}\right)\,{\bf i}+2\sin\left(\frac{3\pi}{4}\right)\,{\bf j}&\mbox{}\\
\displaystyle &\displaystyle= 3\left(-\frac{\sqrt{2}}{2}\right){\bf i}+2\left(\frac{\sqrt{2}}{2}\right){\bf j}&\mbox{}\\
\displaystyle &\displaystyle=-\frac{3\sqrt{2}}{2}{\bf i}+\sqrt{2}\,{\bf j}&\mbox{}\\
\displaystyle &\displaystyle=\left\langle-\frac{3\sqrt{2}}{2},\sqrt{2}\right\rangle&\mbox{}\\
\end{array}
$$
Vector-Valued Functions in Space
A vector-valued function in $\mathbb{R}^3$ has the form $${\bf r}(t)=f(t)\,{\bf i}+g(t)\,{\bf j}+h(t)\,{\bf k}=\langle f(t),g(t),h(t)\rangle$$ where $f(t),$ $g(t),$ and $h(t)$ are real valued functions of a single variable (or parameter) $t.$
Example
For the vector-valued function ${\bf r}(t)=4\cos t\,{\bf i}+4\sin t\,{\bf j}+t\,{\bf k}$ find
$\displaystyle {\bf r}\left(0\right)$
$$
\begin{array}{lll}
\displaystyle {\bf r}\left(0\right)&\displaystyle=4\cos\left(0\right)\,{\bf i}+4\sin \left(0\right)\,{\bf j}+0\,{\bf k} &\mbox{}\\
\displaystyle &\displaystyle=4{\bf i}+0{\bf j}+0{\bf k} &\mbox{}\\
\displaystyle &\displaystyle=4{\bf i}&\mbox{}\\
\displaystyle &\displaystyle=\langle 4,0,0\rangle &\mbox{}\\
\end{array}
$$
$\displaystyle {\bf r}\left(\frac{3\pi}{4}\right)$
$$
\begin{array}{lll}
\displaystyle {\bf r}\left(\frac{3\pi}{4}\right)&\displaystyle=4\cos\left(\frac{3\pi}{4}\right)\,{\bf i}+4\sin \left(\frac{3\pi}{4}\right)\,{\bf j}+\frac{3\pi}{4}\,{\bf k} &\mbox{}\\
\displaystyle &\displaystyle=4\left(-\frac{\sqrt{2}}{2}\right){\bf i}+4\cdot\frac{\sqrt{2}}{2}{\bf j}+\frac{3\pi}{4}{\bf k} &\mbox{}\\
\displaystyle &\displaystyle=-2\sqrt{2}{\bf i}+2\sqrt{2}{\bf j}+\frac{3\pi}{4}{\bf k} &\mbox{}\\
\displaystyle &\displaystyle=\left\langle -2\sqrt{2},2\sqrt{2},\frac{3\pi}{4}\right\rangle &\mbox{}\\
\end{array}
$$
Domain of Vector-Valued Functions
The domain of a vector valued function is all values of $t$ such that ${\bf r}(t)$ is defined.
Examples
Find the domain of the following vector valued functions.
(a) $\displaystyle {\bf r}(t) = 3\cos t \, {\bf i} + 2\sin t \, {\bf j}$
Since $\cos t$ and $\sin t$ can take any real number $t$ as an input, the domain of ${\bf r}$ is all real numbers $\mathbb{R}.$
(b) $\displaystyle {\bf r}(t) = 3\tan t \,{\bf i} + 4 \sec t \,{\bf j} + 5t \,{\bf k}$
Since the ${\bf r}$ is undefined when $\cos t=0,$ we must find these values and exclude them from the domain.
We know $\cos t=0$ precisely when $t$ is $\displaystyle \frac{\pi}{2}$ plus any integer multiple of $\displaystyle \pi.$
Thus, the domain of ${\bf r}$ is all real numbers except $t=\displaystyle \frac{\pi}{2}+k\pi$ where $k$ is an integer.
In fancy schmancy mathematical notation we can write the domain as $$ \left\{t\in\mathbb{R}\Bigr|t\neq \frac{\pi}{2}+k\pi, k \in \mathbb{Z} \right\} $$
We know $\cos t=0$ precisely when $t$ is $\displaystyle \frac{\pi}{2}$ plus any integer multiple of $\displaystyle \pi.$
Thus, the domain of ${\bf r}$ is all real numbers except $t=\displaystyle \frac{\pi}{2}+k\pi$ where $k$ is an integer.
In fancy schmancy mathematical notation we can write the domain as $$ \left\{t\in\mathbb{R}\Bigr|t\neq \frac{\pi}{2}+k\pi, k \in \mathbb{Z} \right\} $$
Graphing Vector-Valued Functions
The graph of a vector-valued function $${\bf r}(t)=f(t)\,{\bf i}+g(t)\,{\bf j}=\langle f(t),g(t)\rangle$$ or $${\bf r}(t)=f(t)\,{\bf i}+g(t)\,{\bf j}+h(t)\,{\bf k}=\langle f(t),g(t),h(t)\rangle$$ is a curve consisting of all terminal points of ${\bf r}(t)$ when graphed in standard position.
Graphing Vector-Valued Functions
For every value of $t,$ a vector-valued function assigns a vector. The graph of ${\bf r}(t)$ is the collection of terminal points of the vector in standard position. $${\bf r}(t)=f(t)\,{\bf i}+g(t)\,{\bf j}=\langle f(t),g(t)\rangle$$
Example
Graph the plane curve represented by ${\bf r}(t) = 3\cos t \, {\bf i} + 2\sin t \, {\bf j}$ where $0 \leq t \leq 2\pi.$
${\bf r}($$)=3\cos($$)\,{\bf i}+2\sin($$)\,{\bf j}=$$\,{\bf i}+$$\,{\bf j}$
Example
Graph the space curve represented by ${\bf r}(t) = 4\cos t \,{\bf i} + 4\sin t \, {\bf j} + t \,{\bf k}.$
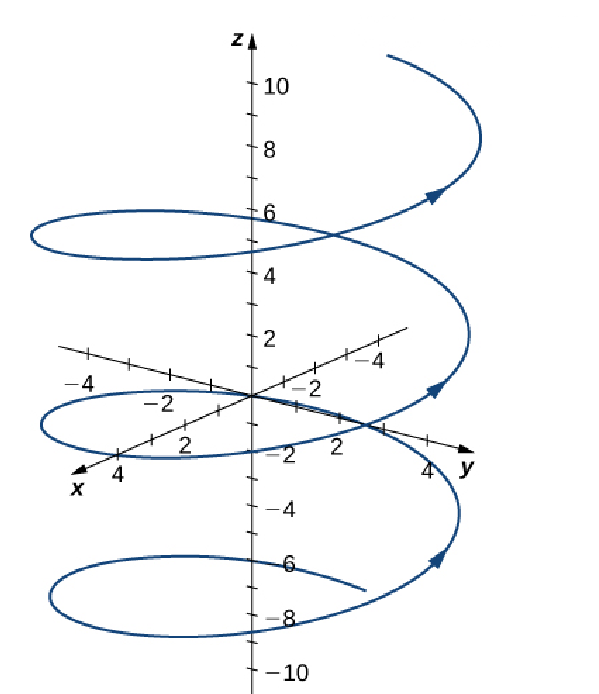
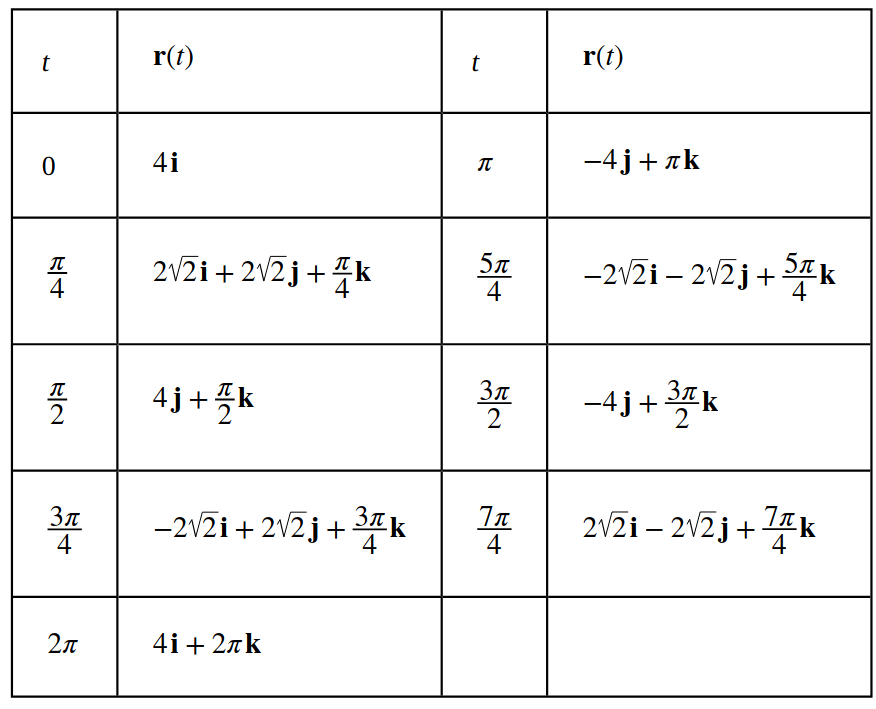
Application
A low-flying plane is dropping off a supply package to a remote Alaskan village. At the moment the package is released, the plane's altitude is $250$ meters and its speed is $50$ meters per second. Ignoring air resistance, the trajectory of the package is modelled by the vector-valued function ${\bf s}(t)=50t\,{\bf i}+(250-4.9t^2)\,{\bf j}.$
${\bf s}($$t$$)=$$50t$$\,{\bf i}$$+(250-4.9t^2)$$\,{\bf j}$
$, \,\,$
Orientation of the Curve
Notice the arrows on the graph of a vector-valued function indicating the direction of travel.
Vector-valued functions have an orientation which is the direction $x,$ $y,$ and possibly $z$ move as the parameter $t$ increases.
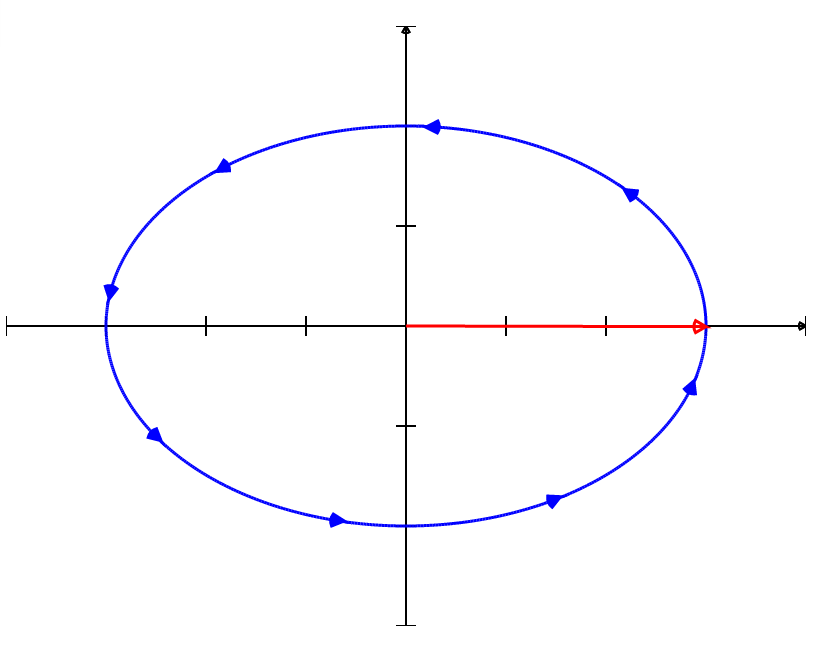

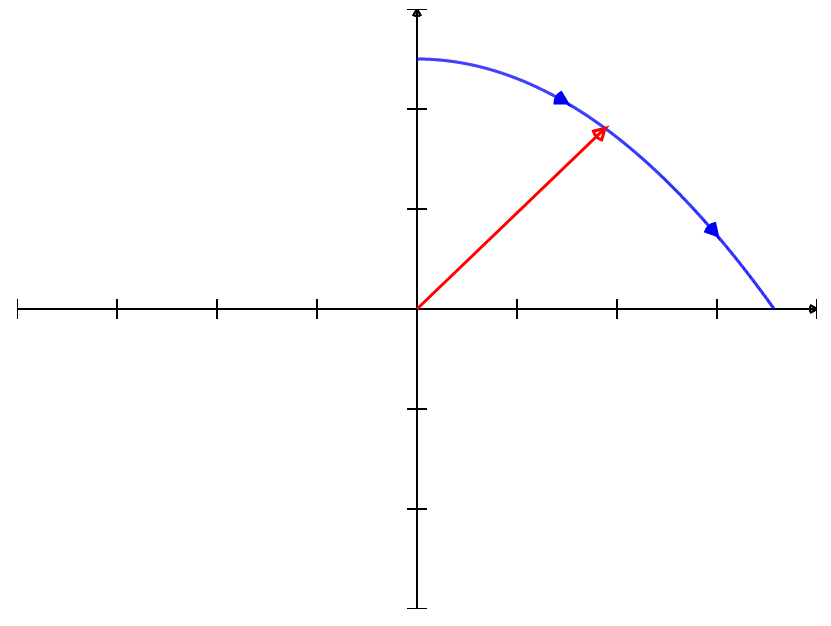
You May Have Already Noticed...
A vector valued function $${\bf r}(t)=f(t){\bf i}+g(t){\bf j}=\langle f(t),g(t)\rangle$$ or $${\bf r}(t)=f(t){\bf i}+g(t){\bf j}+h(t){\bf k}=\langle f(t),g(t),h(t)\rangle$$ is essentially the same thing as a parametrically defined curve either in the plane $$ x=f(t)\\ y=g(t)\\ $$ or in space $$ x=f(t)\\ y=g(t)\\ z=h(t)\\ $$
Restricting the Domain
Sometimes we might restrict the domain of of the parameter $t$ when modelling a particular situation.
Example: Graph the plane curve ${\bf r}(t)=(t^2-3){\bf i}+(2t+1){\bf j}$ on the restricted domain $-2 \leq t \leq 3.$
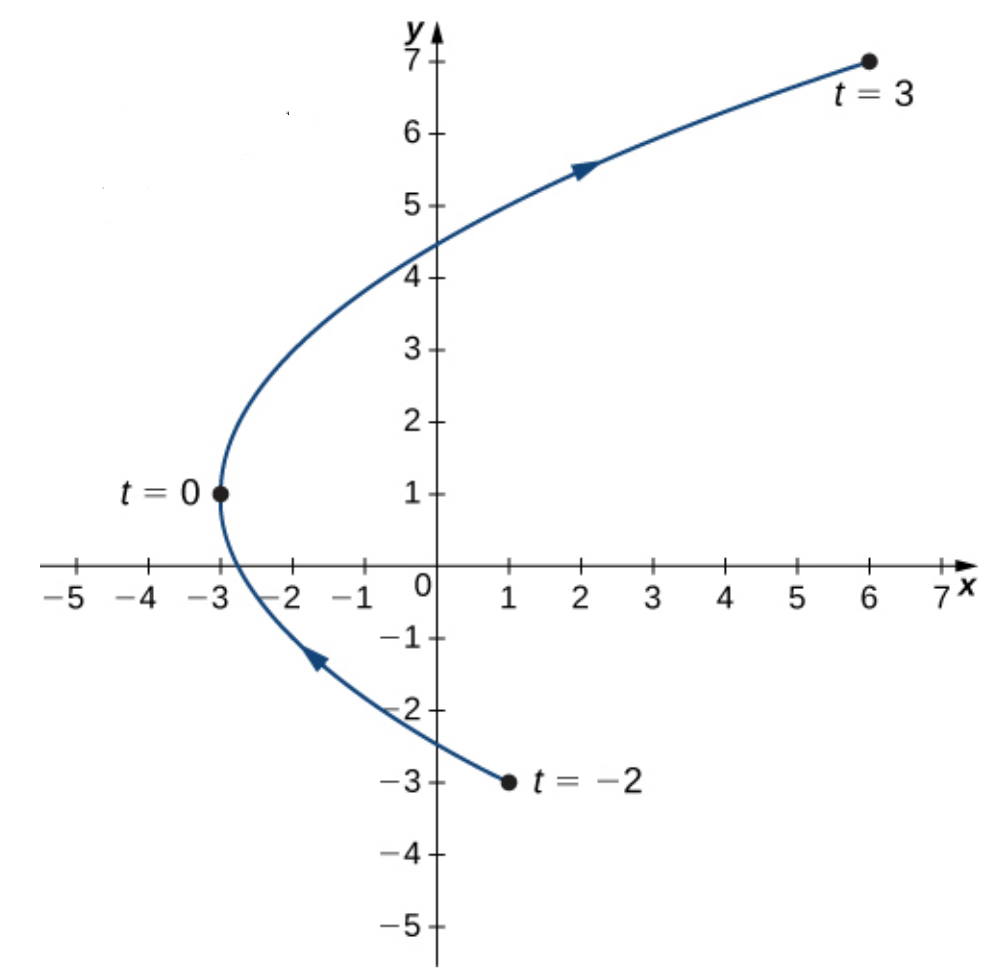 $\,\,\,
\begin{array}{|l|l|}
\hline
t& {\bf r}(t)\\
\hline
-2 &{\bf i}-3{\bf j}\\
\hline
-1&-2{\bf i}-{\bf j}\\
\hline
0&-3{\bf i}+{\bf j}\\
\hline
1&-2{\bf i}+3{\bf j}\\
\hline
2&{\bf i}+5{\bf j}\\
\hline
3&6{\bf i}+7{\bf j}\\
\hline
\end{array}
$
$\,\,\,
\begin{array}{|l|l|}
\hline
t& {\bf r}(t)\\
\hline
-2 &{\bf i}-3{\bf j}\\
\hline
-1&-2{\bf i}-{\bf j}\\
\hline
0&-3{\bf i}+{\bf j}\\
\hline
1&-2{\bf i}+3{\bf j}\\
\hline
2&{\bf i}+5{\bf j}\\
\hline
3&6{\bf i}+7{\bf j}\\
\hline
\end{array}
$
Reparameterizations: Parameterizations are not unique. For example, vector-valued functions
${\bf r}(t) = 3\cos t \, {\bf i} + 2\sin t \, {\bf j}$ and
${\bf r}(t) = 3\cos t^3 \, {\bf i} + 2\sin t^3 \, {\bf j}$
trace out the same curve. However, these are not equivalent representations. If the above functions represent the location of a physical object at time $t,$ then they would give different locations at different times.
Eliminating the Parameter
Setting up a table is a sure-fire way to graph a vector-valued function.
But there are other ways to know what the curve will look like.
One way is to eliminate the parameter.
Eliminating the Parameter
Example: Eliminate the parameter $t$ in the vector-valued function below to obtain a direct relationship between $x$ and $y.$ $$ \begin{array}{l} {\bf s}(t)=50t\,{\bf i}+(250-4.9t^2)\,{\bf j} \end{array} $$

The first equation is $x(t)=50t.$ Then $\displaystyle t=\frac{x(t)}{50}.$ Substituting into the second equation,
$$
y(t)=250-4.9\left(\frac{x(t)}{50}\right)^2
$$
We may now drop the $t$ (eliminate the parameter!) since it is no longer explicit, we simplify and rewrite the above as
$
\displaystyle y=250-\frac{4.9}{2500}x^2
$
which becomes
$$
y=250-0.00196x^2
$$
Eliminating the Parameter
Example: Eliminate the parameter $t$ for the vector-valued function $${\bf r}(t)=(t^2-3)\,{\bf i}+(2t+1)\,{\bf j}$$ to obtain a direct relationship between $x$ and $y.$

We'll first solve for $t$ in the second component $y(t)=2t+1$ to get
$$
t=\frac{y(t)-1}{2}
$$
Substituting $t$ into the first component we have
$$
x(t)=\left(\frac{y(t)-1}{2}\right)^2-3
$$
Since the parameter has now been eliminated, we drop the $t$ and simplify.
$$
\begin{array}{lll}
&\displaystyle x=\left(\frac{y-1}{2}\right)^2-3 &\mbox{}\\
\implies &\displaystyle x=\frac{y^2-2y+1}{4}-3 &\mbox{}\\
\implies &\displaystyle x=\frac{y^2-2y+1-12}{4} &\mbox{}\\
\implies &\displaystyle x=\frac{y^2-2y-11}{4} &\mbox{}\\
\implies &\displaystyle x=\frac{1}{4}y^2-\frac{1}{2}y-\frac{11}{4} &\mbox{}\\
\end{array}
$$
Eliminating the Parameter
Example: Eliminate the parameter $t$ for the vector-valued function $$ \begin{array}{l} {\bf r}(t)=3 \cos t\,{\bf i}+2 \sin t\,{\bf j} \end{array} $$ to obtain a direct relationship between $x$ and $y.$
We will use the Pythagorean Identity again, but we must first solve for $\cos t$ and $\sin t$ knowing that
$$
\begin{array}{l}
x(t)= 3\cos t\\
y(t)= 2\sin t
\end{array}
$$
Then
$$
\begin{array}{l}
\displaystyle \frac{x(t)}{3}= \cos t\\
\displaystyle \frac{y(t)}{2}= \sin t
\end{array}
$$
We then have
$$
\left(\frac{x(t)}{3}\right)^2+\left(\frac{y(t)}{2}\right)^2=\cos^2 t+\sin^2 t=1
$$
or
$$
\frac{x^2}{9}+\frac{y^2}{4}=1
$$
which is the equation of an ellipse.
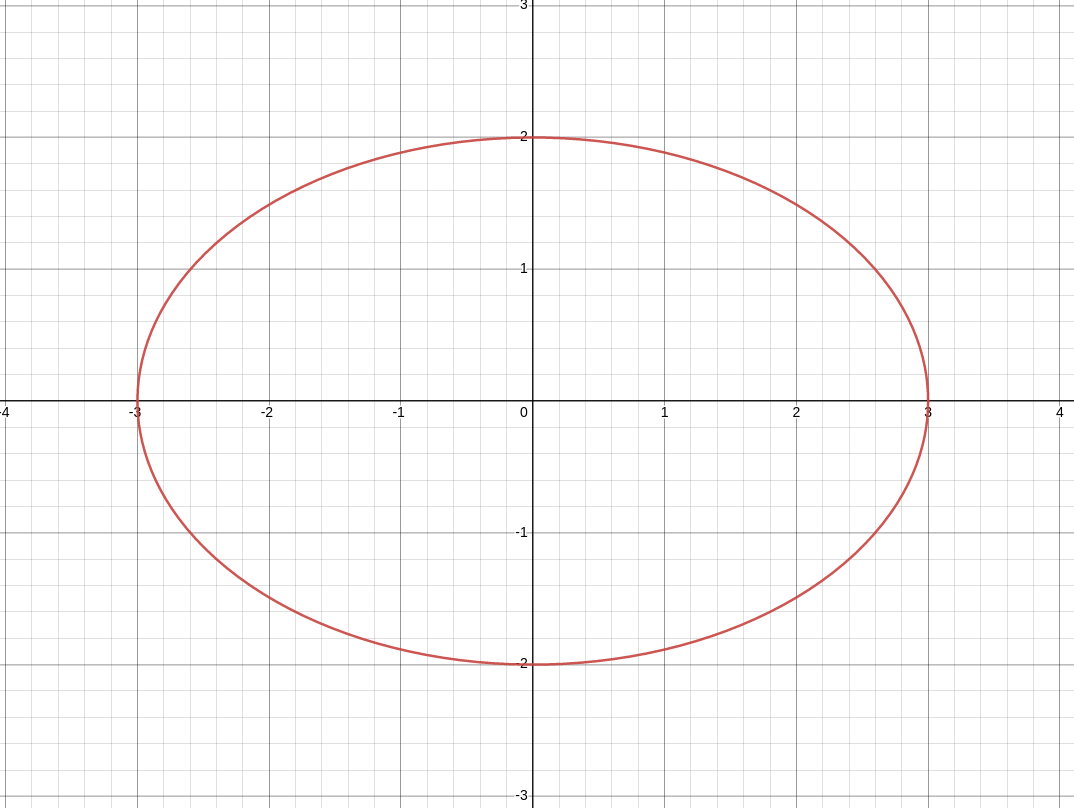

Limits of Vector-Valued Functions
The limit of the vector-valued function $$ \lim_{t \rightarrow a}{\bf r}(t)={\bf L} $$ means that $$ \lim_{t \rightarrow a} \Vert {\bf r}(t)-{\bf L}\Vert=0 $$
Limits of Vector-Valued Functions
If ${\bf r}(t)=f(t)\,{\bf i}+g(t)\,{\bf j}=\langle f(t),g(t)\rangle$ is a vector-valued function in the plane, then $$ \lim_{t \rightarrow a}{\bf r}(t) =\left[\lim_{t \rightarrow a}f(t)\right]\,{\bf i}+\left[\lim_{t \rightarrow a}g(t)\right]\,{\bf j} =\left\langle \lim_{t \rightarrow a}f(t),\lim_{t \rightarrow a} g(t)\right\rangle $$
If ${\bf r}(t)=f(t)\,{\bf i}+g(t)\,{\bf j}+h(t)\,{\bf k}=\langle f(t),g(t),h(t)\rangle$ is a vector-valued function in space, then $$ \lim_{t \rightarrow a}{\bf r}(t) =\left[\lim_{t \rightarrow a}f(t)\right]\,{\bf i}+\left[\lim_{t \rightarrow a}g(t)\right]\,{\bf j}+\left[\lim_{t \rightarrow a}h(t)\right]\,{\bf k} =\left\langle \lim_{t \rightarrow a}f(t),\lim_{t \rightarrow a} g(t),\lim_{t \rightarrow a} h(t)\right\rangle $$
Example
If ${\bf r}(t)=(t^2-3){\bf i}+(2t+1){\bf j},$ find $ \displaystyle \lim_{t \rightarrow 1} {\bf r}(t). $
$$
\begin{array}{lll}
\displaystyle \lim_{t \rightarrow 1} {\bf r}(t)&\displaystyle= \lim_{t \rightarrow 1} \left[(t^2-3){\bf i}+(2t+1){\bf j}\right]&\mbox{}\\
\displaystyle &\displaystyle= \lim_{t \rightarrow 1}(t^2-3){\bf i}+\lim_{t \rightarrow 1}(2t+1){\bf j}&\mbox{}\\
\displaystyle &\displaystyle= (1^2-3){\bf i}+(2\cdot 1+1){\bf j}&\mbox{}\\
\displaystyle &\displaystyle= -2{\bf i}+3{\bf j}&\mbox{}\\
\displaystyle &\displaystyle= \langle-2,3\rangle&\mbox{}\\
\end{array}
$$
If ${\bf r}(t)=\sqrt{t^2-3t-1}{\bf i}+(4t+3){\bf j}+\sin\left(\frac{(t+1)\pi}{2}\right){\bf k},$ find $ \displaystyle \lim_{t \rightarrow -2} {\bf r}(t). $
$$
\begin{array}{lll}
\displaystyle \lim_{t \rightarrow -2} {\bf r}(t)&\displaystyle= \lim_{t \rightarrow -2} \left[\sqrt{t^2-3t-1}{\bf i}+(4t+3){\bf j}+\sin\left(\frac{(t+1)\pi}{2}\right){\bf k}\right] &\mbox{}\\
\displaystyle &\displaystyle= \left(\lim_{t \rightarrow -2}\sqrt{t^2-3t-1}\right){\bf i}+\lim_{t \rightarrow -2}(4t+3){\bf j}+\lim_{t \rightarrow -2}\sin\left(\frac{(t+1)\pi}{2}\right){\bf k} &\mbox{}\\
\displaystyle &\displaystyle= \sqrt{9}\,{\bf i}+(-5){\bf j}+\left(-1\right){\bf k} &\mbox{}\\
\displaystyle &\displaystyle= 3{\bf i}-5{\bf j}-{\bf k} &\mbox{}\\
\displaystyle &\displaystyle= \langle 3,-5,-1 \rangle&\mbox{}\\
\end{array}
$$
Continuity of Vector-Valued Functions
A vector valued function ${\bf r}(t)$ in either the plane or space is continuous at a point $t=a$ provided
${\bf r}(a)$ is defined
$\displaystyle \lim_{t \rightarrow a} {\bf r}(t)$ exists, and
$\displaystyle \lim_{t \rightarrow a} {\bf r}(t)={\bf r}(a)$
Example
Show that the plane curve ${\bf r}(t)=(t^2-3){\bf i}+(2t+1){\bf j}$ is continuous at $t=2.$
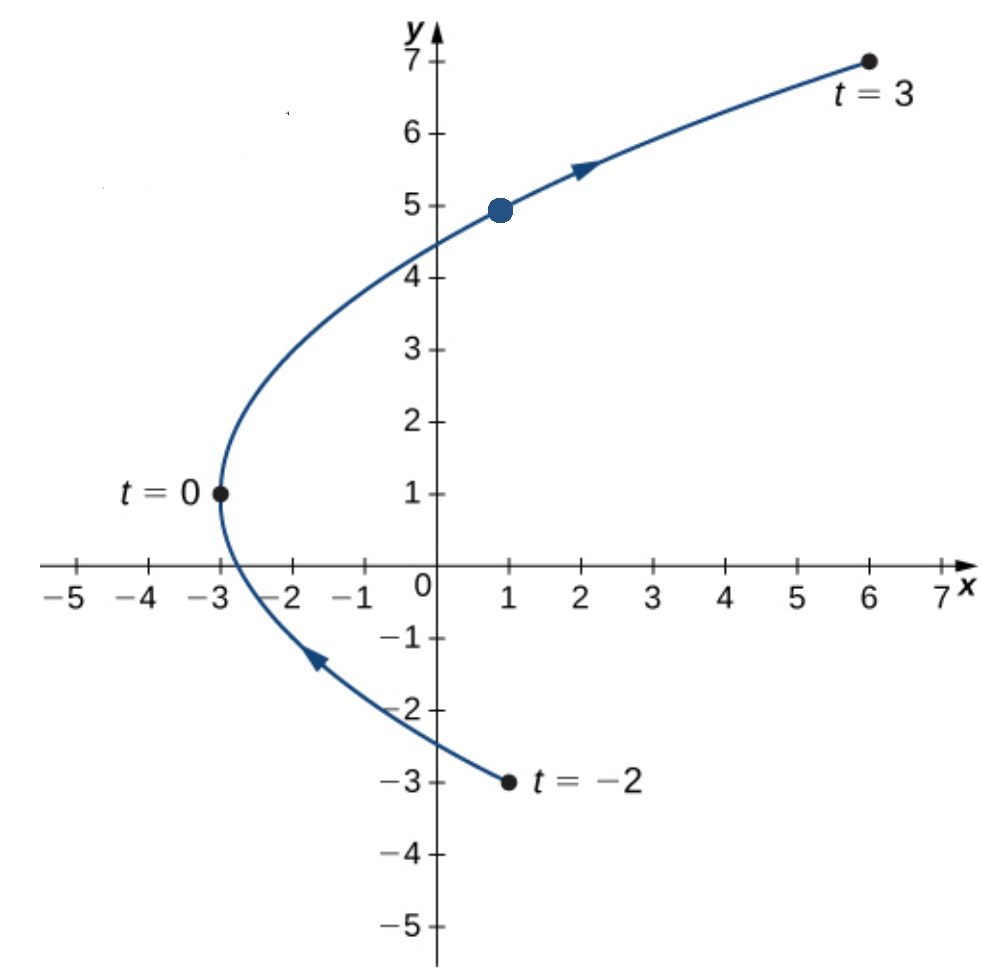
The quantity ${\bf r}(2)$ exists since ${\bf r}(2)=(2^2-3){\bf i}+(2\cdot 2+1){\bf j}={\bf i}+5{\bf j}.$
We now show that $\displaystyle \lim_{t \rightarrow 2}{\bf r}(t)$ exists. Since it is true in general that $$\lim_{t \rightarrow a}{\bf r}(t)=\left[\lim_{t \rightarrow a}f(t)\right]\,{\bf i}+\left[\lim_{t \rightarrow a}g(t)\right]\,{\bf j}$$ all we need to show is that $\displaystyle\lim_{t \rightarrow 2}(t^2-3)$ and $\displaystyle\lim_{t \rightarrow 2}(2t+1)$ exist. From first-term calculus we know that all polynomial functions are continuous.
So, we know that $\displaystyle\lim_{t \rightarrow 2}(t^2-3)=2^2-3=1$ and $\displaystyle\lim_{t \rightarrow 2}(2t+1)=2\cdot 2+1=5.$
Then $$ \lim_{t \rightarrow a}{\bf r}(t)=\lim_{t \rightarrow 2}(t^2-3){\bf i}+\lim_{t \rightarrow 2}(2t+1)={\bf i}+5{\bf j} $$ and we have shown that the limit exists.
From the above arguments we have that $$ \begin{array}{lll} \displaystyle \lim_{t \rightarrow 2}{\bf r}(t)&\displaystyle={\bf i}+5{\bf j}&\mbox{}\\ \displaystyle &\displaystyle={\bf r}(2)&\mbox{}\\ \end{array} $$ which proves that ${\bf r}(t)$ is continuous at $2.$
We now show that $\displaystyle \lim_{t \rightarrow 2}{\bf r}(t)$ exists. Since it is true in general that $$\lim_{t \rightarrow a}{\bf r}(t)=\left[\lim_{t \rightarrow a}f(t)\right]\,{\bf i}+\left[\lim_{t \rightarrow a}g(t)\right]\,{\bf j}$$ all we need to show is that $\displaystyle\lim_{t \rightarrow 2}(t^2-3)$ and $\displaystyle\lim_{t \rightarrow 2}(2t+1)$ exist. From first-term calculus we know that all polynomial functions are continuous.
So, we know that $\displaystyle\lim_{t \rightarrow 2}(t^2-3)=2^2-3=1$ and $\displaystyle\lim_{t \rightarrow 2}(2t+1)=2\cdot 2+1=5.$
Then $$ \lim_{t \rightarrow a}{\bf r}(t)=\lim_{t \rightarrow 2}(t^2-3){\bf i}+\lim_{t \rightarrow 2}(2t+1)={\bf i}+5{\bf j} $$ and we have shown that the limit exists.
From the above arguments we have that $$ \begin{array}{lll} \displaystyle \lim_{t \rightarrow 2}{\bf r}(t)&\displaystyle={\bf i}+5{\bf j}&\mbox{}\\ \displaystyle &\displaystyle={\bf r}(2)&\mbox{}\\ \end{array} $$ which proves that ${\bf r}(t)$ is continuous at $2.$