In the last section we looked at a planes. Planes are examples of surfaces.
We shall now look at other equations in $3$-dimensional space which result in other kinds of surfaces.
Cylindrical Surfaces
As we shall soon see, the word "cylinder" has a much broader meaning than you're probably used to.
However, our first example is very much in line with the notion which is already familiar to us.
Example
Consider the collection of all ordered triples $(x,y,z)$ which satisfy the equation $x^2+y^2=9.$
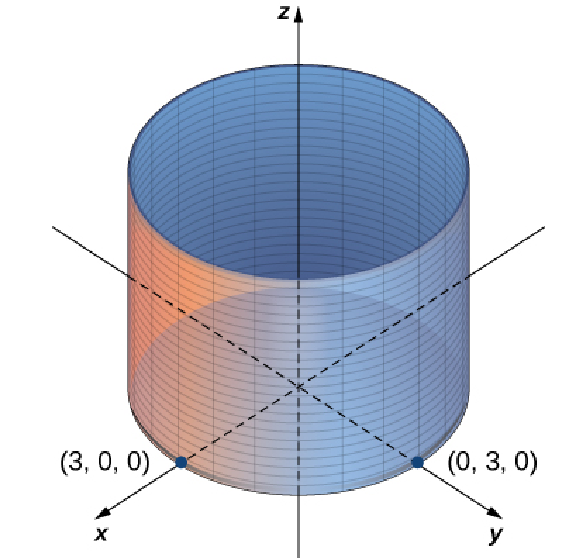
$z$ is a "free" variable, whereas $x$ and $y$ are "constrained" to the circle $x^2+y^2=9.$
Cylindrical Surfaces
A set of lines parallel to a given line passing through a given curve is known as a cylindrical surface, or cylinder.
The parallel lines are called rulings.
Example
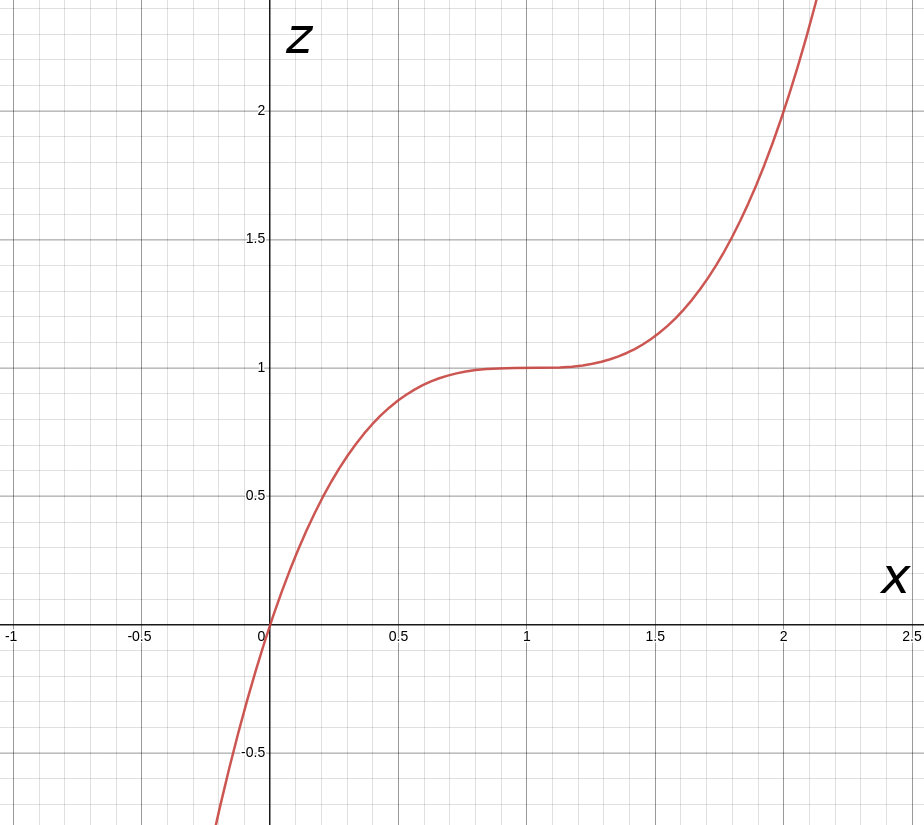
Consider the equation $z=(x-1)^3+1.$ Notice that $y$ is a free variable, but $z$ and $x$ are constrained.
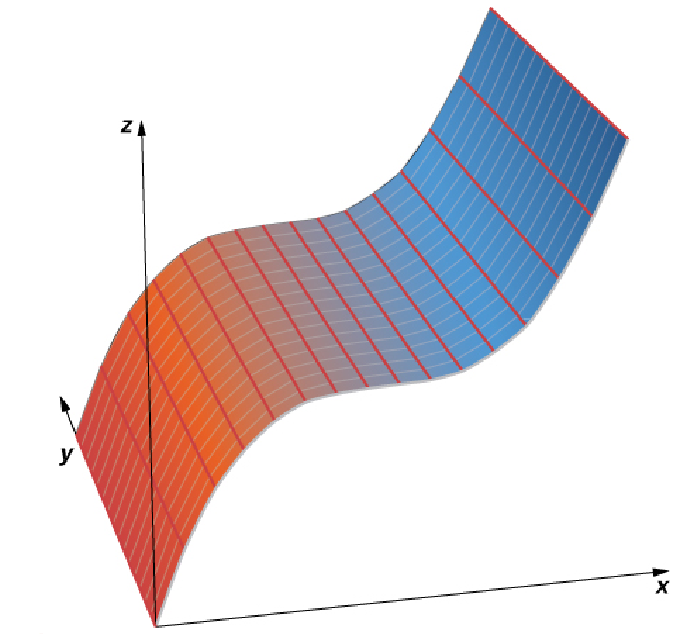
Example
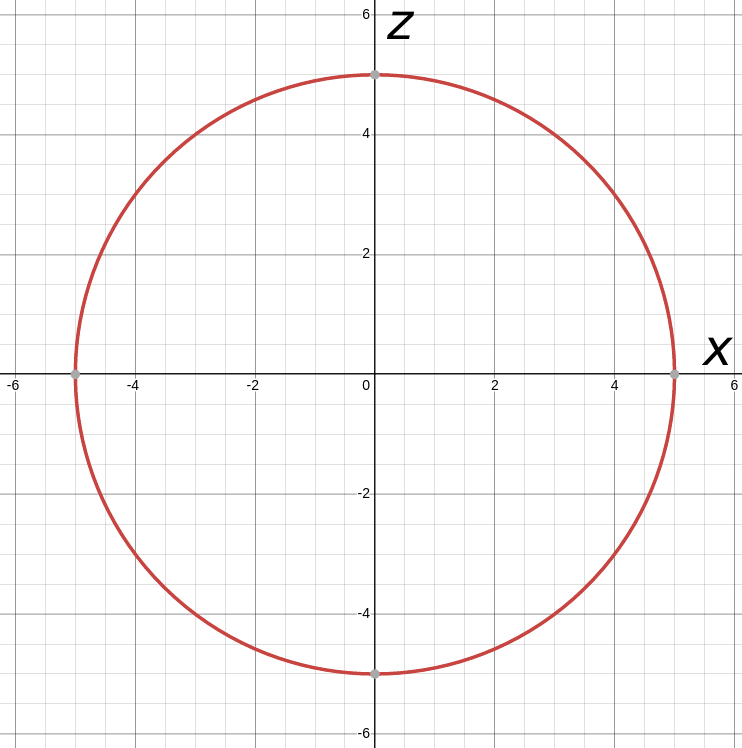
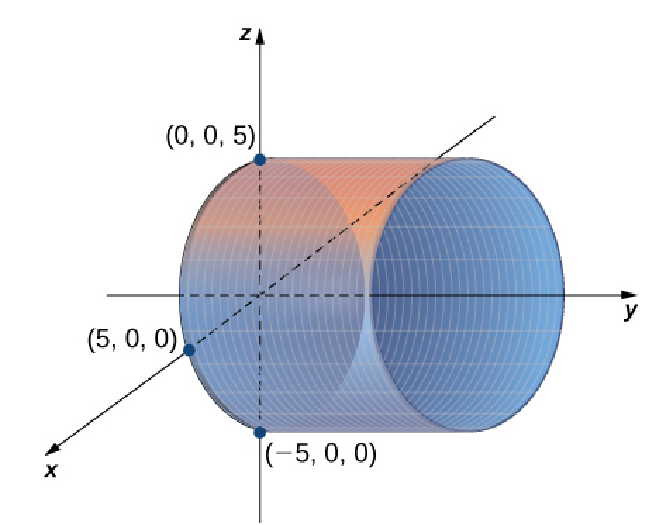
Sketch the graph of the cylindrical surface $x^2+z^2=25.$
Solution
Example
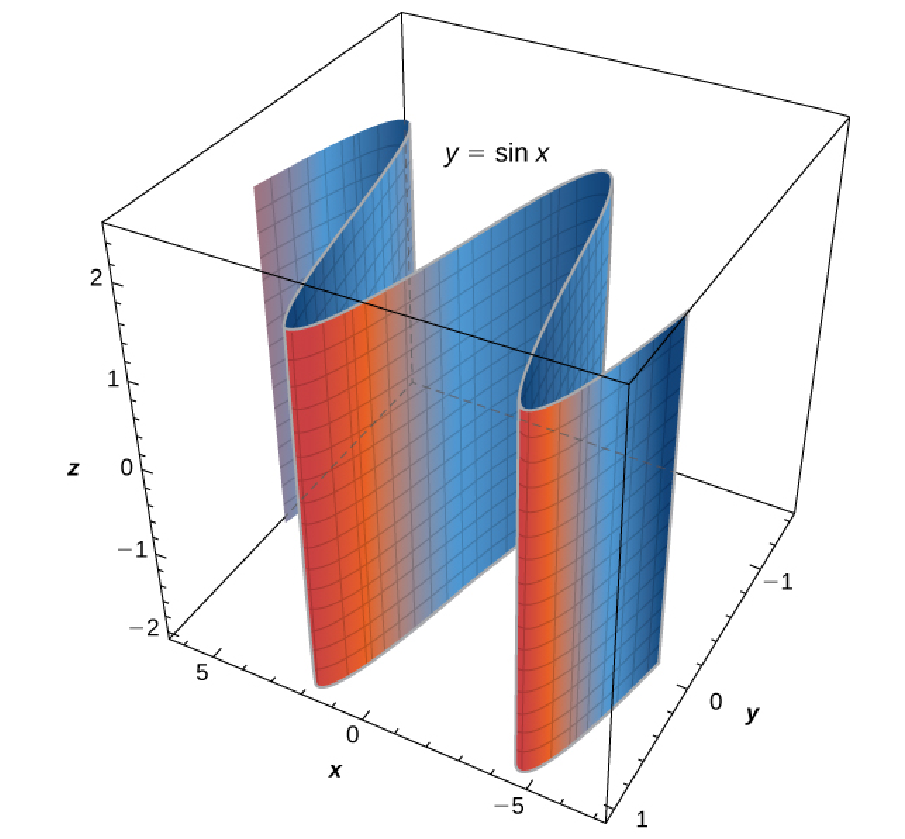
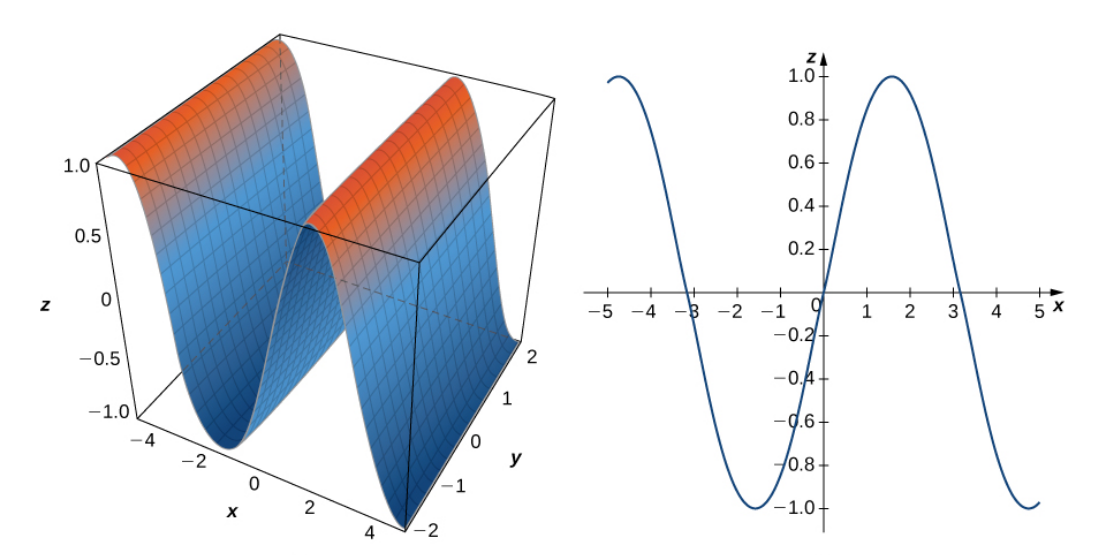
Sketch the graph of the cylindrical surface $y=\sin x.$
Solution
Example
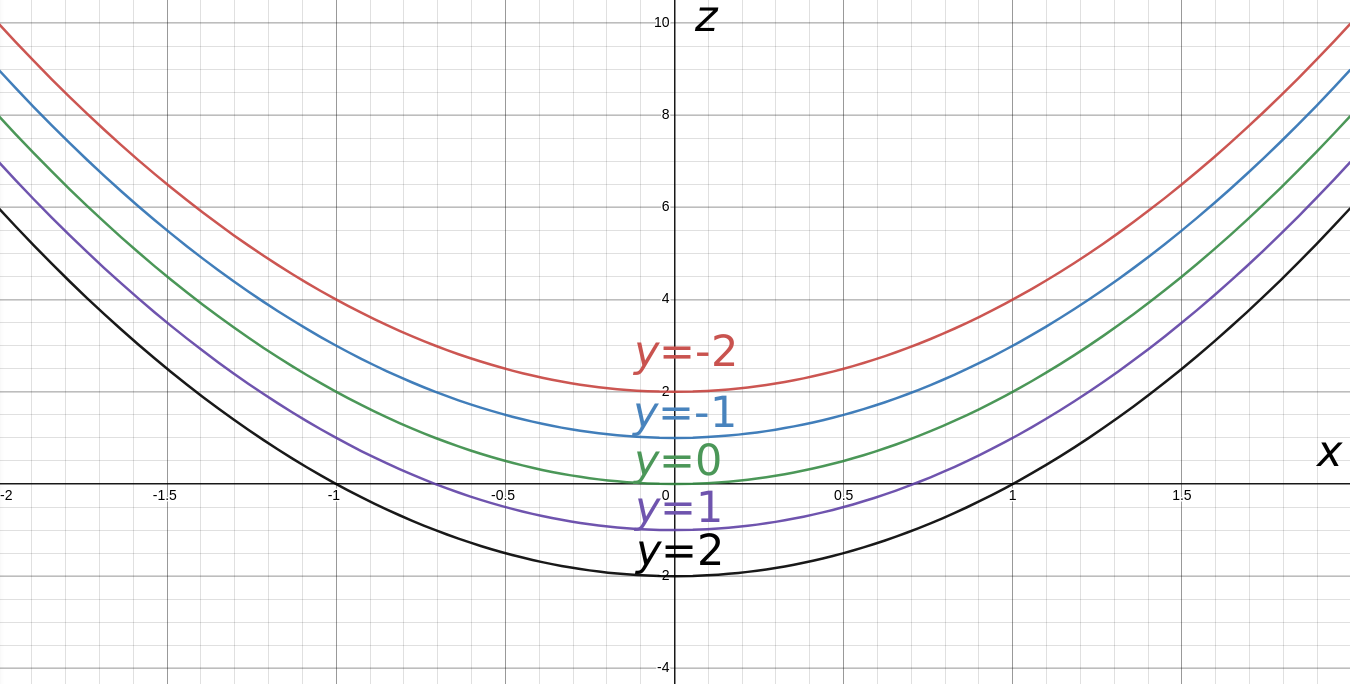
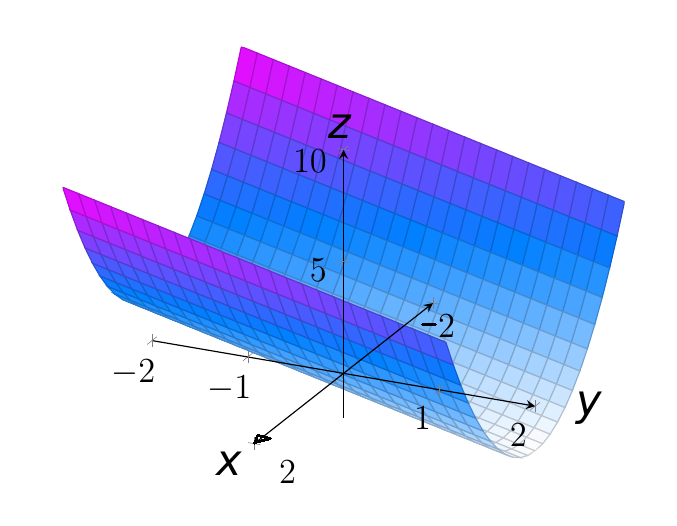
Sketch the graph of the cylindrical surface $z=2x^2-y.$
Solution
For the equation $z=2x^2-y,$ we can think of the variable $y$ as an "ever-changing" vertical intercept (in this case, a $z$-intercept).
More General Surfaces
To visualize more general surfaces, we often look at the curves that result when we slice the surface with a plane.
When we slice using planes parallel to the coordinate axes, these curves have a special name...
Traces
The traces of a surface are the cross-sections created when the surface intersects a plane parallel to one of the coordinate planes.
Example
Letting a plane parallel to the $xz$-plane intersect the surface results in a curve.
Quadric Surfaces
Quadric surfaces are determined by equations with three variables with quadratic terms.
More precisely, they are surfaces that arise from equations of the form $$Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Jz + K = 0.$$ Quadric surfaces are the three-dimensional equivalent of the conic sections.
Example
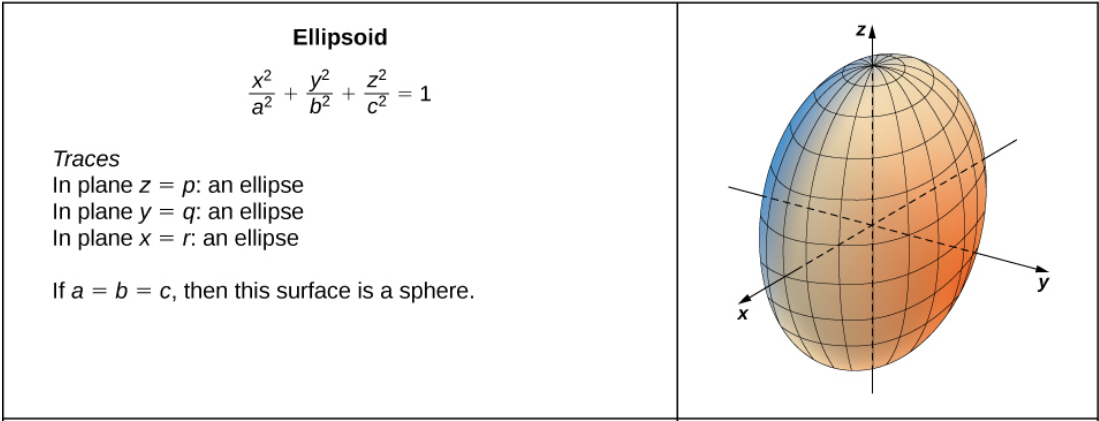
Use traces to sketch a graph of the quadric surface determined by the equation $$\frac{x^2}{4}+\frac{y^2}{9}+\frac{z^2}{25}=1$$
Solution
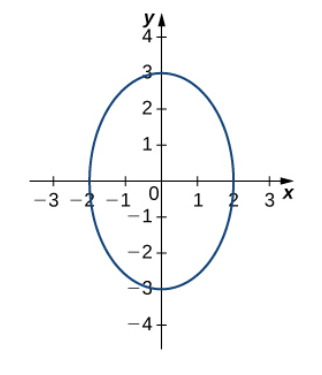
Setting $z=0,$ the trace in the $xy$-plane is $\displaystyle \frac{x^2}{4}+\frac{y^2}{9}=1$
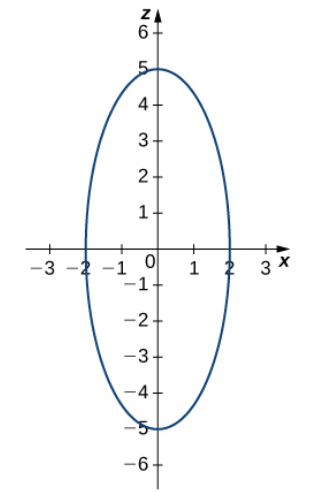
Setting $y=0,$ the trace in the $xz$-plane is $\displaystyle\frac{x^2}{4}+\frac{z^2}{25}=1$
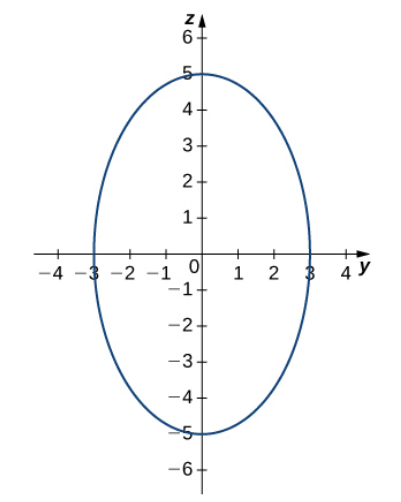
Setting $x=0,$ the trace in the $yz$-plane is $\displaystyle \frac{y^2}{9}+\frac{z^2}{25}=1$
Putting all of this together we can sketch a three-dimensional figure.

This figure is called an ellipsoid since all its traces are ellipses.
Example
Use traces to sketch a graph of the quadric surface determined by the equation $$x^2+\frac{y^2}{4}=\frac{z}{5}$$
Solution
Setting $z$ equal to a constant $c,$ the traces in the $xy$-plane are $\displaystyle x^2+\frac{y^2}{4}=c.$ The trace below is for $c=1.$

Setting $y=0,$ the trace in the $xz$-plane is $\displaystyle x^2=\frac{z}{5}$
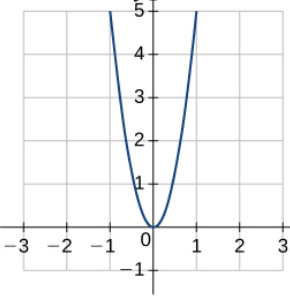
Setting $x=0,$ the trace in the $yz$-plane is $\displaystyle \frac{y^2}{4}=\frac{z}{5}$
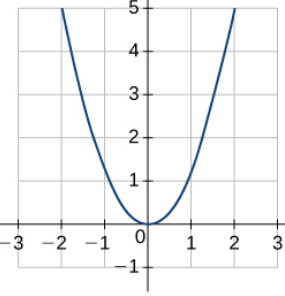
Putting all of this together we can sketch a three-dimensional figure.
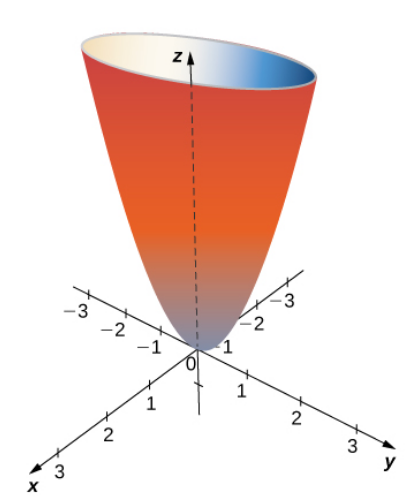
This figure is called an elliptic paraboloid since all its traces are ellipses and parabolas.
Example
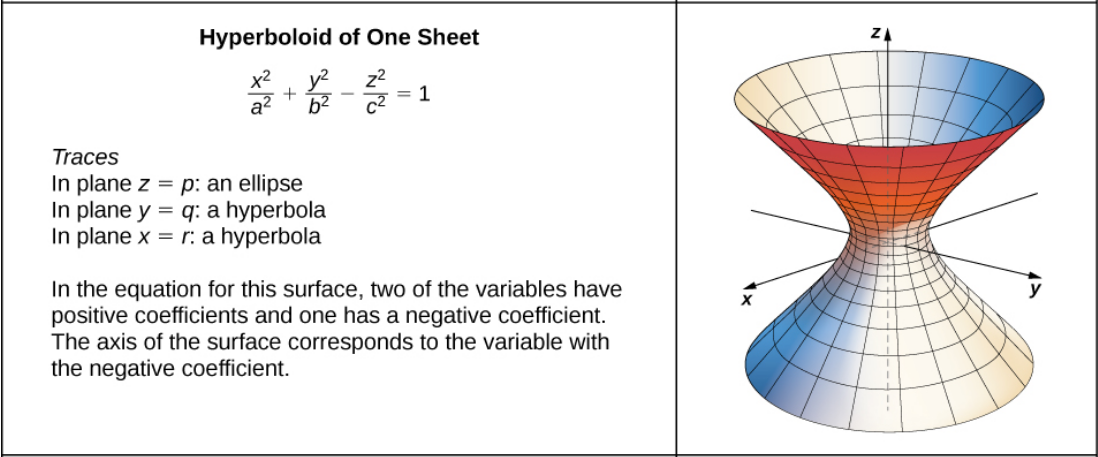
Use traces to sketch a graph of the quadric surface surface determined by the equation $$\frac{x^2}{9}+\frac{y^2}{4}-\frac{z^2}{25}=1$$
Solution
Setting $z$ equal to $0,$ the trace in the $xy$-plane are $\displaystyle \frac{x^2}{9}+\frac{y^2}{4}=1.$

Setting $y=0,$ the trace in the $xz$-plane is $\displaystyle \frac{x^2}{9}-\frac{z^2}{25}=1.$
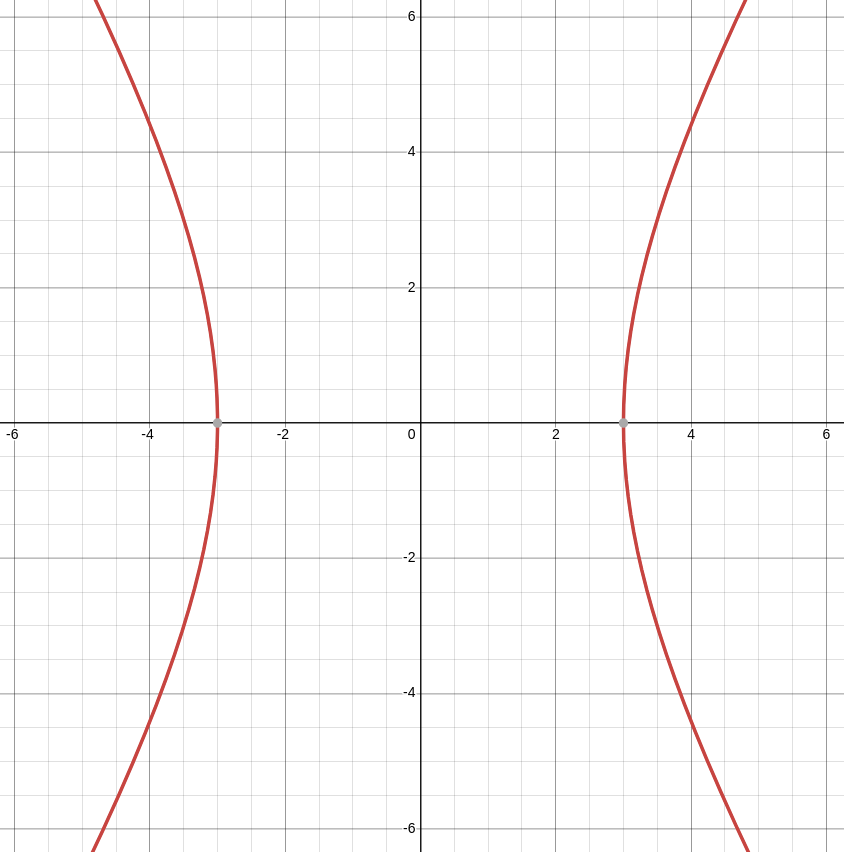
Setting $x=0,$ the trace in the $yz$-plane is $\displaystyle \frac{y^2}{4}-\frac{z^2}{25}=1.$
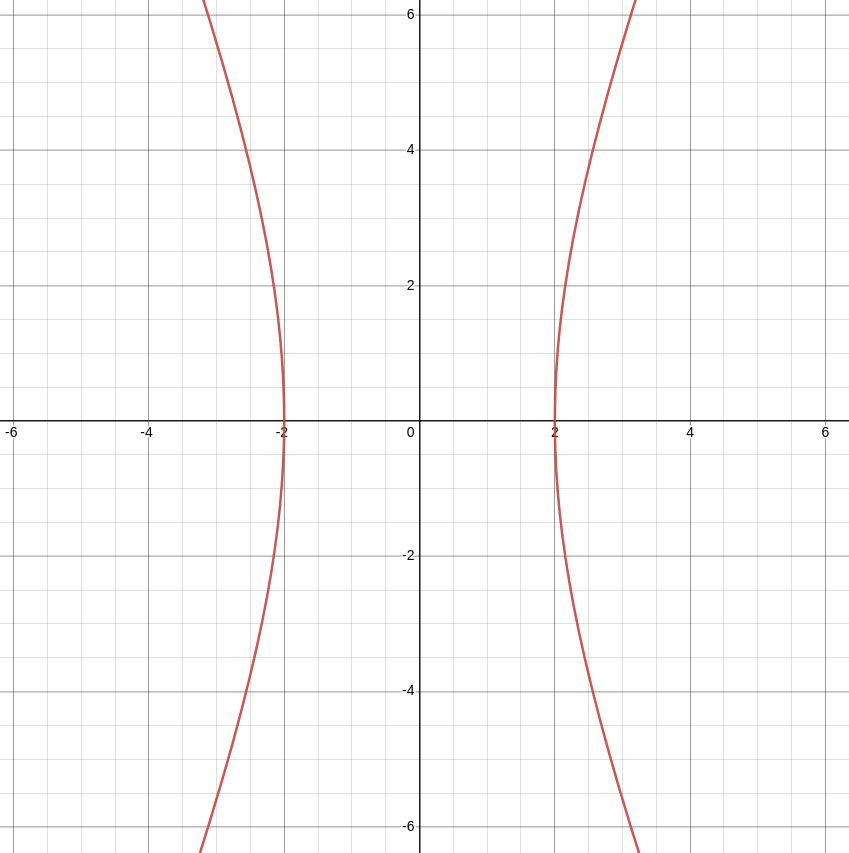
We may now sketch this figure in three dimensions.
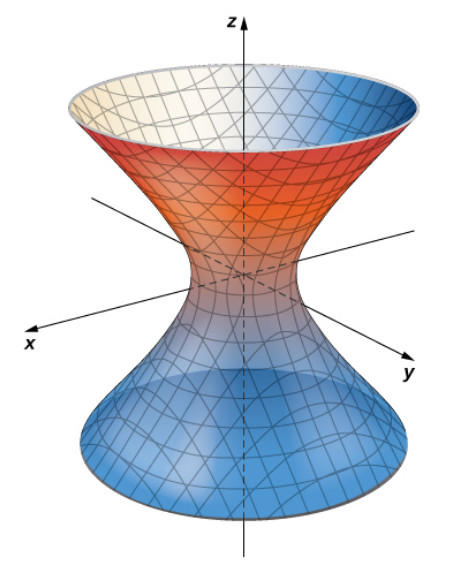
The resulting figure is called a hyperboloid of one sheet
A Veritable Menagerie of Quadric Surfaces
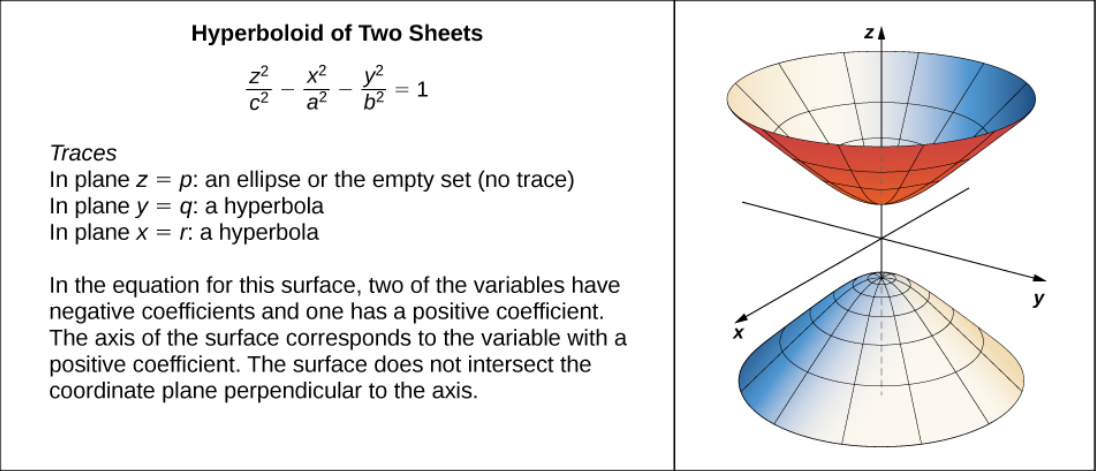
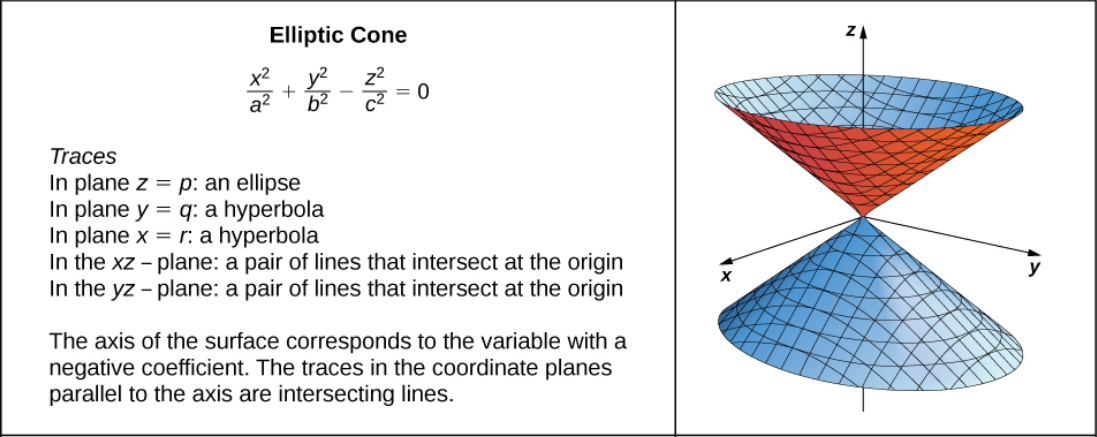
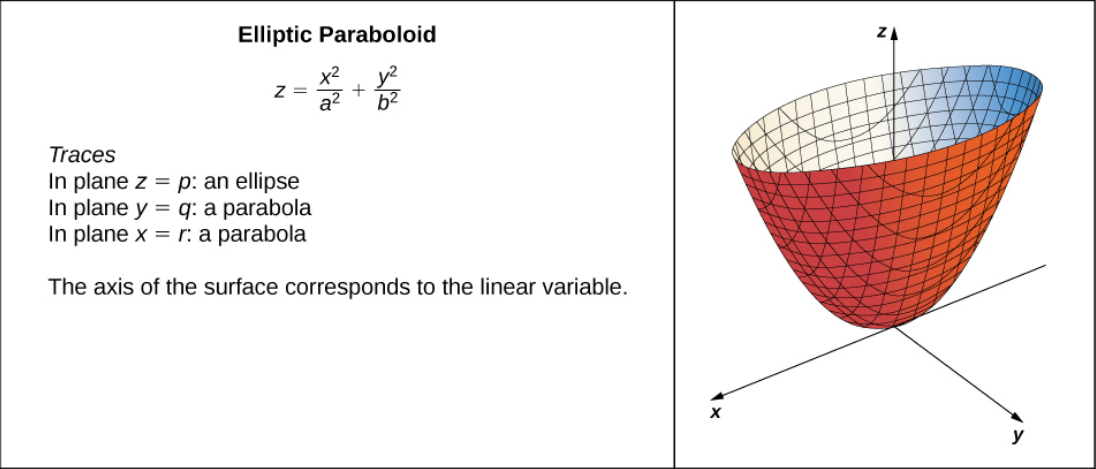
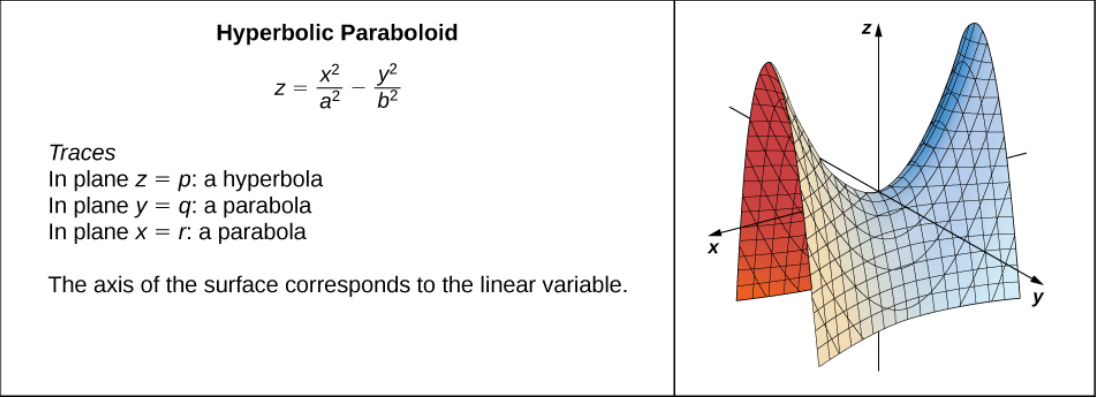
Example
Classify the quadric surface given by the equation $$9x^2 - 18x + 4y^2 + 16y - 36z + 25 = 0$$
Solution
We will massage the equation $9x^2 - 18x + 4y^2 + 16y - 36z + 25 = 0$ into a form we recognize.
First, we complete the square in $x$ and $y.$ $$ \begin{array}{lrll} & \displaystyle 9x^2 - 18x + 4y^2 + 16y - 36z + 25&\displaystyle= 0&\mbox{}\\ \implies & 9(x^2 - 2x) + 4(y^2 + 4y) - 36z + 25&\displaystyle=0 &\displaystyle &\mbox{}\\ \implies & 9(x^2 - 2x\color{magenta}{+1-1}) + 4(y^2 + 4y\color{magenta}{+4-4}) - 36z + 25&\displaystyle=0 &\displaystyle &\mbox{}\\ \implies & 9((x-1)^2-1) + 4((y+2)^2-4) - 36z + 25&\displaystyle=0 &\displaystyle &\mbox{}\\ \implies & 9(x-1)^2-9 + 4(y+2)^2)-16 - 36z + 25&\displaystyle=0 &\displaystyle &\mbox{}\\ \implies & 9(x-1)^2 + 4(y+2)^2 - 36z &\displaystyle=0 &\displaystyle &\mbox{}\\ \implies & 9(x-1)^2 + 4(y+2)^2 &\displaystyle=36z &\displaystyle &\mbox{}\\ \end{array} $$ Then $\displaystyle z=\frac{(x-1)^2}{4}+\frac{(y+2)^2}{9}$ so that $$ z=\frac{(x-1)^2}{2^2}+\frac{(y+2)^2}{3^2} $$ This is an elliptic paraboloid shifted $1$ in the positive $x$ direction and $2$ units in the negative $y$ direction.