Last time we saw that the dot product is a form of vector multiplication which results in a scalar.
Today, we look at another product of vectors called the cross product whose result is another vector.
Definition
Let ${\bf u}=\langle u_1, u_2, u_3 \rangle$ and ${\bf v}=\langle v_1, v_2, v_3 \rangle,$ be vectors.
The the cross product of ${\bf u}$ and ${\bf v},$ denoted ${\bf u}\times {\bf v},$ is defined to be the vector $$ \begin{array}{ll} {\bf u} \times {\bf v}& = (u_2 v_3 - u_3 v_2){\bf i} - (u_1 v_3 - u_3 v_1){\bf j} + (u_1 v_2 - u_2 v_1){\bf k}\\ &= \langle u_2 v_3 - u_3 v_2, u_3 v_1-u_1 v_3 ,u_1 v_2 - u_2 v_1\rangle \end{array} $$
A Word of Advice: Don't bother trying to memorize this definition.
The Cross Product
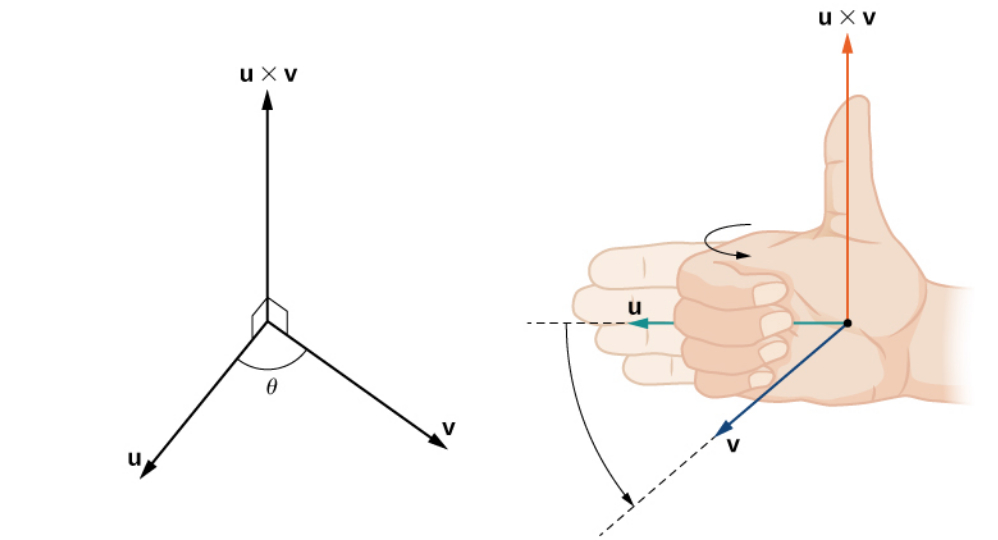
In words, the cross product of the vectors ${\bf u}$ and ${\bf v},$ denoted ${\bf u}\times {\bf v},$ is a vector which is orthogonal to ${\bf u}$ and ${\bf v}$ and has a magnitude equal to the area of the parallelogram formed by ${\bf u}$ and ${\bf v}.$
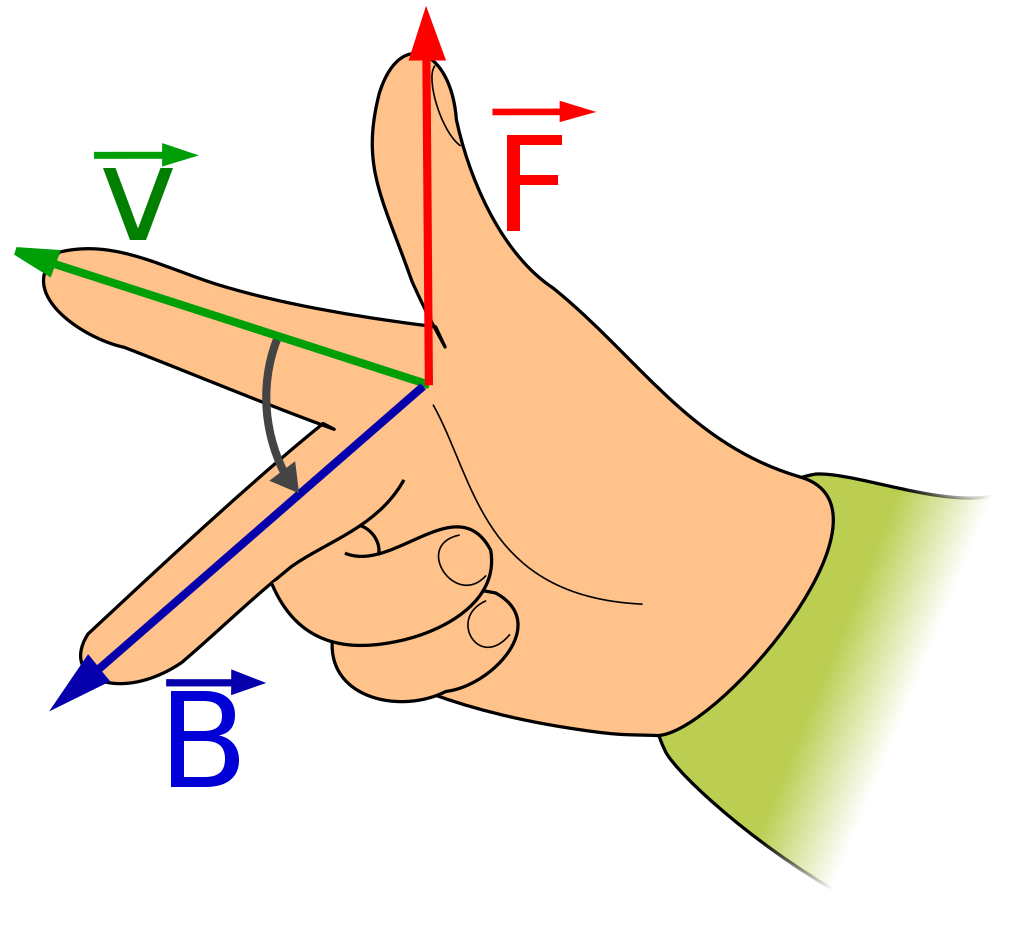
The orientation of ${\bf u}\times {\bf v}$ is determined by the right-hand rule.
Example
Let ${\bf u} = \langle 0, 2, 1 \rangle$ and ${\bf v} = \langle 3, -1, 0 \rangle.$ Calculate ${\bf u}\times {\bf v}$ and ${\bf v}\times {\bf u}.$
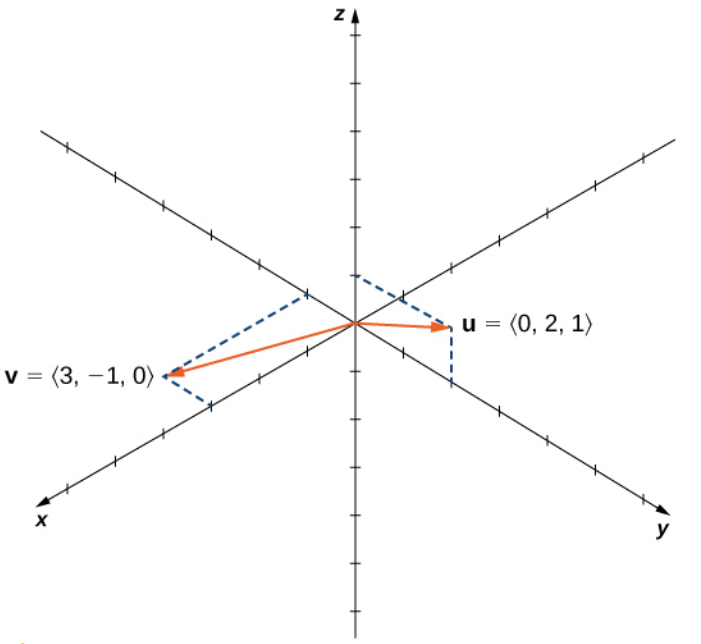
Solution $$ \begin{array}{lll} \displaystyle {\bf u}\times {\bf v}&\displaystyle=\langle 0, 2, 1 \rangle \times \langle 3, -1, 0 \rangle&\mbox{}\\ \displaystyle &\displaystyle=\langle u_1, u_2, u_3 \rangle \times \langle v_1, v_2, v_3 \rangle&\mbox{}\\ \displaystyle &\displaystyle=\langle u_2 v_3 - u_3 v_2, u_3 v_1-u_1 v_3 ,u_1 v_2 - u_2 v_1\rangle &\mbox{}\\ \displaystyle &\displaystyle=\langle 2 \cdot 0 - 1 \cdot (-1), 1 \cdot 3-0 \cdot 0 ,0 \cdot (-1) - 2 \cdot 3\rangle &\mbox{}\\ \displaystyle &\displaystyle=\langle 1, 3, -6\rangle &\mbox{}\\ \end{array} $$ $$ \begin{array}{lll} \displaystyle {\bf v}\times {\bf u}&\displaystyle= \langle 3, -1, 0 \rangle \times \langle 0, 2, 1 \rangle&\mbox{}\\ \displaystyle &\displaystyle=\langle v_1, v_2, v_3 \rangle \times \langle u_1, u_2, u_3 \rangle &\mbox{}\\ \displaystyle &\displaystyle=\langle v_2 u_3 - v_3 u_2, v_3 u_1-v_1 u_3 ,v_1 u_2 - v_2 u_1\rangle &\mbox{}\\ \displaystyle &\displaystyle=\langle -1 \cdot 1-0 \cdot 2 , 0 \cdot 0-3 \cdot 1 ,3 \cdot 2 - (-1) \cdot 0\rangle &\mbox{}\\ \displaystyle &\displaystyle=\langle -1, -3, 6\rangle &\mbox{}\\ \end{array} $$
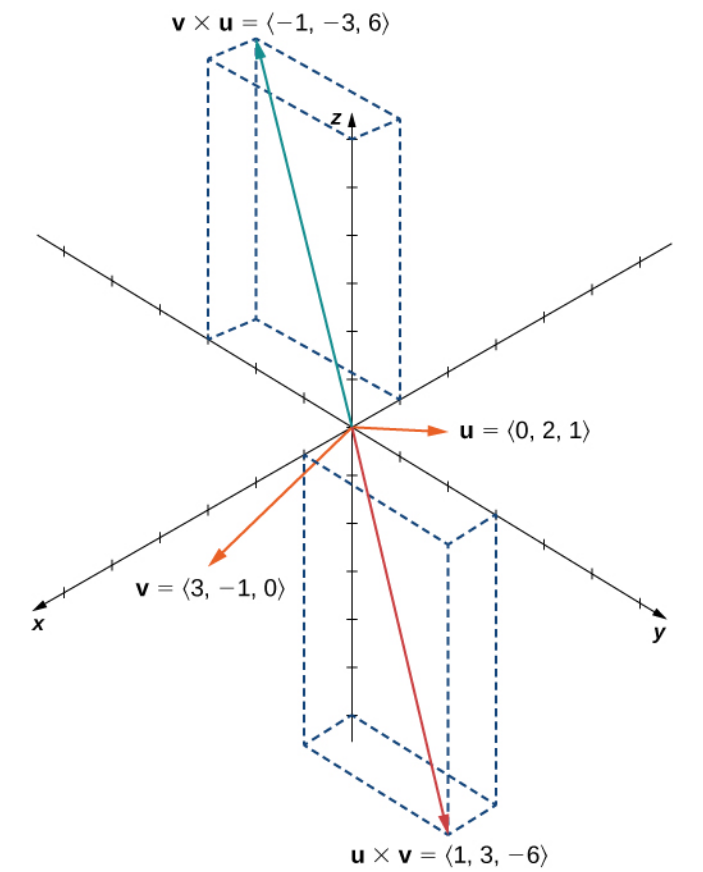
Cross Products of ${\bf i},$ ${\bf j},$ and ${\bf k}$ $$ \begin{array}{ll} {\bf i}\times {\bf j}={\bf k} & {\bf j}\times {\bf i}=-{\bf k}\\ {\bf j}\times {\bf k}={\bf i} & {\bf k}\times {\bf j}=-{\bf i}\\ {\bf k}\times {\bf i}={\bf j} & {\bf i}\times {\bf k}=-{\bf j}\\ \end{array} $$
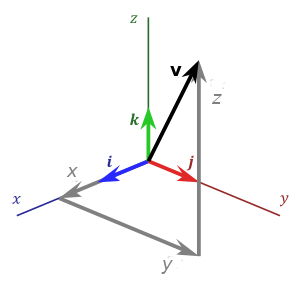
General Properties of Cross Products
Let ${\bf u},$ ${\bf v},$ and ${\bf w}$ be vectors in $\mathbb{R}^3,$ and let $k$ be a scalar. Then $$ \begin{array}{ll} {\bf u}\times {\bf v}=-{\bf v}\times {\bf u} & \mbox{Property 1: The cross product is anticommutative.}\\ {\bf u}\times ({\bf v}+{\bf w})={\bf u}\times {\bf v}+{\bf u}\times {\bf w} & \mbox{Property 2: The cross product distributes over vector addition.}\\ ({\bf v}+{\bf w})\times{\bf u} ={\bf v}\times {\bf u}+{\bf w}\times {\bf u} & \mbox{Property 2: The cross product distributes over vector addition.}\\ k({\bf u}\times{\bf v})=(k{\bf u})\times {\bf v}={\bf u}\times (k{\bf v}) & \mbox{Property 3}\\ {\bf u}\times {\bf 0}={\bf 0} & \mbox{Property 4}\\ {\bf u}\times {\bf u}={\bf 0} & \mbox{Property 5: The cross product of a vector with itself is the zero vector.}\\ {\bf u}\cdot({\bf v}\times {\bf w})=({\bf u}\times {\bf v})\cdot {\bf w} & \mbox{Property 6: The Scalar Triple Product}\\ \end{array} $$
Example
Use the properties of the cross product to calculate $({\bf i} \times {\bf k}) \times ({\bf k} \times {\bf j}).$
Solution
$$ \begin{array}{lll} \displaystyle ({\bf i} \times {\bf k}) \times ({\bf k} \times {\bf j}) &\displaystyle= (-{\bf j} ) \times (-{\bf i})&\mbox{}\\ \displaystyle &\displaystyle= -({\bf j}\times (-{\bf i})) &\mbox{by Property 3}\\ \displaystyle &\displaystyle= {\bf j}\times {\bf i} &\mbox{by Property 3}\\ \displaystyle &\displaystyle=-{\bf i}\times {\bf j} &\mbox{by Property 1}\\ \displaystyle &\displaystyle= -{\bf k} &\mbox{}\\ \end{array} $$
Application
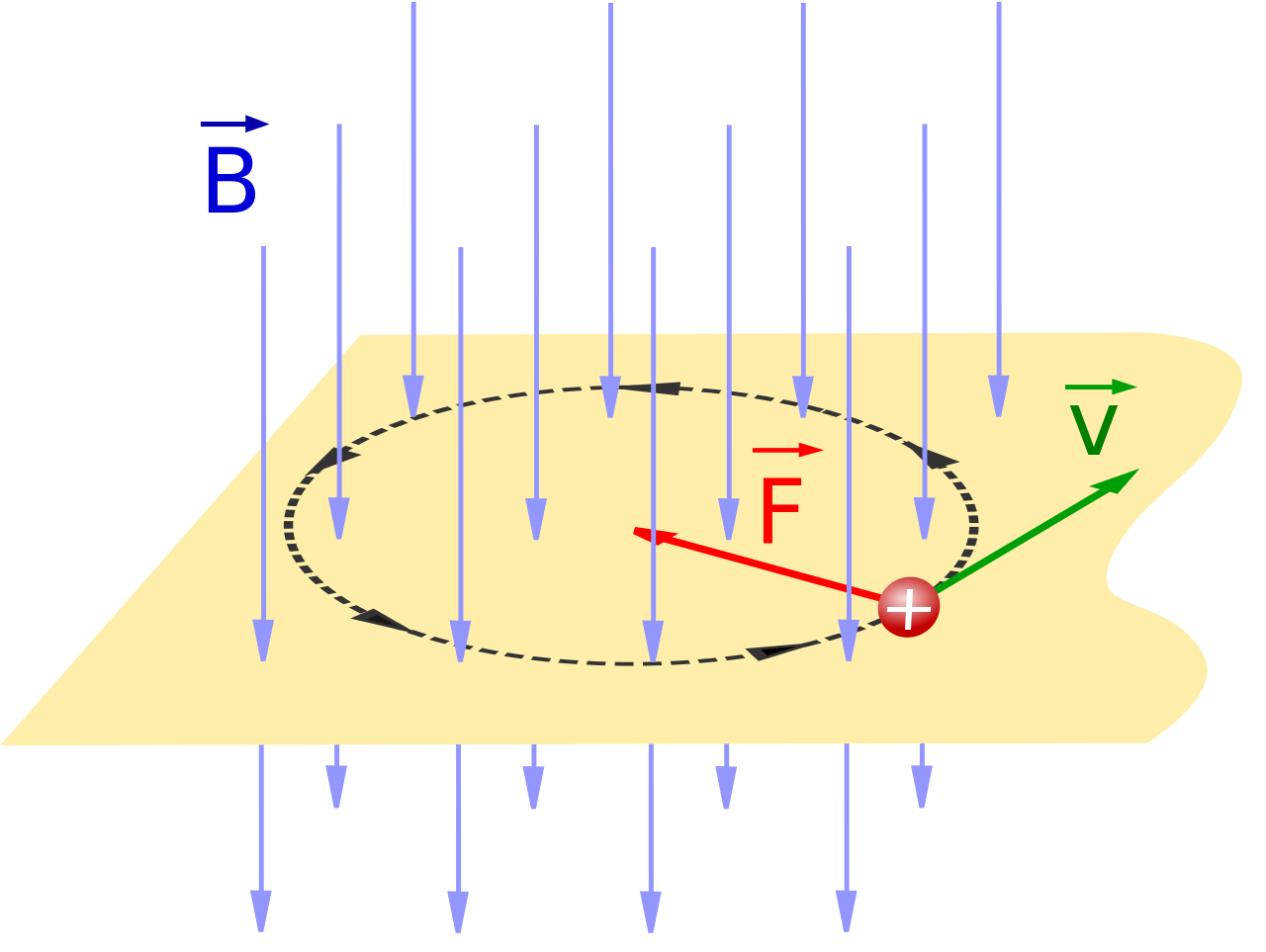
An electrically charged particle with charge $q$ moving with velocity ${\bf v}$ at point where the magnetic field is ${\bf B}$ experiences a force ${\bf F}$ given by $$ {\bf F}=q({\bf v} \times {\bf B}) $$
Find the force that acts on a proton ($q=1.6 \times 10^{-19}$ (in coulombs) that moves in the $xy$-plane at velocity ${\bf v} = 105 {\bf i} + 105 {\bf j}$ (in meters per second) in a magnetic field given by ${\bf B} = -0.3{\bf k}$ (in tesla).
Solution
$$ \begin{array}{lll} \displaystyle {\bf F} &\displaystyle= q({\bf v} \times {\bf B})&\mbox{}\\ \displaystyle &\displaystyle=1.6 \times 10^{-19}((105 {\bf i} + 105 {\bf j})\times(-0.3{\bf k})) &\mbox{}\\ \displaystyle &\displaystyle=1.6 \times 10^{-19}((105({\bf i} + {\bf j}))\times(-0.3{\bf k})) &\mbox{scalar multiplication}\\ \displaystyle &\displaystyle=1.6 \times 10^{-19}(105(-0.3)({\bf i} + {\bf j})\times{\bf k}) &\mbox{Property 3}\\ \displaystyle &\displaystyle=1.6 \times 10^{-19}\cdot 105(-0.3)(({\bf i} + {\bf j})\times{\bf k}) &\mbox{Property 3}\\ \displaystyle &\displaystyle=-5.04\times 10^{-18}(({\bf i} + {\bf j})\times{\bf k}) &\mbox{simplify}\\ \displaystyle &\displaystyle=-5.04\times 10^{-18}(({\bf i}\times{\bf k}) + ({\bf j}\times{\bf k})) &\mbox{Property 2}\\ \displaystyle &\displaystyle=-5.04\times 10^{-18}(-{\bf j}+ {\bf i}) &\mbox{}\\ \displaystyle &\displaystyle=-5.04\times 10^{-18}({\bf i}-{\bf j}) &\mbox{simplify}\\ \displaystyle &\displaystyle=-5.04\times 10^{-18}{\bf i}+5.04\times 10^{-18}{\bf j} &\mbox{scalar multiplication}\\ \end{array} $$
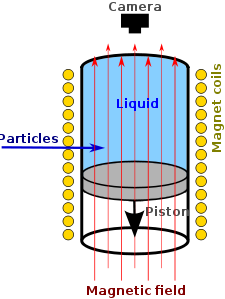
Bubble Chambers
Early experiments in particle physics used bubble chambers to learn more about subatomic particles.
Slight Detour: Determinants
The determinant of a $2\times 2$ matrix, $\left[\begin{array}{cc} a_1&b_1\\a_2&b_2\\ \end{array}\right],$ is the number $$ \left|\begin{array}{cc} a_1&b_1\\a_2&b_2\\ \end{array}\right|=a_1b_2-b_1a_2 $$
Example $$\left|\begin{array}{cc} 3&-2\\5&1\\ \end{array}\right|=3\cdot 1-(-2)\cdot 5=3+10=13$$
Determinants
Determinants, important in their own right, can be applied to solving systems of equations. For example, the general $2 \times 2$ system $$ \begin{cases} a_1x+b_1y&=n_1\\ a_2x+b_2y&=n_2\\ \end{cases} $$ can be solved using determinants: $$ x=\frac{\left|\begin{array}{cc} n_1 & b_1\\n_2 & b_2\\ \end{array}\right|}{\left|\begin{array}{cc} a_1&b_1\\a_2&b_2\\ \end{array}\right|}, \,\,\,\, y=\frac{\left|\begin{array}{cc} a_1 & n_1\\a_2 & n_2\\ \end{array}\right|}{\left|\begin{array}{cc} a_1&b_1\\a_2&b_2\\ \end{array}\right|} $$
$3 \times 3$ Determinants
The determinant of a $3\times 3$ matrix, $\left[\begin{array}{ccc} a_1&b_1&c_1\\a_2&b_2&c_2\\ a_3 & b_3 & c_3 \end{array}\right],$ is the number $$ \begin{array}{ll} \left|\begin{array}{ccc} a_1&b_1&c_1\\a_2&b_2&c_2\\ a_3 & b_3 & c_3 \end{array}\right|&=a_1\left|\begin{array}{cc} b_2&c_2\\b_3&c_3\\ \end{array}\right|-b_1\left|\begin{array}{cc} a_2&c_2\\a_3&c_3\\ \end{array}\right|+c_1\left|\begin{array}{cc} a_2&b_2\\a_3&b_3\\ \end{array}\right|\\ &=a_1(b_2c_3-c_2b_3)-b_1(a_2c_3-c_2a_3)+c_1(a_2b_3-b_2a_3) \end{array} $$
Example
$$ \begin{array}{ll} \left|\begin{array}{ccc} -1&-2&1\\4&3&2\\ 0 & -5 & -2 \end{array}\right|&=(-1)\left|\begin{array}{cc} 3&2\\-5&-2\\ \end{array}\right|-(-2)\left|\begin{array}{cc} 4&2\\0&-2\\ \end{array}\right|+1\left|\begin{array}{cc} 4&3\\0&-5\\ \end{array}\right|\\ &=(-1)(3\cdot (-2)-2\cdot (-5))-(-2)(4\cdot (-2)-2\cdot 0)+1(4\cdot (-5)-3\cdot 0)\\ &=(-1)(-6+10)+2(-8)-20\\ &=(-1)(4)-16-20\\ &=-4-36\\ &=-40 \end{array} $$
Solving $3 \times 3$ Systems of Equations
The solution to the general $3 \times 3$ system of equations $$ \begin{cases} a_1x+b_1y+c_1 z&=n_1\\ a_2x+b_2y+c_2 z&=n_2\\ a_3x+b_3y+c_3 z&=n_3\\ \end{cases} $$ is given by $$ x=\frac{\left|\begin{array}{ccc} n_1&b_1&c_1\\n_2&b_2&c_2\\ n_3 & b_3 & c_3 \end{array}\right|}{\left|\begin{array}{ccc} a_1&b_1&c_1\\a_2&b_2&c_2\\ a_3 & b_3 & c_3 \end{array}\right|},\, y=\frac{\left|\begin{array}{ccc} a_1&n_1&c_1\\a_2&n_2&c_2\\ a_3 & n_3 & c_3 \end{array}\right|}{\left|\begin{array}{ccc} a_1&b_1&c_1\\a_2&b_2&c_2\\ a_3 & b_3 & c_3 \end{array}\right|},\, z=\frac{\left|\begin{array}{ccc} a_1&b_1&n_1\\a_2&b_2&n_2\\ a_3 & b_3 & n_3 \end{array}\right|}{\left|\begin{array}{ccc} a_1&b_1&c_1\\a_2&b_2&c_2\\ a_3 & b_3 & c_3 \end{array}\right|} $$
The Big Deal: $$ \begin{array}{lll} {\bf u} \times {\bf v} &= \langle u_2 v_3 - u_3 v_2, u_3 v_1-u_1 v_3 ,u_1 v_2 - u_2 v_1\rangle&\mbox{the definition}\\\\ &= (u_2 v_3 - u_3 v_2){\bf i} - (u_1 v_3 - u_3 v_1){\bf j} + (u_1 v_2 - u_2 v_1){\bf k}&\mbox{using ${\bf i}$-${\bf j}$-${\bf k}$ notation}\\\\ &= \left|\begin{array}{cc} u_2&v_2\\u_3&v_3\\ \end{array}\right|{\bf i} - \left|\begin{array}{cc} u_1&v_1\\u_3&v_3\\ \end{array}\right|{\bf j} + \left|\begin{array}{cc} u_1&v_1\\u_2&v_2\\ \end{array}\right|{\bf k}&\mbox{expressing components as determinants}\\\\ &=\left|\begin{array}{ccc} {\bf i}&{\bf j}&{\bf k}\\u_1&u_2&u_3\\ v_1 & v_2 & v_3 \end{array}\right|&\mbox{expressing previous result as a determinant}\\ \end{array} $$
Formal Statement
Let ${\bf u}=\langle u_1,u_2,u_3\rangle$ and ${\bf v}=\langle v_1,v_2,v_3\rangle$ be vectors. Then $$ {\bf u} \times {\bf v} =\left|\begin{array}{ccc} {\bf i}&{\bf j}&{\bf k}\\u_1&u_2&u_3\\ v_1 & v_2 & v_3 \end{array}\right| $$
This is how we easily remember the cross product formula.
Magnitude of the Cross Product
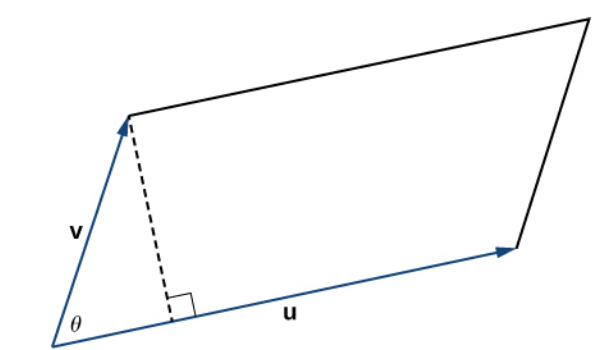
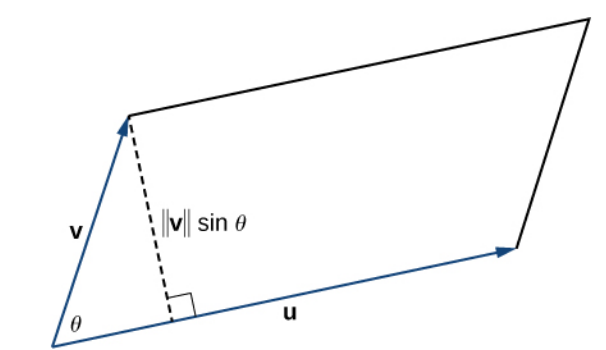
Let ${\bf u}$ and ${\bf v}$ be vectors, and let $\theta$ be the angle between them. Then $$ \Vert {\bf u}\times{\bf v}\Vert=\Vert {\bf u} \Vert \Vert {\bf v}\Vert \sin \theta $$ Moreover, if we locate vectors ${\bf u}$ and ${\bf v}$ such that they form adjacent sides of a parallelogram, then the area of the parallelogram is given by $\Vert {\bf u}\times{\bf v}\Vert.$
Example
Find the magnitude of $\Vert {\bf u}\times{\bf v}\Vert,$ where ${\bf u} = \langle -8, 0, 0 \rangle$ and ${\bf v} = \langle 0, 2, 0 \rangle.$
Solution
For the perpendicular vectors ${\bf u} = \langle -8, 0, 0 \rangle$ and ${\bf v} = \langle 0, 2, 0 \rangle,$ $$ \begin{array}{lll} \displaystyle \Vert {\bf u}\times{\bf v}\Vert&\displaystyle= \Vert {\bf u} \Vert \Vert {\bf v}\Vert \sin \theta&\mbox{}\\ \displaystyle &\displaystyle= \sqrt{(-8)^2+0^2+0^2} \cdot \sqrt{0^2+2^2+0^2} \cdot \sin \frac{\pi}{2}&\mbox{}\\ \displaystyle &\displaystyle= 8 \cdot 2 \cdot 1&\mbox{}\\ \displaystyle &\displaystyle= 16&\mbox{}\\ \end{array} $$
Example
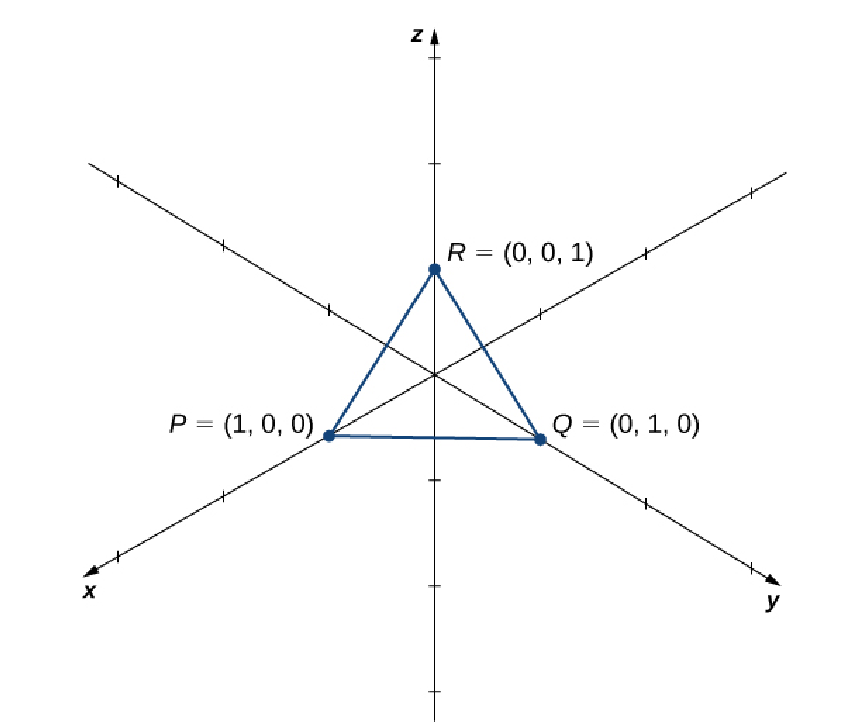
Let $P = (1, 0, 0),$ $Q = (0, 1, 0),$ and $R = (0, 0, 1)$ be the vertices of a triangle. Find its area.
Solution
The area of the triangle is half the area of the parallelogram formed by the vectors ${\bf u}$ and ${\bf v}.$
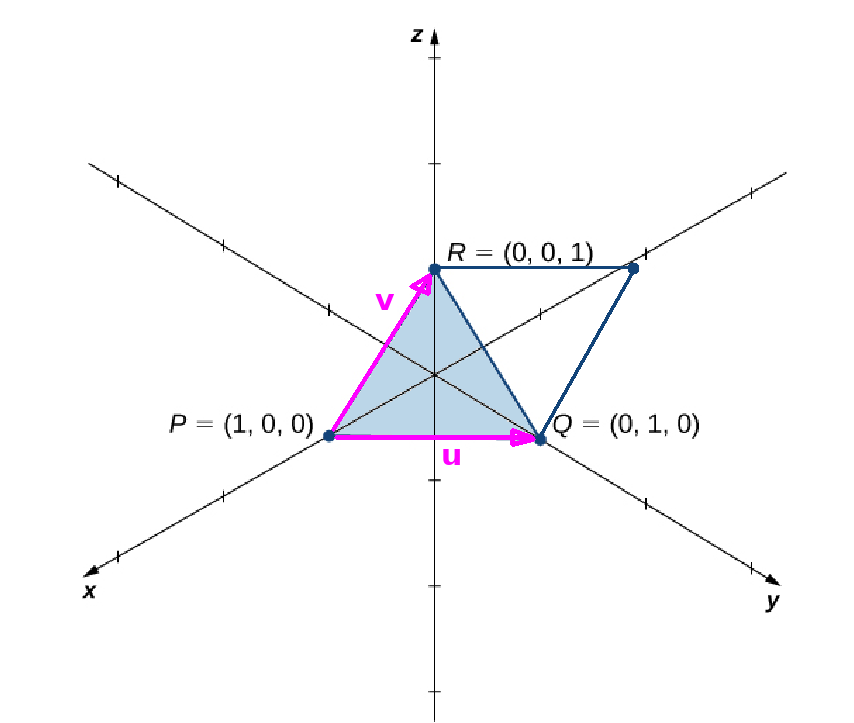
Since the area of the parallelogram is $\Vert {\bf u}\times{\bf v}\Vert$ so that the area of the triangle is $\displaystyle \frac{1}{2}\Vert {\bf u}\times{\bf v}\Vert.$
All we need now to do now to perform the calculation is find ${\bf u}$ and ${\bf v}.$ $$ {\bf u}=\overrightarrow{PR}=\langle 0-1,1-0,0-0\rangle=\langle -1,1,0\rangle $$ and $$ {\bf v}=\overrightarrow{PQ}\langle 0-1,0-0,1-0\rangle=\langle -1,0,1\rangle $$
We may now calculate ${\bf u}\times{\bf v}.$ $$ \begin{array}{lll} \displaystyle {\bf u}\times{\bf v}&\displaystyle=\langle -1,1,0\rangle \times \langle -1,0,1\rangle &\mbox{}\\ \displaystyle &\displaystyle=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\-1&1&0\\-1&0&1\end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(1-0){\bf i}-(-1-0){\bf j}+(0-(-1)){\bf k}&\mbox{}\\ \displaystyle &\displaystyle={\bf i}+{\bf j}+{\bf k}&\mbox{}\\ \end{array} $$ The area of the triangle is then $$ \begin{array}{lll} \displaystyle \frac{1}{2}\Vert {\bf u}\times{\bf v}\Vert&\displaystyle= \frac{1}{2}\Vert {\bf i}+{\bf j}+{\bf k}\Vert&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{2}\Vert \langle 1,1,1\rangle\Vert&\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{2}\sqrt{1^2+1^2+1^2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\sqrt{3}}{2} &\mbox{}\\ \end{array} $$
Application
An electrically charged particle with charge $q$ moving with velocity ${\bf v}$ at point where the magnetic field is ${\bf B}$ experiences a force ${\bf F}$ given by $$ {\bf F}=q({\bf v} \times {\bf B}) $$
Solution
We observe that $$ \begin{array}{lll} \displaystyle \Vert{\bf F}\Vert &\displaystyle= \Vert q({\bf v}\times{\bf B})\Vert&\mbox{}\\ \displaystyle &\displaystyle= |q|\Vert {\bf v}\times{\bf B}\Vert&\mbox{}\\ \displaystyle &\displaystyle= |q|\Vert {\bf v} \Vert \Vert {\bf B}\Vert \sin \theta&\mbox{magnitude of cross product}\\ \displaystyle &\displaystyle= |q|\Vert {\bf v} \Vert \Vert {\bf B}\Vert \sin \theta&\mbox{property of vector length}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle \sin \theta &\displaystyle= \frac{\Vert{\bf F}\Vert}{|q|\Vert {\bf v} \Vert \Vert {\bf B}\Vert}&\mbox{}\\ \end{array} $$ so that $$ \begin{array}{lll} \displaystyle \theta &\displaystyle=\sin^{-1}\left( \frac{\Vert{\bf F}\Vert}{|q|\Vert {\bf v} \Vert \Vert {\bf B}\Vert}\right)&\mbox{}\\ \displaystyle &\displaystyle=\sin^{-1}\left( \frac{5.9 \times 10^{-17}}{|1.6 \times 10^{-19}|\cdot 300 \cdot 2.4}\right) &\mbox{}\\ \displaystyle &\displaystyle\approx 30.80733187^{\circ} &\mbox{}\\ \end{array} $$ Thus, the angle between ${\bf v}$ and ${\bf B}$ is about $30.8^{\circ}.$
The Triple Scalar Product
The triple scalar product of the vectors ${\bf u},$ ${\bf v},$ and ${\bf w}$ is the quantity $$ {\bf u}\cdot({\bf v}\times {\bf w}) $$
The Triple Scalar Product
We note that the triple scalar product of ${\bf u}=\langle u_1,u_2,u_3\rangle,$ ${\bf v}=\langle v_1,v_2,v_3\rangle,$ and ${\bf w}=\langle w_1,w_2,w_3\rangle$ can be expressed as a determinant. $$ {\bf u}\cdot({\bf v}\times {\bf w})=\left|\begin{array}{ccc} u_1&u_2&u_3\\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3\end{array}\right| $$
Example
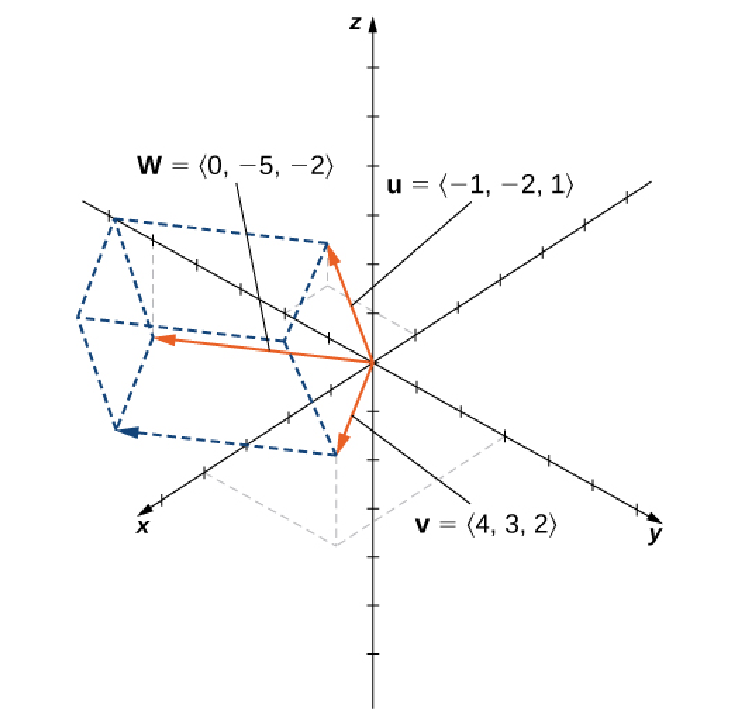
If ${\bf u}=\langle -1,-2,1\rangle,$ ${\bf v}=\langle 4,3,2\rangle,$ and ${\bf w}=\langle 0,-5,-2\rangle,$ then the triple scalar product is $$ \begin{array}{ll} {\bf u}\cdot({\bf v}\times {\bf w}) &=\langle -1,-2,1\rangle \cdot (\langle 4,3,2\rangle \times \langle 0,-5,-2\rangle)\\ &=\left|\begin{array}{ccc} -1&-2&1\\4&3&2\\ 0 & -5 & -2 \end{array}\right|\\ %&=(-1)\left|\begin{array}{cc} 3&2\\-5&-2\\ \end{array}\right|-(-2)\left|\begin{array}{cc} 4&2\\0&-2\\ \end{array}\right|+1\left|\begin{array}{cc} 4&3\\0&-5\\ \end{array}\right|\\ &=-40 \end{array} $$
The Volume of a Parallelepiped
The volume $V$ of a parallelepiped with adjacent edges given by the vectors ${\bf u,}$ ${\bf v,}$ and ${\bf w}$ is the absolute value of the triple scalar product. $$ V=|{\bf u}\cdot({\bf v}\times {\bf w})| $$
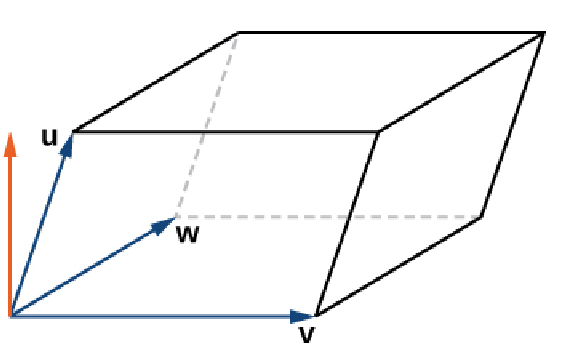
Example
Find the volume of the parallelepiped with adjacent edges given by the vectors ${\bf u}=\langle -1,-2,1\rangle,$ ${\bf v}=\langle 4,3,2\rangle,$ and ${\bf w}=\langle 0,-5,-2\rangle.$
Solution
Since $$ {\bf u}\cdot({\bf v}\times {\bf w})=\left|\begin{array}{ccc} -1&-2&1\\4&3&2\\ 0 & -5 & -2 \end{array}\right|=-40 $$ as shown earlier, we have $$ \begin{array}{ll} V &=|{\bf u}\cdot({\bf v}\times {\bf w})|\\ &=|-40|\\ &=40\\ \end{array} $$
Application: Torque
Torque, denoted by the Greek letter tau ${\bf \tau}$, measures the tendency of a force to produce rotation about an axis. Let ${\bf r}$ be a vector with an initial point located on the axis of rotation and with a terminal point located at the point where the force is applied, and let vector ${\bf F}$ represent the force. Then torque is equal to the cross product of ${\bf r}$ and ${\bf F}.$ $${\bf \tau} = {\bf r}\times {\bf F}.$$
Example
A bolt is tightened by applying a force of $6$ newtons to a $0.15$-meter wrench. The angle between the wrench and the force vector is $40^{\circ}.$ Find the magnitude of the torque about the center of the bolt. Round the answer to two decimal places.
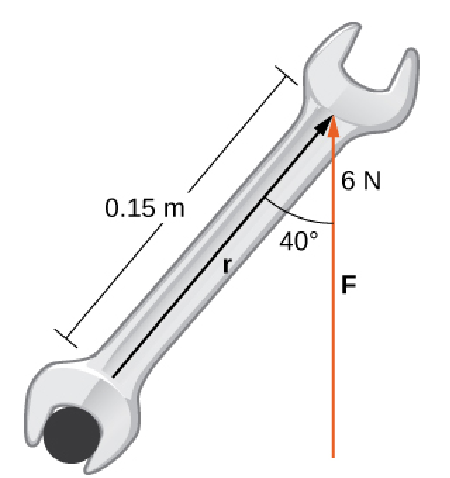
Solution
From the figure we see that $\Vert{\bf r}\Vert=0.15$ meters and $\Vert{\bf F}\Vert=6$ newtons.
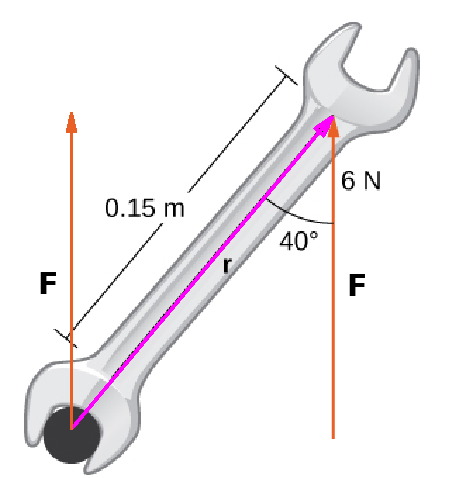
Using basic geometry, we can also deduce that the angle between ${\bf r}$ meters and ${\bf F}$ id $40^{\circ}.$ We may now calculate the magnitude of the torque. $$ \begin{array}{lll} \displaystyle \Vert \tau \Vert &\displaystyle= \Vert{\bf r}\times {\bf F}\Vert&\mbox{}\\ \displaystyle &\displaystyle= \Vert{\bf r}\Vert \Vert{\bf F}\Vert \sin 40^{\circ}&\mbox{magnitude of the cross product}\\ \displaystyle &\displaystyle= 0.15 \cdot 6 \sin 40^{\circ}&\mbox{}\\ \displaystyle &\displaystyle= 0.9 \sin 40^{\circ}&\mbox{}\\ \displaystyle &\displaystyle\approx 0.5785088487&\mbox{}\\ \end{array} $$ Thus, the magnitude of the torque is about $0.58$ $\mbox{N $\cdot$ m}$