We've seen scalar multiplication which multiplies a vector times a number.
Today, we begin to multiply vectors with other vectors.
The flavor of vector multiplication we deal with today is the dot product.
As we shall see, the dot product is central to understanding the physical notion of work.
The Dot Product
In $\mathbb{R}^2:$ Let ${\bf u}=\langle x_1,y_1\rangle$ and ${\bf v}=\langle x_2,y_2\rangle$ be vectors in $\mathbb{R}^2.$ Then the dot product ${\bf u}\cdot {\bf v}$ is given by $$ {\bf u}\cdot {\bf v}=\langle x_1,y_1\rangle \cdot \langle x_2,y_2\rangle=x_1x_2+y_1y_2. $$
In $\mathbb{R}^3:$ Let ${\bf u}=\langle x_1,y_1,z_1\rangle$ and ${\bf v}=\langle x_2,y_2,z_2\rangle$ be vectors in $\mathbb{R}^3.$ Then the dot product ${\bf u}\cdot {\bf v}$ is given by $$ {\bf u}\cdot {\bf v}=\langle x_1,y_1,z_1\rangle \cdot \langle x_2,y_2,z_2\rangle=x_1x_2+y_1y_2+z_1z_2. $$
In Words: The dot product is the sum of the products of components.
Example
(a) Find ${\bf u}\cdot {\bf v}$ if ${\bf u}=\langle 6,8\rangle=6{\bf i}+8{\bf j}$ and ${\bf v}=\langle -2,4 \rangle=-2{\bf i}+4{\bf j}.$
(b) Find ${\bf u}\cdot {\bf v}$ if ${\bf u}=\langle 1,-2,3\rangle={\bf i}-2{\bf j}+3{\bf k}$ and ${\bf v}=\langle -2,3,-1 \rangle=-2{\bf i}+3{\bf j}-{\bf k}.$
Solution
(a) $$ \begin{array}{lll} \displaystyle {\bf u}\cdot {\bf v} &\displaystyle= \langle 6,8\rangle \cdot \langle -2,4 \rangle &\mbox{}\\ \displaystyle &\displaystyle=6(-2)+8 \cdot 4 &\mbox{}\\ \displaystyle &\displaystyle=-12+32 &\mbox{}\\ \displaystyle &\displaystyle=20 &\mbox{}\\ \end{array} $$ (b) $$ \begin{array}{lll} \displaystyle {\bf u}\cdot {\bf v} &\displaystyle= \langle 1,-2,3\rangle \cdot \langle -2,3,-1 \rangle &\mbox{}\\ \displaystyle &\displaystyle=1(-2)+(-2)3+3(-1) &\mbox{}\\ \displaystyle &\displaystyle=-2+(-6)+(-3) &\mbox{}\\ \displaystyle &\displaystyle=-11 &\mbox{}\\ \end{array} $$
In Words: The dot product is the sum of the products of components.
The Dot Product
Notice that the dot product takes two vectors and maps them to a scalar.
For this reason, the dot product is sometimes called the scalar product.
Another name for the dot product is the inner product.
Properties of the Dot Product
Let ${\bf u},$ ${\bf v},$ and ${\bf w}$ be vectors and $k$ be a scalar. Then the following properties hold. $$ \begin{array}{ll} {\bf u}\cdot {\bf v}={\bf v}\cdot{\bf u} & \mbox{The dot product is commutative.}\\ {\bf u}\cdot({\bf v}+{\bf w})={\bf u}\cdot{\bf v}+{\bf u}\cdot {\bf w} & \mbox{The dot product distributes over vector addition.}\\ k({\bf u}\cdot {\bf v})=(k{\bf u})\cdot {\bf v}={\bf u}\cdot(k{\bf v}) & \mbox{The dot product plays nice with scalar multiplication}\\ {\bf v}\cdot {\bf v}=\Vert {\bf v} \Vert^2& \mbox{The dot product of ${\bf v}$ with itself is the square of its magnitude.}\\ \end{array} $$ Using components, these properties are not too difficult to prove.
Example
For vectors in $\mathbb{R}^3,$ prove that the dot product is commutative.
That is, show that ${\bf u}\cdot {\bf v}={\bf v}\cdot{\bf u}$ for any vectors in $\mathbb{R}^3.$
Solution
Let ${\bf u}$ and ${\bf v}$ be vectors in $\mathbb{R}^3.$
Proof: Let ${\bf u}=\langle u_1,u_2,u_3\rangle$ and ${\bf v}=\langle v_1,v_2,v_3\rangle$ be vectors in $\mathbb{R}^3.$ $$ \begin{array}{ll} {\bf u}\cdot {\bf v}= \langle u_1,u_2,u_3\rangle \cdot \langle v_1,v_2,v_3\rangle& \mbox{}\\ = u_1v_1+u_2v_2+u_3v_3& \mbox{by the definition of the dot product}\\ = v_1u_1+v_2u_2+v_3u_3& \mbox{since multiplication of real numbers is commutative}\\ = \langle v_1,v_2,v_3\rangle \cdot \langle u_1,u_2,u_3\rangle& \mbox{by the definition of the dot product}\\ = {\bf u}\cdot {\bf v}& \mbox{}\\ \end{array} $$ $\square$
Example
Find the following for ${\bf p} = \langle 7, 0, 2 \rangle,$ ${\bf q} = \langle -2, 2, -2 \rangle,$ and ${\bf r} = \langle 0, 2, -3 \rangle.$
(a) $({\bf r} + {\bf p})\cdot {\bf q}$
(b) $\Vert {\bf p} \Vert^2$
Solution
(a) There are two possibilities.
(i) Distribute first: $$ \begin{array}{lll} \displaystyle ({\bf r}+{\bf p})\cdot {\bf q} &\displaystyle= {\bf r}\cdot {\bf q}+{\bf p}\cdot {\bf q}&\mbox{dot product distributes over vector addition}\\ \displaystyle &=\langle 0,2,-3\rangle \cdot \langle -2,2,-2 \rangle+\langle 7,0,2 \rangle \cdot \langle -2,2,-2 \rangle &\mbox{}\\ \displaystyle &\displaystyle=0(-2)+2\cdot 2+(-3)(-2)+7(-2)+0\cdot 2+2(-2) &\mbox{}\\ \displaystyle &\displaystyle=0+4+6+(-14)+0+(-4) &\mbox{}\\ \displaystyle &\displaystyle=-8 &\mbox{}\\ \end{array} $$ (ii) Do vector addition first: $$ \begin{array}{lll} \displaystyle ({\bf r}+{\bf p})\cdot {\bf q} &\displaystyle= (\langle 0,2,-3\rangle+\langle 7,0,2 \rangle)\cdot \langle -2, 2, -2 \rangle&\mbox{}\\ \displaystyle &=\langle 7,2,-1\rangle\cdot \langle -2, 2, -2 \rangle &\mbox{do vector addition first}\\ \displaystyle &= 7(-2)+2\cdot 2+(-1)(-2) &\mbox{}\\ \displaystyle &= -14+4+2 &\mbox{}\\ \displaystyle &= -8 &\mbox{same answer as above!}\\ \end{array} $$ (b) $$ \begin{array}{lll} \displaystyle \Vert {\bf p}\Vert^2 &\displaystyle= {\bf p}\cdot {\bf p} &\mbox{dot product of ${\bf p}$ with itself is the square of its magnitude}\\ \displaystyle &\displaystyle= \langle 7, 0, 2 \rangle \cdot \langle 7, 0, 2 \rangle&\mbox{}\\ \displaystyle &\displaystyle= 7^2+0^2+2^2&\mbox{}\\ \displaystyle &\displaystyle= 49+4&\mbox{}\\ \displaystyle &\displaystyle= 53&\mbox{}\\ \end{array} $$
The Angle Between Vectors
An important consideration is the the angle $\theta$ between two vectors ${\bf u}$ and ${\bf v}.$
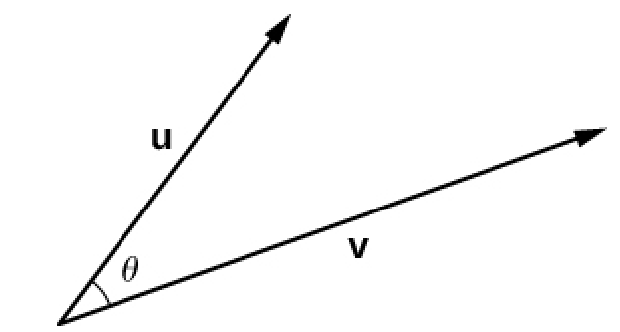
The dot product is related to this angle.
Theorem
For any two vectors ${\bf u}$ and ${\bf v},$ $$ {\bf u}\cdot {\bf v}=\Vert {\bf u}\Vert \Vert {\bf v} \Vert \cos \theta $$

Example
Find the measure of the angle, in radians, formed by vectors ${\bf a} = \langle 1, 2, 0\rangle$ and ${\bf b} = \langle 2, 4, 1 \rangle.$
Solution
We use the above theorem which states that $$ {\bf a}\cdot {\bf b}=\Vert {\bf a}\Vert \Vert {\bf b} \Vert \cos \theta $$ We begin by computing the magnitudes of ${\bf a}$ and ${\bf b}.$ $$ \Vert {\bf a}\Vert=\sqrt{{\bf a}\cdot {\bf a}}=\sqrt{1^2+2^2+0^2}=\sqrt{5} $$ $$ \Vert {\bf b}\Vert=\sqrt{{\bf b}\cdot {\bf b}}=\sqrt{2^2+4^2+1^2}=\sqrt{21} $$ We then have that $$ \begin{array}{lll} \displaystyle \cos \theta &\displaystyle= \frac{{\bf a}\cdot {\bf b}}{\Vert {\bf a}\Vert \Vert {\bf b} \Vert}&\mbox{}\\ \displaystyle &\displaystyle= \frac{\langle 1, 2, 0\rangle\cdot\langle 2, 4, 1 \rangle}{\sqrt{5}\sqrt{21}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{2+8+0}{\sqrt{105}}&\mbox{}\\ \displaystyle &\displaystyle= \frac{10}{\sqrt{105}}&\mbox{}\\ \end{array} $$ Thus, $$ \begin{array}{lll} \displaystyle \theta&\displaystyle= \cos^{-1}\left(\frac{10}{\sqrt{105}}\right)&\mbox{}\\ \displaystyle &\displaystyle\approx 0.2199879774&\mbox{}\\ \end{array} $$
Interpretation
The above result tells us that ${\bf u}\cdot {\bf v}$ is the magnitude of ${\bf u}$ in the direction of ${\bf v}$ times the magnitude of ${\bf v}.$
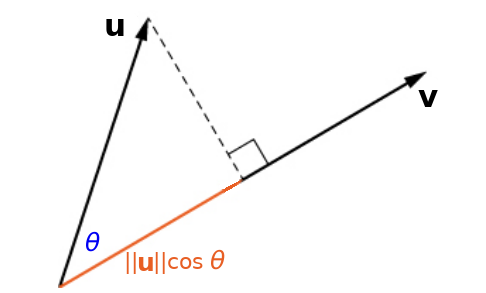
We will see later that this fact is quite relevant to ideas from physics.
The Sign of the Dot Product ${\bf u}\cdot {\bf v}=\Vert {\bf u}\Vert \Vert {\bf v} \Vert \cos \theta$
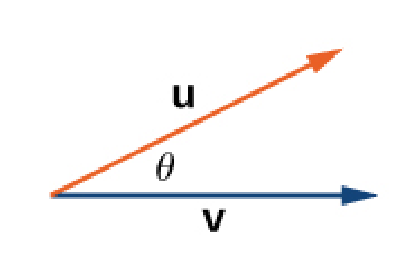 | ${\bf u}\cdot {\bf v} \gt 0$ |
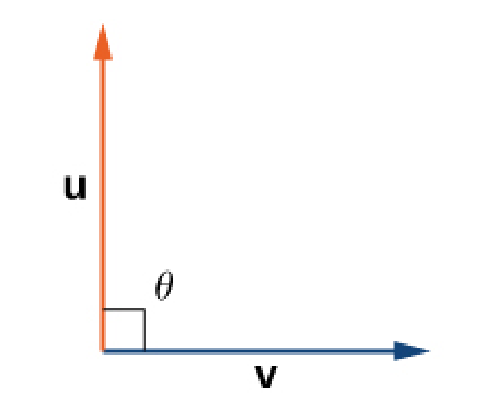 | ${\bf u}\cdot {\bf v} =0$ |
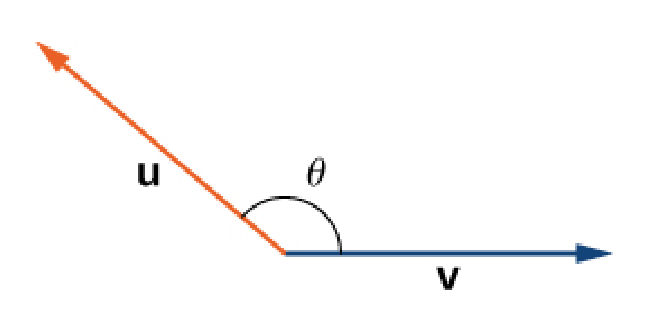 | ${\bf u}\cdot {\bf v} \lt 0$ |
The Sign of the Dot Product ${\bf u}\cdot {\bf v}=\Vert {\bf u}\Vert \Vert {\bf v} \Vert \cos \theta$
 | ${\bf u}\cdot {\bf v} =\Vert {\bf u}\Vert \Vert {\bf v}\Vert$ |
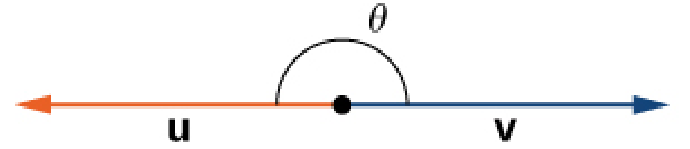 | ${\bf u}\cdot {\bf v} =-\Vert {\bf u}\Vert \Vert {\bf v}\Vert$ |
Orthogonal Vectors
Two vectors ${\bf u}$ and ${\bf v}$ are said to be orthogonal if the angle between them is a right angle.

Special Note: The terms orthogonal, perpendicular, and normal all indicate that mathematical objects are intersecting at right angles.
Orthogonality plays a huge role in pure and applied mathematics.
Theorem
Two vectors ${\bf u}$ and ${\bf v}$ are orthogonal if and only if ${\bf u}\cdot {\bf v}=0.$
Examples
(a) Verify that ${\bf p} = \langle 1, 0, 5 \rangle$ and ${\bf q} = \langle 10, 3, -2 \rangle$ are orthogonal vectors.
(b) For which value of $x$ is ${\bf p} = \langle 2, 8, -1 \rangle$ orthogonal to ${\bf q} = \langle x, -1, 2 \rangle ?$
Solution
(a) For ${\bf p} = \langle 1, 0, 5 \rangle$ and ${\bf q} = \langle 10, 3, -2 \rangle$ $$ \begin{array}{lll} \displaystyle {\bf p}\cdot {\bf q}&\displaystyle= \langle 1, 0, 5 \rangle \cdot \langle 10, 3, -2 \rangle&\mbox{}\\ \displaystyle &\displaystyle=10+0+(-10) &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$ Thus, ${\bf p}$ and ${\bf q}$ are perpendicular.
(b) For ${\bf p} = \langle 2, 8, -1 \rangle$ orthogonal to ${\bf q} = \langle x, -1, 2 \rangle ,$ $$ \begin{array}{lll} \displaystyle {\bf p}\cdot {\bf q}&\displaystyle= \langle 2,8,-1 \rangle \cdot \langle x,-1,2 \rangle&\mbox{}\\ \displaystyle &\displaystyle=2x+(-8)+(-2) &\mbox{}\\ \displaystyle &\displaystyle=2x-10 &\mbox{}\\ \end{array} $$ For ${\bf p}$ and ${\bf q}$ to be perpendicular it must then be that $2x-10=0.$ Thus, ${\bf p}$ and ${\bf q}$ are perpendicular when $x=5.$
Direction Angles
The angles $\alpha,$ $\beta,$ and $\gamma$ between a vector ${\bf v}$ and the standard unit vectors ${\bf i},$ ${\bf j},$ and ${\bf k}$ are called the direction angles of ${\bf v}.$
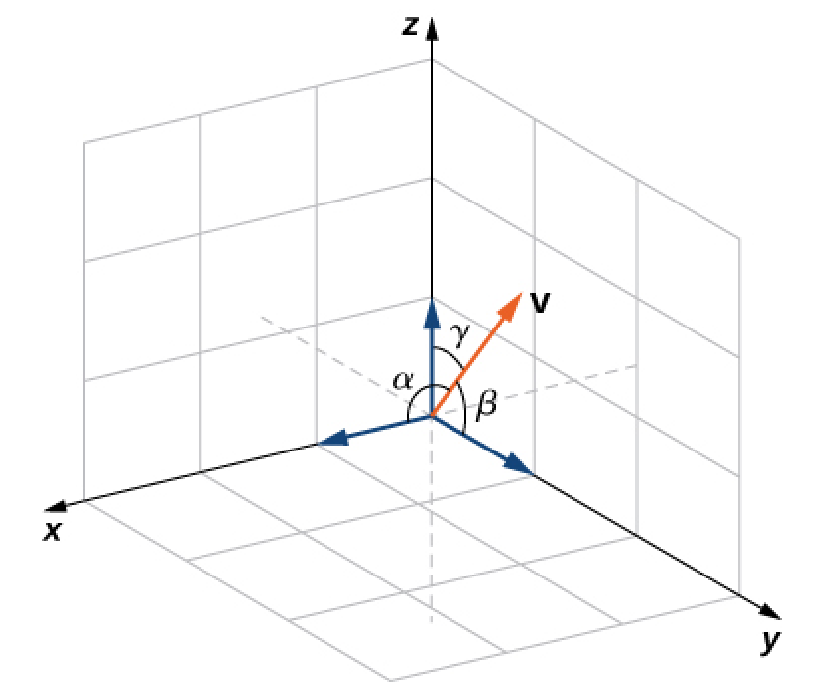
The cosines of these angles are called the direction cosines.
Direction Angles

From the above figure we see that $$\displaystyle \cos \alpha =\frac{{\bf v}\cdot {\bf i}}{\Vert {\bf v} \Vert \Vert {\bf i} \Vert}=\frac{{\bf v}\cdot {\bf i}}{\Vert {\bf v} \Vert }$$ $$\displaystyle \cos \beta =\frac{{\bf v}\cdot {\bf j}}{\Vert {\bf v} \Vert \Vert {\bf j} \Vert}=\frac{{\bf v}\cdot {\bf j}}{\Vert {\bf v} \Vert }$$ $$\displaystyle \cos \gamma =\frac{{\bf v}\cdot {\bf k}}{\Vert {\bf v} \Vert \Vert {\bf k} \Vert}=\frac{{\bf v}\cdot {\bf k}}{\Vert {\bf v} \Vert }$$
Direction Angles

It follows that $$\displaystyle \alpha =\cos^{-1}\left(\frac{{\bf v}\cdot {\bf i}}{\Vert {\bf v} \Vert }\right)$$ $$\displaystyle \beta =\cos^{-1}\left(\frac{{\bf v}\cdot {\bf j}}{\Vert {\bf v} \Vert }\right)$$ $$\displaystyle \gamma =\cos^{-1}\left(\frac{{\bf v}\cdot {\bf k}}{\Vert {\bf v} \Vert }\right)$$
Example
Find the direction angles of ${\bf v} = \langle 2, 3, 3\rangle$ in radians.
Solution
For ${\bf v} = \langle 2, 3, 3\rangle,$ we first note that $$ \Vert {\bf v} \Vert=\sqrt{{\bf v}\cdot {\bf v}}=\sqrt{2^2+3^2+3^2}=\sqrt{22} $$ Then
$$\displaystyle \alpha =\cos^{-1}\left(\frac{{\bf v}\cdot {\bf i}}{\Vert {\bf v} \Vert }\right)=\cos^{-1}\left(\frac{2}{\sqrt{22}}\right)\approx 1.130285664$$ $$\displaystyle \beta =\cos^{-1}\left(\frac{{\bf v}\cdot {\bf j}}{\Vert {\bf v} \Vert }\right)\cos^{-1}\left(\frac{3}{\sqrt{22}}\right)\approx 0.8768157319$$ $$\displaystyle \gamma =\cos^{-1}\left(\frac{{\bf v}\cdot {\bf k}}{\Vert {\bf v} \Vert }\right)\cos^{-1}\left(\frac{3}{\sqrt{22}}\right)\approx 0.8768157319$$
Projections
The vector ${\bf u}$ orthogonally projected onto ${\bf v}$ has a special name, $\mbox{proj}_{{\bf v}} {\bf u},$ and is called the projection of ${\bf u}$ onto ${\bf v}.$
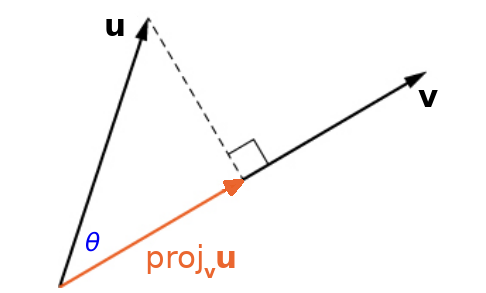
Projections

From the figure we can see that $$ \Vert \mbox{proj}_{{\bf v}} {\bf u}\Vert=\Vert {\bf u} \Vert \cos \theta =\Vert {\bf u} \Vert \left(\frac{{\bf u}\cdot {\bf v}}{\Vert{\bf u}\Vert\Vert{\bf v}\Vert}\right)=\frac{{\bf u}\cdot {\bf v}}{\Vert{\bf v}\Vert} $$
Projections

Multiply by a unit vector in the direction of ${\bf v}$ to get $$ \mbox{proj}_{{\bf v}} {\bf u}= \frac{{\bf u}\cdot {\bf v}}{\Vert{\bf v}\Vert} \frac{{\bf v}}{\Vert{\bf v}\Vert}= \frac{{\bf u}\cdot {\bf v}}{\Vert{\bf v}\Vert^2} {\bf v}%=\frac{{\bf u}\cdot {\bf v}}{{\bf v}\cdot {\bf v}} {\bf v} $$
Scalar Projections
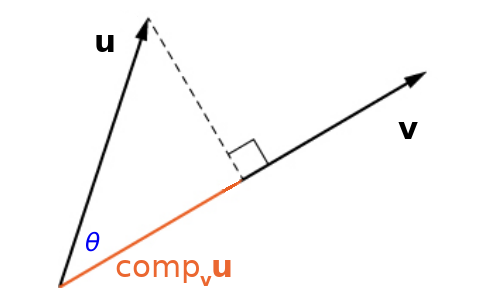
The magnitude of the projection is called scalar projection of ${\bf u}$ onto ${\bf v}$ and is denoted by $\mbox{comp}_{{\bf v}} {\bf u}.$
The reason for the notation is that we may think of the above as component of ${\bf u}$ in the direction of ${\bf v}.$ That is, the magnitude of ${\bf u}$ in the direction of ${\bf v}.$
It may be expressed as $$\mbox{comp}_{{\bf v}} {\bf u}=\Vert \mbox{proj}_{{\bf v}} {\bf u}\Vert=\Vert {\bf u}\Vert \cos \theta=\frac{{\bf u}\cdot {\bf v}}{\Vert{\bf v}\Vert}$$
Example
Consider the vectors ${\bf u} = 3{\bf i} + 2{\bf j}$ and ${\bf v} = 4{\bf i} - 3{\bf j}.$
(a) Find the component form of vector ${\bf w} = \mbox{proj}_{{\bf v}} {\bf u}$ that represents the projection of ${\bf u}$ onto ${\bf v}.$
(b) Write the decomposition ${\bf u} = {\bf w} + {\bf q}$ of vector ${\bf u}$ into the orthogonal components ${\bf w}$ and ${\bf q},$ where ${\bf w}$ is the projection of ${\bf u}$ onto ${\bf v}$ and ${\bf q}$ is a vector orthogonal to the direction of ${\bf v}.$
Solution
(a) For ${\bf u} = 3{\bf i} + 2{\bf j}$ and ${\bf v} = 4{\bf i} - 3{\bf j},$ $$ \begin{array}{lll} \displaystyle {\bf w} &\displaystyle= \mbox{proj}_{{\bf v}} {\bf u}&\mbox{}\\ %\displaystyle &\displaystyle= \frac{{\bf u}\cdot {\bf v}}{{\bf v}\cdot {\bf v}} {\bf v}&\mbox{}\\ \displaystyle &\displaystyle= \frac{{\bf u}\cdot {\bf v}}{\Vert{\bf v}\Vert^2} {\bf v}&\mbox{}\\ %\displaystyle &\displaystyle= \frac{(3{\bf i} + 2{\bf j})\cdot (4{\bf i} - 3{\bf j})}{(4{\bf i} - 3{\bf j})\cdot (4{\bf i} - 3{\bf j})}(4{\bf i} - 3{\bf j})&\mbox{}\\ \displaystyle &\displaystyle= \frac{(3{\bf i} + 2{\bf j})\cdot (4{\bf i} - 3{\bf j})}{4^2+3^2}(4{\bf i} - 3{\bf j})&\mbox{}\\ \displaystyle &\displaystyle= \frac{12-6}{16+9}(4{\bf i} - 3{\bf j})&\mbox{}\\ \displaystyle &\displaystyle= \frac{6}{25}(4{\bf i} - 3{\bf j})&\mbox{}\\ \displaystyle &\displaystyle= \frac{24}{25}{\bf i} - \frac{18}{25}{\bf j}&\mbox{}\\ \displaystyle &\displaystyle= \left\langle\frac{24}{25},-\frac{18}{25}\right\rangle&\mbox{}\\ \end{array} $$ (b) From part (a) we have that $\displaystyle {\bf w}=\left\langle\frac{24}{25},-\frac{18}{25}\right\rangle.$ We want a vector ${\bf q}$ which satisfies $ {\bf u}= {\bf w}+{\bf q}$ and ${\bf q}$ is orthogonal to ${\bf v}$, that is, ${\bf q}\cdot {\bf v}=0.$
First, $$ \begin{array}{lrll} &\displaystyle {\bf u}&\displaystyle= {\bf w}+{\bf q}&\mbox{}\\ \implies &\displaystyle \langle 3,2\rangle&\displaystyle= \left\langle\frac{24}{25},-\frac{18}{25}\right\rangle+{\bf q}&\mbox{}\\ \implies &\displaystyle \left\langle \frac{75}{25},\frac{50}{25}\right\rangle-\left\langle\frac{24}{25},-\frac{18}{25}\right\rangle&\displaystyle= {\bf q} &\mbox{}\\ \implies &\displaystyle &\displaystyle {\bf q}= \left\langle \frac{51}{25},\frac{68}{25}\right\rangle&\mbox{}\\ \end{array} $$ Second, we verify that ${\bf q}$ is orthogonal to ${\bf v}.$ $$ \begin{array}{lll} \displaystyle {\bf q}\cdot {\bf v} &\displaystyle= \left\langle \frac{51}{25},\frac{68}{25}\right\rangle \cdot \langle 4,-3\rangle&\mbox{}\\ \displaystyle &\displaystyle= \frac{51}{25}\cdot 4+\frac{68}{25}\cdot(-3)&\mbox{}\\ \displaystyle &\displaystyle= \frac{204-204}{25}\cdot 4+\frac{68}{25}\cdot(-3)&\mbox{}\\ \displaystyle &\displaystyle= 0 &\mbox{}\\ \end{array} $$ Thus, the desired decomposition is $$ {\bf u}=\langle 3,2 \rangle={\bf w} + {\bf q}=\left\langle\frac{24}{25},-\frac{18}{25}\right\rangle+\left\langle \frac{51}{25},\frac{68}{25}\right\rangle $$
Application
A container ship leaves port travelling $15^{\circ}$ north of east. Its engine generates a speed of $20$ knots along that path. In addition, the ocean current moves the ship southeast at a speed of $2$ knots.
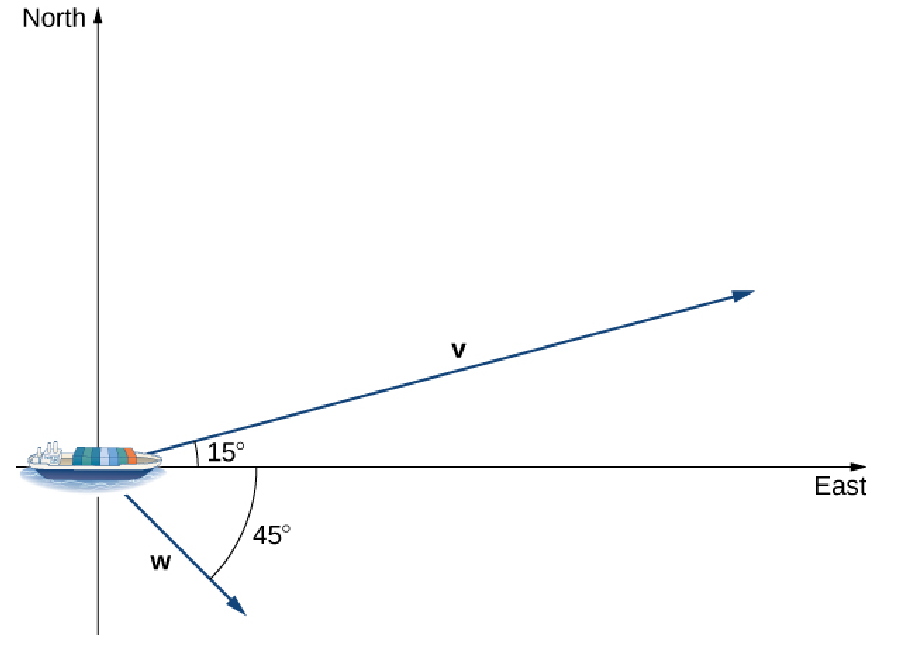
Considering both the engine and the current, how fast is the ship moving in the direction $15^{\circ}$ north of east?
Solution
The current has a positive component along ${\bf v}$ which will add to the speed in the direction of ${\bf v}.$ The increase in speed is the scalar projection of ${\bf w}$ onto ${\bf v},$ or $\color{magenta}{\mbox{comp}_{{\bf v}}{\bf w}}.$
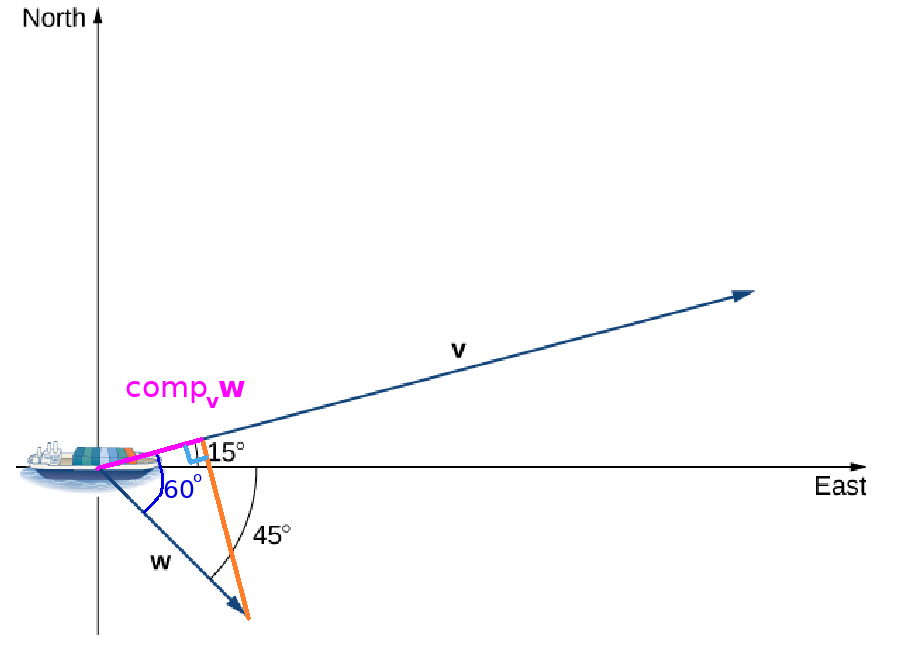
From the information given $ \Vert {\bf v}\Vert=20$ and $ \Vert {\bf w}\Vert=2$ The total speed of the ship is then $$ \begin{array}{lll} \displaystyle \Vert {\bf v}\Vert+ \color{magenta}{\mbox{comp}_{{\bf v}}{\bf w}}&\displaystyle=\Vert {\bf v}\Vert + \color{magenta}{\Vert {\bf w} \Vert \cos \theta}&\mbox{}\\ \displaystyle &\displaystyle=20 + \color{magenta}{2 \cos \color{blue}{60^{\circ}}}&\mbox{}\\ \displaystyle &\displaystyle=20 + \color{magenta}{2\cdot \frac{1}{2}}&\mbox{}\\ \displaystyle &\displaystyle=20 + 1&\mbox{}\\ \displaystyle &\displaystyle=21&\mbox{}\\ \end{array} $$ The ship is moving $21$ knots in the direction of ${\bf v}.$
Work
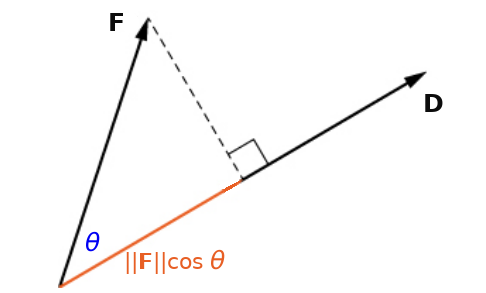
Work is defined as the magnitude of the force applied in the direction of an objects motion times the distance to object travels.
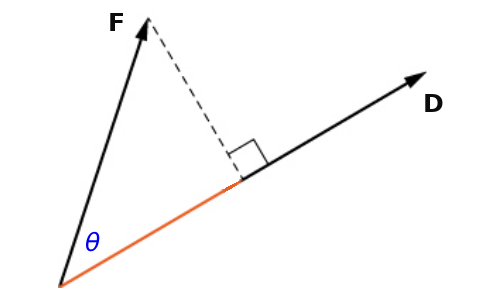
That is, if a force ${\bf F}$ is applied to an object over a straight-line distance ${\bf D},$ the work done on that object is the magnitude of force ${\bf F}$ in direction of ${\bf D}$ times the magnitude of ${\bf D}.$
Work
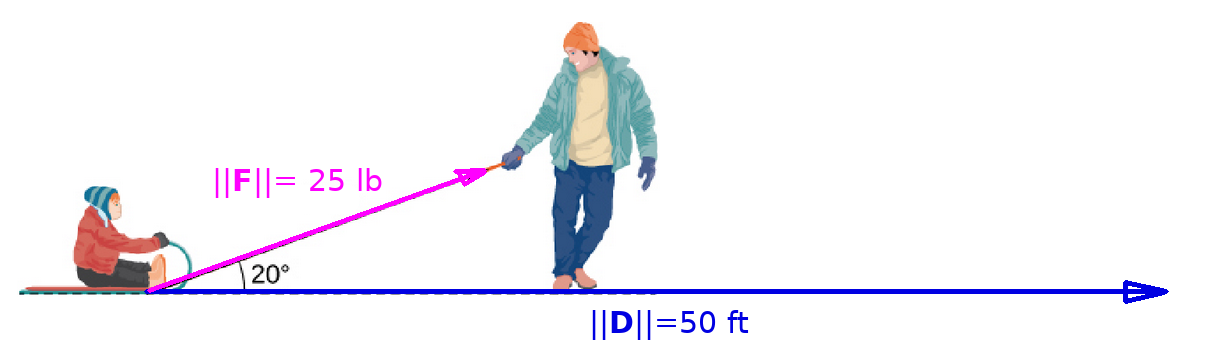
Example
A father is pulling his son on a sled at an angle of $20^{\circ}$ with the horizontal with a force of $25$ lb. He pulls the sled in a straight path of $50$ ft.
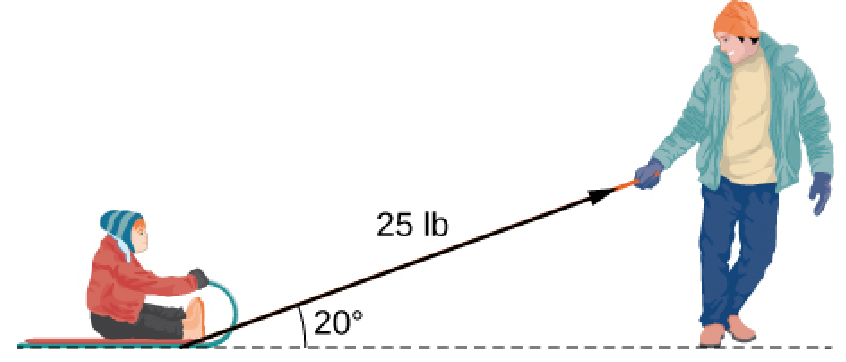
How much work was done by the man pulling the sled?
Solution