We discussed vectors in two-dimensional space.
Now, very naturally, we broaden this notion to vectors living in three dimensions.
First, however, we must get a brief tour of the basics of three-dimensional space.
Three-Dimensional Space: $\mathbb{R}^3$
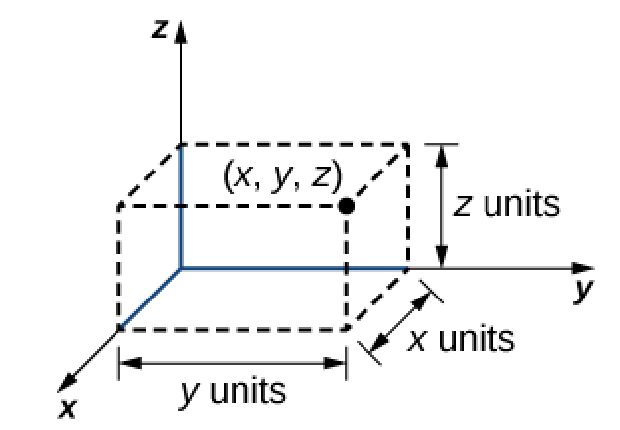
Just as any point in two-dimensional space, $\mathbb{R}^2,$ can be located by using two perpendicular axes $x$ and $y,$ we can locate any point in in $\mathbb{R}^3$ with three perpendicular axes $x,$ $y,$ and $z.$
Three-Dimensional Space: $\mathbb{R}^3$
Just as any point in two-dimensional space, $\mathbb{R}^2,$ can be located by using two perpendicular axes $x$ and $y,$ we can locate any point in in $\mathbb{R}^3$ with three perpendicular axes $x,$ $y,$ and $z.$
Three-Dimensional Space: $\mathbb{R}^3$
The coordinate system we use is a "right-handed" coordinate system.

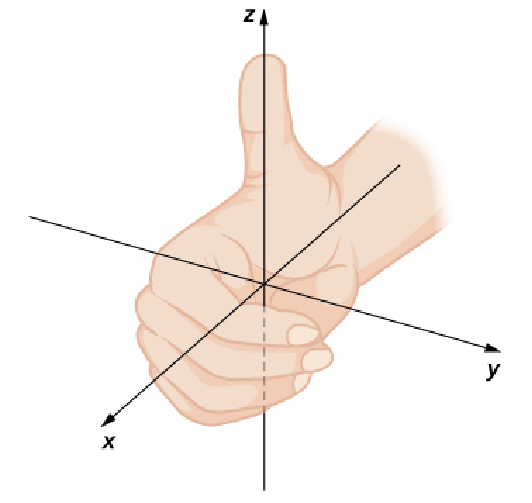
Imagine the fingers on your right hand aligned with the positive $x$-axis, then swinging your fingers into the positive $y$-axis, the thumb which represents the $z$-axis points up. That is, "up" is the positive $z$ direction.
The reason for this terminology is that the orientation of a coordinate system is not unique. A "left-handed" coordinate system would result in the positive $z$-axis pointing down.
Example
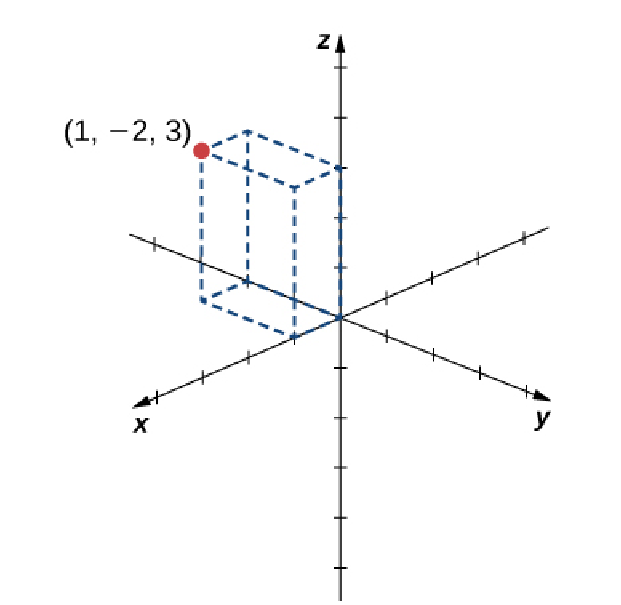
Sketch the points $(1,-2,3)$ and $(-2, 3, -1).$

Solution
Three-Dimensional Space: Coordinate Planes and Octants
Three perpendicular axes give us three coordinate planes and 8 octants.
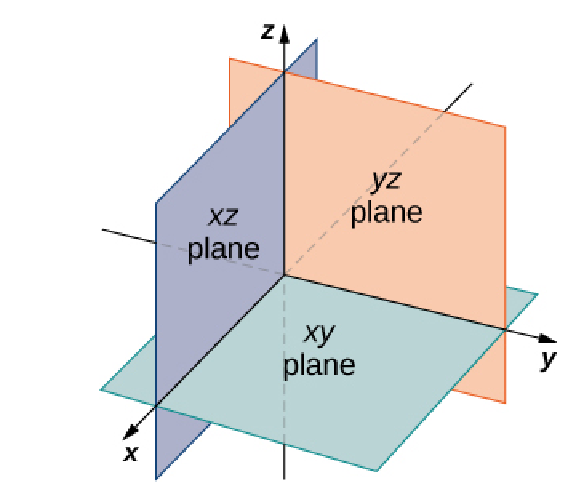
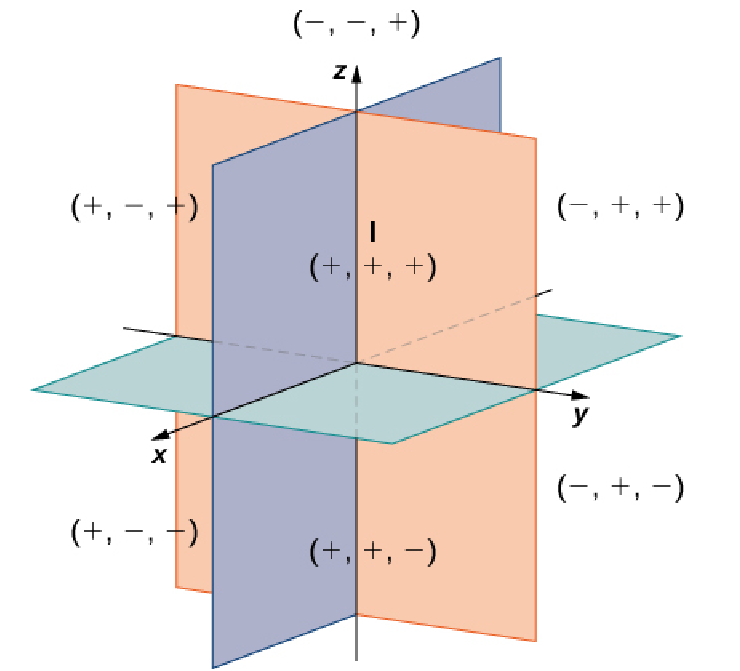
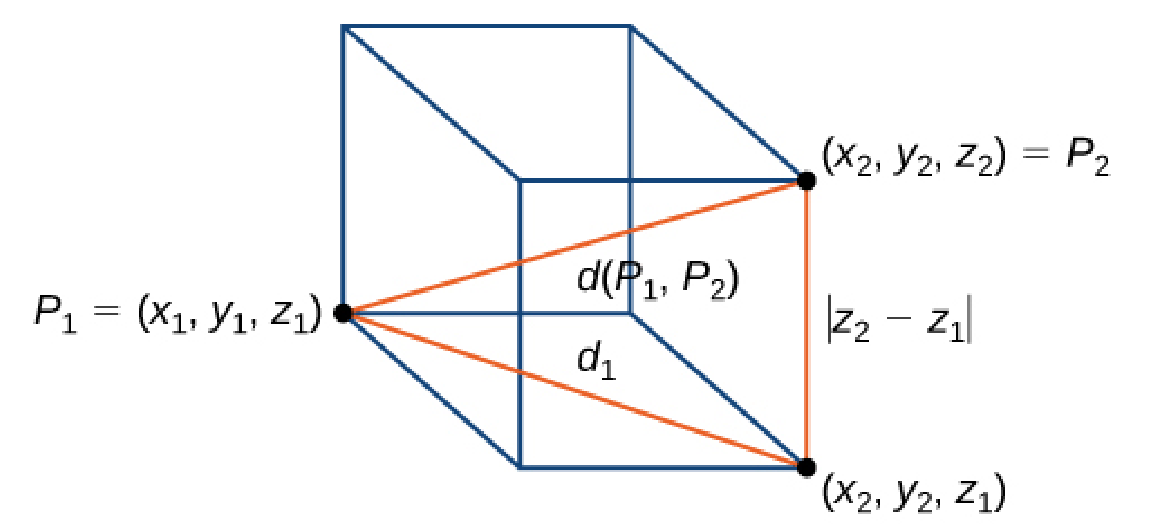
The Distance Between Two Points in $\mathbb{R}^3$
The distance $d$ between points $P_1=(x_1, y_1, z_1)$ and $P_2=(x_2, y_2, z_2)$ is given by the formula $$ d(P_1,P_2)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}=\sqrt{\Delta x^2+\Delta y^2+\Delta z^2} $$
Example
Find the distance between points $P_1 = (3, -1, 5)$ and $P_2 = (2, 1, -1).$
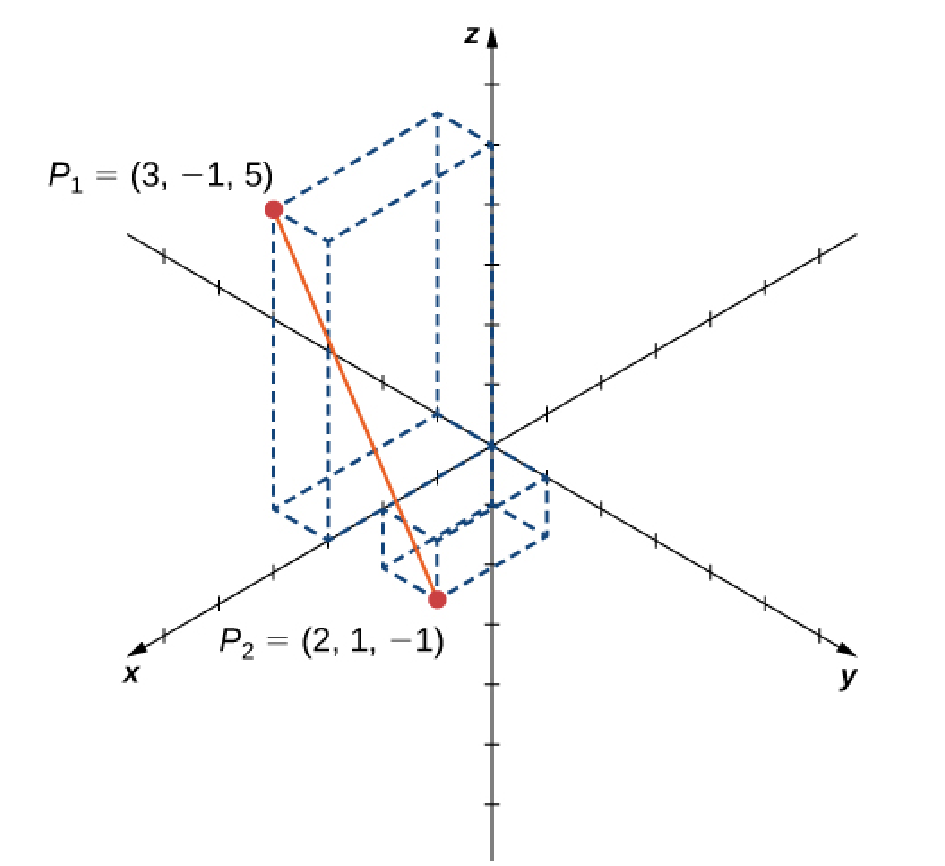
Solution
$$ \begin{array}{lll} \displaystyle d(P_1,P_2)&=\displaystyle \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}&\mbox{}\\ \displaystyle &=\displaystyle \sqrt{(2-3)^2+(1-(-1))^2+(-1-5)^2}&\mbox{}\\ \displaystyle &=\displaystyle \sqrt{1+4+36}&\mbox{}\\ \displaystyle &=\displaystyle \sqrt{41}&\mbox{}\\ \displaystyle &\approx \displaystyle 6.403124237&\mbox{}\\ \end{array} $$

Equations in Three-Dimensional Space
Equations in one variable in one-dimensional space give us points.
Equations in two variables in two-dimensional space give us curves.
Equations in three variables in three dimensions give us surfaces.
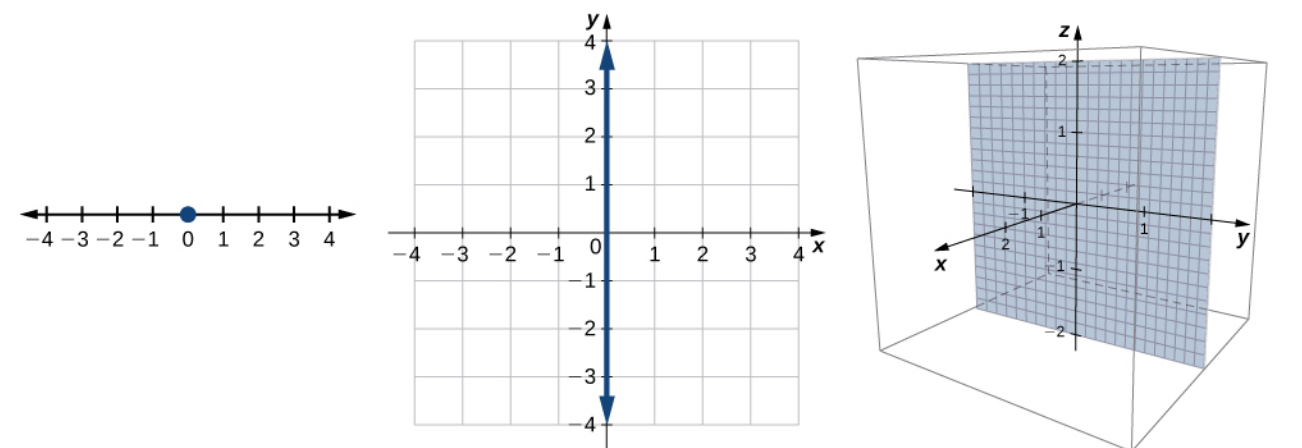
Example
The equations $x=0,$ $y=0,$ and $z=0$ give us the planes below.
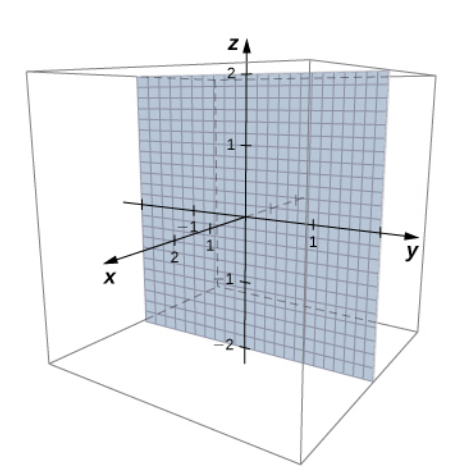
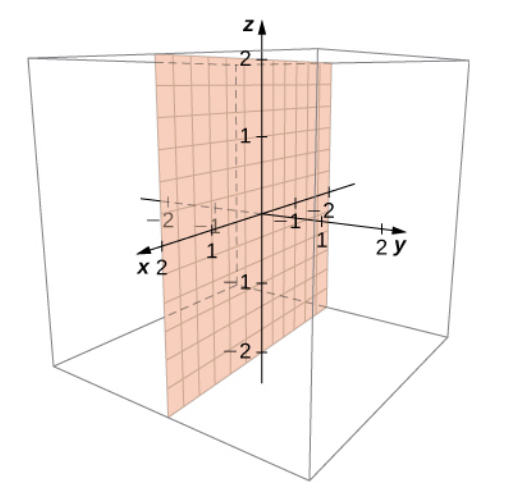
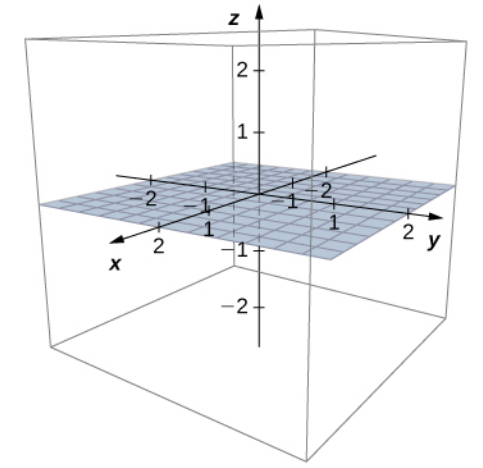
Example of a Surface: Spheres
Suppose we are interested in the collection of points $(x,y,z)$ a distance $r$ away from some point, say $(a,b,c)$ Then, $ r=\sqrt{(x-a)^2+(y-b)^2+(z-c)^2} $ or, $$(x-a)^2+(y-b)^2+(z-c)^2=r^2$$
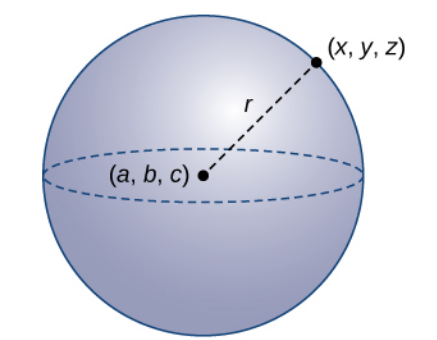
A sphere is the collection of all points $(x,y,z)$ which are a fixed distance away from $(a,b,c).$
Example
Find the standard equation of the sphere with center $(10, 7, 4)$ and containing the point $(-1, 3, -2).$
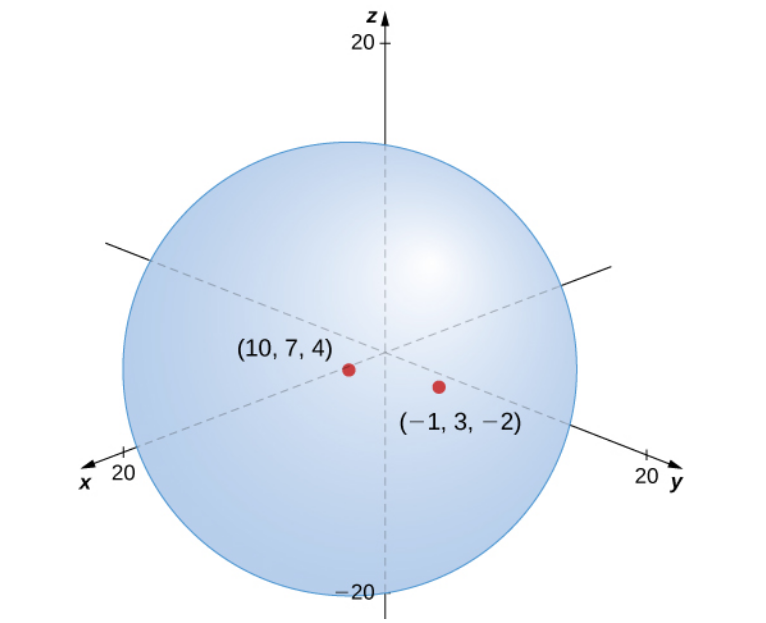
Solution
We first find the distance between the center, $C=(10, 7, 4),$ and the particular point $P=(-1, 3, -2)$ to determine the radius of the sphere. $$ \begin{array}{lll} \displaystyle d(C,P)&=\displaystyle \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}&\mbox{}\\ \displaystyle &=\displaystyle \sqrt{(-1-10)^2+(3-7)^2+(-2-4)^2}&\mbox{}\\ \displaystyle &=\displaystyle \sqrt{121+16+36}&\mbox{}\\ \displaystyle &=\displaystyle \sqrt{173}&\mbox{}\\ \end{array} $$ Thus, the distance between any point $A=(x,y,z)$ on the sphere and the center is $\sqrt{173}$
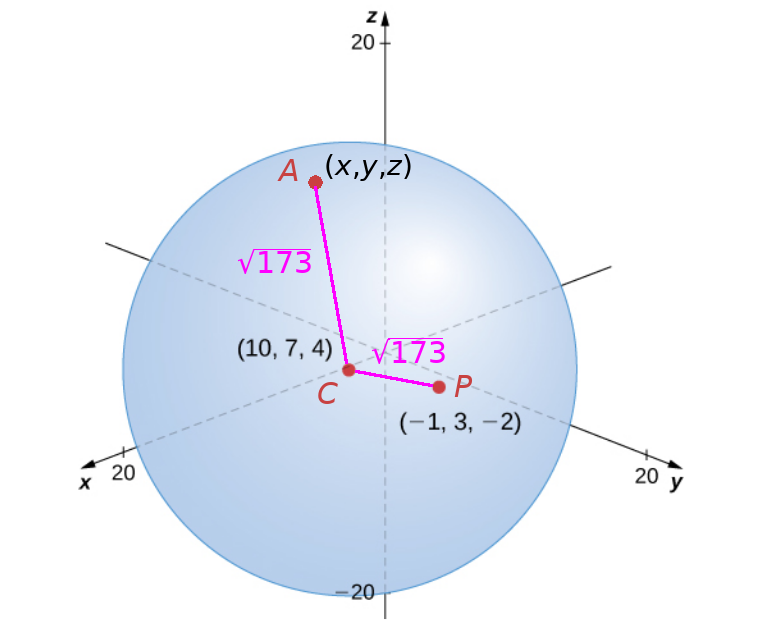
The above translates to $$ d(C,A)=\sqrt{173}=\sqrt{(x-10)^2+(y-7)^2+(z-4)^2} $$ or $$ (x-10)^2+(y-7)^2+(z-4)^2=173. $$
Example
Describe the set of points in three dimensional space that satisfies $x^2 + (z - 2)^2 = 16,$ and graph the surface.

Solution
In two dimensions, the graph of $x^2 + (z - 2)^2 = 16$ is a circle of radius $4$ centered at $(0,2)$ in the $xz$-plane.
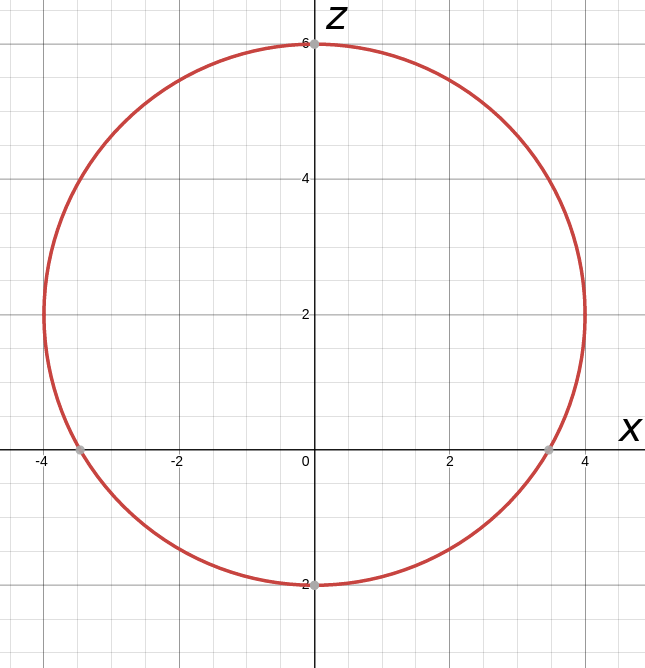
In three dimensions, $y$ doesn't appear in the equation $x^2 + (z - 2)^2 = 16.$ This means that $y$ is a "free" variable. That is, the surface is the "extended" circle in the $y$ direction.
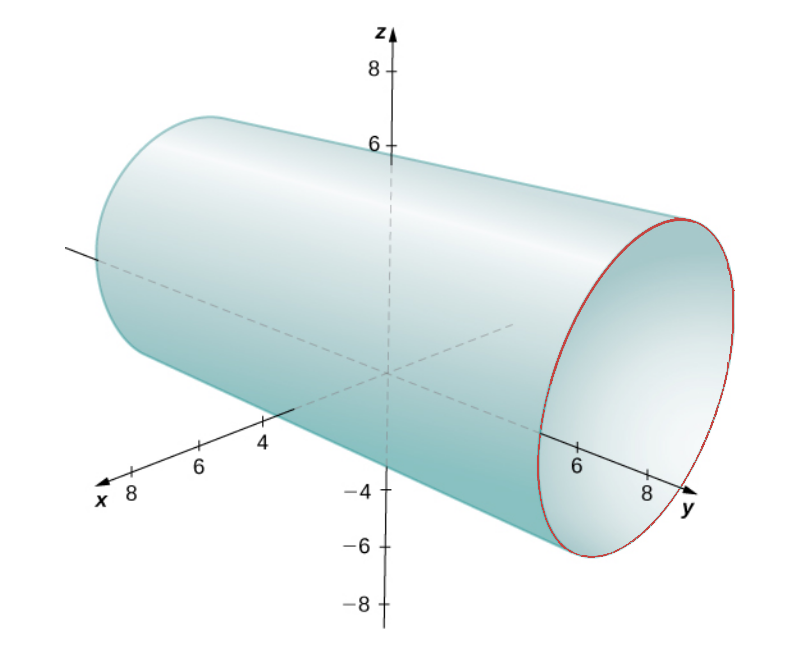
To understand why this is the case, we note that if the point $(x,y,z)$ is on the surface, $x$ and $z$ are constrained to satisfy the equation $x^2 + (z - 2)^2 = 16,$ whereas $y$ can be any number.
Example
Sketch or use a graphing tool to view the graph of the cylindrical surface defined by equation $z = y^2.$

Solution Solution
In two dimensions, the graph of $z=y^2$ is a parabola in the $yz$-plane.
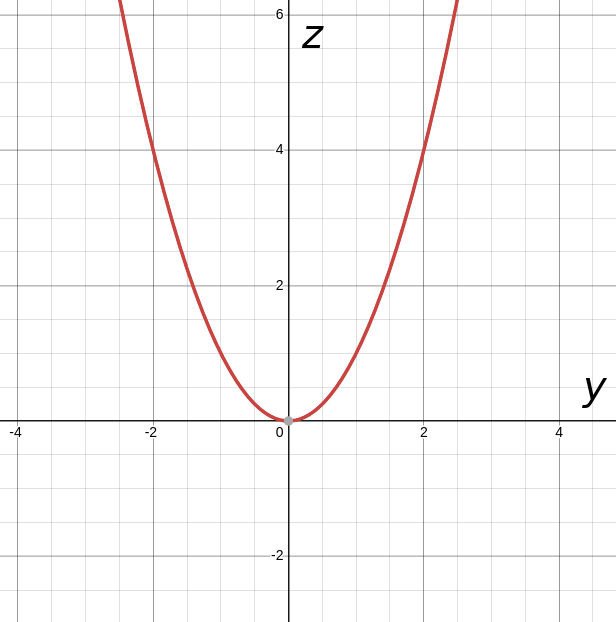
In three dimensions, $x$ doesn't appear in the equation $z=y^2$ This means that $x$ is a "free" variable. That is, the surface is the "extended" circle in the $x$ direction.
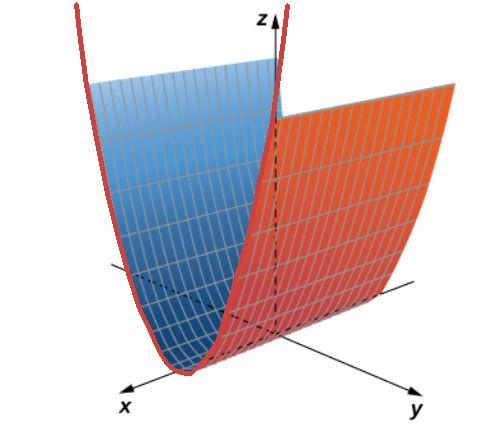
To understand why this is the case, we note that if the point $(x,y,z)$ is on the surface, $y$ and $z$ are constrained to satisfy the equation $z=y^2,$ whereas $x$ can be any number.
This surface is called a "parabolic cylinder."
Vectors in Spaaaace!
Vectors can live in three dimensions just as well as two dimensions.
We simply lift our vectors off the page an into space.
The analogies between three and two dimensional vectors are perfect as we shall see in the results we use to do computations with vectors.
Vectors in $\mathbb{R}^3$
To define the initial and terminal point of a vector in $\mathbb{R}^2,$ we need $2$ coordinates.
To define the initial and terminal point of a vector in $\mathbb{R}^3,$ we need $3$ coordinates.
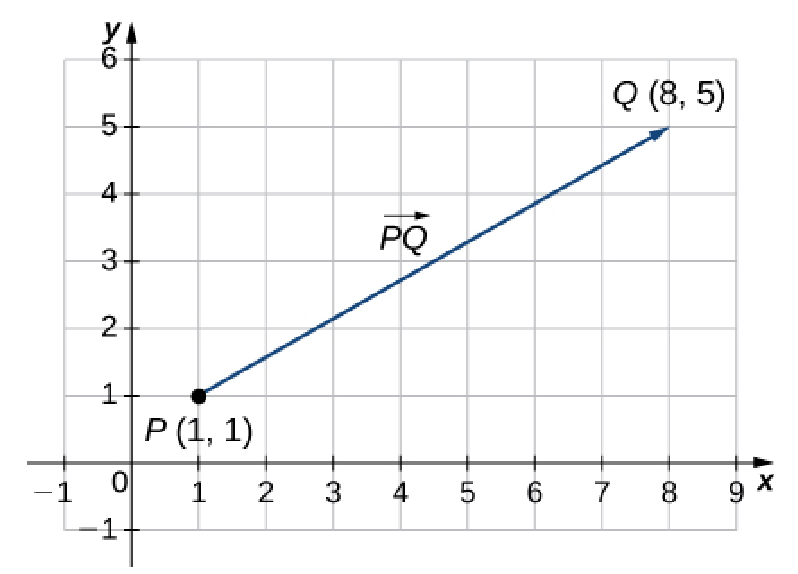
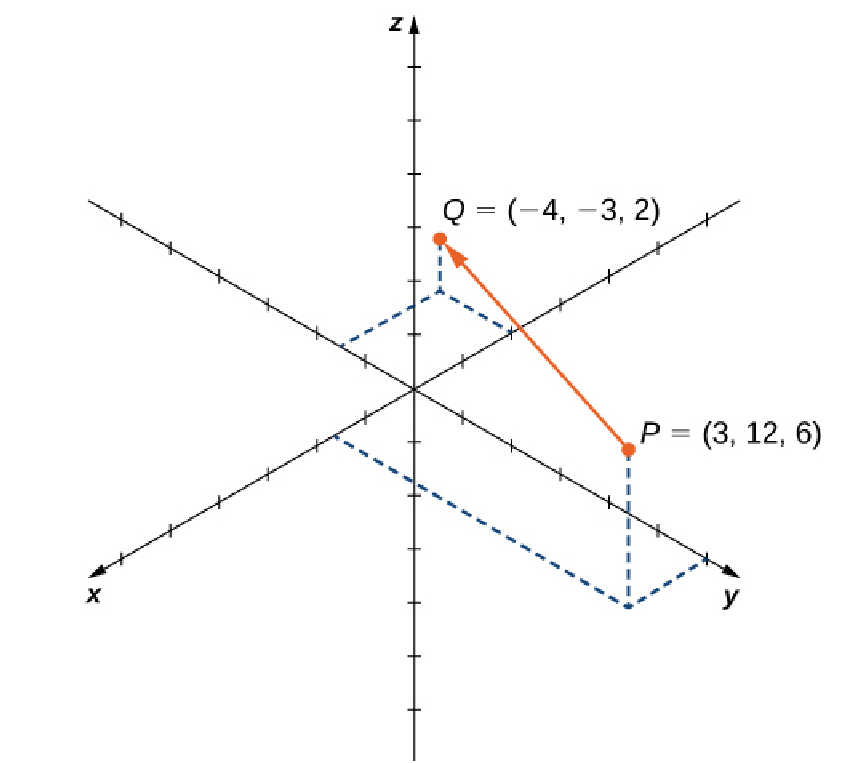
Vectors in $\mathbb{R}^3$
A three-dimensional vector in component form has $3$ components.
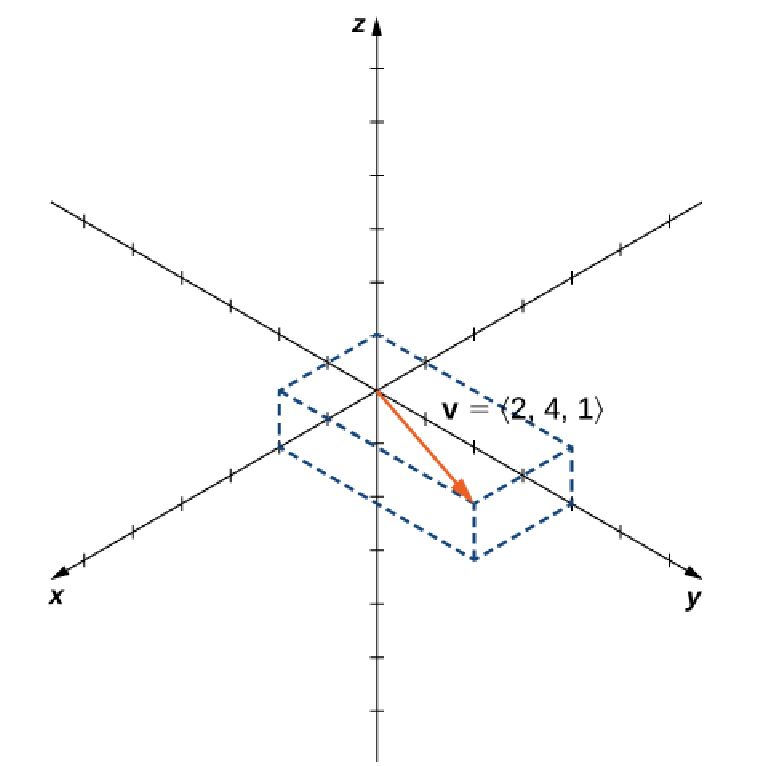
Vectors in $\mathbb{R}^3$
A vector ${\bf v}$ whose initial point $(x_i,y_i,z_i)$ and terminal point is $(x_t,y_t,z_t)$ is written in component form as $$ {\bf v}=\langle x_t-x_i, y_t-y_i, z_t-z_i\rangle $$ Example: Write the vector below in component form.

Solution
$$ \begin{array}{lll} \displaystyle {\bf v} &\displaystyle= \langle x_t-x_i, y_t-y_i, z_t-z_i\rangle &\mbox{}\\ \displaystyle &\displaystyle=\langle -4-3, -3-12, 2-6\rangle &\mbox{}\\ \displaystyle &\displaystyle=\langle -7, -15, -4\rangle &\mbox{}\\ \end{array} $$

Vector Addition in $\mathbb{R}^3$
To add the vectors ${\bf A}$ and ${\bf B},$ place the initial point of ${\bf B}$ at the terminal point of ${\bf A}.$
Then, the sum of the vectors ${\bf A}$ and ${\bf B}$ is denoted ${\bf A}+{\bf B}$ and is defined to be the vector whose initial point is that of ${\bf A}$ and whose terminal point is that of ${\bf B}.$
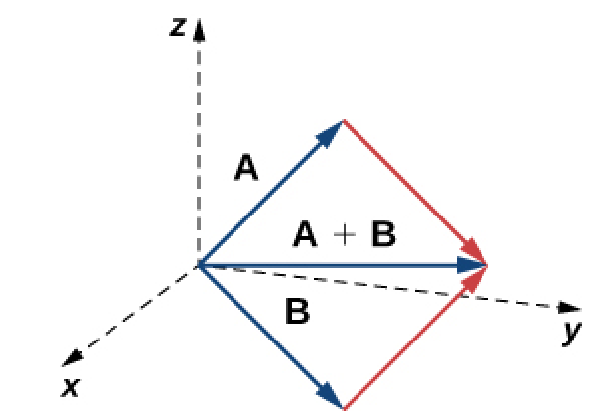
Essential Properties of Vectors in $\mathbb{R}^3$
Let ${\bf u},$ ${\bf v},$ and ${\bf w}$ be vectors in $\mathbb{R}^3$ and let $r$ and $s$ be scalars. Then the following properties hold. $$ \begin{array}{ll} {\bf u} + {\bf v} = {\bf v} + {\bf u} & \mbox{Vector addition is commutative.}\\ ({\bf u} + {\bf v}) + {\bf w} = {\bf u} + ({\bf v} + {\bf w}) & \mbox{Vector addition is associative.}\\ {\bf u} + {\bf 0} = {\bf u} & \mbox{The zero vector ${\bf 0}$ is the additive identity.}\\ {\bf u} + (-{\bf u}) = {\bf 0} & \mbox{Every vector has an additive inverse.}\\ r(s{\bf u}) = (rs){\bf u} & \mbox{Associativity of scalar multiplication.}\\ (r + s){\bf u} = r{\bf u} + s{\bf u} & \mbox{Vectors distribute over scalar addition.}\\ r({\bf u} + {\bf v}) = r{\bf u} + r{\bf v} & \mbox{Scalars distribute over vector addition.}\\ 1{\bf u} = {\bf u}, 0{\bf u} = {\bf 0} & \mbox{Identity and zero properties.}\\ \end{array} $$ The proofs of these properties are very straightforward.
Standard Unit Vectors
The standard unit vectors are the vectors ${\bf i} = \langle 1, 0, 0 \rangle,$ ${\bf j} = \langle 0, 1, 0 \rangle,$ and ${\bf k} = \langle 0, 0, 1 \rangle,$
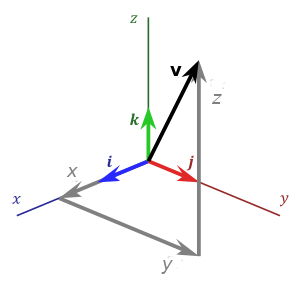
Standard Unit Vectors
The standard unit vectors allow us to write the component form ${\bf v}=\langle x,y,z\rangle$ as ${\bf v}=x{\bf i}+y{\bf j}+z{\bf k}.$

Vectors Operations in $\mathbb{R}^3$
Letting ${\bf v} = \langle x_1, y_1,z_1 \rangle$ and ${\bf w} = \langle x_2, y_2, z_2 \rangle$ be vectors, and letting $k$ be a scalar, we can define vector operations algebraically.
$$ \begin{array}{ll} \mbox{Scalar Multiplication:} & k{\bf v}=k\langle x_1, y_1,z_1 \rangle=\langle kx_1, ky_1 kz_1\rangle\\ \\ \mbox{Vector Addition:} & {\bf v} + {\bf w} = \langle x_1, y_1, z_1 \rangle + \langle x_2, y_2, z_2 \rangle = \langle x_1 + x_2, y_1 + y_2, z_1+z_2 \rangle\\\\ \mbox{Vector Subtraction:} & {\bf v} - {\bf w} = \langle x_1, y_1, z_1 \rangle - \langle x_2, y_2, z_2 \rangle = \langle x_1 - x_2, y_1 - y_2, z_1-z_2 \rangle\\\\ \mbox{Vector Magnitude:} & \Vert{\bf v}\Vert =\sqrt{ x_1^2+y_1^2+z_1^2}\\\\ \mbox{Unit Vectors:} & \displaystyle {\bf u}=\frac{{\bf v}}{\Vert{\bf v}\Vert} =\frac{1}{\Vert{\bf v}\Vert}{\bf v}=\frac{1}{\Vert{\bf v}\Vert}\langle x_1, y_1,z_1 \rangle=\left\langle\frac{x_1}{\Vert{\bf v}\Vert},\frac{y_1}{\Vert{\bf v}\Vert},\frac{z_1}{\Vert{\bf v}\Vert}\right\rangle\\\\ \end{array} $$
Example
Let ${\bf v} = \langle 1,-2,3 \rangle$ and ${\bf w} = \langle -2, 3, -1 \rangle$ Find the following vectors.
(a) $3{\bf v} - 2{\bf w}$
(b) $5 \Vert {\bf w} \Vert$
(c) $\Vert 5{\bf w} \Vert$
(d) A unit vector in the direction of ${\bf v}$
Solution
${\bf v} = \langle 1,-2,3 \rangle$ and ${\bf w} = \langle -2, 3, -1 \rangle$
(a) $$ \begin{array}{lll} \displaystyle 3{\bf v} - 2{\bf w}&\displaystyle= 3\langle 1,-2,3 \rangle -2\langle -2, 3, -1 \rangle&\mbox{}\\ \displaystyle &\displaystyle= \langle 3 \cdot 1,3(-2),3\cdot 3 \rangle -\langle 2(-2), 2\cdot 3, 2(-1) \rangle&\mbox{scalar multiplication}\\ \displaystyle &\displaystyle= \langle 3,-6,9 \rangle -\langle -4, 6, -2 \rangle&\mbox{}\\ \displaystyle &\displaystyle= \langle 3-(-4),-6-6,9-(-2) \rangle &\mbox{vector subtraction}\\ \displaystyle &\displaystyle= \langle 7,-12,11 \rangle &\mbox{}\\ \end{array} $$ (b) $$ \begin{array}{lll} \displaystyle 5\Vert {\bf w}\Vert&\displaystyle= 5\Vert\langle -2, 3, -1 \rangle \Vert&\mbox{}\\ &\displaystyle= 5\sqrt{(-2)^2+3^2+(-1)^2}&\mbox{}\\ &\displaystyle= 5\sqrt{4+9+1}&\mbox{}\\ &\displaystyle= 5\sqrt{14}&\mbox{}\\ \end{array} $$ (c) $$ \begin{array}{lll} \displaystyle \Vert 5{\bf w}\Vert&\displaystyle= \Vert 5\langle -2, 3, -1 \rangle \Vert&\mbox{}\\ &\displaystyle= \Vert \langle -10, 15, -5 \rangle \Vert&\mbox{}\\ &\displaystyle= \sqrt{(-10)^2+15^2+(5)^2}&\mbox{}\\ &\displaystyle= \sqrt{100+225+25}&\mbox{}\\ &\displaystyle= \sqrt{350}&\mbox{}\\ &\displaystyle= \sqrt{25\cdot 14}&\mbox{}\\ &\displaystyle= \sqrt{25}\cdot \sqrt{14}&\mbox{}\\ &\displaystyle= 5\sqrt{14}&\mbox{}\\ \end{array} $$ (d) A unit vector ${\bf u}$ in the direction of ${\bf v}$ is $$ \begin{array}{lll} \displaystyle {\bf u}&\displaystyle= \frac{1}{\Vert{\bf v}\Vert}{\bf v}&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{\Vert\langle 1,-2,3 \rangle\Vert}\langle 1,-2,3 \rangle&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{\sqrt{1^2+(-2)^2+3^2}}\langle 1,-2,3 \rangle&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{\sqrt{1^2+(-2)^2+3^2}}\langle 1,-2,3 \rangle&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{\sqrt{1+4+9}}\langle 1,-2,3 \rangle&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{\sqrt{14}}\langle 1,-2,3 \rangle&\mbox{}\\ \displaystyle &\displaystyle=\left \langle \frac{1}{\sqrt{14}},-\frac{2}{\sqrt{14}},\frac{3}{\sqrt{14}} \right \rangle&\mbox{scalar multiplication}\\ \displaystyle &\displaystyle=\left \langle \frac{\sqrt{14}}{14},-\frac{\sqrt{14}}{7},\frac{3\sqrt{14}}{14} \right \rangle&\mbox{rationalize denominators}\\ \end{array} $$
Application
A quarterback is standing on the football field preparing to throw a pass. His receiver is standing $20$ yd down the field and $15$ yd to the quarterback’s left. The quarterback throws the ball at a velocity of $60$ mph toward the receiver at an upward angle of $30^{\circ}$ (see the following figure).
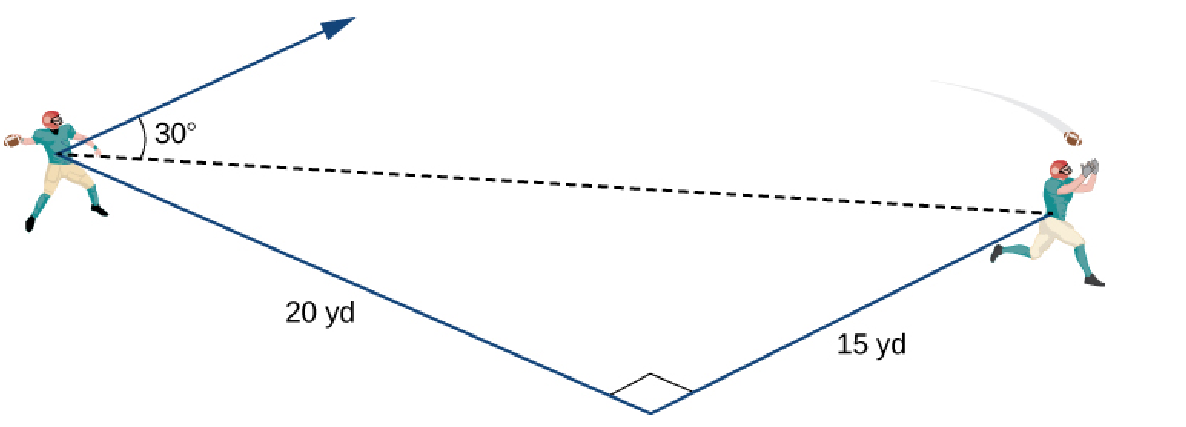
Write the initial velocity vector of the ball, ${\bf v},$ in component form.
Solution
Imposing a three-dimensional coordinate system on the situation, we have the following picture.
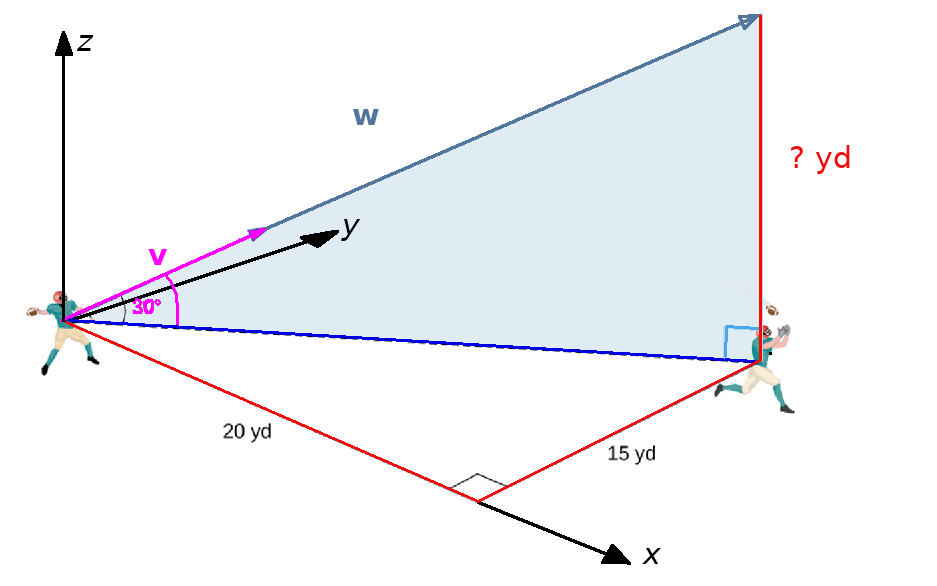
We would like to find the velocity vector $\color{magenta}{{\bf v}}.$
The first step in our strategy will be to find the longer vector, ${\bf w},$ which points in the same direction.
To find the $z$-coordinate of ${\bf w},$ we must first find the distance from the quarterback to the receiver. This is a matter of using Pythagorean Theorem (or the distance formula in the plane). $$ d=\sqrt{20^2+15^2}=\sqrt{625}=25 $$ Thus the distance is $25$ yards.
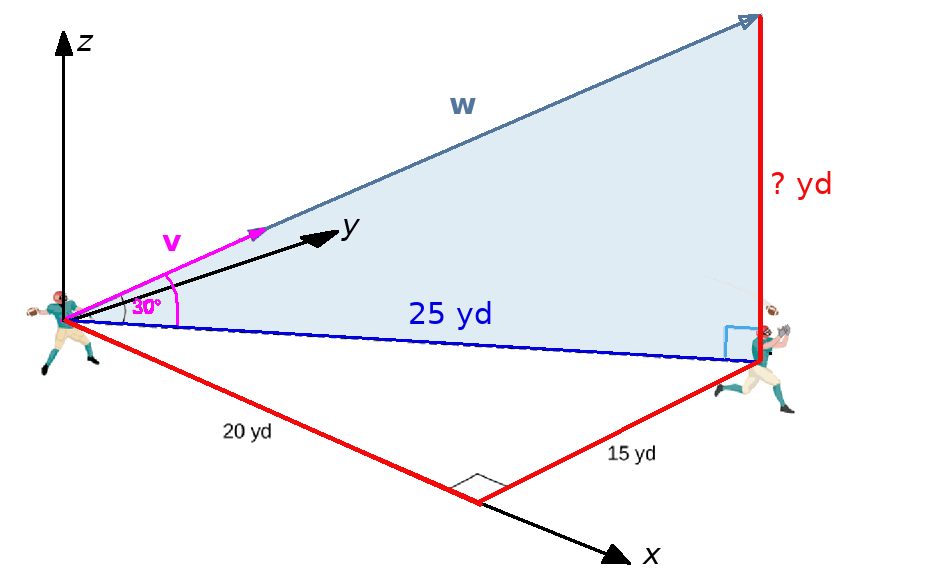
We now find the $z$ component of ${\bf w}.$ We know that $\displaystyle \tan 30^{\circ}=\frac{z}{25}$ so that $\displaystyle z=25 \tan 30^{\circ}.$ We then have $$\displaystyle {\bf w}=\left \langle 20,15,25\tan 30^{\circ} \right \rangle = \left \langle 20,15,\frac{25}{\sqrt{3}}\right \rangle$$ We now find a unit vector which points in the same direction as ${\bf v}$ and ${\bf w}.$ First, we find the length of ${\bf w}.$ $$\displaystyle\Vert {\bf w}\Vert=\left \Vert \left \langle 20,15,\frac{25}{\sqrt{3}}\right \rangle \right \Vert=\sqrt{20^2+15^2+\frac{25^2}{3}}=\sqrt{\frac{2500}{3}}=\frac{50}{\sqrt{3}}$$ Thus, the unit vector ${\bf u}$ which points in the direction of ${\bf v}$ and ${\bf w}$ is $$ \begin{array}{lll} \displaystyle {\bf u}&\displaystyle= \frac{1}{\Vert{\bf w}\Vert}{\bf w}&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{\left\Vert\left \langle 20,15,\frac{25}{\sqrt{3}}\right \rangle\right\Vert}\left \langle 20,15,\frac{25}{\sqrt{3}}\right \rangle&\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{\frac{50}{\sqrt{3}}}\left \langle 20,15,\frac{25}{\sqrt{3}}\right \rangle&\mbox{}\\ \displaystyle &\displaystyle= \frac{\sqrt{3}}{50}\left \langle 20,15,\frac{25}{\sqrt{3}}\right \rangle&\mbox{}\\ \displaystyle &\displaystyle= \left \langle \frac{\sqrt{3}}{50} \cdot 20,\frac{\sqrt{3}}{50} \cdot 15,\frac{\sqrt{3}}{50}\cdot\frac{25}{\sqrt{3}}\right \rangle&\mbox{scalar multiplication}\\ \displaystyle &\displaystyle= \left \langle \frac{2\sqrt{3}}{5},\frac{3\sqrt{3}}{10},\frac{1}{2}\right \rangle&\mbox{}\\ \end{array} $$ Since $\Vert {\bf u}\Vert=1$ (verify!), we know that $60\Vert {\bf u}\Vert=\Vert 60{\bf u}\Vert=60.$
Thus, since $60 {\bf u}$ is a vector of length $60$ pointing in the same direction as ${\bf v},$ we must have $$ \begin{array}{lll} \displaystyle {\bf v}&\displaystyle=60{\bf u} &\mbox{}\\ \displaystyle &\displaystyle=60 \left \langle \frac{2\sqrt{3}}{5},\frac{3\sqrt{3}}{10},\frac{1}{2}\right \rangle&\mbox{}\\ \displaystyle &\displaystyle= \left \langle 60 \cdot\frac{2\sqrt{3}}{5},60 \cdot\frac{3\sqrt{3}}{10},60 \cdot\frac{1}{2}\right \rangle&\mbox{scalar multiplication}\\ \displaystyle &\displaystyle= \left \langle 24\sqrt{3},18\sqrt{3},30\right \rangle&\mbox{}\\ \end{array} $$