Vectors are fundamental idea in both the physical sciences, and pure and applied mathematics.
For example, to understand the physics of electricity and magnetism at a deeper level, one must truly grasp the arithmetic, algebra, and calculus of vectors.
Vectors in General: A Hand-Wavy Definition
Vectors are quantities with two parts: magnitude and direction.
Such quantities include:
- Position (or Displacement)
- Velocity
- Acceleration
- Forces
- Electric Fields
- Magnetic Fields
Vectors in the Plane: A Hand-Wavy Definition
Vectors are quantities with two parts: magnitude and direction.
We can visualize a vector as an arrow whose length is the magnitude of the quantity and points in the direction of the quantity.
Vectors: History and Origins
"Vector" is a Latin word for "carrier." That is, a vector "carries" an initial point to a terminal point.
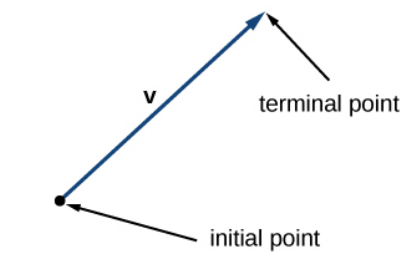
Vectors: Some Notation
Note that vector quantities in the book and in the online lecture notes will be denoted in bold.
However, it is common in handwritten calculations to put a right-pointing arrow over then quantity.
For example, we can write ${\bf v}$ by hand as $\overrightarrow{v}$
Vectors: Some Notation
The "carrying" (displacement) of the point $P$ to the point $Q$ as seen below.
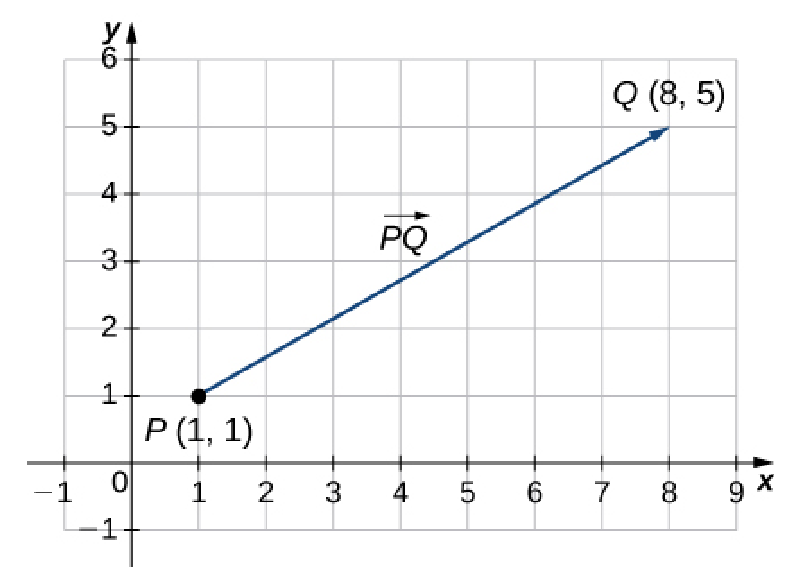
Vectors will allow us a broader means of describing processes involving work (energy) required to perform such a displacement.
Definition: Vector Equivalence
Two vectors are equal if they have the same direction and magnitude.
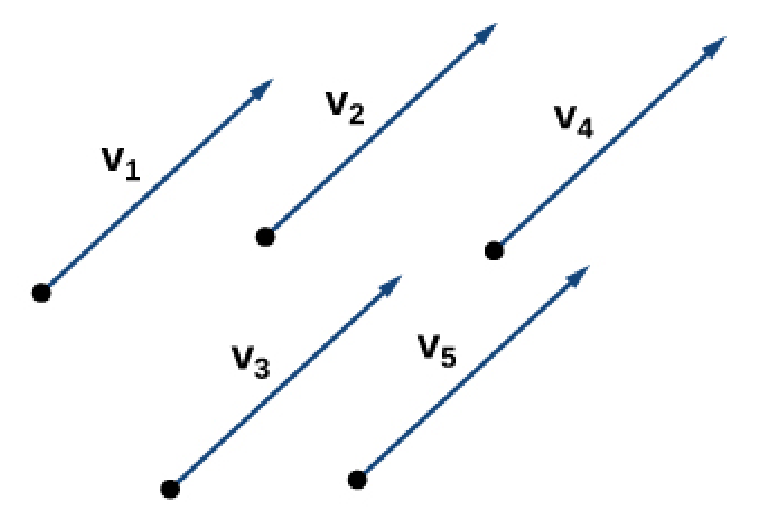
Definition: Vector Equivalence
Which of the vectors below are equal?

Operations on Vectors: Scalar Multiplication
Scalar quantities have only magnitude. Real numbers here will be considered scalar quantities.
We can multiply a vector by a scalar quantity by multiplying its length by the scalar.
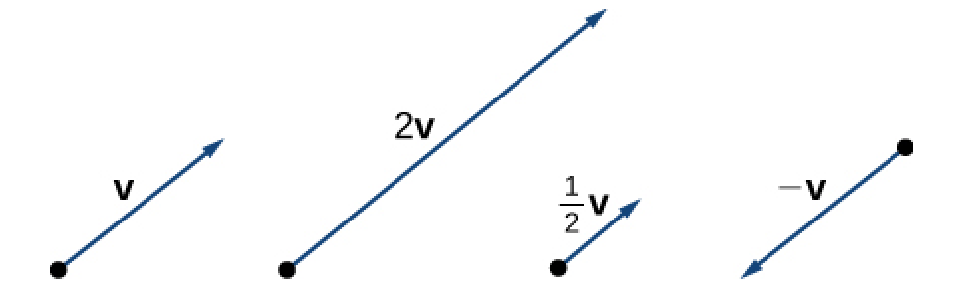
In the above figure, the vector ${\bf v}$ is being multiplied by the scalars $2,$ $\displaystyle \frac{1}{2},$ and $-1.$
Note that $(-1){\bf v}=-{\bf v}.$ Also, $-{\bf v}$ is a vector of the same magnitude as ${\bf v}$ but points in the opposite direction.
Definition: Vector Addition
To add the vectors ${\bf v}$ and ${\bf w},$ place the initial point of ${\bf w}$ at the terminal point of ${\bf v}.$
Then, the sum of the vectors ${\bf v}$ and ${\bf w}$ is denoted ${\bf v}+{\bf w}$ and is defined to be the vector whose initial point is that of ${\bf v}$ and whose terminal point is that of ${\bf w}.$
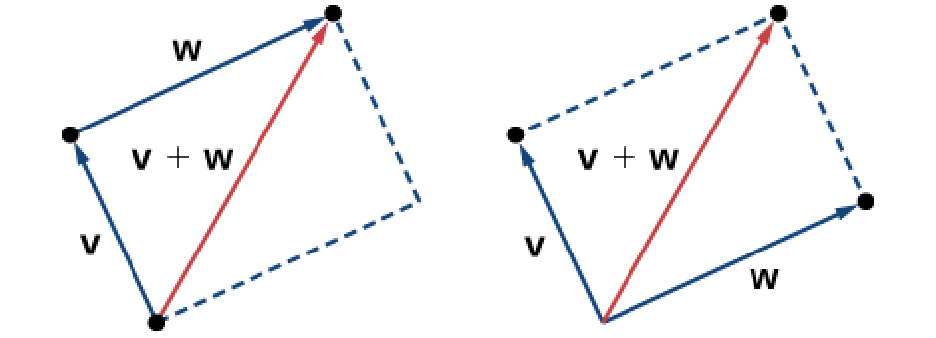
The above method is called the parallelogram method for adding two vectors.
Definition: Vector Subtraction
The difference of the vectors ${\bf v}$ and ${\bf w}$ is denoted ${\bf v}-{\bf w}$ and is defined to be the sum ${\bf v}+(-{\bf w}).$
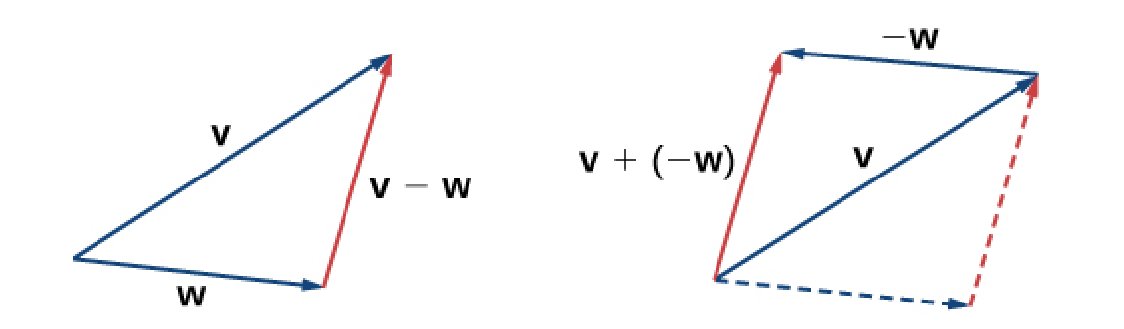
Example
Draw the vectors ${\bf v}+{\bf w},$ $\frac{1}{2}{\bf v},$ $-3{\bf w},$ and $\frac{1}{2}{\bf v}-3{\bf w}$
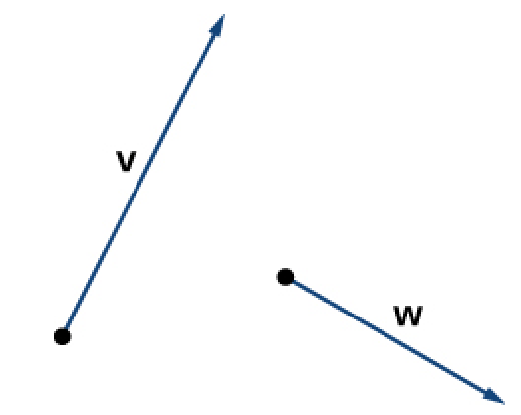
Solution
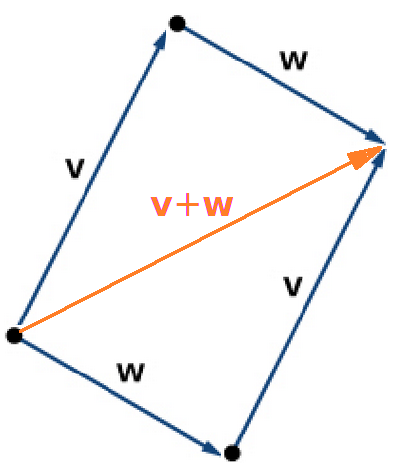 $
{\bf v}+{\bf w}
$
$
{\bf v}+{\bf w}
$
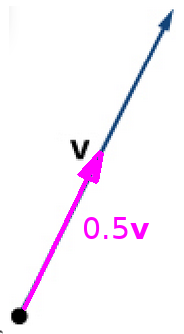 $
\frac{1}{2}{\bf v}
$
$
\frac{1}{2}{\bf v}
$
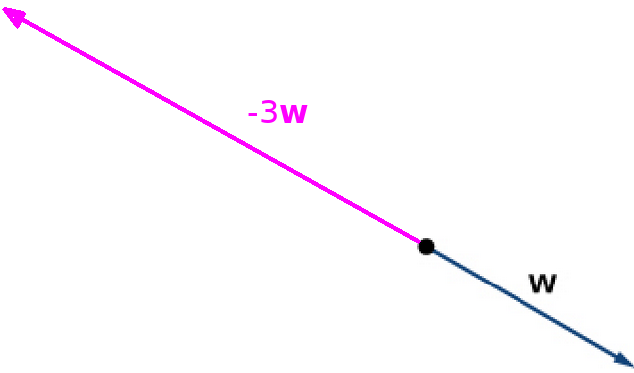 $
-3{\bf w}
$
$
-3{\bf w}
$
 $
\frac{1}{2}{\bf v}-3{\bf w}=\frac{1}{2}{\bf v}+(-3{\bf w})
$
$
\frac{1}{2}{\bf v}-3{\bf w}=\frac{1}{2}{\bf v}+(-3{\bf w})
$
Drawing vectors is tedious, so we need a better, more mathematical way of representing them.
We shall impose a coordinate system...
Component Form of Vectors
Definition: A vector ${\bf v}$ with its initial point $(0,0)$ and terminal point $(x,y)$ is denoted as $${\bf v}=\langle x,y\rangle$$ $\star$ Any vector with the same magnitude and direction can be written as $\langle x,y\rangle$
Example
Express the vector ${\bf v}$ below in component form.
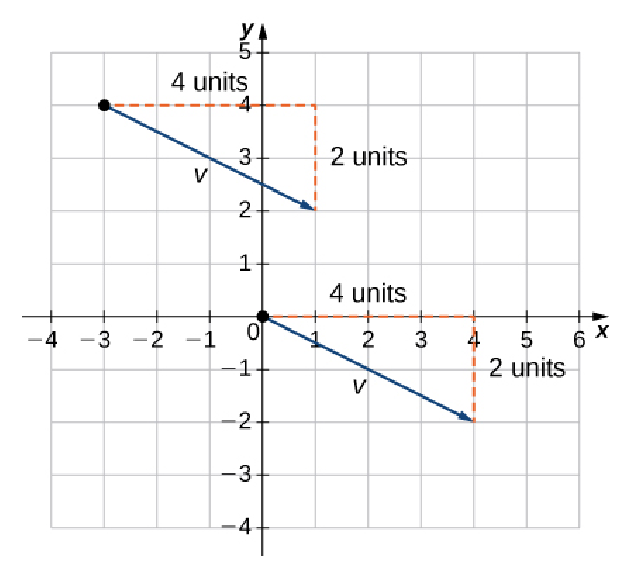
Solution
$$ {\bf v}=\langle 4,-2\rangle $$

Component Form of Vectors
If the vector ${\bf v}$ has initial point $(x_i,y_i)$ and terminal point $(x_t,y_t),$ then the component form of ${\bf v}$ is $${\bf v}=\langle x_t-x_i,y_t-y_i\rangle$$
Magnitude of Vectors in Component Form
The magnitude of the vector ${\bf v}=\langle x,y\rangle$ is denoted as $\Vert {\bf v} \Vert$ and is given by $$\Vert {\bf v} \Vert = \sqrt{x^2+y^2}$$ Note that this is merely the distance between the point $(0,0)$ to the point $(x,y)$ using the distance formula.
Example: Find the magnitude of the vector ${\bf v}=\langle 4,-2 \rangle$
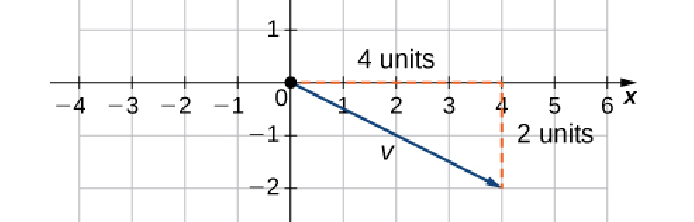
Solution

Operations on Vectors Revisited
The component form of vectors makes vector operations much easier.
In fact, letting ${\bf v} = \langle x_1, y_1 \rangle$ and ${\bf w} = \langle x_2, y_2 \rangle$ be vectors, and letting $k$ be a scalar, we can define vector operations algebraically.
Scalar Multiplication: $$k{\bf v}=k\langle x_1, y_1 \rangle=\langle kx_1, ky_1 \rangle$$
Vector Addition: $${\bf v} + {\bf w} = \langle x_1, y_1 \rangle + \langle x_2, y_2 \rangle = \langle x_1 + x_2, y_1 + y_2 \rangle$$
Example
Let ${\bf v}$ be the vector with initial point $(2, 5)$ and terminal point $(8, 13),$ and let ${\bf w} = 〈 -2, 4 〉.$
(a) Express ${\bf v}$ in component form and find $\Vert {\bf v} \Vert.$
(b) Find ${\bf v} + {\bf w}$ in component form.
(c) Find $3{\bf v}$ in component form.
(d) Find $\frac{1}{2}{\bf v} - 3{\bf w}$ in component form.
Solution
(a) In component form, $$ \begin{array}{ll} {\bf v}&=\langle 8-2,13-5\rangle\\\\ &=\langle 6,8\rangle\\\\ \end{array} $$ The magnitude is $$ \begin{array}{ll} \Vert {\bf v} \Vert&=\Vert \langle 6,8 \rangle \Vert\\ &=\sqrt{6^2+8^2}\\ &=\sqrt{36+64}\\ &=\sqrt{100}\\ &=10\\ \end{array} $$ (b) $$ \begin{array}{lll} {\bf v}+{\bf w}&=\langle 6,8 \rangle + \langle -2,4 \rangle & \mbox{vector addition}\\ &=\langle 6+(-2),8+4 \rangle & \mbox{}\\ &=\langle 4,12 \rangle & \mbox{}\\ \end{array} $$ (c) $$ \begin{array}{lll} 3{\bf v}&=3 \langle 6,8 \rangle&\\ &=\langle 3\cdot 6,3 \cdot 8 \rangle&\mbox{scalar multiplication}\\ &=\langle 18,24 \rangle&\\ \end{array} $$ (d) $$ \begin{array}{lll} \frac{1}{2}{\bf v}-3{\bf w}&=\frac{1}{2}\langle 6,8 \rangle - 3\langle -2,4 \rangle & \mbox{}\\ &=\left \langle \frac{1}{2}\cdot 6,\frac{1}{2} \cdot 8 \right\rangle - \langle 3(-2),3\cdot 4 \rangle & \mbox{scalar multiplication}\\ &=\left \langle 3,4 \right\rangle - \langle -6,12 \rangle & \mbox{}\\ &=\left \langle 3-(-6),4-12 \right\rangle & \mbox{vector subtraction}\\ &=\left \langle 9,-8 \right\rangle & \mbox{}\\ \end{array} $$
Essential Properties of Vectors
Let ${\bf u},$ ${\bf v},$ and ${\bf w}$ be vectors in a plane. Let $r$ and $s$ be scalars. Then the following properties hold. $$ \begin{array}{ll} {\bf u} + {\bf v} = {\bf v} + {\bf u} & \mbox{Vector addition is commutative}\\ ({\bf u} + {\bf v}) + {\bf w} = {\bf u} + ({\bf v} + {\bf w}) & \mbox{Vector addition is associative}\\ {\bf u} + {\bf 0} = {\bf u} & \mbox{The zero vector ${\bf 0}$ is the additive identity}\\ {\bf u} + (-{\bf u}) = {\bf 0} & \mbox{Every vector has an additive inverse}\\ r(s{\bf u}) = (rs){\bf u} & \mbox{Associativity of scalar multiplication}\\ (r + s){\bf u} = r{\bf u} + s{\bf u} & \mbox{Vectors distribute over scalar addition}\\ r({\bf u} + {\bf v}) = r{\bf u} + r{\bf v} & \mbox{Scalars distribute over vector addition}\\ 1{\bf u} = {\bf u} & \mbox{Multiplicative identity property}\\ 0{\bf u} = {\bf 0} & \mbox{Multiplication by $0$ gives ${\bf 0}$}\\ \end{array} $$ The proofs of these properties are very straightforward.
Finding Vector Components
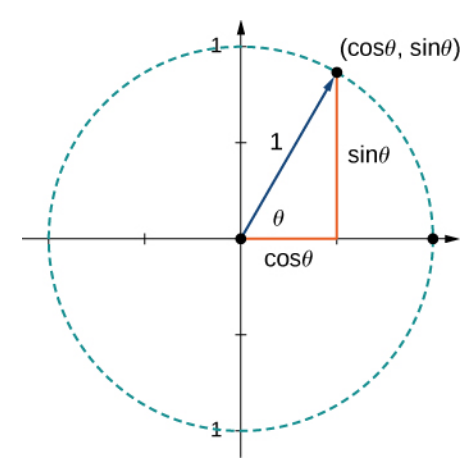
It is often the case that we must find the components of a vector ${\bf v}$ given only its magnitude $\Vert v \Vert$ and direction given by an angle $\theta.$ In this case, $$ {\bf v}=\langle \Vert {\bf v} \Vert \cos \theta, \Vert {\bf v} \Vert \sin \theta \rangle $$
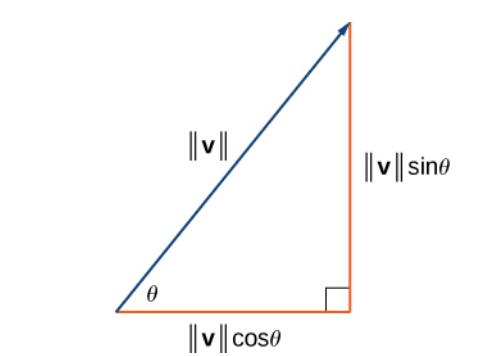
Example
Express the vector below in component form.
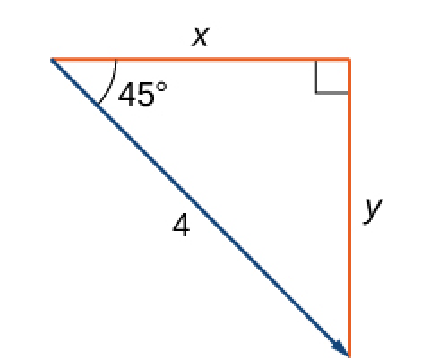
Solution
$$ \begin{array}{ll} {\bf v}&= \langle \Vert {\bf v} \Vert\cos \theta,\Vert {\bf v} \Vert\sin \theta \rangle\\ &=\langle 4\cos (-45^{\circ}),4\sin (-45^{\circ}) \rangle\\ &=\displaystyle \left \langle 4\cdot \frac{\sqrt{2}}{2},4\cdot \left(-\frac{\sqrt{2}}{2}\right) \right\rangle\\ &=\displaystyle \left \langle 2\sqrt{2},-2\sqrt{2} \right\rangle\\ \end{array} $$

Unit Vectors
Vectors of magnitude $1$ have a particular significance in mathematics and even have a special name: unit vectors.
We can find the unit vector ${\bf u}$ which points in the direction of ${\bf v}$ by simply dividing it by its magnitude: $$ {\bf u}=\frac{1}{\Vert{\bf v}\Vert}{\bf v} $$

Example: Let ${\bf v} = \langle 9, 2 \rangle.$
(a) Find a vector with magnitude $1$ in the direction as ${\bf v}.$
(b) Find a vector with magnitude $5$ in the opposite direction as ${\bf v}.$
Solution
(a) For ${\bf v} = \langle 9, 2 \rangle,$ $$ \begin{array}{ll} \Vert {\bf v} \Vert&=\Vert \langle 9,2 \rangle \Vert\\ &=\sqrt{9^2+2^2}\\ &=\sqrt{81+4}\\ &=\sqrt{85}\\ \end{array} $$ Thus, a unit vector ${\bf u}$ in the direction of ${\bf v}$ is $$ \begin{array}{lll} \displaystyle {\bf u} &\displaystyle= \frac{1}{\Vert {\bf v} \Vert} {\bf v} &\mbox{}\\ \displaystyle &\displaystyle= \frac{1}{\sqrt{85}}\langle 9, 2 \rangle&\mbox{}\\ \displaystyle &\displaystyle= \left\langle \frac{9}{\sqrt{85}}, \frac{2}{\sqrt{85}} \right\rangle&\mbox{scalar multiplication}\\ \end{array} $$ (b) A vector with magnitude $5$ in the opposite direction as ${\bf v}$ is $5$ times $-{\bf u},$ $$ \begin{array}{lll} \displaystyle -5{\bf u} &\displaystyle= -5\left\langle \frac{9}{\sqrt{85}}, \frac{2}{\sqrt{85}} \right\rangle&\mbox{}\\ \displaystyle &\displaystyle= \left\langle -\frac{45}{\sqrt{85}}, -\frac{10}{\sqrt{85}} \right\rangle&\mbox{scalar multiplication}\\ \end{array} $$
Standard Unit Vectors
The standard unit vectors are the vectors ${\bf i} = \langle 1, 0 \rangle$ and ${\bf j} = \langle 0, 1 \rangle$
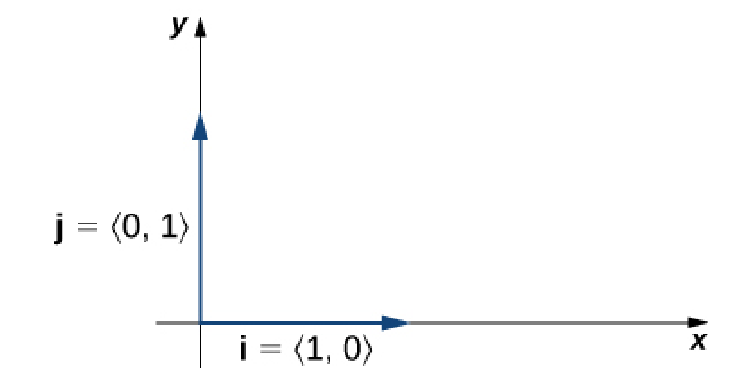
Standard Unit Vectors
The standard unit vectors allow us to write the component form ${\bf v}=\langle x,y\rangle$ as ${\bf v}=x{\bf i}+y{\bf j}.$

We say that we may write ${\bf v}$ as a linear combination of ${\bf i}$ and ${\bf j}.$
Examples: Standard Unit Vectors
(a) Express the vector ${\bf w} = \langle 3, -4 \rangle$ in terms of standard unit vectors.
(b) Let ${\bf u}$ be a unit vector that forms an angle of $60^{\circ}$ with the positive $x$-axis. Use standard unit vectors to describe ${\bf u}.$
Solution
(a) $${\bf w} = \langle 3, -4 \rangle = 3 {\bf i}-4{\bf j} $$ (b) Let ${\bf u}$ be a unit vector that forms an angle of $60^{\circ}$ with the positive $x$-axis. Then $$ \begin{array}{ll} {\bf v}&= \langle \Vert {\bf v} \Vert\cos \theta,\Vert {\bf v} \Vert\sin \theta \rangle\\ &=\langle 1\cdot \cos 60^{\circ},1\cdot \sin 60^{\circ} \rangle\\ &=\displaystyle \left\langle \frac{1}{2},\frac{\sqrt{3}}{2} \right \rangle\\ &=\displaystyle \frac{1}{2}{\bf i}+\frac{\sqrt{3}}{2}{\bf j}\\ \end{array} $$
Applications of Vectors to Physics
As mentioned earlier, vectors are one of the most fundamental and basic tools of physics.
We shall now apply the above ideas to understand two physical situations: one involving velocity, and the other involving force.
Application: Velocity & Bearing
An airplane flies due west at an airspeed of $425$ mph. The wind is blowing from the northeast at $40$ mph.
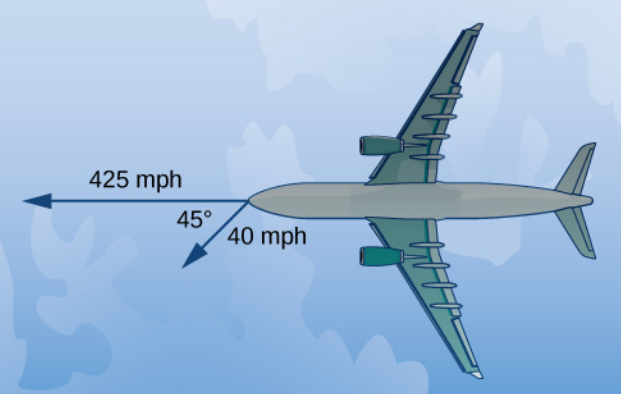
(a) Find the vector which describes the velocity of the airplane.
(b) Find the ground speed of the airplane.
(c) Find the bearing of the airplane.
Solution
(a) Imposing a coordinate system on the image, we see that the velocity ${\bf v}$ of the plane is ${\bf v}=-425{\bf i}=\langle -425,0\rangle.$
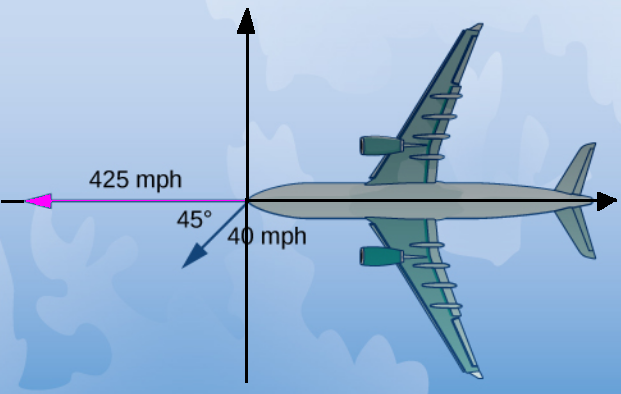
(b) To find the ground speed, we must find the vector modelling the plane's velocity with the wind.
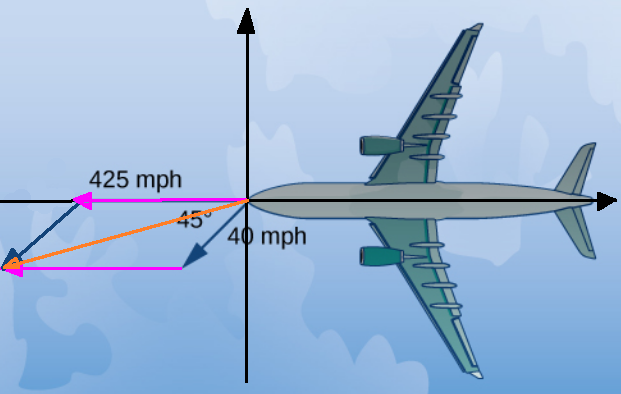
Letting ${\bf w}$ be the wind velocity, we have that $$ \begin{array}{lll} \displaystyle {\bf w} &\displaystyle= \langle \Vert {\bf w} \Vert\cos \theta,\Vert {\bf w} \Vert\sin \theta \rangle&\mbox{}\\ \displaystyle &\displaystyle= \langle 40\cos 225^{\circ},40\sin 225^{\circ} \rangle &\mbox{}\\ \displaystyle &\displaystyle= \left \langle 40\cdot \left(-\frac{\sqrt{2}}{2}\right),40\left(-\frac{\sqrt{2}}{2}\right) \right\rangle &\mbox{}\\ \displaystyle &\displaystyle= \left \langle -20\sqrt{2},-20\sqrt{2}\right\rangle &\mbox{}\\ \end{array} $$
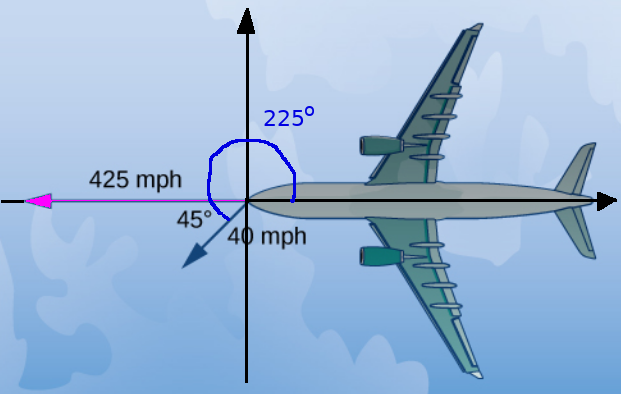
Thus, the vector which describes the plane's direction of travel with the wind is $$ \begin{array}{lll} \displaystyle {\bf v}+{\bf w} &\displaystyle= \langle -425,0\rangle+\left \langle -20\sqrt{2},-20\sqrt{2}\right\rangle &\mbox{}\\ &\displaystyle= \left \langle -425 -20\sqrt{2},-20\sqrt{2}\right\rangle &\mbox{}\\ &\displaystyle \approx \left \langle -453.28,-28.28\right\rangle &\mbox{}\\ \end{array} $$ The ground speed is the magnitude of the above vector. $$ \begin{array}{lll} \displaystyle \Vert{\bf v}+{\bf w}\Vert &\displaystyle= \Vert\left \langle -425 -20\sqrt{2},-20\sqrt{2}\right\rangle\Vert &\mbox{}\\ \displaystyle &\displaystyle= \sqrt{(-425 -20\sqrt{2})^2+(-20\sqrt{2})^2} &\mbox{}\\ \displaystyle &\displaystyle \approx 454.17&\mbox{}\\ \end{array} $$ The plane's ground speed is about $454.17$ miles per hour.
(c) To find the bearing of the plane, we must find the angle $\theta$ of the resultant velocity vector with the horizontal axis.
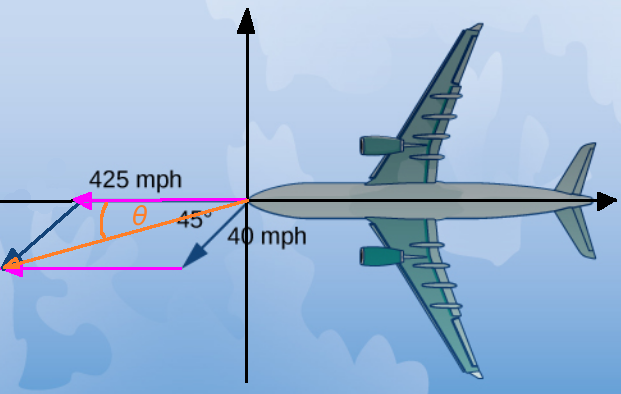
The vertical component of the velocity is $-20\sqrt{2},$ and the horizontal component of the velocity is $-425 -20\sqrt{2}.$
Thus, $$\tan \theta=\frac{-20\sqrt{2}}{-425 -20\sqrt{2}}$$ so that $$\theta=\tan^{-1}\left(\frac{-20\sqrt{2}}{-425 -20\sqrt{2}}\right)\approx 3.57^{\circ}$$
So, the planes bearing is $3.57^{\circ}$ south of west.
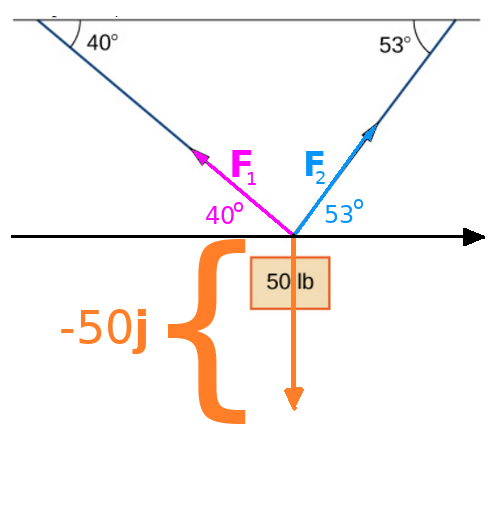
Application: Static Forces
A $50$ pound weight is hung by a cable so that the two portions of the cable make angles of $40^{\circ}$ and $53^{\circ},$ respectively, with the horizontal. Find the magnitudes of the forces of tension ${\bf F}_1$ and ${\bf F}_2$ in the cables if the resultant force acting on the object is zero.
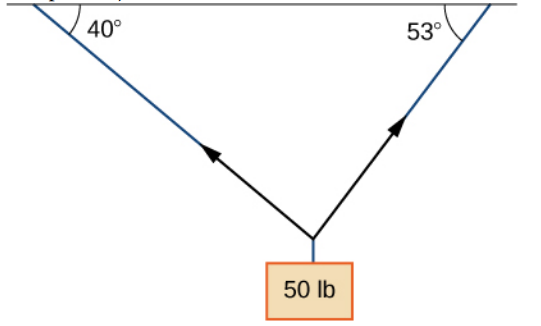
Solution
Each force acting on the weight is modelled as a vector: the two tensile forces and the force of gravity.
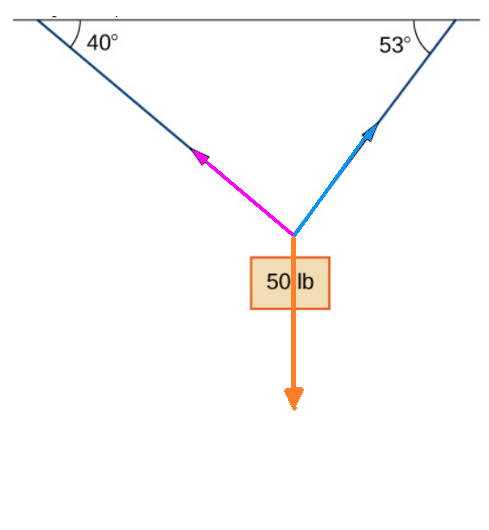
Since the weight is in equilibrium (not moving), the forces acting on it must sum to the zero vector ${\bf 0}.$
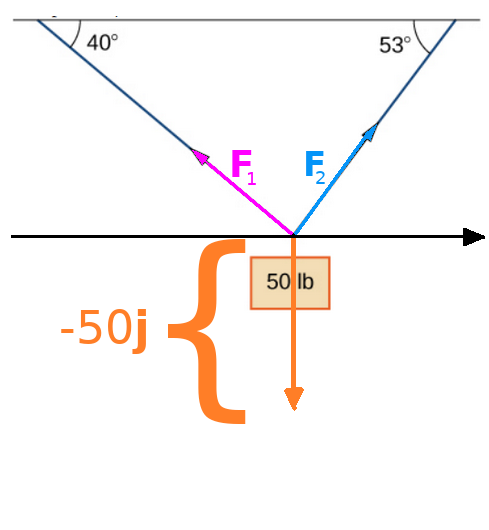
Using some basic geometry, wave the following.
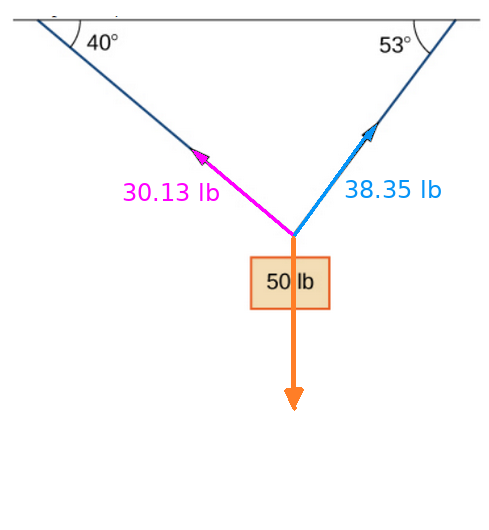
Application: Dynamic Forces
When we begin incorporating the techniques of calculus into our understanding of vectors, we will be able to model more dynamic situations such as a pendulum.