What happens to the value of an integral when either:
- the interval of integration becomes infinite or
- the integrand becomes infinite?
Improper Integrals: Infinite Interval
Consider the integral $\displaystyle \int_{a}^{t}f(x) \, dx$ as the upper limit $t$ gets larger and larger.

The Big Question: As $t \rightarrow \infty,$ does the integral approach a finite value?
Definition: Infinite Limits of Integration
$\displaystyle \int_{a}^{\infty} f(x) \, dx=\lim_{b \rightarrow \infty} \int_{a}^{b} f(x) \, dx$
$\displaystyle \int_{-\infty}^{b} f(x) \, dx=\lim_{a \rightarrow -\infty} \int_{a}^{b} f(x) \, dx$
$\displaystyle \int_{-\infty}^{\infty} f(x) \, dx= \int_{-\infty}^{c} f(x) \, dx+ \int_{c}^{\infty} f(x) \, dx$
In each case, if the limit exists and is finite, then the integral is said to converge. Otherwise, the integral is said to diverge.
Example: Infinite Limits of Integration
Find the value of the improper integral. $\displaystyle \int_{1}^{\infty} \frac{\ln x}{x^2} \, dx$
We first find an antiderivative by parts.
$$
\begin{array}{lll}
\displaystyle \int \frac{\ln x}{x^2} \, dx&=\displaystyle \int \ln x\frac{1}{x^2} \, dx&\mbox{}\\
&=\displaystyle \int uv' \, dx&\mbox{letting $u=\ln x$ and $v'=\frac{1}{x^2}$}\\
&=\displaystyle uv-\int u'v \, dx&\mbox{}\\
&=\displaystyle \ln x \left(-\frac{1}{x}\right)-\int \frac{1}{x} \left(-\frac{1}{x}\right) \, dx&\mbox{since $u'=\frac{1}{x}$ and $v=-\frac{1}{x}$}\\
&=\displaystyle -\frac{\ln x }{x}+\int \frac{1}{x^2} \, dx&\mbox{}\\
&=\displaystyle -\frac{\ln x }{x}-\frac{1}{x} +C&\mbox{}\\
\end{array}
$$
We may now evaluate the improper integral.
$$
\begin{array}{lll}
\displaystyle \int_{1}^{\infty} \frac{\ln x}{x^2} \, dx&=\displaystyle \lim_{b \rightarrow \infty}\int_{1}^{b} \frac{\ln x}{x^2} \, dx&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} \left[-\frac{\ln x }{x}-\frac{1}{x}\right]_{1}^{b}&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} \left[\left(-\frac{\ln b }{b}-\frac{1}{b}\right)-\left(-\frac{\ln 1 }{1}-\frac{1}{1}\right)\right]&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} \left[-\frac{\ln b }{b}\right]-0+1&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} \left[-\frac{(\ln b)' }{b'}\right]+1&\mbox{L'Hopital!}\\
&=\displaystyle \lim_{b \rightarrow \infty} \left[-\frac{1/b }{1}\right]+1&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} \left[-\frac{1}{b}\right]+1&\mbox{}\\
&=\displaystyle 0+1&\mbox{}\\
&=\displaystyle 1&\mbox{}\\
\end{array}
$$

Example: Infinite Limits of Integration
Find the value of the improper integral. $\displaystyle \int_{1}^{\infty} \frac{1}{x} \, dx$
$$
\begin{array}{lll}
\displaystyle \int_{1}^{\infty} \frac{1}{x} \, dx &=\displaystyle \lim_{b \rightarrow \infty} \int_{1}^{b} \frac{1}{x} \, dx&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} [\ln x]_{1}^{b} \, dx&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} [\ln b-1] \, dx&\mbox{}\\
\end{array}
$$
This limit goes to $\infty.$ Thus, the integral diverges.


Example: Infinite Limits of Integration
Find the value of the improper integral. $\displaystyle \int_{-\infty}^{\infty} \frac{1}{x^2+1} \, dx$
$$
\begin{array}{lll}
\displaystyle \int_{-\infty}^{\infty} \frac{1}{x^2+1} \, dx&=\displaystyle \int_{-\infty}^{0} \frac{1}{x^2+1} \, dx + \int_{0}^{\infty} \frac{1}{x^2+1} \, dx&\mbox{}\\
&=\displaystyle \lim_{a \rightarrow -\infty} \int_{a}^{0} \frac{1}{x^2+1} \, dx + \lim_{b \rightarrow \infty}\int_{0}^{b} \frac{1}{x^2+1} \, dx&\mbox{}\\
&=\displaystyle \lim_{a \rightarrow -\infty} \left[\tan^{-1}x\right]_{a}^{0} + \lim_{b \rightarrow \infty}\left[\tan^{-1}x\right]_{0}^{b}&\mbox{}\\
&=\displaystyle \lim_{a \rightarrow -\infty} \left[\tan^{-1}0-\tan^{-1}a\right] + \lim_{b \rightarrow \infty}\left[\tan^{-1}b-\tan^{-1}0\right]_{0}^{b}&\mbox{}\\
&=\displaystyle \lim_{a \rightarrow -\infty} \left[-\tan^{-1}a\right] + \lim_{b \rightarrow \infty}\left[\tan^{-1}b\right]_{0}^{b}&\mbox{}\\
&=\displaystyle \frac{\pi}{2} + \frac{\pi}{2}&\mbox{}\\
&=\displaystyle \pi &\mbox{}\\
\end{array}
$$

Example: Find $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ where $p$ can take on any value.
We must examine three cases: $p \gt 1,$ $p=1,$ and $p \lt 1.$
If $p \gt 1,$ then $$ \begin{array}{lll} \displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx&=\displaystyle \lim_{b \rightarrow \infty} \int_{1}^{b} \frac{1}{x^p} \, dx&\mbox{}\\ &=\displaystyle \lim_{b \rightarrow \infty} \int_{1}^{b} x^{-p} \, dx&\mbox{}\\ &=\displaystyle \lim_{b \rightarrow \infty} \left[\frac{1}{-p+1}x^{-p+1}\right]_{1}^{b}&\mbox{}\\ &=\displaystyle \lim_{b \rightarrow \infty} \frac{1}{1-p}\left[\frac{1}{x^{p-1}}\right]_{1}^{b}&\mbox{}\\ &=\displaystyle \frac{1}{1-p} \lim_{b \rightarrow \infty} \left[\frac{1}{x^{p-1}}\right]_{1}^{b}&\mbox{}\\ &=\displaystyle \frac{1}{1-p} \lim_{b \rightarrow \infty} \left[\frac{1}{b^{p-1}}-1\right]&\mbox{}\\ &=\displaystyle \frac{1}{1-p} \left[0-1\right]&\mbox{since $p \gt 1$}\\ %&=\displaystyle \frac{1}{1-p}(-1)&\mbox{}\\ &=\displaystyle \frac{1}{p-1}&\mbox{}\\ \end{array} $$ If $p=1,$ then $$ \begin{array}{lll} \displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx&=\displaystyle \int_{1}^{\infty} \frac{1}{x} \, dx&\mbox{}\\ \end{array} $$ which is a divergent integral as we saw in a previous example.
If $p \lt 1,$ then, by a calculation similar to the above, $$ \begin{array}{lll} \displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx&=\displaystyle \frac{1}{1-p} \lim_{b \rightarrow \infty} \left[\frac{1}{b^{p-1}}-1\right]&\mbox{}\\ \end{array} $$ which diverges since $p \lt 1.$ That is, $\displaystyle \frac{1}{b^{p-1}}\rightarrow \infty.$
In Summary:
If $p \gt 1,$ then $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ converges.
If $p \leq 1,$ then $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ diverges.
If $p \gt 1,$ then $$ \begin{array}{lll} \displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx&=\displaystyle \lim_{b \rightarrow \infty} \int_{1}^{b} \frac{1}{x^p} \, dx&\mbox{}\\ &=\displaystyle \lim_{b \rightarrow \infty} \int_{1}^{b} x^{-p} \, dx&\mbox{}\\ &=\displaystyle \lim_{b \rightarrow \infty} \left[\frac{1}{-p+1}x^{-p+1}\right]_{1}^{b}&\mbox{}\\ &=\displaystyle \lim_{b \rightarrow \infty} \frac{1}{1-p}\left[\frac{1}{x^{p-1}}\right]_{1}^{b}&\mbox{}\\ &=\displaystyle \frac{1}{1-p} \lim_{b \rightarrow \infty} \left[\frac{1}{x^{p-1}}\right]_{1}^{b}&\mbox{}\\ &=\displaystyle \frac{1}{1-p} \lim_{b \rightarrow \infty} \left[\frac{1}{b^{p-1}}-1\right]&\mbox{}\\ &=\displaystyle \frac{1}{1-p} \left[0-1\right]&\mbox{since $p \gt 1$}\\ %&=\displaystyle \frac{1}{1-p}(-1)&\mbox{}\\ &=\displaystyle \frac{1}{p-1}&\mbox{}\\ \end{array} $$ If $p=1,$ then $$ \begin{array}{lll} \displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx&=\displaystyle \int_{1}^{\infty} \frac{1}{x} \, dx&\mbox{}\\ \end{array} $$ which is a divergent integral as we saw in a previous example.
If $p \lt 1,$ then, by a calculation similar to the above, $$ \begin{array}{lll} \displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx&=\displaystyle \frac{1}{1-p} \lim_{b \rightarrow \infty} \left[\frac{1}{b^{p-1}}-1\right]&\mbox{}\\ \end{array} $$ which diverges since $p \lt 1.$ That is, $\displaystyle \frac{1}{b^{p-1}}\rightarrow \infty.$
In Summary:
If $p \gt 1,$ then $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ converges.
If $p \leq 1,$ then $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ diverges.
Improper Integrals: Infinite Integrand
Consider the integral $\displaystyle \int_{a}^{t}f(x) \, dx$ as the upper limit $t$ gets close to an asymptote at $b.$
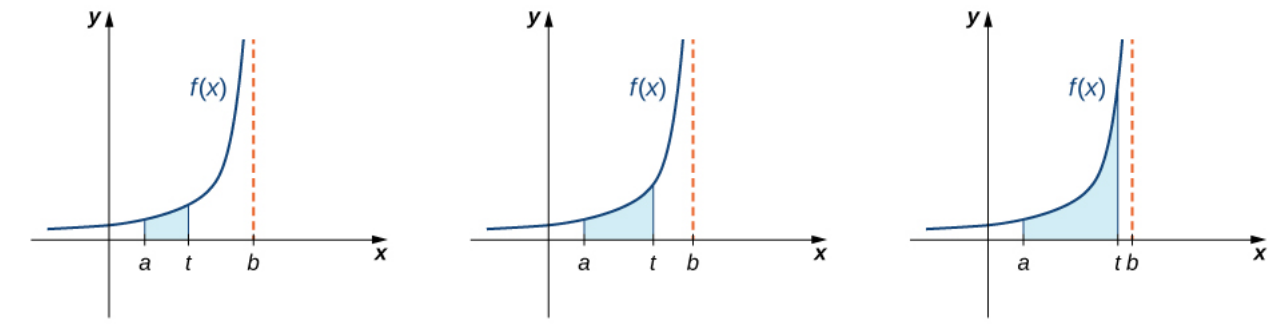
The Big Question: As $t \rightarrow b,$ does the integral approach a finite value?
Definition: When the Integrand Becomes Infinite.
If $f(x)$ is continuous on $(a,b]$ but discontinuous at $a,$ then $\displaystyle \int_{a}^{b} f(x) \, dx=\lim_{c \rightarrow a^+} \int_{c}^{b} f(x) \, dx$
If $f(x)$ is continuous on $[a,b)$ but discontinuous at $b,$ then $\displaystyle \int_{a}^{b} f(x) \, dx=\lim_{c \rightarrow b^-} \int_{a}^{c} f(x) \, dx$
If $f(x)$ is continuous on $[a,c) \cup (c,b]$ but discontinuous at $c,$ then $$\displaystyle \int_{a}^{b} f(x) \, dx= \int_{a}^{c} f(x) \, dx+ \int_{c}^{b} f(x) \, dx$$ In each case, if the limit exists and is finite, then the integral is said to converge. Otherwise, the integral is said to diverge.
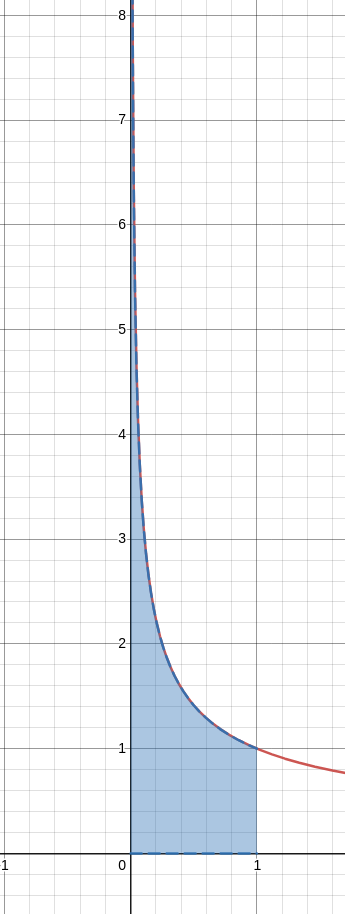
Example: When The Integrand Becomes Infinite
Find the value of the improper integral. $\displaystyle \int_{0}^{1} \frac{1}{\sqrt{x}} \, dx$
The integrand becomes infinite at $x=0.$ Nonetheless, the area under the curve may still be finite. Let's find out!
$$
\begin{array}{lll}
\displaystyle \int_{0}^{1} \frac{1}{\sqrt{x}} \, dx&=\displaystyle \lim_{a \rightarrow 0^+}\int_{a}^{1} \frac{1}{\sqrt{x}} \, dx&\mbox{}\\
&=\displaystyle \lim_{a \rightarrow 0^+}\left[2\sqrt{x}\right]_{a}^{1} &\mbox{}\\
&=\displaystyle \lim_{a \rightarrow 0^+}\left[2\sqrt{1}-2\sqrt{a}\right] &\mbox{}\\
&=\displaystyle 2 &\mbox{}\\
\end{array}
$$

Example: When The Integrand Becomes Infinite
Find the value of the improper integral. $\displaystyle \int_{0}^{1} \frac{1}{1-x} \, dx$
The integrand becomes infinite at $x=1.$ Nonetheless, the area under the curve may still be finite. Let's find out!
$$
\begin{array}{lll}
\displaystyle \int_{0}^{1} \frac{1}{1-x} \, dx&=\displaystyle \lim_{b \rightarrow 1^-} \int_{0}^{b} \frac{1}{1-x} \, dx&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow 1^-} \left[-\ln|1-x|\right]_{0}^{b}&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow 1^-} \left[-\ln|1-b|-(-\ln|1-0|)\right]&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow 1^-} \left[-\ln|1-b|\right]&\mbox{}\\
\end{array}
$$
Since $\ln|1-b|\rightarrow \infty$ as $b \rightarrow 1^-,$ the integral diverges.
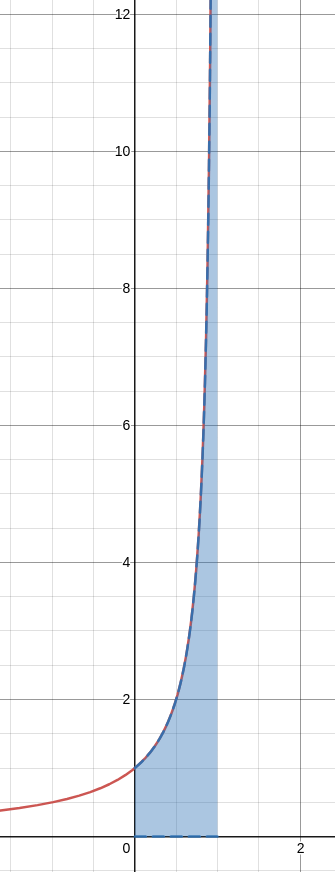

Example: When The Integrand Becomes Infinite
Find the value of the improper integral. $\displaystyle \int_{0}^{3} \frac{1}{(x-1)^{2/3}} \, dx$
The integrand becomes infinite at $x=1.$ This time, we need to break up the integral since the "singularity" lies between $0$ and $3.$
$$
\begin{array}{lll}
\displaystyle \int_{0}^{3} \frac{1}{(x-1)^{2/3}} \, dx&=\displaystyle \int_{0}^{1} \frac{1}{(x-1)^{2/3}} \, dx+\int_{1}^{3} \frac{1}{(x-1)^{2/3}} \, dx&\mbox{}\\
&=\displaystyle\lim_{b \rightarrow 1^-} \int_{0}^{b} \frac{1}{(x-1)^{2/3}} \, dx+\lim_{a \rightarrow 1^+}\int_{a}^{3} \frac{1}{(x-1)^{2/3}} \, dx&\mbox{}\\
&=\displaystyle\lim_{b \rightarrow 1^-} \int_{0}^{b} (x-1)^{-2/3} \, dx+\lim_{a \rightarrow 1^+}\int_{a}^{3} (x-1)^{-2/3} \, dx&\mbox{}\\
&=\displaystyle\lim_{b \rightarrow 1^-} \left[3(x-1)^{1/3}\right]_{0}^{b}+\lim_{a \rightarrow 1^+}\left[3(x-1)^{1/3}\right]_{a}^{3}&\mbox{}\\
&=\displaystyle\lim_{b \rightarrow 1^-} \left[3(b-1)^{1/3}-3(0-1)^{1/3}\right]+\lim_{a \rightarrow 1^+}\left[3(3-1)^{1/3}-3(a-1)^{1/3}\right]&\mbox{}\\
&=\displaystyle\lim_{b \rightarrow 1^-} \left[3(b-1)^{1/3}+3\right]+\lim_{a \rightarrow 1^+}\left[3\sqrt[3]{2}-3(a-1)^{1/3}\right]&\mbox{}\\
&=\displaystyle 3+3\sqrt[3]{2}&\mbox{}\\
\end{array}
$$
The integral converges.
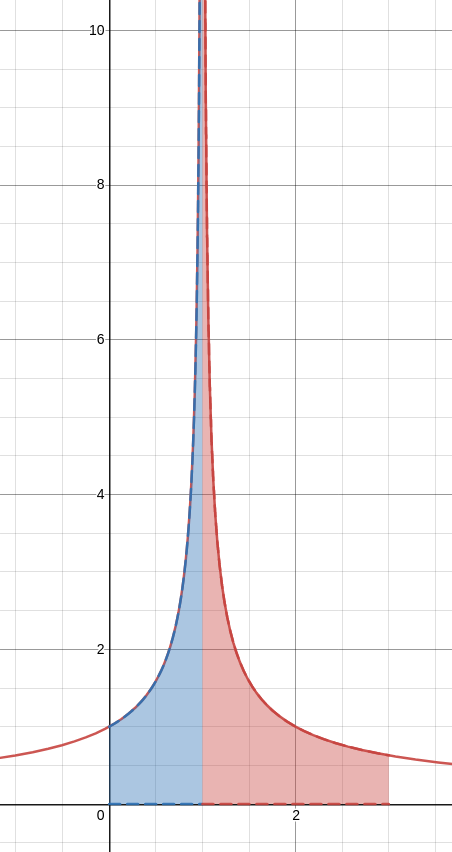

Comparison Theorem
If $f$ and $g$ are continuous on $[a,\infty)$ and $0 \leq f(x) \leq g(x)$ for $x \geq a,$ then the following hold:
1) If $\displaystyle \int_{a}^{\infty} g(x) \, dx$ converges, then $\displaystyle \int_{a}^{\infty} f(x) \, dx$ also converges.
2) If $\displaystyle \int_{a}^{\infty} f(x) \, dx$ diverges, then $\displaystyle \int_{a}^{\infty} g(x) \, dx$ also diverges.
Example: Use of the Comparison Theorem
Determine whether the following integrals converge or diverge.
$\displaystyle \int_{1}^{\infty} \frac{\sin^2 x}{x^2} \, dx$
Since $\displaystyle 0\leq \frac{\sin^2 x}{x^2}\leq \frac{1}{x^2}$ for all $x\geq 1,$ and since $\displaystyle \int_{1}^{\infty} \frac{1}{x^2} \, dx$ converges ($p=2$ from above!),
the integral $\displaystyle \int_{1}^{\infty} \frac{\sin^2 x}{x^2} \, dx$ also converges.
Since $\displaystyle 0 \leq \frac{1}{x}\leq \frac{1}{\sqrt{x^2-0.1}}$ for all $x\geq 1,$ and since $\displaystyle \int_{1}^{\infty} \frac{1}{x} \, dx$ diverges ($p=1$ from above!),
the integral $\displaystyle \int_{1}^{\infty} \frac{1}{\sqrt{x^2-0.1}} \, dx$ also diverges.
We shall compare $\displaystyle \int_{1}^{\infty} e^{-x^2} \, dx$ to the integral $\displaystyle \int_{1}^{\infty} e^{-x} \, dx$ which converges since
$$
\begin{array}{lll}
\displaystyle \int_{1}^{\infty} e^{-x} \, dx&=\displaystyle \lim_{b \rightarrow \infty} \int_{1}^{b} e^{-x} \, dx&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} [-e^{-x}]_{1}^{b}&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} [-e^{-b}-(-e^{-1})]&\mbox{}\\
&=\displaystyle \lim_{b \rightarrow \infty} [-e^{-b}+e^{-1}]&\mbox{}\\
&=\displaystyle e^{-1}&\mbox{}\\
\end{array}
$$
Thus, since $\displaystyle 0\leq e^{-x}\leq e^{-x^2}$ for all $x \geq 1$ (as seen below) and since $\displaystyle \int_{1}^{\infty} e^{-x} \, dx$ converges as shown above,
the integral $\displaystyle \int_{1}^{\infty} e^{-x^2} \, dx$ also converges.


Example: Gabriel's Horn
Gabriel's Horn is the surface obtained by rotating the curve $\displaystyle f(x)=\frac{1}{x}$ around the $x$-axis over $[1,\infty)$ as seen below.

1) Find the volume of Gabriel's Horn. (A convergent integral.)
This is an infinite volume of revolution!
$$
\begin{array}{lll}
\displaystyle V&=\displaystyle \int_{a}^{b}\pi\left[f(x)\right]^2\,dx&\mbox{}\\
&=\displaystyle \int_{1}^{\infty}\pi\left[\frac{1}{x}\right]^2\,dx&\mbox{}\\
&=\displaystyle \pi \int_{1}^{\infty}\frac{1}{x^2}\,dx&\mbox{}\\
&=\displaystyle \pi \lim_{b \rightarrow \infty}\int_{1}^{b}\frac{1}{x^2}\,dx&\mbox{}\\
&=\displaystyle \pi \lim_{b \rightarrow \infty}\left[-\frac{1}{x}\right]_{1}^{b}&\mbox{}\\
&=\displaystyle \pi \lim_{b \rightarrow \infty}\left[-\frac{1}{b}-\left(-\frac{1}{1}\right)\right]&\mbox{}\\
&=\displaystyle \pi \cdot 1&\mbox{}\\
&=\displaystyle \pi &\mbox{}\\
\end{array}
$$
Gabriel's horn has a volume of $\pi$ cubic units.
2) Show that the surface area is infinite. (A divergent integral.)
This is an infinite surface area of revolution!
$$
\begin{array}{lll}
\displaystyle S&=\displaystyle \int_{a}^{b}2\pi f(x)\sqrt{1+[f'(x)]^2}\,dx&\mbox{}\\
&=\displaystyle \int_{1}^{\infty}2\pi \frac{1}{x}\sqrt{1+\left[-\frac{1}{x^2}\right]^2}\,dx&\mbox{}\\
&=\displaystyle 2\pi\int_{1}^{\infty} \frac{1}{x}\sqrt{1+\frac{1}{x^4}}\,dx&\mbox{}\\
\end{array}
$$
It is here that we put the brakes on our computational zeal and realize that $\displaystyle \frac{1}{x} \leq \frac{1}{x}\sqrt{1+\frac{1}{x^4}}$ for all $x \geq 1.$
Since we know quite well that $\displaystyle \int_{1}^{\infty} \frac{1}{x}\,dx$ diverges, the Comparison Theorem tells us that $\displaystyle \int_{1}^{\infty} \frac{1}{x}\sqrt{1+\frac{1}{x^4}}\,dx$ also diverges.
Therefore, Gabriel's horn has an infinite surface area! (Yet, it has a finite volume. Hmmm.....)
Since we know quite well that $\displaystyle \int_{1}^{\infty} \frac{1}{x}\,dx$ diverges, the Comparison Theorem tells us that $\displaystyle \int_{1}^{\infty} \frac{1}{x}\sqrt{1+\frac{1}{x^4}}\,dx$ also diverges.
Therefore, Gabriel's horn has an infinite surface area! (Yet, it has a finite volume. Hmmm.....)
Example: Escape Velocity
The gravitational force a planet of mass $M$ exerts on an object of mass $m$ is given by $$F(r)=\frac{GMm}{r^2}$$ where $G=6.674 \times 10^{-11}$ is the universal gravitational constant given in $\displaystyle \frac{\mbox{N}\cdot \mbox{m}^2}{\mbox{kg}^2}.$
(a) Compute the amount of work it would take to move an object of mass $m$ away from the gravitational pull of a planet of mass $M$ and radius $R.$
We recall that the amount of work to move an object from $a$ to $b$ along an axis with variable force is given by
$$
W=\int_{a}^{b} F(x)\,dx
$$
where $F(x)$ is the force on the object at $x.$
Thus, the amount of work it takes to move an object $r_1$ units from the center of the planet to $r_2$ units is given by $$\int_{r_1}^{r_2}F(r)\,dr$$
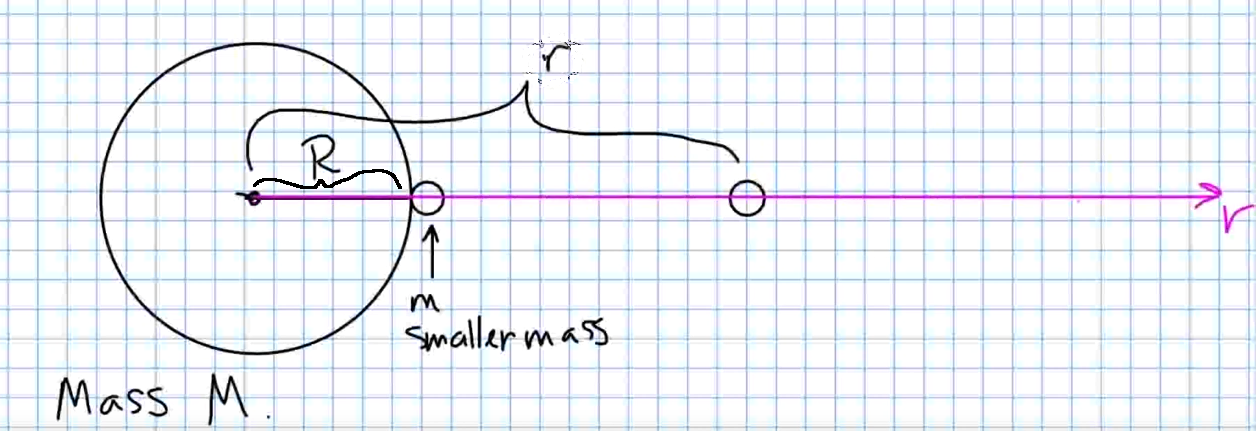
Consequently, the work required to hurl the object into space so that it never comes back is $$ \begin{array}{lll} \displaystyle \int_{R}^{\infty}F(r)\,dr&=\displaystyle \int_{R}^{\infty}\frac{GMm}{r^2}\,dr&\mbox{}\\ &=\displaystyle GMm\int_{R}^{\infty}\frac{1}{r^2}\,dr&\mbox{}\\ &=\displaystyle GMm\lim_{b\rightarrow \infty}\int_{R}^{b}\frac{1}{r^2}\,dr&\mbox{}\\ &=\displaystyle GMm\lim_{b\rightarrow \infty}\left[-\frac{1}{r}\right]_{R}^{b}&\mbox{}\\ &=\displaystyle GMm\lim_{b\rightarrow \infty}\left[-\frac{1}{b}+\frac{1}{R}\right]&\mbox{}\\ &=\displaystyle \frac{GMm}{R}&\mbox{}\\ \end{array} $$
Thus, the amount of work it takes to move an object $r_1$ units from the center of the planet to $r_2$ units is given by $$\int_{r_1}^{r_2}F(r)\,dr$$

Consequently, the work required to hurl the object into space so that it never comes back is $$ \begin{array}{lll} \displaystyle \int_{R}^{\infty}F(r)\,dr&=\displaystyle \int_{R}^{\infty}\frac{GMm}{r^2}\,dr&\mbox{}\\ &=\displaystyle GMm\int_{R}^{\infty}\frac{1}{r^2}\,dr&\mbox{}\\ &=\displaystyle GMm\lim_{b\rightarrow \infty}\int_{R}^{b}\frac{1}{r^2}\,dr&\mbox{}\\ &=\displaystyle GMm\lim_{b\rightarrow \infty}\left[-\frac{1}{r}\right]_{R}^{b}&\mbox{}\\ &=\displaystyle GMm\lim_{b\rightarrow \infty}\left[-\frac{1}{b}+\frac{1}{R}\right]&\mbox{}\\ &=\displaystyle \frac{GMm}{R}&\mbox{}\\ \end{array} $$
(b) Using part (a), how much work would it take to move a $70 \mbox{ kg}$ mass (about $154 \mbox{ lb}$) away from earth's gravitational influence? Note that the mass of earth is $M=5.972 \times 10^{24} \mbox{ kg}$ and its radius is $R=6371000 \mbox{ m}.$
It would take
$$
\frac{GMm}{R}=\frac{6.674 \times 10^{-11}\cdot 5.972 \times 10^{24} \cdot 70}{6371000}=4.3792167\times 10^9 \mbox{ J}
$$
Fun Fact: This amount of energy could power a $60 \mbox{ W}$ light bulb for about $2.3$ years.
(c) Using information in part (b), and that the kinetic energy $K$ of an object of mass $m$ with velocity $v$ is given by $\displaystyle K=\frac{1}{2}mv^2,$ compute the escape velocity from earth.
Assuming we could covert all this energy into kinetic energy, we see that
$$
\begin{array}{lll}
\displaystyle& K &=\displaystyle 4.3792167\times 10^9\\
\implies &\displaystyle \frac{1}{2}mv^2 &=\displaystyle 4.3792167\times 10^9\\
\implies &\displaystyle \frac{1}{2}70v^2 &=\displaystyle 4.3792167\times 10^9\\
\implies &\displaystyle 35v^2 &=\displaystyle 4.3792167\times 10^9\\
\implies &\displaystyle v^2 &=\displaystyle 125120477.2\\
\implies &\displaystyle v &\approx \displaystyle 11185.72649\\
\end{array}
$$
That is, the escape velocity of earth (neglecting air resistance, as well as several other things) is about $\mbox{11,186 m/s}$ (this is about $\mbox{25022.369 mph}!$)