Hard Fact of Life: Not all functions have a nice, closed-form antiderivative.
For instance, the important and useful function $\displaystyle f(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2}$ has no antiderivative which can be expressed in terms of elementary functions.
$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2}$ is the probability density function of a standard normal random variable.
Also, approximating definite integrals involving $e^{-x^2}$ occurs often in practice.
But tables of integrals and CAS's (at least symbolically) aren't going to help.
When the tried and true fails, what do we do???
Numerical Integration!
Today we learn methods for approximating definite integrals $\displaystyle \int_{a}^{b} f(x) \, dx$ when we don't necessarily have an antiderivative.
Numerical Integration
There are a veritable variety of numerical methods for approximating a definite integrals.
In fact, we already know of two methods...
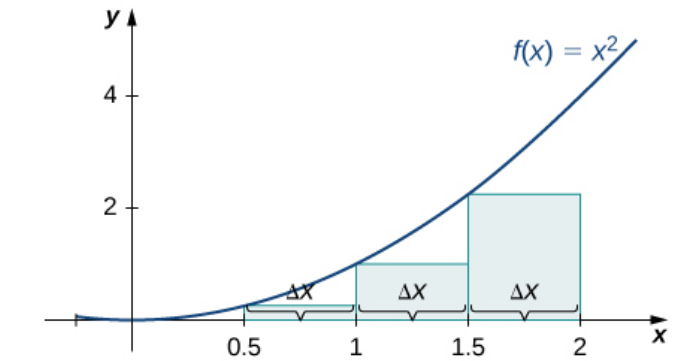
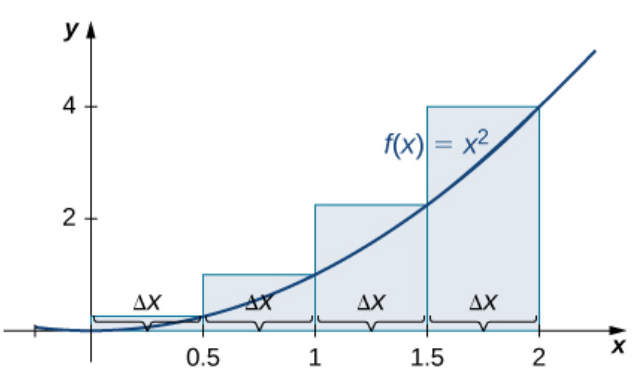
Numerical Integration Method: Left and Right-Hand Riemann Sums
The Left and Right-Hand sums evaluate at the endpoints $x_i^*=a+i\Delta x$ of each interval.
 |  |
| $\displaystyle L_n=\sum_{i=0}^{n-1}f(a+i\Delta x)\Delta x$ | $\displaystyle R_n=\sum_{i=1}^{n}f(a+i\Delta x)\Delta x$ |
Numerical Integration Method: Left and Right-Hand Riemann Sums
For $\displaystyle \int_{0}^{2} x^2 \, dx,$
| |
| $\displaystyle L_n=\sum_{i=0}^{n-1}f(a+i\Delta x)\Delta x$ | $\displaystyle R_n=\sum_{i=1}^{n}f(a+i\Delta x)\Delta x$ |
| $\displaystyle=\sum_{i=0}^{3}(0+i \cdot 0.5)^2\cdot 0.5$ | $\displaystyle=\sum_{i=1}^{4}(0+i \cdot 0.5)^2\cdot 0.5$ |
| $=1.75$ | $=3.75$ |
Numerical Integration Method: Left and Right-Hand Riemann Sums
For $\displaystyle \int_{0}^{2} x^2 \, dx,$
| |
| $\displaystyle \mbox{Error}=\left|\displaystyle \int_{0}^{2} x^2 \, dx-L_4\right|$ | $\displaystyle \mbox{Error}=\left|\displaystyle \int_{0}^{2} x^2 \, dx-R_4\right|$ |
| $=\displaystyle \left|\frac{8}{3}-1.75\right|$ | $=\displaystyle \left|\frac{8}{3}-3.75\right|$ |
| $=0.91\overline{6}.$ | $=1.08\overline{3}$ |
We now learn several more more accurate and sophisticated approximations.
The first of these we consider uses the trapezoids instead of rectangles to estimate the area under the curve.
Naturally, it's called the trapezoid rule.
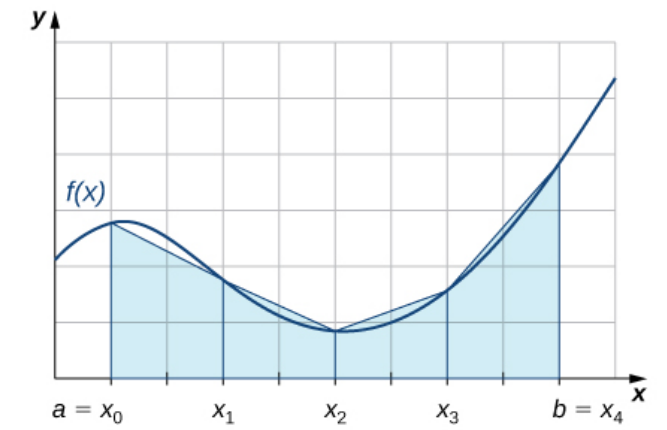
The Trapezoid Rule
The trapezoid rule uses linear approximations between the endpoints of each subinterval. Break up $[a,b]$ into subintervals $[a,x_1],$ $[x_1,x_2],$ $[x_2,x_3],$ $\cdots,$ $[x_{n-3},x_{n-2}],$ $[x_{n-2},x_{n-1}],$ $[x_{n-1},b].$
Example
Approximate the integral $\displaystyle \int_{0}^{2} x^2 \, dx$ by computing $T_4,$ the trapezoid rule approximation with $n=4$ subdivisions. Compare the result with the actual value of this integral.
$T_4 = \frac{1}{2}\Delta x\left[f(a)+2f(x_1)+2f(x_2)+2f(x_3)+f(b)\right]$
$=\frac{1}{2}\cdot 0.5\left[f(0)+2f(0.5)+2f(1)+2f(1.5)+f(2)\right]$
$=0.25\left[0^2+2 \cdot 0.5^2+2 \cdot 1^2+2 \cdot 1.5^2+2^2\right]$
$=2.75$
The error of this approximation is $\displaystyle \left|\int_{0}^{2} x^2 \, dx-T_4\right|=\left|\frac{8}{3}-2.75\right|=0.08\overline{3}.$
Nice Fact
$$T_n=\frac{1}{2}(L_n+R_n).$$ That is, the trapezoid approximation is the average of the left and right-hand sum approximations.
Example: For $\displaystyle \int_{0}^{2} x^2 \, dx,$ $$T_4=2.75=\frac{1}{2}(1.75+3.75)=\frac{1}{2}(L_n+R_n).$$
Question: Can we do better?
The Midpoint Rule
The midpoint rule evaluates at $x_i^*=m_i=a+(i-0.5)\Delta x$ which is the point between the left and right endpoints.
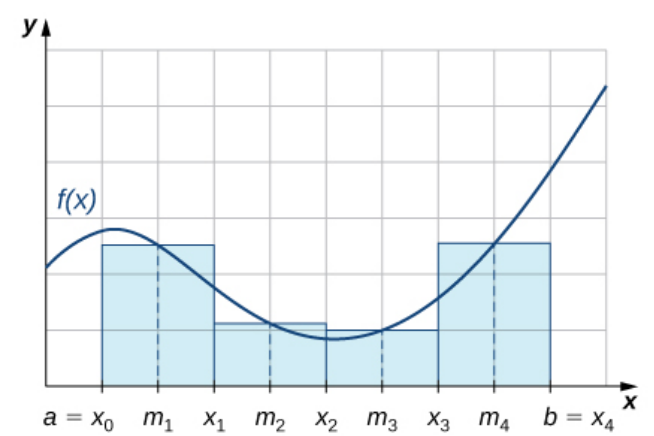$$\displaystyle M_n=\sum_{i=1}^{n}f(a+(i-0.5)\Delta x)\Delta x$$
Example
Approximate the integral $\displaystyle \int_{0}^{2} x^2 \, dx$ by computing $M_4,$ the midpoint rule approximation with $n=4$ subdivisions. Compare the result with the actual value of this integral.
$M_4 =\displaystyle \sum_{i=1}^{4}f(a+(i-0.5)\Delta x)\Delta x$
$=\displaystyle \Delta x \sum_{i=1}^{4}f(a+(i-0.5)\Delta x)$
$=\displaystyle 0.5 \sum_{i=1}^{4}f(0+(i-0.5)0.5)$
$= 0.5[f(0+(1-0.5)\cdot 0.5)+f(0+(2-0.5)\cdot 0.5)+f(0+(3-0.5)\cdot 0.5)+f(0+(4-0.5)\cdot 0.5)]$
$= 0.5[f(0.5 \cdot 0.5)+f(1.5 \cdot 0.5)+f(2.5 \cdot 0.5)+f(3.5 \cdot 0.5)]$
$= 0.5[f(0.25)+f(0.75)+f(1.25)+f(1.75)]$
$= 0.5[0.25^2+0.75^2+1.25^2+1.75^2]$
$= 2.625$
The error of this approximation is $\displaystyle \left|\int_{0}^{2} x^2 \, dx-M_4\right|=\left|\frac{8}{3}-2.625\right|=0.041\overline{6}.$
Question: Can we do better?
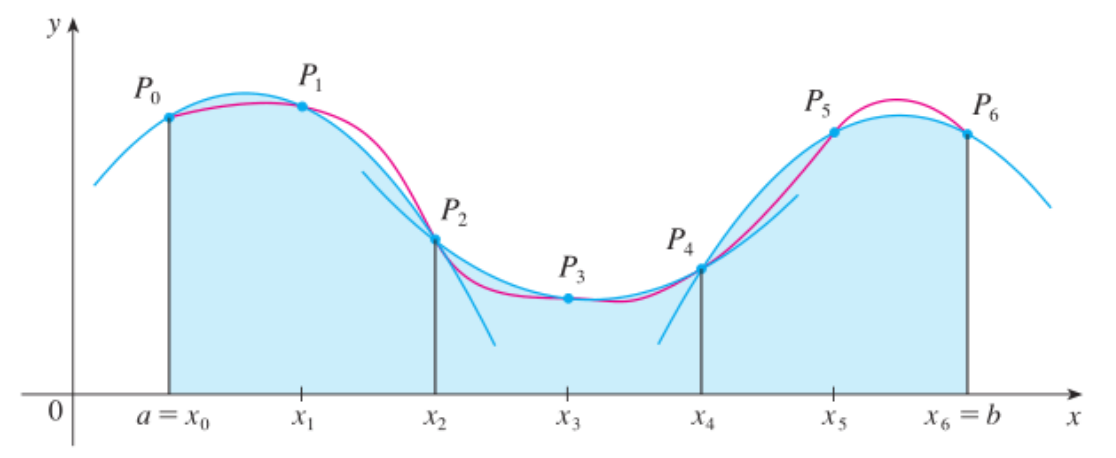
Simpson's Rule
Simpson's rule uses quadratic approximations (parabolas) between the endpoints of each subinterval. Break up $[a,b]$ into subintervals $[a,x_1],$ $[x_1,x_2],$ $[x_2,x_3],$ $\cdots,$ $[x_{n-3},x_{n-2}],$ $[x_{n-2},x_{n-1}],$ $[x_{n-1},b].$
Example
Approximate the integral $\displaystyle \int_{0}^{2} x^2 \, dx$ by computing $S_4,$ Simpson's rule approximation with $n=4$ subdivisions. Compare the result with the actual value of this integral.
$S_4 = \frac{1}{3}\Delta x\left[f(a)+4f(x_1)+2f(x_2)+4f(x_3)+f(b)\right]$
$= \frac{1}{3}\cdot 0.5\left[f(0)+4f(0.5)+2f(1)+4f(1.5)+f(2)\right]$
$= \frac{1}{6}\left[0^2+4 \cdot 0.5^2+2 \cdot 1^2+4 \cdot 1.5^2+2^2\right]$
$= 2.\overline{6}$
The error of this approximation is $\displaystyle \left|\int_{0}^{2} x^2 \, dx-S_4\right|=\left|\frac{8}{3}-2.\overline{6}\right|=0.$ Wow!
Another Nice Fact
$$S_{2n}=\frac{2}{3}M_n+\frac{1}{3}T_n.$$ That is, Simpson's rule is a weighted average of the midpoint and trapezoid sum approximations.
Example: For $\displaystyle \int_{0}^{2} x^2 \, dx,$ $$S_4=2.\overline{6}=\frac{2}{3} \cdot \frac{5}{2}+\frac{1}{3} \cdot 3 =\frac{2}{3}M_2+\frac{1}{3}T_2.$$
Example: Exact Value Unknown
Approximate the integral $\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx$ by computing $S_4,$ Simpson's rule approximation with $n=4$ subdivisions.
$S_4 = \frac{1}{\sqrt{2\pi}} \frac{1}{3}\Delta x\left[f(a)+4f(x_1)+2f(x_2)+4f(x_3)+f(b)\right]$
$= \frac{1}{\sqrt{2\pi}} \frac{1}{3}\cdot 0.25\left[f(0)+4f(0.25)+2f(0.5)+4f(0.75)+f(1)\right]$
$= \frac{1}{12\sqrt{2\pi}}\left[e^{-0^2/2}+4 \cdot e^{-0.25^2/2}+2 \cdot e^{-0.5^2/2}+4 \cdot e^{-0.75^2/2}+e^{-1^2/2}\right]$
$\approx 0.341355.$
The error of this approximation is ?????????????????????????
Error Bounds: How Good is Our Approximation?
When approximating some value (an integral or otherwise), it is quite rare that we actually know the exact value. (Otherwise, why would we go to all this trouble to approximate! :P)
In order to understand how far off we could be, we need to know the maximum amount of error in our approximation.
For the midpoint, the trapezoid, and Simpson's rule, we have error bounds.
We will return to the example $\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx.$ First, however, we will need to learn how to bound the error of our approximations.
Error Bound: The Trapezoid Rule
Let $f(x)$ be a continuous function over $[a, b],$ having a second derivative $f''(x)$ over this interval. If $M$ is the maximum value of $|f''(x)|$ over $[a, b],$ then the upper bound for the error in using $T_n$ to estimate $\displaystyle \int_{a}^{b} f(x) \, dx$ satisfies $$\left|\displaystyle \int_{a}^{b} f(x) \, dx-T_n\right| \leq \frac{M(b-a)^3}{12n^2}.$$
Example: Error Bound Using The Trapezoid Rule
Estimate the value of $\ln 2$ by approximating $\displaystyle \int_{1}^{2} \frac{dx}{x}$ with the trapezoid rule using $n=4$ subdivisions.
Compute the maximum error of this estimate.
We first estimate the integral.
$$
\begin{array}{lll}
\displaystyle \int_{1}^{2} \frac{dx}{x}&\approx\displaystyle T_4&\mbox{}\\
&=\displaystyle \frac{1}{2}\Delta x\left[f(a)+2f(x_1)+2f(x_2)+2f(x_3)+f(b)\right] &\mbox{}\\
&=\displaystyle \frac{1}{2} \cdot \frac{1}{4}\left[f(1)+2f(1.25)+2f(1.5)+2f(1.75)+f(2)\right] &\mbox{ since $\displaystyle \Delta x=\frac{b-a}{n}=\frac{2-1}{4}=\frac{1}{4}$}\\
&=\displaystyle \frac{1}{8}\left[\frac{1}{1}+2\cdot \frac{1}{1.25}+2\cdot\frac{1}{1.5}+2\cdot\frac{1}{1.75}+\frac{1}{2}\right] &\mbox{}\\
&=\displaystyle \frac{1171}{1680} &\mbox{}\\
&\approx 0.6970238095 &\mbox{}\\
\end{array}
$$
To compute the maximum error of the above estimate $\displaystyle \frac{M(b-a)^3}{12n^2},$ we must first compute the maximum value, $M,$ of
$f''(x)$ on the interval $[1,2].$ Computing $f''(x),$
$$
\begin{array}{lll}
&\displaystyle f(x)&=\displaystyle \frac{1}{x}\\
\implies &\displaystyle f'(x)&=\displaystyle-\frac{1}{x^2}\\
\implies &\displaystyle f''(x)&=\displaystyle \frac{2}{x^3}\\
\end{array}
$$
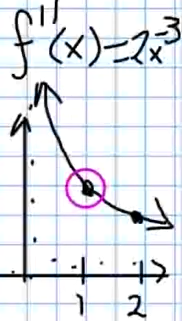
Thus, we must find the maximum value of $\displaystyle f''(x)=\frac{2}{x^3}$ on $[1,2].$
Since this function is decreasing on the entire interval as seen below, the maximum occurs at $x=1.$
$$\displaystyle M=\max_{[1,2]} f''(x)=\max_{[1,2]} \frac{2}{x^3}=\frac{2}{1^3}=2.$$
We may now determine the max error of our estimate $T_4.$ $$ \begin{array}{lll} \displaystyle \left|\displaystyle \int_{a}^{b} f(x) \, dx-T_n\right|&= \left|\displaystyle \int_{1}^{2} \frac{1}{x} \, dx-\frac{1171}{1680}\right| &\mbox{}\\ &\leq \displaystyle \frac{M(b-a)^3}{12n^2}&\mbox{}\\ &= \displaystyle \frac{2\cdot (2-1)^3}{12 \cdot 4^2}&\mbox{}\\ &= \displaystyle \frac{1}{96}&\mbox{}\\ &= \displaystyle 0.01041\overline{6}&\mbox{}\\ \end{array} $$ The above maximum error tells us that $$ \begin{array}{lll} &\displaystyle -\frac{1}{96} \leq \int_{1}^{2} \frac{1}{x} \, dx-\frac{1171}{1680}\leq \frac{1}{96}&\\ \implies &\displaystyle \frac{1171}{1680}-\frac{1}{96} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{1171}{1680}+\frac{1}{96}&\\ \implies &\displaystyle 0.6866071429 \approx \frac{769}{1120} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{2377}{3360} \approx 0.7074404762&\\ \end{array} $$
We may now determine the max error of our estimate $T_4.$ $$ \begin{array}{lll} \displaystyle \left|\displaystyle \int_{a}^{b} f(x) \, dx-T_n\right|&= \left|\displaystyle \int_{1}^{2} \frac{1}{x} \, dx-\frac{1171}{1680}\right| &\mbox{}\\ &\leq \displaystyle \frac{M(b-a)^3}{12n^2}&\mbox{}\\ &= \displaystyle \frac{2\cdot (2-1)^3}{12 \cdot 4^2}&\mbox{}\\ &= \displaystyle \frac{1}{96}&\mbox{}\\ &= \displaystyle 0.01041\overline{6}&\mbox{}\\ \end{array} $$ The above maximum error tells us that $$ \begin{array}{lll} &\displaystyle -\frac{1}{96} \leq \int_{1}^{2} \frac{1}{x} \, dx-\frac{1171}{1680}\leq \frac{1}{96}&\\ \implies &\displaystyle \frac{1171}{1680}-\frac{1}{96} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{1171}{1680}+\frac{1}{96}&\\ \implies &\displaystyle 0.6866071429 \approx \frac{769}{1120} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{2377}{3360} \approx 0.7074404762&\\ \end{array} $$
Error Bound: The Midpoint Rule
Let $f(x)$ be a continuous function over $[a, b],$ having a second derivative $f''(x)$ over this interval. If $M$ is the maximum value of $|f''(x)|$ over $[a, b],$ then the upper bound for the error in using $M_n$ to estimate $\displaystyle \int_{a}^{b} f(x) \, dx$ satisfies $$\left|\displaystyle \int_{a}^{b} f(x) \, dx-M_n\right| \leq \frac{M(b-a)^3}{24n^2}.$$
Example: Error Bound Using The Midpoint Rule
Estimate the value of $\ln 2$ by approximating $\displaystyle \int_{1}^{2} \frac{dx}{x}$ with the midpoint rule using $n=4$ subdivisions.
Compute the maximum error of this estimate.
We first estimate the integral.
$$
\begin{array}{lll}
\displaystyle \int_{1}^{2} \frac{dx}{x}&\approx\displaystyle M_4&\mbox{}\\
&=\displaystyle \sum_{i=1}^{4}f(a+(i-0.5)\Delta x)\Delta x &\mbox{}\\
&=\displaystyle \Delta x \sum_{i=1}^{4}f(a+(i-0.5)\Delta x) &\mbox{}\\
&=\displaystyle 0.25 \sum_{i=1}^{4}f(1+(i-0.5)0.25) \,\,\,\,\,\,\,\,\,\,\mbox{ since $\displaystyle \Delta x=\frac{b-a}{n}=\frac{2-1}{4}=0.25$}&\\
&=\displaystyle 0.25 \left[f(1+(1-0.5)0.25)+f(1+(2-0.5)0.25)+f(1+(3-0.5)0.25)+f(1+(4-0.5)0.25)\right] &\mbox{}\\
&=\displaystyle 0.25 \left[f(1.125)+f(1.375)+f(1.625)+f(1.875)\right] &\mbox{}\\
&=\displaystyle 0.25 \left[\frac{1}{1.125}+\frac{1}{1.375}+\frac{1}{1.625}+\frac{1}{1.875}\right] &\mbox{}\\
&=\displaystyle \frac{4448}{6435} &\mbox{}\\
&\approx \displaystyle 0.6912198912 &\mbox{}\\
\end{array}
$$
We now compute the maximum error of the above estimate $\displaystyle \frac{M(b-a)^3}{24n^2}.$ In the previous example we found that
$\displaystyle M=\max_{[1,2]} f''(x)=\max_{[1,2]} \frac{2}{x^3}=\frac{2}{1^3}=2.$
Thus, we may now determine the max error of our estimate $M_4.$
$$
\begin{array}{lll}
\displaystyle \left|\displaystyle \int_{a}^{b} f(x) \, dx-M_n\right|&= \left|\displaystyle \int_{1}^{2} \frac{1}{x} \, dx-\frac{4448}{6435}\right| &\mbox{}\\
&\leq \displaystyle \frac{M(b-a)^3}{24n^2}&\mbox{}\\
&= \displaystyle \frac{2\cdot (2-1)^3}{24 \cdot 4^2}&\mbox{}\\
&= \displaystyle \frac{1}{192}&\mbox{}\\
&= \displaystyle 0.005208\overline{3}&\mbox{}\\
\end{array}
$$
The above maximum error tells us that
$$
\begin{array}{lll}
&\displaystyle -\frac{1}{192} \leq \int_{1}^{2} \frac{1}{x} \, dx-\frac{4448}{6435}\leq \frac{1}{192}&\\
\implies &\displaystyle \frac{4448}{6435}-\frac{1}{192} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{4448}{6435}+\frac{1}{192}&\\
\implies &\displaystyle 0.6860115579 \approx \frac{282527}{411840} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{286817}{411840}\approx 0.6964282246&\\
\end{array}
$$
Error Bound: Simpson's Rule
Let $f(x)$ be a continuous function over $[a, b],$ having a fourth derivative $f^{(4)}(x)$ over this interval. If $M$ is the maximum value of $|f^{(4)}(x)|$ over $[a, b],$ then the upper bound for the error in using $S_n$ to estimate $\displaystyle \int_{a}^{b} f(x) \, dx$ satisfies $$\left|\displaystyle \int_{a}^{b} f(x) \, dx-S_n\right| \leq \frac{M(b-a)^5}{180n^4}.$$
Example: Error Bound Using Simpson's Rule
Estimate the value of $\ln 2$ by approximating $\displaystyle \int_{1}^{2} \frac{dx}{x}$ with Simpson's rule using $n=8$ subdivisions. (Hint: Use the estimates $M_4$ and $T_4$ above.)
Compute the maximum error of this estimate.
We first estimate the integral.
$$
\begin{array}{lll}
\displaystyle \int_{1}^{2} \frac{dx}{x}&\approx\displaystyle S_8&\mbox{}\\
&=\displaystyle \frac{2}{3}M_4+\frac{1}{3}T_4&\mbox{}\\
&=\displaystyle \frac{2}{3}\frac{4448}{6435}+\frac{1}{3}\frac{1171}{1680}&\mbox{ from the previous two examples}\\
&=\displaystyle \frac{1498711}{2162160}&\mbox{}\\
&=\displaystyle 0.6931\overline{545306}&\mbox{}\\
\end{array}
$$
To compute the maximum error of the above estimate $\displaystyle \frac{M(b-a)^5}{180n^4},$ we must first compute the maximum value, $M,$ of
$f''(x)$ on the interval $[1,2].$ Computing $f''(x),$
$$
\begin{array}{lll}
&\displaystyle f''(x)&=\displaystyle \frac{2}{x^3}\\
\implies &\displaystyle f'''(x)&=\displaystyle-\frac{6}{x^4}\\
\implies &\displaystyle f^{(4)}(x)&=\displaystyle \frac{24}{x^5}\\
\end{array}
$$
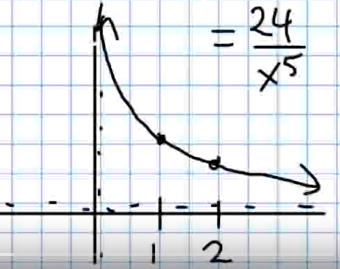
Thus, we must find the maximum value of $\displaystyle f^{(4)}(x)=\frac{24}{x^5}$ on $[1,2].$
Since this function is decreasing on the entire interval as seen below, the maximum occurs at $x=1.$
$$\displaystyle M=\max_{[1,2]} f^{(4)}(x)=\max_{[1,2]} \frac{24}{x^5}=\frac{24}{1^3}=24.$$
We may now determine the max error of our estimate $S_8.$ $$ \begin{array}{lll} \displaystyle \left|\displaystyle \int_{a}^{b} f(x) \, dx-S_n\right|&= \left|\displaystyle \int_{1}^{2} \frac{1}{x} \, dx-\frac{1498711}{2162160}\right| &\mbox{}\\ &\leq \displaystyle \frac{M(b-a)^5}{180n^4}&\mbox{}\\ &= \displaystyle \frac{24\cdot (2-1)^5}{180 \cdot 8^4}&\mbox{}\\ &= \displaystyle \frac{1}{30720}&\mbox{}\\ &= 0.00003255208\overline{3}&\mbox{}\\ \end{array} $$ The above maximum error tells us that $$ \begin{array}{lll} &\displaystyle -\frac{1}{30720} \leq \int_{1}^{2} \frac{1}{x} \, dx-\frac{1171}{1680}\leq \frac{1}{30720}&\\ \implies &\displaystyle \frac{1498711}{2162160}-\frac{1}{30720} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{1498711}{2162160}+\frac{1}{30720}&\\ \implies &\displaystyle 0.69312197857119732 \approx \frac{191825999}{276756480} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{191844017}{276756480} \approx 0.69318708273786398&\\ \end{array} $$
We may now determine the max error of our estimate $S_8.$ $$ \begin{array}{lll} \displaystyle \left|\displaystyle \int_{a}^{b} f(x) \, dx-S_n\right|&= \left|\displaystyle \int_{1}^{2} \frac{1}{x} \, dx-\frac{1498711}{2162160}\right| &\mbox{}\\ &\leq \displaystyle \frac{M(b-a)^5}{180n^4}&\mbox{}\\ &= \displaystyle \frac{24\cdot (2-1)^5}{180 \cdot 8^4}&\mbox{}\\ &= \displaystyle \frac{1}{30720}&\mbox{}\\ &= 0.00003255208\overline{3}&\mbox{}\\ \end{array} $$ The above maximum error tells us that $$ \begin{array}{lll} &\displaystyle -\frac{1}{30720} \leq \int_{1}^{2} \frac{1}{x} \, dx-\frac{1171}{1680}\leq \frac{1}{30720}&\\ \implies &\displaystyle \frac{1498711}{2162160}-\frac{1}{30720} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{1498711}{2162160}+\frac{1}{30720}&\\ \implies &\displaystyle 0.69312197857119732 \approx \frac{191825999}{276756480} \leq \int_{1}^{2} \frac{1}{x} \, dx\leq \frac{191844017}{276756480} \approx 0.69318708273786398&\\ \end{array} $$
Example: Error Bound Using Simpson's Rule
Recall that $\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx \approx 0.341355$ using $n=4$ subdivisions.
Compute the maximum error of this estimate.
Noting that $\displaystyle \frac{d^4}{dx^4}e^{-x^2/2}=(x^4-6x^2+3)e^{-x^2/2}$ and considering its graph
below, we see that the maximum absolute value of the fourth derivative of $e^{-x^2/2}$ on $[0,1]$ is $3.$
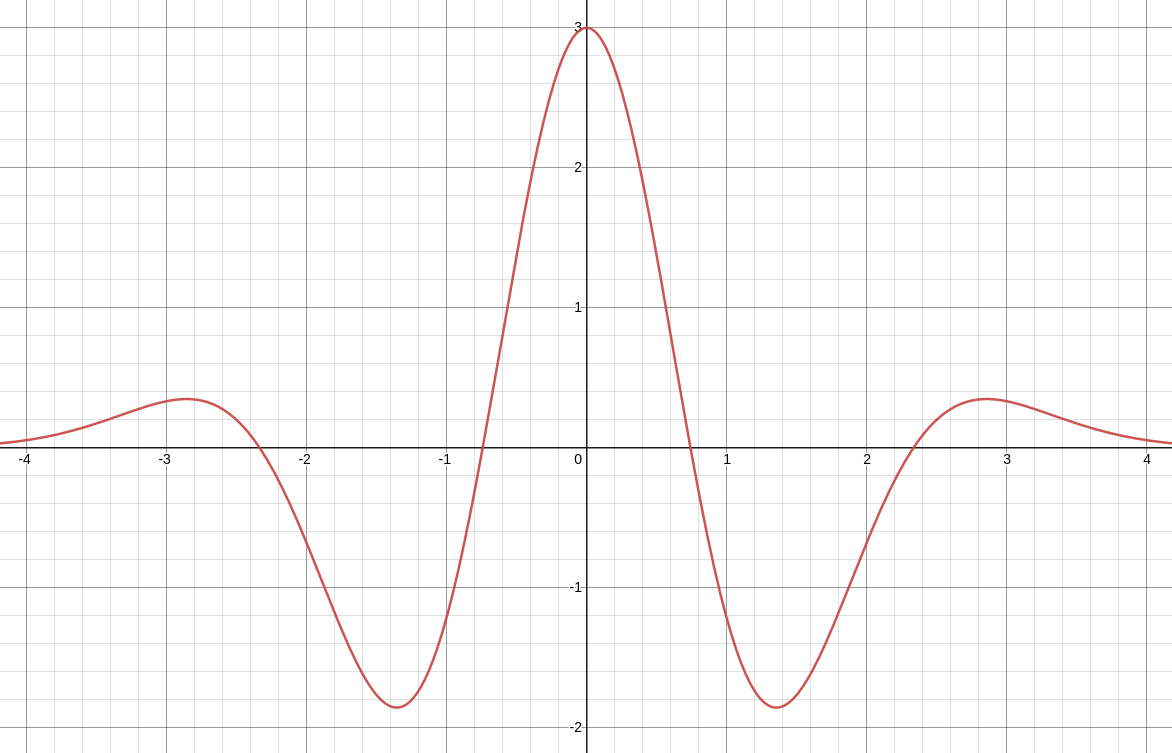
Thus, the maximum value of the fourth derivative of $\displaystyle \frac{1}{\sqrt{2\pi}}e^{-x^2/2}$ on $[0,1]$ is $\displaystyle \frac{3}{\sqrt{2\pi}}.$ That is, $\displaystyle M=\frac{3}{\sqrt{2\pi}}.$
It follows that $$ \begin{array}{ll} \displaystyle \left|\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-S_4\right|&=\left|\displaystyle \int_{0}^{1} \frac{1}{\sqrt{2\pi}}e^{-x^2/2} \, dx-S_4\right| \\ &\displaystyle\leq \frac{\frac{3}{\sqrt{2 \pi}}(1-0)^5}{180 \cdot 4^4}\\ &\displaystyle=\frac{1}{60 \cdot 256 \cdot \sqrt{2\pi}}\\ &\displaystyle=\frac{1}{15360\sqrt{2\pi}} \\ &\displaystyle\lt 0.000026.\\ \end{array} $$ From the inequality $\displaystyle \left|\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-S_4\right| \lt 0.000026$ established above, we have that $$0.341329 \approx S_4-0.000026 \lt \displaystyle \displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx \lt S_4+0.000026\approx 0.341381.$$
Thus, the maximum value of the fourth derivative of $\displaystyle \frac{1}{\sqrt{2\pi}}e^{-x^2/2}$ on $[0,1]$ is $\displaystyle \frac{3}{\sqrt{2\pi}}.$ That is, $\displaystyle M=\frac{3}{\sqrt{2\pi}}.$
It follows that $$ \begin{array}{ll} \displaystyle \left|\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-S_4\right|&=\left|\displaystyle \int_{0}^{1} \frac{1}{\sqrt{2\pi}}e^{-x^2/2} \, dx-S_4\right| \\ &\displaystyle\leq \frac{\frac{3}{\sqrt{2 \pi}}(1-0)^5}{180 \cdot 4^4}\\ &\displaystyle=\frac{1}{60 \cdot 256 \cdot \sqrt{2\pi}}\\ &\displaystyle=\frac{1}{15360\sqrt{2\pi}} \\ &\displaystyle\lt 0.000026.\\ \end{array} $$ From the inequality $\displaystyle \left|\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-S_4\right| \lt 0.000026$ established above, we have that $$0.341329 \approx S_4-0.000026 \lt \displaystyle \displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx \lt S_4+0.000026\approx 0.341381.$$
Using Error Bounds for Desired Accuracy
Find the minimum number of subdivisions $n$ that would be required so that the approximation of the integral $\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx$ is less than $0.00001$ using
- The Trapezoid Rule
- The Midpoint Rule
- Simpson's Rule
Trapezoid Rule:
Using the trapezoid rule we need to choose the number of subdivisions $n$ such that
$$\displaystyle \left| \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-T_n\right|=\left| \int_{0}^{1} \frac{1}{\sqrt{2\pi}} e^{-x^2/2} \, dx-T_n\right| \leq \frac{M(b-a)^3}{12n^2}\lt 0.00001$$
To find $M,$ we note that
$$\displaystyle \max_{[0,1]} \left|\frac{d^2}{dx^2}e^{-x^2/2}\right|=\max_{[0,1]} \left|(x^2-1)e^{-x^2/2}\right|=|-1|= 1$$
as seen from the graph of $(x^2-1)e^{-x^2/2}$ below.
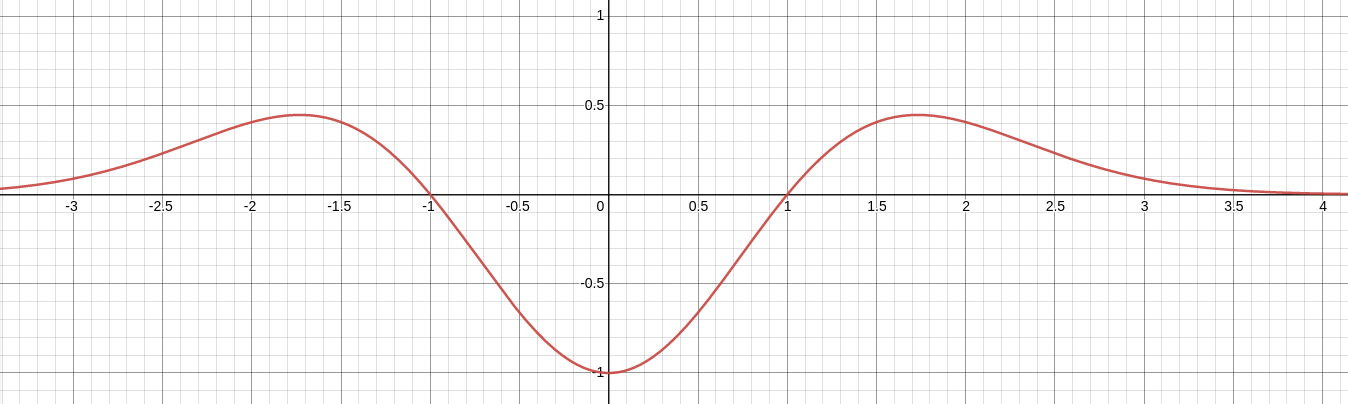From this we obtain
$$\displaystyle M=\max_{[0,1]}|f''(x)|=\max_{[0,1]} \left|\frac{d^2}{dx^2}\frac{1}{\sqrt{2\pi}}e^{-x^2/2}\right|= \frac{1}{\sqrt{2\pi}}.$$
Then,
$$
\begin{array}{lll}
&\displaystyle \frac{M(b-a)^3}{12n^2} \lt 0.00001&\\
\implies &\displaystyle 10^5\frac{M(b-a)^3}{12n^2} \lt \displaystyle 1&\\
\implies &\displaystyle 10^5\frac{M(b-a)^3}{12} \lt \displaystyle n^2&\\
\implies &\displaystyle \sqrt{10^5\frac{M(b-a)^3}{12}} \lt \displaystyle n&\\
\implies &\displaystyle \sqrt{10^5\frac{\frac{1}{\sqrt{2\pi}}(1-0)^3}{12}} \lt \displaystyle n&\mbox{}\\
\implies &\displaystyle 57.65864205 \lt \displaystyle n&\\
\implies &\displaystyle n \geq 58&\\
\end{array}
$$
Thus, using the trapezoid rule, we would need at least $58$ subdivisions to achieve a maximum error of less than $0.00001.$
Midpoint Rule: Using the midpoint rule we need to choose the number of subdivisions $n$ such that $$\displaystyle \left| \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-M_n\right|= \left|\int_{0}^{1} \frac{1}{\sqrt{2\pi}}e^{-x^2/2} \, dx-M_n\right| \leq \frac{M(b-a)^3}{24n^2}\lt 0.00001.$$ Then, $$ \begin{array}{lll} &\displaystyle \frac{M(b-a)^3}{12n^2} \lt 0.00001&\\ \implies &\displaystyle 10^5\frac{M(b-a)^3}{24n^2} \lt \displaystyle 1&\\ \implies &\displaystyle 10^5\frac{M(b-a)^3}{24} \lt \displaystyle n^2&\\ \implies &\displaystyle \sqrt{10^5\frac{M(b-a)^3}{24}} \lt \displaystyle n&\\ \implies &\displaystyle \sqrt{10^5\frac{\frac{1}{\sqrt{2\pi}}(1-0)^3}{24}} \lt \displaystyle n&\mbox{ in this case $M=\frac{1}{\sqrt{2\pi}}$ as well}\\ \implies &\displaystyle 40.77081679 \lt \displaystyle n&\\ \implies &\displaystyle n \geq 41 &\\ \end{array} $$ Thus, using the midpoint rule, we would need at least $41$ subdivisions to achieve a maximum error of less than $0.00001.$
Simpson's Rule: Using Simpson's rule we need to choose the number of subdivisions $n$ such that $$\displaystyle \left|\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-S_n\right| =\left|\displaystyle \int_{0}^{1} \frac{1}{\sqrt{2\pi}} e^{-x^2/2} \, dx-S_n\right| \leq \frac{M(b-a)^5}{180n^4}\lt 0.00001.$$ Then, $$ \begin{array}{lll} &\displaystyle \frac{M(b-a)^5}{180n^4}\lt 0.00001 &\\ \implies &\displaystyle 10^5\frac{M(b-a)^5}{180n^4} \lt \displaystyle 1&\\ \implies &\displaystyle 10^5\frac{M(b-a)^5}{180}\lt \displaystyle n^4&\\ \implies &\displaystyle \sqrt[4]{10^5\frac{M(b-a)^5}{180}} \lt \displaystyle n&\\ \implies &\displaystyle \sqrt[4]{10^5\frac{\frac{3}{\sqrt{2\pi}}(1-0)^5}{180}} \lt \displaystyle n&\mbox{ since $M=\frac{3}{\sqrt{2\pi}}$ as shown in a previous example}\\ \implies &\displaystyle 5.077965008 \lt \displaystyle n&\\ \implies &\displaystyle n \geq 6&\\ \end{array} $$ Thus, using Simpson's rule, we would need at least $6$ subdivisions to achieve a maximum error of less than $0.00001.$
Midpoint Rule: Using the midpoint rule we need to choose the number of subdivisions $n$ such that $$\displaystyle \left| \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-M_n\right|= \left|\int_{0}^{1} \frac{1}{\sqrt{2\pi}}e^{-x^2/2} \, dx-M_n\right| \leq \frac{M(b-a)^3}{24n^2}\lt 0.00001.$$ Then, $$ \begin{array}{lll} &\displaystyle \frac{M(b-a)^3}{12n^2} \lt 0.00001&\\ \implies &\displaystyle 10^5\frac{M(b-a)^3}{24n^2} \lt \displaystyle 1&\\ \implies &\displaystyle 10^5\frac{M(b-a)^3}{24} \lt \displaystyle n^2&\\ \implies &\displaystyle \sqrt{10^5\frac{M(b-a)^3}{24}} \lt \displaystyle n&\\ \implies &\displaystyle \sqrt{10^5\frac{\frac{1}{\sqrt{2\pi}}(1-0)^3}{24}} \lt \displaystyle n&\mbox{ in this case $M=\frac{1}{\sqrt{2\pi}}$ as well}\\ \implies &\displaystyle 40.77081679 \lt \displaystyle n&\\ \implies &\displaystyle n \geq 41 &\\ \end{array} $$ Thus, using the midpoint rule, we would need at least $41$ subdivisions to achieve a maximum error of less than $0.00001.$
Simpson's Rule: Using Simpson's rule we need to choose the number of subdivisions $n$ such that $$\displaystyle \left|\displaystyle \frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-x^2/2} \, dx-S_n\right| =\left|\displaystyle \int_{0}^{1} \frac{1}{\sqrt{2\pi}} e^{-x^2/2} \, dx-S_n\right| \leq \frac{M(b-a)^5}{180n^4}\lt 0.00001.$$ Then, $$ \begin{array}{lll} &\displaystyle \frac{M(b-a)^5}{180n^4}\lt 0.00001 &\\ \implies &\displaystyle 10^5\frac{M(b-a)^5}{180n^4} \lt \displaystyle 1&\\ \implies &\displaystyle 10^5\frac{M(b-a)^5}{180}\lt \displaystyle n^4&\\ \implies &\displaystyle \sqrt[4]{10^5\frac{M(b-a)^5}{180}} \lt \displaystyle n&\\ \implies &\displaystyle \sqrt[4]{10^5\frac{\frac{3}{\sqrt{2\pi}}(1-0)^5}{180}} \lt \displaystyle n&\mbox{ since $M=\frac{3}{\sqrt{2\pi}}$ as shown in a previous example}\\ \implies &\displaystyle 5.077965008 \lt \displaystyle n&\\ \implies &\displaystyle n \geq 6&\\ \end{array} $$ Thus, using Simpson's rule, we would need at least $6$ subdivisions to achieve a maximum error of less than $0.00001.$
Application
The mean height of women in their 20's in the United States is $\mu=64.3$ inches with a standard deviation of $\sigma=2.7$ inches. What is the probability that a randomly chosen woman in her 20's is between $64.3$ and $67$ inches tall? That is, what is the probability that her height will be within $0$ to $1$ standard deviations above the mean?
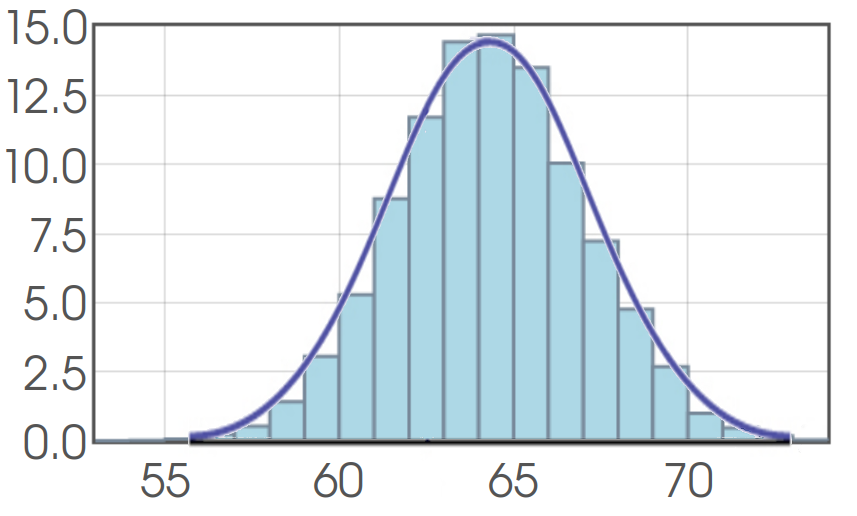
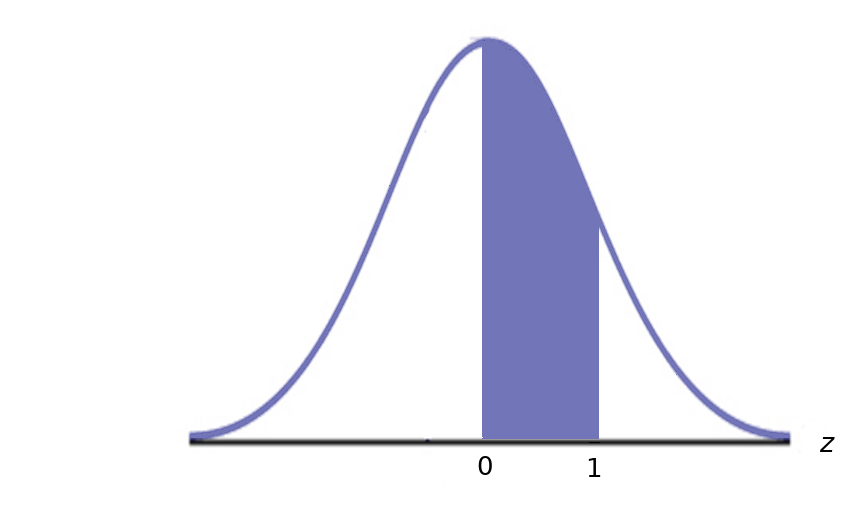
$$\displaystyle P(64.3 \lt \mbox{Height} \lt 67)=P(0 \lt z \lt 1)=\frac{1}{\sqrt{2\pi}}\int_{0}^{1} e^{-z^2/2} \, dz \approx 0.341355$$