Today we handle integrals that contain the forms $\sqrt{x^2+a^2},$ $\sqrt{a^2-x^2},$ and $\sqrt{x^2-a^2}.$
Using these techniques we can also integrate many forms containing $x^2+a^2,$ $a^2-x^2,$ and $x^2-a^2.$
Application #1: WiFi-Passwords

Forms Involving $\sqrt{x^2+a^2}$
To deal with integrals involving the expression $\sqrt{x^2+a^2},$ construct a reference triangle
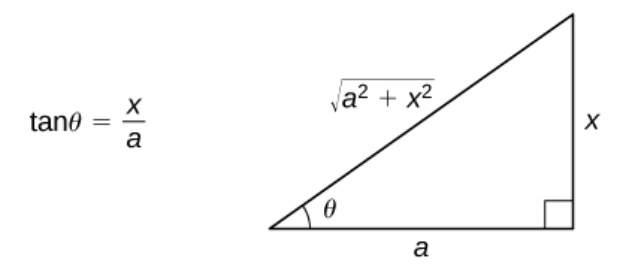
Example
Find the indefinite integral. $\displaystyle \int \frac{1}{\sqrt{x^2+4}} \, dx$
We first construct our reference triangle.

In the original integral we need to replace both $\displaystyle \frac{1}{\sqrt{x^2+4}}$ and $dx$ with equivalent trigonometric expressions using our triangle.
We see that $\displaystyle \frac{2}{\sqrt{x^2+4}}=\cos \theta$ so that $\displaystyle \frac{1}{\sqrt{x^2+4}}=\frac{1}{2}\cos \theta.$
Also, since $\displaystyle \tan \theta =\frac{x}{2},$ we have $x=2\tan \theta$ so that $dx=2\sec^2 \theta \,d\theta.$
We may now make our trigonometric substitutions and integrate: $$ \begin{array}{lll} \displaystyle \int \frac{1}{\sqrt{x^2+4}} \, dx&=\displaystyle \int \frac{1}{2}\cos \theta \cdot 2 \sec^2 \theta \,d\theta &\mbox{}\\ &=\displaystyle \int \sec\theta \,d\theta &\mbox{}\\ &=\displaystyle \ln\left|\sec \theta + \tan \theta \right|+C &\mbox{from a table of integrals}\\ &=\displaystyle \ln\left|\frac{\sqrt{x^2+4}}{2} + \frac{x}{2} \right|+C &\mbox{from our reference triangle}\\ \end{array} $$

In the original integral we need to replace both $\displaystyle \frac{1}{\sqrt{x^2+4}}$ and $dx$ with equivalent trigonometric expressions using our triangle.
We see that $\displaystyle \frac{2}{\sqrt{x^2+4}}=\cos \theta$ so that $\displaystyle \frac{1}{\sqrt{x^2+4}}=\frac{1}{2}\cos \theta.$
Also, since $\displaystyle \tan \theta =\frac{x}{2},$ we have $x=2\tan \theta$ so that $dx=2\sec^2 \theta \,d\theta.$
We may now make our trigonometric substitutions and integrate: $$ \begin{array}{lll} \displaystyle \int \frac{1}{\sqrt{x^2+4}} \, dx&=\displaystyle \int \frac{1}{2}\cos \theta \cdot 2 \sec^2 \theta \,d\theta &\mbox{}\\ &=\displaystyle \int \sec\theta \,d\theta &\mbox{}\\ &=\displaystyle \ln\left|\sec \theta + \tan \theta \right|+C &\mbox{from a table of integrals}\\ &=\displaystyle \ln\left|\frac{\sqrt{x^2+4}}{2} + \frac{x}{2} \right|+C &\mbox{from our reference triangle}\\ \end{array} $$
Forms Involving $\sqrt{a^2-x^2}$
To deal with integrals involving the expression $\sqrt{a^2-x^2},$ construct a reference triangle
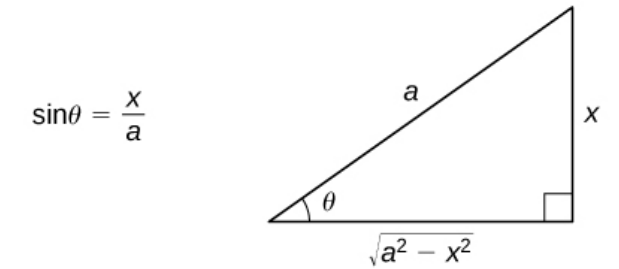
Example
Find the indefinite integral. $\displaystyle \int \frac{x^2}{\sqrt{9-x^2}} \, dx$
We first construct our reference triangle.
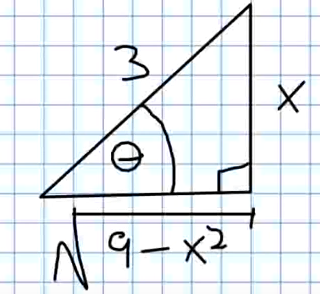
In the original integral we need to replace both $\displaystyle \frac{x^2}{\sqrt{9-x^2}}$ and $dx$ with equivalent trigonometric expressions using our triangle.
We see that $\displaystyle \sin \theta =\frac{x}{3}.$ Thus, we have $x=3\sin \theta$ so that $dx=3 \cos \theta \,d\theta$ and $x^2=9\sin ^2 \theta.$
Also, $\displaystyle \sec \theta =\frac{3}{\sqrt{9-x^2}}$ so that $\displaystyle \frac{1}{3}\sec \theta =\frac{1}{\sqrt{9-x^2}}.$
We may now make our trigonometric substitutions and integrate: $$ \begin{array}{lll} \displaystyle \int \frac{x^2}{\sqrt{9-x^2}} \, dx&=\displaystyle \int x^2\frac{1}{\sqrt{9-x^2}} \, dx &\mbox{}\\ &=\displaystyle \int 9\sin^2 \theta \cdot \frac{1}{3}\sec \theta \cdot 3 \cos \theta \,d\theta &\mbox{}\\ &=\displaystyle \int 9\sin^2 \theta \,d\theta &\mbox{}\\ &=\displaystyle 9 \int \sin^2 \theta \,d\theta &\mbox{}\\ &=\displaystyle 9 \int \frac{1-\cos(2\theta)}{2} \,d\theta &\mbox{using half-angle identity}\\ &=\displaystyle \frac{9}{2} \int 1-\cos(2\theta)\,d\theta &\mbox{}\\ &=\displaystyle \frac{9}{2}\left( \theta-\frac{1}{2}\sin(2\theta)\right)+C &\mbox{}\\ &=\displaystyle \frac{9}{2}\theta-\frac{9}{4}\sin(2\theta)+C &\mbox{}\\ &=\displaystyle \frac{9}{2}\theta-\frac{9}{4}2\sin \theta \cos \theta+C &\mbox{using a double-angle identity}\\ &=\displaystyle \frac{9}{2}\theta-\frac{9}{2}\sin \theta \cos \theta+C &\mbox{}\\ &=\displaystyle \frac{9}{2}\sin^{-1}\left(\frac{x}{3}\right)-\frac{9}{2}\frac{x}{3}\frac{\sqrt{9-x^2}}{3}+C &\mbox{from our reference triangle}\\ &=\displaystyle \frac{9}{2}\sin^{-1}\left(\frac{x}{3}\right)-\frac{1}{2}x\sqrt{9-x^2}+C &\mbox{}\\ \end{array} $$
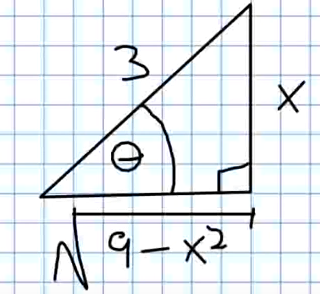
In the original integral we need to replace both $\displaystyle \frac{x^2}{\sqrt{9-x^2}}$ and $dx$ with equivalent trigonometric expressions using our triangle.
We see that $\displaystyle \sin \theta =\frac{x}{3}.$ Thus, we have $x=3\sin \theta$ so that $dx=3 \cos \theta \,d\theta$ and $x^2=9\sin ^2 \theta.$
Also, $\displaystyle \sec \theta =\frac{3}{\sqrt{9-x^2}}$ so that $\displaystyle \frac{1}{3}\sec \theta =\frac{1}{\sqrt{9-x^2}}.$
We may now make our trigonometric substitutions and integrate: $$ \begin{array}{lll} \displaystyle \int \frac{x^2}{\sqrt{9-x^2}} \, dx&=\displaystyle \int x^2\frac{1}{\sqrt{9-x^2}} \, dx &\mbox{}\\ &=\displaystyle \int 9\sin^2 \theta \cdot \frac{1}{3}\sec \theta \cdot 3 \cos \theta \,d\theta &\mbox{}\\ &=\displaystyle \int 9\sin^2 \theta \,d\theta &\mbox{}\\ &=\displaystyle 9 \int \sin^2 \theta \,d\theta &\mbox{}\\ &=\displaystyle 9 \int \frac{1-\cos(2\theta)}{2} \,d\theta &\mbox{using half-angle identity}\\ &=\displaystyle \frac{9}{2} \int 1-\cos(2\theta)\,d\theta &\mbox{}\\ &=\displaystyle \frac{9}{2}\left( \theta-\frac{1}{2}\sin(2\theta)\right)+C &\mbox{}\\ &=\displaystyle \frac{9}{2}\theta-\frac{9}{4}\sin(2\theta)+C &\mbox{}\\ &=\displaystyle \frac{9}{2}\theta-\frac{9}{4}2\sin \theta \cos \theta+C &\mbox{using a double-angle identity}\\ &=\displaystyle \frac{9}{2}\theta-\frac{9}{2}\sin \theta \cos \theta+C &\mbox{}\\ &=\displaystyle \frac{9}{2}\sin^{-1}\left(\frac{x}{3}\right)-\frac{9}{2}\frac{x}{3}\frac{\sqrt{9-x^2}}{3}+C &\mbox{from our reference triangle}\\ &=\displaystyle \frac{9}{2}\sin^{-1}\left(\frac{x}{3}\right)-\frac{1}{2}x\sqrt{9-x^2}+C &\mbox{}\\ \end{array} $$
Forms Involving $\sqrt{x^2-a^2}$
To deal with integrals involving the expression $\sqrt{x^2-a^2},$ there are two cases to consider: $x<-a,$ and $x>a.$
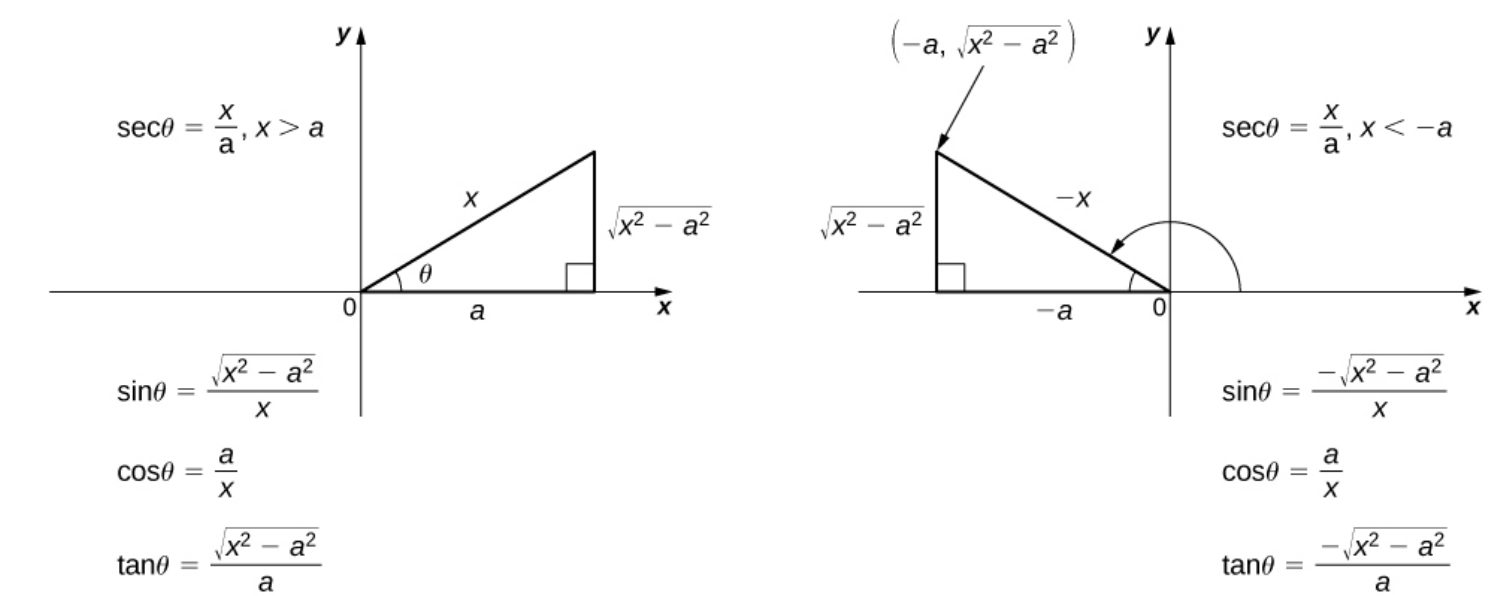
Examples
Find the indefinite integral. $\displaystyle \int \frac{x^2}{\sqrt{25x^2-4}} \, dx$ when $\displaystyle x \gt \frac{2}{5}.$
Find the indefinite integral. $\displaystyle \int \frac{x^2}{\sqrt{25x^2-4}} \, dx$ when $\displaystyle x \lt -\frac{2}{5}.$
The initial calculation for both integrals is the same. However, when restating our integral from $\theta$ back into $x,$
we will need to take into consideration the where $x$ lives.
We construct our reference triangle.
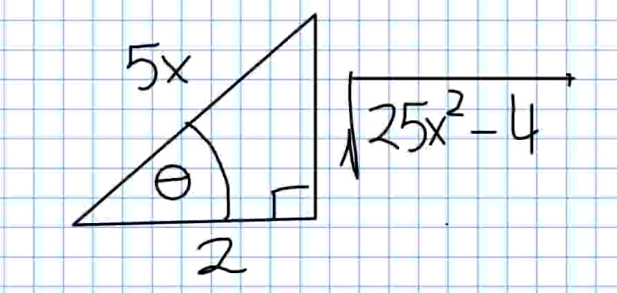
In the original integral we need to replace both $\displaystyle \frac{x^2}{\sqrt{25x^2-4}}$ and $dx$ with equivalent trigonometric expressions using our triangle.
We see that $\displaystyle \sec \theta =\frac{5x}{2}.$ Thus, we have $\displaystyle x=\frac{2}{5}\sec \theta$ so that $\displaystyle dx= \frac{2}{5}\sec \theta \tan \theta \,d\theta$ and $\displaystyle x^2=\frac{4}{25}\sec^2 \theta.$
Also, $\displaystyle \cot \theta =\frac{2}{\sqrt{25x^2-4}}$ so that $\displaystyle \frac{1}{2}\cot \theta =\frac{1}{\sqrt{25x^2-4}}.$
We may now make our trigonometric substitutions and integrate: $$ \begin{array}{lll} \displaystyle \int \frac{x^2}{\sqrt{25x^2-4}} \, dx&=\displaystyle \int x^2 \frac{1}{\sqrt{25x^2-4}} \, dx &\mbox{}\\ &=\displaystyle \int\frac{4}{25}\sec^2 \theta \cdot \frac{1}{2}\cot \theta \cdot \frac{2}{5}\sec \theta \tan \theta \,d\theta &\mbox{}\\ &=\displaystyle \int\frac{4}{125}\sec^3 \theta \,d\theta &\mbox{}\\ &=\displaystyle \frac{4}{125} \int\sec^3 \theta \,d\theta &\mbox{}\\ &=\displaystyle \frac{4}{125} \left(\frac{1}{2}\sec \theta \tan \theta+\frac{1}{2}\ln\left|\sec \theta + \tan \theta \right| \right)+C &\mbox{recall boomerang!}\\ &=\displaystyle \frac{2}{125}\sec \theta \tan \theta+\frac{2}{125}\ln\left|\sec \theta + \tan \theta \right|+C &\mbox{}\\ \end{array} $$ It is here that we must be particularly careful translating the integral back into $x.$ $$ \begin{array}{lll} \mbox{When $\displaystyle x \gt \frac{2}{5}:$}&&\mbox{When $\displaystyle x \lt \frac{2}{5}:$}\\ \displaystyle \frac{2}{125}\sec \theta \tan \theta+\frac{2}{125}\ln\left|\sec \theta + \tan \theta \right|+C&&\displaystyle \frac{2}{125}\sec \theta \tan \theta+\frac{2}{125}\ln\left|\sec \theta + \tan \theta \right|+C\\ \displaystyle=\frac{2}{125}\frac{5x}{2} \frac{\sqrt{25x^2-4}}{2}+\frac{2}{125}\ln\left|\frac{5x}{2} + \frac{\sqrt{25x^2-4}}{2} \right|+C&&\displaystyle=\frac{2}{125}\frac{5x}{2} \left(-\frac{\sqrt{25x^2-4}}{2}\right)+\frac{2}{125}\ln\left|\frac{5x}{2} + \left(-\frac{\sqrt{25x^2-4}}{2}\right)\right|+C\\ \displaystyle=\frac{1}{50}x\sqrt{25x^2-4}+\frac{2}{125}\ln\left|\frac{5x}{2} + \frac{\sqrt{25x^2-4}}{2} \right|+C&&\displaystyle=-\frac{1}{50}x\sqrt{25x^2-4}+\frac{2}{125}\ln\left|\frac{5x}{2} -\frac{\sqrt{25x^2-4}}{2}\right|+C\\ \end{array} $$ Thus, $$\int \frac{x^2}{\sqrt{25x^2-4}} \, dx=\frac{1}{50}x\sqrt{25x^2-4}+\frac{2}{125}\ln\left|\frac{5x}{2} + \frac{\sqrt{25x^2-4}}{2} \right|+C \mbox { when $\displaystyle x \gt \frac{2}{5}$}$$ and $$\int \frac{x^2}{\sqrt{25x^2-4}} \, dx=-\frac{1}{50}x\sqrt{25x^2-4}+\frac{2}{125}\ln\left|\frac{5x}{2} - \frac{\sqrt{25x^2-4}}{2} \right|+C \mbox { when $\displaystyle x \lt \frac{2}{5}$}$$
We construct our reference triangle.
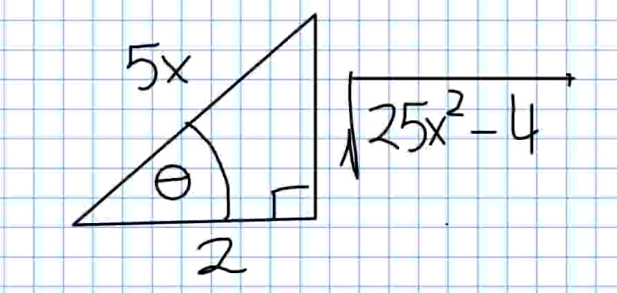
In the original integral we need to replace both $\displaystyle \frac{x^2}{\sqrt{25x^2-4}}$ and $dx$ with equivalent trigonometric expressions using our triangle.
We see that $\displaystyle \sec \theta =\frac{5x}{2}.$ Thus, we have $\displaystyle x=\frac{2}{5}\sec \theta$ so that $\displaystyle dx= \frac{2}{5}\sec \theta \tan \theta \,d\theta$ and $\displaystyle x^2=\frac{4}{25}\sec^2 \theta.$
Also, $\displaystyle \cot \theta =\frac{2}{\sqrt{25x^2-4}}$ so that $\displaystyle \frac{1}{2}\cot \theta =\frac{1}{\sqrt{25x^2-4}}.$
We may now make our trigonometric substitutions and integrate: $$ \begin{array}{lll} \displaystyle \int \frac{x^2}{\sqrt{25x^2-4}} \, dx&=\displaystyle \int x^2 \frac{1}{\sqrt{25x^2-4}} \, dx &\mbox{}\\ &=\displaystyle \int\frac{4}{25}\sec^2 \theta \cdot \frac{1}{2}\cot \theta \cdot \frac{2}{5}\sec \theta \tan \theta \,d\theta &\mbox{}\\ &=\displaystyle \int\frac{4}{125}\sec^3 \theta \,d\theta &\mbox{}\\ &=\displaystyle \frac{4}{125} \int\sec^3 \theta \,d\theta &\mbox{}\\ &=\displaystyle \frac{4}{125} \left(\frac{1}{2}\sec \theta \tan \theta+\frac{1}{2}\ln\left|\sec \theta + \tan \theta \right| \right)+C &\mbox{recall boomerang!}\\ &=\displaystyle \frac{2}{125}\sec \theta \tan \theta+\frac{2}{125}\ln\left|\sec \theta + \tan \theta \right|+C &\mbox{}\\ \end{array} $$ It is here that we must be particularly careful translating the integral back into $x.$ $$ \begin{array}{lll} \mbox{When $\displaystyle x \gt \frac{2}{5}:$}&&\mbox{When $\displaystyle x \lt \frac{2}{5}:$}\\ \displaystyle \frac{2}{125}\sec \theta \tan \theta+\frac{2}{125}\ln\left|\sec \theta + \tan \theta \right|+C&&\displaystyle \frac{2}{125}\sec \theta \tan \theta+\frac{2}{125}\ln\left|\sec \theta + \tan \theta \right|+C\\ \displaystyle=\frac{2}{125}\frac{5x}{2} \frac{\sqrt{25x^2-4}}{2}+\frac{2}{125}\ln\left|\frac{5x}{2} + \frac{\sqrt{25x^2-4}}{2} \right|+C&&\displaystyle=\frac{2}{125}\frac{5x}{2} \left(-\frac{\sqrt{25x^2-4}}{2}\right)+\frac{2}{125}\ln\left|\frac{5x}{2} + \left(-\frac{\sqrt{25x^2-4}}{2}\right)\right|+C\\ \displaystyle=\frac{1}{50}x\sqrt{25x^2-4}+\frac{2}{125}\ln\left|\frac{5x}{2} + \frac{\sqrt{25x^2-4}}{2} \right|+C&&\displaystyle=-\frac{1}{50}x\sqrt{25x^2-4}+\frac{2}{125}\ln\left|\frac{5x}{2} -\frac{\sqrt{25x^2-4}}{2}\right|+C\\ \end{array} $$ Thus, $$\int \frac{x^2}{\sqrt{25x^2-4}} \, dx=\frac{1}{50}x\sqrt{25x^2-4}+\frac{2}{125}\ln\left|\frac{5x}{2} + \frac{\sqrt{25x^2-4}}{2} \right|+C \mbox { when $\displaystyle x \gt \frac{2}{5}$}$$ and $$\int \frac{x^2}{\sqrt{25x^2-4}} \, dx=-\frac{1}{50}x\sqrt{25x^2-4}+\frac{2}{125}\ln\left|\frac{5x}{2} - \frac{\sqrt{25x^2-4}}{2} \right|+C \mbox { when $\displaystyle x \lt \frac{2}{5}$}$$
Hyperbolic Substitutions
Example: Use the substitution $x=\sinh \theta$ to find the indefinite integral $$\displaystyle \int \frac{\sqrt{x^2+1}}{x} \, dx.$$ Express the final answer in terms of the original variable.
Hint: Use the half-argument hyperbolic identity $$\displaystyle \tanh\left(\frac{\theta}{2}\right)=\frac{\sinh \theta}{\cosh \theta +1}.$$
If we let $x=\sinh \theta,$ then $dx=\cosh \theta \,d\theta.$ Then,
$$
\begin{array}{lll}
\displaystyle \int \frac{\sqrt{x^2+1}}{x} \, dx&=\displaystyle \int \frac{\sqrt{\sinh^2\theta+1}}{\sinh \theta} \, \cosh \theta \,d\theta&\mbox{}\\
&=\displaystyle \int \frac{\sqrt{\cosh^2\theta}}{\sinh \theta} \, \cosh \theta \,d\theta&\mbox{using the hyperbolic identity $\cosh^2 x - \sinh^2 x = 1$}\\
&=\displaystyle \int \frac{|\cosh\theta|}{\sinh \theta} \, \cosh \theta \,d\theta&\mbox{}\\
&=\displaystyle \int \frac{\cosh\theta}{\sinh \theta} \, \cosh \theta \,d\theta&\mbox{since $\cosh \theta \gt 0$ for all $\theta$}\\
&=\displaystyle \int \frac{\cosh^2\theta}{\sinh \theta} \,d\theta&\mbox{}\\
&=\displaystyle \int \frac{\sinh^2\theta+1}{\sinh \theta} \,d\theta&\mbox{}\\
&=\displaystyle \int \sinh\theta+\mbox{csch } \theta \,d\theta&\mbox{}\\
&=\displaystyle \cosh\theta+\ln\left|\tanh\left(\frac{\theta}{2}\right)\right|+C&\mbox{using an integral table}\\
&=\displaystyle \cosh\theta+\ln\left|\frac{\sinh \theta}{\cosh \theta +1}\right|+C&\mbox{using half-argument hyperbolic identity}\\
&=\displaystyle \sqrt{\sinh^2 \theta +1}+\ln\left|\frac{\sinh \theta}{\sqrt{\sinh^2 \theta +1} +1}\right|+C&\mbox{using the hyperbolic identity $\cosh^2 x - \sinh^2 x = 1$}\\
&=\displaystyle \sqrt{x^2+1}+\ln\left|\frac{x}{\sqrt{x^2+1}+1}\right|+C&\mbox{}\\
\end{array}
$$
Converting Quadratic Forms to Trig Substitutions by Completing the Square
Use the technique of completing the square to evaluate the following integral. $\displaystyle \int \frac{1}{\sqrt{-x^2+2x+8}} \, dx$
$$
\begin{array}{lll}
\displaystyle \int \frac{1}{\sqrt{-x^2+2x+8}} \, dx&=\displaystyle \int \frac{1}{\sqrt{-(x^2-2x)+8}} \, dx&\mbox{get into $x^2+bx$ form}\\
&=\displaystyle \int \frac{1}{\sqrt{-(x^2-2x+1-1)+8}} \, dx&\mbox{adding $\left(\frac{b}{2}\right)^2=\left(\frac{-2}{2}\right)^2=1$ completes the square}\\
&=\displaystyle \int \frac{1}{\sqrt{-((x-1)^2-1)+8}} \, dx&\mbox{ factor $x^2-2x+1$ into $(x-1)^2$}\\
&=\displaystyle \int \frac{1}{\sqrt{-(x-1)^2+1+8}} \, dx&\mbox{distribute minus}\\
&=\displaystyle \int \frac{1}{\sqrt{9-(x-1)^2}} \, dx&\mbox{}\\
&=\displaystyle \int \frac{1}{\sqrt{9-u^2}} \, du&\mbox{letting $u=x-1$ so that $du=dx$}\\
\end{array}
$$
We recognize the above as a classic trigonometric substitution and make a reference triangle.

In the above integral we need to replace both $\displaystyle \frac{1}{\sqrt{9-u^2}}$ and $du$ with equivalent trigonometric expressions using our triangle.
We see that $\displaystyle \sin \theta =\frac{u}{3}.$ We then have $u=3\sin \theta$ so that $du=3 \cos \theta \,d\theta.$
Also, $\displaystyle \sec \theta =\frac{3}{\sqrt{9-u^2}}$ so that $\displaystyle \frac{1}{3}\sec \theta =\frac{1}{\sqrt{9-u^2}}.$
We may now make our trigonometric substitutions and integrate: $$ \begin{array}{lll} \displaystyle \int \frac{1}{\sqrt{9-u^2}} \, du&=\displaystyle \int \frac{1}{3}\sec \theta \cdot 3 \cos \theta \,d\theta &\mbox{}\\ &=\displaystyle \int \,d\theta &\mbox{}\\ &=\displaystyle \theta +C&\mbox{}\\ &=\displaystyle \sin^{-1}\left(\frac{u}{3}\right)+C &\mbox{}\\ &=\displaystyle \sin^{-1}\left(\frac{x-1}{3}\right)+C &\mbox{}\\ \end{array} $$

In the above integral we need to replace both $\displaystyle \frac{1}{\sqrt{9-u^2}}$ and $du$ with equivalent trigonometric expressions using our triangle.
We see that $\displaystyle \sin \theta =\frac{u}{3}.$ We then have $u=3\sin \theta$ so that $du=3 \cos \theta \,d\theta.$
Also, $\displaystyle \sec \theta =\frac{3}{\sqrt{9-u^2}}$ so that $\displaystyle \frac{1}{3}\sec \theta =\frac{1}{\sqrt{9-u^2}}.$
We may now make our trigonometric substitutions and integrate: $$ \begin{array}{lll} \displaystyle \int \frac{1}{\sqrt{9-u^2}} \, du&=\displaystyle \int \frac{1}{3}\sec \theta \cdot 3 \cos \theta \,d\theta &\mbox{}\\ &=\displaystyle \int \,d\theta &\mbox{}\\ &=\displaystyle \theta +C&\mbox{}\\ &=\displaystyle \sin^{-1}\left(\frac{u}{3}\right)+C &\mbox{}\\ &=\displaystyle \sin^{-1}\left(\frac{x-1}{3}\right)+C &\mbox{}\\ \end{array} $$
Any Takers?
