Integration by Parts is our second general technique for finding antiderivatives after integration by substitution.
Recall: The Product Rule $$\frac{d}{dx}[u(x)v(x)]=u'(x)v(x)+u(x)v'(x)$$ Restating the above in integral form we have...
The Reverse Product Rule $$\int [u'(x)v(x)+u(x)v'(x)] \, dx = u(x)v(x)$$ In another form we have...
Integration by Parts $$\int u(x)v'(x) \, dx = u(x)v(x)-\int u'(x)v(x) \, dx$$ This is a form of the integration by parts formula.
Notice that if we are integrating a product of functions, but we only know how to integrate one of the factors (i.e., $v'(x)$), we can transform the integral into an equivalent form which "transfers" the derivative to the other factor.
Integration by Parts
We may restate the integration by parts formula as $$\int u \, dv = uv-\int v \, du$$ since $du=u'(x) \, dx$ and $dv=v'(x) \, dx.$
Integration by Parts: A Personal Preference
I always preferred to remembering integration by parts as $$\int uv' \, dx = uv-\int u'v \, dx$$ since it's easy to say:
"The integral of $uv'$ is $uv$ minus the integral of $u'v.$"
Example
Find the indefinite integral. $\displaystyle \int x \cos x \, dx$
Let $u=x$ and $v'=\cos x.$ Then $u'=1$ and $v=\sin x.$ Thus,
$$
\begin{array}{lll}
\displaystyle \int x \cos x \, dx&=\displaystyle \int uv' \,dx&\mbox{}\\
&=\displaystyle uv-\int u'v \, dx&\mbox{}\\
&=\displaystyle x\sin x -\int 1\cdot \sin x \, dx&\mbox{}\\
&=\displaystyle x\sin x -\int \sin x \, dx&\mbox{}\\
&=\displaystyle x\sin x +\cos x +C&\mbox{}\\
\end{array}
$$
Differentiation Check: $$ \begin{array}{lll} \displaystyle \frac{d}{dx}\left(x\sin x +\cos x +C\right) &\displaystyle=x'\sin x+x(\sin x)'-\sin x&\mbox{}\\ &\displaystyle=\sin x+x\cos x-\sin x&\mbox{}\\ &\displaystyle=x\cos x&\checkmark\mbox{}\\ \end{array} $$
Differentiation Check: $$ \begin{array}{lll} \displaystyle \frac{d}{dx}\left(x\sin x +\cos x +C\right) &\displaystyle=x'\sin x+x(\sin x)'-\sin x&\mbox{}\\ &\displaystyle=\sin x+x\cos x-\sin x&\mbox{}\\ &\displaystyle=x\cos x&\checkmark\mbox{}\\ \end{array} $$
Example
Find the indefinite integral. $\displaystyle \int x^2 e^x \, dx$
The $x^2$ in the integrand means we'll need to apply parts twice:
Round 1:
Let $u=x^2$ and $v'=e^x.$ Then $u'=2x$ and $v=e^x.$ Thus,
$$
\begin{array}{lll}
\displaystyle \int x^2 e^x \, dx&=\displaystyle \int uv' \,dx&\mbox{}\\
&=\displaystyle uv-\int u'v \, dx&\mbox{}\\
&=\displaystyle x^2e^x -\int 2x e^x \, dx&\mbox{}\\
&=\displaystyle x^2e^x -2\int x e^x \, dx&\mbox{}\\
\end{array}
$$
We see that $\displaystyle \int x e^x \, dx$ requires another round of parts.
Round 2: Let $u=x$ and $v'=e^x.$ Then $u'=1$ and $v=e^x.$ Thus, $$ \begin{array}{lll} \displaystyle \int x^2 e^x \, dx&=\displaystyle x^2e^x -2\int x e^x \, dx&\mbox{}\\ &=\displaystyle x^2e^x -2\left(\int uv' \,dx\right)&\mbox{}\\ &=\displaystyle x^2e^x -2\left(uv-\int u'v \,dx\right)&\mbox{}\\ &=\displaystyle x^2e^x -2\left(xe^x-\int e^x \,dx\right)&\mbox{}\\ &=\displaystyle x^2e^x -2\left(xe^x-e^x \right)+C&\mbox{}\\ &=\displaystyle x^2e^x -2xe^x+2e^x+C&\mbox{}\\ \end{array} $$
Differentiation Check: $$ \begin{array}{lll} \displaystyle \frac{d}{dx}\left(x^2e^x -2xe^x+2e^x+C\right) &\displaystyle= (x^2)'e^x+x^2(e^x)' -(2x)'e^x-2x(e^x)'+2e^x&\mbox{}\\ &\displaystyle=2xe^x+x^2 e^x -2e^x-2xe^x+2e^x&\mbox{}\\ &\displaystyle=x^2 e^x&\checkmark\mbox{}\\ \end{array} $$
Round 2: Let $u=x$ and $v'=e^x.$ Then $u'=1$ and $v=e^x.$ Thus, $$ \begin{array}{lll} \displaystyle \int x^2 e^x \, dx&=\displaystyle x^2e^x -2\int x e^x \, dx&\mbox{}\\ &=\displaystyle x^2e^x -2\left(\int uv' \,dx\right)&\mbox{}\\ &=\displaystyle x^2e^x -2\left(uv-\int u'v \,dx\right)&\mbox{}\\ &=\displaystyle x^2e^x -2\left(xe^x-\int e^x \,dx\right)&\mbox{}\\ &=\displaystyle x^2e^x -2\left(xe^x-e^x \right)+C&\mbox{}\\ &=\displaystyle x^2e^x -2xe^x+2e^x+C&\mbox{}\\ \end{array} $$
Differentiation Check: $$ \begin{array}{lll} \displaystyle \frac{d}{dx}\left(x^2e^x -2xe^x+2e^x+C\right) &\displaystyle= (x^2)'e^x+x^2(e^x)' -(2x)'e^x-2x(e^x)'+2e^x&\mbox{}\\ &\displaystyle=2xe^x+x^2 e^x -2e^x-2xe^x+2e^x&\mbox{}\\ &\displaystyle=x^2 e^x&\checkmark\mbox{}\\ \end{array} $$
Example
Find the indefinite integral. $\displaystyle \int \ln x \, dx$
This one is a little trickier. Sometimes you just have to play around with substitutions until you get something that works.
Here, we let $u=\ln x$ and $v'=1.$ Then $u'=\frac{1}{x}$ and $v=x.$ Thus, $$ \begin{array}{lll} \displaystyle \int \ln x \, dx&=\displaystyle \int \ln x \cdot 1 \,dx&\mbox{}\\ &=\displaystyle \int uv' \,dx&\mbox{}\\ &=\displaystyle uv-\int u'v \, dx&\mbox{}\\ &=\displaystyle (\ln x)\cdot x-\int \frac{1}{x} \cdot x \, dx&\mbox{}\\ &=\displaystyle x\ln x-\int 1 \, dx&\mbox{}\\ &=\displaystyle x\ln x-x+C&\mbox{}\\ \end{array} $$
Differentiation Check: $$ \begin{array}{lll} \displaystyle \frac{d}{dx}\left(x\ln x-x+C\right) &\displaystyle= x'\ln x+x(\ln x)'-1&\mbox{}\\ &\displaystyle=\ln x+x \cdot \frac{1}{x}-1&\mbox{}\\ &\displaystyle=\ln x+1-1&\mbox{}\\ &\displaystyle=\ln x &\checkmark\mbox{}\\ \end{array} $$
Here, we let $u=\ln x$ and $v'=1.$ Then $u'=\frac{1}{x}$ and $v=x.$ Thus, $$ \begin{array}{lll} \displaystyle \int \ln x \, dx&=\displaystyle \int \ln x \cdot 1 \,dx&\mbox{}\\ &=\displaystyle \int uv' \,dx&\mbox{}\\ &=\displaystyle uv-\int u'v \, dx&\mbox{}\\ &=\displaystyle (\ln x)\cdot x-\int \frac{1}{x} \cdot x \, dx&\mbox{}\\ &=\displaystyle x\ln x-\int 1 \, dx&\mbox{}\\ &=\displaystyle x\ln x-x+C&\mbox{}\\ \end{array} $$
Differentiation Check: $$ \begin{array}{lll} \displaystyle \frac{d}{dx}\left(x\ln x-x+C\right) &\displaystyle= x'\ln x+x(\ln x)'-1&\mbox{}\\ &\displaystyle=\ln x+x \cdot \frac{1}{x}-1&\mbox{}\\ &\displaystyle=\ln x+1-1&\mbox{}\\ &\displaystyle=\ln x &\checkmark\mbox{}\\ \end{array} $$
Example: The Boomerang
Find the indefinite integral. $\displaystyle \int e^x \cos x \, dx$
You'll soon see why I like to call this the "Boomerang."
Again we take this in two rounds.
Round 1: Let $u=\cos x$ and $v'=e^x.$ Then $u'=-\sin x$ and $v=e^x.$ Thus, $$ \begin{array}{lll} \displaystyle \int e^x \cos x \, dx&=\displaystyle \int v'u \,dx&\mbox{}\\ &=\displaystyle \int uv' \,dx&\mbox{}\\ &=\displaystyle uv-\int u'v \,dx&\mbox{}\\ &=\displaystyle (\cos x)e^x-\int (-\sin x)e^x \, dx&\mbox{}\\ &=\displaystyle e^x \cos x+\int e^x\sin x \, dx&\mbox{}\\ \end{array} $$ Round 2: We now deal with the integral $\displaystyle \int e^x \sin x \, dx:$
Let $u=\sin x$ and $v'=e^x.$ Then $u'=\cos x$ and $v=e^x.$ Thus, $$ \begin{array}{lll} \displaystyle \int e^x \cos x \, dx&=\displaystyle e^x \cos x+\int e^x\sin x \, dx&\mbox{}\\ &=\displaystyle e^x \cos x+\int uv' \,dx&\mbox{}\\ &=\displaystyle e^x \cos x+uv-\int u'v \,dx&\mbox{}\\ &=\displaystyle e^x \cos x+ (\sin x)e^x-\int (\cos x)e^x \,dx&\mbox{}\\ &=\displaystyle e^x \cos x+ e^x \sin x-\int e^x \cos x \,dx&\mbox{}\\ \end{array} $$ From the above, do you see where we go next? If so, great! If not, read on!
The above gives $$ \begin{array}{crl} &\displaystyle \int e^x \cos x \, dx&=\displaystyle e^x \cos x+ e^x \sin x-\int e^x \cos x \,dx\\ \implies&\displaystyle \int e^x \cos x \, dx+\int e^x \cos x \,dx&=\displaystyle e^x \cos x+ e^x \sin x-\int e^x \cos x \,dx+\int e^x \cos x \,dx\\ \implies&\displaystyle 2\int e^x \cos x \, dx&=\displaystyle e^x \cos x+ e^x \sin x\\ \implies&\displaystyle \int e^x \cos x \, dx&=\displaystyle \frac{1}{2}e^x (\cos x+ \sin x)\\ \end{array} $$ Of course, let's not forget the $C!$ $$ \begin{array}{crl} &\displaystyle \int e^x \cos x \, dx&=\displaystyle \frac{1}{2}e^x (\cos x+ \sin x)+C\\ \end{array} $$
Differentiation Check: $$ \begin{array}{lll} \displaystyle \frac{d}{dx}\left(\frac{1}{2}e^x (\cos x+ \sin x)+C\right) &\displaystyle=\left(\frac{1}{2}e^x\right)'(\cos x+ \sin x)+\frac{1}{2}e^x (\cos x+ \sin x)'&\mbox{}\\ &\displaystyle=\frac{1}{2}e^x(\cos x+ \sin x)+\frac{1}{2}e^x (-\sin x+ \cos x)&\mbox{}\\ &\displaystyle=\frac{1}{2}e^x\cos x+ \frac{1}{2}e^x\sin x-\frac{1}{2}e^x\sin x+ \frac{1}{2}e^x\cos x&\mbox{}\\ &\displaystyle=e^x\cos x&\checkmark\mbox{}\\ \end{array} $$
Again we take this in two rounds.
Round 1: Let $u=\cos x$ and $v'=e^x.$ Then $u'=-\sin x$ and $v=e^x.$ Thus, $$ \begin{array}{lll} \displaystyle \int e^x \cos x \, dx&=\displaystyle \int v'u \,dx&\mbox{}\\ &=\displaystyle \int uv' \,dx&\mbox{}\\ &=\displaystyle uv-\int u'v \,dx&\mbox{}\\ &=\displaystyle (\cos x)e^x-\int (-\sin x)e^x \, dx&\mbox{}\\ &=\displaystyle e^x \cos x+\int e^x\sin x \, dx&\mbox{}\\ \end{array} $$ Round 2: We now deal with the integral $\displaystyle \int e^x \sin x \, dx:$
Let $u=\sin x$ and $v'=e^x.$ Then $u'=\cos x$ and $v=e^x.$ Thus, $$ \begin{array}{lll} \displaystyle \int e^x \cos x \, dx&=\displaystyle e^x \cos x+\int e^x\sin x \, dx&\mbox{}\\ &=\displaystyle e^x \cos x+\int uv' \,dx&\mbox{}\\ &=\displaystyle e^x \cos x+uv-\int u'v \,dx&\mbox{}\\ &=\displaystyle e^x \cos x+ (\sin x)e^x-\int (\cos x)e^x \,dx&\mbox{}\\ &=\displaystyle e^x \cos x+ e^x \sin x-\int e^x \cos x \,dx&\mbox{}\\ \end{array} $$ From the above, do you see where we go next? If so, great! If not, read on!
The above gives $$ \begin{array}{crl} &\displaystyle \int e^x \cos x \, dx&=\displaystyle e^x \cos x+ e^x \sin x-\int e^x \cos x \,dx\\ \implies&\displaystyle \int e^x \cos x \, dx+\int e^x \cos x \,dx&=\displaystyle e^x \cos x+ e^x \sin x-\int e^x \cos x \,dx+\int e^x \cos x \,dx\\ \implies&\displaystyle 2\int e^x \cos x \, dx&=\displaystyle e^x \cos x+ e^x \sin x\\ \implies&\displaystyle \int e^x \cos x \, dx&=\displaystyle \frac{1}{2}e^x (\cos x+ \sin x)\\ \end{array} $$ Of course, let's not forget the $C!$ $$ \begin{array}{crl} &\displaystyle \int e^x \cos x \, dx&=\displaystyle \frac{1}{2}e^x (\cos x+ \sin x)+C\\ \end{array} $$
Differentiation Check: $$ \begin{array}{lll} \displaystyle \frac{d}{dx}\left(\frac{1}{2}e^x (\cos x+ \sin x)+C\right) &\displaystyle=\left(\frac{1}{2}e^x\right)'(\cos x+ \sin x)+\frac{1}{2}e^x (\cos x+ \sin x)'&\mbox{}\\ &\displaystyle=\frac{1}{2}e^x(\cos x+ \sin x)+\frac{1}{2}e^x (-\sin x+ \cos x)&\mbox{}\\ &\displaystyle=\frac{1}{2}e^x\cos x+ \frac{1}{2}e^x\sin x-\frac{1}{2}e^x\sin x+ \frac{1}{2}e^x\cos x&\mbox{}\\ &\displaystyle=e^x\cos x&\checkmark\mbox{}\\ \end{array} $$
Example
Use integration by parts to find a reduction formula for the indefinite integral $\displaystyle \int \cos^n x \, dx.$
We first write the integrand as $\cos^{n-1} x \cdot \cos x.$
Let $u=\cos^{n-1} x$ and $v'=\cos x.$ Then $u'=(n-1)\cos^{n-2} x (-\sin x)=-(n-1)\sin x \cos^{n-2} x$ and $v=\sin x.$ $$ \begin{array}{lll} \displaystyle \int \cos^n x \, dx&=\displaystyle \int \cos^{n-1} x \cdot \cos x \, dx&\mbox{}\\ &=\displaystyle \int uv'\, dx&\mbox{}\\ &=\displaystyle uv-\int u'v\, dx&\mbox{}\\ &=\displaystyle \cos^{n-1} x \sin x-\int (-(n-1)\sin x \cos^{n-2} x)\sin x\, dx&\mbox{}\\ &=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \sin^2 x \cos^{n-2} x\, dx&\mbox{}\\ &=\displaystyle \cos^{n-1} x \sin x+(n-1)\int (1-\cos^2 x) \cos^{n-2} x\, dx&\mbox{Pythagorean Identity!}\\ &=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x-\cos^{n} x \, dx&\mbox{}\\ &=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x \,dx- (n-1)\int \cos^{n} x \, dx&\mbox{}\\ \end{array} $$ We have another boomerang! $$ \begin{array}{crl} &\displaystyle \int \cos^n x \, dx&=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x \,dx- (n-1)\int \cos^{n} x \, dx\\ %\implies&\displaystyle \int \cos^n x \, dx+(n-1)\int \cos^{n} x \, dx&=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x \,dx- (n-1)\int \cos^{n} x \, dx+ (n-1)\int \cos^{n} x \, dx\\ \implies&\displaystyle n\int \cos^n x \, dx&=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x \,dx\\ \implies&\displaystyle \int \cos^n x \, dx&=\displaystyle \frac{1}{n}\cos^{n-1} x \sin x+\frac{n-1}{n}\int \cos^{n-2} x \,dx\\ \end{array} $$ Thus, the reduction formula is $$\displaystyle \int \cos^n x \, dx= \frac{1}{n}\cos^{n-1} x \sin x+\frac{n-1}{n}\int \cos^{n-2} x \,dx$$
Let $u=\cos^{n-1} x$ and $v'=\cos x.$ Then $u'=(n-1)\cos^{n-2} x (-\sin x)=-(n-1)\sin x \cos^{n-2} x$ and $v=\sin x.$ $$ \begin{array}{lll} \displaystyle \int \cos^n x \, dx&=\displaystyle \int \cos^{n-1} x \cdot \cos x \, dx&\mbox{}\\ &=\displaystyle \int uv'\, dx&\mbox{}\\ &=\displaystyle uv-\int u'v\, dx&\mbox{}\\ &=\displaystyle \cos^{n-1} x \sin x-\int (-(n-1)\sin x \cos^{n-2} x)\sin x\, dx&\mbox{}\\ &=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \sin^2 x \cos^{n-2} x\, dx&\mbox{}\\ &=\displaystyle \cos^{n-1} x \sin x+(n-1)\int (1-\cos^2 x) \cos^{n-2} x\, dx&\mbox{Pythagorean Identity!}\\ &=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x-\cos^{n} x \, dx&\mbox{}\\ &=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x \,dx- (n-1)\int \cos^{n} x \, dx&\mbox{}\\ \end{array} $$ We have another boomerang! $$ \begin{array}{crl} &\displaystyle \int \cos^n x \, dx&=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x \,dx- (n-1)\int \cos^{n} x \, dx\\ %\implies&\displaystyle \int \cos^n x \, dx+(n-1)\int \cos^{n} x \, dx&=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x \,dx- (n-1)\int \cos^{n} x \, dx+ (n-1)\int \cos^{n} x \, dx\\ \implies&\displaystyle n\int \cos^n x \, dx&=\displaystyle \cos^{n-1} x \sin x+(n-1)\int \cos^{n-2} x \,dx\\ \implies&\displaystyle \int \cos^n x \, dx&=\displaystyle \frac{1}{n}\cos^{n-1} x \sin x+\frac{n-1}{n}\int \cos^{n-2} x \,dx\\ \end{array} $$ Thus, the reduction formula is $$\displaystyle \int \cos^n x \, dx= \frac{1}{n}\cos^{n-1} x \sin x+\frac{n-1}{n}\int \cos^{n-2} x \,dx$$
Example
Find the definite integral. $\displaystyle \int_{0}^{4} xe^{-x} \, dx$
Lest we get too lost in the clouds, let's not forget one of the main reasons we love antiderivatives so much is that they
allow us to find areas under curves!
This is a garden variety parts!
Let $u=x$ and $v'=e^{-x}.$ Then $u'=1$ and $v=-e^{-x}.$ Thus, $$ \begin{array}{lll} \displaystyle \int_{0}^{4} xe^{-x} \, dx&=\displaystyle \int_{0}^{4} uv' \,dx&\mbox{}\\ &=\displaystyle [uv]_{0}^{4}-\int_{0}^{4} u'v \, dx&\mbox{}\\ &=\displaystyle [-xe^{-x}]_{0}^{4} -\int_{0}^{4} 1\cdot (-e^{-x}) \, dx&\mbox{}\\ &=\displaystyle [-xe^{-x}]_{0}^{4} +\int_{0}^{4} e^{-x} \, dx&\mbox{}\\ &=\displaystyle [-xe^{-x}]_{0}^{4} +[-e^{-x}]_{0}^{4}&\mbox{}\\ &=\displaystyle -4e^{-4} +[-e^{-4}-(-1)]&\mbox{}\\ &=\displaystyle -4e^{-4} -e^{-4}+1&\mbox{}\\ &=\displaystyle 1-5e^{-4}&\mbox{}\\ &\approx\displaystyle 0.9084218056 \mbox{ units}^2 &\mbox{}\\ \end{array} $$
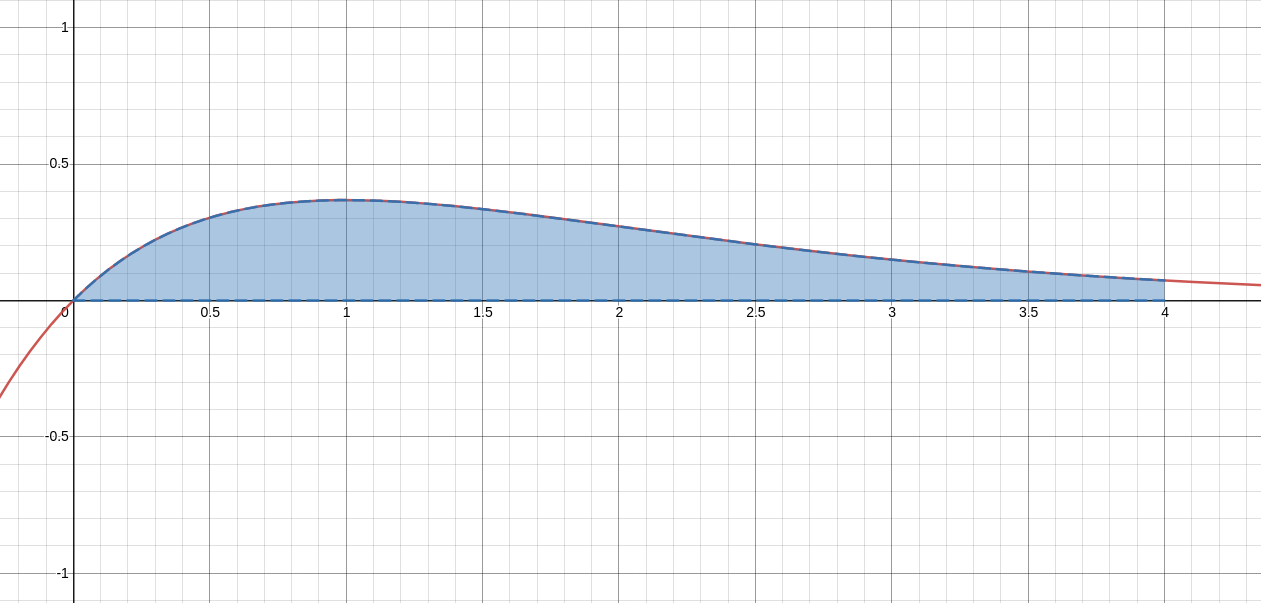
This is a garden variety parts!
Let $u=x$ and $v'=e^{-x}.$ Then $u'=1$ and $v=-e^{-x}.$ Thus, $$ \begin{array}{lll} \displaystyle \int_{0}^{4} xe^{-x} \, dx&=\displaystyle \int_{0}^{4} uv' \,dx&\mbox{}\\ &=\displaystyle [uv]_{0}^{4}-\int_{0}^{4} u'v \, dx&\mbox{}\\ &=\displaystyle [-xe^{-x}]_{0}^{4} -\int_{0}^{4} 1\cdot (-e^{-x}) \, dx&\mbox{}\\ &=\displaystyle [-xe^{-x}]_{0}^{4} +\int_{0}^{4} e^{-x} \, dx&\mbox{}\\ &=\displaystyle [-xe^{-x}]_{0}^{4} +[-e^{-x}]_{0}^{4}&\mbox{}\\ &=\displaystyle -4e^{-4} +[-e^{-4}-(-1)]&\mbox{}\\ &=\displaystyle -4e^{-4} -e^{-4}+1&\mbox{}\\ &=\displaystyle 1-5e^{-4}&\mbox{}\\ &\approx\displaystyle 0.9084218056 \mbox{ units}^2 &\mbox{}\\ \end{array} $$

Bonus Example
What is the volume of the Bundt cake that comes from rotating $y = \sin x$ around the $y$-axis from $x = 0$ to $x = \pi ?$
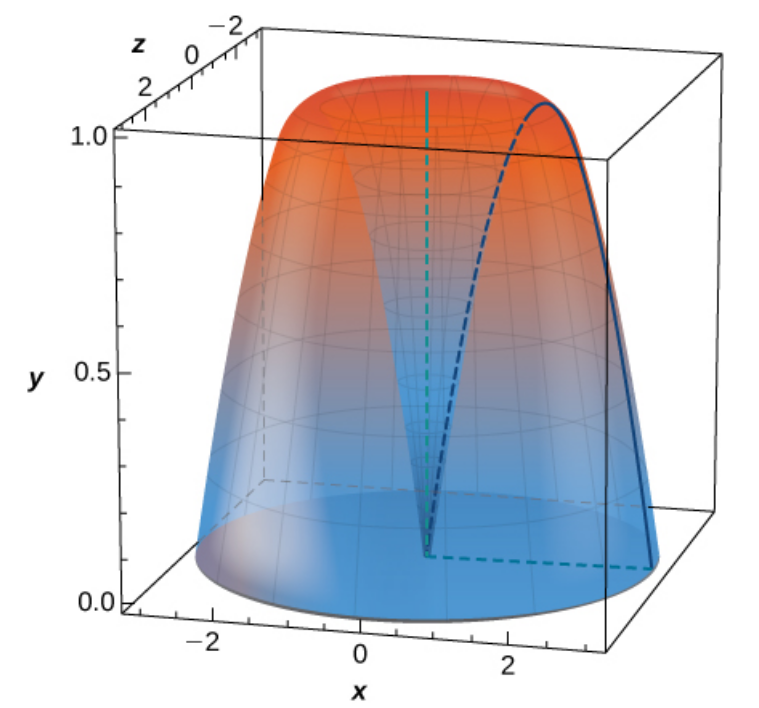
Here we dust off our formula for a volume of revolution by shells around the $x$-axis!
The volume of revolution is: $$ \begin{array}{lll} \displaystyle V &=\displaystyle \int_{a}^{b} 2 \pi x f(x) \,dx&\mbox{}\\ &=\displaystyle \int_{0}^{\pi} 2 \pi x \sin x \,dx&\mbox{}\\ &=\displaystyle 2 \pi \int_{0}^{\pi} x \sin x \,dx&\mbox{}\\ \end{array} $$ We're now faced with a situation which requires parts.
Let $u=x$ and $v'=\sin x.$ Then $u'=1$ and $v=-\cos x.$ Thus, $$ \begin{array}{lll} \displaystyle V&=\displaystyle 2 \pi \int_{0}^{\pi} x \sin x \,dx&\mbox{}\\ &=\displaystyle 2\pi\int_{0}^{\pi} uv' \, dx&\mbox{}\\ &=\displaystyle 2\pi \left([uv]_{0}^{\pi}-\int_{0}^{\pi} u'v \, dx\right)&\mbox{}\\ &=\displaystyle 2\pi \left([-x\cos x]_{0}^{\pi} -\int_{0}^{\pi} 1 \cdot (-\cos x) \, dx\right)&\mbox{}\\ &=\displaystyle 2\pi \left([-x\cos x]_{0}^{\pi} +\int_{0}^{\pi} \cos x \, dx\right)&\mbox{}\\ &=\displaystyle 2\pi \left([-x\cos x]_{0}^{\pi} +[\sin x]_{0}^{\pi}\right)&\mbox{}\\ &=\displaystyle 2\pi \left(-\pi\cos \pi-0 +\sin \pi -\sin 0\right)&\mbox{}\\ &=\displaystyle 2\pi \left(-\pi(-1)-0 +0 -0\right)&\mbox{}\\ &=\displaystyle 2\pi^2&\mbox{}\\ &\approx \displaystyle 19.7392088 \mbox{ units}^3&\mbox{}\\ \end{array} $$
The volume of revolution is: $$ \begin{array}{lll} \displaystyle V &=\displaystyle \int_{a}^{b} 2 \pi x f(x) \,dx&\mbox{}\\ &=\displaystyle \int_{0}^{\pi} 2 \pi x \sin x \,dx&\mbox{}\\ &=\displaystyle 2 \pi \int_{0}^{\pi} x \sin x \,dx&\mbox{}\\ \end{array} $$ We're now faced with a situation which requires parts.
Let $u=x$ and $v'=\sin x.$ Then $u'=1$ and $v=-\cos x.$ Thus, $$ \begin{array}{lll} \displaystyle V&=\displaystyle 2 \pi \int_{0}^{\pi} x \sin x \,dx&\mbox{}\\ &=\displaystyle 2\pi\int_{0}^{\pi} uv' \, dx&\mbox{}\\ &=\displaystyle 2\pi \left([uv]_{0}^{\pi}-\int_{0}^{\pi} u'v \, dx\right)&\mbox{}\\ &=\displaystyle 2\pi \left([-x\cos x]_{0}^{\pi} -\int_{0}^{\pi} 1 \cdot (-\cos x) \, dx\right)&\mbox{}\\ &=\displaystyle 2\pi \left([-x\cos x]_{0}^{\pi} +\int_{0}^{\pi} \cos x \, dx\right)&\mbox{}\\ &=\displaystyle 2\pi \left([-x\cos x]_{0}^{\pi} +[\sin x]_{0}^{\pi}\right)&\mbox{}\\ &=\displaystyle 2\pi \left(-\pi\cos \pi-0 +\sin \pi -\sin 0\right)&\mbox{}\\ &=\displaystyle 2\pi \left(-\pi(-1)-0 +0 -0\right)&\mbox{}\\ &=\displaystyle 2\pi^2&\mbox{}\\ &\approx \displaystyle 19.7392088 \mbox{ units}^3&\mbox{}\\ \end{array} $$
Super-Duper-Ultra-Mega Bonus Example: Radial Density
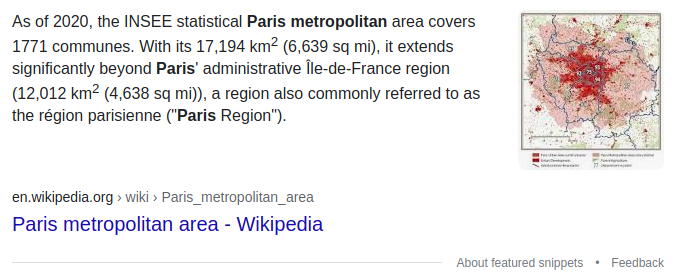
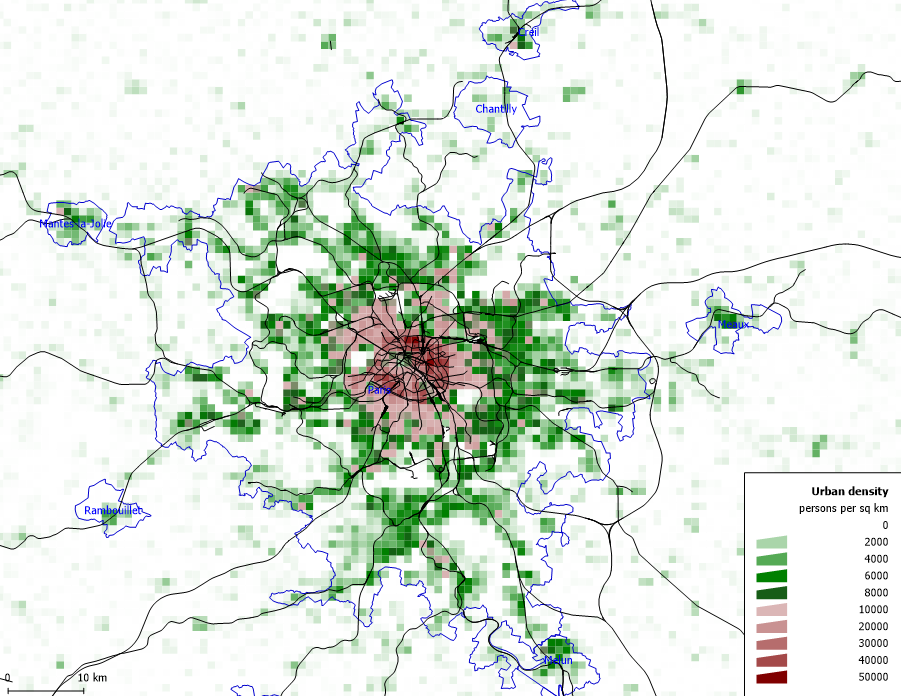
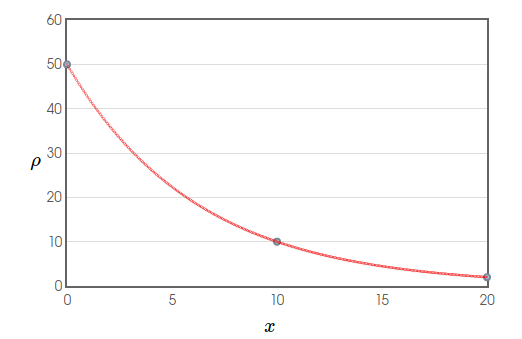
Consider the approximately radially-symmetric map of Paris Metropolitan Area on the left which gives the population density $\rho$ at each point over the area shown in persons per square kilometer $(2015).$ The function on the right $\rho(x)=50e^{-0.161x}$ approximates the population density (in thousands of people) at a distance $x$ kilometers from the city center.
$$
\begin{array}{lll}
\displaystyle \mbox{Number of People} &= \displaystyle \int_{0}^{r} 2 \pi x \rho(x)\, dx&\mbox{}\\
&=\displaystyle \int_{0}^{74} 2\pi x\left(50e^{-0.161x}\right) \,dx&\mbox{}\\
&=\displaystyle 100\pi\int_{0}^{74} xe^{-0.161x} \,dx&\mbox{}\\
&=\displaystyle 100\pi\int_{0}^{74} uv' \,dx \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mbox{ taking $u=x,$ $v'=e^{-0.161x},$ $u'=1,$ and $v=-\frac{1}{0.161}e^{-0.161x}$}&\\
&=\displaystyle 100\pi\left([uv]_{0}^{74}-\int_{0}^{74} u'v \,dx\right)&\mbox{}\\
&=\displaystyle 100\pi\left(\left[-\frac{x}{0.161}e^{-0.161x}\right]_{0}^{74}-\int_{0}^{74} 1\cdot\left(-\frac{1}{0.161} e^{-0.161x}\right) \,dx\right)&\mbox{}\\
&=\displaystyle 100\pi\left(\left[-\frac{x}{0.161}e^{-0.161x}\right]_{0}^{74}+\frac{1}{0.161}\int_{0}^{74} e^{-0.161x} \,dx\right)&\mbox{}\\
&=\displaystyle 100\pi\left(\left[-\frac{x}{0.161}e^{-0.161x}\right]_{0}^{74}+\frac{1}{0.161}\left[\left(-\frac{1}{0.161} e^{-0.161x}\right)\right]_{0}^{74} \right)&\mbox{}\\
&=\displaystyle 100\pi\left(\left[-\frac{x}{0.161}e^{-0.161x}\right]_{0}^{74}+\frac{1}{0.161}\left[-\frac{1}{0.161}e^{-0.161x}\right]_{0}^{74}\right)&\mbox{}\\
&=\displaystyle 100\pi\left(-\frac{74}{0.161}e^{-0.161\cdot 74}+\frac{1}{0.161}\left[-\frac{1}{0.161}e^{-0.161\cdot 74}+\frac{1}{0.161}e^{0}\right]\right)&\mbox{}\\
&=\displaystyle 100\pi\left(-\frac{74}{0.161}e^{-11.914}-\frac{1}{0.161^2}e^{-11.914}+\frac{1}{0.161^2}\right)&\mbox{}\\
&\approx \displaystyle 12118.8 \mbox{ thousand people}&\mbox{}\\
&= \displaystyle \mbox{12,118,800} \mbox{ people}&\mbox{}\\
\end{array}
$$