Today, we learn more about the hyperbolic equivalent of the trigonometric (circular) functions.
Definitions of Hyperbolic Sine and Cosine
$$\sinh x = \frac{e^x-e^{-x}}{2}$$ $$\cosh x = \frac{e^x+e^{-x}}{2}$$
The Graph of Hyperbolic Sine

The Graph of Hyperbolic Cosine
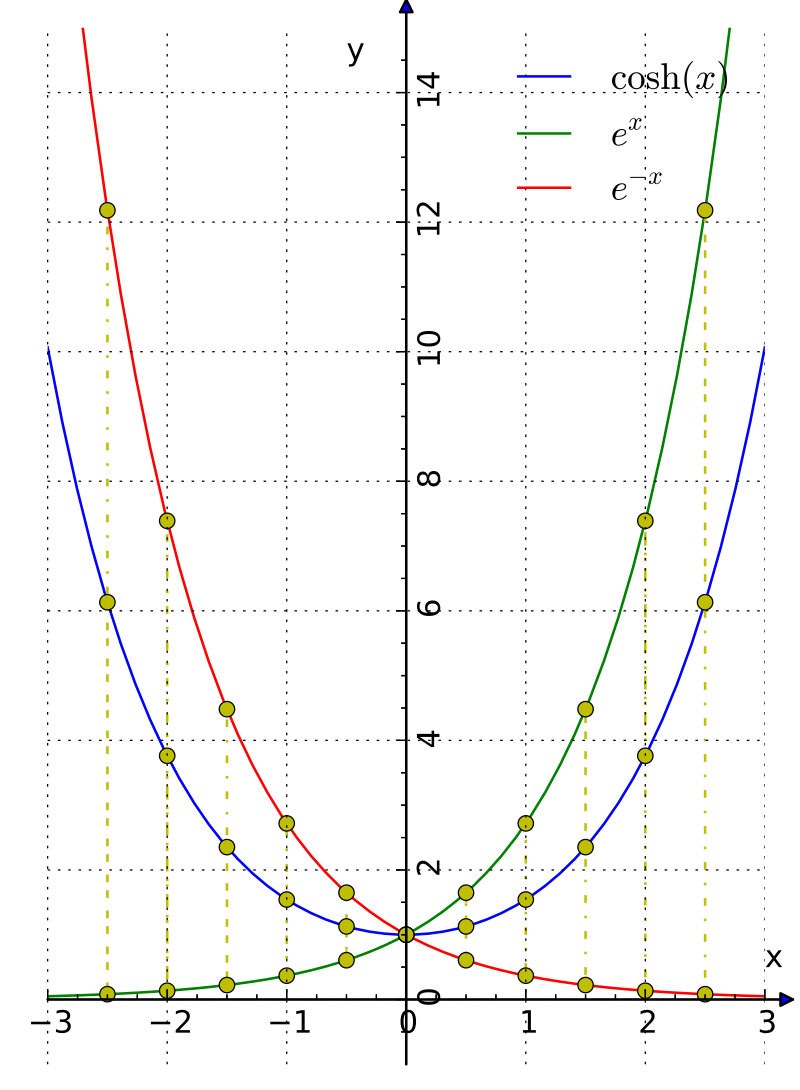
Relationship to Trig Functions

Definitions of the Other Four
$$\tanh x = \frac{\sinh x}{\cosh x}$$ $$\coth x = \frac{1}{\tanh x}$$ $$\mbox{sech } x = \frac{1}{\cosh x}$$ $$\mbox{csch } x = \frac{1}{\sinh x}$$
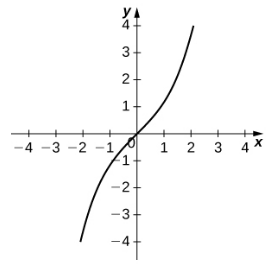 | 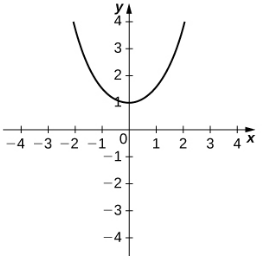 | 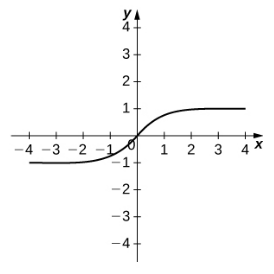 |
| $y=\sinh x$ | $y=\cosh x$ | $y=\tanh x$ |
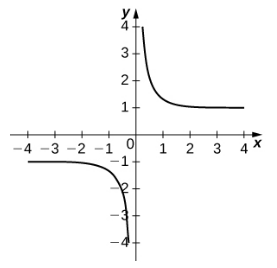 | 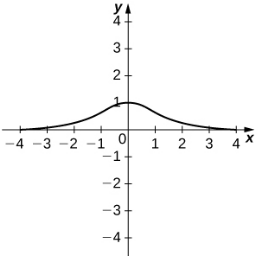 |  |
| $y=\coth x$ | $y=\mbox{sech } x$ | $y=\mbox{csch } x$ |
Some Hyperbolic Identities
1. $\cosh(-x) = \cosh x$
2. $\sinh(-x) = -\sinh x$
3. $\cosh^2 x - \sinh^2 x = 1$
4. $1 - \tanh^2 x = \mbox{sech}^2 x$
5. $\coth^2 x - 1 = \mbox{csch}^2 x$
6. $\sinh(x \pm y) = \sinh x \cosh y \pm \cosh x \sinh y$
7. $\cosh(x \pm y) = \cosh x \cosh y \pm \sinh x \sinh y$
8. $\cosh x + \sinh x = e^x$
9. $\cosh x - \sinh x = e^{-x}$
Derivatives of Hyperbolic Functions $$\frac{d}{dx}\sinh x=\cosh x$$ $$\frac{d}{dx}\cosh x=\sinh x$$ $$\frac{d}{dx}\tanh x=\mbox{sech}^2 x$$ $$\frac{d}{dx}\coth x=-\mbox{csch}^2 x$$ $$\frac{d}{dx}\mbox{sech } x= -\mbox{sech } x \tanh x$$ $$\frac{d}{dx}\mbox{csch } x=-\mbox{csch } x \coth x$$
Some Integrals of Hyperbolic Functions $$\int \cosh x \,dx = \sinh x +C$$ $$\int \sinh x \,dx =\cosh x +C$$ $$\int \mbox{sech}^2 x \,dx = \tanh x +C$$ $$\int \mbox{csch}^2 x \,dx =-\coth x +C$$ $$\int \mbox{sech } x \tanh x \,dx =-\mbox{sech } x +C$$ $$\int \mbox{csch } x \coth x \,dx = -\mbox{csch } x+C$$
Hyperbolic Cosine is a Catenary Curve
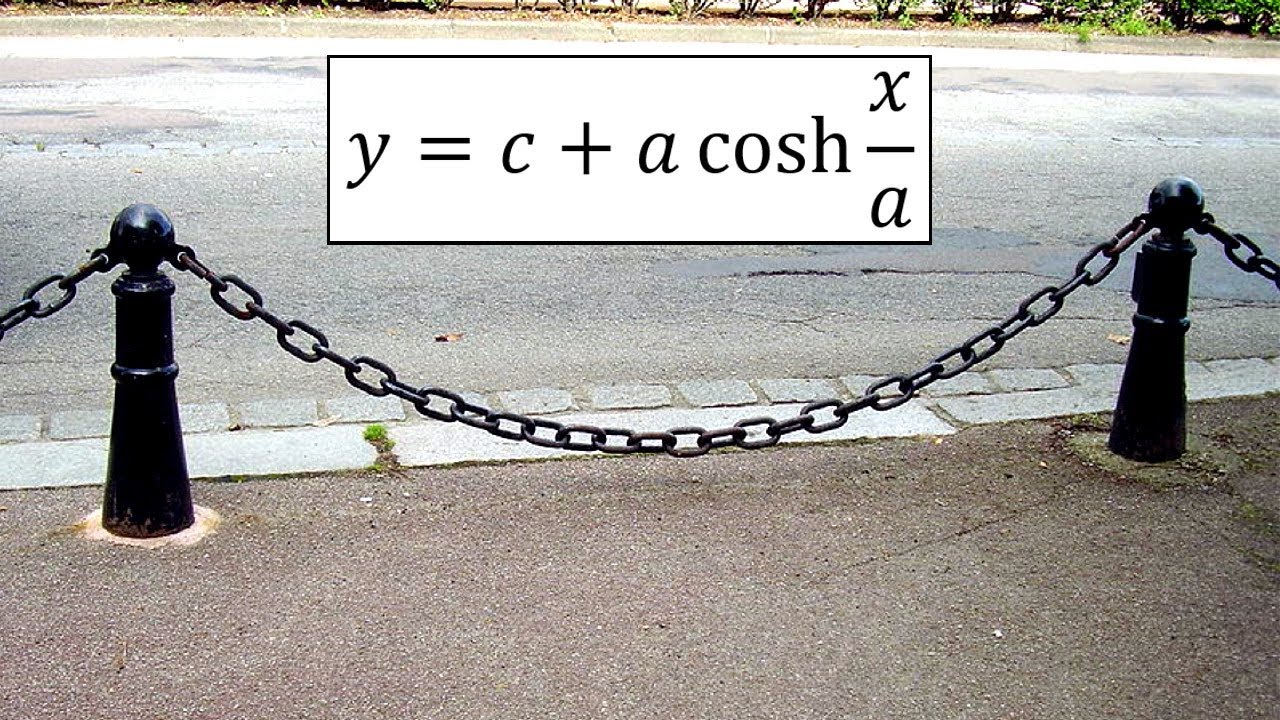
Hyperbolic Functions in Engineering and Architecture



Hyperbolic Functions in Engineering and Architecture
The Budapest Keleti Railway Station

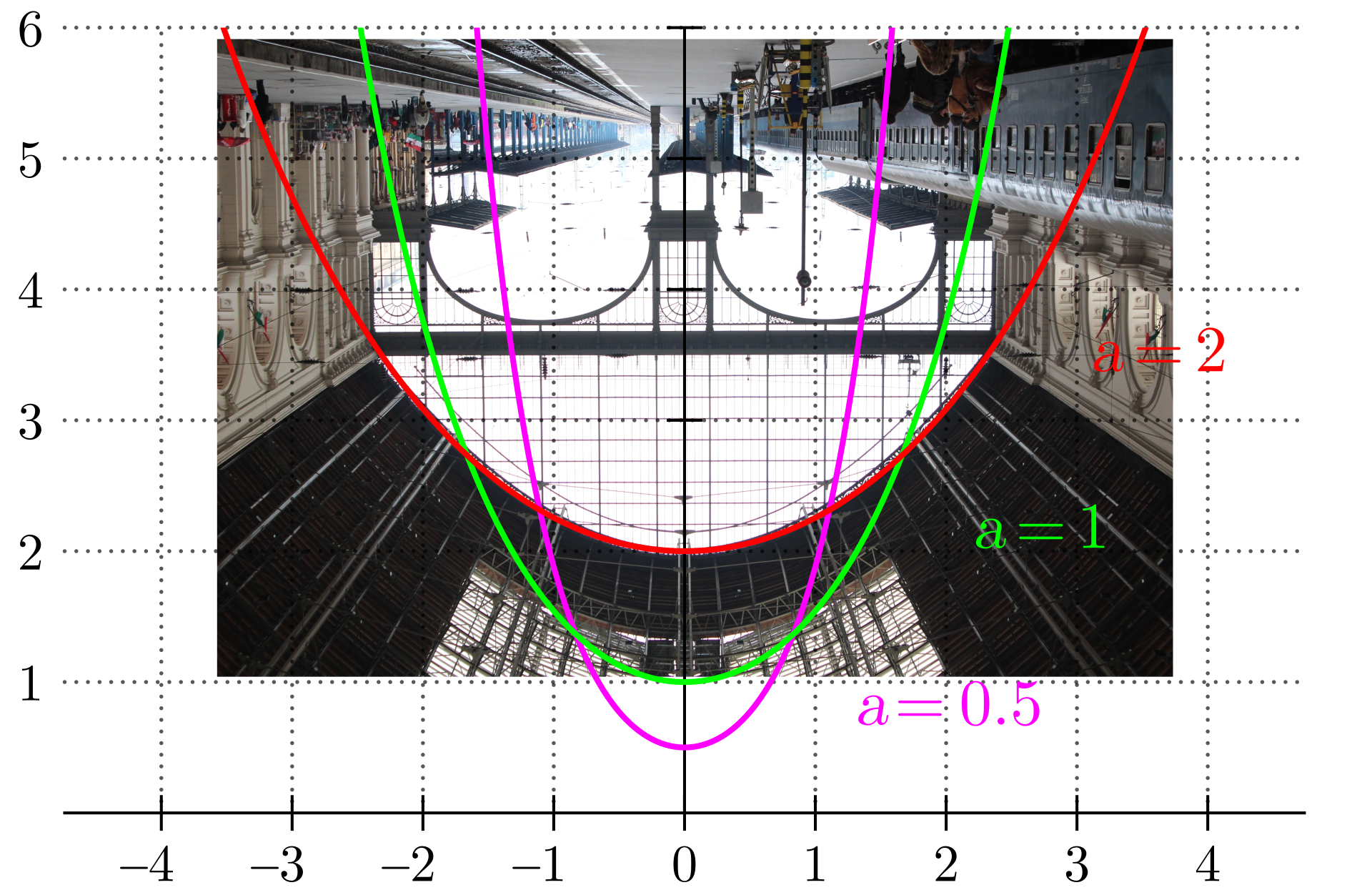
Hyperbolic Functions in Engineering and Architecture
The Conde McCullough Memorial Bridge


Example
Find the derivative of the given function: $y=\ln ( \mbox{sech}(x) + \tanh(x) )$
$$
\begin{array}{lll}
\displaystyle \frac{d}{dx}\ln ( \mbox{sech}(x) + \tanh(x) )&=\displaystyle \frac{1}{\mbox{sech}(x) + \tanh(x)}\frac{d}{dx}(\mbox{sech}(x) + \tanh(x))&\mbox{}\\
&=\displaystyle \frac{1}{\mbox{sech}(x) + \tanh(x)}(-\mbox{sech}(x) \tanh(x) + \mbox{sech}^2(x))&\mbox{}\\
&=\displaystyle \frac{\mbox{sech}^2(x)-\mbox{sech}(x) \tanh(x)}{\mbox{sech}(x) + \tanh(x)}&\mbox{}\\
&=\displaystyle \mbox{sech}(x) \frac{\mbox{sech}(x)-\tanh(x)}{\mbox{sech}(x) + \tanh(x)}&\mbox{}\\
\end{array}
$$
We could stop here, but identities are great for making expressions neater.
So, let's do some shenanigans!
$$
\begin{array}{lll}
\displaystyle \frac{d}{dx}\ln ( \mbox{sech}(x) + \tanh(x) )&=\displaystyle \mbox{sech}(x) \frac{\mbox{sech}(x)-\tanh(x)}{\mbox{sech}(x) + \tanh(x)}&\mbox{}\\
&=\displaystyle \mbox{sech}(x) \frac{\mbox{sech}(x)-\tanh(x)}{\mbox{sech}(x) + \tanh(x)}\cdot \frac{\cosh(x)}{\cosh(x)}&\mbox{}\\
&=\displaystyle \mbox{sech}(x) \frac{1-\sinh(x)}{1 + \sinh(x)}&\mbox{}\\
&=\displaystyle \frac{\mbox{sech}(x)-\tanh(x)}{1 + \sinh(x)}&\mbox{}\\
\end{array}
$$
Examples
Find the following integrals:
$\displaystyle \int \cosh^2 (x)\sinh(x) \, dx$
$$
\begin{array}{lll}
\displaystyle \int \cosh^2 (x)\sinh(x) \, dx&=\displaystyle \int u^2 du &\mbox{letting $u=\cosh(x)$ so that $du=\sinh(x)dx$}\\
&=\displaystyle \frac{1}{3}u^3+C&\mbox{}\\
&=\displaystyle \frac{1}{3}\cosh^3(x)+C &\mbox{}\\
\end{array}
$$
$\displaystyle \int \tanh x \, dx$
$$
\begin{array}{lll}
\displaystyle \int \tanh x \, dx&=\displaystyle \int \frac{\sinh x}{\cosh x} \, dx&\mbox{}\\
&=\displaystyle \int \frac{1}{u}\,du&\mbox{letting $u=\cosh(x)$ so that $du=\sinh(x)dx$}\\
&=\displaystyle \ln(u)+C &\mbox{}\\
&=\displaystyle \ln(\cosh x)+C &\mbox{}\\
\end{array}
$$
Inverse Hyperbolic Functions
Before looking at the graphs of the inverse hyperbolic functions, let's first take a look back at the graphs of the original hyperbolic functions.
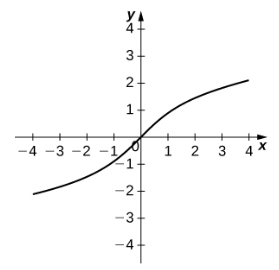 |  | 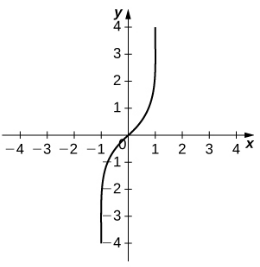 |
| $y=\sinh^{-1} x$ | $y=\cosh^{-1} x$ | $y=\tanh^{-1} x$ |
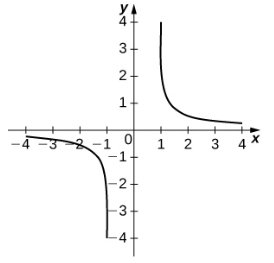 |  | 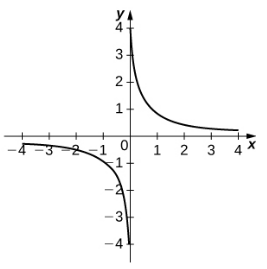 |
| $y=\coth^{-1} x$ | $y=\mbox{sech}^{-1} x$ | $y=\mbox{csch}^{-1} x$ |
Derivatives of Inverse Hyperbolic Functions
Example
Find $\displaystyle \frac{d}{dx} \sinh^{-1} x.$
Note: A nice trick for remembering these derivatives is to write $y=\sinh^{-1} x$ and then implicitly differentiate $x=\sinh(y)$ with respect to $x.$
Suppose $x=\sinh(y).$ Then
$$
\begin{array}{lcll}
&\displaystyle \frac{d}{dx}x &=\displaystyle \frac{d}{dx}\sinh(y)&\mbox{}\\
\implies &\displaystyle 1 &=\displaystyle \cosh(y)\frac{dy}{dx}&\mbox{}\\
\implies &\displaystyle \frac{dy}{dx} &=\displaystyle \frac{1}{\cosh(y)}&\mbox{}\\
\implies &\displaystyle \frac{dy}{dx} &=\displaystyle \frac{1}{\cosh(\sinh^{-1} x)}&\mbox{}\\
\end{array}
$$
But wait! There's more!
Let's recall the identity $\cosh^2(y)-\sinh^2(y)=1.$
Since this identity is valid for any input $y,$ let's suppose $y=\sinh^{-1} x.$ Then $$ \begin{array}{lcll} &\displaystyle \cosh^2(\sinh^{-1} x)-\sinh^2(\sinh^{-1} x) &=\displaystyle 1&\mbox{}\\ \implies &\displaystyle \cosh^2(\sinh^{-1} x)-x^2 &=\displaystyle 1&\mbox{}\\ \implies &\displaystyle \cosh^2(\sinh^{-1} x) &=\displaystyle 1+x^2&\mbox{}\\ \implies &\displaystyle \cosh(\sinh^{-1} x) &=\displaystyle \sqrt{1+x^2}&\mbox{take positive root since $\cosh x \gt 0$ for all $x$}\\ \end{array} $$ Thus, from our previous calculations, we have $$ \begin{array}{lcll} &\displaystyle \frac{dy}{dx} &=\displaystyle \frac{1}{\cosh(\sinh^{-1} x)}&\mbox{}\\ \implies &\displaystyle \frac{dy}{dx} &=\displaystyle \frac{1}{\sqrt{1+x^2}}&\mbox{}\\ \end{array} $$ In conclusion, we have shown that $\displaystyle \frac{d}{dx} \sinh^{-1} x=\frac{1}{\sqrt{1+x^2}}$
But wait! There's more!
Let's recall the identity $\cosh^2(y)-\sinh^2(y)=1.$
Since this identity is valid for any input $y,$ let's suppose $y=\sinh^{-1} x.$ Then $$ \begin{array}{lcll} &\displaystyle \cosh^2(\sinh^{-1} x)-\sinh^2(\sinh^{-1} x) &=\displaystyle 1&\mbox{}\\ \implies &\displaystyle \cosh^2(\sinh^{-1} x)-x^2 &=\displaystyle 1&\mbox{}\\ \implies &\displaystyle \cosh^2(\sinh^{-1} x) &=\displaystyle 1+x^2&\mbox{}\\ \implies &\displaystyle \cosh(\sinh^{-1} x) &=\displaystyle \sqrt{1+x^2}&\mbox{take positive root since $\cosh x \gt 0$ for all $x$}\\ \end{array} $$ Thus, from our previous calculations, we have $$ \begin{array}{lcll} &\displaystyle \frac{dy}{dx} &=\displaystyle \frac{1}{\cosh(\sinh^{-1} x)}&\mbox{}\\ \implies &\displaystyle \frac{dy}{dx} &=\displaystyle \frac{1}{\sqrt{1+x^2}}&\mbox{}\\ \end{array} $$ In conclusion, we have shown that $\displaystyle \frac{d}{dx} \sinh^{-1} x=\frac{1}{\sqrt{1+x^2}}$
Derivatives of Inverse Hyperbolic Functions $$\frac{d}{dx} \sinh^{-1} x=\frac{1}{\sqrt{1+x^2}}$$ $$\frac{d}{dx} \cosh^{-1} x=\frac{1}{\sqrt{x^2-1}}$$ $$\frac{d}{dx} \tanh^{-1} x=\frac{1}{1-x^2}$$ $$\frac{d}{dx} \coth^{-1} x=\frac{1}{1-x^2}$$ $$\frac{d}{dx} \mbox{sech}^{-1} x=-\frac{1}{x\sqrt{1-x^2}}$$ $$\frac{d}{dx} \mbox{csch}^{-1} x=-\frac{1}{|x|\sqrt{1+x^2}}$$
Some Sweet Integrals $$\int \frac{1}{\sqrt{1+x^2}} \, dx = \sinh^{-1} x+C$$ $$\int \frac{1}{\sqrt{x^2-1}} \, dx = \cosh^{-1} x+C$$ $$\int \frac{1}{1-x^2} \, dx = \tanh^{-1} x+C, \mbox{ if } |x| \lt 1$$ $$\int \frac{1}{1-x^2} \, dx = \coth^{-1} x+C, \mbox{ if } |x| \gt 1$$ $$\int\frac{1}{x\sqrt{1-x^2}} \, dx = -\mbox{sech}^{-1} |x|+C$$ $$\int \frac{1}{|x|\sqrt{1+x^2}} \, dx = -\mbox{csch}^{-1} |x|+C$$
Examples
Find the following integrals:
$\displaystyle \int \frac{dx}{4-x^2}$ if $|x| \lt 2.$
$$
\begin{array}{lll}
\displaystyle \int \frac{dx}{4-x^2}&=\displaystyle \int \frac{1}{4}\frac{dx}{1-\frac{x^2}{4}}&\mbox{}\\
&=\displaystyle \displaystyle \frac{1}{4} \int \frac{dx}{1-\left(\frac{x}{2}\right)^2}&\mbox{}\\
&=\displaystyle \displaystyle \frac{1}{4} \int \frac{2\,du}{1-u^2}&\mbox{letting $u=\frac{x}{2}$ so that $dx=2\,du$}\\
&=\displaystyle \displaystyle \frac{1}{2} \int \frac{\,du}{1-u^2}&\mbox{}\\
&=\displaystyle \displaystyle \frac{1}{2} \tanh^{-1} u + C&\mbox{since $|x| \lt 2,$ we have $|u|=\left|\frac{x}{2}\right|\lt 1$}\\
&=\displaystyle \displaystyle \frac{1}{2} \tanh^{-1} \left(\frac{x}{2}\right) + C&\mbox{}\\
\end{array}
$$
$\displaystyle \int \frac{e^x}{\sqrt{e^{2x}-1}}\, dx$
Let $u=e^x.$ Then $du=e^x\,dx$ so that
$$
\begin{array}{lll}
\displaystyle \int \frac{e^x}{\sqrt{e^{2x}-1}}\, dx&=\displaystyle \int \frac{du}{\sqrt{u^2-1}}&\mbox{}\\
&=\displaystyle \cosh^{-1}(u)+C&\mbox{}\\
&=\displaystyle \cosh^{-1}(e^x)+C&\mbox{}\\
\end{array}
$$