Today, we apply our knowledge of integration to some applications in physics and beyond.
Physical Applications Part 1: Density
Physical Applications: Mass from Density
Recall: $$\mbox{Density}=\frac{\mbox{Mass}}{\mbox{Volume}}$$
Using typical variable names of $m$ for mass, $V$ for volume, and $\rho$ for density, we have $$\rho=\frac{m}{V}.$$
Physical Applications: Mass from Density
If we know an object's density and volume, we can recover its mass $$m=\rho V.$$
A Broader Notion of Density $$\mbox{Density}=\frac{\mbox{Amount of Stuff}}{\mbox{Amount of Space}}$$
Here $\mbox{Amount of Space}$ could refer to a volume, and area or a length.
$\mbox{Amount of Stuff}$ could refer to mass, cars, people, anything whose density could vary over space.
A Broader Notion of Density
We may recover the $\mbox{Amount of Stuff}$ from $\mbox{Amount of Space}$ and $\mbox{Density}$ as $$\mbox{Amount of Stuff}=\mbox{Density}\cdot \mbox{Amount of Space}$$
Physical Applications: Mass from Density
Problem: The density of an object is not always the same throughout the object.
In an object, some regions of space might have more "stuff," i.e., mass, than other regions.
A Broader Notion of Density: Examples
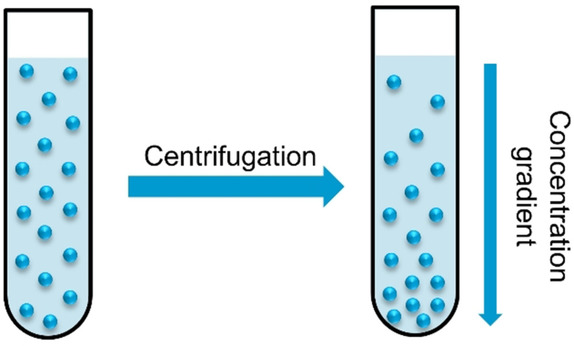 | Linear Density: The amount of a substance in solution is variable under centrifugation. |
A Broader Notion of Density: Examples
 | Linear Density: The number of cars per mile is generally non-uniform. |
A Broader Notion of Density: Examples
 | Area Density: The amount of people per square mile is non-uniform. |
A Broader Notion of Density: Examples
 | Volumetric Density: The amount of soil in a given region of a soil sample is generally non-uniform. |
Fact: The techniques of calculus enable us to deal with cases of non-uniform density.
Today we shall cover two cases:
- linear density
- radially symmetric density over a circular area.
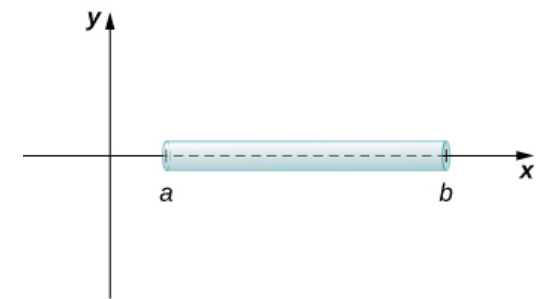
Linear Density
Consider a thin rod of variable density $\rho(x)$ at the point $x.$
Linear Density
The amount of "stuff" between $x_{i-1}$ and $x_i$ is approximately $$\rho(x_i^*)\Delta x.$$
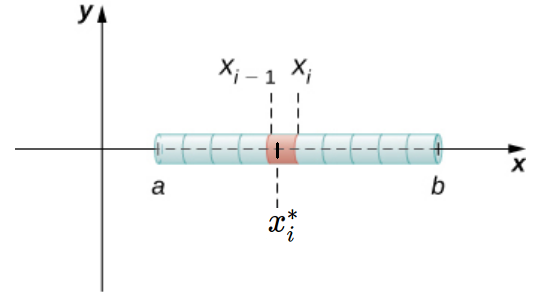
Linear Density
The total amount $A$ of "stuff" between $a$ and $b$ is then approximately $$\sum_{i=1}^{n}\rho(x_i^*)\Delta x.$$

Linear Density
| $$\lim_{n \rightarrow \infty} \sum_{i=1}^{n} \rho(x_i^*) \Delta x$$ | ||
| $\displaystyle \sum_{i=1}^{n} \rho(x_i^*)\Delta x$ | $\longrightarrow$ | $\displaystyle \int_{a}^{b} \rho(x) \,dx$ |
 | $\longrightarrow$ |  |
Linear Density
Given a thin rod oriented along the $x$-axis over the interval $[a,b],$ let $\rho(x)$ denote a linear density function giving the density of the rod at a point $x$ in the interval. Then the mass (or amount of "stuff": people, cars, etc.) of the rod is given by $$\displaystyle \int_{a}^{b} \rho(x) \,dx$$

Example: Linear Density.
Find the mass of a wire that is $2$ feet long (starting at $x = 0$) and has a density function of $\rho(x) = x^2 + 2x$ lb/ft.

$$
\begin{array}{lll}
\displaystyle \mbox{Mass} &=\displaystyle \int_{a}^{b} \rho(x) \,dx&\mbox{}\\
&=\displaystyle \int_{0}^{2} x^2 + 2x \,dx&\mbox{}\\
&=\displaystyle \left[\frac{1}{3}x^3+x^2\right]_{0}^{2}&\mbox{}\\
&=\displaystyle \frac{1}{3}2^3+2^2&\mbox{}\\
&=\displaystyle \frac{8}{3}+4&\mbox{}\\
&=\displaystyle \frac{20}{3}&\mbox{}\\
&\approx \displaystyle 6.67 \mbox{ lb}&\mbox{}\\
\end{array}
$$
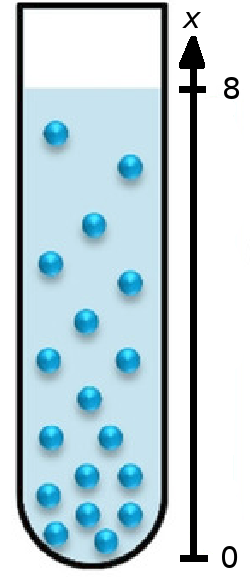
Example: Linear Density.
The density $\rho$ in g/cm of a solute under centrifugation at a distance $x$ from the bottom of a test tube is given by the function $\rho(x)=0.5e^{-0.2x}$ Find the mass of the solute in the tube.
$$
\begin{array}{lll}
\displaystyle \mbox{Mass} &=\displaystyle \int_{a}^{b} \rho(x) \,dx&\mbox{}\\
&=\displaystyle \int_{0}^{8} 0.5e^{-0.2x} \,dx&\mbox{}\\
&=\displaystyle \left[-2.5e^{-0.2x}\right]_{0}^{8}&\mbox{}\\
&=\displaystyle \left[-2.5e^{-0.2\cdot 8}\right]-\left[-2.5e^{-0.2\cdot 0}\right]&\mbox{}\\
&=\displaystyle -2.5e^{-1.6}+2.5 &\mbox{}\\
&=\displaystyle 2.5-2.5e^{-1.6} &\mbox{}\\
&=\displaystyle 2.5(1-e^{-1.6}) &\mbox{}\\
&\approx \displaystyle 1.995258705 \mbox{ grams of solute}&\mbox{}\\
\end{array}
$$
Bonus Example: Linear Density. Coming into Portland on Interstate 5 North during rush hour, the traffic density $\rho$ (in cars/mile) from $10$ miles out of town ($x=0$ mi) to the center of the city ($x=10$ mi) is given by $$\rho(x)=200e^{0.1386x}$$ Find the total amount of cars on this stretch of road during rush hour.

$$
\begin{array}{lll}
\displaystyle \mbox{Number of Cars} &= \displaystyle \int_{a}^{b} \rho(x) \,dx&\mbox{}\\
&=\displaystyle \int_{0}^{10} 200e^{0.1386x} \,dx&\mbox{}\\
&=\displaystyle \left[\frac{200}{0.1386}e^{0.1386x}\right]_{0}^{10} &\mbox{}\\
&=\displaystyle \frac{200}{0.1386}\left[e^{0.1386x}\right]_{0}^{10} &\mbox{}\\
&=\displaystyle \frac{200}{0.1386}\left[e^{0.1386\cdot 10}-e^{0.1386\cdot 0}\right] &\mbox{}\\
&=\displaystyle \frac{200}{0.1386}\left[e^{1.386}-e^{0}\right] &\mbox{}\\
&=\displaystyle \frac{200}{0.1386}\left[e^{1.386}-1\right] &\mbox{}\\
&\approx\displaystyle 4327.305525 &\mbox{}\\
&\approx \displaystyle 4327 \mbox{ cars}&\mbox{}\\
\end{array}
$$
Radial Density
Suppose a disk has a density of $\rho$ at a radial distance of $x$ units away from the center.
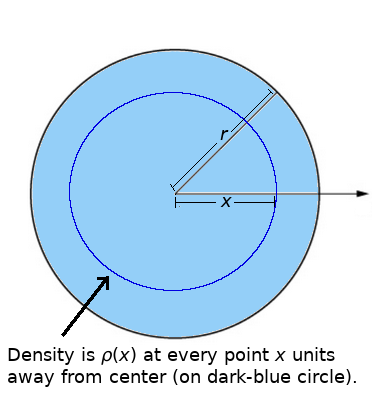
Note: In this case $\rho$ gives the amount of stuff per unit area.
Radial Density
Consider a thin washer-shaped region of our disk with width $\Delta x$ containing the point $x_i^*.$

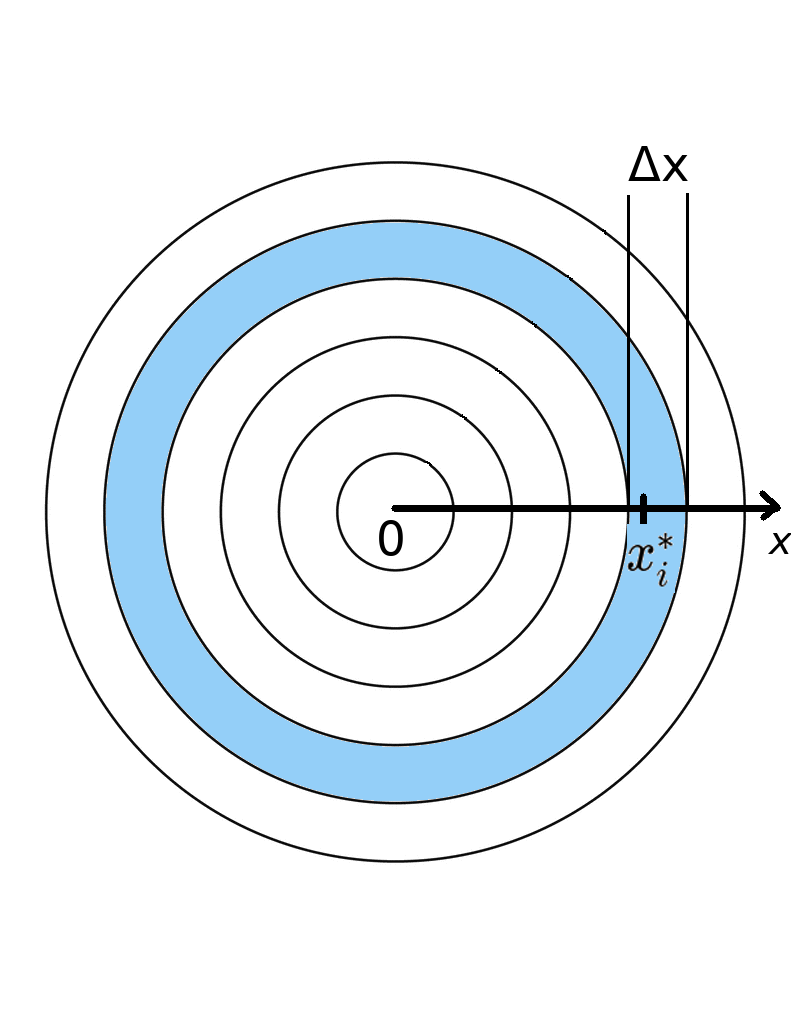
Radial Density
The area of the washer-shaped region is approximately $$2 \pi x_i^* \Delta x.$$

Radial Density
If $\Delta x$ is small, $\rho$ is approximately constant over the washer-shaped region. Then amount of stuff in the washer-shaped region is approximately $$2 \pi x_i^* \rho(x_{i}^*)\Delta x.$$

Radial Density
Adding up all the concentric washer-shaped regions, we get an approximation for the total amount of stuff as $$\sum_{i=1}^{n} 2 \pi x_i^* \rho(x_{i}^*)\Delta x.$$
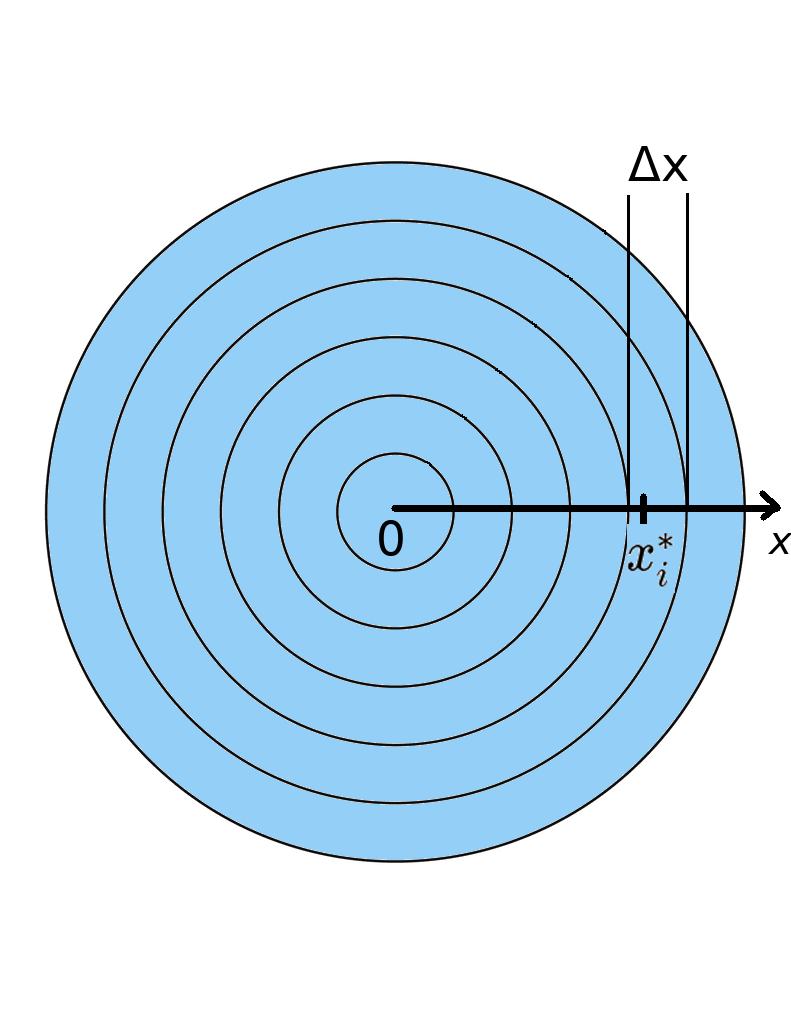
Radial Density
In the limit, the total amount of stuff (mass, cars, people, etc.) in the disk from $0$ to $r$ is given by $$\int_{0}^{r} 2 \pi x \rho(x)\, dx.$$

Example: Radial Density
Find the mass of a hockey puck having a standard radius of $3$ inches and a radial density function $\rho(x) = 2x + 2$ in grams per square inch.

$$
\begin{array}{lll}
\displaystyle \mbox{Mass} &= \displaystyle \int_{0}^{r} 2 \pi x \rho(x)\, dx&\mbox{}\\
&=\displaystyle \int_{0}^{3} 2\pi x(2x+2) \,dx&\mbox{}\\
&=\displaystyle 2\pi \int_{0}^{3} 2x^2+2x \,dx&\mbox{}\\
&=\displaystyle 2\pi \left[\frac{2}{3}x^3+x^2\right]_{0}^{3}&\mbox{}\\
&=\displaystyle 2\pi \left[\frac{2}{3}3^3+3^2\right]&\mbox{}\\
&=\displaystyle 2\pi \left[2\cdot 9+9\right]&\mbox{}\\
&=\displaystyle 2\pi\cdot 27&\mbox{}\\
&=\displaystyle 54\pi&\mbox{}\\
&\approx \displaystyle 169.6460033 \mbox{ grams}&\mbox{}\\
&\approx \displaystyle 5.9840866653026 \mbox{ oz}&\mbox{}\\
\end{array}
$$
Bonus Example: Radial Density
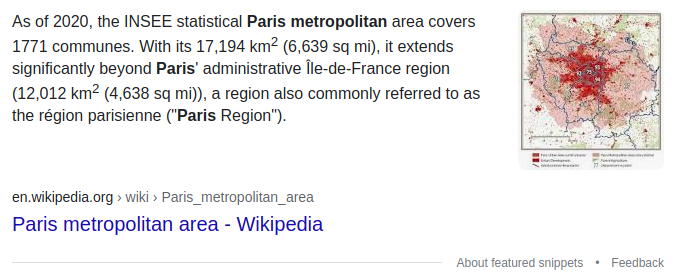
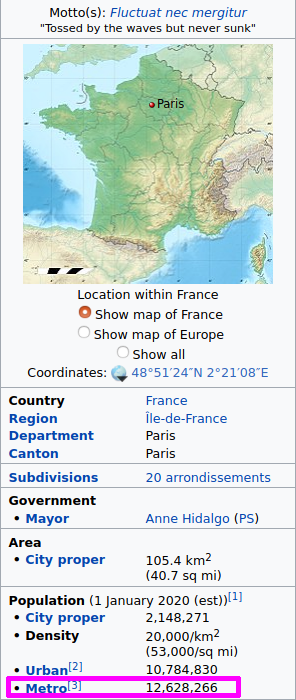
Consider the approximately radially-symmetric map of Paris Metropolitan Area on the left which gives the population density $\rho$ at each point over the area shown in persons per square kilometer $(2015).$ The function on the right $\rho(x)=50e^{-0.161x}$ approximates the population density (in thousands of people) at a distance $x$ kilometers from the city center.
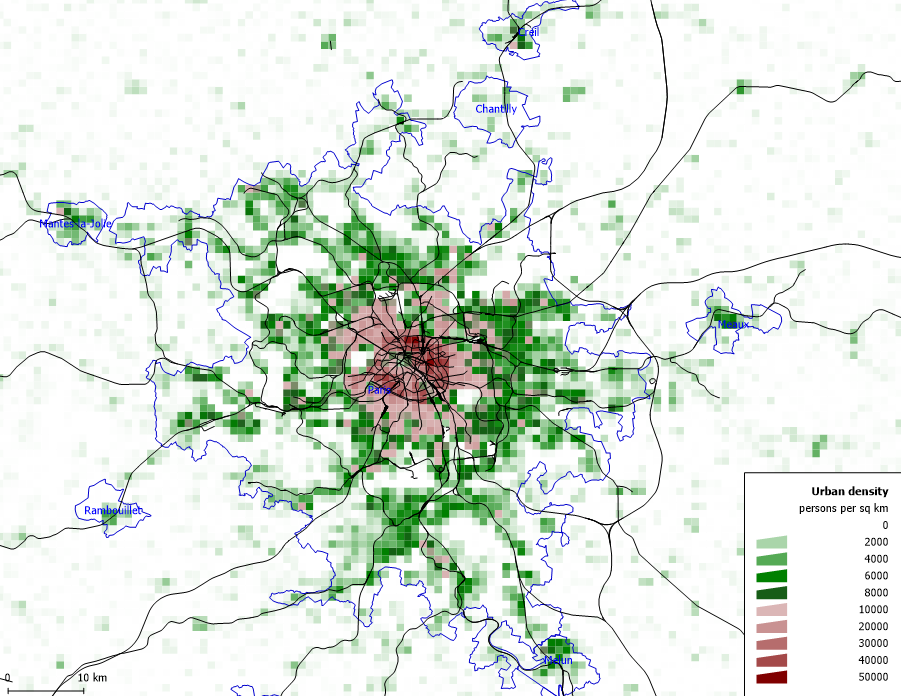
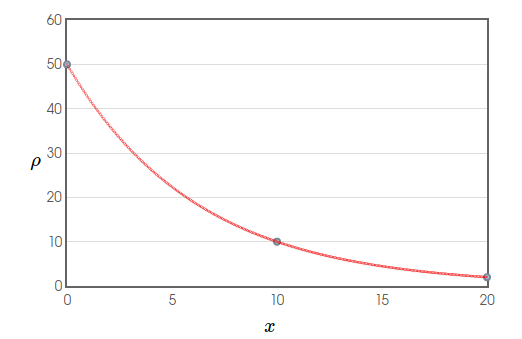
$$
\begin{array}{lll}
\displaystyle \mbox{Number of People} &= \displaystyle \int_{0}^{r} 2 \pi x \rho(x)\, dx&\mbox{}\\
&=\displaystyle \int_{0}^{74} 2\pi x\left(50e^{-0.161x}\right) \,dx&\mbox{}\\
&=\displaystyle 100\pi\int_{0}^{74} xe^{-0.161x} \,dx&\mbox{}\\
&\displaystyle \vdots&\mbox{}\\
&\displaystyle \mbox{using techniques from Chapter 3}&\mbox{}\\
&\displaystyle \vdots&\mbox{}\\
&\approx \displaystyle 12118.8 \mbox{ thousand people}&\mbox{}\\
&= \displaystyle \mbox{12,118,800} \mbox{ people}&\mbox{}\\
\end{array}
$$
Bonus Example: Radial Density
Physical Applications Part 2: Work
Work
Physicists define the amount of work performed on an object to be the product of the force $F$ exerted on the object and the the distance $d$ over which the force was exerted.
That is, $W=F \cdot d.$
Example
How much work is done when a person lifts a $50$-lb box of comics onto a truck that is $3$ feet off the ground?

$$
W=F\cdot d=50 \cdot 3=150 \mbox{ ft $\cdot$ lb}
$$
Units of Force: The newton $\mbox{N}.$
One newton is the amount of force required to accelerate a $1$-kg mass to $1$ meter per second over a one-second time interval.

The newton is expressed in base units as $\displaystyle \mbox{kg}\frac{\mbox{m}}{\mbox{s}^2}.$
Also note that $1 \mbox{ lb}=4.45 \mbox{ N}.$
Units of Work: The $\mbox{N$\cdot$m},$ or joule $(\mbox{J})$.
One joule, or newton-meter, is the amount of work done by applying a force of $1$ newton over $1$ meter.
Example
Find the amount of work done in joules when a person lifts a $50$-lb box of comics onto a truck that is $3$ ft off the ground?

Note that $1 \mbox{ lb}=4.45 \mbox{ N}$ and $1 \mbox{ m}=3.28 \mbox{ ft}.$
$$
150 \mbox{ ft $\cdot$ lb} \cdot \frac{4.45 \mbox{ N}}{1 \mbox{ lb}} \cdot \frac{1 \mbox{ m}}{3.28 \mbox{ ft}}\approx 203.51 \mbox{ N $\cdot$ m}=203.51 \mbox{ J}
$$
Fun Fact: The amount of energy required to do this could power a $60 \mbox{ W}$ light bulb for about $3.4$ seconds.
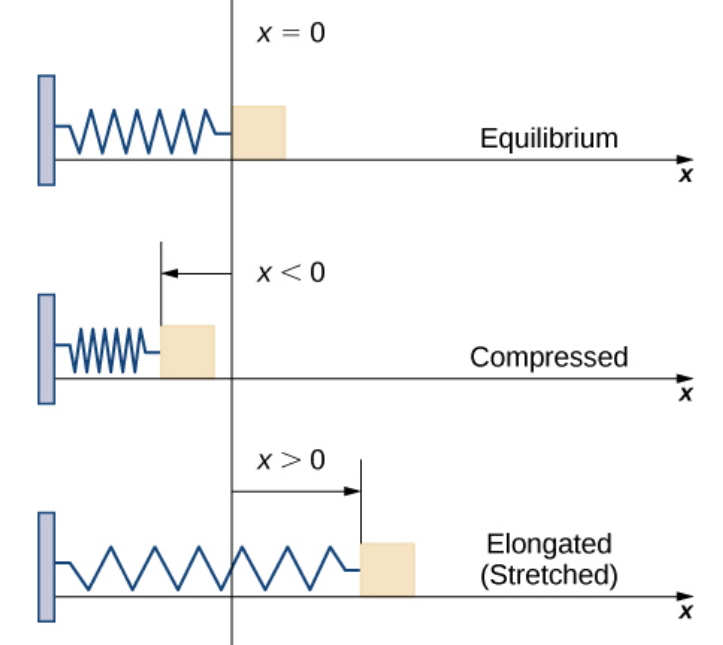
Variable Force
Some forces are variable to move an object. For example to stretch or compress a spring requires more effort the farther you push or pull.
When launching satellites the force of gravity changes depending on how far the satellite is away from a planetary body.
If a variable force $F(x)$ moves an object in a positive direction along the $x$-axis from point $a$ to point $b,$ then the work done on the object is $$W=\int_{a}^{b} F(x) dx.$$
Variable Force
Some forces are variable to move an object. For example to stretch or compress a spring requires more effort the farther you push or pull. The law which quantifies this is Hooke's Law:
Hooke's Law: To stretch or compress a spring by $x$ units requires $F(x)=kx$ units of force where $k$ is a constant which is particular to the spring.
Example: Variable Force, Springs
A spring has a natural length of $10$ cm. It takes $2$ newtons of force to keep a spring stretched to $15$ cm. How much work would it take to stretch the spring from $15 \mbox{ cm}$ to $20 \mbox{ cm}?$
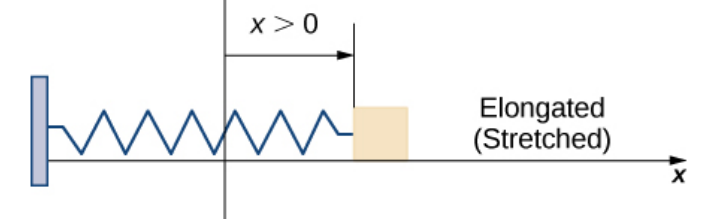
We will use the information provided to determine the spring constant $k$ in Hooke's Law: $F(x)=kx.$
It takes $2$ newtons of force to keep the spring stretched at $15 \mbox{ cm}.$ That is, $F(5)=k\cdot 5=2.$
Thus, $\displaystyle k=\frac{2}{5}$ so that $\displaystyle F(x)=\frac{2}{5}x.$
From this we can now find the work to stretch the spring from $15 \mbox{ cm}$ to $20 \mbox{ cm}:$ $$ \begin{array}{lll} \displaystyle W&=\displaystyle \int_{5}^{10} F(x) \,dx &\mbox{}\\ &=\displaystyle \int_{5}^{10} \frac{2}{5}x \,dx &\mbox{}\\ &=\displaystyle \frac{2}{5}\int_{5}^{10}x \,dx &\mbox{}\\ &=\displaystyle \frac{2}{5}\left[\frac{1}{2}x^2\right]_{5}^{10}&\mbox{}\\ &=\displaystyle \frac{2}{5}\cdot \frac{1}{2}\left[x^2\right]_{5}^{10}&\mbox{}\\ &=\displaystyle \frac{1}{5}\left[10^2-5^2\right]&\mbox{}\\ &=\displaystyle \frac{1}{5}\cdot 75&\mbox{}\\ &= \displaystyle 15 \mbox{ J}&\mbox{}\\ \end{array} $$ Thus, it takes about $15 \mbox{ J}$ of work to stretch the spring from $15 \mbox{ cm}$ to $20 \mbox{ cm}?$
Fun Fact: The amount of energy required to do this could power a $60 \mbox{ W}$ light bulb for about $0.25$ seconds.
It takes $2$ newtons of force to keep the spring stretched at $15 \mbox{ cm}.$ That is, $F(5)=k\cdot 5=2.$
Thus, $\displaystyle k=\frac{2}{5}$ so that $\displaystyle F(x)=\frac{2}{5}x.$
From this we can now find the work to stretch the spring from $15 \mbox{ cm}$ to $20 \mbox{ cm}:$ $$ \begin{array}{lll} \displaystyle W&=\displaystyle \int_{5}^{10} F(x) \,dx &\mbox{}\\ &=\displaystyle \int_{5}^{10} \frac{2}{5}x \,dx &\mbox{}\\ &=\displaystyle \frac{2}{5}\int_{5}^{10}x \,dx &\mbox{}\\ &=\displaystyle \frac{2}{5}\left[\frac{1}{2}x^2\right]_{5}^{10}&\mbox{}\\ &=\displaystyle \frac{2}{5}\cdot \frac{1}{2}\left[x^2\right]_{5}^{10}&\mbox{}\\ &=\displaystyle \frac{1}{5}\left[10^2-5^2\right]&\mbox{}\\ &=\displaystyle \frac{1}{5}\cdot 75&\mbox{}\\ &= \displaystyle 15 \mbox{ J}&\mbox{}\\ \end{array} $$ Thus, it takes about $15 \mbox{ J}$ of work to stretch the spring from $15 \mbox{ cm}$ to $20 \mbox{ cm}?$
Fun Fact: The amount of energy required to do this could power a $60 \mbox{ W}$ light bulb for about $0.25$ seconds.
Example: Variable Force, Springs
A spring has a natural length of $10$ cm. It takes $2$ joules of work to stretch the spring to $15$ cm. How much work would it take to stretch the spring from $15$ cm to $20$ cm?

We will use the information provided to determine the spring constant $k$ in Hooke's Law: $F(x)=kx.$
It takes $2$ joules of of work to stretch the spring to $15 \mbox{ cm}.$ That is, $$ \begin{array}{lll} \displaystyle &\displaystyle \int_{0}^{5} F(x) \,dx &=2\\ \displaystyle \implies &\displaystyle \int_{0}^{5} kx \,dx &=2\\ \displaystyle \implies &\displaystyle k\int_{0}^{5} x \,dx &=2\\ \displaystyle \implies &\displaystyle k\left[\frac{1}{2}x^2\right]_{0}^{5} &=2\\ \displaystyle \implies &\displaystyle \frac{k}{2}\left[x^2\right]_{0}^{5} &=2\\ \displaystyle \implies &\displaystyle \frac{k}{2}\cdot 25 &=2\\ \displaystyle \implies &\displaystyle k&=\frac{4}{25}\\ \end{array} $$
Since $\displaystyle k=\frac{4}{25},$ we can now find the work to stretch the spring from $15 \mbox{ cm}$ to $20 \mbox{ cm}:$ $$ \begin{array}{lll} \displaystyle W&=\displaystyle \int_{5}^{10} F(x) \,dx &\mbox{}\\ &=\displaystyle \int_{5}^{10} \frac{4}{25}x \,dx &\mbox{}\\ &=\displaystyle \frac{4}{25}\int_{5}^{10}x \,dx &\mbox{}\\ &=\displaystyle \frac{4}{25}\left[\frac{1}{2}x^2\right]_{5}^{10}&\mbox{}\\ &=\displaystyle \frac{4}{25}\cdot \frac{1}{2}\left[x^2\right]_{5}^{10}&\mbox{}\\ &=\displaystyle \frac{2}{25}\left[10^2-5^2\right]&\mbox{}\\ &=\displaystyle \frac{2}{25}\cdot 75&\mbox{}\\ &= \displaystyle 6 \mbox{ J}&\mbox{}\\ \end{array} $$
Thus, it takes about $6 \mbox{ J}$ of work to stretch the spring from $15 \mbox{ cm}$ to $20 \mbox{ cm}?$
It takes $2$ joules of of work to stretch the spring to $15 \mbox{ cm}.$ That is, $$ \begin{array}{lll} \displaystyle &\displaystyle \int_{0}^{5} F(x) \,dx &=2\\ \displaystyle \implies &\displaystyle \int_{0}^{5} kx \,dx &=2\\ \displaystyle \implies &\displaystyle k\int_{0}^{5} x \,dx &=2\\ \displaystyle \implies &\displaystyle k\left[\frac{1}{2}x^2\right]_{0}^{5} &=2\\ \displaystyle \implies &\displaystyle \frac{k}{2}\left[x^2\right]_{0}^{5} &=2\\ \displaystyle \implies &\displaystyle \frac{k}{2}\cdot 25 &=2\\ \displaystyle \implies &\displaystyle k&=\frac{4}{25}\\ \end{array} $$
Since $\displaystyle k=\frac{4}{25},$ we can now find the work to stretch the spring from $15 \mbox{ cm}$ to $20 \mbox{ cm}:$ $$ \begin{array}{lll} \displaystyle W&=\displaystyle \int_{5}^{10} F(x) \,dx &\mbox{}\\ &=\displaystyle \int_{5}^{10} \frac{4}{25}x \,dx &\mbox{}\\ &=\displaystyle \frac{4}{25}\int_{5}^{10}x \,dx &\mbox{}\\ &=\displaystyle \frac{4}{25}\left[\frac{1}{2}x^2\right]_{5}^{10}&\mbox{}\\ &=\displaystyle \frac{4}{25}\cdot \frac{1}{2}\left[x^2\right]_{5}^{10}&\mbox{}\\ &=\displaystyle \frac{2}{25}\left[10^2-5^2\right]&\mbox{}\\ &=\displaystyle \frac{2}{25}\cdot 75&\mbox{}\\ &= \displaystyle 6 \mbox{ J}&\mbox{}\\ \end{array} $$
Fun Fact: The amount of energy required to do this could power a $60 \mbox{ W}$ light bulb for about $0.1$ seconds.
Doing Work on a Fluid
With the idea of density in mind, we are now going to apply the idea of integrals for calculating the amount of work required to lift (pump) fluids out of both regular and oddly-shaped tanks.
The Problem
A tank has the shape of an inverted cone with a height of $10$ meters and a base radius of $4$ meters. It is filled with water to a height of $6$ meters. Find the work required to empty the tank by pumping all the water to the top of the tank.
The Solution: The pic slab v m f w sum int method.
pic slab v m f w sum int
Step 1. Draw a picture of the situation.
In this case, it's an inverted cone.
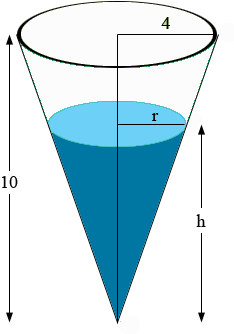
pic slab v m f w sum int
Step 2. Approximate the fluid volume as a column of horizontally stacked "slabs."
In this particular case, our slabs are cylinders.
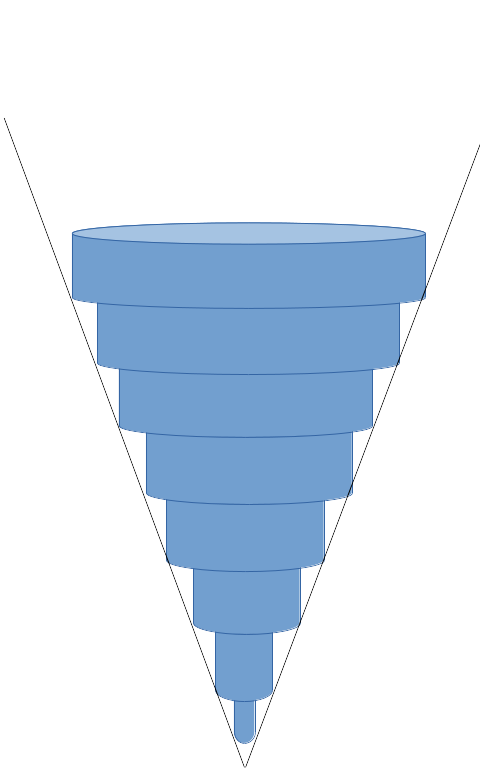
pic slab v m f w sum int
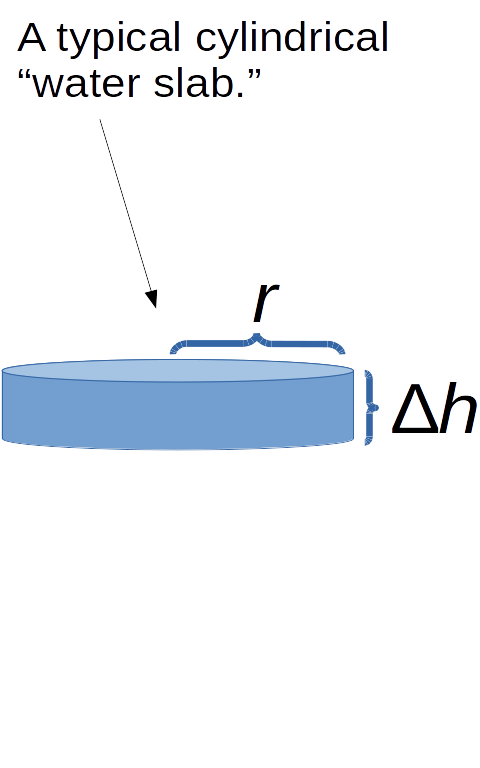
Step 3. Find the volume of a typical slab.
Note: If we have a funny-shaped container, this will involve having to express the each variable of the volume expression in terms of the height.
In our case, we need to express the radius of our cylindrical slab in terms of the height.


The volume of the slab is $\displaystyle V=\pi r^2 \, \Delta h,$ but we must express $r$ in terms of $h.$
We will use the geometry of the cone to do this.
By similar triangles we have $\displaystyle \frac{r}{h}=\frac{4}{10},$ or $\displaystyle r=\frac{2}{5}h.$ We may now express the volume in terms of height alone: $$ \begin{array}{lll} &\displaystyle V&=\displaystyle \pi r^2 \, \Delta h\\ \implies & V &=\displaystyle \pi \left(\frac{2}{5}h\right)^2 \, \Delta h\\ \implies & V &=\displaystyle \frac{4\pi}{25}h^2 \, \Delta h\\ \end{array} $$
By similar triangles we have $\displaystyle \frac{r}{h}=\frac{4}{10},$ or $\displaystyle r=\frac{2}{5}h.$ We may now express the volume in terms of height alone: $$ \begin{array}{lll} &\displaystyle V&=\displaystyle \pi r^2 \, \Delta h\\ \implies & V &=\displaystyle \pi \left(\frac{2}{5}h\right)^2 \, \Delta h\\ \implies & V &=\displaystyle \frac{4\pi}{25}h^2 \, \Delta h\\ \end{array} $$
pic slab v m f w sum int
Step 4. From the volume, use the density $\rho$ to find the mass of a typical slab.
Recall: Since the density of water is uniform, $\rho$ is simply mass divided by volume. Then $$m=\rho V.$$
Since our tank is filled with water, we know $\rho=1000$ $\mbox{kg}/\mbox{m}^3$.
Then,
$$
\begin{array}{lll}
&\displaystyle m&=\displaystyle \rho V\\
\implies & m &=\displaystyle 1000 \cdot \frac{4\pi}{25}h^2 \, \Delta h\\
\implies & m &=\displaystyle 160 \pi h^2 \, \Delta h\\
\end{array}
$$
pic slab v m f w sum int
Step 5. From the mass, find the force of gravity on a typical slab.
Note: The force $F$ that gravity exerts on an object of mass $m$ is
given by
$$F=mg,$$
where $g=9.8$ $\mbox{m}/\mbox{s}^2.$
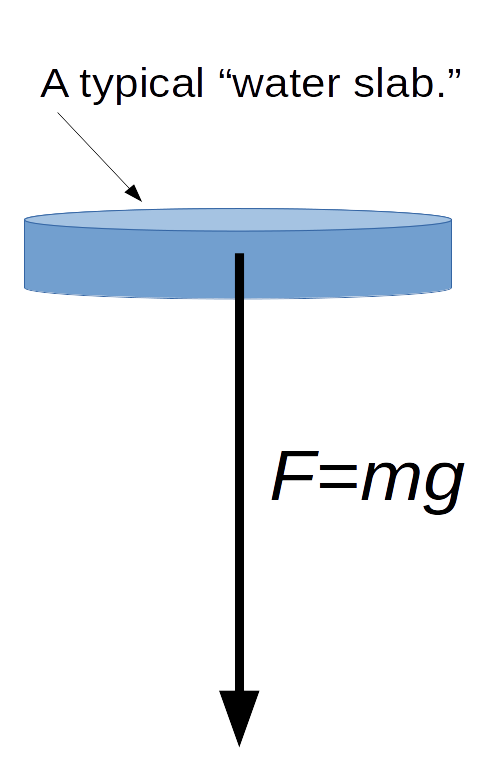
$$
\begin{array}{lll}
&\displaystyle F&=\displaystyle mg\\
\implies & F &=\displaystyle 160 \pi h^2 \, \Delta h \cdot 9.8 \\
\implies & F &=\displaystyle 1568 \pi h^2 \, \Delta h \\
\end{array}
$$
pic slab v m f w sum int
Step 6. Once you know the force of gravity on a typical slab, you may now find the amount of work to lift that slab to the top of the tank.
Note: The work $W$ done on an object by exerting a force $F$ over a distance $d$
is given by
$$W=F \cdot d.$$


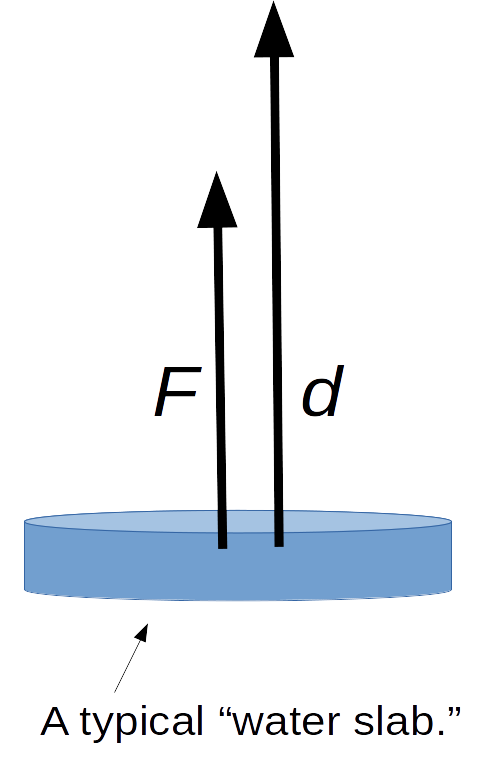
From the diagram, we see that the distance a slab must travel to the top of the tank is $10-h.$
Thus, the work to lift our slab at height $h$ a distance of $d=10-h$ is
$$
\begin{array}{lll}
&\displaystyle W&=\displaystyle F\cdot d\\
\implies & W &=\displaystyle 1568 \pi h^2 \, \Delta h \cdot (10-h) \\
\implies & W &=\displaystyle 1568 \pi (10-h) h^2 \, \Delta h \\
\implies & W &=\displaystyle 1568 \pi (10h^2-h^3) \, \Delta h \\
\end{array}
$$
pic slab v m f w sum int
Step 7. Now that we know the amount of work to lift a typical slab from height $h$ to the top of the tank, we now add up the work required to lift each individual slab to the top. That is, we take the sum of the "works."
Big Question: What kind of sum is this?
$$\mbox{Work} \approx \sum_{i=1}^{n} W(h_i^{*})$$
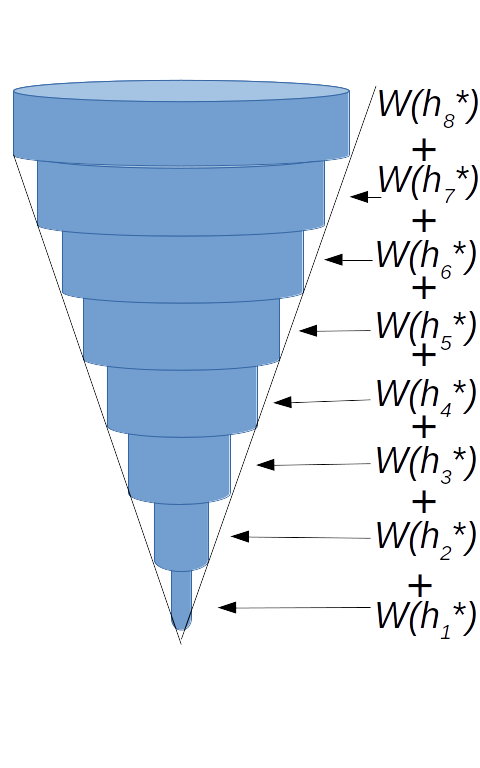
Let $h_i^*$ be the height of the $i$th slab. Then,
$$
\begin{array}{lll}
&\displaystyle W&\approx\displaystyle \sum_{i=1}^{n} W(h_i^{*})\\
\implies & W &\approx\displaystyle \sum_{i=1}^{n} 1568 \pi (10(h_i^*)^2-(h_i^*)^3) \, \Delta h \\
\implies & W &\approx\displaystyle 1568 \pi \sum_{i=1}^{n} (10(h_i^*)^2-(h_i^*)^3) \, \Delta h \\
\end{array}
$$
pic slab v m f w sum int
Step 8. We now take the limit of the sum we wrote in Step 7 to obtain the integral representing the exact amount of work required to lift all the fluid in the tank.
$$
\begin{array}{lll}
&\displaystyle W&=\displaystyle \lim_{n \rightarrow \infty}\sum_{i=1}^{n} W(h_i^{*})\\
\implies & W &=\displaystyle \lim_{n \rightarrow \infty}\left[1568 \pi \sum_{i=1}^{n} (10(h_i^*)^2-(h_i^*)^3) \, \Delta h\right] \\
\implies & W &=\displaystyle 1568 \pi \lim_{n \rightarrow \infty} \sum_{i=1}^{n} (10(h_i^*)^2-(h_i^*)^3) \, \Delta h \\
\implies & W &=\displaystyle 1568 \pi \int_{0}^{6} 10h^2-h^3 \, dh \\
\end{array}
$$
Note: The upper limit of integration is $6$ since that is the initial height of the water in the tank.
Don't Forget to Evaluate!
Let's evaluate the integral!
$$
\begin{array}{lll}
W &=\displaystyle 1568 \pi \int_{0}^{6} 10h^2-h^3 \, dh & \\
&=\displaystyle 1568 \pi \left[\frac{10}{3}h^3-\frac{1}{4}h^4\right]_{0}^{6} & \\
&=\displaystyle 1568 \pi \left[\frac{10}{3}6^3-\frac{1}{4}6^4\right] & \\
&=\displaystyle 1568 \pi \left[\frac{10}{3}\cdot 6 \cdot 6^2-\frac{1}{4}\cdot 6^2 \cdot 6^2\right] & \\
&=\displaystyle 1568 \pi \cdot 396 & \\
&=\displaystyle 620928 \pi& \\
&\approx \displaystyle \mbox{1,950,702.8} \mbox{ J} & \\
\end{array}
$$
Fun Fact: This amount of energy could power a $60 \mbox{ W}$ light bulb for about $32511.7$ seconds,
which is about $9$ hours.
Method Summary
Step 1: Draw a picture
Step 2: Visualize fluid as a stack of slabs.
Step 3: Determine the volume of a typical slab.
Step 4: Determine the mass of a typical slab.
Step 5: Determine the force to lift a typical slab.
Step 6: Determine the work to lift a typical slab.
Step 7: Sum the work of each slab.
Step 8: Take the limit of the sum to get an integral.
Bonus Example
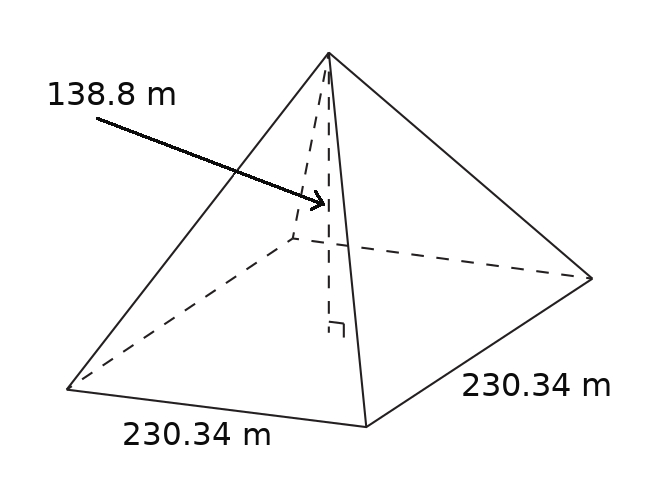
The Pyramid of Giza is $138.8$ meters tall with a square base having a side length of $230.34$ meters. It was built out of granite and limestone which both have respective densities of $2750$ kg/m3 and $2711$ kg/m3.
Calculate the amount of work it took to build The Pyramid of Giza.

Step 1: Pic. We first draw a picture of the situation.
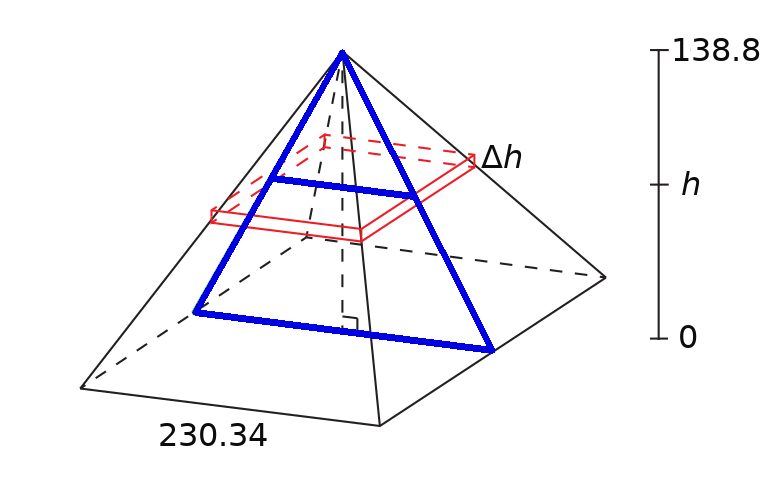
Step 2: Slab. We draw a picture of a typical slab that will be lifted to the necessary height.
Step 3: v. We now find the volume of a typical slab: $$ \begin{array}{llll} &\displaystyle V&=\displaystyle \mbox{length $\cdot$ width $\cdot$ height}&\\ \implies & V &= LWH &\\ \implies & V &= LW\,\Delta h &\mbox{letting the height be $\Delta h$}\\ \implies & V &= L^2\,\Delta h &\mbox{$L=W$ since the pyramid has a square base}\\ \end{array} $$
As with the previous example, we must use the geometry of the situation of express the length of the base $L$ in terms of the height $h$ of a slab. To do so, we look at a vertical cross-section of the pyramid from the previous figure.
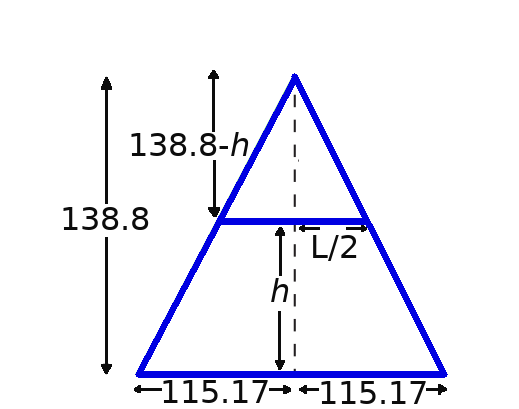
From the figure we see that $$\frac{L/2}{138.8-h}=\frac{115.17}{138.8}$$ This gives $$L=\frac{230.34}{138.8}(138.8-h)$$ The volume of a slab of height $\Delta h$ is then $$ \begin{array}{llll} & V &= L^2\,\Delta h &\mbox{}\\ \implies & V &=\displaystyle \left(\frac{230.34}{138.8}(138.8-h)\right)^2\,\Delta h= \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h&\mbox{}\\ \end{array} $$
Step 4: m. We now find the mass of a slab. Since granite and limestone have densities of $2750$ kg/m3 and $2711$ kg/m3, and we don't know the proportion of granite to limestone, we'll assume that both are present in equal amounts. Since both values are quite similar, this assumption isn't asking too much. With this assumption, we can take the average of the two densities so that $\displaystyle \rho=\frac{2750+2711}{2}=2730.5.$
Since $m=\rho V,$ we have that the mass of a slab lifted to height $h$ is $$m=2730.5\cdot \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h$$
Step 5: f. The force $F$ of gravity on an object of mass $m \mbox{ kg}$ is given by $F=mg.$ So, the force gravity exerts on the slab is $$ \begin{array}{llll} &\displaystyle F&=\displaystyle 2730.5 \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h \cdot 9.8&\\ \implies & F &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h &\\ \end{array} $$
Step 6: w. The work on to lift our slab to height $h$ is given by $W=F\cdot d.$ Since the distance the slab was moved is $h$ meters, we may say that $d=h.$ That is, $$ \begin{array}{llll} &\displaystyle W&=F\cdot d&\\ \implies &\displaystyle W&=F\cdot h&\\ \implies & W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h \cdot h &\mbox{ from Step 5 above}\\ \implies & W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 h \left(138.8-h\right)^2\,\Delta h &\\ \end{array} $$
Step 7: Sum. Letting $h_i^*$ be the height of the $i$th slab, we may now write the approximation of the total work to build the pyramid. $$ \begin{array}{llll} &\displaystyle W&\approx \displaystyle \sum_{i=1}^{n} W_i&\\ \implies & W &\approx \displaystyle \sum_{i=1}^{n}\displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 h_i^* \left(138.8-h_i^*\right)^2\,\Delta h &\\ \implies & W &\approx \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \sum_{i=1}^{n}\displaystyle h_i^* \left(138.8-h_i^*\right)^2\,\Delta h &\\ \end{array} $$
Step 8: int. Taking the limit of the sum obtained in Step 7 we have an integral which gives the work required to build the pyramid.
$$ \begin{array}{llll} &\displaystyle W&= \displaystyle \lim_{n \rightarrow \infty} \sum_{i=1}^{n} W_i&\\ \implies & W &= \displaystyle \lim_{n \rightarrow \infty}\left[26758.9 \left(\frac{230.34}{138.8}\right)^2 \sum_{i=1}^{n} h_i^* \left(138.8-h_i^*\right)^2\,\Delta h\right] &\\ \implies & W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \lim_{n \rightarrow \infty}\sum_{i=1}^{n} h_i^* \left(138.8-h_i^*\right)^2\,\Delta h &\\ \implies & W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \int_{0}^{138.8} h \left(138.8-h\right)^2\, dh &\\ \end{array} $$ Let's evaluate! $$ \begin{array}{lll} W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \int_{0}^{138.8} h \left(138.8-h\right)^2\, dh &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \int_{0}^{138.8} h (138.8^2-2\cdot 138.8 h+h^2)\, dh &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \int_{0}^{138.8} 138.8^2h-2\cdot 138.8h^2+h^3\, dh &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \left[\frac{138.8^2}{2}h^2-\frac{2\cdot 138.8}{3}h^3+\frac{1}{4}h^4\right]_{0}^{138.8} &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \left[\frac{138.8^2}{2}(138.8)^2-\frac{2\cdot 138.8}{3}(138.8)^3+\frac{1}{4}(138.8)^4\right] &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 (138.8)^4\left[\frac{1}{2}-\frac{2}{3}+\frac{1}{4}\right] &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 (138.8)^4\left[\frac{1}{12}\right] &\\ &= \displaystyle 26758.9 \left(230.34\right)^2 (138.8)^2\left[\frac{1}{12}\right] &\\ &\approx \displaystyle 2.28 \times 10^{12} \mbox{ J} &\\ \end{array} $$ Fun Fact: This amount of energy could power a $60 \mbox{ W}$ light bulb for about $1205$ years.

Step 2: Slab. We draw a picture of a typical slab that will be lifted to the necessary height.

Step 3: v. We now find the volume of a typical slab: $$ \begin{array}{llll} &\displaystyle V&=\displaystyle \mbox{length $\cdot$ width $\cdot$ height}&\\ \implies & V &= LWH &\\ \implies & V &= LW\,\Delta h &\mbox{letting the height be $\Delta h$}\\ \implies & V &= L^2\,\Delta h &\mbox{$L=W$ since the pyramid has a square base}\\ \end{array} $$
As with the previous example, we must use the geometry of the situation of express the length of the base $L$ in terms of the height $h$ of a slab. To do so, we look at a vertical cross-section of the pyramid from the previous figure.

From the figure we see that $$\frac{L/2}{138.8-h}=\frac{115.17}{138.8}$$ This gives $$L=\frac{230.34}{138.8}(138.8-h)$$ The volume of a slab of height $\Delta h$ is then $$ \begin{array}{llll} & V &= L^2\,\Delta h &\mbox{}\\ \implies & V &=\displaystyle \left(\frac{230.34}{138.8}(138.8-h)\right)^2\,\Delta h= \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h&\mbox{}\\ \end{array} $$
Step 4: m. We now find the mass of a slab. Since granite and limestone have densities of $2750$ kg/m3 and $2711$ kg/m3, and we don't know the proportion of granite to limestone, we'll assume that both are present in equal amounts. Since both values are quite similar, this assumption isn't asking too much. With this assumption, we can take the average of the two densities so that $\displaystyle \rho=\frac{2750+2711}{2}=2730.5.$
Since $m=\rho V,$ we have that the mass of a slab lifted to height $h$ is $$m=2730.5\cdot \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h$$
Step 5: f. The force $F$ of gravity on an object of mass $m \mbox{ kg}$ is given by $F=mg.$ So, the force gravity exerts on the slab is $$ \begin{array}{llll} &\displaystyle F&=\displaystyle 2730.5 \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h \cdot 9.8&\\ \implies & F &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h &\\ \end{array} $$
Step 6: w. The work on to lift our slab to height $h$ is given by $W=F\cdot d.$ Since the distance the slab was moved is $h$ meters, we may say that $d=h.$ That is, $$ \begin{array}{llll} &\displaystyle W&=F\cdot d&\\ \implies &\displaystyle W&=F\cdot h&\\ \implies & W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2\left(138.8-h\right)^2\,\Delta h \cdot h &\mbox{ from Step 5 above}\\ \implies & W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 h \left(138.8-h\right)^2\,\Delta h &\\ \end{array} $$
Step 7: Sum. Letting $h_i^*$ be the height of the $i$th slab, we may now write the approximation of the total work to build the pyramid. $$ \begin{array}{llll} &\displaystyle W&\approx \displaystyle \sum_{i=1}^{n} W_i&\\ \implies & W &\approx \displaystyle \sum_{i=1}^{n}\displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 h_i^* \left(138.8-h_i^*\right)^2\,\Delta h &\\ \implies & W &\approx \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \sum_{i=1}^{n}\displaystyle h_i^* \left(138.8-h_i^*\right)^2\,\Delta h &\\ \end{array} $$
Step 8: int. Taking the limit of the sum obtained in Step 7 we have an integral which gives the work required to build the pyramid.
$$ \begin{array}{llll} &\displaystyle W&= \displaystyle \lim_{n \rightarrow \infty} \sum_{i=1}^{n} W_i&\\ \implies & W &= \displaystyle \lim_{n \rightarrow \infty}\left[26758.9 \left(\frac{230.34}{138.8}\right)^2 \sum_{i=1}^{n} h_i^* \left(138.8-h_i^*\right)^2\,\Delta h\right] &\\ \implies & W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \lim_{n \rightarrow \infty}\sum_{i=1}^{n} h_i^* \left(138.8-h_i^*\right)^2\,\Delta h &\\ \implies & W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \int_{0}^{138.8} h \left(138.8-h\right)^2\, dh &\\ \end{array} $$ Let's evaluate! $$ \begin{array}{lll} W &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \int_{0}^{138.8} h \left(138.8-h\right)^2\, dh &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \int_{0}^{138.8} h (138.8^2-2\cdot 138.8 h+h^2)\, dh &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \int_{0}^{138.8} 138.8^2h-2\cdot 138.8h^2+h^3\, dh &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \left[\frac{138.8^2}{2}h^2-\frac{2\cdot 138.8}{3}h^3+\frac{1}{4}h^4\right]_{0}^{138.8} &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 \left[\frac{138.8^2}{2}(138.8)^2-\frac{2\cdot 138.8}{3}(138.8)^3+\frac{1}{4}(138.8)^4\right] &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 (138.8)^4\left[\frac{1}{2}-\frac{2}{3}+\frac{1}{4}\right] &\\ &= \displaystyle 26758.9 \left(\frac{230.34}{138.8}\right)^2 (138.8)^4\left[\frac{1}{12}\right] &\\ &= \displaystyle 26758.9 \left(230.34\right)^2 (138.8)^2\left[\frac{1}{12}\right] &\\ &\approx \displaystyle 2.28 \times 10^{12} \mbox{ J} &\\ \end{array} $$ Fun Fact: This amount of energy could power a $60 \mbox{ W}$ light bulb for about $1205$ years.