Suppose a curve walks up to you on the street and asks: "How long am I?"
Question: How do you answer?
Answer: You ask: "over what interval?"
Example: Consider the curve $y=x^{3/2}$ over the interval $[0,1].$ Let's approximate the exact length $L.$
| $y$ | |
| $x$ |
Question: How can we use the above process to find the exact length of the curve $$y=x^{3/2}$$ on the interval $0 \leq x \leq 1?$
Answer: Remember the distance formula.
Do You Believe It?
Is the following statement true? $$\sqrt{\Delta x^2+\Delta y^2}=\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2} \, \Delta x$$
$$\sum \sqrt{\Delta x^2+\Delta y^2}=\sum \sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2} \, \Delta x$$
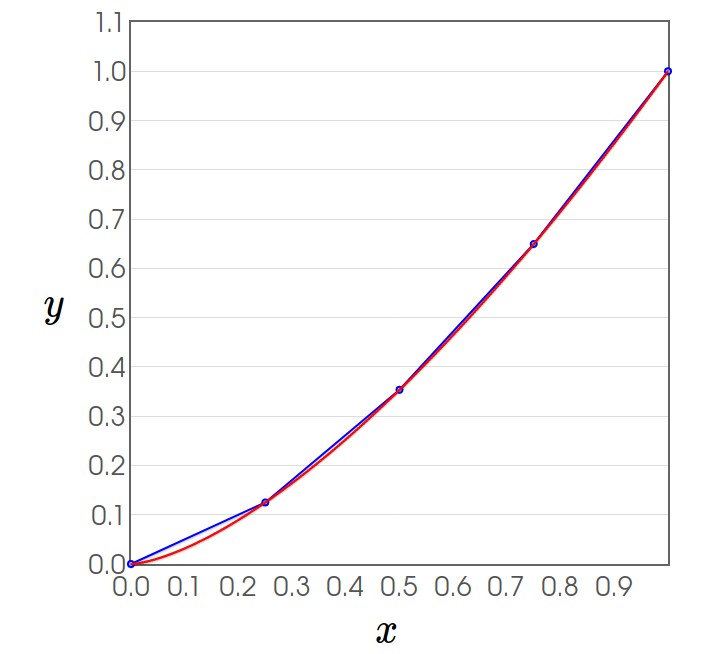
Big Question: What kind of sum is this?
Big Answer: A Riemann sum!
| $$\sum \sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}\Delta x$$ | $$\longrightarrow$$ | $$\int \sqrt{1+\left(\frac{dy}{dx}\right)^2} \, dx$$ |
 |
$\longrightarrow$ | 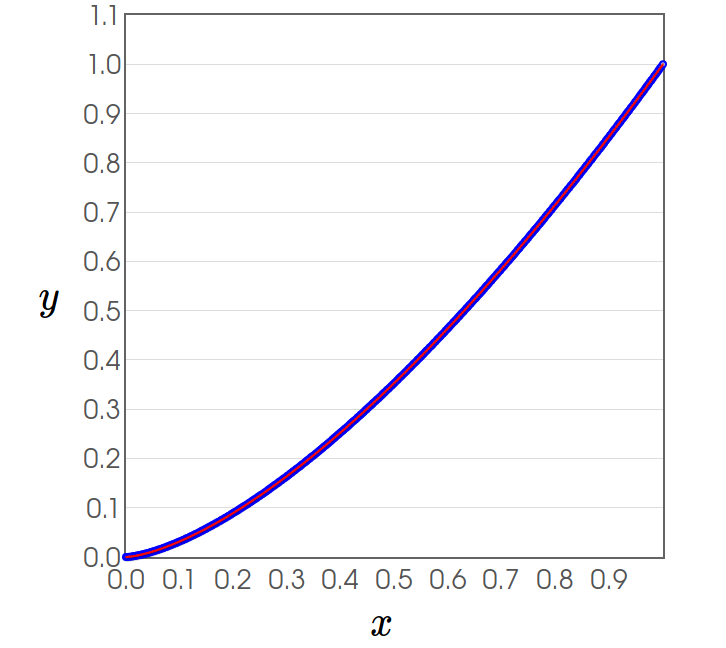 |
Formal Statement of Arc Length: Let $y=f'(x)$ be a continuous function on the interval $a \leq x \leq b.$ Then the length $L$ of the curve of $y=f(x)$ from $x=a$ to $x=b$ is given by $$L=\int_{a}^{b} \sqrt{1+\left[f'(x)\right]^2} \, dx$$
Example: Find the exact length of the curve $y=x^{3/2}$ on the interval $0 \leq x \leq 1.$
Taking $f(x)=x^{3/2}$ so that $\displaystyle f'(x)=\frac{3}{2}x^{1/2},$ we have
$$
\begin{array}{lll}
\displaystyle L &=\displaystyle \int_{a}^{b} \sqrt{1+\left[f'(x)\right]^2} \, dx &\mbox{}\\
&=\displaystyle \int_{0}^{1} \sqrt{1+\left[\frac{3}{2}x^{1/2}\right]^2} \, dx &\mbox{}\\
&=\displaystyle \int_{0}^{1} \sqrt{1+\frac{9}{4}x} \, dx &\mbox{}\\
&=\displaystyle \int_{1}^{13/4} \sqrt{u}\, \frac{4}{9}\, du &\mbox{taking $u=1+\frac{9}{4}x$ so that $dx=\frac{4}{9}\,du$}\\
&=\displaystyle \frac{4}{9}\int_{1}^{13/4} u^{1/2}\, du &\mbox{}\\
&=\displaystyle \frac{4}{9}\left[\frac{2}{3}u^{3/2}\right]_{1}^{13/4} &\mbox{}\\
&=\displaystyle \frac{4}{9}\frac{2}{3}\left[u^{3/2}\right]_{1}^{13/4} &\mbox{}\\
&=\displaystyle \frac{8}{27}\left[\left(\frac{13}{4}\right)^{3/2}-1^{3/2}\right] &\mbox{}\\
&=\displaystyle \frac{8}{27}\left[\frac{\sqrt{2197}}{8}-1\right] &\mbox{}\\
&=\displaystyle \frac{\sqrt{2197}}{27}-\frac{8}{27} &\mbox{}\\
&\approx \displaystyle 1.439709873 \mbox{ units}&\mbox{}\\
\end{array}
$$
Arc Length
Let $g'(y)$ be a continuous function on the interval $c \leq y \leq d.$ Then the length $L$ of the curve of $x=g(y)$ from $y=c$ to $y=d$ is given by $$L=\int_{c}^{d} \sqrt{1+\left[g'(y)\right]^2} \, dy$$
Example: Find the exact length of the curve $x=\sqrt{1-y^2}$ on the interval $-1 \leq y \leq 1.$
Taking $g(y)=\sqrt{1-y^2}$ so that $\displaystyle g'(y)=\frac{-y}{\sqrt{1-y^2}},$ we have
$$
\begin{array}{lll}
\displaystyle L &=\displaystyle \int_{c}^{d} \sqrt{1+\left[g'(y)\right]^2} \, dy &\mbox{}\\
&=\displaystyle \int_{-1}^{1} \sqrt{1+\left[\frac{-y}{\sqrt{1-y^2}}\right]^2} \, dy &\mbox{}\\
&=\displaystyle \int_{-1}^{1} \sqrt{1+\frac{y^2}{1-y^2}} \, dy &\mbox{}\\
&=\displaystyle \int_{-1}^{1} \sqrt{\frac{1-y^2}{1-y^2}+\frac{y^2}{1-y^2}} \, dy &\mbox{}\\
&=\displaystyle \int_{-1}^{1} \sqrt{\frac{1}{1-y^2}} \, dy &\mbox{}\\
&=\displaystyle \int_{-1}^{1} \frac{1}{\sqrt{1-y^2}} \, dy &\mbox{}\\
&=\displaystyle \left[\sin^{-1}y\right]_{-1}^{1} &\mbox{}\\
&=\displaystyle \sin^{-1}(1)-\sin^{-1}(-1) &\mbox{}\\
&=\displaystyle \frac{\pi}{2}-\left(-\frac{\pi}{2}\right) &\mbox{}\\
&=\displaystyle \pi &\mbox{}\\
&\approx \displaystyle 3.141592654 \mbox{ units}&\mbox{}\\
\end{array}
$$
Surface Area of a Solid of Revolution
We can apply the same ideas for finding arc length to finding the exact surface area of a solid of revolution.
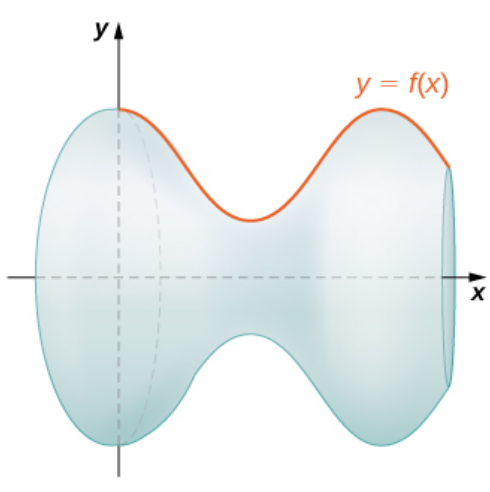
Surface Area of a Solid of Revolution
First, approximate the curve with line segments and revolve around the $x$ axis.
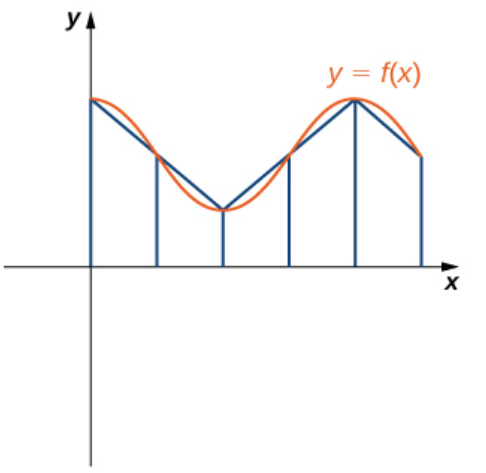

Surface Area of a Solid of Revolution
The surface area of a typical band at at a specially chosen point $x_i^*$ in the interval $[x_{i-1},x_i]$is $$S(x_i^*) =2 \pi f(x_i^*)\sqrt{\Delta x^2+\Delta y^2} \approx 2 \pi f(x_i^*) \sqrt{1+[f'(x_i^*)]^2}\Delta x$$
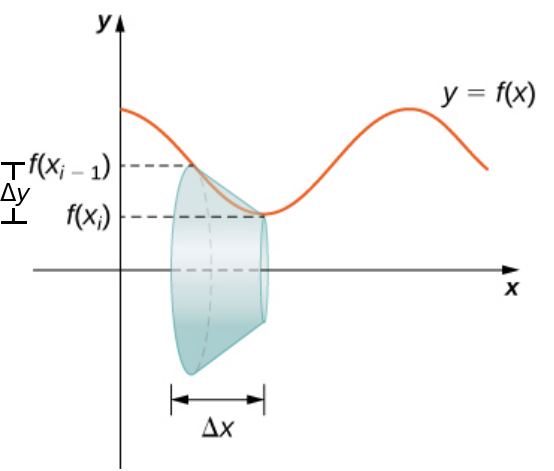
Surface Area of a Solid of Revolution
The exact surface area $S$ of the solid is then approximated by adding up the surface areas of all the individual bands $$S \approx \sum_{i=1}^{n} 2 \pi f(x_i^*) \sqrt{1+[f'(x_i^*)]^2}\Delta x.$$

Surface Area of a Solid of Revolution
| $$\lim_{n \rightarrow \infty} \sum_{i=1}^{n} 2 \pi f(x_i^*) \sqrt{1+[f'(x_i^*)]^2}\Delta x$$ | ||
| $\displaystyle \sum_{i=1}^{n} 2 \pi f(x_i^*) \sqrt{1+[f'(x_i^*)]^2}\Delta x$ | $\longrightarrow$ | $\displaystyle \int_{a}^{b} 2 \pi f(x) \sqrt{1+[f'(x)]^2} \,dx$ |
 | $\longrightarrow$ |  |
Surface Area of a Solid of Revolution
The exact surface area $S$ of the solid formed by revolving $f(x)$ around the $x$-axis is given by $$\displaystyle S = \int_{a}^{b} 2 \pi f(x) \sqrt{1+[f'(x)]^2} \,dx$$

Example: Surface Area of a Solid of Revolution
Let $f (x) = \sqrt{x}$ over the interval $[1, 4].$ Find the surface area of the surface generated by revolving the graph of $f (x)$ around the $x$-axis.
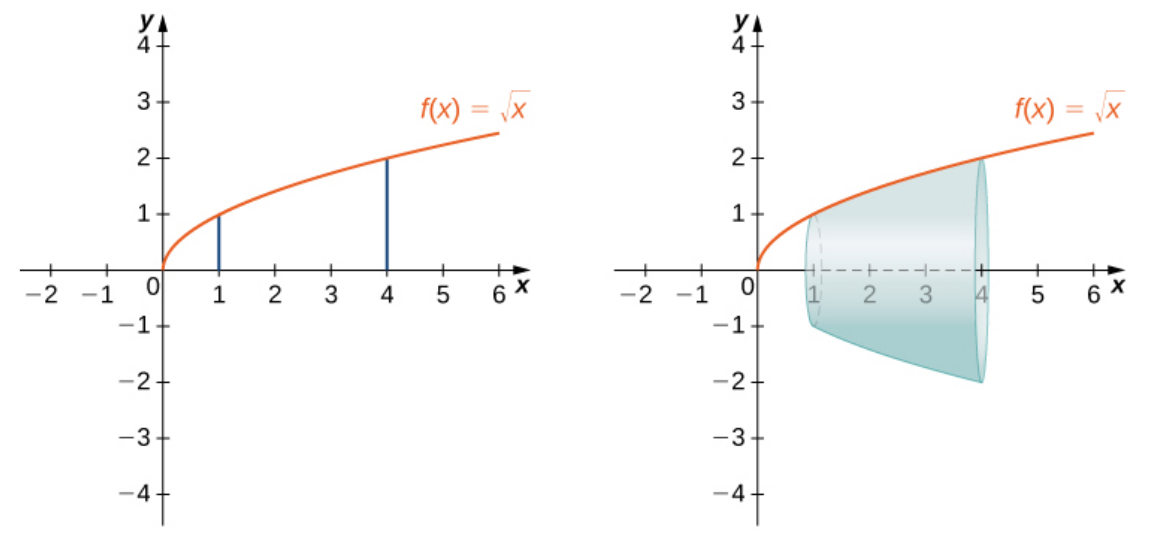
Taking $f(x)=\sqrt{x}$ so that $\displaystyle f'(x)=\frac{1}{2\sqrt{x}},$ we have
$$
\begin{array}{lll}
\displaystyle S &=\displaystyle \int_{a}^{b} 2 \pi f(x) \sqrt{1+[f'(x)]^2} \,dx &\mbox{}\\
&=\displaystyle \int_{1}^{4} 2 \pi \sqrt{x} \sqrt{1+\left[\frac{1}{2\sqrt{x}}\right]^2} \,dx &\mbox{}\\
&=\displaystyle 2 \pi \int_{1}^{4} \sqrt{x} \sqrt{1+\frac{1}{4x}} \,dx &\mbox{}\\
&=\displaystyle 2 \pi \int_{1}^{4} \sqrt{x\left(1+\frac{1}{4x}\right)} \,dx &\mbox{}\\
&=\displaystyle 2 \pi \int_{1}^{4} \sqrt{x+\frac{1}{4}} \,dx &\mbox{}\\
&=\displaystyle 2 \pi \int_{5/4}^{17/4} \sqrt{u} \,du &\mbox{ letting $u=x+\frac{1}{4}$ so that $du=dx$}\\
&=\displaystyle 2 \pi \int_{5/4}^{17/4} u^{1/2} \,du &\mbox{}\\
&=\displaystyle 2 \pi \left[\frac{2}{3}u^{3/2}\right]_{5/4}^{17/4} &\mbox{}\\
&=\displaystyle 2 \pi \cdot \frac{2}{3} \left[u^{3/2}\right]_{5/4}^{17/4} &\mbox{}\\
&=\displaystyle \frac{4\pi}{3} \left[\left(\frac{17}{4}\right)^{3/2}-\left(\frac{5}{4}\right)^{3/2}\right] &\mbox{}\\
&=\displaystyle \frac{4\pi}{3} \left[\left(\frac{17^{3/2}}{8}\right)-\left(\frac{5^{3/2}}{8}\right)\right] &\mbox{}\\
&=\displaystyle \frac{4\pi}{3} \left(\frac{17^{3/2}-5^{3/2}}{8}\right) &\mbox{}\\
&=\displaystyle \frac{\pi}{6} \left(17^{3/2}-5^{3/2}\right) &\mbox{}\\
&=\displaystyle \frac{\pi}{6} \left((\sqrt{17})^3-(\sqrt{5})^3\right) &\mbox{}\\
&=\displaystyle \frac{\pi}{6} \left(17\sqrt{17}-5\sqrt{5}\right) &\mbox{}\\
&\approx \displaystyle 30.8464897 \mbox{ units}^2&\mbox{}\\
\end{array}
$$
Surface Area of a Solid of Revolution
The exact surface area $S$ of the solid formed by revolving $x=g(y)$ around the $y$-axis is given by $$\displaystyle S = \int_{c}^{d} 2 \pi g(y) \sqrt{1+[g'(y)]^2} \,dy$$
Example: Surface Area of a Solid of Revolution
Consider the portion of the curve $\displaystyle g(y)=\frac{1}{3}y^3$ where $0 \leq y \leq 2.$ Find the surface area of the surface generated by revolving the graph of $f (x)$ around the $y$-axis.
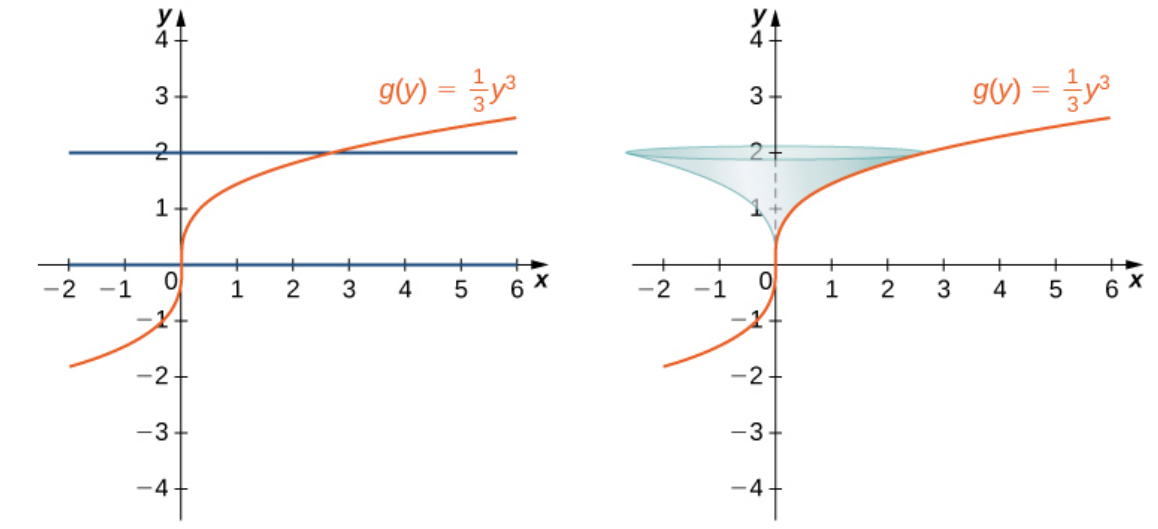
Taking $g(y)=\frac{1}{3}y^3$ so that $\displaystyle g'(y)=y^2,$ we have
$$
\begin{array}{lll}
\displaystyle S &=\displaystyle\int_{c}^{d} 2 \pi g(y) \sqrt{1+[g'(y)]^2} \,dy &\mbox{}\\
&=\displaystyle \int_{0}^{2} 2 \pi\cdot \frac{1}{3}y^3 \sqrt{1+[y^2]^2} \,dy &\mbox{}\\
&=\displaystyle \frac{2\pi}{3}\int_{0}^{2} y^3 \sqrt{1+y^4} \,dy &\mbox{}\\
&=\displaystyle \frac{2\pi}{3}\int_{1}^{17} \sqrt{u} \,\frac{1}{4}\,du &\mbox{ letting $u=1+y^4$ so that $\frac{1}{4}du=y^3\,dy$}\\
&=\displaystyle \frac{2\pi}{3}\cdot \frac{1}{4}\int_{1}^{17} \sqrt{u} \,du &\mbox{}\\
&=\displaystyle \frac{\pi}{6}\left[\frac{2}{3}u^{3/2}\right]_{1}^{17} &\mbox{}\\
&=\displaystyle \frac{\pi}{6}\cdot \frac{2}{3}\left[u^{3/2}\right]_{1}^{17} &\mbox{}\\
&=\displaystyle \frac{\pi}{9}\left[17^{3/2}-1^{3/2}\right] &\mbox{}\\
&=\displaystyle \frac{\pi}{9}\left[17\sqrt{17}-1\right] &\mbox{}\\
&\approx \displaystyle 24.11793546 \mbox{ units}^2&\mbox{}\\
\end{array}
$$
Bonus Example: Surface Area of a Solid of Revolution: Find the lateral surface area of a cone of radius $r$ and height $h$ by using finding the surface area of a solid of revolution
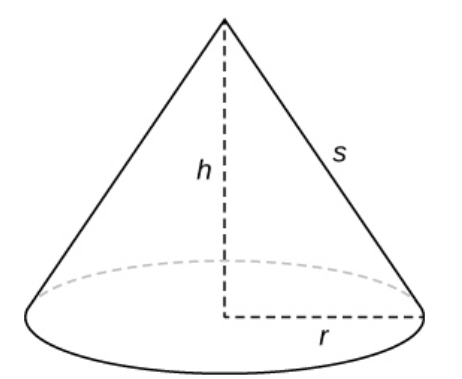
Putting the cone onto a coordinate system, we see that we can obtain the surface area by revolving the line $\displaystyle y=-\frac{h}{r}x+h$ around the $y$-axis.
To do this, we need to express $x$ in terms of $y$ so that $\displaystyle x=-\frac{r}{h}(y-h)=-\frac{r}{h}y+r.$
Thus, we take $\displaystyle g(y)=-\frac{r}{h}y+r$ so that $\displaystyle g'(y)=-\frac{r}{h}.$ Then, the surface area $S$ is $$ \begin{array}{lll} \displaystyle S &=\displaystyle\int_{c}^{d} 2 \pi g(y) \sqrt{1+[g'(y)]^2} \,dy &\mbox{}\\ &=\displaystyle \int_{0}^{h} 2 \pi\cdot \left(-\frac{r}{h}y+r\right) \sqrt{1+\left[-\frac{r}{h}\right]^2} \,dy &\mbox{}\\ &=\displaystyle 2 \pi\sqrt{1+\left[-\frac{r}{h}\right]^2} \int_{0}^{h}-\frac{r}{h}y+r \,dy &\mbox{ note that $r$ and $h$ are constants}\\ &=\displaystyle 2 \pi\sqrt{1+\frac{r^2}{h^2}} \left[-\frac{r}{2h}y^2+ry\right]_{0}^{h}&\mbox{}\\ &=\displaystyle 2 \pi\sqrt{\frac{h^2+r^2}{h^2}} \left[-\frac{rh}{2}+rh\right]&\mbox{}\\ &=\displaystyle 2 \pi\frac{\sqrt{h^2+r^2}}{h} \left[\frac{rh}{2}\right]&\mbox{}\\ &= \displaystyle \pi r \sqrt{h^2+r^2}\mbox{ units}^2&\mbox{}\\ \end{array} $$
To do this, we need to express $x$ in terms of $y$ so that $\displaystyle x=-\frac{r}{h}(y-h)=-\frac{r}{h}y+r.$
Thus, we take $\displaystyle g(y)=-\frac{r}{h}y+r$ so that $\displaystyle g'(y)=-\frac{r}{h}.$ Then, the surface area $S$ is $$ \begin{array}{lll} \displaystyle S &=\displaystyle\int_{c}^{d} 2 \pi g(y) \sqrt{1+[g'(y)]^2} \,dy &\mbox{}\\ &=\displaystyle \int_{0}^{h} 2 \pi\cdot \left(-\frac{r}{h}y+r\right) \sqrt{1+\left[-\frac{r}{h}\right]^2} \,dy &\mbox{}\\ &=\displaystyle 2 \pi\sqrt{1+\left[-\frac{r}{h}\right]^2} \int_{0}^{h}-\frac{r}{h}y+r \,dy &\mbox{ note that $r$ and $h$ are constants}\\ &=\displaystyle 2 \pi\sqrt{1+\frac{r^2}{h^2}} \left[-\frac{r}{2h}y^2+ry\right]_{0}^{h}&\mbox{}\\ &=\displaystyle 2 \pi\sqrt{\frac{h^2+r^2}{h^2}} \left[-\frac{rh}{2}+rh\right]&\mbox{}\\ &=\displaystyle 2 \pi\frac{\sqrt{h^2+r^2}}{h} \left[\frac{rh}{2}\right]&\mbox{}\\ &= \displaystyle \pi r \sqrt{h^2+r^2}\mbox{ units}^2&\mbox{}\\ \end{array} $$