Today we will find volumes of revolution using a slightly different method than in the previous section. Instead of using disks to find a volume of revolution, we are going to use shells.
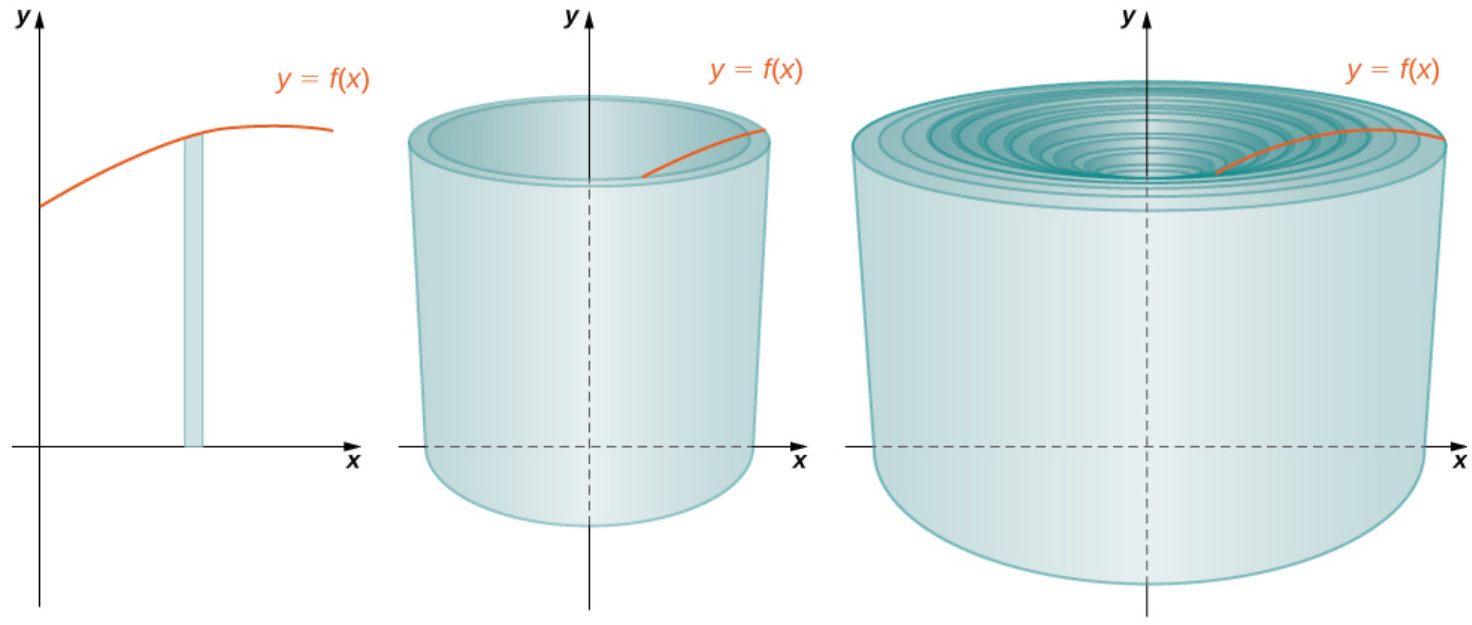
The Big Difference: The disk method integrates along the axis of revolution, whereas the shell method integrates in a direction perpendicular to the axis of revolution.
Volumes of Revolution: Cylindrical Shells
The volume of a typical shell at $x_i^*$ is $$V(x_i^*)=2 \pi x_i^* f(x_i^*)\Delta x$$
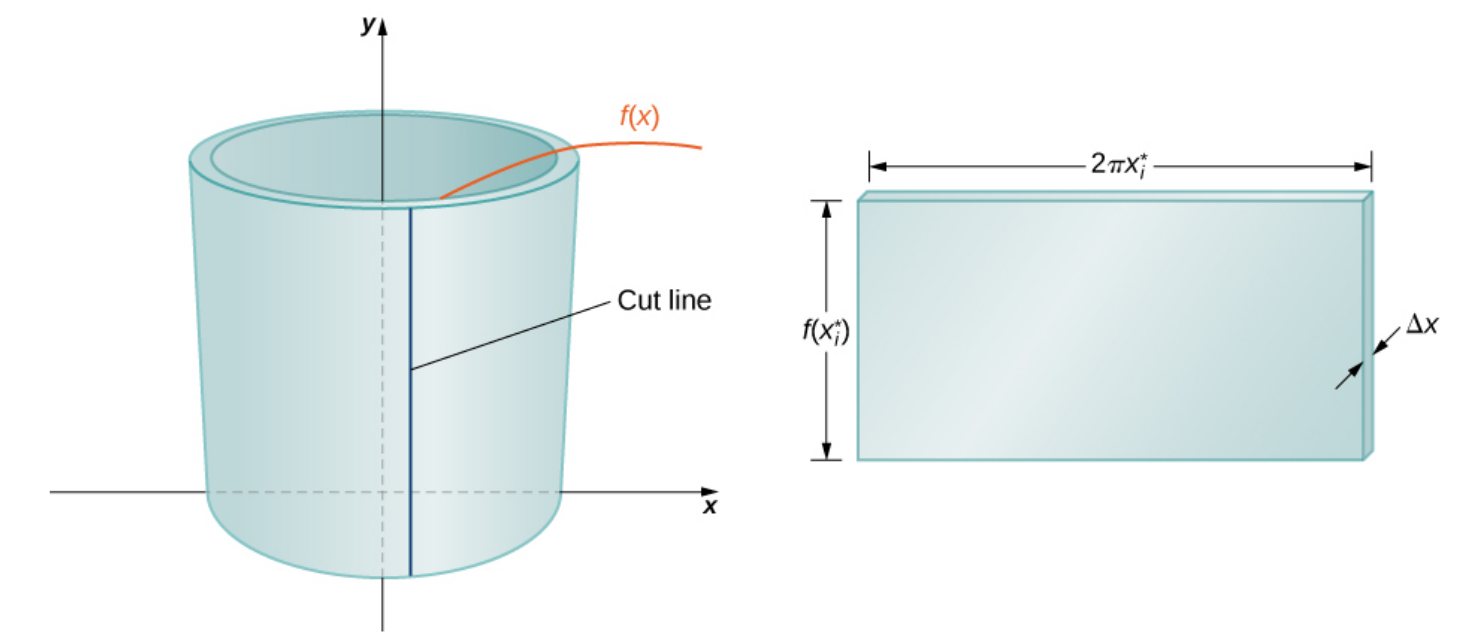
Volumes of Revolution: Cylindrical Shells
The exact volume $V$ of the solid is then approximated by adding up the volumes of all the individual shells $$V \approx \sum_{i=1}^{n} 2\pi x_i^* f(x_i^*)\Delta x.$$
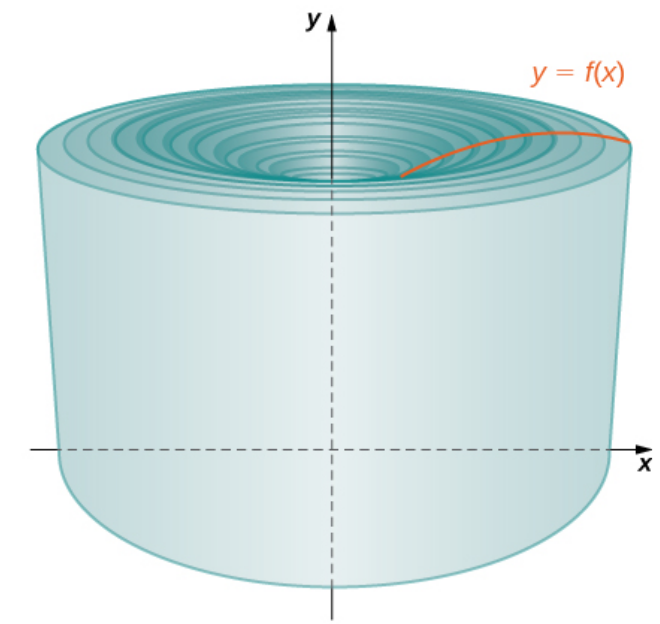
Volumes of Revolution: Cylindrical Shells
| $$\lim_{n \rightarrow \infty} \sum_{i=1}^{n} 2\pi x_i^* f(x_i^*)\Delta x$$ | ||
| $\displaystyle \sum_{i=1}^{n} 2\pi x_i^* f(x_i^*)\Delta x$ | $\longrightarrow$ | $\displaystyle \int_{a}^{b} 2 \pi x f(x) \,dx$ |
| | $\longrightarrow$ |  |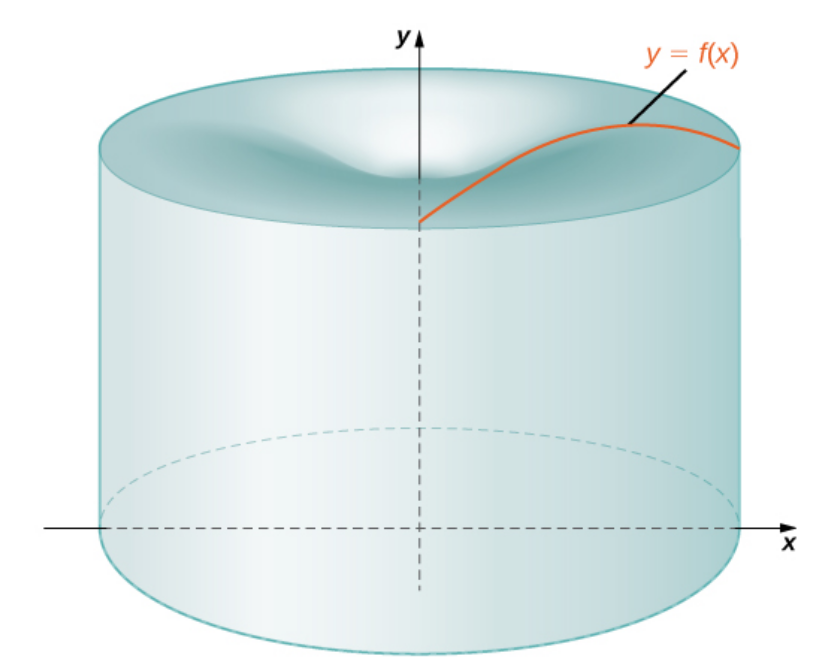
Volumes of Revolution: Cylindrical Shells
The exact volume $V$ of the solid formed by revolving $R$ around the $y$-axis is given by $$\displaystyle V=\int_{a}^{b} 2 \pi x f(x) \,dx$$
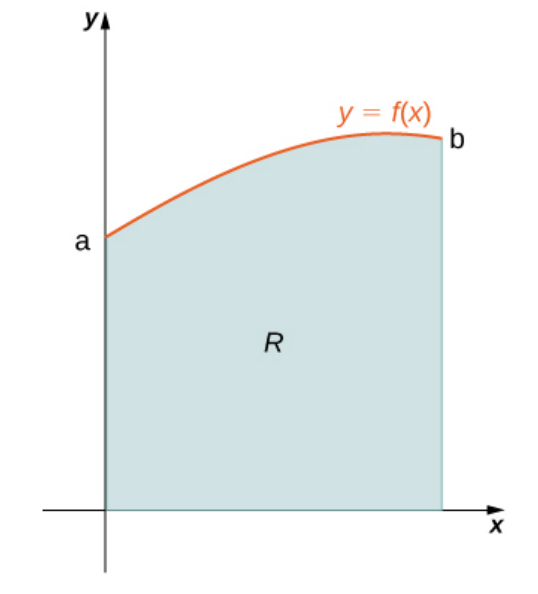
Example: Cylindrical Shells
Define $R$ as the region bounded above by the graph of $f (x) = 2x - x^2$ and below by the $x$-axis over the interval $[0, 2].$ Find the volume of the solid of revolution formed by revolving $R$ around the $y$-axis.
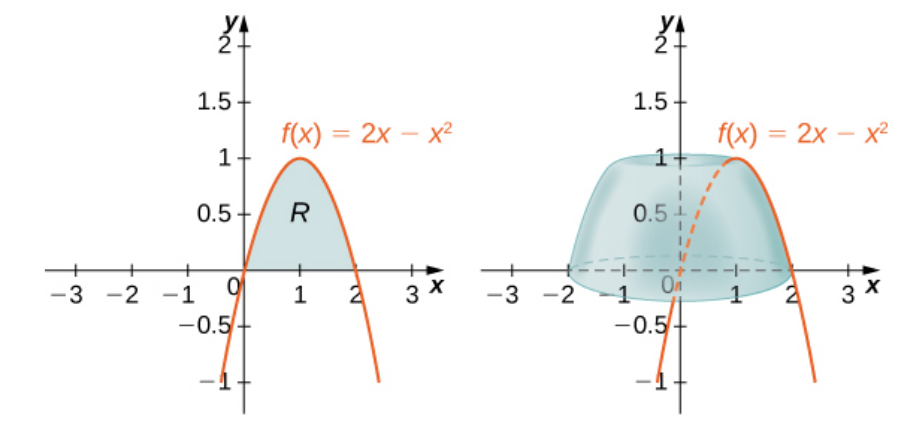
The volume of revolution $V$ is
$$
\begin{array}{lll}
\displaystyle V &=\displaystyle \int_{a}^{b} 2 \pi x f(x) \,dx &\mbox{}\\
&=\displaystyle \int_{0}^{2} 2 \pi x (2x - x^2) \,dx &\mbox{}\\
&=\displaystyle 2 \pi \int_{0}^{2} 2x^2 - x^3 \,dx &\mbox{}\\
&=\displaystyle 2 \pi \left[\frac{2}{3}x^3-\frac{1}{4}x^4\right]_{0}^{2} &\mbox{}\\
&=\displaystyle 2 \pi \left[\frac{2}{3}2^3-\frac{1}{4}2^4\right] &\mbox{}\\
&=\displaystyle 2 \pi \left[\frac{16}{3}-\frac{16}{4}\right] &\mbox{}\\
&=\displaystyle 2 \pi \cdot \frac{4}{3} &\mbox{}\\
&=\displaystyle \frac{8\pi}{3} &\mbox{}\\
&\approx \displaystyle 8.37758041 \mbox{ units}^3&\mbox{}\\
\end{array}
$$
Example: Cylindrical Shells
Draw the region bounded by the curves and use shells to find the volume generated when the region is rotated around the $y$-axis. $$y=\frac{1}{1+x^2}, \,\,\,\, x=0, \,\,\,\, \mbox{ and } \,\,\,\, x=3$$
We first sketch the region described in the statement of the problem:
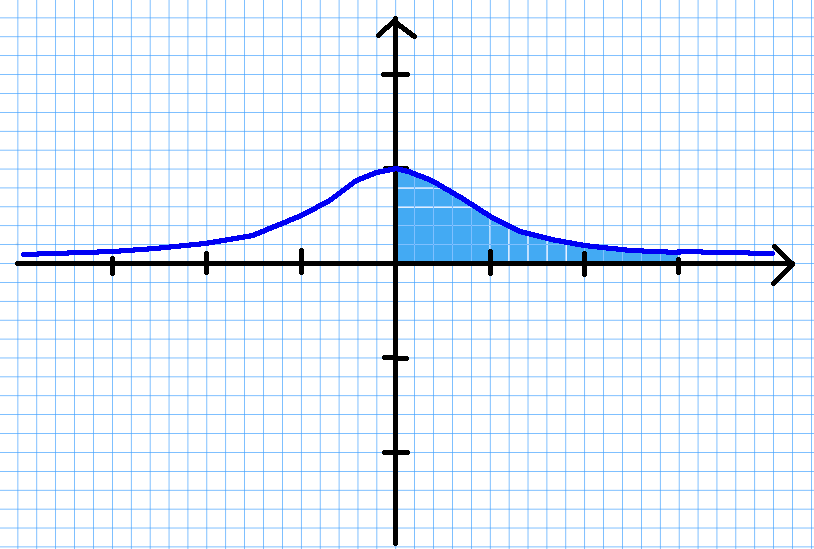The volume of revolution $V$ is
$$
\begin{array}{lll}
\displaystyle V &=\displaystyle \int_{a}^{b} 2 \pi x f(x) \,dx &\mbox{}\\
&=\displaystyle \int_{0}^{3} 2 \pi x \frac{1}{1+x^2} \,dx &\mbox{}\\
&=\displaystyle \pi\int_{0}^{3}\frac{2x}{1+x^2} \,dx &\mbox{}\\
&=\displaystyle \pi\int_{1}^{10}\frac{1}{u} \,du &\mbox{ letting $u=1+x^2$ so that $dx=2x\,dx$ }\\
&=\displaystyle \pi\left[\ln u\right]_{1}^{10}&\mbox{}\\
&=\displaystyle \pi \ln 10&\mbox{}\\
&\approx \displaystyle 7.233784412 \mbox{ units}^3&\mbox{}\\
\end{array}
$$
Volumes of Revolution: Cylindrical Shells
Nice Fact: We can use the shell method with solids of revolution by revolving around the $x$-axis too when $x$ is a function of $y,$ that is when $x=g(y)$ for $y \in [c,d].$ In this case $$V=\int_{c}^{d} 2\pi \, y \, g(y) \, dy$$
Example: Cylindrical Shells
Define $Q$ as the region bounded on the right by the graph of $g(y) = 2 \sqrt{y}$ and on the left by the $y$-axis for $y \in [0, 4].$ Find the volume of the solid of revolution formed by revolving $Q$ around the $x$-axis.
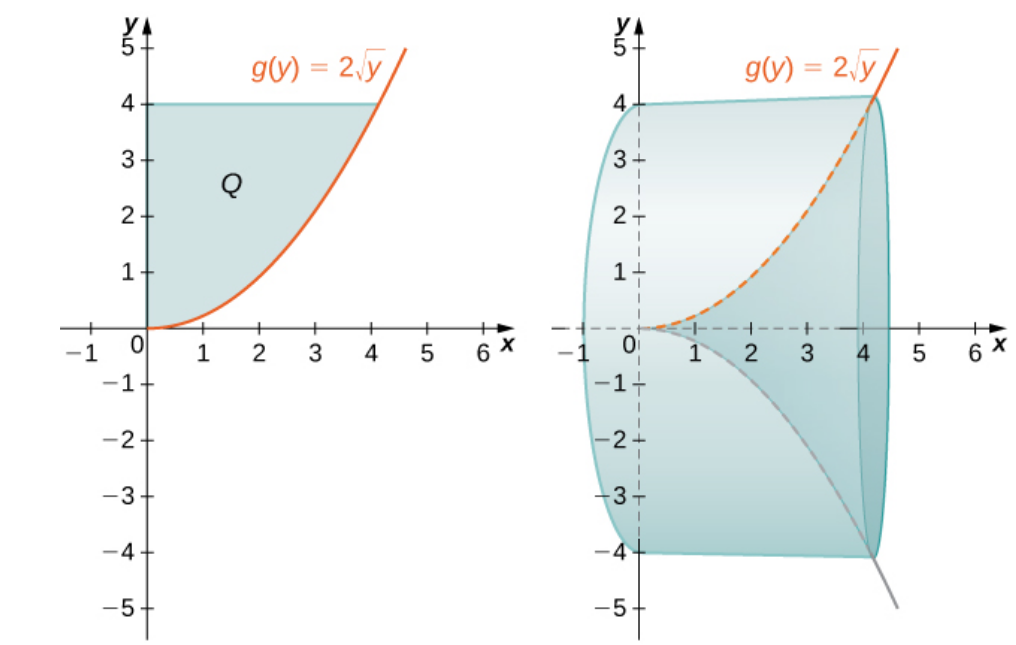
The volume of revolution $V$ is
$$
\begin{array}{lll}
\displaystyle V &=\displaystyle \int_{c}^{d} 2\pi \, y \, g(y) \, dy &\mbox{}\\
&=\displaystyle \int_{0}^{4} 2 \pi y (2\sqrt{y}) \,dy &\mbox{}\\
&=\displaystyle 4\pi \int_{0}^{4} y^{3/2} \,dy &\mbox{}\\
&=\displaystyle 4\pi \left[\frac{2}{5}y^{5/2}\right]_{0}^{4} &\mbox{}\\
&=\displaystyle 4\pi \left[\frac{2}{5}4^{5/2}\right] &\mbox{}\\
&=\displaystyle 4\pi \cdot \frac{2}{5}\cdot 32&\mbox{}\\
&=\displaystyle \frac{256\pi}{5} &\mbox{}\\
&\approx \displaystyle 160.849543864 \mbox{ units}^3&\mbox{}\\
\end{array}
$$
Example: Disk Method & Cylindrical Shells
Draw the region bounded by the curves and use both the shell and disk/washer methods to find the volume generated when the above region is rotated around the $y$-axis. $$y=x^2 \,\,\,\, \mbox{ and } \,\,\,\, y=x$$
We first sketch the region described in the statement of the problem:
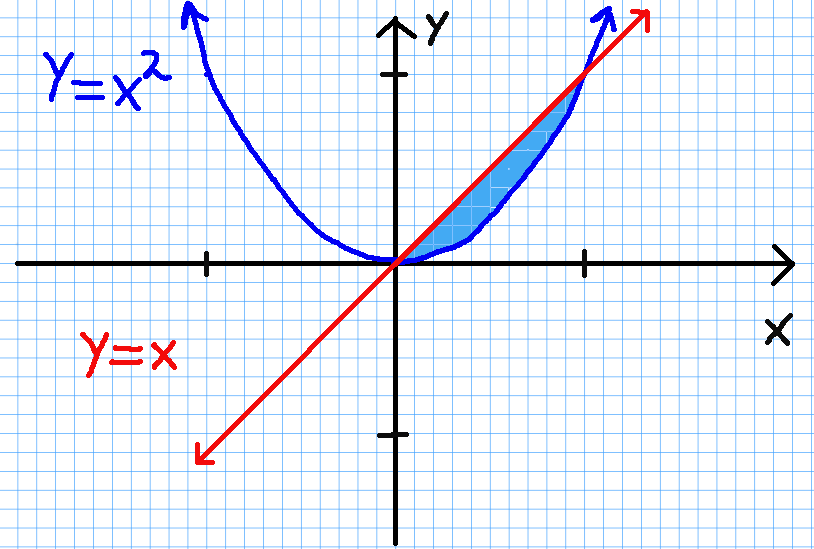
Shell Method: The shell method requires that we subtract a lower volume (below $y=x^2$) from an upper volume (below $y=x$):
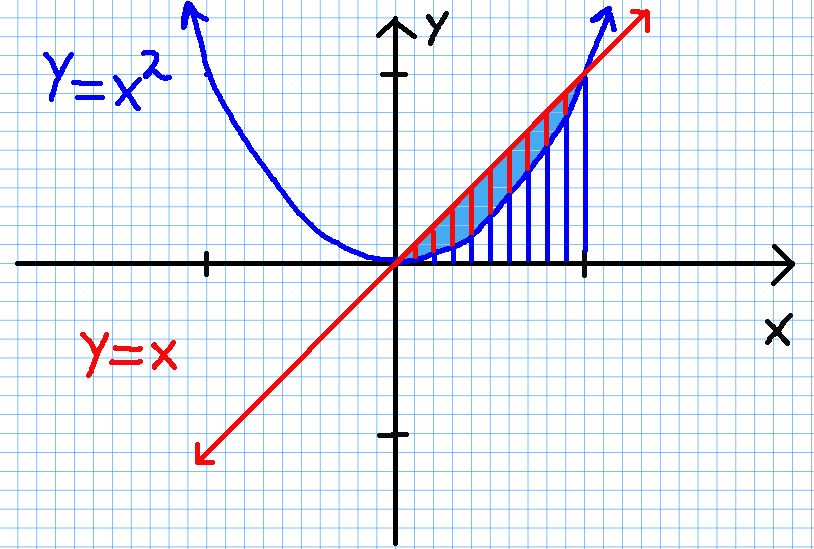
Note that this is similar to the washer method from the previous section.
The volume of revolution $V$ is $$ \begin{array}{lll} \displaystyle V &=\displaystyle \mbox{Upper Volume}-\mbox{Lower Volume}&\mbox{}\\ &=\displaystyle \int_{a}^{b} 2 \pi x f(x) \,dx-\int_{a}^{b} 2 \pi x g(x) \,dx &\mbox{}\\ &=\displaystyle \int_{0}^{1} 2 \pi x \cdot x \,dx-\int_{0}^{1} 2 \pi x \cdot x^2 \,dx &\mbox{}\\ &=\displaystyle 2 \pi \int_{0}^{1} x^2 \,dx-2 \pi \int_{0}^{1} x^3 \,dx &\mbox{}\\ &=\displaystyle 2 \pi \left[\frac{1}{3}x^3\right]_{0}^{1}-2 \pi \left[\frac{1}{4}x^4\right]_{0}^{1} &\mbox{}\\ &=\displaystyle 2 \pi \cdot \frac{1}{3}-2 \pi \cdot \frac{1}{4} &\mbox{}\\ &=\displaystyle \frac{2\pi}{12} &\mbox{}\\ &=\displaystyle \frac{\pi}{6} &\mbox{}\\ &\approx \displaystyle 0.523598776 \mbox{ units}^3&\mbox{}\\ \end{array} $$ Note that for the shell method, the direction of integration is perpendicular to the axis of revolution.
Disk/Washer Method: The disk/washer method requires that we first express $x$ as a function of $y$ and then integrate with respect to $y.$ From there we can understand which volume is the inner volume (to the left of $x=y$) and which is the outer volume (to the left of $x=\sqrt{y}$):
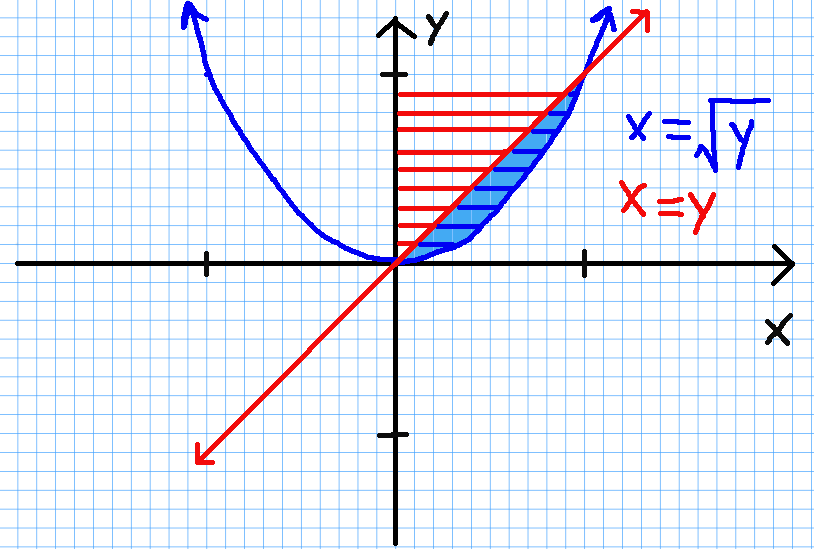
The volume of revolution $V$ is $$ \begin{array}{lll} \displaystyle V &=\displaystyle \mbox{Outer Volume}-\mbox{Inner Volume}&\mbox{}\\ &=\displaystyle \int_{c}^{d} \pi[u(y)]^2\, dy -\int_{c}^{d} \pi[v(y)]^2\, dy &\mbox{}\\ &=\displaystyle \int_{c}^{d} \pi[u(y)^2-v(y)^2]\, dy &\mbox{this is simply the washer formula from last section}\\ &=\displaystyle \int_{0}^{1} \pi[(\sqrt{y})^2-y^2]\, dy &\mbox{}\\ &=\displaystyle \pi\int_{0}^{1} y-y^2\, dy &\mbox{}\\ &=\displaystyle \pi\left[\frac{1}{2}y^2-\frac{1}{3}y^3\right]_{0}^{1} &\mbox{}\\ &=\displaystyle \pi\left[\frac{1}{2}-\frac{1}{3}\right] &\mbox{}\\ &=\displaystyle \pi\cdot\frac{1}{6} &\mbox{}\\ &=\displaystyle \frac{\pi}{6} &\mbox{}\\ &\approx \displaystyle 0.523598776 \mbox{ units}^3&\mbox{}\\ \end{array} $$ Note that for the disk/washer method, the direction of integration is parallel to the axis of revolution.
Shell Method: The shell method requires that we subtract a lower volume (below $y=x^2$) from an upper volume (below $y=x$):
Note that this is similar to the washer method from the previous section.
The volume of revolution $V$ is $$ \begin{array}{lll} \displaystyle V &=\displaystyle \mbox{Upper Volume}-\mbox{Lower Volume}&\mbox{}\\ &=\displaystyle \int_{a}^{b} 2 \pi x f(x) \,dx-\int_{a}^{b} 2 \pi x g(x) \,dx &\mbox{}\\ &=\displaystyle \int_{0}^{1} 2 \pi x \cdot x \,dx-\int_{0}^{1} 2 \pi x \cdot x^2 \,dx &\mbox{}\\ &=\displaystyle 2 \pi \int_{0}^{1} x^2 \,dx-2 \pi \int_{0}^{1} x^3 \,dx &\mbox{}\\ &=\displaystyle 2 \pi \left[\frac{1}{3}x^3\right]_{0}^{1}-2 \pi \left[\frac{1}{4}x^4\right]_{0}^{1} &\mbox{}\\ &=\displaystyle 2 \pi \cdot \frac{1}{3}-2 \pi \cdot \frac{1}{4} &\mbox{}\\ &=\displaystyle \frac{2\pi}{12} &\mbox{}\\ &=\displaystyle \frac{\pi}{6} &\mbox{}\\ &\approx \displaystyle 0.523598776 \mbox{ units}^3&\mbox{}\\ \end{array} $$ Note that for the shell method, the direction of integration is perpendicular to the axis of revolution.
Disk/Washer Method: The disk/washer method requires that we first express $x$ as a function of $y$ and then integrate with respect to $y.$ From there we can understand which volume is the inner volume (to the left of $x=y$) and which is the outer volume (to the left of $x=\sqrt{y}$):
The volume of revolution $V$ is $$ \begin{array}{lll} \displaystyle V &=\displaystyle \mbox{Outer Volume}-\mbox{Inner Volume}&\mbox{}\\ &=\displaystyle \int_{c}^{d} \pi[u(y)]^2\, dy -\int_{c}^{d} \pi[v(y)]^2\, dy &\mbox{}\\ &=\displaystyle \int_{c}^{d} \pi[u(y)^2-v(y)^2]\, dy &\mbox{this is simply the washer formula from last section}\\ &=\displaystyle \int_{0}^{1} \pi[(\sqrt{y})^2-y^2]\, dy &\mbox{}\\ &=\displaystyle \pi\int_{0}^{1} y-y^2\, dy &\mbox{}\\ &=\displaystyle \pi\left[\frac{1}{2}y^2-\frac{1}{3}y^3\right]_{0}^{1} &\mbox{}\\ &=\displaystyle \pi\left[\frac{1}{2}-\frac{1}{3}\right] &\mbox{}\\ &=\displaystyle \pi\cdot\frac{1}{6} &\mbox{}\\ &=\displaystyle \frac{\pi}{6} &\mbox{}\\ &\approx \displaystyle 0.523598776 \mbox{ units}^3&\mbox{}\\ \end{array} $$ Note that for the disk/washer method, the direction of integration is parallel to the axis of revolution.
Example: Cylindrical Shells
Use the method of shells to find the volume of a cone with radius $r$ and height $h.$
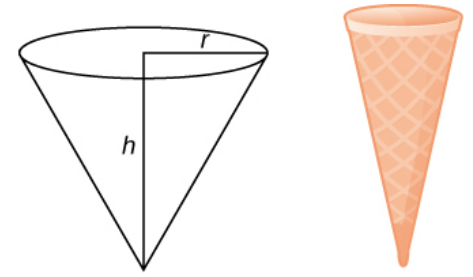
We can find the volume of a cone by rotating a non-vertical line about the $y$-axis.
To do so, we first establish a coordinate system in which the rotation will take place:
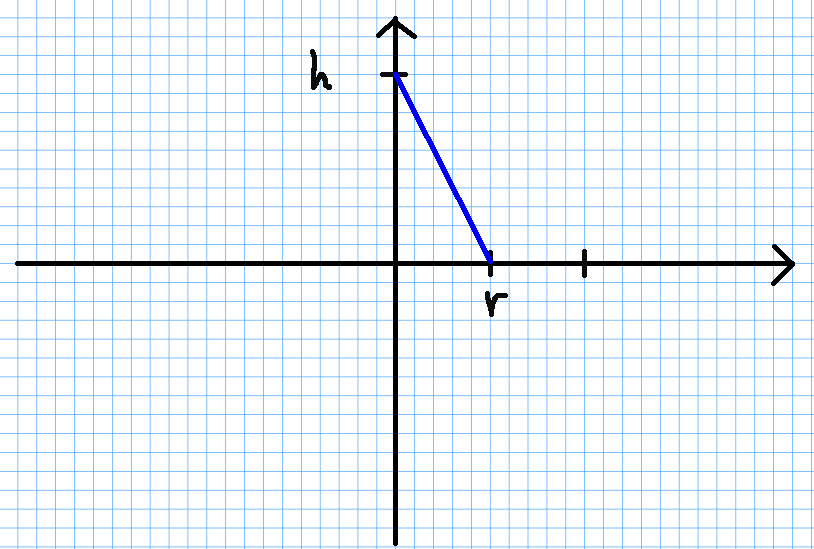We shall rotate the line $\displaystyle y=f(x)=-\frac{h}{r}x+h$ around the $y$ axis using the shell method:
$$
\begin{array}{lll}
\displaystyle V &=\displaystyle \int_{a}^{b} 2 \pi x f(x) \,dx &\mbox{}\\
&=\displaystyle \int_{0}^{r} 2 \pi x \left(-\frac{h}{r}x+h\right) \,dx &\mbox{}\\
&=\displaystyle 2\pi \int_{0}^{r} -\frac{h}{r}x^2+hx \,dx &\mbox{}\\
&=\displaystyle 2\pi \left[-\frac{h}{3r}x^3+\frac{h}{2}x^2\right]_{0}^{r} &\mbox{}\\
&=\displaystyle 2\pi \left[-\frac{h}{3r}r^3+\frac{h}{2}r^2\right] &\mbox{}\\
&=\displaystyle 2\pi \left[-\frac{h}{3}r^2+\frac{h}{2}r^2\right] &\mbox{}\\
&=\displaystyle 2\pi r^2h \left[-\frac{1}{3}+\frac{1}{2}\right] &\mbox{}\\
&=\displaystyle 2\pi r^2h \cdot \frac{1}{6} &\mbox{}\\
&=\displaystyle \frac{1}{3}\pi r^2h &\mbox{}\\
\end{array}
$$
Bonus Example: Different Axis
Draw the region bounded by the curves and find the volume generated when the above region is rotated around the line $x=4.$ $$y=\frac{1}{4-x}, \,\,\,\, x=1, \,\,\,\, \mbox{ and } \,\,\,\, x=2$$
We first sketch the region described in the statement of the problem:
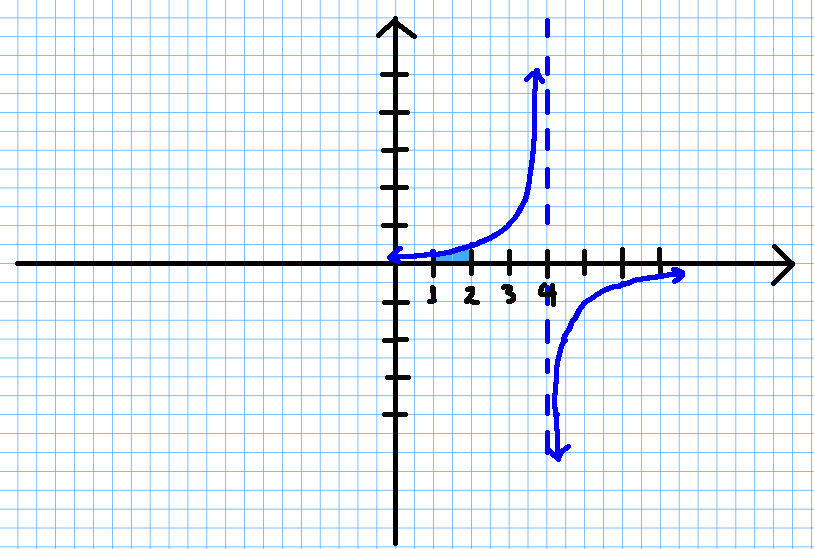
From our figure, the radius of a shell spun around the vertical line $x=4$ is $4-x:$
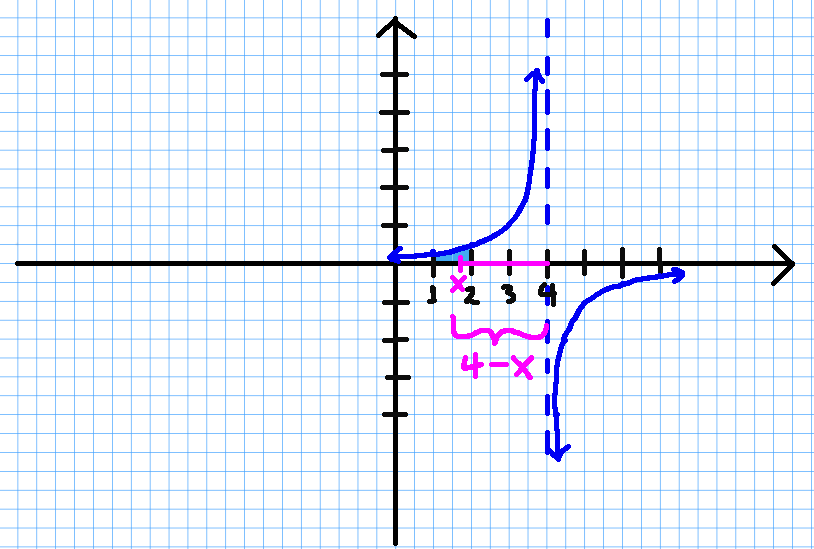
Thus, the volume of revolution $V$ is $$ \begin{array}{lll} \displaystyle V &=\displaystyle \int_{a}^{b} 2 \pi \cdot \mbox{radius of shell at $x$ } \cdot \mbox{ height of shell at $x$} \,dx &\mbox{}\\ &=\displaystyle \int_{1}^{2} 2 \pi \cdot (4-x) \cdot \frac{1}{4-x} \,dx &\mbox{}\\ &=\displaystyle 2 \pi \int_{1}^{2} 1 \,dx &\mbox{}\\ &=\displaystyle 2 \pi \left[x\right]_{1}^{2} &\mbox{}\\ &=\displaystyle 2 \pi \cdot 1 &\mbox{}\\ &=\displaystyle 2 \pi &\mbox{}\\ &\approx \displaystyle 6.283185307 \mbox{ units}^3&\mbox{}\\ \end{array} $$
From our figure, the radius of a shell spun around the vertical line $x=4$ is $4-x:$
Thus, the volume of revolution $V$ is $$ \begin{array}{lll} \displaystyle V &=\displaystyle \int_{a}^{b} 2 \pi \cdot \mbox{radius of shell at $x$ } \cdot \mbox{ height of shell at $x$} \,dx &\mbox{}\\ &=\displaystyle \int_{1}^{2} 2 \pi \cdot (4-x) \cdot \frac{1}{4-x} \,dx &\mbox{}\\ &=\displaystyle 2 \pi \int_{1}^{2} 1 \,dx &\mbox{}\\ &=\displaystyle 2 \pi \left[x\right]_{1}^{2} &\mbox{}\\ &=\displaystyle 2 \pi \cdot 1 &\mbox{}\\ &=\displaystyle 2 \pi &\mbox{}\\ &\approx \displaystyle 6.283185307 \mbox{ units}^3&\mbox{}\\ \end{array} $$