As we have already seen, many applied problems can be reduced to finding areas. The same can also be said for volumes.
Today, we will apply our understanding of integration to finding certain volumes.
The Situash
Suppose we want to find the volume of a weird shape like the one below.

Step 1: Put the solid on a coordinate system.
Notice that the cross-sectional area changes with respect to $x.$
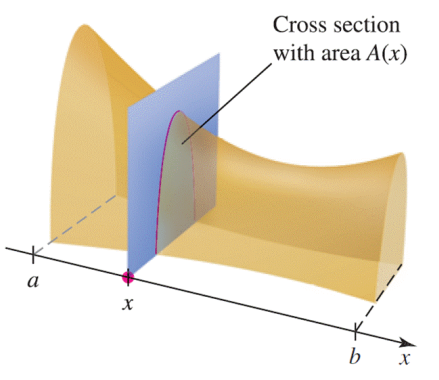
Step 2: Find the volume of a "wafer-thin" cross-sectional volume with width $\Delta x.$
Choose a point $x_i^*$ between $x$ and $x+\Delta x.$
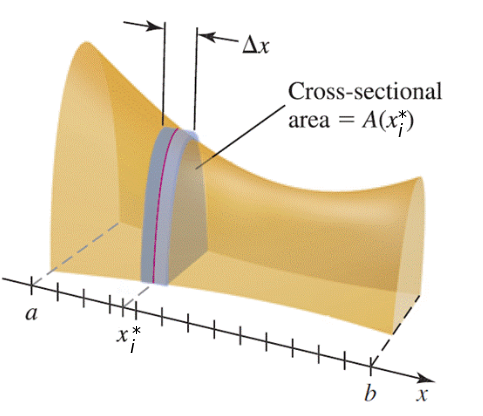
The "wafer-thin" volume is $A(x_i^*)\Delta x.$
Step 3: Add up all the "wafer-thin" volumes to get an approximation of the solid's volume.
| $\displaystyle \sum_{i=1}^{10} A(x_i^*)\Delta x$ | $\approx$ | $\mbox{Exact Volume}$ |
 | $\approx$ |  |
Step 4: Start taking finer and finer approximations by increasing the number of "wafers."
| $\displaystyle \sum_{i=1}^{20} A(x_i^*)\Delta x$ | $\approx$ | $\mbox{Exact Volume}$ |
 | $\approx$ |  |
As we take more slices the wafers get even thinner!
...and thinner!
| $\displaystyle \sum_{i=1}^{30} A(x_i^*)\Delta x$ | $\approx$ | $\mbox{Exact Volume}$ |
 | $\approx$ |  |
Volumes by Slicing: If a solid has a cross-sectional area $A(x)$ at height or length $x,$ we can approximate the volume with a Riemann sum.
| $$\lim_{n \rightarrow \infty} \sum_{i=1}^{n} A(x_i^*)\Delta x$$ | ||
| $\displaystyle \sum_{i=1}^{n} A(x_i^*)\Delta x$ | $\longrightarrow$ | $\displaystyle \int_{a}^{b} A(x) \,dx$ |
 | $\longrightarrow$ |  |
The exact volume is the limit of the Riemann sum.
Volumes by Slicing

Example: Volumes by Slicing
Use the slicing method to find the volume of a right cone with radius of $2$ inches and height of $8$ inches
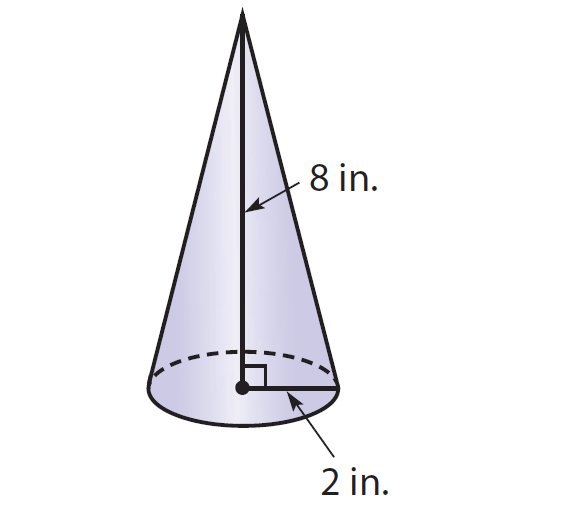
First we embed the cone into a coordinate system:
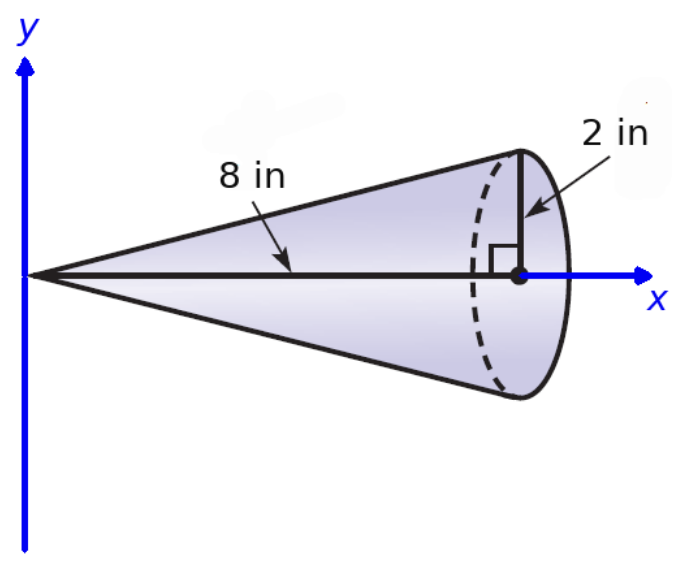
At a point $x$ in $[0,8]$ on the $x$-axis, a cross-section is a circle with radius $\displaystyle \frac{1}{4}x.$
Thus, $$\displaystyle A(x)=\pi r(x)^2=\pi \left(\frac{1}{4}x\right)^2=\frac{\pi}{16}x^2.$$ So, the volume is $$ \begin{array}{lll} V&=\displaystyle \int_{a}^{b} A(x) \, dx&\mbox{}\\ &=\displaystyle \int_{0}^{8} \frac{\pi}{16}x^2 \, dx&\mbox{}\\ &=\displaystyle \frac{\pi}{16} \int_{0}^{8} x^2 \, dx&\mbox{}\\ &=\displaystyle \frac{\pi}{16} \left[\frac{1}{3}x^3\right]_{0}^{8}&\mbox{}\\ &=\displaystyle \frac{\pi}{16}\frac{1}{3}8^3&\mbox{}\\ &=\displaystyle \frac{32\pi}{3}&\mbox{}\\ &\approx\displaystyle 33.510321638 \mbox{ units}^3&\mbox{}\\ \end{array} $$

At a point $x$ in $[0,8]$ on the $x$-axis, a cross-section is a circle with radius $\displaystyle \frac{1}{4}x.$
Thus, $$\displaystyle A(x)=\pi r(x)^2=\pi \left(\frac{1}{4}x\right)^2=\frac{\pi}{16}x^2.$$ So, the volume is $$ \begin{array}{lll} V&=\displaystyle \int_{a}^{b} A(x) \, dx&\mbox{}\\ &=\displaystyle \int_{0}^{8} \frac{\pi}{16}x^2 \, dx&\mbox{}\\ &=\displaystyle \frac{\pi}{16} \int_{0}^{8} x^2 \, dx&\mbox{}\\ &=\displaystyle \frac{\pi}{16} \left[\frac{1}{3}x^3\right]_{0}^{8}&\mbox{}\\ &=\displaystyle \frac{\pi}{16}\frac{1}{3}8^3&\mbox{}\\ &=\displaystyle \frac{32\pi}{3}&\mbox{}\\ &\approx\displaystyle 33.510321638 \mbox{ units}^3&\mbox{}\\ \end{array} $$
Volumes by Slicing
Problem-Solving Strategy: Finding Volumes by the Slicing Method
1. Examine the solid and determine the shape of a cross-section of the solid. It is often helpful to draw a picture if one is not provided.
2. Determine a formula for the area of the cross-section.
3. Integrate the area formula over the appropriate interval to get the volume.
Example: Volumes by Slicing
Find the volume of a solid whose base is a circle of radius $2.$ The slices perpendicular to the base are squares.
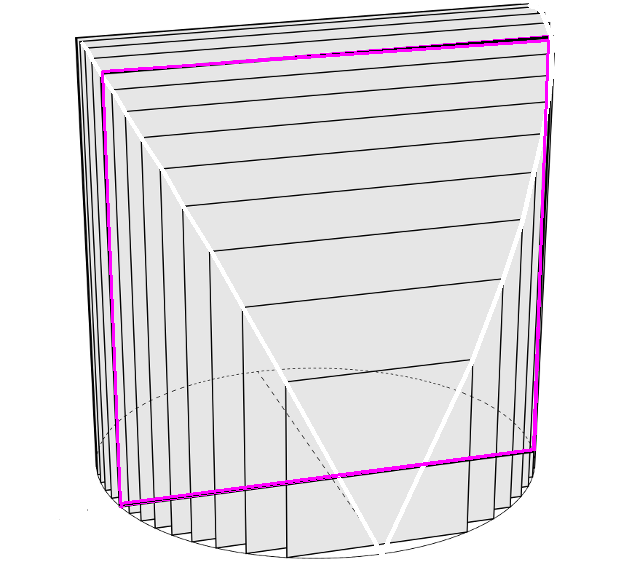
From the figure we see that the cross-sectional area of the solid is the square of the length of vertical chord on the circle in the $xy$-plane
which forms the base.
The length of side of this square cross-section is shown in pink below:
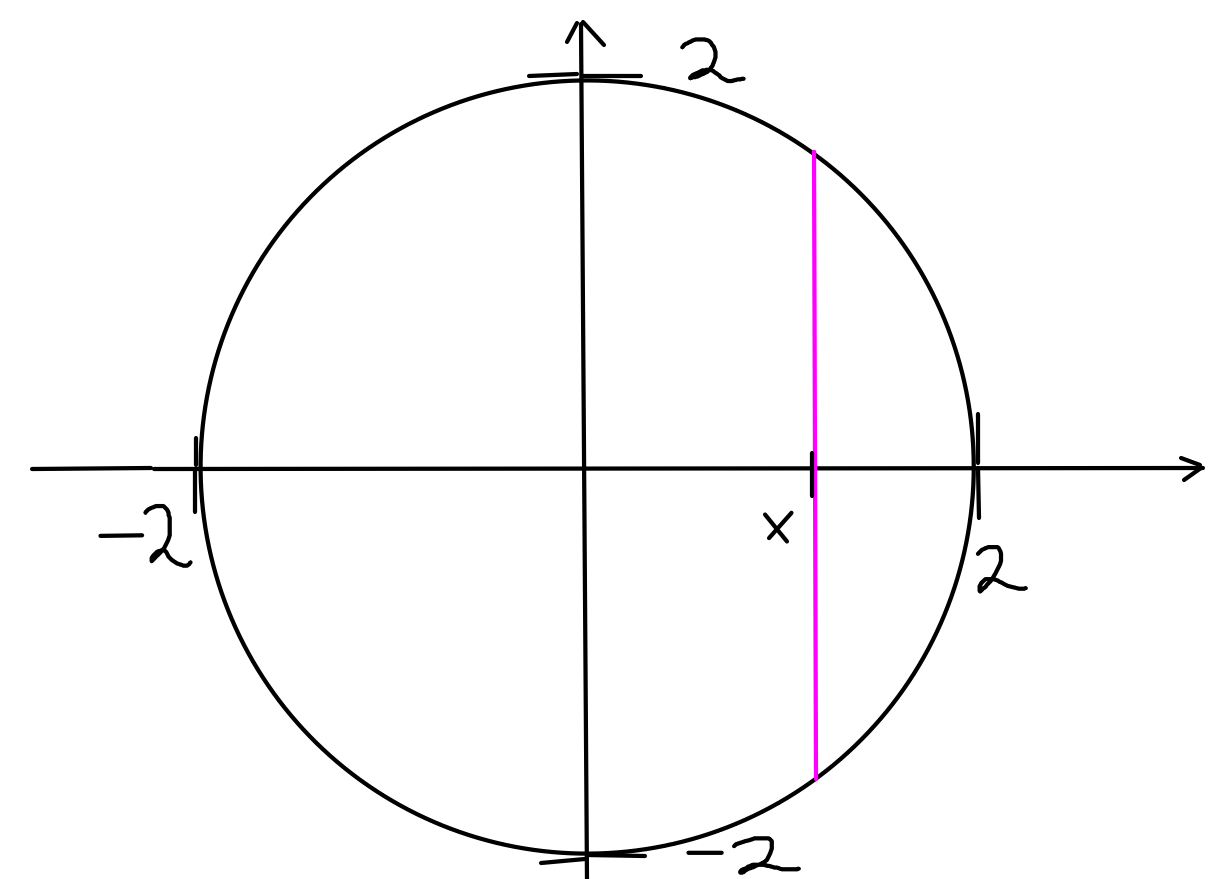
The equation for the upper half of the circle is $y=\sqrt{4-x^2}.$
Since the height of the curve above the $x$-axis is the function value, $\sqrt{4-x^2}$ represents half of the pink length. Thus, $$\mbox{Pink Length}=\mbox{Square Side Length}=2\sqrt{4-x^2}$$ It follows that the area of a cross-section located at $x$ is $$A(x)=\mbox{Square Side Length}^2=\left(2\sqrt{4-x^2}\right)^2=4(4-x^2)=16-4x^2$$ So, the volume is $$ \begin{array}{lll} V&=\displaystyle \int_{a}^{b} A(x) \, dx&\mbox{}\\ &=\displaystyle \int_{-2}^{2} 16-4x^2 \, dx&\mbox{}\\ &=\displaystyle \left[16x-\frac{4}{3}x^3\right]_{-2}^{2}&\mbox{}\\ &=\displaystyle \left[16\cdot 2-\frac{4}{3}2^3\right]-\left[16(-2)-\frac{4}{3}(-2)^3\right]&\mbox{}\\ &=\displaystyle \frac{128}{3}&\mbox{}\\ &\approx\displaystyle 42.67 \mbox{ units}^3&\mbox{}\\ \\ \end{array} $$
The length of side of this square cross-section is shown in pink below:

The equation for the upper half of the circle is $y=\sqrt{4-x^2}.$
Since the height of the curve above the $x$-axis is the function value, $\sqrt{4-x^2}$ represents half of the pink length. Thus, $$\mbox{Pink Length}=\mbox{Square Side Length}=2\sqrt{4-x^2}$$ It follows that the area of a cross-section located at $x$ is $$A(x)=\mbox{Square Side Length}^2=\left(2\sqrt{4-x^2}\right)^2=4(4-x^2)=16-4x^2$$ So, the volume is $$ \begin{array}{lll} V&=\displaystyle \int_{a}^{b} A(x) \, dx&\mbox{}\\ &=\displaystyle \int_{-2}^{2} 16-4x^2 \, dx&\mbox{}\\ &=\displaystyle \left[16x-\frac{4}{3}x^3\right]_{-2}^{2}&\mbox{}\\ &=\displaystyle \left[16\cdot 2-\frac{4}{3}2^3\right]-\left[16(-2)-\frac{4}{3}(-2)^3\right]&\mbox{}\\ &=\displaystyle \frac{128}{3}&\mbox{}\\ &\approx\displaystyle 42.67 \mbox{ units}^3&\mbox{}\\ \\ \end{array} $$
Volumes of Revolution
Volumes of revolution are obtained by rotating a curve around an axis.
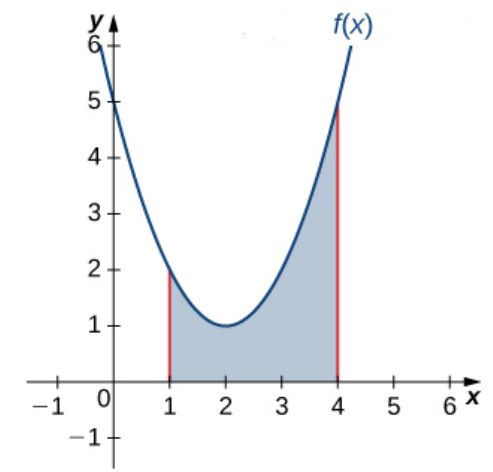
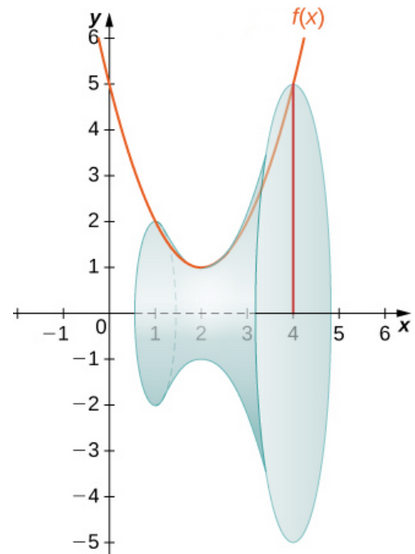
Volumes of Revolution
Volumes of revolution are determined by using the slicing method. In this case we have the advantage of knowing that the cross-sectional shape is...

Volumes of Revolution $$A(x)=$$

Volumes of Revolution
The volume $V$ of a solid of revolution about the $x$-axis is $$V= \int_{a}^{b} A(x) \, dx=\int_{a}^{b} \pi[f(x)]^2 \, dx.$$

Volumes of Revolution
The above method for finding volumes of revolution is called the disk method since the cross-sectional are of a volume of revolution is always a disk.
Example: The Disk Method
Use the disk method to find the volume of the solid of revolution formed by revolving the region between the graph of the function $\displaystyle f (x) = \frac{1}{x}$ and the $x$-axis over the interval $[1, 2]$ around the $x$-axis.
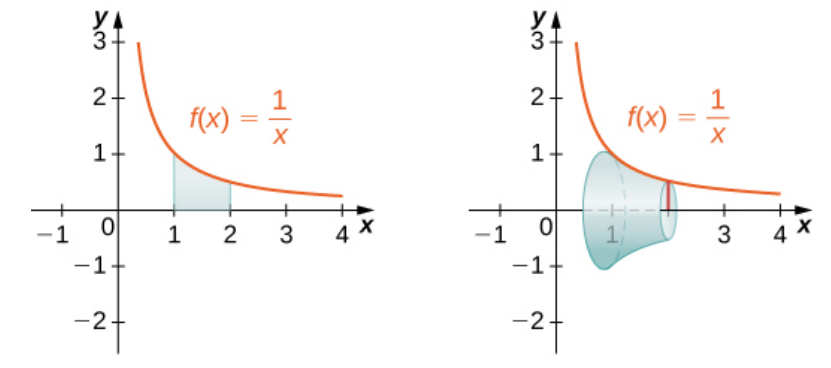
The volume of revolution $V$ is
$$
\begin{array}{lll}
\displaystyle V &=\displaystyle \int_{a}^{b} A(x) \, dx&\mbox{}\\
&=\displaystyle \int_{a}^{b}\pi[f(x)]^2 \, dx&\mbox{ $\pi[f(x)]^2$ is the area of each disk}\\
&=\displaystyle \int_{1}^{2}\pi\left[\frac{1}{x}\right]^2 \, dx&\mbox{}\\
&=\displaystyle \int_{1}^{2}\pi\frac{1}{x^2} \, dx&\mbox{}\\
&=\displaystyle \pi \int_{1}^{2}\frac{1}{x^2} \, dx&\mbox{}\\
&=\displaystyle \pi \left[-\frac{1}{x}\right]_{1}^{2}&\mbox{}\\
&=\displaystyle \pi \left(\left[-\frac{1}{2}\right]-\left[-\frac{1}{1}\right]\right)&\mbox{}\\
&=\displaystyle \pi \left(-\frac{1}{2}+1\right)&\mbox{}\\
&=\displaystyle \frac{\pi}{2}&\mbox{}\\
&\approx \displaystyle 1.570796327 \mbox{ units}^3&\mbox{}\\
\end{array}
$$
Volumes of Revolution
If we can express $x$ as a function of $y,$ finding volumes of revolution around the $y$-axis are found in a very similar fashion: $$V=\int_{c}^{d} \pi[g(y)]^2 \, dy.$$
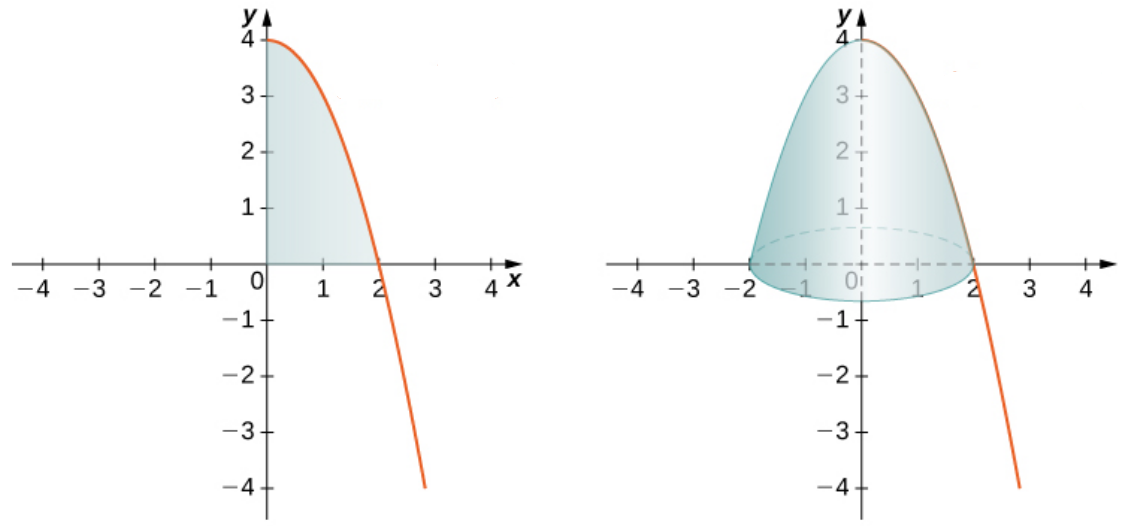
Example: The Disk Method
Let $R$ be the region bounded by the graph of $g(y) = \sqrt{4 - y}$ and the $y$-axis over the y-axis interval $[0, 4].$ Use the disk method to find the volume of the solid of revolution generated by rotating $R$ around the $y$-axis.
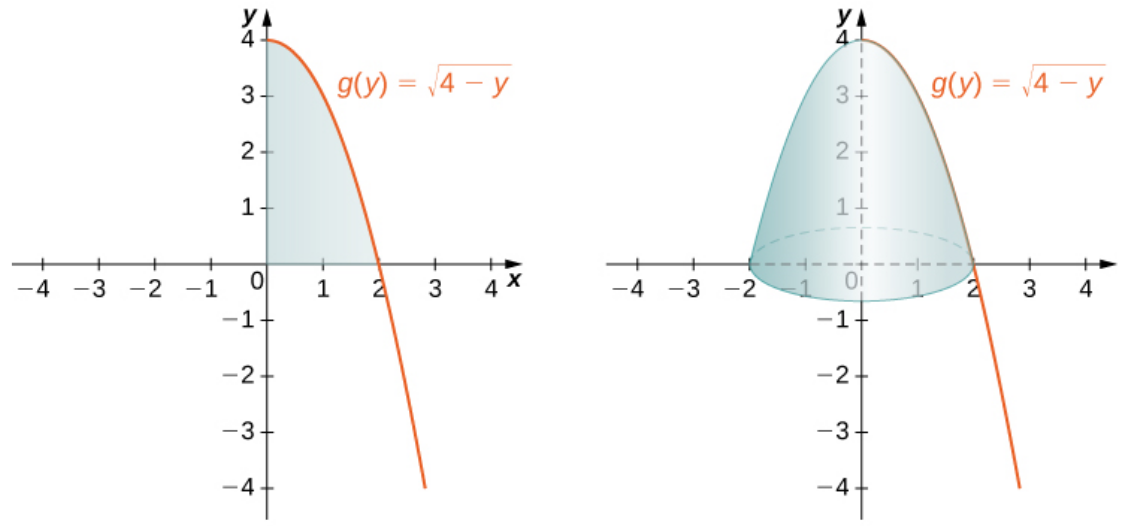
The volume of revolution $V$ is
$$
\begin{array}{lll}
\displaystyle V &=\displaystyle \int_{a}^{b} A(y) \, dy&\mbox{}\\
&=\displaystyle \int_{a}^{b}\pi[g(y)]^2 \, dy&\mbox{}\\
&=\displaystyle \int_{0}^{4}\pi\left[\sqrt{4-y}\right]^2 \, dy&\mbox{}\\
&=\displaystyle \pi \int_{0}^{4}4-y \, dy&\mbox{}\\
&=\displaystyle \pi \left[4y-\frac{1}{2}y^2\right]_{0}^{4}&\mbox{}\\
&=\displaystyle \pi \left[4\cdot 4-\frac{1}{2}(4)^2\right]&\mbox{}\\
&=\displaystyle \pi \left[16-8\right]&\mbox{}\\
&=\displaystyle 8\pi&\mbox{}\\
&\approx \displaystyle 25.13274123 \mbox{ units}^3&\mbox{}\\
\end{array}
$$
The Washer Method
When the solid of revolution has a cavity in the middle, the slices used to approximate the volume are not disks, but washers (disks with holes in the center).
The Washer Method
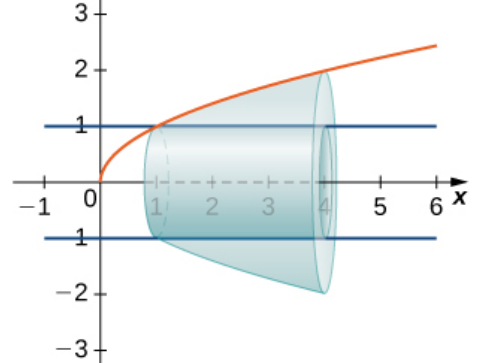
$$\mbox{Volume}=\mbox{Outer Volume}-\mbox{Inner Volume}=\int_{a}^{b}\pi[f(x)]^2 \, dx-\int_{a}^{b}\pi[g(x)]^2 \, dx$$
The Washer Method
The volume $V$ of a solid of revolution about the $x$-axis is $$V= \int_{a}^{b} \pi[f(x)^2-g(x)^2]\, dx.$$


Example: The Washer Method
Find the volume of a solid of revolution formed by revolving the region bounded above by the graph of $f (x) = x$ and below by the graph of $\displaystyle g(x) = \frac{1}{x}$ over the interval $[1, 4]$ around the $x$-axis.
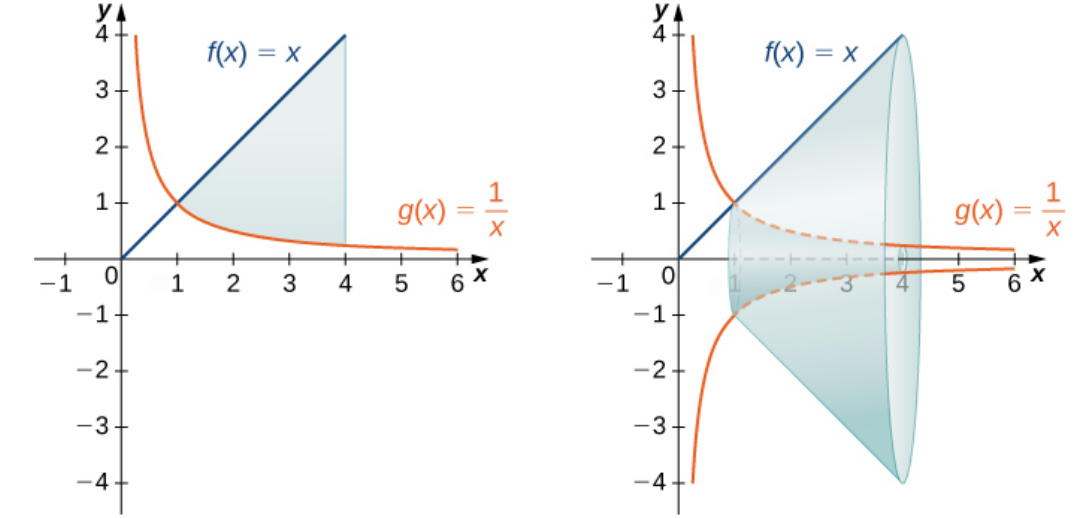
The volume of revolution $V$ is
$$
\begin{array}{lll}
\displaystyle V &=\displaystyle \int_{a}^{b} \pi[f(x)^2-g(x)^2]\, dx&\mbox{}\\
&=\displaystyle \int_{1}^{4} \pi\left[x^2-\left(\frac{1}{x}\right)^2\right]\, dx&\mbox{}\\
&=\displaystyle \pi \int_{1}^{4} \left[x^2-\frac{1}{x^2}\right]\, dx&\mbox{}\\
&=\displaystyle \pi \left[\frac{1}{3}x^3+\frac{1}{x}\right]_{1}^{4} &\mbox{}\\
&=\displaystyle \pi \left(\left[\frac{1}{3}4^3+\frac{1}{4}\right]-\left[\frac{1}{3}1^3+\frac{1}{1}\right]\right) &\mbox{}\\
&=\displaystyle \pi \left(\frac{64}{3}+\frac{1}{4}-\frac{1}{3}-1\right) &\mbox{}\\
&=\displaystyle \frac{81\pi}{4} &\mbox{}\\
&\approx \displaystyle 63.61725124 \mbox{ units}^3&\mbox{}\\
\end{array}
$$
The Washer Method
The volume $V$ of a solid of revolution about the $y$-axis is $$V= \int_{c}^{d} \pi[u(y)^2-v(y)^2]\, dy.$$
Example: The Washer Method
Draw the region bounded by the curves and use the washer method to find the volume when the above region is rotated around the $y$-axis. $$y=\sqrt[3]{x}, \,\,\,\, y=x^3, \,\,\,\, x=0, \,\,\,\, \mbox{ and } \,\,\,\, x=1$$
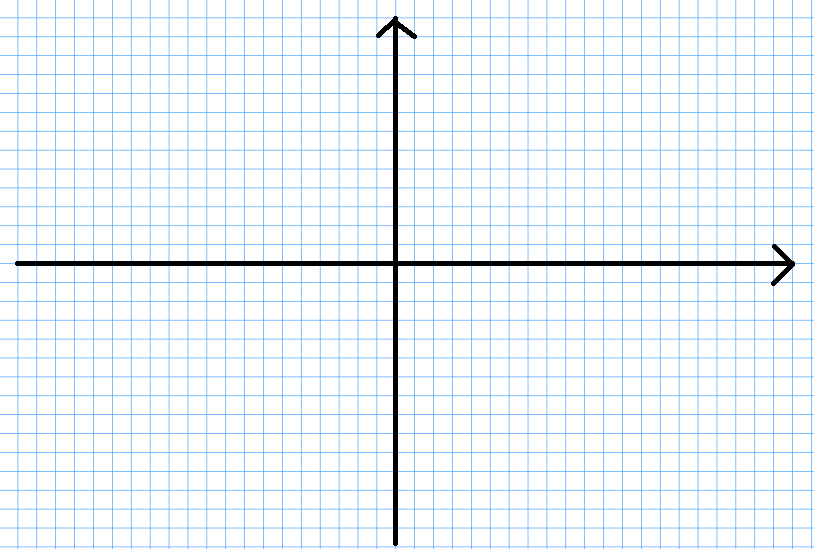
We first sketch the region described in the statement of the problem:
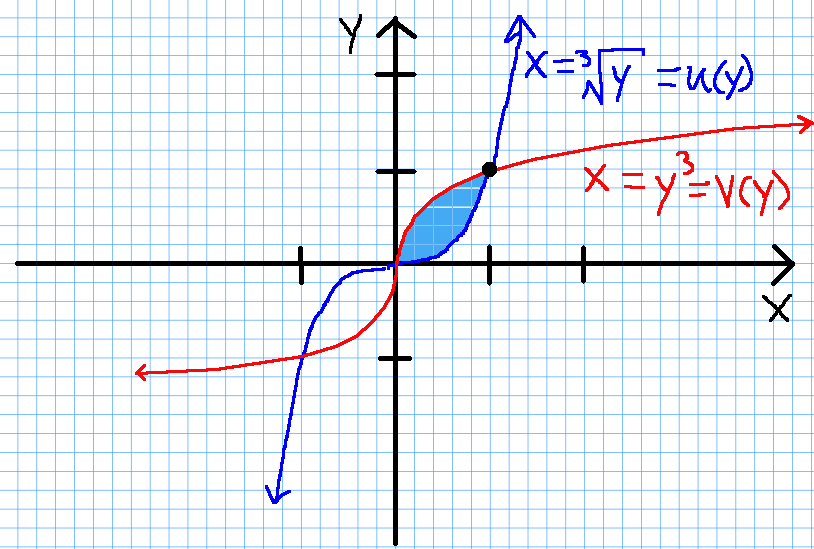 As seen in the above figure, we re-expressed $x$ as a function of $y$ in order to use the
washer method integrating along the $y$-axis.
As seen in the above figure, we re-expressed $x$ as a function of $y$ in order to use the
washer method integrating along the $y$-axis.
$$ \begin{array}{lll} \displaystyle V &=\displaystyle \int_{a}^{b} \pi[u(y)^2-v(y)^2]\, dy&\mbox{}\\ &=\displaystyle \int_{0}^{1} \pi\left[(\sqrt[3]{y})^2-(y^3)^2\right]\, dy&\mbox{}\\ &=\displaystyle \pi\int_{0}^{1} \left[y^{2/3}-y^6\right]\, dy&\mbox{}\\ &=\displaystyle \pi\left[\frac{3}{5}y^{5/3}-\frac{1}{7}y^7\right]_{0}^{1}&\mbox{}\\ &=\displaystyle \pi\left[\frac{3}{5}-\frac{1}{7}\right]&\mbox{}\\ &=\displaystyle \frac{16 \pi}{35}&\mbox{}\\ &\approx \displaystyle 1.436156642 \mbox{ units}^3&\mbox{}\\ \end{array} $$

$$ \begin{array}{lll} \displaystyle V &=\displaystyle \int_{a}^{b} \pi[u(y)^2-v(y)^2]\, dy&\mbox{}\\ &=\displaystyle \int_{0}^{1} \pi\left[(\sqrt[3]{y})^2-(y^3)^2\right]\, dy&\mbox{}\\ &=\displaystyle \pi\int_{0}^{1} \left[y^{2/3}-y^6\right]\, dy&\mbox{}\\ &=\displaystyle \pi\left[\frac{3}{5}y^{5/3}-\frac{1}{7}y^7\right]_{0}^{1}&\mbox{}\\ &=\displaystyle \pi\left[\frac{3}{5}-\frac{1}{7}\right]&\mbox{}\\ &=\displaystyle \frac{16 \pi}{35}&\mbox{}\\ &\approx \displaystyle 1.436156642 \mbox{ units}^3&\mbox{}\\ \end{array} $$