As we have already seen, many applied problems can be reduced to finding areas. Today, we learn the important skill of finding areas between curves.
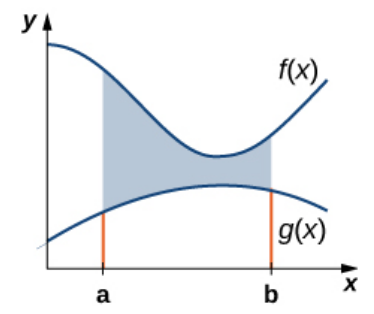
Area Between Two Curves
Area Between Two Curves
Example
Determine the area of the region between the two curves in the given figure by integrating over the $x$-axis.
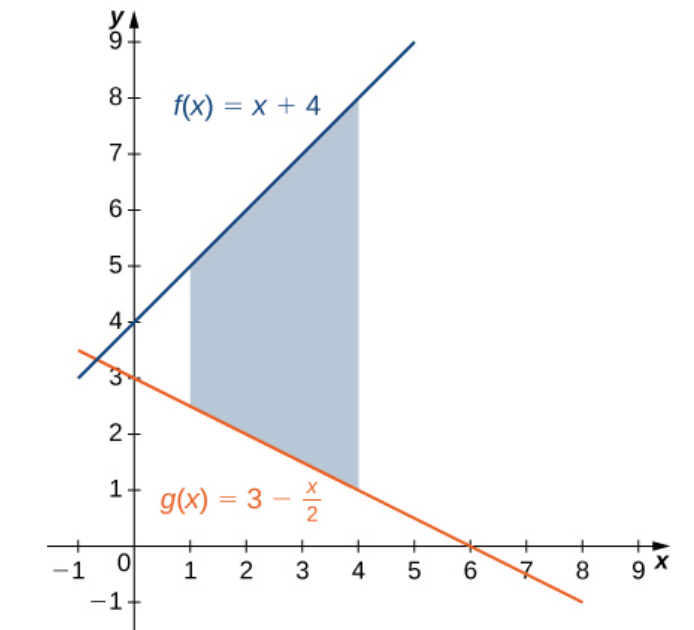
$$
\begin{array}{lll}
\mbox{Area Between $f(x)$ and $g(x)$ on $[a,b]$}&=\displaystyle \int_{a}^{b} [f(x)-g(x)] \, dx&\mbox{}\\
&=\displaystyle \int_{1}^{4} \left[x+4-\left(3-\frac{x}{2}\right)\right] \, dx&\mbox{}\\
&=\displaystyle \int_{1}^{4} \left[\frac{3}{2}x+1\right] \, dx&\mbox{}\\
&=\displaystyle \left[\frac{3}{4}x^2+x\right]_{1}^{4} &\mbox{}\\
&=\displaystyle \left[\frac{3}{4}\cdot 4^2+4\right]-\left[\frac{3}{4}\cdot 1^2+1\right] &\mbox{}\\
&=\displaystyle \frac{3}{4}\cdot 4^2 +4-\frac{3}{4}\cdot 1^2-1 &\mbox{}\\
&=\displaystyle \frac{3}{4}\cdot 16+3-\frac{3}{4} &\mbox{}\\
&=\displaystyle 12+3-\frac{3}{4} &\mbox{}\\
&=\displaystyle 15-\frac{3}{4} &\mbox{}\\
&=\displaystyle \frac{60}{4}-\frac{3}{4} &\mbox{}\\
&=\displaystyle \frac{57}{4} &\mbox{}\\
&=\displaystyle 14.25 &\mbox{}\\
\end{array}
$$
Area Between Two Curves
Fact #1: It is often the case that we want to define our interval of interest based on where the graphs of two functions intersect.
Example
Determine the area of the region between the two curves in the given figure by integrating over the $x$-axis.
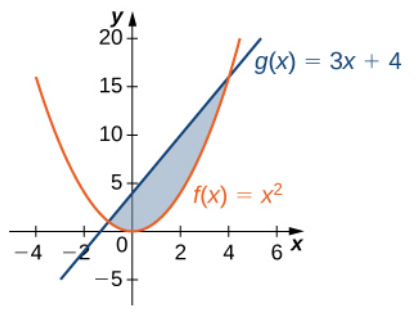
First, we need to determine what the limits of integration by solving $f(x)=g(x)$:
$$
\begin{array}{lll}
&f(x)=g(x)&\\
\implies &x^2=3x+4&\\
\implies &x^2-3x-4=0&\\
\implies &(x+1)(x-4)=0&\\
\implies &x=-1 \mbox{ OR } x=4&\\
\end{array}
$$
Thus,
$$
\begin{array}{lll}
\mbox{Area Between $f(x)$ and $g(x)$ on $[a,b]$}&=\displaystyle \int_{a}^{b} [f(x)-g(x)] \, dx&\mbox{}\\
&=\displaystyle \int_{-1}^{4} \left[3x+4-x^2\right] \, dx&\mbox{}\\
&=\displaystyle \left[\frac{3}{2}x^2+4x-\frac{1}{3}x^3\right]_{-1}^{4}&\mbox{}\\
&=\displaystyle \left[\frac{3}{2}\cdot 4^2+4\cdot 4-\frac{1}{3}\cdot 4^3\right]-\left[\frac{3}{2}\cdot (-1)^2+4\cdot (-1)-\frac{1}{3}\cdot (-1)^3\right]&\mbox{}\\
&=\displaystyle \left[3\cdot 8+16-\frac{64}{3}\right]-\left[\frac{3}{2}-4+\frac{1}{3}\right]&\mbox{}\\
&=\displaystyle \left[40-\frac{64}{3}\right]-\left[\frac{3}{2}-4+\frac{1}{3}\right]&\mbox{}\\
%&=\displaystyle \left[\frac{120}{3}-\frac{64}{3}\right]-\left[\frac{9}{6}-\frac{24}{6}+\frac{2}{6}\right]&\mbox{}\\
&=\displaystyle \left[\frac{240}{6}-\frac{128}{6}\right]-\left[\frac{9}{6}-\frac{24}{6}+\frac{2}{6}\right]&\mbox{}\\
&=\displaystyle \frac{240}{6}-\frac{128}{6}-\frac{9}{6}+\frac{24}{6}-\frac{2}{6}&\mbox{}\\
&=\displaystyle \frac{125}{6}&\mbox{}\\
&\approx \displaystyle 20.833333333&\mbox{}\\
\end{array}
$$
When Two Curves Intersect
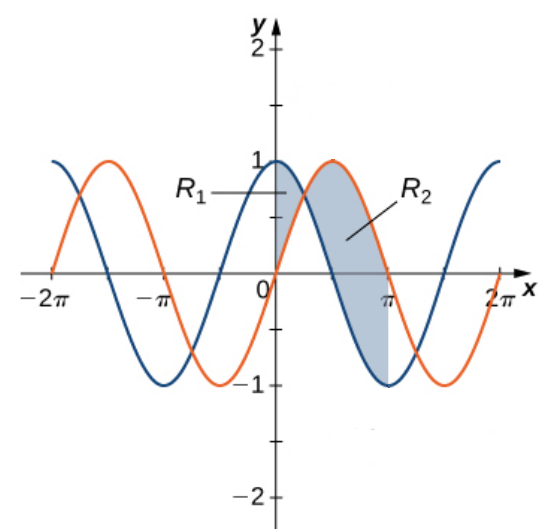
Area Between Two Curves
Fact #2: Applying the above theorem requires us to break up the interval $[a,b]$ and evaluate several integrals, depending on which of the function values is greater over a given part of the interval.
Example
Determine the area of the region between the two curves in the given figure by integrating over the $x$-axis.
The point of intersection on the interval $[0,\pi]$ is $\displaystyle \frac{\pi}{4}.$
Thus, the area between $f(x)$ and $g(x)$ on $[0,\pi]$ is $$ \begin{array}{lll} &\displaystyle \int_{a}^{b} |f(x)-g(x)| \, dx&\mbox{}\\ &=\displaystyle \int_{0}^{\pi} |\sin x-\cos x| \, dx&\mbox{}\\ &=\displaystyle \int_{0}^{\pi/4} [\cos x-\sin x] \, dx+\int_{\pi/4}^{\pi} [\sin x-\cos x] \, dx&\mbox{}\\ &=\displaystyle [\sin x+\cos x]_{0}^{\pi/4}+ [-\cos x-\sin x]_{\pi/4}^{\pi}&\mbox{}\\ &=\displaystyle \left[\sin \frac{\pi}{4}+\cos \frac{\pi}{4}\right]-[\sin 0+\cos 0]+ [-\cos \pi-\sin \pi]-\left[-\cos \frac{\pi}{4}-\sin \frac{\pi}{4}\right]&\mbox{}\\ &=\displaystyle \left[\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}\right]-[0+1]+ [-(-1)-0]-\left[-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}\right]&\mbox{}\\ &=\displaystyle \sqrt{2}-1+ 1+\sqrt{2}&\mbox{}\\ &=\displaystyle 2\sqrt{2}&\mbox{}\\ &\approx \displaystyle 2.828427125 &\mbox{}\\ \end{array} $$
Thus, the area between $f(x)$ and $g(x)$ on $[0,\pi]$ is $$ \begin{array}{lll} &\displaystyle \int_{a}^{b} |f(x)-g(x)| \, dx&\mbox{}\\ &=\displaystyle \int_{0}^{\pi} |\sin x-\cos x| \, dx&\mbox{}\\ &=\displaystyle \int_{0}^{\pi/4} [\cos x-\sin x] \, dx+\int_{\pi/4}^{\pi} [\sin x-\cos x] \, dx&\mbox{}\\ &=\displaystyle [\sin x+\cos x]_{0}^{\pi/4}+ [-\cos x-\sin x]_{\pi/4}^{\pi}&\mbox{}\\ &=\displaystyle \left[\sin \frac{\pi}{4}+\cos \frac{\pi}{4}\right]-[\sin 0+\cos 0]+ [-\cos \pi-\sin \pi]-\left[-\cos \frac{\pi}{4}-\sin \frac{\pi}{4}\right]&\mbox{}\\ &=\displaystyle \left[\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}\right]-[0+1]+ [-(-1)-0]-\left[-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}\right]&\mbox{}\\ &=\displaystyle \sqrt{2}-1+ 1+\sqrt{2}&\mbox{}\\ &=\displaystyle 2\sqrt{2}&\mbox{}\\ &\approx \displaystyle 2.828427125 &\mbox{}\\ \end{array} $$
Example
Graph the equations and shade the area of the region between the curves. Determine its area by integrating over the $x$-axis. $$y=\sqrt{x}, \,\,\,\, y=\frac{3}{2}-\frac{x}{2}, \,\,\,\, \mbox{ and } y=0$$
We first graph our region in order to understand how to set up the integral:
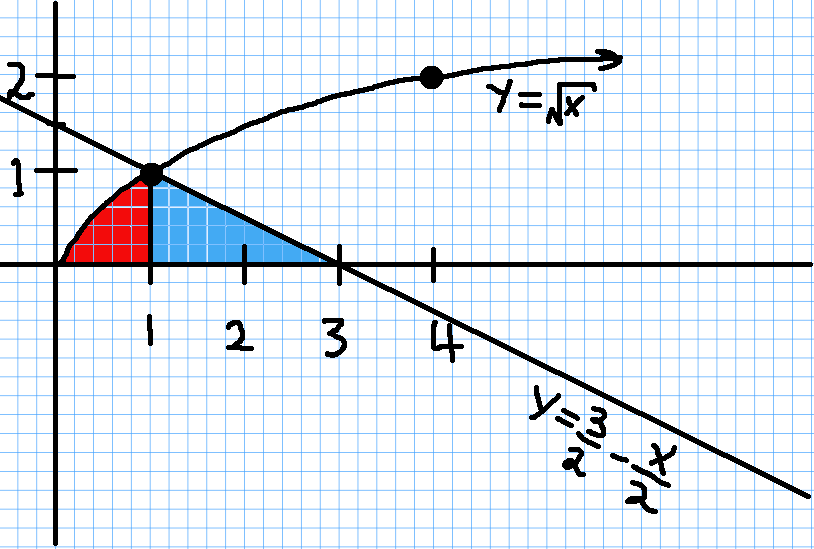
From the above, we see that we must break the region into two pieces and express the area as a sum of two integrals: $$ \begin{array}{lll} \mbox{Total Area}&=\displaystyle \mbox{Red Area}+\mbox{Blue Area}&\mbox{}\\ &=\displaystyle \int_{0}^{1} \sqrt{x} \, dx+\int_{1}^{3} \frac{3}{2}-\frac{x}{2} \, dx&\mbox{}\\ &=\displaystyle \left[\frac{2}{3}x^{3/2}\right]_{0}^{1}+\left[\frac{3x}{2}-\frac{x^2}{4}\right]_{1}^{3}&\mbox{}\\ &=\displaystyle \frac{2}{3}+\left[\frac{3\cdot 3}{2}-\frac{3^2}{4}\right]-\left[\frac{3\cdot 1}{2}-\frac{1^2}{4}\right]&\mbox{}\\ &=\displaystyle \frac{2}{3}+\left[\frac{9}{2}-\frac{9}{4}\right]-\left[\frac{3}{2}-\frac{1}{4}\right]&\mbox{}\\ &=\displaystyle \frac{2}{3}+\frac{9}{4}-\frac{5}{4}&\mbox{}\\ &=\displaystyle \frac{2}{3}+1&\mbox{}\\ &=\displaystyle \frac{5}{3}&\mbox{}\\ &\approx\displaystyle 1.67&\mbox{}\\ \end{array} $$
From the above, we see that we must break the region into two pieces and express the area as a sum of two integrals: $$ \begin{array}{lll} \mbox{Total Area}&=\displaystyle \mbox{Red Area}+\mbox{Blue Area}&\mbox{}\\ &=\displaystyle \int_{0}^{1} \sqrt{x} \, dx+\int_{1}^{3} \frac{3}{2}-\frac{x}{2} \, dx&\mbox{}\\ &=\displaystyle \left[\frac{2}{3}x^{3/2}\right]_{0}^{1}+\left[\frac{3x}{2}-\frac{x^2}{4}\right]_{1}^{3}&\mbox{}\\ &=\displaystyle \frac{2}{3}+\left[\frac{3\cdot 3}{2}-\frac{3^2}{4}\right]-\left[\frac{3\cdot 1}{2}-\frac{1^2}{4}\right]&\mbox{}\\ &=\displaystyle \frac{2}{3}+\left[\frac{9}{2}-\frac{9}{4}\right]-\left[\frac{3}{2}-\frac{1}{4}\right]&\mbox{}\\ &=\displaystyle \frac{2}{3}+\frac{9}{4}-\frac{5}{4}&\mbox{}\\ &=\displaystyle \frac{2}{3}+1&\mbox{}\\ &=\displaystyle \frac{5}{3}&\mbox{}\\ &\approx\displaystyle 1.67&\mbox{}\\ \end{array} $$
Area Between Two Curves Integrating Over $y$-Axis
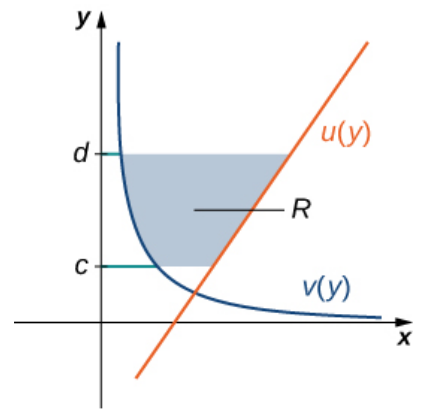
Example
Graph the equations and shade the area of the region between the two curves. Determine its area by integrating over the $y$-axis for $y \in [1,2].$ $$x=\frac{1}{y} \,\,\,\, \mbox{ and } \,\,\,\, x=2y+1$$
We first graph our region in order to understand how to set up the integral:
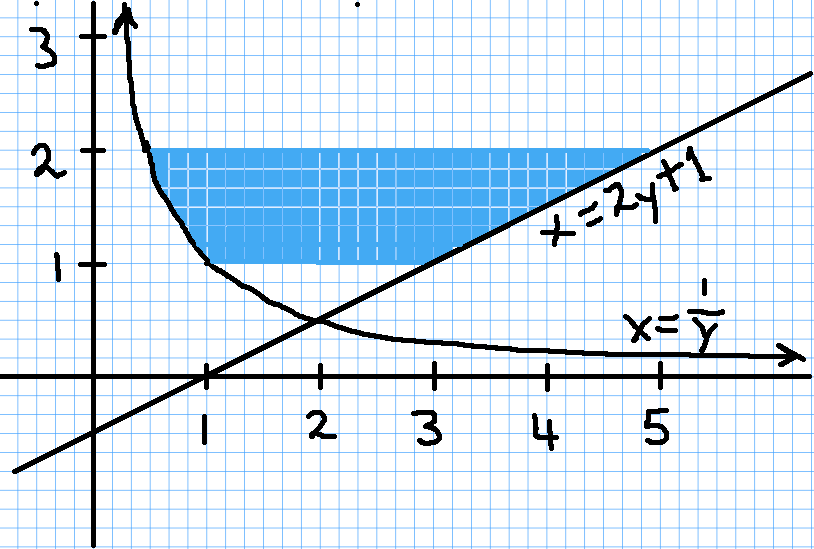From the above,
$$
\begin{array}{lll}
\mbox{Area}&=\displaystyle \int_{c}^{d} [u(y)-v(y)] \, dy&\mbox{}\\
&=\displaystyle \int_{1}^{2} 2y+1-\frac{1}{y} \, dy&\mbox{}\\
&=\displaystyle \left[y^2+y-\ln y\right]_{1}^{2}&\mbox{}\\
&=\displaystyle \left[2^2+2-\ln 2\right]-\left[1^2+1-\ln 1\right]&\mbox{}\\
&=\displaystyle \left[6-\ln 2\right]-\left[2-0\right]&\mbox{}\\
&=\displaystyle 4-\ln 2&\mbox{}\\
&\approx \displaystyle 3.31&\mbox{}\\
\end{array}
$$
Example with Signed Areas
An amusement park has a marginal cost function $C(x) = 1000e^{-x} + 5,$ where $x$ represents the number of tickets sold, and a marginal revenue function given by $R(x) = 60 − 0.1x.$ Find the total profit generated when selling $550$ tickets.
Recall that marginal profit $P(x)$ can be expressed in terms of the marginal revenue $R(x)$ and marginal cost $C(x)$ as
$$P(x)=R(x)-C(x).$$
Since the marginal profit is the derivative of profit, the Net Change Theorem says that the net change in profit from selling $550$ tickets is given by
$$\int_{0}^{550} P(x) \, dx$$
To understand this integral as a signed area, we make a very rough sketch of $R(x)-C(x)$ below
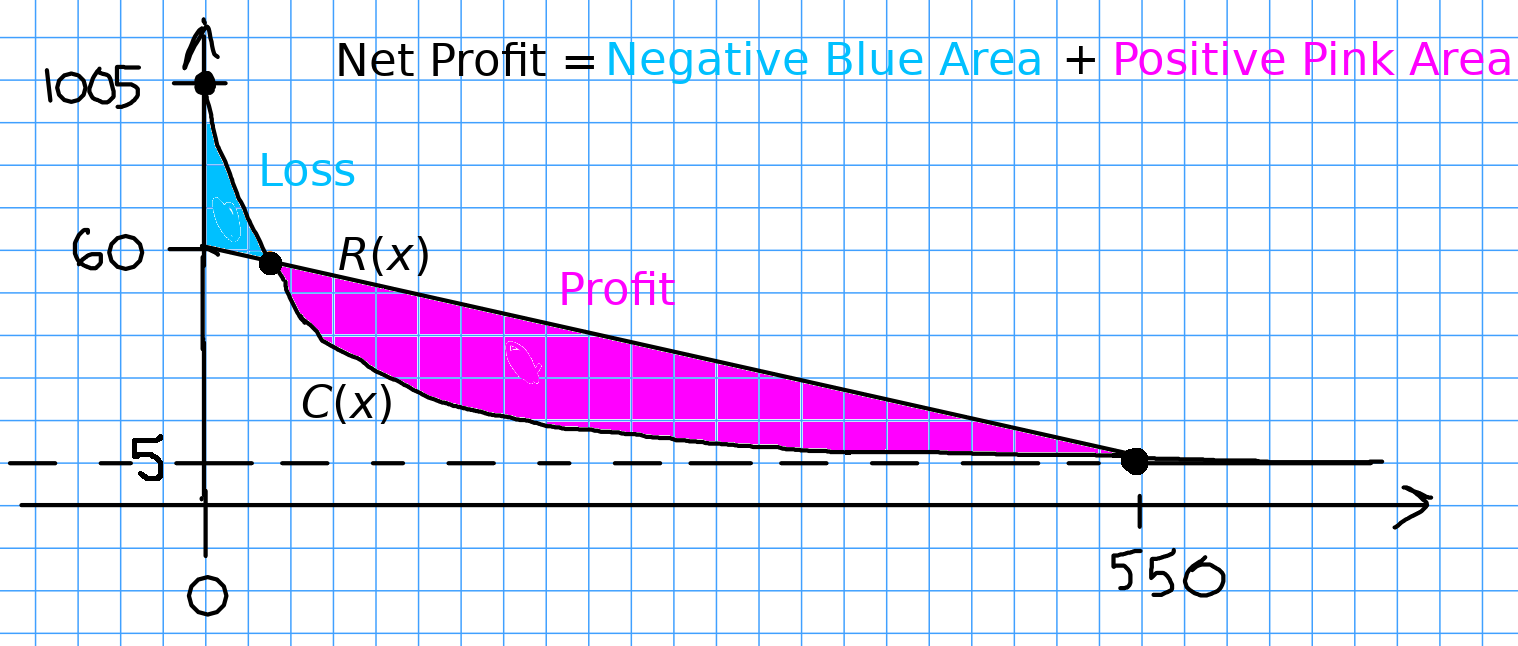Thus,
$$
\begin{array}{lll}
\mbox{Net Profit}&=\mbox{Net Signed Area}&\mbox{}\\
&=\displaystyle \int_{0}^{550} P(x) \, dx&\mbox{}\\
&=\displaystyle \int_{0}^{550} R(x)-C(x) \, dx&\mbox{}\\
&=\displaystyle \int_{0}^{550} 60-0.1x-(1000e^{-x} + 5) \, dx&\mbox{}\\
&=\displaystyle \int_{0}^{550} 55-0.1x-1000e^{-x} \, dx&\mbox{}\\
&=\displaystyle \left[55x-0.05x^2+1000e^{-x}\right]_{0}^{550} &\mbox{}\\
&=\displaystyle \left[55\cdot 550-0.05\cdot 550^2+1000e^{-550}\right]-\left[55\cdot 0-0.05\cdot 0^2+1000e^{-0}\right] &\mbox{}\\
&=\displaystyle \left[15125+1000e^{-550}\right]-\left[1000\right] &\mbox{}\\
&=\displaystyle 14125 &\mbox{}\\
\end{array}
$$
So, the net profit is $\$14125$ when $550$ tickets are sold.