Funny Math Joke: What is $\displaystyle \int \frac{d\mbox{Cabin}}{\mbox{Cabin}}?$
A houseboat party!


Integrals Resulting in Inverse Trigonometric Functions $$\int \frac{dx}{\sqrt{a^2-x^2}} =\sin^{-1} \left(\frac{x}{a}\right)+C$$ $$\int \frac{dx}{a^2+x^2} =\frac{1}{a}\tan^{-1} \left(\frac{x}{a}\right)+C$$ $$\int \frac{dx}{x\sqrt{x^2-a^2}} =\frac{1}{a}\sec^{-1} \left(\frac{x}{a}\right)+C$$
Examples
Find the integrals
$\displaystyle \int \frac{1}{\sqrt{1-16x^2}} \, dx$
Let $u=4x.$ Then $\displaystyle dx=\frac{1}{4}\,du$ so that
$$
\begin{array}{lll}
\displaystyle \int \frac{1}{\sqrt{1-16x^2}} \, dx&=\displaystyle \int \frac{1}{\sqrt{1-(4x)^2}} \, dx &\mbox{}\\
&=\displaystyle \int \frac{1}{\sqrt{1-u^2}} \left(\frac{1}{4}\, du \right) &\mbox{}\\
&=\displaystyle \frac{1}{4}\int \frac{1}{\sqrt{1-u^2}} \, du &\mbox{}\\
&=\displaystyle \frac{1}{4}\sin^{-1}(u)+C &\mbox{}\\
&=\displaystyle \frac{1}{4}\sin^{-1}(4x)+C &\mbox{}\\
\end{array}
$$
$\displaystyle \int \frac{1}{25+16x^2} \, dx$
Again, let $u=4x.$ Then $\displaystyle dx=\frac{1}{4}\,du$ so that
$$
\begin{array}{lll}
\displaystyle \int \frac{1}{25+16x^2} \, dx&=\displaystyle \int \frac{1}{25+(4x)^2} \, dx &\mbox{}\\
&=\displaystyle \int \frac{1}{25+u^2} \left(\frac{1}{4}\,du\right) &\mbox{}\\
&=\displaystyle \frac{1}{4}\int \frac{1}{25+u^2} \,du &\mbox{}\\
&=\displaystyle \frac{1}{4} \cdot \frac{1}{5}\tan^{-1}\left(\frac{u}{5}\right)+C &\mbox{}\\
&=\displaystyle \frac{1}{20}\tan^{-1}\left(\frac{4x}{5}\right)+C &\mbox{}\\
\end{array}
$$
$\displaystyle \int_{1}^{\sqrt{3}} \frac{dx}{1+x^2}$
$$
\begin{array}{lll}
\displaystyle \int_{1}^{\sqrt{3}} \frac{dx}{1+x^2}&=\displaystyle \left[\tan^{-1}x\right]_{1}^{\sqrt{3}} &\mbox{}\\
&=\displaystyle \tan^{-1}(\sqrt{3})-\tan^{-1}(1) &\mbox{}\\
&=\displaystyle \frac{\pi}{3}-\frac{\pi}{4} &\mbox{}\\
&=\displaystyle \frac{\pi}{12} &\mbox{}\\
&\approx 0.261799388
\end{array}
$$

$\displaystyle \int \frac{dx}{x\sqrt{4x^2-16}}$
Let $u=2x.$ Then $\displaystyle dx=\frac{1}{2}\,du$ so that
$$
\begin{array}{lll}
\displaystyle \int \frac{dx}{x\sqrt{4x^2-16}}&=\displaystyle \int \frac{1}{x\sqrt{(2x)^2-16}}\,dx &\mbox{}\\
&=\displaystyle \int \frac{1}{\frac{u}{2}\sqrt{u^2-16}} \left(\frac{1}{2}\, du \right) &\mbox{}\\
&=\displaystyle \frac{1}{2}\int \frac{1}{\frac{1}{2}u\sqrt{u^2-16}} \, du &\mbox{}\\
&=\displaystyle \int \frac{1}{u\sqrt{u^2-16}} \, du &\mbox{}\\
&=\displaystyle \frac{1}{4}\sec^{-1}\left(\frac{1}{4}u\right)+C &\mbox{}\\
&=\displaystyle \frac{1}{4}\sec^{-1}\left(\frac{1}{4}\cdot 2x\right)+C &\mbox{}\\
&=\displaystyle \frac{1}{4}\sec^{-1}\left(\frac{1}{2}x\right)+C &\mbox{}\\
\end{array}
$$

Examples
Find the integrals
$\displaystyle \int \frac{t \tan^{-1}(t^2)}{1+t^4} \, dt$
Method 1: The Double Sustitoosh
Let $u=t^2.$ Then $\displaystyle t \,dt=\frac{1}{2}\,du$ so that $$ \begin{array}{lll} \displaystyle \int \frac{t \tan^{-1}(t^2)}{1+t^4} \, dt&=\displaystyle \int \frac{ \tan^{-1}(t^2)}{1+(t^2)^2} t \, dt&\mbox{}\\ &=\displaystyle \int \frac{ \tan^{-1}(u)}{1+u^2} \left(\frac{1}{2}\,du\right)&\mbox{}\\ &=\displaystyle \frac{1}{2}\int \frac{ \tan^{-1}(u)}{1+u^2} \,du&\mbox{}\\ \end{array} $$ Now let $w=\tan^{-1}(u).$ Then $dw=\displaystyle \frac{1}{1+u^2}\,du$ so that $$ \begin{array}{lll} \displaystyle \int \frac{t \tan^{-1}(t^2)}{1+t^4} \, dt&=\displaystyle \frac{1}{2}\int \frac{ \tan^{-1}(u)}{1+u^2} \,du&\mbox{}\\ &=\displaystyle \frac{1}{2}\int \tan^{-1}(u) \frac{1}{1+u^2} \,du&\mbox{}\\ &=\displaystyle \frac{1}{2}\int w \,dw&\mbox{}\\ &=\displaystyle \frac{1}{2}\cdot \frac{1}{2}w^2+C&\mbox{}\\ &=\displaystyle \frac{1}{4}\left(\tan^{-1}(u)\right)^2+C&\mbox{}\\ &=\displaystyle \frac{1}{4}\left(\tan^{-1}(t^2)\right)^2+C&\mbox{}\\ \end{array} $$ Method 2: In One Fell Swoop
Let $u=\tan^{1}(t^2).$ Then $\displaystyle \frac{du}{dt}=\frac{1}{1+(t^2)^2}\frac{d}{dx}t^2=\frac{2t}{1+t^4}$ so that $\displaystyle \frac{1}{2}du=\frac{t}{1+t^4}\,dt$ Thus, $$ \begin{array}{lll} \displaystyle \int \frac{t \tan^{-1}(t^2)}{1+t^4} \, dt&=\displaystyle \int \tan^{-1}(t^2) \frac{t}{1+t^4} \, dt&\mbox{}\\ &=\displaystyle \int u\left(\frac{1}{2}\,du\right)&\mbox{}\\ &=\displaystyle \frac{1}{2}\int u\,du&\mbox{}\\ &=\displaystyle \frac{1}{2}\cdot \frac{1}{2}u^2+C&\mbox{}\\ &=\displaystyle \frac{1}{4}(\tan^{-1}(t^2))^2+C&\mbox{}\\ \end{array} $$
Let $u=t^2.$ Then $\displaystyle t \,dt=\frac{1}{2}\,du$ so that $$ \begin{array}{lll} \displaystyle \int \frac{t \tan^{-1}(t^2)}{1+t^4} \, dt&=\displaystyle \int \frac{ \tan^{-1}(t^2)}{1+(t^2)^2} t \, dt&\mbox{}\\ &=\displaystyle \int \frac{ \tan^{-1}(u)}{1+u^2} \left(\frac{1}{2}\,du\right)&\mbox{}\\ &=\displaystyle \frac{1}{2}\int \frac{ \tan^{-1}(u)}{1+u^2} \,du&\mbox{}\\ \end{array} $$ Now let $w=\tan^{-1}(u).$ Then $dw=\displaystyle \frac{1}{1+u^2}\,du$ so that $$ \begin{array}{lll} \displaystyle \int \frac{t \tan^{-1}(t^2)}{1+t^4} \, dt&=\displaystyle \frac{1}{2}\int \frac{ \tan^{-1}(u)}{1+u^2} \,du&\mbox{}\\ &=\displaystyle \frac{1}{2}\int \tan^{-1}(u) \frac{1}{1+u^2} \,du&\mbox{}\\ &=\displaystyle \frac{1}{2}\int w \,dw&\mbox{}\\ &=\displaystyle \frac{1}{2}\cdot \frac{1}{2}w^2+C&\mbox{}\\ &=\displaystyle \frac{1}{4}\left(\tan^{-1}(u)\right)^2+C&\mbox{}\\ &=\displaystyle \frac{1}{4}\left(\tan^{-1}(t^2)\right)^2+C&\mbox{}\\ \end{array} $$ Method 2: In One Fell Swoop
Let $u=\tan^{1}(t^2).$ Then $\displaystyle \frac{du}{dt}=\frac{1}{1+(t^2)^2}\frac{d}{dx}t^2=\frac{2t}{1+t^4}$ so that $\displaystyle \frac{1}{2}du=\frac{t}{1+t^4}\,dt$ Thus, $$ \begin{array}{lll} \displaystyle \int \frac{t \tan^{-1}(t^2)}{1+t^4} \, dt&=\displaystyle \int \tan^{-1}(t^2) \frac{t}{1+t^4} \, dt&\mbox{}\\ &=\displaystyle \int u\left(\frac{1}{2}\,du\right)&\mbox{}\\ &=\displaystyle \frac{1}{2}\int u\,du&\mbox{}\\ &=\displaystyle \frac{1}{2}\cdot \frac{1}{2}u^2+C&\mbox{}\\ &=\displaystyle \frac{1}{4}(\tan^{-1}(t^2))^2+C&\mbox{}\\ \end{array} $$
$\displaystyle \int \frac{dt}{t\sqrt{1-\ln^2 t}} $
Let $u=\ln t.$ Then $\displaystyle du=\frac{dt}{t}$ so that
$$
\begin{array}{lll}
\displaystyle \int \frac{dt}{t\sqrt{1-\ln^2 t}}&=\displaystyle \int \frac{1}{\sqrt{1-\ln^2 t}}\frac{dt}{t}&\mbox{}\\
&=\displaystyle \int \frac{1}{\sqrt{1-u^2}}\,du&\mbox{}\\
&=\displaystyle \sin^{-1}(u)+C&\mbox{}\\
&=\displaystyle \sin^{-1}(\ln t)+C&\mbox{}\\
\end{array}
$$
$\displaystyle \int \frac{e^t \cos^{-1}(e^t)}{\sqrt{1-e^{2t}}} \, dt$
Let $u=\cos^{-1}(e^t).$ Then $\displaystyle \frac{du}{dt}=-\frac{1}{\sqrt{1-(e^t)^2}}\frac{d}{dx}e^t=-\frac{1}{\sqrt{1-e^{2t}}}e^t=-\frac{e^t}{\sqrt{1-e^{2t}}}$ so that
$\displaystyle -du=\frac{e^t}{\sqrt{1-e^{2t}}}\,dt$
$$
\begin{array}{lll}
\displaystyle \int \frac{e^t \cos^{-1}(e^t)}{\sqrt{1-e^{2t}}} \, dt&=\displaystyle \int \cos^{-1}(e^t) \frac{e^t}{\sqrt{1-e^{2t}}} \, dt&\mbox{}\\
&=\displaystyle \int u (-du)&\mbox{}\\
&=\displaystyle -\int u \,du&\mbox{}\\
&=\displaystyle -\frac{1}{2}u^2+C&\mbox{}\\
&=\displaystyle -\frac{1}{2}(\cos^{-1}(e^t))^2+C&\mbox{}\\
\end{array}
$$
$\displaystyle \int_{0}^{1/2} \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt$
This time, we'll first find the antiderivative, and then evaluate at the limits of integration.
Let $u=\sin^{-1}t.$ Then $\displaystyle du=\frac{1}{\sqrt{1-t^{2}}}\,dt$ so that $$ \begin{array}{lll} \displaystyle \int \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt&=\displaystyle \int \tan(\sin^{-1} t)\frac{1}{\sqrt{1-t^2}} \, dt&\mbox{}\\ &=\displaystyle \int \tan(u)\,du&\mbox{}\\ &=\displaystyle \int \frac{\sin u}{\cos u}\,du&\mbox{}\\ \end{array} $$ We now make another substitution $w=\cos{u}.$ Then $-dw=\sin u \,du$ so that $$ \begin{array}{lll} \displaystyle \int \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt&=\displaystyle \int \frac{\sin u}{\cos u}\,du&\mbox{}\\ &=\displaystyle \int \frac{1}{\cos u}\sin u\,du&\mbox{}\\ &=\displaystyle \int \frac{1}{w}(-\,dw)&\mbox{}\\ &=\displaystyle -\int \frac{1}{w}\,dw&\mbox{}\\ &=\displaystyle -\ln|w|+C&\mbox{}\\ &=\displaystyle -\ln|\cos u|+C&\mbox{}\\ &=\displaystyle -\ln|\cos(\sin^{-1}t)|+C&\mbox{}\\ &=\displaystyle -\ln|\sqrt{1-t^2}|+C&\mbox{see remarks below}\\ &=\displaystyle -\ln(\sqrt{1-t^2})+C&\mbox{since the principal square root is defined to be positive}\\ \end{array} $$ With the above antiderivative, we find the definite integral: $$ \begin{array}{lll} \displaystyle \int_{0}^{1/2} \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt&=\displaystyle \left[-\ln(\sqrt{1-t^2})\right]_{0}^{1/2}&\mbox{}\\ &=\displaystyle -\ln\left(\sqrt{1-\left(\frac{1}{2}\right)^2}\right)-(-\ln(\sqrt{1-0^2}))&\mbox{}\\ &=\displaystyle -\ln\left(\sqrt{1-\frac{1}{4}}\right)+\ln(\sqrt{1})&\mbox{}\\ &=\displaystyle -\ln\left(\sqrt{\frac{3}{4}}\right)+\ln(1)&\mbox{}\\ &=\displaystyle -\ln\left(\frac{\sqrt{3}}{2}\right)\mbox{}\\ &=\displaystyle \ln\left(\left(\frac{\sqrt{3}}{2}\right)^{-1}\right)\mbox{}\\ &=\displaystyle \ln\left(\frac{2}{\sqrt{3}}\right)\mbox{}\\ %&=\displaystyle \ln\left(2\right)-\ln\left(\sqrt{3}\right)&\mbox{}\\ %&=\displaystyle \ln\left(2\right)-\ln\left(3^{1/2}\right)&\mbox{}\\ %&=\displaystyle \ln\left(2\right)-\frac{1}{2}\ln\left(3\right)&\mbox{}\\ &\approx 0.1438410362&\\ \end{array} $$
Remarks
Taking $\sin^{-1}t$ to be an angle such that its sine is $t,$ we take the cosine of that angle to get $\sqrt{1-t^2}.$
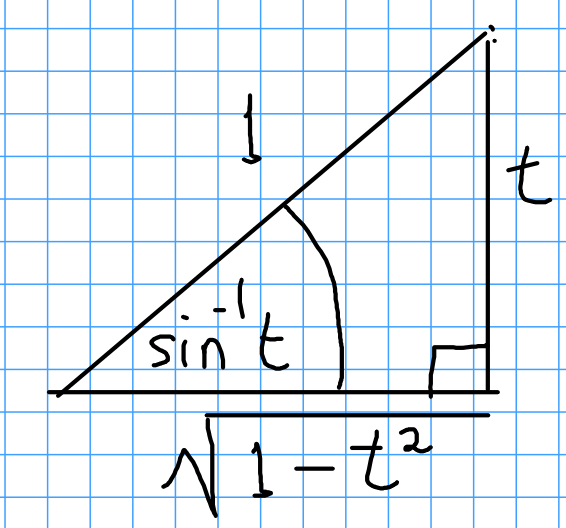
We could also say that $$|\cos(\sin^{-1}t)|=\sqrt{\cos^2(\sin^{-1}t)}=\sqrt{1-\sin^2(\sin^{-1}t)}=\sqrt{1-t^2}$$
Note that using the reasoning of the above figure, we could have rewritten the original integral as $$ \displaystyle \int_{0}^{1/2} \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt =\int_{0}^{1/2} \frac{\frac{t}{\sqrt{1-t^2}}}{\sqrt{1-t^2}} \, dt =\int_{0}^{1/2} \frac{t}{1-t^2} \, dt $$
Let $u=\sin^{-1}t.$ Then $\displaystyle du=\frac{1}{\sqrt{1-t^{2}}}\,dt$ so that $$ \begin{array}{lll} \displaystyle \int \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt&=\displaystyle \int \tan(\sin^{-1} t)\frac{1}{\sqrt{1-t^2}} \, dt&\mbox{}\\ &=\displaystyle \int \tan(u)\,du&\mbox{}\\ &=\displaystyle \int \frac{\sin u}{\cos u}\,du&\mbox{}\\ \end{array} $$ We now make another substitution $w=\cos{u}.$ Then $-dw=\sin u \,du$ so that $$ \begin{array}{lll} \displaystyle \int \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt&=\displaystyle \int \frac{\sin u}{\cos u}\,du&\mbox{}\\ &=\displaystyle \int \frac{1}{\cos u}\sin u\,du&\mbox{}\\ &=\displaystyle \int \frac{1}{w}(-\,dw)&\mbox{}\\ &=\displaystyle -\int \frac{1}{w}\,dw&\mbox{}\\ &=\displaystyle -\ln|w|+C&\mbox{}\\ &=\displaystyle -\ln|\cos u|+C&\mbox{}\\ &=\displaystyle -\ln|\cos(\sin^{-1}t)|+C&\mbox{}\\ &=\displaystyle -\ln|\sqrt{1-t^2}|+C&\mbox{see remarks below}\\ &=\displaystyle -\ln(\sqrt{1-t^2})+C&\mbox{since the principal square root is defined to be positive}\\ \end{array} $$ With the above antiderivative, we find the definite integral: $$ \begin{array}{lll} \displaystyle \int_{0}^{1/2} \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt&=\displaystyle \left[-\ln(\sqrt{1-t^2})\right]_{0}^{1/2}&\mbox{}\\ &=\displaystyle -\ln\left(\sqrt{1-\left(\frac{1}{2}\right)^2}\right)-(-\ln(\sqrt{1-0^2}))&\mbox{}\\ &=\displaystyle -\ln\left(\sqrt{1-\frac{1}{4}}\right)+\ln(\sqrt{1})&\mbox{}\\ &=\displaystyle -\ln\left(\sqrt{\frac{3}{4}}\right)+\ln(1)&\mbox{}\\ &=\displaystyle -\ln\left(\frac{\sqrt{3}}{2}\right)\mbox{}\\ &=\displaystyle \ln\left(\left(\frac{\sqrt{3}}{2}\right)^{-1}\right)\mbox{}\\ &=\displaystyle \ln\left(\frac{2}{\sqrt{3}}\right)\mbox{}\\ %&=\displaystyle \ln\left(2\right)-\ln\left(\sqrt{3}\right)&\mbox{}\\ %&=\displaystyle \ln\left(2\right)-\ln\left(3^{1/2}\right)&\mbox{}\\ %&=\displaystyle \ln\left(2\right)-\frac{1}{2}\ln\left(3\right)&\mbox{}\\ &\approx 0.1438410362&\\ \end{array} $$

Remarks
Taking $\sin^{-1}t$ to be an angle such that its sine is $t,$ we take the cosine of that angle to get $\sqrt{1-t^2}.$
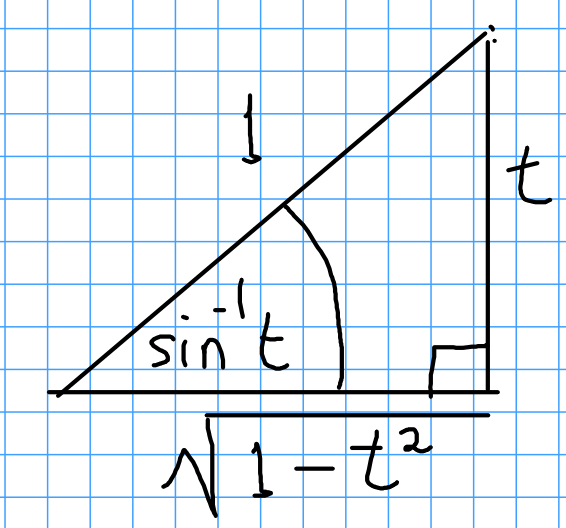
We could also say that $$|\cos(\sin^{-1}t)|=\sqrt{\cos^2(\sin^{-1}t)}=\sqrt{1-\sin^2(\sin^{-1}t)}=\sqrt{1-t^2}$$
Note that using the reasoning of the above figure, we could have rewritten the original integral as $$ \displaystyle \int_{0}^{1/2} \frac{\tan(\sin^{-1} t)}{\sqrt{1-t^2}} \, dt =\int_{0}^{1/2} \frac{\frac{t}{\sqrt{1-t^2}}}{\sqrt{1-t^2}} \, dt =\int_{0}^{1/2} \frac{t}{1-t^2} \, dt $$