Warm-Up Question: Find the indefinite integral. $$\int 2x^{-1} \, dx$$
Recall $$\displaystyle \frac{d}{dx}(e^x+C)=e^x.$$ $$\displaystyle \frac{d}{dx}(a^x+C)=(\ln a) a^x.$$
Restating the above in integral form gives us...
Integral Formulas for Exponentials $$\int e^x \, dx=e^x+C$$ $$\int a^x \, dx=\frac{1}{\ln a} a^x+C$$
Recall: Integration by Substitution
Let $u = g(x)$ where $g'(x)$ is continuous over an interval, $f (x)$ be continuous over the corresponding range of $g$, and let $F(x)$ be an antiderivative of $f (x).$ Then, $$\int f(g(x)) g'(x) \, dx=\int f(u) \, du =F(u)+C=F(g(x))+C$$ Note: When we let $u=g(x),$ this is the substitution that gives the technique its name.
Examples
Find the indefinite integrals
$\displaystyle \int e^{3x} \, dx$
Let $u=3x.$ Then $du=3\,dx,$ or $\displaystyle dx=\frac{1}{3}\,du.$ Thus,
$$
\begin{array}{lll}
\displaystyle \int e^{3x} \, dx&=\displaystyle \int e^{u} \cdot \frac{1}{3}\,du &\mbox{}\\
&=\displaystyle \frac{1}{3}\int e^{u}\,du &\mbox{}\\
&=\displaystyle \frac{1}{3} e^{u}+C &\mbox{}\\
&=\displaystyle \frac{1}{3} e^{3x}+C &\mbox{}\\
\end{array}
$$
$\displaystyle \int 2^{-x} \, dx$
Let $u=-x.$ Then $dx=-du.$ Thus,
$$
\begin{array}{lll}
\displaystyle \int 2^{-x} \, dx&=\displaystyle \int 2^{u}(-\, du) &\mbox{}\\
&=\displaystyle -\int 2^{u}\, du &\mbox{}\\
&=\displaystyle -\frac{1}{\ln 2} 2^{u}+C &\mbox{}\\
&=\displaystyle -\frac{1}{\ln 2} 2^{-x}+C &\mbox{}\\
\end{array}
$$
$\displaystyle \int x^2e^{-x^3} \, dx$
Let $u=-x^3.$ Then $du=-3x^2\,dx,$ or $\displaystyle x^2 \,dx=-\frac{1}{3}\,du.$ Thus,
$$
\begin{array}{lll}
\displaystyle \int x^2e^{-x^3} \, dx&=\displaystyle \int e^{-x^3} x^2 \, dx&\mbox{}\\
&=\displaystyle \int e^{u} \cdot \left(-\frac{1}{3}\,du\right)&\mbox{}\\
&=\displaystyle -\frac{1}{3} \int e^{u} \,du&\mbox{}\\
&=\displaystyle -\frac{1}{3}e^{u}+C&\mbox{}\\
&=\displaystyle -\frac{1}{3}e^{-x^3}+C&\mbox{}\\
\end{array}
$$
$\displaystyle \int e^{\tan x} \sec^2 x\, dx$
Let $u=\tan x.$ Then $du=sec^2 x\,dx.$ Thus,
$$
\begin{array}{lll}
\displaystyle \int e^{\tan x} \sec^2 x\, dx&=\displaystyle \int e^{u}\,du&\mbox{}\\
&=\displaystyle e^{u}+C&\mbox{}\\
&=\displaystyle e^{\tan x}+C&\mbox{}\\
\end{array}
$$
Recall $$\displaystyle \frac{d}{dx}(\ln |x|+C)=\frac{1}{x}.$$
Restating the above in integral form gives us...
Integral Formula for $x^{-1}$ $$\int \frac{1}{x} \, dx=\int x^{-1}\, dx=\ln |x| +C$$
Integral Formula for Logarithms $$\int \ln x \, dx=x\ln x - x+C=x(\ln x-1)+C$$ $$\int \log_a x \, dx=\frac{1}{\ln a}(x\ln x - x)+C=\frac{1}{\ln a}x(\ln x-1)+C$$
Examples
Find the following indefinite integrals
$\displaystyle \int \frac{dx}{x\ln x}$
Let $u=\ln x.$ Then $du=\displaystyle \frac{1}{x}dx=\frac{dx}{x}.$ Thus,
$$
\begin{array}{lll}
\displaystyle \int \frac{dx}{x\ln x}&=\displaystyle \int \frac{1}{\ln x} \frac{dx}{x}&\mbox{}\\
&=\displaystyle \int \frac{1}{u}\,du&\mbox{}\\
&=\displaystyle \ln|u|+C&\mbox{}\\
&=\displaystyle \ln|\ln x|+C&\mbox{}\\
\end{array}
$$
$\displaystyle \int \frac{\ln(\sin x)}{\tan x} \, dx$
Since we are looking for an inside function and a multiple of its derivative, we look to the $\tan x$
in the denominator of the integrand. Rewriting the integrand we have:
$$
\frac{\ln(\sin x)}{\tan x}=\frac{\ln(\sin x)}{\frac{\sin x}{\cos x}}=\frac{\ln(\sin x)\cos x}{\sin x}
$$
A possible substitution then becomes a little more apparent:
$u=\sin x.$ Then $du=\cos dx.$ Thus,
$$
\begin{array}{lll}
\displaystyle \int \frac{\ln(\sin x)}{\tan x} \, dx&=\displaystyle \int \frac{\ln(\sin x)\cos x}{\sin x} \,dx&\mbox{}\\
&=\displaystyle \int \frac{\ln(\sin x)}{\sin x}\cos x \,dx&\mbox{}\\
&=\displaystyle \int \frac{\ln(u)}{u}\,du&\mbox{}\\
\end{array}
$$
We may now make another substitution; let $w=\ln(u).$ Then $dw=\displaystyle \frac{1}{u}du$ so that
$$
\begin{array}{lll}
\displaystyle \int \frac{\ln(u)}{u}\,du&=\displaystyle \int \ln(u) \frac{1}{u}\,du&\mbox{}\\
&=\displaystyle \int w \,dw&\mbox{}\\
&=\displaystyle \frac{1}{2}w^2+C \,dw&\mbox{}\\
&=\displaystyle \frac{1}{2}(\ln(u))^2+C \,dw&\mbox{}\\
\end{array}
$$
Thus,
$$
\int \frac{\ln(\sin x)}{\tan x} \, dx=\frac{1}{2}(\ln(u))^2+C=\frac{1}{2}(\ln(\sin x))^2+C
$$
Scenic Alternative
Let $u=\ln(\sin x).$ Then $$ \displaystyle \frac{du}{dx}=\frac{1}{\sin x}\frac{d}{dx}\sin x=\frac{1}{\sin x}\cos x=\frac{1}{\tan x}. $$ so that $\displaystyle du=\frac{1}{\tan x}\,dx.$ It follows that $$ \begin{array}{lll} \displaystyle \int \frac{\ln(\sin x)}{\tan x} \, dx&=\displaystyle \int \ln(\sin x)\frac{1}{\tan x} \,dx&\mbox{}\\ &=\displaystyle \int u \,du&\mbox{}\\ &=\displaystyle \frac{1}{2}u^2+C&\mbox{}\\ &=\displaystyle \frac{1}{2}(\ln(\sin x))^2+C&\mbox{}\\ \end{array} $$
Scenic Alternative
Let $u=\ln(\sin x).$ Then $$ \displaystyle \frac{du}{dx}=\frac{1}{\sin x}\frac{d}{dx}\sin x=\frac{1}{\sin x}\cos x=\frac{1}{\tan x}. $$ so that $\displaystyle du=\frac{1}{\tan x}\,dx.$ It follows that $$ \begin{array}{lll} \displaystyle \int \frac{\ln(\sin x)}{\tan x} \, dx&=\displaystyle \int \ln(\sin x)\frac{1}{\tan x} \,dx&\mbox{}\\ &=\displaystyle \int u \,du&\mbox{}\\ &=\displaystyle \frac{1}{2}u^2+C&\mbox{}\\ &=\displaystyle \frac{1}{2}(\ln(\sin x))^2+C&\mbox{}\\ \end{array} $$
$\displaystyle \int \frac{\sin(3x)-\cos(3x)}{\sin(3x)+\cos(3x)} \, dx$
Let $u=\sin(3x)+\cos(3x).$
Then $\displaystyle \frac{du}{dx}=3\cos(3x)-3\sin(3x)=-3(\sin(3x)-\cos(3x))$ so that $$\displaystyle -\frac{1}{3}du=(\sin(3x)-\cos(3x))\,dx.$$ Thus, $$ \begin{array}{lll} \displaystyle \int \frac{\sin(3x)-\cos(3x)}{\sin(3x)+\cos(3x)} \, dx&=\displaystyle \int \frac{1}{\sin(3x)+\cos(3x)}(\sin(3x)-\cos(3x)) \, dx&\mbox{}\\ &\displaystyle =\int \frac{1}{u}\left(-\frac{1}{3}du\right)&\mbox{}\\ &\displaystyle =-\frac{1}{3}\int \frac{1}{u}\,du&\mbox{}\\ &\displaystyle =-\frac{1}{3}\ln |u| +C&\mbox{}\\ &\displaystyle =-\frac{1}{3}\ln |\sin(3x)+\cos(3x)| +C&\mbox{}\\ \end{array} $$
Then $\displaystyle \frac{du}{dx}=3\cos(3x)-3\sin(3x)=-3(\sin(3x)-\cos(3x))$ so that $$\displaystyle -\frac{1}{3}du=(\sin(3x)-\cos(3x))\,dx.$$ Thus, $$ \begin{array}{lll} \displaystyle \int \frac{\sin(3x)-\cos(3x)}{\sin(3x)+\cos(3x)} \, dx&=\displaystyle \int \frac{1}{\sin(3x)+\cos(3x)}(\sin(3x)-\cos(3x)) \, dx&\mbox{}\\ &\displaystyle =\int \frac{1}{u}\left(-\frac{1}{3}du\right)&\mbox{}\\ &\displaystyle =-\frac{1}{3}\int \frac{1}{u}\,du&\mbox{}\\ &\displaystyle =-\frac{1}{3}\ln |u| +C&\mbox{}\\ &\displaystyle =-\frac{1}{3}\ln |\sin(3x)+\cos(3x)| +C&\mbox{}\\ \end{array} $$
And Don't Forget...
You can always check your work by differentiating!

And let's not forget, let's NOT forget that the reason we're so interested in antiderivatives is...
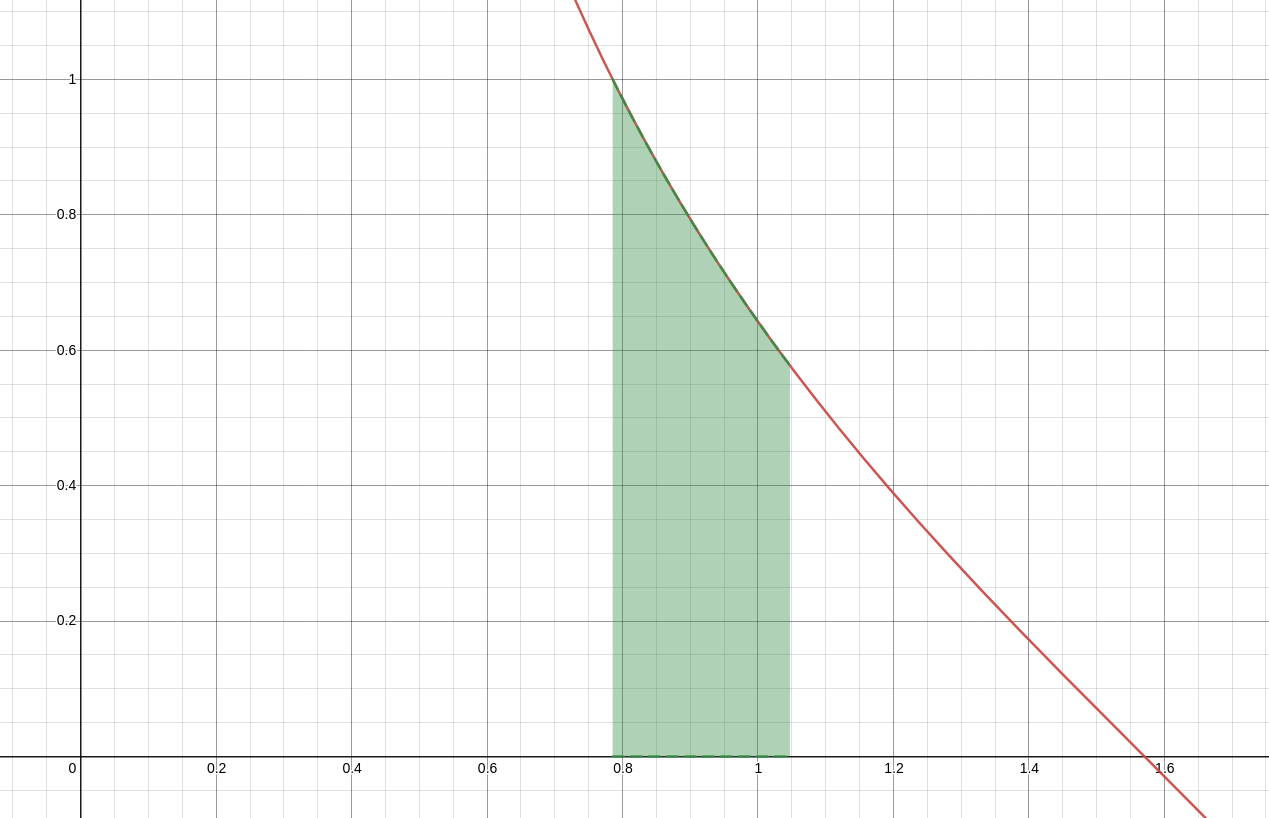
A Definite Integral
$\displaystyle \int_{\pi/4}^{\pi/3} \cot x \, dx$
We notice that the integrand contains an inside function and a multiple of its derivative:
$\displaystyle \cot x=\frac{\cos x}{\sin x}.$
Then, letting $u=\sin x,$ we have $du=\cos x \,dx$ so that
$$
\begin{array}{lll}
\displaystyle \int \cot x \, dx&=\displaystyle \int \frac{\cos x}{\sin x} \, dx&\mbox{}\\
&=\displaystyle \int \frac{1}{\sin x}\cos x \, dx&\mbox{}\\
&=\displaystyle \int \frac{1}{u}\, du&\mbox{}\\
&=\displaystyle \ln u+C&\mbox{}\\
&=\displaystyle \ln(\sin x)+C&\mbox{}\\
\end{array}
$$
Thus,
$$
\begin{array}{lll}
\displaystyle \int_{\pi/4}^{\pi/3} \cot x \, dx&=\displaystyle [\ln(\sin x)]_{\pi/4}^{\pi/3}&\mbox{}\\
&=\displaystyle [\ln(\sin x)]_{\pi/4}^{\pi/3}&\mbox{}\\
&=\displaystyle \ln\left(\sin \left(\frac{\pi}{3}\right)\right)-\ln\left(\sin \left(\frac{\pi}{4}\right)\right)&\mbox{}\\
&=\displaystyle \ln\left(\frac{\sqrt{3}}{2}\right)-\ln\left(\frac{\sqrt{2}}{2}\right)&\mbox{}\\
&=\displaystyle \ln\left(\frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}\right)&\mbox{}\\
&=\displaystyle \ln\left(\frac{\sqrt{3}}{\sqrt{2}}\right)&\mbox{}\\
&=\displaystyle \ln\left(\sqrt{\frac{3}{2}}\right)&\mbox{}\\
&=\displaystyle \ln\left(\left(\frac{3}{2}\right)^{1/2}\right)&\mbox{}\\
&=\displaystyle \frac{1}{2}\ln\left(\frac{3}{2}\right)&\mbox{}\\
&\approx 0.202732554
\end{array}
$$