Net Change Theorem

The Net Change Theorem

Recall: Let's recall the following form of the Fundamental Theorem: $$\int_{a}^{b}F'(x) \, dx=F(b)-F(a).$$ We may restate this as the following...

The Net Change Theorem

The integral of a rate of change over $[a,b]$ gives the net change. We may state this as: $$F(b)=F(a)+\int_{a}^{b}F'(x) \, dx$$ or $$\int_{a}^{b}F'(x) \, dx=F(b)-F(a)$$

In words, the NCT says that "the integral of a rate gives total change."

The Net Change Theorem

Example: Consider the graph of a delivery driver's velocity $v(t)$ versus time. How far away is the driver from their initial position at $3$ hours? At $5$ hours?

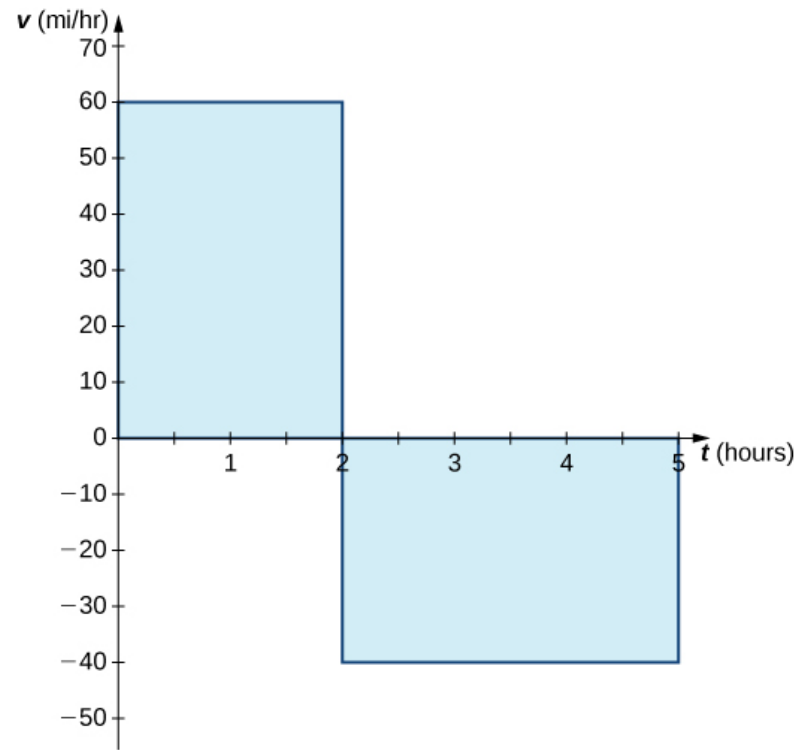
Hint: The Net Change Theorem tells us that $\displaystyle s(t)=s(0)+\int_{0}^{t} v(x) \, dx.$

To find the net change in the driver's distance after $3$ hours, we evaluate $s(3):$ $$ \begin{array}{lll} \displaystyle s(3)&=\displaystyle s(0)+\int_{0}^{3} v(x) \, dx&\mbox{}\\ &=\displaystyle 0+\int_{0}^{3} v(x) \, dx&\mbox{$s(0)=0$ by definition of $s$}\\ &\displaystyle =\int_{0}^{2} v(x) \, dx+\int_{2}^{3} v(x) \, dx&\mbox{break up interval of integration}\\ &\displaystyle =120+(-40)&\mbox{}\\ &\displaystyle =80&\mbox{}\\ \end{array} $$ Thus, after $3$ hours, the driver will be $80$ miles from their initial starting point.

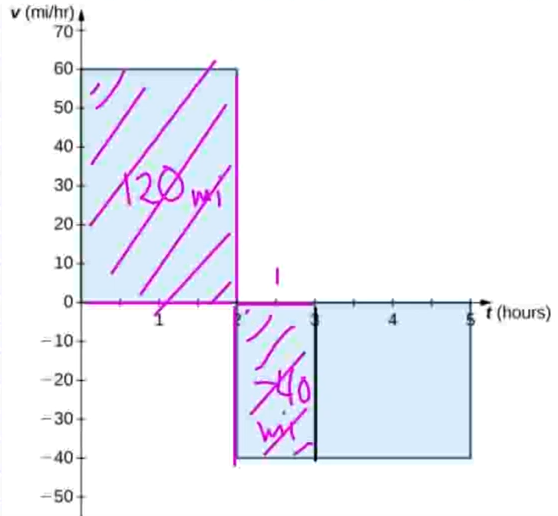
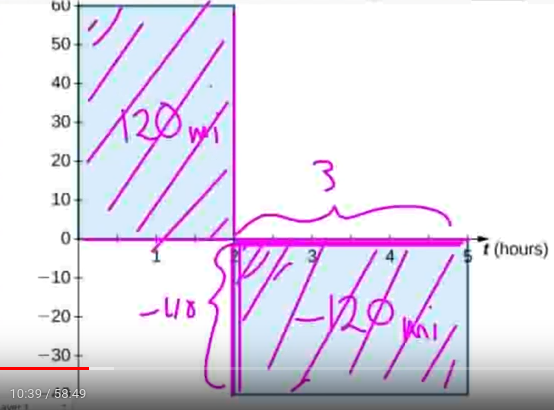
Similarly, for $5$ hours, we evaluate $s(5):$ $$ \begin{array}{lll} \displaystyle s(5)&=\displaystyle s(0)+\int_{0}^{5} v(x) \, dx&\mbox{}\\ &=\displaystyle 0+\int_{0}^{5} v(x) \, dx&\mbox{}\\ &\displaystyle =\int_{0}^{2} v(x) \, dx+\int_{2}^{5} v(x) \, dx&\mbox{break up interval of integration}\\ &\displaystyle =120+(-120)&\mbox{}\\ &\displaystyle =0&\mbox{}\\ \end{array} $$ That is, after $5$ hours, the driver will be $0$ miles from their initial starting point. (They made it home!)

Example: The Net Change Theorem

A ball is thrown upward from a height of $1.5$ m at an initial speed of $40$ m/sec. Acceleration resulting from gravity is $-9.8$ $\mbox{m}/\mbox{sec}^2.$ Neglecting air resistance, solve for the velocity $v(t)$ and the height $h(t)$ of the ball $t$ seconds after it is thrown and before it returns to the ground.

Since acceleration $a(t)$ is the derivative of velocity $v(t),$ the NCT says $$v(t)=v(0)+\int_{0}^{t}a(x)\,dx$$ Using the information provided, we rewrite the above as $$v(t)=40+\int_{0}^{t}(-9.8)\,dx=40+(-9.8t)=-9.8t+40$$ Now, since velocity $v(t)$ is the derivative of position $h(t),$ the NCT says $$h(t)=h(0)+\int_{0}^{t}v(x)\,dx$$ Again, using the information provided, we rewrite the above as $$v(t)=1.5+\int_{0}^{t}(-9.8t+40)\,dx=1.5-4.9t^2+40t=-4.9t^2+40t+1.5$$

In words, the NCT says that "the integral of a rate gives total change."

Example: An integral of a rate of change of distance (velocity) gives the net change in distance.

Example: An integral of a rate of change of velocity (acceleration) gives the net change in velocity.

Example: The Net Change Theorem

Suppose water is draining from a tank at a rate $R( t )$ gallons per hour where $R( t ) = 4.9 - 0.341 t$ and $t$ is the number of hours since $7$ AM.

(a) Write an integral which expresses the the total amount of water lost from $7$ AM to $10$ AM.

Let $V(t)$ be the cumulative volume of water which has leaked out of the tank up to time $t$. Then, the NTC says that $$V(3)-V(0)=\int_{0}^{3}V'(t)\,dt=\int_{0}^{3}R(t)\,dt=\int_{0}^{3}4.9 - 0.341 t\,dt$$

(b) Evaluate the integral in part (a) to find the amount of water that leaked from the tank from $7$ AM to $10$ AM.

$$ \begin{array}{lll} \displaystyle \int_{0}^{3}4.9 - 0.341 t\,dt&=\displaystyle \left[4.9t-0.341\cdot \frac{1}{2}t^2\right]_{0}^{3}&\mbox{}\\ &=\left[4.9t-0.1705t^2\right]_{0}^{3}&\mbox{}\\ &=\left[4.9\cdot 3-0.1705 \cdot 3^2\right]-\left[4.9\cdot 0-0.1705\cdot 0^2\right]&\mbox{}\\ &=\left[14.7-0.1705 \cdot 9\right]-0&\mbox{}\\ &=14.7-1.5345&\mbox{}\\ &=13.1655&\mbox{}\\ \end{array} $$ That is, from $7$ AM to $10$ AM a total of $13.1655$ gallons drained from the tank.

In words, the NCT says that "the integral of a rate gives total change."

Example: An integral of a volume's rate of change gives the net change in volume.

Example: The Net Change Theorem

A motor vehicle has a maximum efficiency of $33$ mpg at a cruising speed of $40$ mph. The efficiency drops at a rate of $0.1$ mpg/mph between $40$ mph and $50$ mph, and at a rate of $0.4$ mpg/mph between $50$ mph and $80$ mph.

What is the efficiency in miles per gallon if the car is cruising at $50$ mph?

Let $E(v)$ be the efficiency of the the vehicle at velocity $v.$ The information above tells us the rate at which efficiency drops over the specified intervals of velocity. We write this information as $$ E'(v)=\begin{cases} -0.1 & \mbox{ if $40 \lt v \lt 50$} \\ -0.4 & \mbox{ if $50 \lt v \lt 80$} \end{cases} $$ At $v=40$ mph, the efficiency begins to drop. The net change in efficiency over the interval from $40$ mph to $50$ mph is then $$ E(50)-E(40)=\int_{40}^{50} E'(v) dv $$ Since the maximum efficiency of the vehicle is $33$ mpg and only begins to drop off at $40$ mph, we may say that $E(40)=33.$ Then, $$ \begin{array}{lll} &\displaystyle E(50)-E(40)=\displaystyle \int_{40}^{50} (-0.1) dv&\mbox{$E'(v)=-0.1$ on $40 \lt v \lt 50$}\\ \implies &E(50)=\displaystyle E(40)+ \int_{40}^{50} (-0.1) dv&\mbox{}\\ \implies &E(50)=\displaystyle 33 +[-0.1t]_{40}^{50}&\mbox{since $E(40)=33$}\\ \implies &E(50)=\displaystyle 33+[-0.1\cdot 50]-[-0.1\cdot 40]&\mbox{}\\ \implies &E(50)=33+[-5]-[-4]&\mbox{}\\ \implies &E(50)=33-1&\mbox{}\\ \implies &E(50)=32&\mbox{}\\ \end{array} $$ Thus, the efficiency at $50$ mph is $32$ mpg.

What is the efficiency in miles per gallon if the car is cruising at $80$ mph?

The net change in efficiency over the interval from $50$ mph to $80$ mph $$ E(80)-E(50)=\int_{50}^{80} E'(v) dv $$ Since $E(50)=32$ from above, we have $$ \begin{array}{lll} &\displaystyle E(80)-E(50)=\displaystyle \int_{50}^{80} (-0.4) dv&\mbox{$E'(v)=-0.4$ on $50 \lt v \lt 80$}\\ \implies &E(80)=\displaystyle E(50)+ \int_{50}^{80} (-0.4) dv&\mbox{}\\ \implies &E(80)=\displaystyle 32 +[-0.4t]_{50}^{80}&\mbox{since $E(50)=32$}\\ \implies &E(80)=\displaystyle 32+[-0.4\cdot 80]-[-0.4\cdot 50]&\mbox{}\\ \implies &E(80)=32+[-32]-[-20]&\mbox{}\\ \implies &E(80)=32-12&\mbox{}\\ \implies &E(80)=20&\mbox{}\\ \end{array} $$ Thus, the efficiency at $80$ mph drops to $20$ mpg.

In words, the NCT says that "the integral of a rate gives total change."

Example: An integral of a rate of change of efficiency gives the net change in efficiency.

Nerdy Example: The Net Change Theorem

An icosahedron is a Platonic solid with a surface that consists of $20$ equilateral triangles. Write an integral which expresses the change in surface area of an icosahedron as the side length of each triangle doubles from $a$ units to $2a$ units.

Let $S(a)$ be the surface area of an icosahedron made up of triangles with a side length of $a$ units. By the NCT, we know that $$S(2a)-S(a)=\int_{a}^{2a}S'(x)\,dx$$ To write the integral, we must first find a formula for $S(a),$ the surface area of an icosahedron where each triangle has a side length of $a.$ Since each triangle has side length $a,$ we use the following figure to find the area of a single triangle:

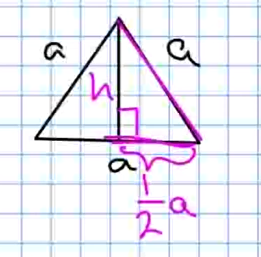From this figure we see that $\displaystyle \left(\frac{1}{2}a\right)^2+h^2=a^2.$ Then $$ \begin{array}{lll} & \displaystyle \frac{1}{4}a^2+h^2=a^2 &\mbox{}\\ \implies & \displaystyle h^2=a^2-\frac{1}{4}a^2 &\mbox{}\\ \implies & \displaystyle h^2=\frac{3}{4}a^2 &\mbox{}\\ \implies & \displaystyle h=\sqrt{\frac{3}{4}a^2} &\mbox{taking the positive root}\\ \implies & \displaystyle h=\frac{\sqrt{3}}{2}a &\mbox{simplifying}\\ \end{array} $$ Thus, the base of each triangle is $a$ and the height is $\displaystyle h=\frac{\sqrt{3}}{2}a.$ We then have that the area of a single triangle is given by $$\displaystyle \frac{1}{2}\mbox{base}\cdot\mbox{height}=\frac{1}{2}a\cdot \frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{4}a^2$$ The surface area of the icosahedron is $$S(a)=20\cdot \frac{\sqrt{3}}{4}a^2=5\sqrt{3}a^2$$ so that $$S'(a)=(10\sqrt{3})a.$$ We may now rewrite our initial statement of the NCT as $$S(2a)-S(a)=\int_{a}^{2a}(10\sqrt{3})x\,dx$$ which expresses the change in surface area as the side length of each triangle doubles from $a$ units to $2a$ units.