Fact: Rarely in life do we ever get a lot in return for a little.
The Fundamental Theorem of Calculus, is one such rare case.
The Fundamental Theorem of Calculus
We shall soon see that the Fundamental Theorem of Calculus is really two theorems.
What these two theorems say standing side-by-side is one of the great intellectual achievements of humankind.
The Fundamental Theorem of Calculus (Part 1)
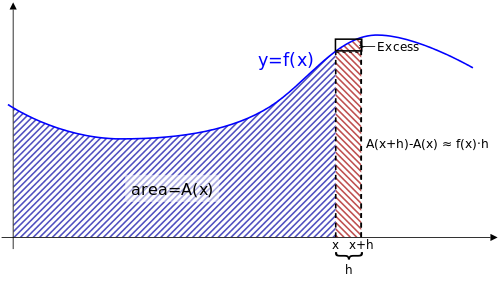
The Fundamental Theorem of Calculus (Part 1): Formally Stated
If $f (x)$ is continuous over an interval $[a, b],$ and the function $F(x)$ is defined by $$F(x)=\int_{a}^{x}f(t) \, dt,$$ then $F'(x)=f(x)$ over $[a,b].$
The Fundamental Theorem of Calculus (Part 1): Not-So-Formally Stated
$$\frac{d}{dx}\int_{a}^{x}f(t) \, dt=f(x)$$
The Fundamental Theorem of Calculus (Part 1)
Examples: Use Part 1 of the Fundamental Theorem of Calculus to find the following:
$\displaystyle \frac{d}{dx}\int_{1}^{x} \frac{ds}{\sqrt{16-s^2}}$
$\displaystyle \frac{d}{dx}\int_{1}^{x} \frac{ds}{\sqrt{16-s^2}}=\frac{1}{\sqrt{16-x^2}}$
$\displaystyle \frac{d}{dx}\int_{0}^{\sin x} \sqrt{1-t^2} \, dt$
Let $F(x)=\displaystyle \int_{0}^{x} \sqrt{1-t^2} \, dt$ so that $F'(x)=\displaystyle \frac{d}{dx}\displaystyle \int_{0}^{x} \sqrt{1-t^2} \, dt=\displaystyle \sqrt{1-x^2}.$
Then, $F(\sin x)=\displaystyle \int_{0}^{\sin x} \sqrt{1-t^2} \, dt$
and $$ \begin{array}{lll} \displaystyle \frac{d}{dx} \int_{0}^{\sin x} \sqrt{1-t^2} \, dt &=\displaystyle \frac{d}{dx}F(\sin x)&\\ &=F'(\sin x)\displaystyle \frac{d}{dx}\sin x&\mbox{Chain Rule!}\\ &=\sqrt{1-(\sin x)^2} \cos x&\mbox{}\\ &=\sqrt{1-\sin^2 x} \cos x&\\ &=\sqrt{\cos^2 x} \cos x&\\ &=|\cos x| \cos x&\\ \end{array} $$
Then, $F(\sin x)=\displaystyle \int_{0}^{\sin x} \sqrt{1-t^2} \, dt$
and $$ \begin{array}{lll} \displaystyle \frac{d}{dx} \int_{0}^{\sin x} \sqrt{1-t^2} \, dt &=\displaystyle \frac{d}{dx}F(\sin x)&\\ &=F'(\sin x)\displaystyle \frac{d}{dx}\sin x&\mbox{Chain Rule!}\\ &=\sqrt{1-(\sin x)^2} \cos x&\mbox{}\\ &=\sqrt{1-\sin^2 x} \cos x&\\ &=\sqrt{\cos^2 x} \cos x&\\ &=|\cos x| \cos x&\\ \end{array} $$
The Fundamental Theorem of Calculus (Part 2): Formally Stated.
If $f$ is continuous over the interval $[a,b]$ and $F(x)$ is any antiderivative of $f (x),$ then $$\int_{a}^{b}f(x) \, dx=F(b)-F(a).$$
The Fundamental Theorem of Calculus (Part 2): Not-So-Formally Stated.
$$\int_{a}^{b}F'(x) \, dx=F(b)-F(a).$$
Do you realize how AWESOME the above statement is?!?!?


Let's Take a Moment to Reflect
Recall that $\displaystyle \int_{0}^{2} x^2 \,dx=\frac{8}{3},$ but also recall the amount of work we had to do to find it...
Let's Take a Moment to Reflect
First, $$\sum_{i=1}^{n}f(x_i^*)\Delta x=\sum_{i=1}^{n}(i\Delta x)^2\Delta x=\sum_{i=1}^{n}\left(\frac{2i}{n}\right)^2\frac{2}{n}=\sum_{i=1}^{n}\left(\frac{4i^2}{n^2}\right)\frac{2}{n}=\sum_{i=1}^{n}\frac{8i^2}{n^3}=\frac{8}{n^3}\sum_{i=1}^{n}i^2$$ and then $$\frac{8}{n^3}\sum_{i=1}^{n}i^2=\frac{8}{n^3}\frac{n(n+1)(2n+1)}{6}=\frac{8}{n^3}\frac{2n^3+3n^2+n}{6}=\frac{16n^3+24n^2+8n}{6n^3}=\frac{8}{3}+\frac{4}{n}+\frac{4}{3n^2}$$ so that FINALLY $$\displaystyle \int_{0}^{2} x^2 \,dx=\lim_{n \rightarrow \infty}\sum_{i=1}^{n}f(x_i^*)\Delta x=\lim_{n \rightarrow \infty} \left(\frac{8}{3}+\frac{4}{n}+\frac{4}{3n^2}\right)=\frac{8}{3}.$$

But with the The Fundamental Theorem of Calculus...
It's so eeeeaaaasyyy!
1. Find an antiderivative for $f(x)=x^2.$ Ok, $F(x)=\displaystyle \frac{1}{3}x^3.$ Done.
2. Evaluate $\displaystyle \int_{0}^{2}x^2 \,dx =F(2)-F(0)=\frac{1}{3}2^3-\frac{1}{3}0^3=\frac{8}{3}.$

I love you, Fundamental Theorem of Calculus!
Examples
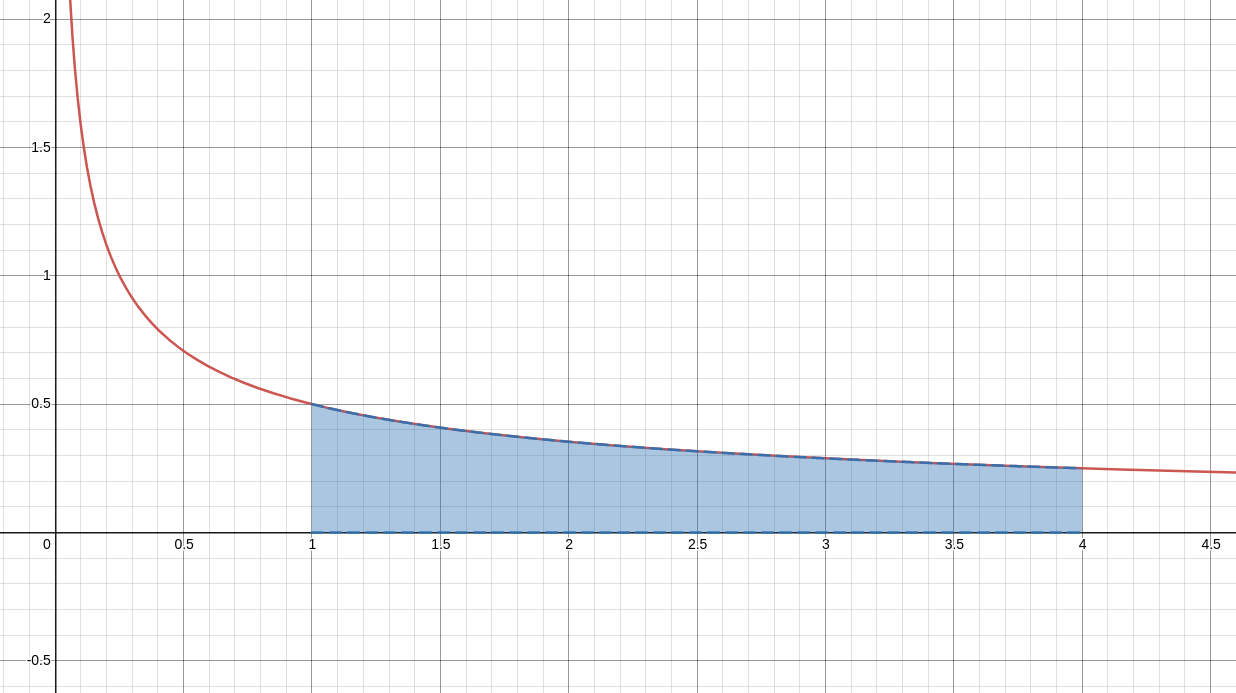
$\displaystyle \int_{1}^{4} \frac{1}{2\sqrt{x}} \, dx$
$$
\begin{array}{lll}
\displaystyle \int_{1}^{4} \frac{1}{2\sqrt{x}} \, dx &=\displaystyle \int_{1}^{4} \frac{1}{2}\frac{1}{\sqrt{x}} \, dx&\mbox{}\\
&=\displaystyle \frac{1}{2} \int_{1}^{4} \frac{1}{\sqrt{x}} \, dx&\mbox{pull out constant multiple}\\
&=\displaystyle \frac{1}{2} \int_{1}^{4} x^{-1/2} \, dx&\mbox{rewrite in exponential form}\\
&=\displaystyle \frac{1}{2} \left[2 x^{1/2}\right]_{1}^{4} &\mbox{find antiderivative (using power rule)}\\
&=\displaystyle \frac{1}{2} \left[2 \sqrt{x}\right]_{1}^{4} &\mbox{rewrite in radical form}\\
&=\displaystyle \frac{1}{2} \left[2 \sqrt{4}-2 \sqrt{1}\right] &\mbox{evaluate antiderivative at endpoints}\\
&=\displaystyle \frac{1}{2} \left[2\cdot 2-2 \cdot 1\right] &\mbox{}\\
&=\displaystyle \frac{1}{2} \left[4-2\right] &\mbox{}\\
&=\displaystyle \frac{1}{2} \cdot 2 &\mbox{}\\
&=\displaystyle 1 &\mbox{}\\
\end{array}
$$

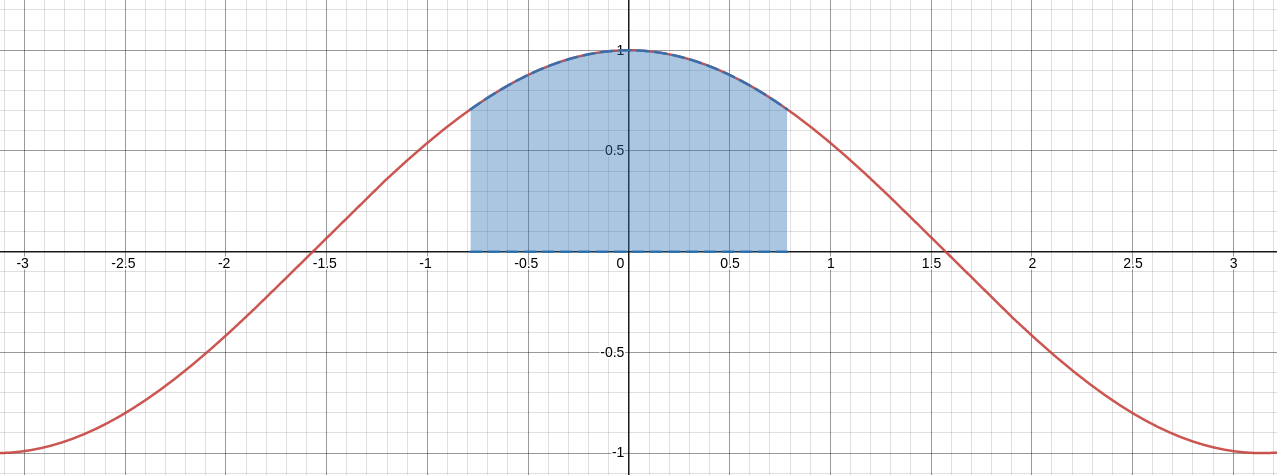
$\displaystyle \int_{-\pi/4}^{\pi/4} \cos \theta \, d\theta$
$$
\begin{array}{lll}
\displaystyle \int_{-\pi/4}^{\pi/4} \cos \theta \, d\theta &=\displaystyle [\sin \theta]_{-\pi/4}^{\pi/4}&\mbox{find antiderivative}\\
&=\displaystyle \sin \left(\frac{\pi}{4}\right)-\sin\left(-\frac{\pi}{4}\right) &\mbox{}\\
&=\displaystyle \frac{\sqrt{2}}{2}- \left(-\frac{\sqrt{2}}{2}\right)&\mbox{}\\
&=\displaystyle \frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}&\mbox{}\\
&=\displaystyle \sqrt{2}&\mbox{}\\
&\displaystyle \approx 1.41&\mbox{}\\
\end{array}
$$

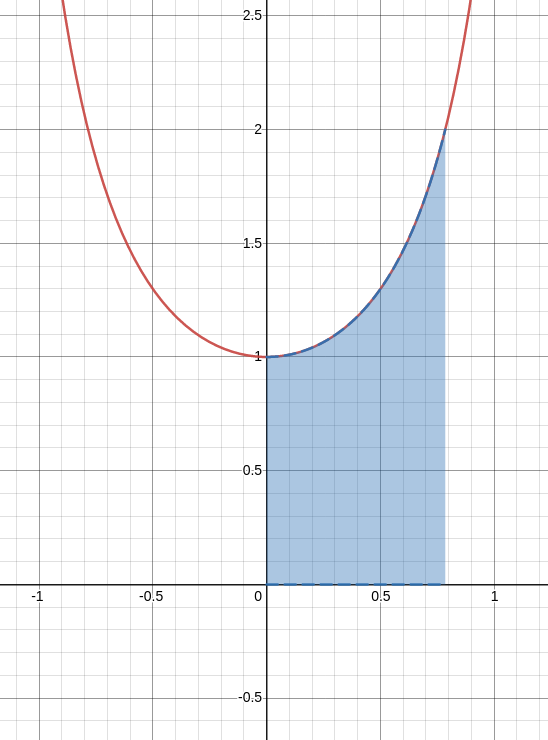
$\displaystyle \int_{0}^{\pi/4} \sec^2 \theta \, d\theta$
$$
\begin{array}{lll}
\displaystyle \displaystyle \int_{0}^{\pi/4} \sec^2 \theta \, d\theta &=\displaystyle [\tan \theta]_{0}^{\pi/4}&\mbox{find antiderivative}\\
&=\displaystyle \tan \frac{\pi}{4}-\tan 0&\mbox{}\\
&=\displaystyle 1- 0&\mbox{}\\
&=\displaystyle 1 &\mbox{}\\
\end{array}
$$

$\displaystyle \int_{4}^{8} (4t^{5/2}-3t^{3/2}) \, dt$
$$
\begin{array}{lll}
\displaystyle \int_{4}^{8} (4t^{5/2}-3t^{3/2}) \, dt &=\displaystyle \int_{4}^{8} 4t^{5/2}\,dt-\int_{4}^{8}3t^{3/2} \, dt&\mbox{integral of a diff is the diff of the integrals}\\
&=\displaystyle 4\int_{4}^{8} t^{5/2}\,dt-3\int_{4}^{8}t^{3/2} \, dt&\mbox{pull out constant multiples}\\
&=\displaystyle 4\left[\frac{2}{7}t^{7/2}\right]_{4}^{8}-3\left[\frac{2}{5}t^{5/2}\right]_{4}^{8}&\mbox{find antiderivative}\\
&=\displaystyle 4\left[\frac{2}{7}(8)^{7/2}-\frac{2}{7}(4)^{7/2}\right]-3\left[\frac{2}{5}(8)^{5/2}-\frac{2}{5}(4)^{5/2}\right]_{4}^{8}&\mbox{evaluate at end points}\\
&=\displaystyle 4\cdot \frac{2}{7}\left[(8)^{7/2}-(4)^{7/2}\right]-3\cdot \frac{2}{5} \left[(8)^{5/2}-(4)^{5/2}\right]&\mbox{factor out fractions}\\
&=\displaystyle \frac{8}{7}\left[(\sqrt{8})^7-2^7\right]-\frac{6}{5} \left[(\sqrt{8})^5-2^5\right]&\mbox{re-express as radicals}\\
&=\displaystyle \frac{8}{7}\left[(2\sqrt{2})^7-128\right]-\frac{6}{5} \left[(2\sqrt{2})^5-32\right]&\mbox{simplify radicals}\\
&=\displaystyle \frac{8}{7}\left[2^7(\sqrt{2})^7-128\right]-\frac{6}{5} \left[2^5(\sqrt{2})^5-32\right]&\mbox{apply exponent rules}\\
&=\displaystyle \frac{8}{7}\left[128(\sqrt{2})^7-128\right]-\frac{6}{5} \left[32(\sqrt{2})^5-32\right]&\mbox{}\\
&=\displaystyle \frac{8}{7}\cdot 128\left[(\sqrt{2})^7-1\right]-\frac{6}{5}\cdot 32 \left[(\sqrt{2})^5-1\right]&\mbox{factor out common factors}\\
%&=\displaystyle \frac{8}{7}\cdot 128\left[8\sqrt{2}-1\right]-\frac{6}{5}\cdot 32 \left[4\sqrt{2}-1\right]&\mbox{}\\
&=\displaystyle \frac{1024}{7}\left[8\sqrt{2}-1\right]-\frac{192}{5} \left[4\sqrt{2}-1\right]&\mbox{}\\
&=\displaystyle \frac{1024}{7}\cdot 8\sqrt{2}-\frac{1024}{7}-\frac{192}{5} \cdot 4\sqrt{2}+\frac{192}{5}&\mbox{}\\
&=\displaystyle \frac{8192}{7}\sqrt{2}-\frac{1024}{7}-\frac{768}{5}\sqrt{2}+\frac{192}{5}&\mbox{}\\
&=\displaystyle \frac{8192}{7}\sqrt{2}-\frac{768}{5}\sqrt{2}-\frac{1024}{7}+\frac{192}{5}&\mbox{}\\
&=\displaystyle \left(\frac{8192}{7}-\frac{768}{5}\right)\sqrt{2}-\frac{3776}{35}&\mbox{}\\
&=\displaystyle \frac{35584}{35}\sqrt{2}-\frac{3776}{35}&\mbox{}\\
&\approx \displaystyle 1329.925012 &\mbox{}\\
\end{array}
$$

The Big Picture $$\frac{d}{dx}\int_{a}^{x}f(t) \, dt=f(x)$$ $$\int_{a}^{b}F'(x) \, dx=F(b)-F(a).$$
Taken together, both parts of the Fundamental of Calculus say that differentiation and integration are inverse processes.
Bonus Example: Below is the graph of $\displaystyle y=\int_{0}^{x} \ell(t) \, dt$ where $\ell$ is a piecwise linear function.
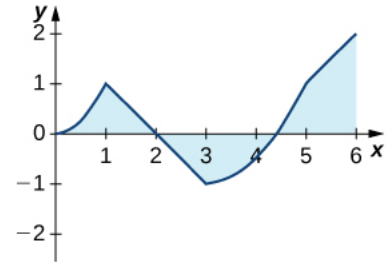
By Part $1$ of the FTC, we have that $\displaystyle \ell(x)=\frac{dy}{dx}=\frac{d}{dx}\int_{0}^{x} \ell(t) \, dt.$
That is, the value of $\ell(x)$ is the slope of the tangent line to the curve shown in the figure above.
Thus, $\ell(x)$ is positive on the interval $(0,1)\cup(3,5)\cup(5,6)$ and is negative on $(1,3).$
That is, the value of $\ell(x)$ is the slope of the tangent line to the curve shown in the figure above.
Thus, $\ell(x)$ is positive on the interval $(0,1)\cup(3,5)\cup(5,6)$ and is negative on $(1,3).$
b. Over which intervals is $\ell$ increasing? Over which is it decreasing? Over which intervals, if any, is it constant?
Since $\displaystyle \ell(x)=\frac{dy}{dx}=\frac{d}{dx}\int_{0}^{x} \ell(t) \, dt,$ we have
$\displaystyle \ell'(x)=\frac{d^2y}{dx^2}.$
Thus, $\ell(x)$ is increasing when $\displaystyle \ell'(x)=\frac{d^2y}{dx^2} \gt 0,$ or when the concavity of the above curve is positive.
It follows that $\ell(x)$ is increasing in the interval $(0,1)\cup(3,5),$ is nowhere decreasing, and is constant on on $(1,3)\cup(5,6).$
Thus, $\ell(x)$ is increasing when $\displaystyle \ell'(x)=\frac{d^2y}{dx^2} \gt 0,$ or when the concavity of the above curve is positive.
It follows that $\ell(x)$ is increasing in the interval $(0,1)\cup(3,5),$ is nowhere decreasing, and is constant on on $(1,3)\cup(5,6).$
c. What is the average value of $\ell?$
The average value of $\ell(x)$ on $[0,6]$ is
$$
\begin{array}{lll}
\displaystyle \frac{1}{6-0}\int_{0}^{6} \ell(t) \, dt&\displaystyle=\frac{1}{6}y(6)&\mbox{by definition of $y$}\\
&\displaystyle =\frac{1}{6}\cdot 2&\mbox{}\\
&\displaystyle =\frac{1}{3} &\mbox{}\\
\end{array}
$$