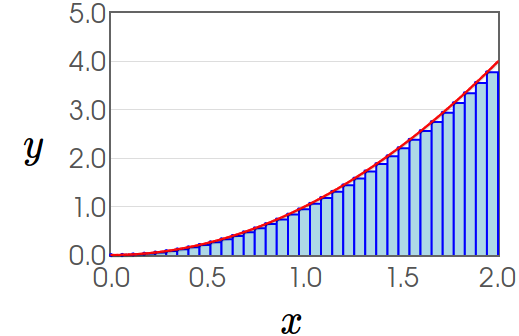
Recall: The exact area under the curve of $f(x)=x^2$ over the interval $[0,2]$ is $\displaystyle \frac{8}{3}.$
$y=x^2, \,\, 0 \leq x \leq 2$
| $y$ | $y$ | ||
| $x$ | $x$ |
The Definite Integral
The exact area under the curve of $f(x)=x^2$ over the interval $[0,2]$ has a special notation: $$\int_{0}^{2} x^2 \,dx$$ This area also has a special name. In this case, it is the definite integral of $x^2$ from $0$ to $2.$
The Definite Integral
Recall that this exact area under the curve, $\displaystyle \int_{0}^{2} x^2 \,dx,$ is the limit of a Riemann sum $\displaystyle \lim_{n \rightarrow \infty} \sum_{i=1}^{n} (x_i^*)^2\Delta x.$
The Definite Integral: Notation
| $$\lim_{n \rightarrow \infty} \sum_{i=1}^{n} (x_i^*)^2\Delta x$$ | ||
| $\displaystyle \sum_{i=1}^{n} (x_i^*)^2\Delta x$ | $\longrightarrow$ | $\displaystyle \int_{0}^{2} x^2 \,dx$ |
 | $\longrightarrow$ | 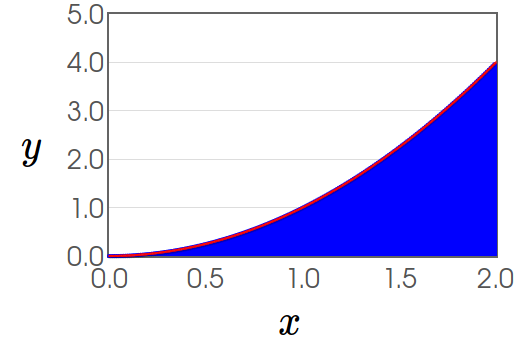 |
Definition: Let $f$ be a function on the interval $[a,b].$ Then the definite integral from $a$ to $b$ is given by $$\int_{a}^{b}f(x) \, dx = \lim_{n \rightarrow \infty} \sum_{i=1}^{n} f(x_i^*)\Delta x$$ provided the limit exists. If it does, then $f$ is said to be integrable on $[a,b].$
The Definite Integral as a Signed Area
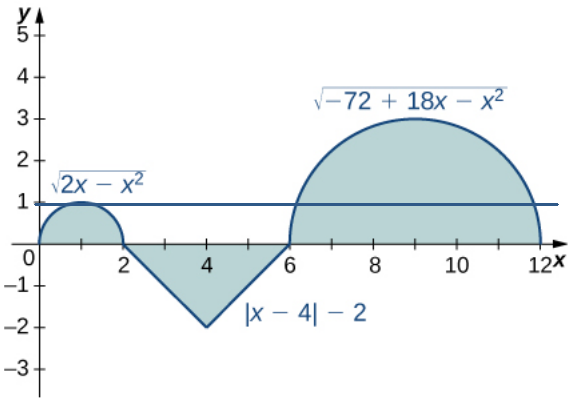
Example: Consider the function $f(x)$ graphed in the figure below. Evaluate the definite integral $$\displaystyle \int_{0}^{12} f(x)\,dx.$$
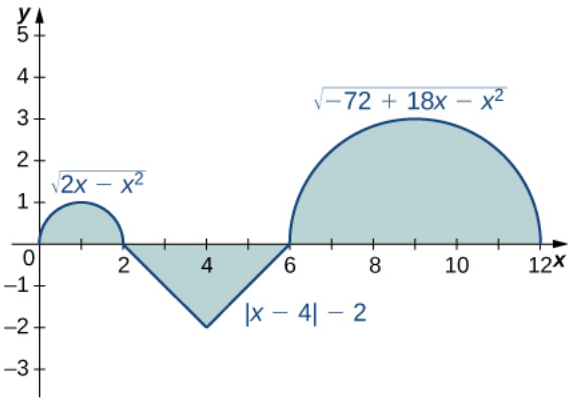
We can break up the integral into three separate areas:
$$\displaystyle \int_{0}^{12} f(x)\,dx=\int_{0}^{2} f(x)\,dx+\int_{2}^{6} f(x)\,dx+\int_{6}^{12} f(x)\,dx=\frac{\pi}{2}+\left(-4\right)+\frac{9\pi}{2}=5\pi-4$$
Without even knowing it, we just used a nice fact about integrals!


Properties of the Definite Integral $$ \int_{a}^{b} f(x)\,dx = \int_{a}^{c} f(x)\,dx+\int_{c}^{b} f(x)\,dx$$
Public Service Announcement
As we've just seen, over intervals where $f(x)$ is negative, the integral (area!) is negative.
Contrary to what we've been told all these years in our algebra courses, an area CAN be negative...

Duhn! Duhn! Duuuuhhhun!
In fact, negative area can actually be quite meaningful!
Negative Area Has a Physical Meaning: The signed area is the net distance travelled.
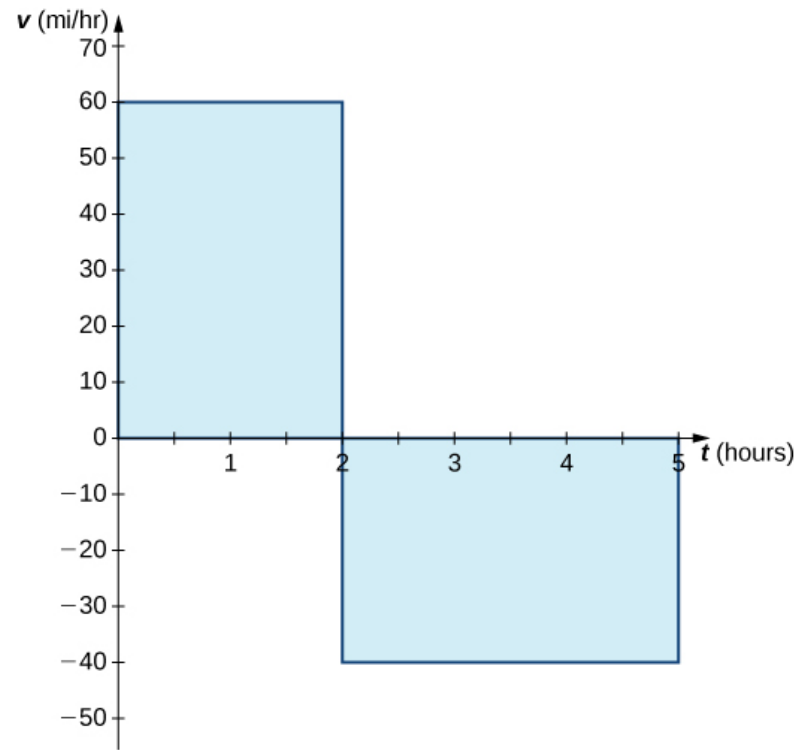
On the other hand, if we want to find the total area as if it were positive, we need to do something a bit different...
The Definite Integral as a Total Area
Example: Consider the function $f(x)$ graphed in the figure below. Evaluate the definite integral $$\displaystyle \int_{0}^{12} |f(x)|\,dx.$$

$$\displaystyle \int_{0}^{12} |f(x)|\,dx=\int_{0}^{2} |f(x)|\,dx+\int_{2}^{6} |f(x)|\,dx+\int_{6}^{12} |f(x)|\,dx=\frac{\pi}{2}+4+\frac{9\pi}{2}=5\pi+4$$
We now consider some properties of the definite integral which we will be using a lot!
Properties of the Definite Integral $$\int_{a}^{b} [f(x)+g(x)]\,dx=\int_{a}^{b} f(x)\,dx+ \int_{a}^{b} g(x)\,dx$$ $$\int_{a}^{b} [f(x)-g(x)]\,dx=\int_{a}^{b} f(x)\,dx- \int_{a}^{b} g(x)\,dx$$ $$\int_{a}^{b} cf(x)\,dx= c \int_{a}^{b} f(x)\,dx$$
Example
Suppose that $\displaystyle \int_{0}^{4} f(x) \, dx=5$ and $\displaystyle \int_{0}^{2} f(x) \, dx=-3,$ and $\displaystyle \int_{0}^{4} g(x) \, dx=-1$ and $\displaystyle \int_{0}^{2} g(x) \, dx=2.$
Compute the following integral: $$\int_{0}^{2}\left[3f(x)-4g(x)\right] \, dx$$
$$
\begin{array}{lll}
\displaystyle \int_{0}^{2}\left[3f(x)-4g(x)\right] \, dx&=\displaystyle \int_{0}^{2}3f(x)\,dx-\int_{0}^{2}4g(x)\,dx &\mbox{integral of diff is the diff of the integrals}\\
&=\displaystyle 3\int_{0}^{2}f(x)\,dx-4\int_{0}^{2}g(x)\,dx &\mbox{pull out constant multiples}\\
&=\displaystyle 3(-3)-4(2) &\mbox{since $\displaystyle \int_{0}^{2} f(x) \, dx=-3$ and $\displaystyle \int_{0}^{2} g(x) \, dx=2$}\\
&=\displaystyle -17 &\mbox{}\\
\end{array}
$$
Average Value of a Function
Definition: The average value $f_{avg}$ of the function $f$ on the interval $[a,b]$ is given by $$f_{avg}=\frac{1}{b-a}\int_{a}^{b}f(x) \, dx.$$
Example: Consider the function $f(x)$ graphed in the figure below.

The average value of $f$ on $[0,12]$ is $$f_{avg}=\frac{1}{12-0}\displaystyle \int_{0}^{12} f(x)\,dx=\frac{1}{12}\displaystyle \int_{0}^{12} f(x)\,dx= \frac{1}{12}(5 \pi -4) \approx 0.976$$

Comparison Theorem
i. If $f(x) \geq 0$ on the interval $[a,b],$ then $\displaystyle \int_{a}^{b}f(x) \, dx \geq 0.$
ii. If $f(x) \geq g(x)$ on the interval $[a,b],$ then $\displaystyle \int_{a}^{b}f(x) \, dx \geq \int_{a}^{b}g(x) \, dx.$
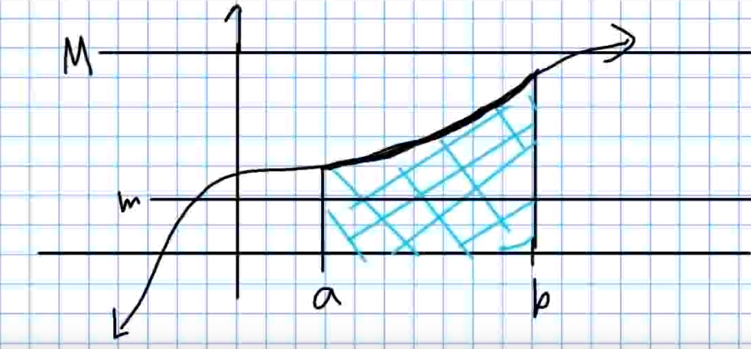
iii. If $m \leq f(x) \leq M$ on the interval $[a,b],$ then $\displaystyle m(b-a) \leq \int_{a}^{b}f(x) \, dx \leq M(b-a).$
Note: Notice that iii. can be rephrased in terms of the average value of a function: $\displaystyle m \leq \frac{1}{b-a}\int_{a}^{b}f(x) \, dx \leq M.$
Special Note on Comparison Theorem Part iii
If $m \leq f(x) \leq M$ on the interval $[a,b],$ then $\displaystyle m(b-a)\leq$ $\displaystyle \int_{a}^{b}f(x) \, dx$ $\leq M(b-a).$
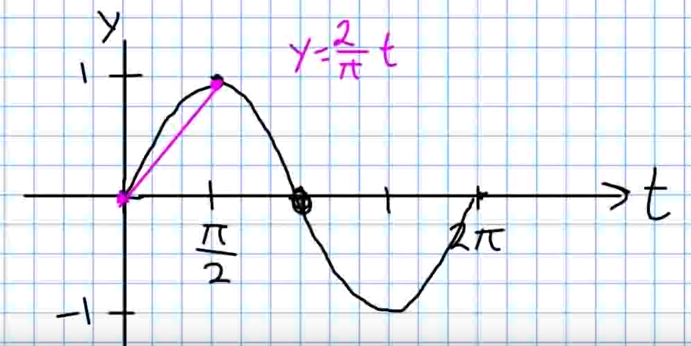
Example: Use the Comparison Theorem to show that $$\int_{0}^{\pi/2} \sin t \,dt \geq \frac{\pi}{4}.$$ (Hint: use that $\displaystyle \sin t \geq \frac{2}{\pi}t$ over $\displaystyle \left[0,\frac{\pi}{2}\right].$)
Miscellaneous Debris
1. $$\int_{a}^{a} f(x)\,dx= 0$$ 2. $$\int_{a}^{b} f(x)\,dx= -\int_{b}^{a} f(x)\,dx$$ 3. All continuous functions on $[a,b]$ are integrable on $[a,b].$
4. The variable of integration is arbitrary. All the following integrals are the same. $$\int_{a}^{b}f(x) \,dx, \,\,\,\, \int_{a}^{b}f(W) \,dW, \,\,\,\, \int_{a}^{b}f(\Phi) \,d\Phi, \,\,\,\, \int_{a}^{b}f(\xi) \,d\xi, \,\,\,\,\int_{a}^{b}f(\mbox{Symbol}) \,d\mbox{Symbol} \,\,\,\,$$