Newton's Method is all about estimating roots (zeros) of general functions.
That is, Newton's Method helps us to solve equations of the form $f(x)=0.$
Example
Solving cubic equations is much harder that quadratic equations.
Suppose we needed to solve the equation $f(x)=x^3-3x^2+3=0.$
Although there is a cubic formula, it's very complicated. What shall we do?
Newton's Method: The Big Idea
| $f(x)=x^3-3x^2+3$ | Initial Guess: $x_0=$ | |
| $y$ | | |
| $x$ |
Newton's Method
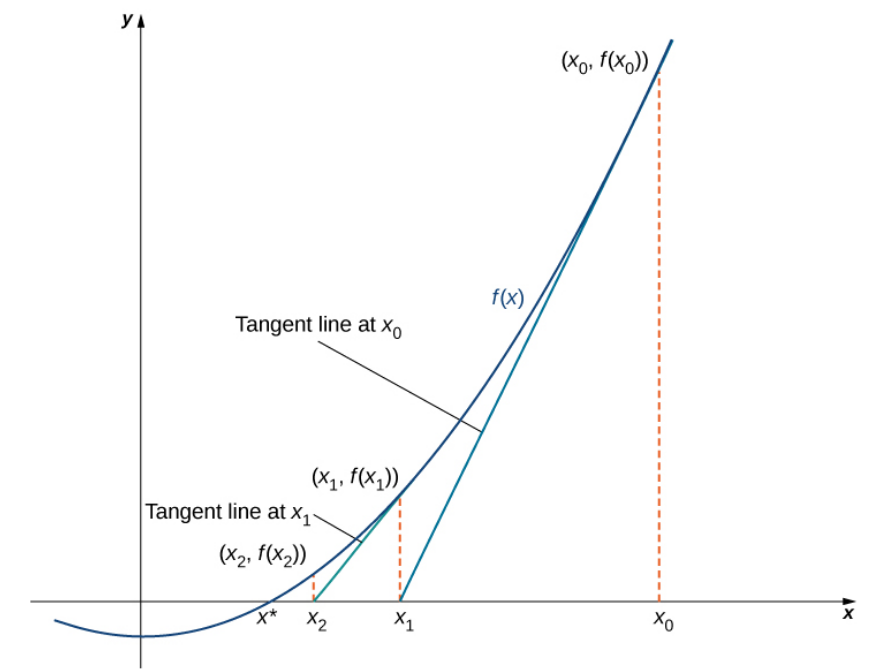
Since the point $(x_1,0)$ is on this line we have that $0-f(x_0)=f'(x_0)(x_1-x_0).$
Newton's Method

Newton's Method

Newton's Method
In general, we have $$\displaystyle x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})}.$$
Example
Let's return to our old friend $f(x)=x^3-3x^2+3.$ To employ Newton's Method, we note that $f'(x)=3x^2-6x.$ Then our formula becomes $\displaystyle x_{n+1}=x_{n}-\frac{x_{n}^3-3x_{n}^2+3}{3x_{n}^2-6x_{n}}.$ Like we did above, we take an initial guess of $x_0=5.$
| $n$ | $\displaystyle x_{n+1}=x_{n}-\frac{x_{n}^3-3x_{n}^2+3}{3x_{n}^2-6x_{n}}$ |
Finding Roots
Have you ever wondered how a calculator finds square roots?
Newton's Method is one way to do so. Suppose we wanted to find the square root of $3.$
We note that $\sqrt{3}$ is a root to the equation $x^2-3=0.$
We may now apply Newton's Method to this equation by taking $f(x)=x^2-3.$
Example
We now find the root of the function $f(x)=x^2-3.$ To employ Newton's Method, we note that $f'(x)=2x.$ Then our formula becomes $\displaystyle x_{n+1}=x_{n}-\frac{x_{n}^2-3}{2x_{n}}.$ Let's take an initial guess of $x_0=1.5.$
| $n$ | $\displaystyle x_{n+1}=x_{n}-\frac{x_{n}^2-3}{2x_{n}}$ |
Finding Maxima and Minima
Since maxima and minima can occur where $f'(x)=0,$ we can apply Newton's Method to the equation $f'(x)=0$ to get $$\displaystyle x_{n+1}=x_{n}-\frac{f'(x_{n})}{f''(x_{n})}.$$
Example
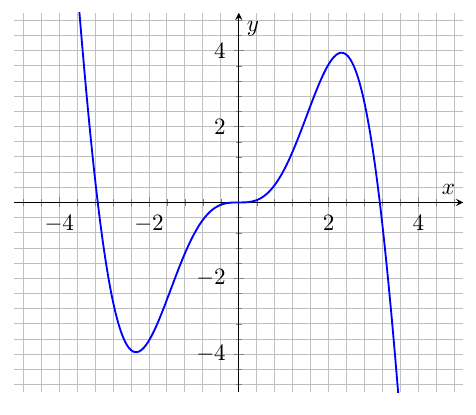
Use Newton's method to find the closest non-zero local minimum to $x=0$ of $\displaystyle f(x)=x^2 \sin x$ to three decimal places. Use the graph below to help make your guess for $x_0.$
Example
We now find the local minimum of the function $f(x)=x^2\sin x$ at $x=-2$ To employ Newton's Method, we note that $$f'(x)=2x\sin x+x^2\cos x$$ and $$ \begin{array}{rl} f''(x)&=2\sin x+2x\cos x+2x\cos x-x^2\sin x\\ &=2\sin x+4x\cos x-x^2\sin x. \end{array} $$ Then our formula becomes $$\displaystyle x_{n+1}=x_{n}-\frac{2x_{n}\sin x_{n}+x_{n}^2\cos x_{n}}{2\sin x_{n}+4x_{n}\cos x_{n}-x_{n}^2\sin x_{n}}.$$ Based upon the graph, let's take an initial guess of $x_0=-2.$
| $n$ | $\displaystyle x_{n+1}=x_{n}-\frac{f'(x_{n})}{f''(x_{n})}$ |
When Newton's Method Fails: Fail #1. At one of the approximations $x_n,$ the derivative $f'$ is zero at $x_n,$ but $f(x_n)\neq 0.$ As a result, the tangent line at $x_n$ does not intersect the $x$-axis. Therefore, we cannot continue the iterative process. As an example, set $x_0=0$ as our initial guess.
| $f(x)=x^3-3x^2+3$ | Initial Guess: $x_0=$ | |
| $y$ | | |
| $x$ |
When Newton's Method Fails: Fail #2. The approximations $x_0,$ $x_1,$ $x_2,\ldots$ may approach a different root. If the function $f$ has more than one root, it is possible that our approximations do not approach the root which we want, but approach a different root. This event most often occurs when we do not choose the approximation $x_0$ close enough to the desired root. As an example, set $x_0=0.1$ as our initial guess.
| $f(x)=x^3-3x^2+3$ | Initial Guess: $x_0=$ | |
| $y$ | | |
| $x$ |
When Newton's Method Fails: Fail #3. The approximations may fail to approach a root entirely. As an example, compare the behavior of the sequence with $x_0=1.16$ and $x_0=1.17$ as our initial guesses.
| $f(x)=x^3-2x+2$ | Initial Guess: $x_0=$ | |
| $y$ | | |
| $x$ |
Bonus Example! Remember the cubic equation $2x^3+3x^2+15x-11=0$ from Section $4.6?$
We can now solve this cubic!
To avoid confusion when referencing the last example of Section $4.6,$ we will say that $g(x)=2x^3+3x^2+15x-11$ so that $g'(x)=6x^2+6x+15.$
Then our recursion formula becomes $\displaystyle x_{n+1}=x_{n}-\frac{2x_{n}^3+3x_{n}^2+15x_{n}-11}{6x_{n}^2+6x_{n}+15}.$
Initial guess: $x_0=$
| $n$ | $\displaystyle x_{n+1}=x_{n}-\frac{g(x_{n})}{g'(x_{n})}$ |