When the input of a function becomes very large in the positive or negative direction, the value of a function can approach a fixed value.
For example, the strength of earth's gravitational pull on an object gets closer to zero as the distance of the object from earth gets bigger and bigger.
Example
Consider the function $f(x)$ below. As $x$ becomes large in the positive direction, the value of $f(x)$ gets closer and closer to $2.$
As $x$ becomes large in the negative direction, the value of $f(x)$ gets closer and closer to $1.$
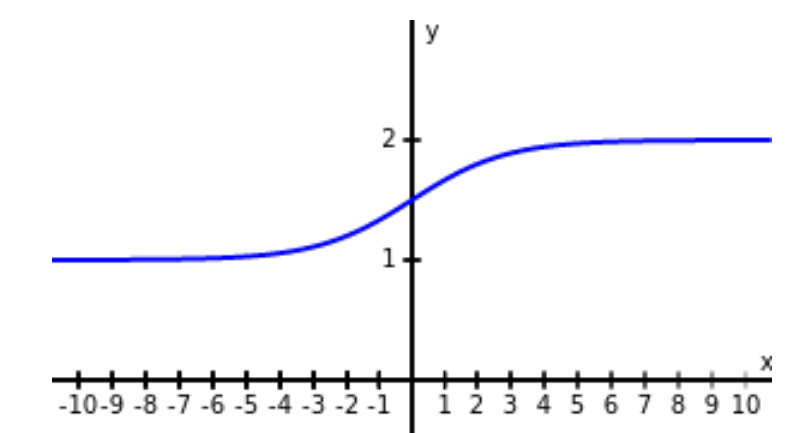
Horizontal Asymptotes & Limits at Infinity
Informal Definition
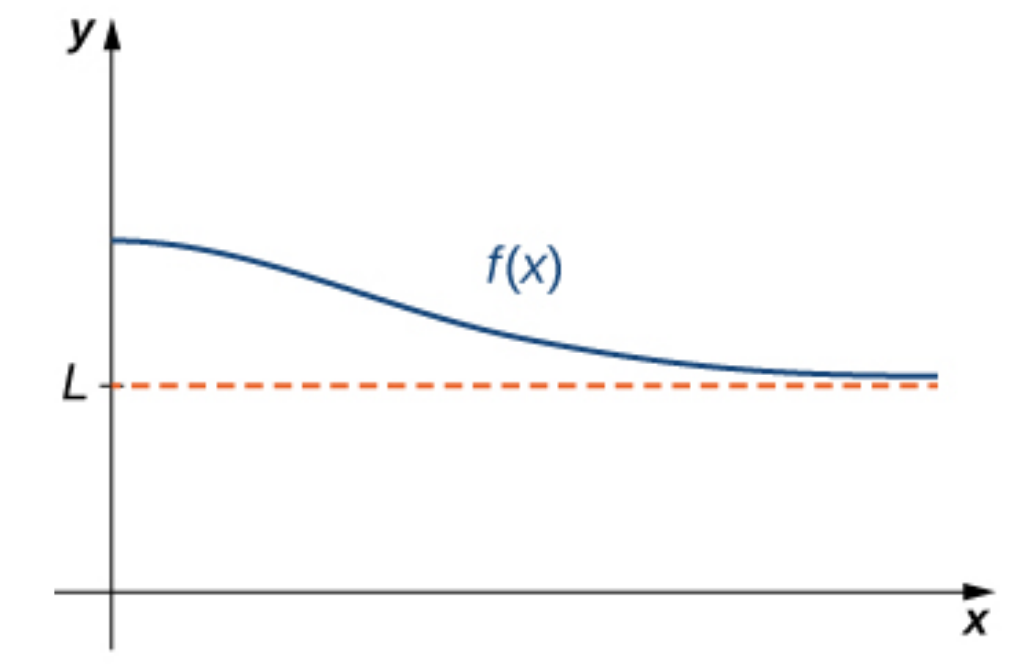
If the values of $f(x)$ become arbitrarily close to $L$ as $x$ becomes sufficiently large, we say the function $f$ has a limit at infinity and write $$\lim_{x \rightarrow \infty}f(x)=L.$$
Horizontal Asymptotes & Limits at Negative Infinity
Informal Definition
If the values of $f(x)$ become arbitrarily close to $L$ as $x \lt 0$ becomes sufficiently large in the negative direction, we say the function $f$ has a limit at negative infinity and write $$\lim_{x \rightarrow -\infty}f(x)=L.$$
Example
For the function $f(x)$ below we would write $$\lim_{x \rightarrow \infty}f(x)=2 \,\,\,\, \mbox{ and } \,\,\,\, \lim_{x \rightarrow -\infty}f(x)=1.$$
Definition: Horizontal Asymptote
If $\displaystyle \lim_{x \rightarrow \infty}f(x)=L$ or $ \displaystyle \lim_{x \rightarrow -\infty}f(x)=L$ we say that the line $y=L$ is a horizontal asymptote of $f.$
Example
For the function $f(x)$ below, since $\displaystyle \lim_{x \rightarrow \infty}f(x)=1$ and $\displaystyle \lim_{x \rightarrow -\infty}f(x)=0,$ we say that $$y=2 \,\,\,\, \mbox{ and } \,\,\,\, y=1$$ are horizontal asymptotes of $f.$
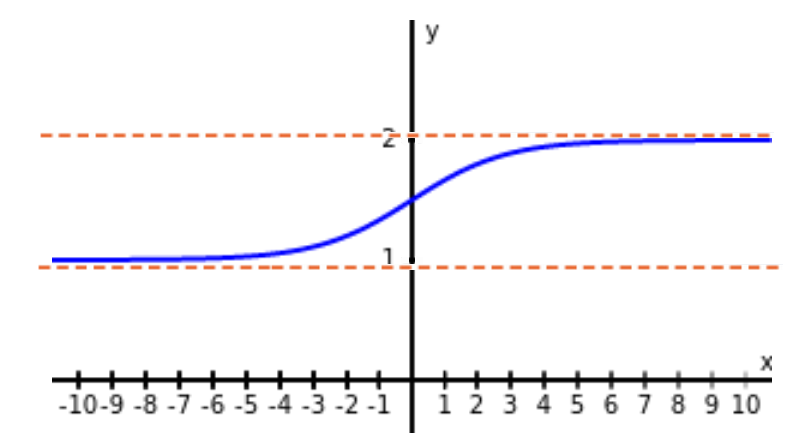
Here comes the formal definition of a limit at infinity! Are you ready?! :D
Formal Definition: Limit at Infinity
We say a function $f$ has a limit $L$ at infinity, if for all $ε \gt 0,$ there exists an $N \gt 0$ such that $$x \gt N \implies |f(x)-L| \lt \varepsilon.$$ In this case we write $$\lim_{x \rightarrow \infty}f(x)=L.$$
The $\varepsilon$-$N$ Definition of a Limit at Infinity (Limit Exists)
$\displaystyle \lim_{x \rightarrow \infty} f(x)=L$ means:
for any $\varepsilon \gt 0$ we choose,
we can find a $N \gt 0$ such that
$x \gt N$ (any $x$-value in pink region)
guarantees that $|f(x)-L| \lt \varepsilon$
(beyond $N$, $f(x)$-values are ALL in blue strip)
for any $\varepsilon \gt 0$ we choose,
we can find a $N \gt 0$ such that
$x \gt N$ (any $x$-value in pink region)
guarantees that $|f(x)-L| \lt \varepsilon$
(beyond $N$, $f(x)$-values are ALL in blue strip)
Example
Use the formal definition of an infinite limit to show $$\lim_{x \rightarrow \infty}\frac{1}{x}=0.$$
$$\lim_{x \rightarrow \infty}\frac{1}{x}=0.$$
Proof: Let $\varepsilon \gt 0.$ Choose $\displaystyle N=\frac{1}{\varepsilon}.$
Then,
$$
\begin{array}{lll}
& \displaystyle x \gt N&\\
\implies & \displaystyle x \gt \frac{1}{\varepsilon}&\\
\implies & \displaystyle \varepsilon \gt \frac{1}{x}&\\
\implies & \displaystyle \left|\frac{1}{x}-0\right|\lt \varepsilon&\\
\end{array}
$$
$\square$
Good News!
All the limit laws and theorems and limit theorems we've studied apply to limits at infinity!
For this reason, we will not need to bother much with the formal definition to show when limits at infinity exist.
All Limit Laws
Example: Since $\displaystyle \lim_{x \rightarrow \infty}\frac{1}{x}=0,$ we have by the limit laws that $$ \displaystyle \lim_{x \rightarrow \infty}\frac{1}{x^2} =\lim_{x \rightarrow \infty}\left(\frac{1}{x}\cdot\frac{1}{x}\right) =\lim_{x \rightarrow \infty}\frac{1}{x}\cdot\lim_{x \rightarrow \infty}\frac{1}{x} =0\cdot 0 =0. $$
Squeeze Theorem
Since $-1\leq \sin x \leq 1,$ it's true that $\displaystyle -\frac{1}{x}\leq \frac{\sin x}{x} \leq \frac{1}{x}.$ By the squeeze theorem we then have $$\lim_{x \rightarrow \infty}\frac{\sin x}{x}=0.$$
Example
Use the limit laws and the basic limit we just proved, $\displaystyle \lim_{x \rightarrow \infty}\frac{1}{x}=0,$ to evaluate $$\displaystyle \lim_{x \rightarrow \infty} \frac{x^2-3x+4}{x^2-1}.$$
$$
\begin{array}{lll}
\displaystyle \lim_{x \rightarrow \infty} \frac{x^2-3x+4}{x^2-1}&=\displaystyle \lim_{x \rightarrow \infty} \frac{x^2-3x+4}{x^2-1}\frac{\frac{1}{x^2}}{\frac{1}{x^2}}&\mbox{}\\
&=\displaystyle \lim_{x \rightarrow \infty} \frac{x^2\frac{1}{x^2}-3x\frac{1}{x^2}+4\frac{1}{x^2}}{x^2\frac{1}{x^2}-1\frac{1}{x^2}}&\mbox{}\\
&=\displaystyle \lim_{x \rightarrow \infty} \frac{1-\frac{3}{x}+\frac{4}{x^2}}{1-\frac{1}{x^2}}&\mbox{}\\
&=\displaystyle \frac{\displaystyle \lim_{x \rightarrow \infty}\left(1-\frac{3}{x}+\frac{4}{x^2}\right)}{\displaystyle \lim_{x \rightarrow \infty} \left(1-\frac{1}{x^2}\right)}&\mbox{Quotient Law}\\
&=\displaystyle \frac{\displaystyle \lim_{x \rightarrow \infty}1-\displaystyle \lim_{x \rightarrow \infty}\frac{3}{x}+\displaystyle \lim_{x \rightarrow \infty}\frac{4}{x^2}}{\displaystyle \lim_{x \rightarrow \infty} 1-\displaystyle \lim_{x \rightarrow \infty}\frac{1}{x^2}}&\mbox{Sum and Difference Law}\\
&=\displaystyle \frac{\displaystyle 1-\displaystyle 3 \lim_{x \rightarrow \infty}\frac{1}{x}+\displaystyle 4 \lim_{x \rightarrow \infty}\frac{1}{x^2}}{\displaystyle 1-0}&\mbox{Limit of a Constant, Constant Multiple Laws}\\
&=\displaystyle \frac{\displaystyle 1-\displaystyle 3 \cdot 0+\displaystyle 4 \cdot 0}{1}&\mbox{}\\
&=\displaystyle 1&\mbox{}\\
\end{array}
$$
Example
Consider the function $\displaystyle f(x)=\frac{1}{1+2^{-x}}+1$ whose graph is seen below.
Use limit laws to show that $\displaystyle \lim_{x \rightarrow \infty} \left(\frac{1}{1+2^{-x}}+1\right)=2.$
$$
\begin{array}{lll}
\displaystyle \lim_{x \rightarrow \infty} \left(\frac{1}{1+2^{-x}}+1\right)&=\displaystyle \lim_{x \rightarrow \infty}\frac{1}{1+2^{-x}}+\displaystyle \lim_{x \rightarrow \infty} 1&\mbox{Sum Law}\\
&=\frac{\displaystyle \lim_{x \rightarrow \infty} 1}{\displaystyle \lim_{x \rightarrow \infty}\left(1+2^{-x}\right)}+1&\mbox{Limit of a Constant and Quotient Laws}\\
&=\frac{\displaystyle 1}{\displaystyle \lim_{x \rightarrow \infty}1+\lim_{x \rightarrow \infty}2^{-x}}+1&\mbox{Limit of a Constant and Sum Laws}\\
&=\frac{\displaystyle 1}{\displaystyle 1+0}+1&\mbox{Limit of a Constant}\\
&=2&\mbox{}\\
\end{array}
$$
Example
Consider the function $\displaystyle f(x)=\frac{1}{1+2^{-x}}+1$ whose graph is seen below.
Use the Squeeze Theorem to show that $\displaystyle \lim_{x \rightarrow -\infty} \left(\frac{1}{1+2^{-x}}+1\right)=1.$
It is true for any $x$ that $\displaystyle 0 \leq \frac{1}{1+2^{-x}} \leq \frac{1}{2^{-x}}=2^x.$ Thus, adding $1$ to all sides, it is also true that
$$1 \leq \frac{1}{1+2^{-x}}+1 \leq 2^x+1.$$
Since $\displaystyle \lim_{x \rightarrow -\infty} 1=1,$ and
$\displaystyle \lim_{x \rightarrow -\infty} \left(2^x+1\right)=\lim_{x \rightarrow -\infty} 2^x+\lim_{x \rightarrow -\infty}1=0+1=1,$
the Squeeze Theorem guarantees that $$\lim_{x \rightarrow -\infty} \left(\frac{1}{1+2^{-x}}+1\right)=1$$
Infinite Limits at Infinity
Consider the function $f(x)$ below. As $x$ becomes large in the positive direction, the value of $f(x)$ just keeps getting bigger and bigger.
As $x$ becomes large in the negative direction, the value of $f(x)$ also keeps getting bigger and bigger but in the negative direction
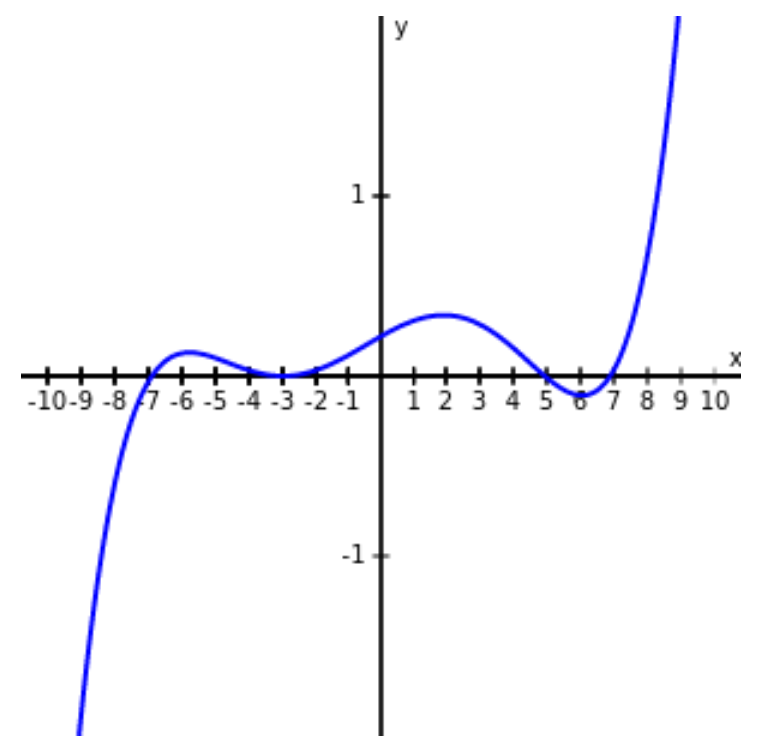
Informal Definition
We say a function $f$ has an infinite limit at infinity and write $$\displaystyle \lim_{x\rightarrow \infty}f(x)= \infty$$ if $f(x)$ becomes arbitrarily large for $x$ sufficiently large.
We say a function has a negative infinite limit at infinity and write $$\displaystyle \lim_{x\rightarrow \infty}f(x)= -\infty$$ if $f(x) \lt 0$ and $|f(x)|$ becomes arbitrarily large for $x$ sufficiently large.
Similarly, we can define infinite limits as $x\rightarrow -\infty.$
Example: Infinite Limits at Infinity
For the function $f(x)$ below we would write $$\lim_{x \rightarrow \infty} f(x)=\infty \,\,\,\, \mbox{ and }\,\,\,\,\lim_{x \rightarrow -\infty} f(x)=-\infty$$
Example: Infinite Limits at Infinity
For the function $f(x)$ below we would write $$\lim_{x \rightarrow \infty} f(x)=-\infty \,\,\,\, \mbox{ and }\,\,\,\,\lim_{x \rightarrow -\infty} f(x)=\infty$$
Formal Definition
We say a function $f$ has an infinite limit at infinity and write $$\lim_{x\rightarrow \infty}f(x)= \infty$$ if for all $M\gt 0,$ there exists an $N \gt 0$ such that $f(x) \gt M$ for all $x>N.$
We say a function has a negative infinite limit at infinity and write $$\lim_{x\rightarrow \infty}f(x)= -\infty$$ if for all $M \lt 0,$there exists an $N \gt 0$ such that $f(x)\lt M$ for all $x \gt N.$
Similarly we can define limits as $x\rightarrow -\infty$
Formal Definition of Infinite Limit
$\displaystyle \lim_{x \rightarrow \infty} f(x)=\infty$ means:
for any $M \gt 0$ we choose,
we can find a $N \gt 0$ such that
$x \gt N$ (any $x$-value in pink region)
guarantees that $f(x) \gt M$
(beyond $N$, $f(x)$-values are ALL in blue region)
for any $M \gt 0$ we choose,
we can find a $N \gt 0$ such that
$x \gt N$ (any $x$-value in pink region)
guarantees that $f(x) \gt M$
(beyond $N$, $f(x)$-values are ALL in blue region)
Example
Use the formal definition of an infinite limit at infinity to show that $$\displaystyle \lim_{x \rightarrow \infty}3x^2=\infty.$$
Proof: Let $M \gt 0.$ Choose $\displaystyle N=\sqrt{\frac{M}{3}}.$
Then,
$$
\begin{array}{lll}
& \displaystyle x \gt N&\\
\implies & \displaystyle x \gt \sqrt{\frac{M}{3}}&\\
\implies & \displaystyle x^2 \gt \frac{M}{3}&\\
\implies & \displaystyle 3x^2 \gt M&\\
\end{array}
$$
$\square$
End Behavior
End Behavior is basically what a function "does at $\pm\infty.$" There are three possibilities:
| 1.The function $f(x)$ approaches a horizontal asymptote $y=L.$ | |
| 2.The function $f(x)\rightarrow \infty$ or $f(x)\rightarrow -\infty.$ | |
| 3.The function does not approach a finite limit, nor does it approach $\infty$ or $-\infty.$ In this case, the function may have some oscillatory or periodic behavior. |   |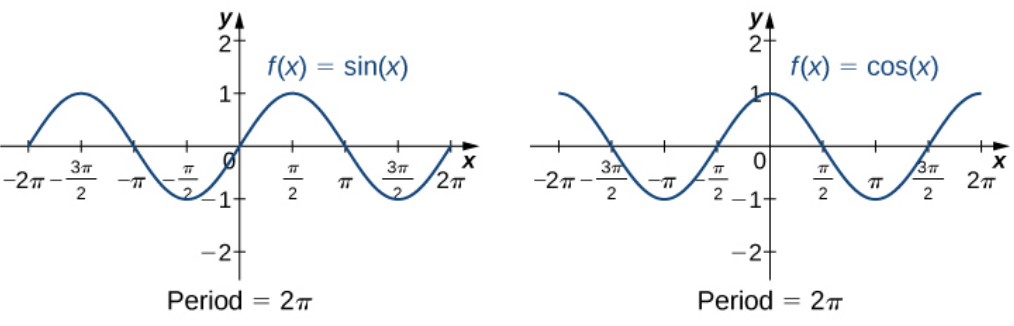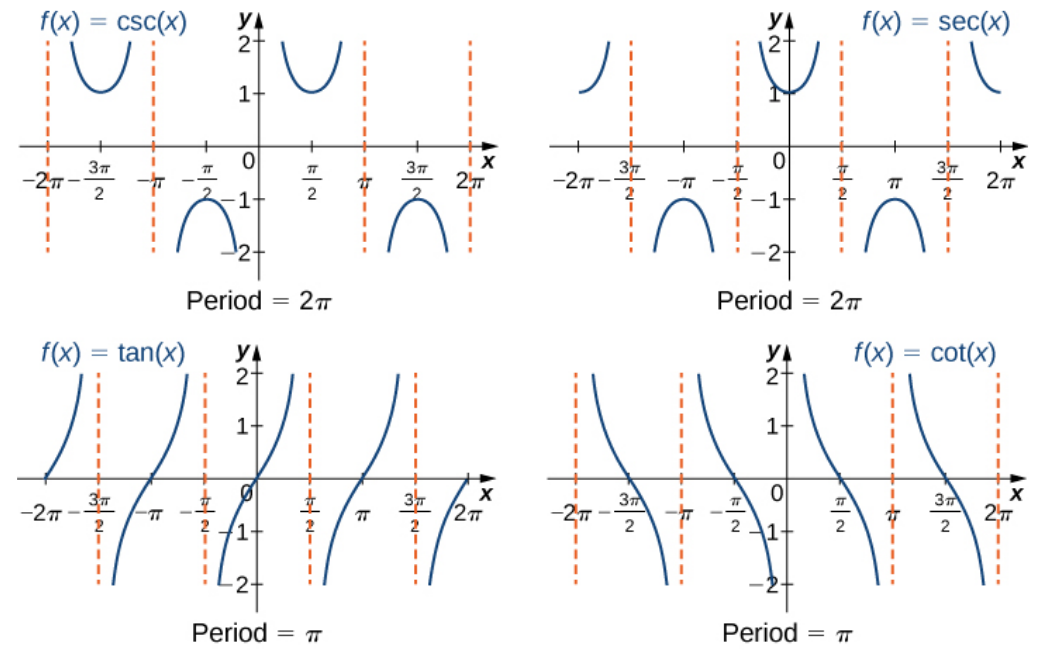
End Behavior: Example
$\displaystyle \lim_{x \rightarrow -\infty} \left(-3x^4\right)$ and $\displaystyle \lim_{x \rightarrow \infty} \left(-3x^4\right)$
$$\displaystyle \lim_{x \rightarrow -\infty} \left(-3x^4\right)=-\infty \mbox{ and } \displaystyle \lim_{x \rightarrow \infty} \left(-3x^4\right)=-\infty$$
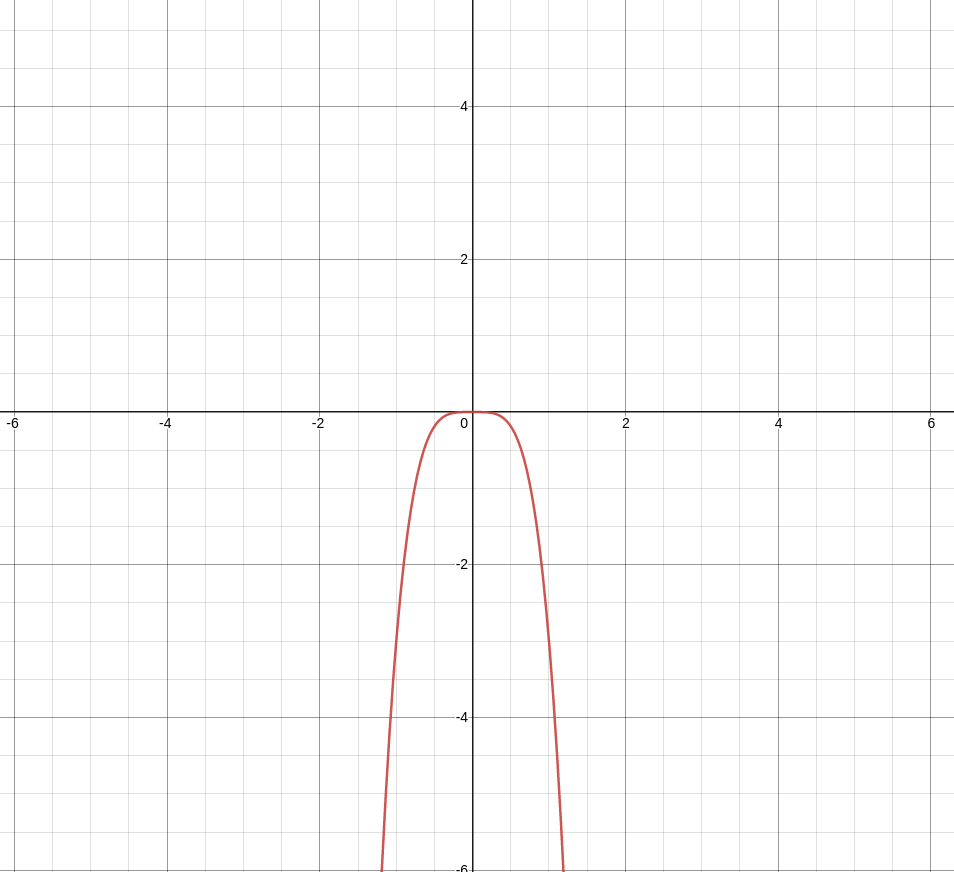$$y=-3x^4$$
$$y=-3x^4$$
$\displaystyle \lim_{x \rightarrow -\infty} \frac{2x-1}{5x^2-4x+7}$ and $\displaystyle \lim_{x \rightarrow \infty} \frac{2x-1}{5x^2-4x+7}$
For large $x$ in either the positive or negative direction, $\displaystyle \frac{2x-1}{5x^2-4x+7}\approx \frac{2x}{5x^2}=\frac{2}{5x}.$
Thus,
$$\displaystyle \lim_{x \rightarrow -\infty} \frac{2x-1}{5x^2-4x+7}=0 \mbox{ and } \displaystyle \lim_{x \rightarrow \infty} \frac{2x-1}{5x^2-4x+7}=0.$$
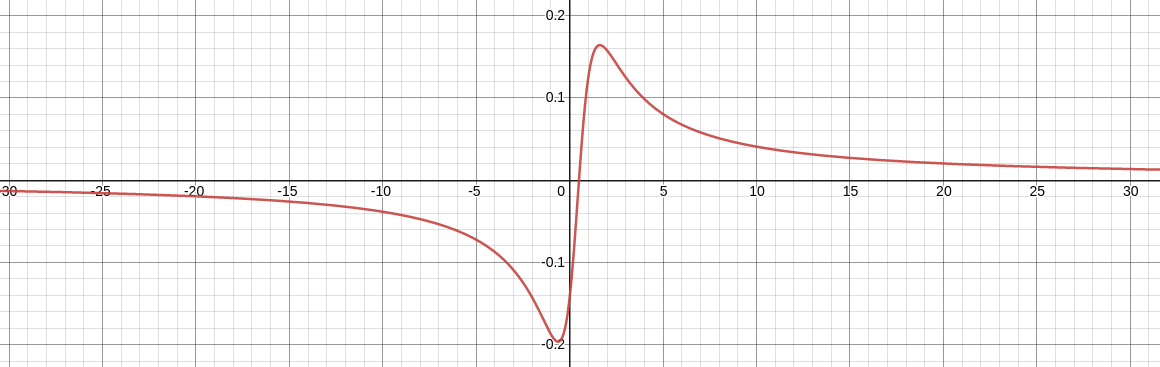$$y=\displaystyle \frac{2x-1}{5x^2-4x+7}$$
$$y=\displaystyle \frac{2x-1}{5x^2-4x+7}$$
End Behavior: Example
$\displaystyle \lim_{x \rightarrow -\infty} \frac{3x^2+2x-1}{5x^2-4x+7}$ and $\displaystyle \lim_{x \rightarrow \infty} \frac{3x^2+2x-1}{5x^2-4x+7}$
For large $x$ in either the positive or negative direction, $\displaystyle \frac{3x^2+2x-1}{5x^2-4x+7}\approx \frac{3x^2}{5x^2}=\frac{3}{5}.$
Thus,
$$\displaystyle \lim_{x \rightarrow -\infty} \frac{3x^2+2x-1}{5x^2-4x+7} = \frac{3}{5} \mbox{ and } \displaystyle \lim_{x \rightarrow \infty} \frac{3x^2+2x-1}{5x^2-4x+7} = \frac{3}{5}$$
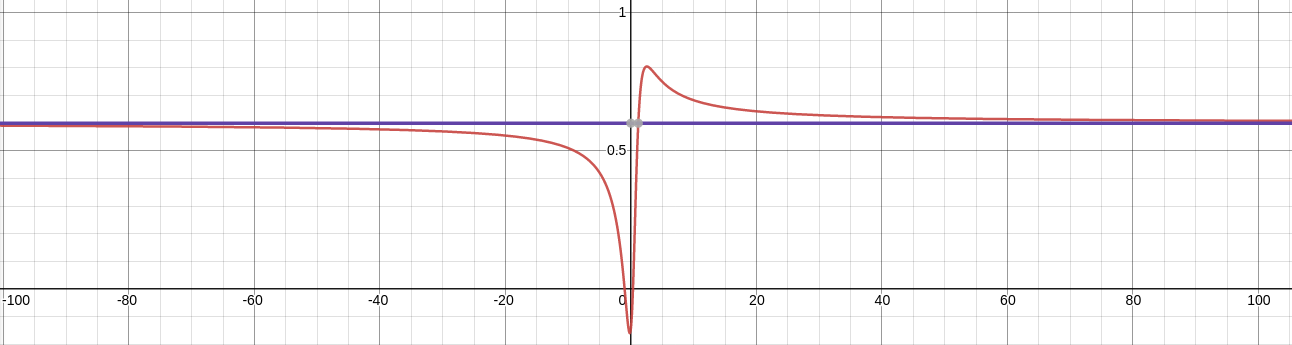$$y=\displaystyle \frac{3x^2+2x-1}{5x^2-4x+7}$$
$$y=\displaystyle \frac{3x^2+2x-1}{5x^2-4x+7}$$
End Behavior: Example
$\displaystyle \lim_{x \rightarrow -\infty} \frac{\sqrt{3x^2+4}}{x+6}$ and $\displaystyle \lim_{x \rightarrow \infty} \frac{\sqrt{3x^2+4}}{x+6}$
For large $x$ in either the positive or negative direction, $\displaystyle \frac{\sqrt{3x^2+4}}{x+6}\approx \frac{\sqrt{3x^2}}{x}=\frac{\sqrt{3}\sqrt{x^2}}{x}=\frac{\sqrt{3}|x|}{x}$
$$\displaystyle \lim_{x \rightarrow -\infty} \frac{\sqrt{3x^2+4}}{x+6}=-\sqrt{3} \mbox{ and } \displaystyle \lim_{x \rightarrow \infty} \frac{\sqrt{3x^2+4}}{x+6}=\sqrt{3}$$
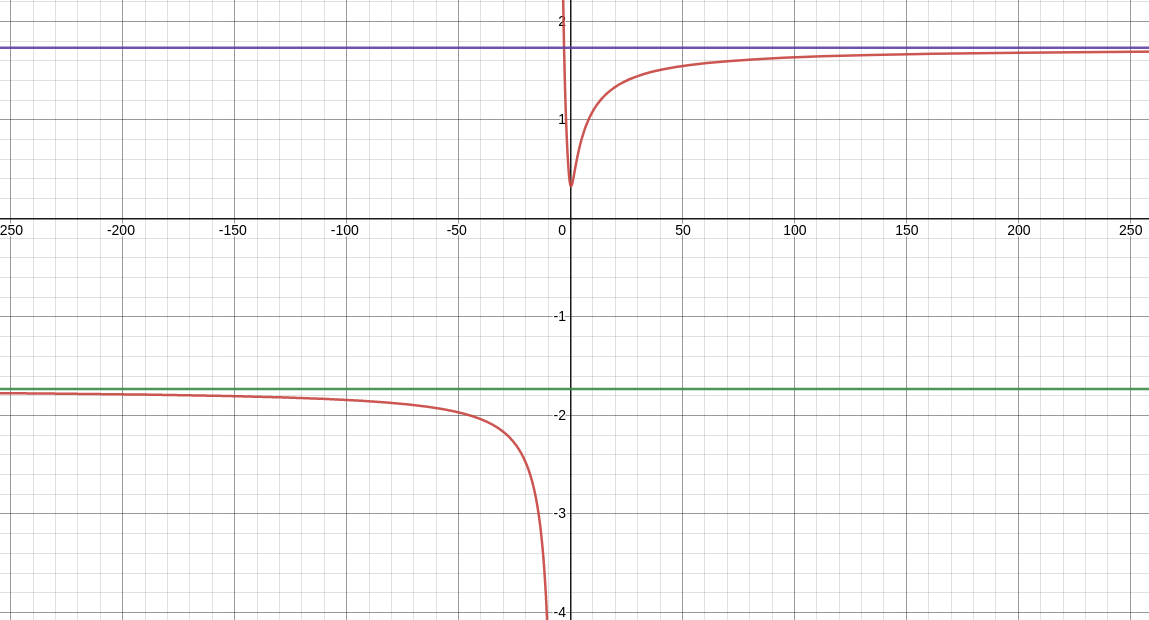$$y=\displaystyle \frac{\sqrt{3x^2+4}}{x+6}$$
$$y=\displaystyle \frac{\sqrt{3x^2+4}}{x+6}$$
End Behavior: Example
$\displaystyle \lim_{x \rightarrow -\infty} \frac{3e^x-4}{5e^x+2}$ and $\displaystyle \lim_{x \rightarrow \infty} \frac{3e^x-4}{5e^x+2}$
For large $x$ in the positive direction, $\displaystyle \frac{3e^x-4}{5e^x+2}\approx \frac{3e^x}{5e^x}=\frac{3}{5}.$
Thus,
$$\displaystyle \lim_{x \rightarrow \infty} \frac{3e^x-4}{5e^x+2}=\frac{3}{5}$$
For large $x$ in the negative direction, $\displaystyle \frac{3e^x-4}{5e^x+2}\approx \frac{-4}{2}=-2.$
Thus,
$$\displaystyle \lim_{x \rightarrow -\infty} \frac{3e^x-4}{5e^x+2}=-2$$
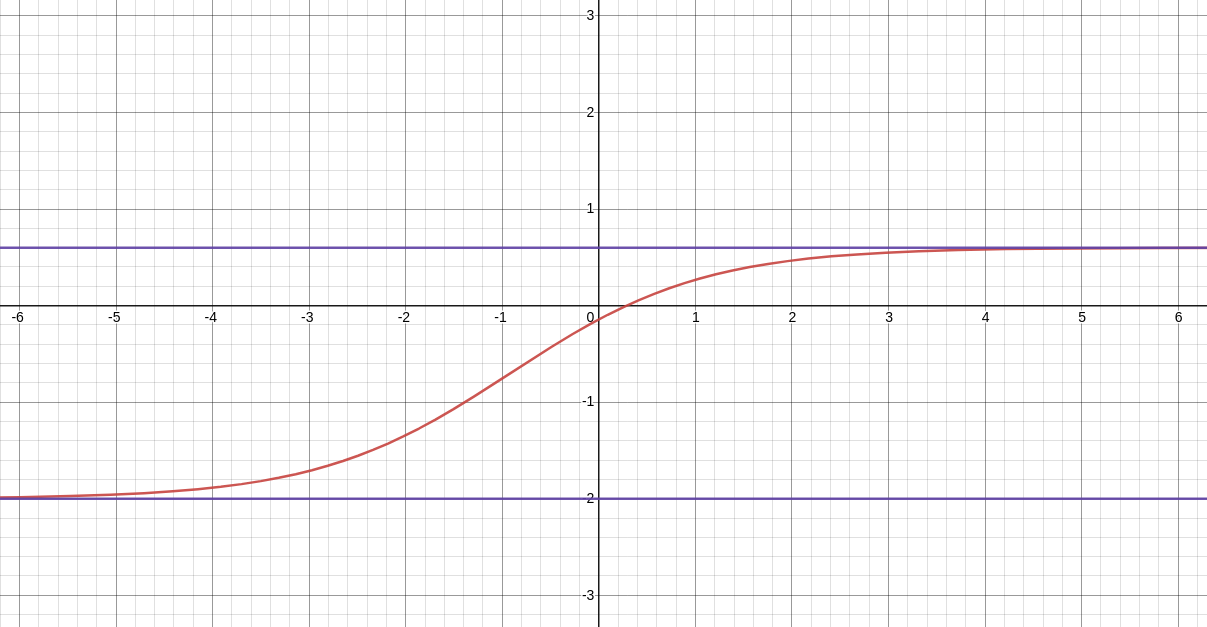$$y=\displaystyle \frac{3e^x-4}{5e^x+2}$$
$$y=\displaystyle \frac{3e^x-4}{5e^x+2}$$
End Behavior: Example
$\displaystyle \lim_{x \rightarrow -\infty} \frac{5x^2-4x+7}{2x-1}$ and $\displaystyle \lim_{x \rightarrow \infty} \frac{5x^2-4x+7}{2x-1}$
For large $x$ in either the positive or negative direction, $\displaystyle \frac{5x^2-4x+7}{2x-1}\approx \frac{5x^2}{2x}=\frac{5x}{2}.$
Thus,
$$\displaystyle \lim_{x \rightarrow -\infty} \frac{5x^2-4x+7}{2x-1}=-\infty \mbox{ and } \displaystyle \frac{5x^2-4x+7}{2x-1}=\infty.$$
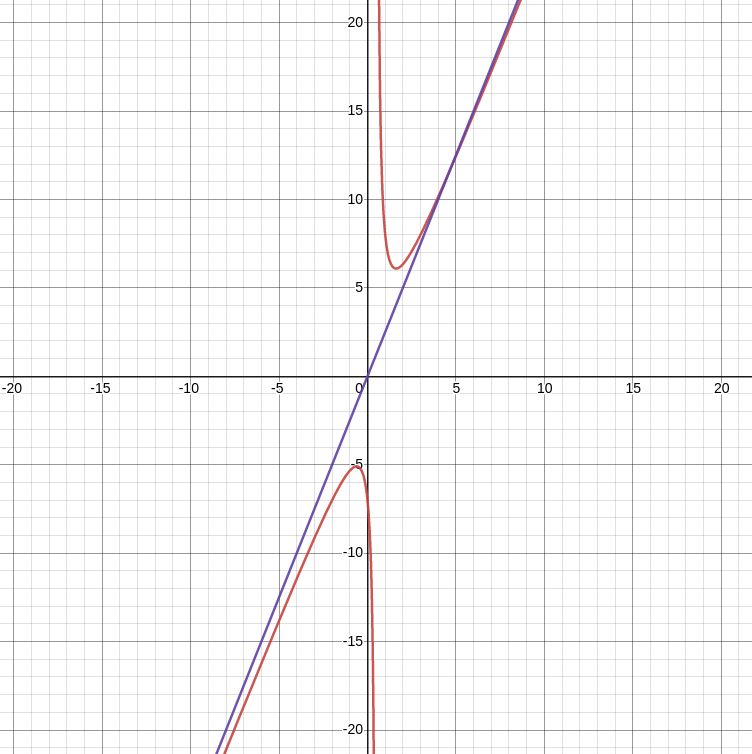$$y=\displaystyle \frac{5x^2-4x+7}{2x-1}$$
$$y=\displaystyle \frac{5x^2-4x+7}{2x-1}$$
Great News!
Combining the above with the techniques we learned in the last section, we can draw very detailed graphs of polynomial and rational functions!
Graphing Functions Using End Behavior
Draw a graph of the following function without using a calculator. Be sure to notice all important features of the graph: $x$ and $y$-intercepts, local maxima and minima, inflection points, vertical asymptotes, and end behavior.
$$\displaystyle f(x)=\frac{x^2+x-2}{x^2-3x-4}$$
Pro-Tip: Make a sign diagram for $f,$ $f',$ and $f''.$
We begin withe the intercepts. The $y$-intercept is $\displaystyle f(0)=\frac{0^2+0-2}{0^2-3\cdot 0-4}=\frac{1}{2}.$ Thus, the
$y$-intercept point is $\displaystyle \left(0,0\right).$
We now find the $x$-intercepts, that is, where $f(x)=0:$ $$ \begin{array}{lll} & \displaystyle f(x)=0&\\ \implies & \displaystyle \frac{x^2+x-2}{x^2-3x-4}=0&\\ \implies & \displaystyle \frac{(x+2)(x-1)}{(x+1)(x-4)}=0&\\ \implies & \displaystyle (x+2)(x-1)=0&\\ \end{array} $$ Thus, $x=-2$ or $x=1,$ and the $x$-intercept points are $(-2,0)$ and $(1,0).$
We'll now look at asymptotes. Vertical asymptotes occur where the denominator is $0,$ that is, where $x^2-3x-4=(x+1)(x-4)=0.$ Since there we no factors that cancelled, vertical asymptotes occur at $x=-1$ and $x=4.$
We can now make our sign diagram for $f:$
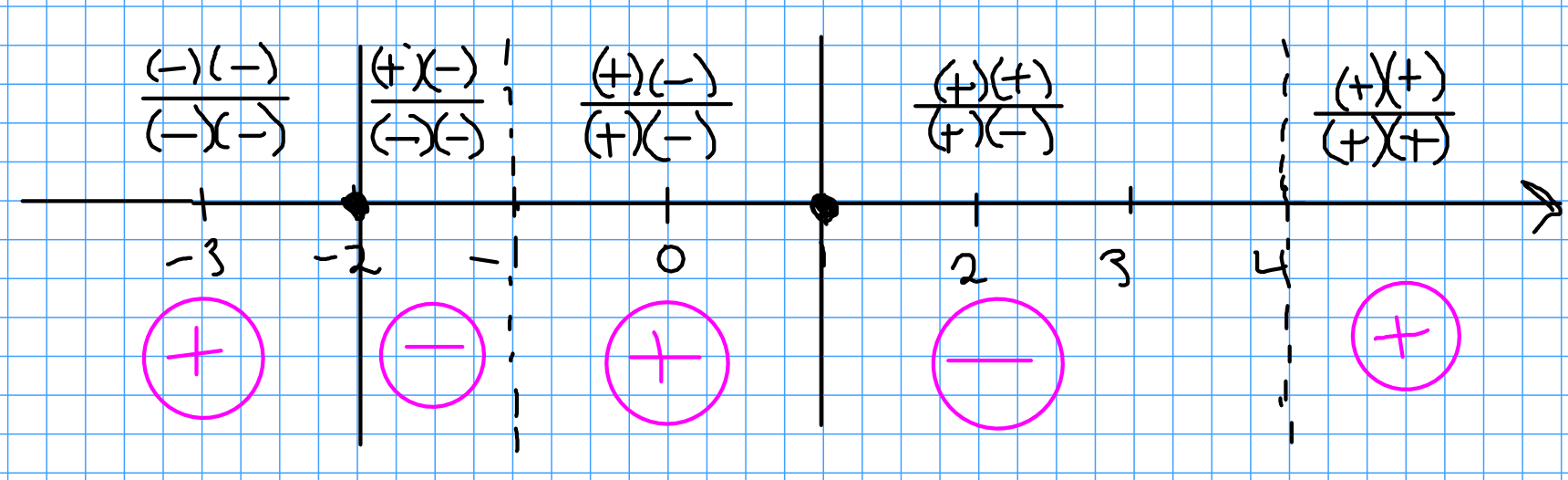
We now consider end behavior. For large $x$ in either the positive or negative direction, we have that $\displaystyle f(x)=\frac{x^2+x-2}{x^2-3x-4}\approx \frac{x^2}{x^2}=1.$ That is, $f(x)$ has a horizontal asymptote $y=1.$ So, $\displaystyle \lim_{x \rightarrow \infty} f(x)=1$ and $\displaystyle \lim_{x \rightarrow -\infty}f(x)=1.$
We now look at the critical points of $f(x):$ $$ \begin{array}{lll} f'(x)&=\displaystyle \frac{d}{dx}\frac{x^2+x-2}{x^2-3x-4}&\\ &=\displaystyle \frac{(x^2-3x-4)(x^2+x-2)'-(x^2+x-2)(x^2-3x-4)'}{(x^2-3x-4)^2}&\\ &=\displaystyle \frac{(x^2-3x-4)(2x+1)-(x^2+x-2)(2x-3)}{(x^2-3x-4)^2}&\\ &=\displaystyle \frac{(2x^3-6x^2-8x+x^2-3x-4)-(2x^3+2x^2-4x-3x^2-3x+6)}{(x^2-3x-4)^2}&\\ &=\displaystyle \frac{2x^3-6x^2-8x+x^2-3x-4-2x^3-2x^2+4x+3x^2+3x-6}{(x^2-3x-4)^2}&\\ &=\displaystyle \frac{-4x^2-4x-10}{(x^2-3x-4)^2}&\\ &=\displaystyle -\frac{4x^2+4x+10}{(x^2-3x-4)^2}&\\ \end{array} $$ Since $4x^2+4x+10=2(2x^2+2x+5)$ is always positive (the discriminant, $2^2-4\cdot 2 \cdot 5=-36.$ is negative), there are no critical points such that $f'(x)=0.$
As for critical points where $f'(x)$ is undefined, the denominator factors as $(x^2-3x-4)^2=(x+1)^2(x-4)^2.$ Thus, $x=-1$ and $x=4$ are the critical points (and vertical asymptotes.)
We may now make a sign diagram for $f':$
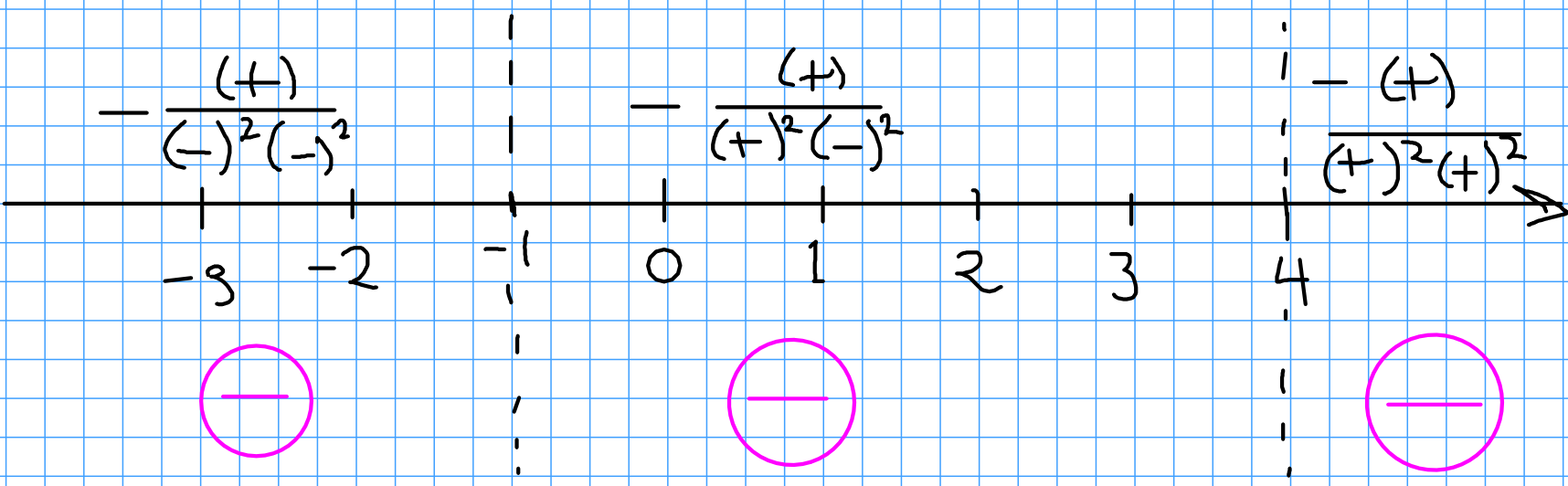
We now consider concavity and inflection points. Thus, we now find $f'':$ $$ \begin{array}{lll} f''(x)&=\displaystyle \frac{d}{dx}\left(-\frac{4x^2+4x+10}{(x^2-3x-4)^2}\right)&\\ &=\displaystyle -\frac{d}{dx}\frac{4x^2+4x+10}{(x^2-3x-4)^2}&\\ &=\displaystyle -\frac{(x^2-3x-4)^2(4x^2+4x+10)'-(4x^2+4x+10)((x^2-3x-4)^2)'}{(x^2-3x-4)^4}&\\ &=\displaystyle -\frac{(x^2-3x-4)^2(8x+4)-(4x^2+4x+10)(2(x^2-3x-4)(2x-3))}{(x^2-3x-4)^4}&\\ &=\displaystyle -(x^2-3x-4)\frac{(x^2-3x-4)(8x+4)-(4x^2+4x+10)(2(2x-3))}{(x^2-3x-4)^4}&\\ &=\displaystyle -\frac{(x^2-3x-4)(8x+4)-(4x^2+4x+10)(4x-6)}{(x^2-3x-4)^3}&\\ &=\displaystyle -\frac{(8x^3-24x^2-32x+4x^2-12x-16)-(16x^3+16x^2+40x-24x^2-24x-60)}{(x^2-3x-4)^3}&\\ &=\displaystyle -\frac{8x^3-24x^2-32x+4x^2-12x-16-16x^3-16x^2-40x+24x^2+24x+60}{(x^2-3x-4)^3}&\\ &=\displaystyle -\frac{-8x^3-12x^2-60x+44}{(x^2-3x-4)^3}&\\ &=\displaystyle \frac{8x^3+12x^2+60x-44}{(x^2-3x-4)^3}&\\ &=\displaystyle \frac{4(2x^3+3x^2+15x-11)}{(x^2-3x-4)^3}&\\ &=\displaystyle \frac{4(2x^3+3x^2+15x-11)}{((x+1)(x-4))^3}&\\ &=\displaystyle \frac{4(2x^3+3x^2+15x-11)}{(x+1)^3(x-4)^3}&\\ \end{array} $$ Inflection points occur where $f''(x)=0:$
$$ \begin{array}{lll} & \displaystyle f''(x)=0&\\ \implies & \displaystyle \frac{4(2x^3+3x^2+15x-11)}{(x^2-3x-4)^3}=0&\\ \implies & \displaystyle 2x^3+3x^2+15x-11=0&\\ \end{array} $$ Now, my dear students. We don't have great methods for solving cubics yet. But, in a few sections, we will! For now I will tell you that $f''(x)=0$ when $x \approx 0.6233.$ Thus, we have an inflection point of about $(0.6233,0.1803)$ to four decimal places. From this, we may now make a sign diagram for $f'':$
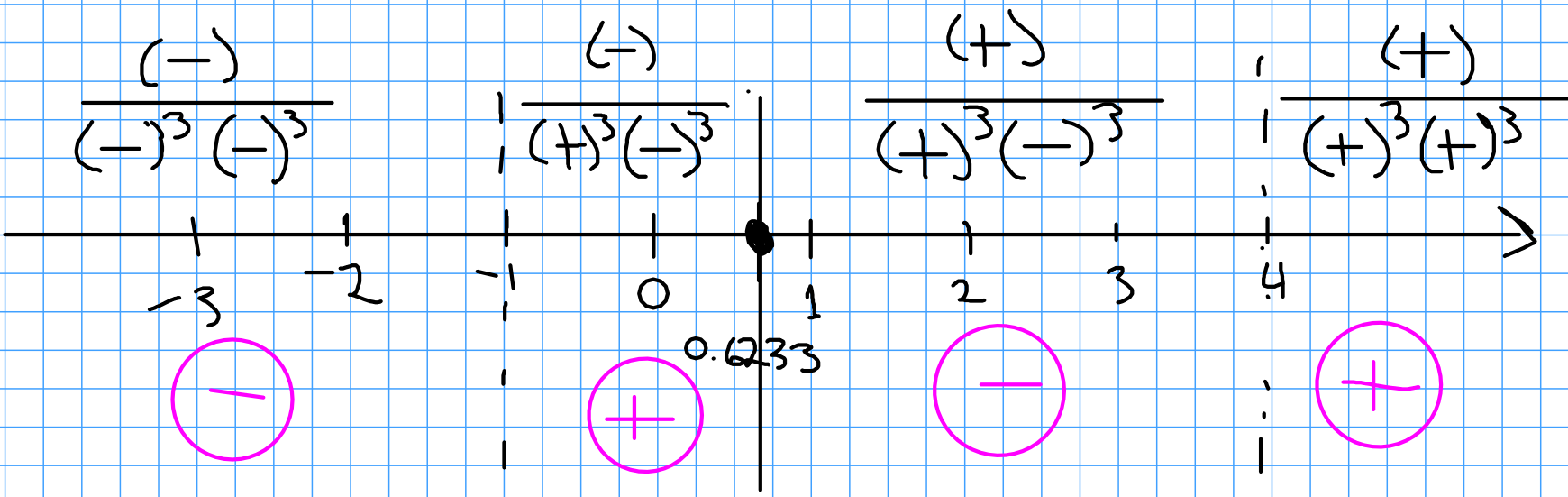
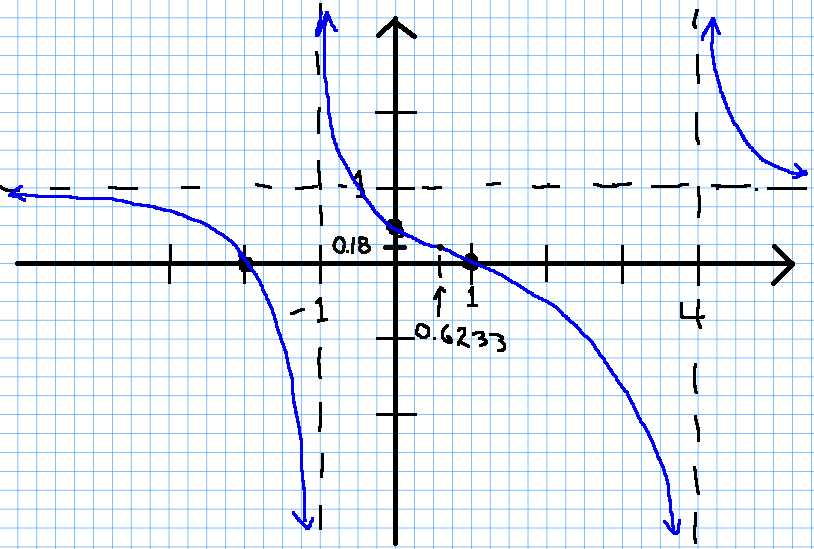
Putting all this information together, we may now sketch a lovely graph:
For comparison, here's a graph sketched earlier with a drawing program:
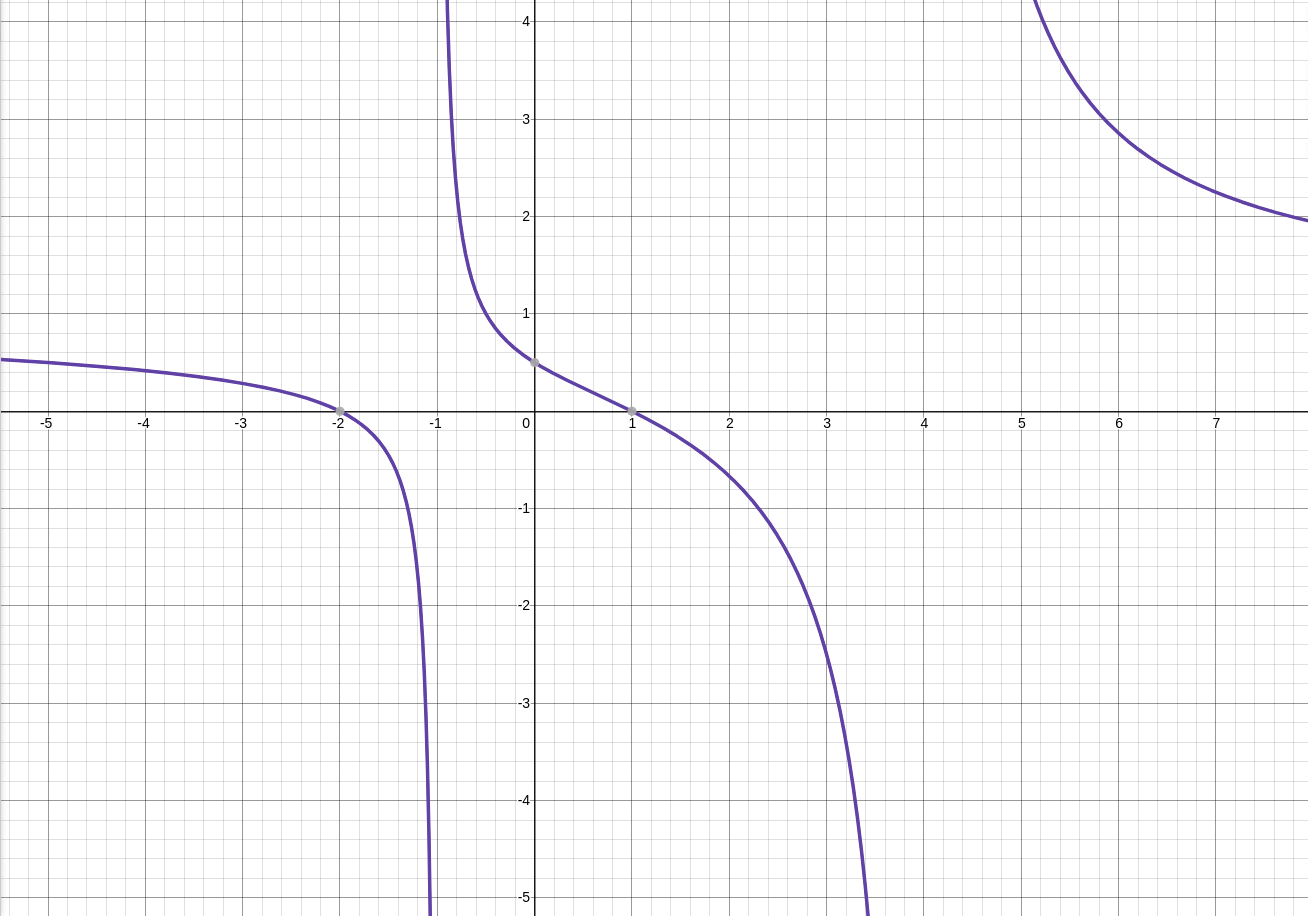
For further comparison, here's a graph generated by a graphing utility:
We now find the $x$-intercepts, that is, where $f(x)=0:$ $$ \begin{array}{lll} & \displaystyle f(x)=0&\\ \implies & \displaystyle \frac{x^2+x-2}{x^2-3x-4}=0&\\ \implies & \displaystyle \frac{(x+2)(x-1)}{(x+1)(x-4)}=0&\\ \implies & \displaystyle (x+2)(x-1)=0&\\ \end{array} $$ Thus, $x=-2$ or $x=1,$ and the $x$-intercept points are $(-2,0)$ and $(1,0).$
We'll now look at asymptotes. Vertical asymptotes occur where the denominator is $0,$ that is, where $x^2-3x-4=(x+1)(x-4)=0.$ Since there we no factors that cancelled, vertical asymptotes occur at $x=-1$ and $x=4.$
We can now make our sign diagram for $f:$
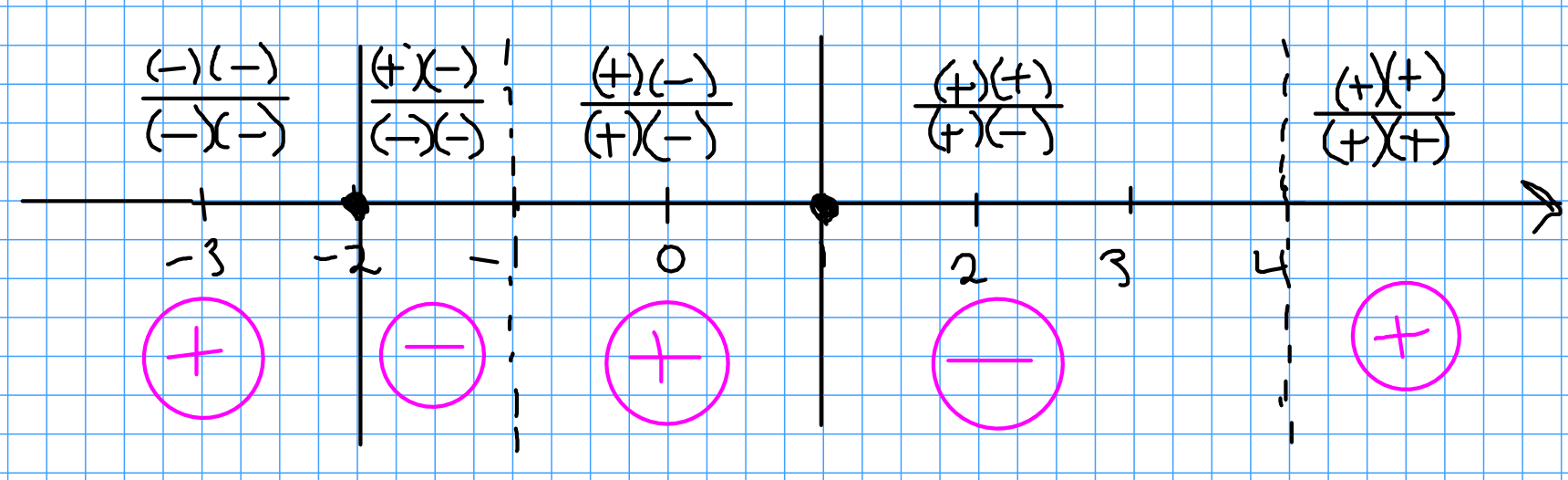
We now consider end behavior. For large $x$ in either the positive or negative direction, we have that $\displaystyle f(x)=\frac{x^2+x-2}{x^2-3x-4}\approx \frac{x^2}{x^2}=1.$ That is, $f(x)$ has a horizontal asymptote $y=1.$ So, $\displaystyle \lim_{x \rightarrow \infty} f(x)=1$ and $\displaystyle \lim_{x \rightarrow -\infty}f(x)=1.$
We now look at the critical points of $f(x):$ $$ \begin{array}{lll} f'(x)&=\displaystyle \frac{d}{dx}\frac{x^2+x-2}{x^2-3x-4}&\\ &=\displaystyle \frac{(x^2-3x-4)(x^2+x-2)'-(x^2+x-2)(x^2-3x-4)'}{(x^2-3x-4)^2}&\\ &=\displaystyle \frac{(x^2-3x-4)(2x+1)-(x^2+x-2)(2x-3)}{(x^2-3x-4)^2}&\\ &=\displaystyle \frac{(2x^3-6x^2-8x+x^2-3x-4)-(2x^3+2x^2-4x-3x^2-3x+6)}{(x^2-3x-4)^2}&\\ &=\displaystyle \frac{2x^3-6x^2-8x+x^2-3x-4-2x^3-2x^2+4x+3x^2+3x-6}{(x^2-3x-4)^2}&\\ &=\displaystyle \frac{-4x^2-4x-10}{(x^2-3x-4)^2}&\\ &=\displaystyle -\frac{4x^2+4x+10}{(x^2-3x-4)^2}&\\ \end{array} $$ Since $4x^2+4x+10=2(2x^2+2x+5)$ is always positive (the discriminant, $2^2-4\cdot 2 \cdot 5=-36.$ is negative), there are no critical points such that $f'(x)=0.$
As for critical points where $f'(x)$ is undefined, the denominator factors as $(x^2-3x-4)^2=(x+1)^2(x-4)^2.$ Thus, $x=-1$ and $x=4$ are the critical points (and vertical asymptotes.)
We may now make a sign diagram for $f':$
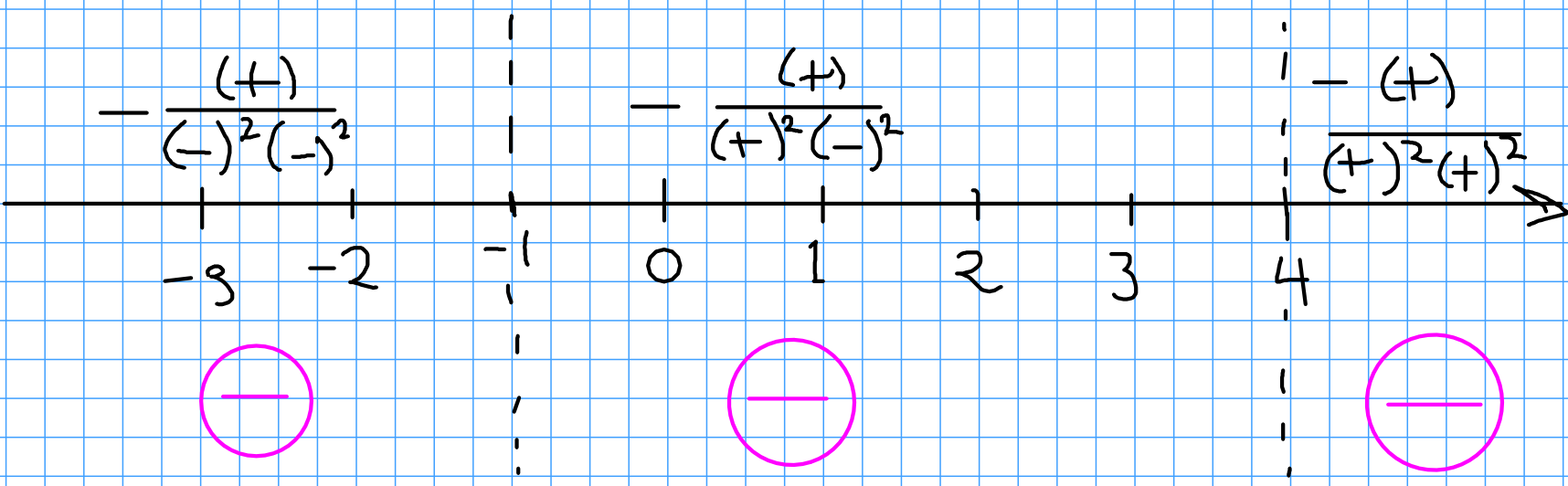
We now consider concavity and inflection points. Thus, we now find $f'':$ $$ \begin{array}{lll} f''(x)&=\displaystyle \frac{d}{dx}\left(-\frac{4x^2+4x+10}{(x^2-3x-4)^2}\right)&\\ &=\displaystyle -\frac{d}{dx}\frac{4x^2+4x+10}{(x^2-3x-4)^2}&\\ &=\displaystyle -\frac{(x^2-3x-4)^2(4x^2+4x+10)'-(4x^2+4x+10)((x^2-3x-4)^2)'}{(x^2-3x-4)^4}&\\ &=\displaystyle -\frac{(x^2-3x-4)^2(8x+4)-(4x^2+4x+10)(2(x^2-3x-4)(2x-3))}{(x^2-3x-4)^4}&\\ &=\displaystyle -(x^2-3x-4)\frac{(x^2-3x-4)(8x+4)-(4x^2+4x+10)(2(2x-3))}{(x^2-3x-4)^4}&\\ &=\displaystyle -\frac{(x^2-3x-4)(8x+4)-(4x^2+4x+10)(4x-6)}{(x^2-3x-4)^3}&\\ &=\displaystyle -\frac{(8x^3-24x^2-32x+4x^2-12x-16)-(16x^3+16x^2+40x-24x^2-24x-60)}{(x^2-3x-4)^3}&\\ &=\displaystyle -\frac{8x^3-24x^2-32x+4x^2-12x-16-16x^3-16x^2-40x+24x^2+24x+60}{(x^2-3x-4)^3}&\\ &=\displaystyle -\frac{-8x^3-12x^2-60x+44}{(x^2-3x-4)^3}&\\ &=\displaystyle \frac{8x^3+12x^2+60x-44}{(x^2-3x-4)^3}&\\ &=\displaystyle \frac{4(2x^3+3x^2+15x-11)}{(x^2-3x-4)^3}&\\ &=\displaystyle \frac{4(2x^3+3x^2+15x-11)}{((x+1)(x-4))^3}&\\ &=\displaystyle \frac{4(2x^3+3x^2+15x-11)}{(x+1)^3(x-4)^3}&\\ \end{array} $$ Inflection points occur where $f''(x)=0:$
$$ \begin{array}{lll} & \displaystyle f''(x)=0&\\ \implies & \displaystyle \frac{4(2x^3+3x^2+15x-11)}{(x^2-3x-4)^3}=0&\\ \implies & \displaystyle 2x^3+3x^2+15x-11=0&\\ \end{array} $$ Now, my dear students. We don't have great methods for solving cubics yet. But, in a few sections, we will! For now I will tell you that $f''(x)=0$ when $x \approx 0.6233.$ Thus, we have an inflection point of about $(0.6233,0.1803)$ to four decimal places. From this, we may now make a sign diagram for $f'':$
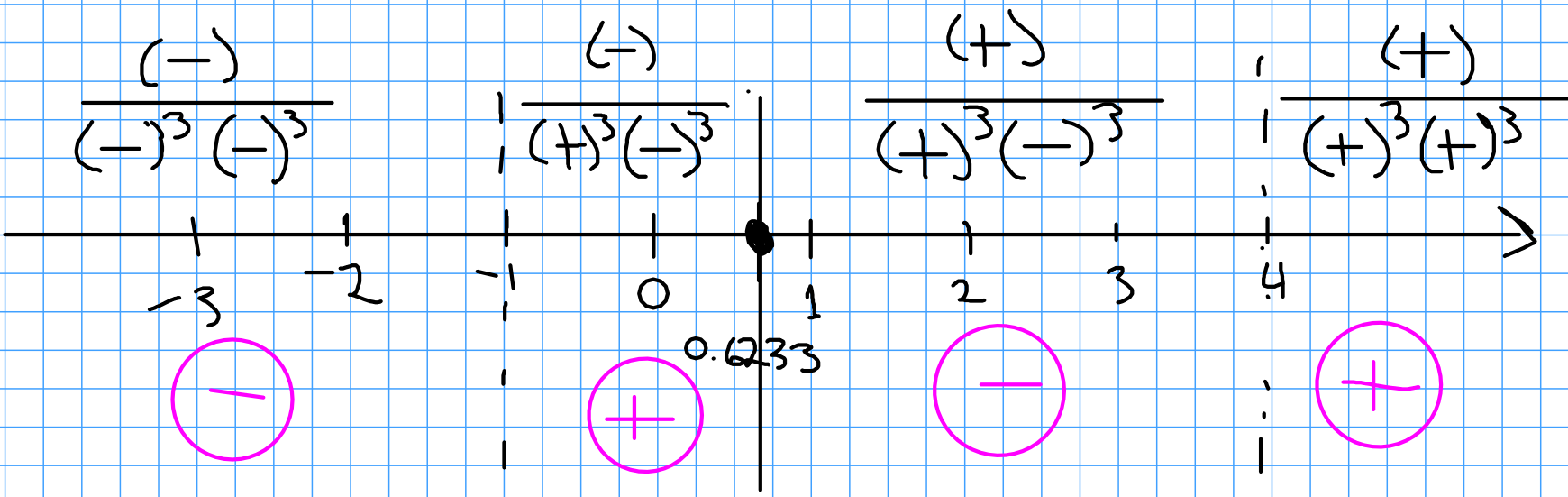
Putting all this information together, we may now sketch a lovely graph:
For comparison, here's a graph sketched earlier with a drawing program:
For further comparison, here's a graph generated by a graphing utility: