The Mean Value Theorem

The Mean Value Theorem

Suppose you made the $220$-mile trip from Coos Bay to Portland in $4$ hours.

This would mean that your average speed was $\displaystyle \frac{220 \mbox{ miles}}{4 \mbox{ hours}}=55 \mbox{ mph}.$

Of course your speed most likely varied as you went, but can you say that there was a point in your journey where were going exactly $55 \mbox{ mph}?$

The Mean Value Theorem

The MVT says "Yes!"

But before we state the MVT, we need a preliminary result.

Rolle's Theorem

Let $f$ be a continuous function over the closed interval $[a,b]$ and differentiable over the open interval $(a,b)$ such that $f(a)=f(b).$ Then there exists at least one $c\in (a,b)$ such that $f'(c)= 0.$

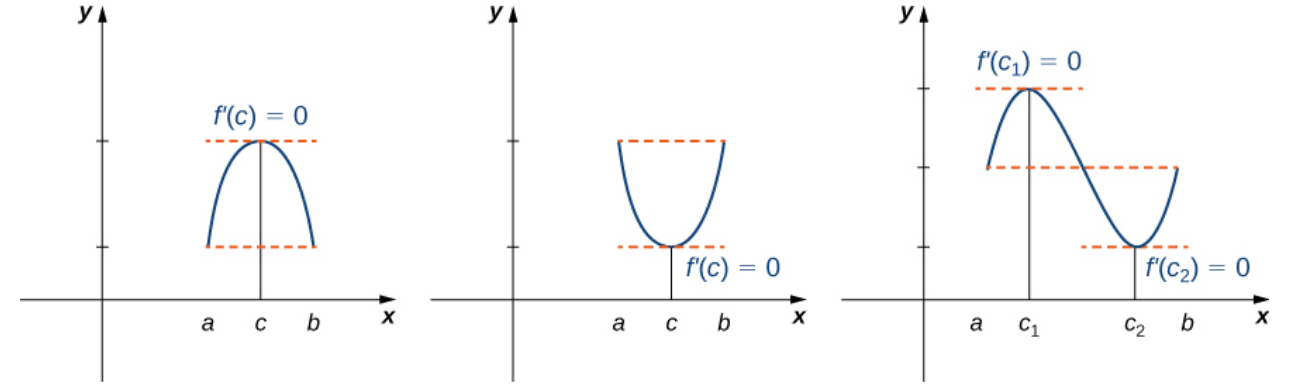
Example

Verify that the function $f(x)= 2x^2- 8x+ 6$ defined over the interval $[1 , 3]$ satisfies the conditions of Rolle's theorem.

Since $f(x)$ is a polynomial, it is both continuous on $[1,3]$ and differentiable on $(1,3).$

Also, $f(1)=2\cdot 1^2- 8\cdot 1+ 6=0$ and $f(3)=2 \cdot 3^2- 8\cdot 3+ 6=0$ so that $f(1)=f(3).$

Find all points $c$ guaranteed by Rolle's theorem.

We need to find a point $c\in(1,3)$ such that $f'(c)=0.$

Now, $f'(x)=4x-8,$ so our point $c$ must satisfy $4c-8=0.$

Thus, the point we seek is $c=2.$

The Mean Value Theorem

Let $f$ be continuous over the closed interval $[a,b]$ and differentiable over the open interval $(a,b).$ Then, there exists at least one point $c \in (a,b)$ such that $$f'(c)=\frac{f(b)-f(a)}{b-a}.$$

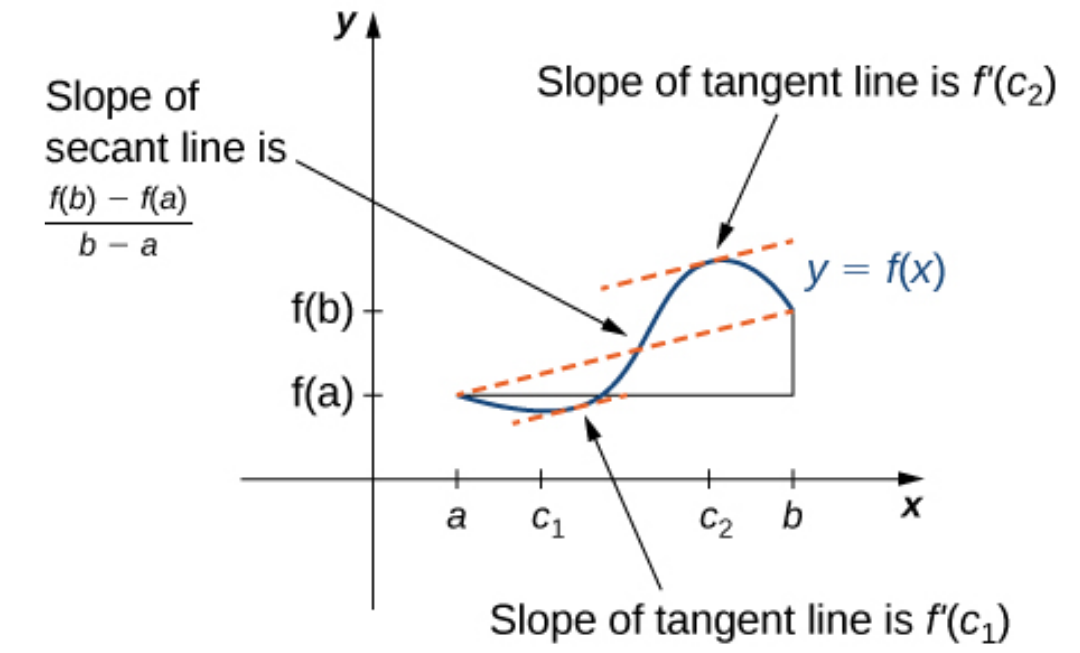
Interpretation: For a "well-behaved" function over an interval $[a,b],$ there is a point somewhere in $(a,b)$ where the instantaneous rate of change equals the average rate of change over the entire interval.

Example

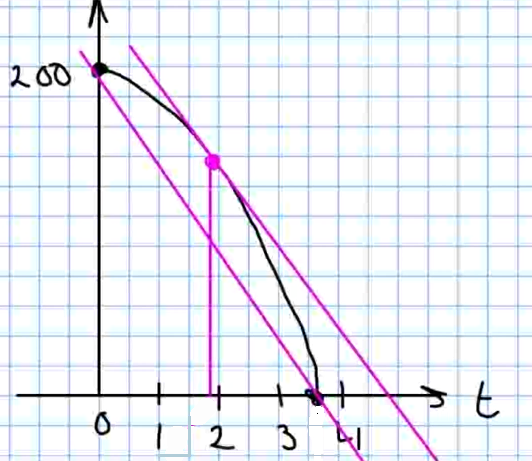
Suppose a ball is dropped from a height of $200$ ft. Its position at time $t$ is $s(t)= -16t^2+ 200.$

Find the time $t$ when the instantaneous velocity of the ball equals its average velocity.

To find the average velocity, we need to know when the ball hits the ground. This occurs when $s(t)=0:$ $$ \begin{array}{lll} &s(t)=0&\\ \implies &-16t^2+ 200=0&\\ \implies &16t^2= 200&\\ \implies &\displaystyle t^2= \frac{200}{16}&\\ \implies &\displaystyle t^2= 12.5&\\ \implies &\displaystyle t=\pm \sqrt{12.5}&\\ \end{array} $$ Taking the positive root (of course!), $t=\sqrt{12.5}\approx 3.535533906.$

We may now find the average velocity over $[0,\sqrt{12.5}]:$ $$ \begin{array}{ll} \displaystyle \frac{f(\sqrt{12.5})-f(0)}{\sqrt{12.5}-0}&=\displaystyle \frac{-16(\sqrt{12.5})^2+200-(-16\cdot 0^2+200)}{\sqrt{12.5}}\\ &=\displaystyle \frac{-16\cdot 12.5+200-200}{\sqrt{12.5}}\\ &=\displaystyle \frac{-200}{\sqrt{12.5}}\\ &\approx -56.568542495\\ \end{array} $$ The average velocity during the ball's free fall is about $-56.57$ feet per second (that is, a downward velocity of about $56.57$ feet per second).

We may now find the point in time $t$ when the instantaneous velocity equals the average velocity. The function describing instantaneous velocity is $s'(t)=-32t.$ Thus, time $t$ we seek satisfies: $$ \begin{array}{lll} &s'(t)=\displaystyle \frac{-200}{\sqrt{12.5}}&\\ \implies &-32t=\displaystyle \frac{-200}{\sqrt{12.5}}&\\ \implies &t=\displaystyle \frac{-200}{-32\sqrt{12.5}}&\\ \implies &t \approx 1.767766953&\\ \end{array} $$ Thus, the ball's average velocity equals its average velocity at approximately $t \approx 1.77$ seconds.

Dire Warning

If the conditions of the MVT are not met, then all bets are off.

If a function $f$ is either

1. not continuous over the entire interval $[a,b]$, or

2. $f$ isn't differentiable at some point $(a,b),$

then $f$ might have a point $c$ in $(a,b)$ such that $\displaystyle f'(c)=\frac{f(b)-f(a)}{b-a}$, but then again, it might not.

In this situation there are no guarantees.

Example

Consider the functions below defined on the interval $[2,4].$


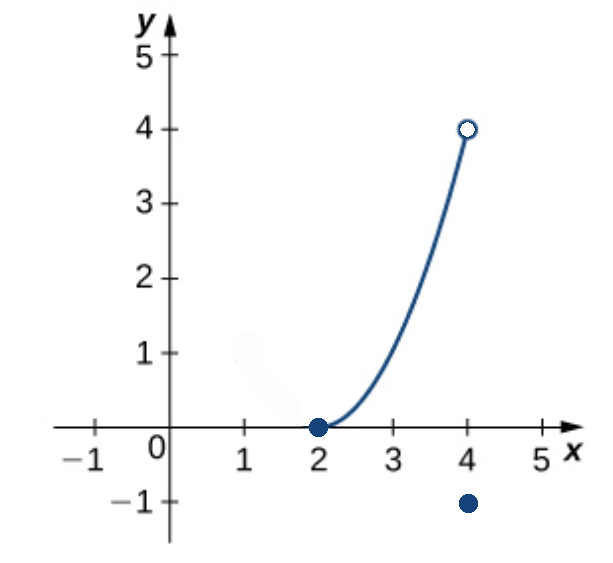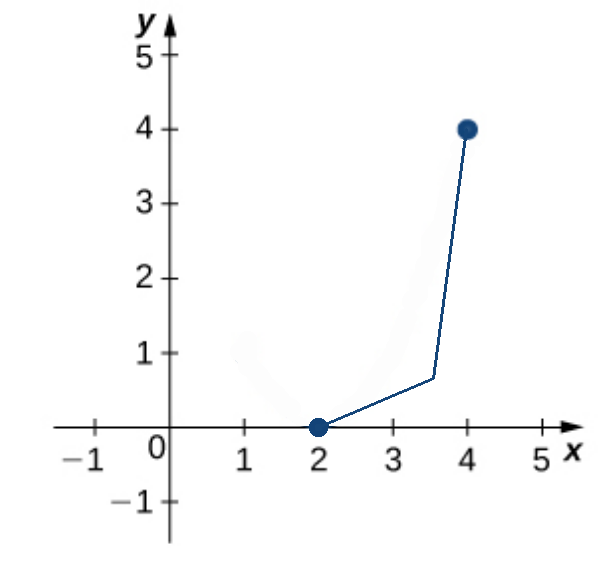MVT Applies	MVT Does Not Apply	MVT Does Not Apply

Examples

Determine whether the Mean Value Theorem applies for the functions over the given interval. Justify your answers.

$f(x)=e^x \,\,\, \mbox{ over } \,\,\, [0,1]$

$f(x)=e^x$ is continuous on the closed and bounded interval $[0,1]$ and differentiable on $(0,1).$

The MVT applies.

$f(x)=\tan(\pi x) \,\,\, \mbox{ over } \,\,\, [0,1]$

$f(x)=\tan(\pi x)$ is not continuous on the closed and bounded interval $[0,1]$ since there is a discontinuity at $\displaystyle x=\frac{1}{2}.$

The MVT does not apply.

$f(x)= 5-|x|\,\,\, \mbox{ over } \,\,\, [-1,1]$

$f(x)=5-|x|$ is continuous on the closed and bounded interval $[-1,1],$ but not differentiable on $(-1,1)$ since there is a corner at $x=0.$

The MVT does not apply.

Back to Our Original Question...

Suppose you made the $220$-mile trip from Coos Bay to Portland in $4$ hours.

This would mean that your average speed was $\displaystyle \frac{220 \mbox{ miles}}{4 \mbox{ hours}}=55 \mbox{ mph}.$

Of course your speed most likely varied as you went, but can you say that there was a point in your journey where were going exactly $55 \mbox{ mph}?$

Corollaries of the Mean Value Theorem

Corollary #1

Let $f$ be differentiable over an interval $I.$ If $f'(x)= 0$ for all $x\in I,$ then $f(x)$ is equal to a constant for all $x\in I.$

Corollaries of the Mean Value Theorem

Corollary #2

If $f$ and $g$ are differentiable over an interval $I$ and $f'(x)=g'(x)$ for all $x\in I,$ then $f(x)=g(x)+C$ for some constant $C.$

Corollaries of the Mean Value Theorem

Corollary #3 (Big Corollary!)

Let $f$ be continuous over the closed interval $[a,b]$ and differentiable over the open interval $(a,b).$

i. If $f'(x) \gt 0$ for all $x\in (a,b),$ then $f$ is an increasing function over $[a,b].$

ii. If $f'(x) \lt 0$ for all $x\in (a,b),$ then $f$ is a decreasing function over $[a,b].$

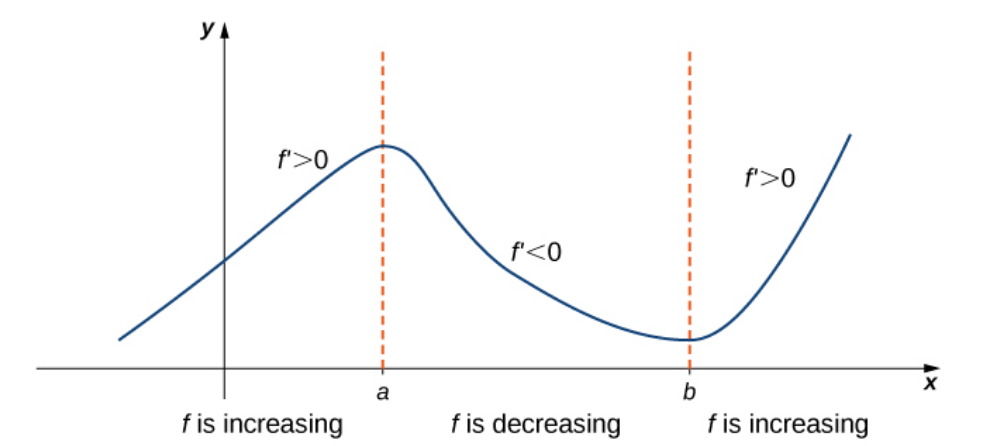
With all of these great results, don't you think we call it the Nice Value Theorem?