In applications, the ability to find points where a function is at its lowest value (minimum) or highest value (maximum) is hugely important. The truth of this statement will become more apparent when we begin the topic of optimization in later sections.
For now, we shall begin with the first steps in determining maxima and minima of a function.
Absolute Maxima & Minima
The blue graph has an absolute maximum near $x=2.$
The red graph has an absolute minimum near $x=2.$
Maxima & Minima
Let $f$ be a function defined over an interval $I$ and let $c \in I.$
We say $f$ has an absolute maximum on $I$ at $c$ if $f(c) \geq f(x)$ for all $x \in I.$
Maxima & Minima
We say $f$ has an absolute minimum on $I$ at $c$ if $f(c) \leq f(x)$ for all $x \in I.$
If$f$ has an absolute maximum on $I$ at $c$ or an absolute minimum on $I$ at $c,$ we say $f$ has an absolute extremum on $I$ at $c.$
The Extreme Value Theorem
If $f$ is a continuous function over the closed and bounded interval $[a,b],$ then there is a point in $[a,b]$ at which $f$ has an absolute maximum over $[a,b]$ and there is a point in $[a,b]$ at which $f$ has an absolute minimum over $[a,b].$
The Extreme Value Theorem
The function $f$ below is a continuous function over the closed and bounded interval $[1,4],$ The Extreme Value Theorem guarantees that this function has an absolute maximum and minimum on the interval $[1,4].$
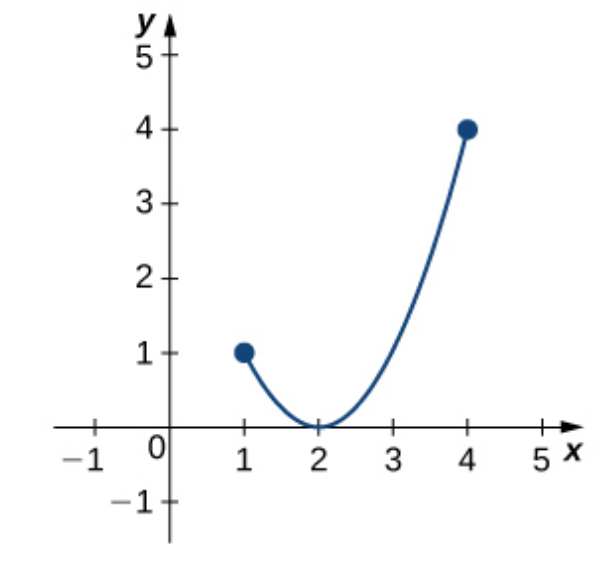
The absolute minimum occurs at $x=2,$ and the absolute maximum occurs at the endpoint $x=4.$
Dire Warning
If the conditions of the EVT are not met, then all bets are off.
If:
1. $f$ is not continuous somewhere in the interval, or
2. the interval being considered is not closed and bounded,
then $f$ might have absolute extrema on the interval, but then again, it might not.
In this situation there are no guarantees.
Examples
The functions below all occur on the unbounded interval $(-\infty,\infty).$ The EVT does not apply.
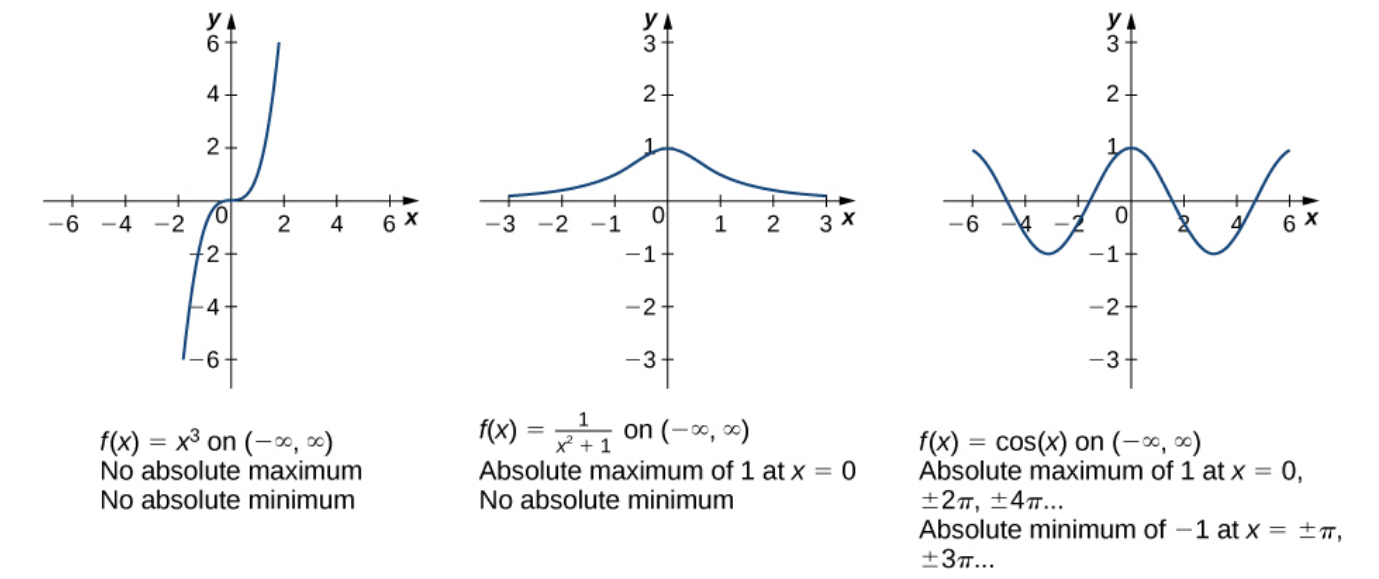
However, notice sometimes there are absolute maxima and minima, and sometimes there are not. This shows there are no guarantees if the conditions (hypotheses) if the EVT are not met.
Example
The functions below take values on a closed and bounded interval, but the function is not continuous. The EVT does not apply.
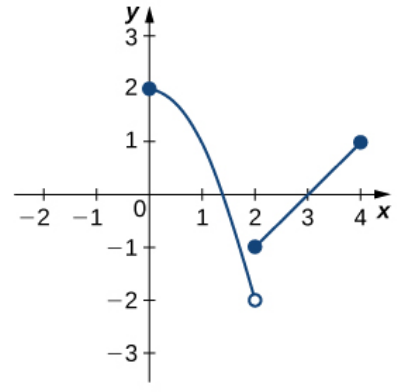
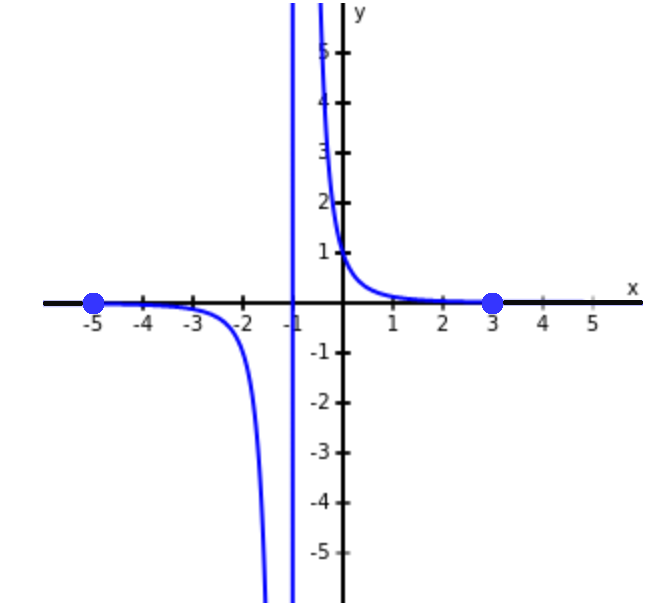
However, notice sometimes there are absolute maxima and minima, and sometimes there are not. This shows there are no guarantees if the conditions (hypotheses) if the EVT are not met.
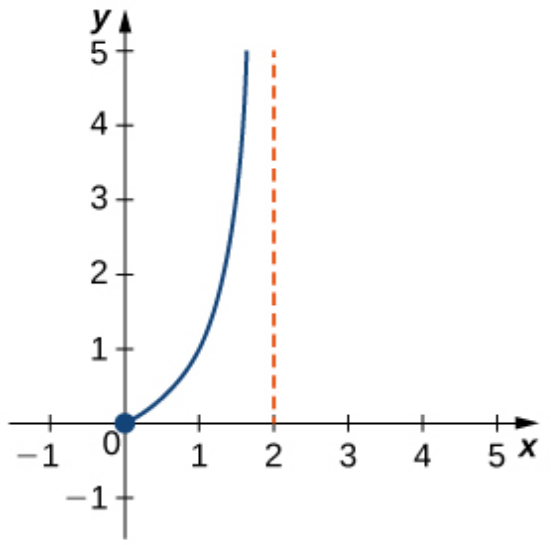
Example
The function below is continuous, but takes values on a bounded interval which is not closed. The EVT does not apply.
Local Extrema
A function $f$ need not have absolute extrema (absolute maxima or minima), especially if $f$ is either not continuous at some point, or the domain of the function is not closed and bounded.
However, there can still be points are "locally" a maximum or a minimum. For example, in the graph below, the point $x=-2$ serves as a local minimum and $x=2$ serves as local maximum.
Local Extrema
A function $f$ has a local maximum at $c$ if there exists an open interval $I$ containing $c$ such that $I$ is contained in the domain of $f$ and $f(c) \geq f(x)$ for all $x\in I.$
A function $f$ has a local minimum at $c$ if there exists an open interval $I$ containing $c$ such that $I$ is contained in the domain of $f$ and $f(c) \leq f(x)$ for all $x\in I.$
A function $f$ has a local extremum at $c$ if $f$ has a local maximum at $c$ or $f$ has a local minimum at $c$.
Critical Points
Let $c$ be an interior point in the domain of $f.$ We say that $c$ is a critical point of $f$ if $f'(c)= 0$ or $f'(c)$ is undefined.
Example
In the graph below, $f'(0)=0,$ $f'(1)=0,$ and $f'(2)$ is undefined.
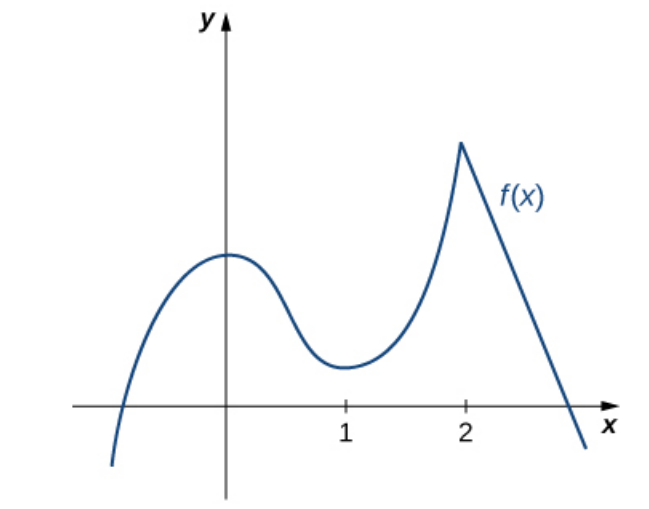
Thus, $x=0,$ $x=1,$ and $x=2$ are all critical points.
Extrema & Critical Points are Related
Fermat's Theorem: If $f$ has a local extremum at $c$ and $f$ is differentiable at $c,$ then $f'(c)= 0.$
This is to say that if $f$ has a local extremum at a point $x=c,$ then $c$ must be a critical point of $f.$
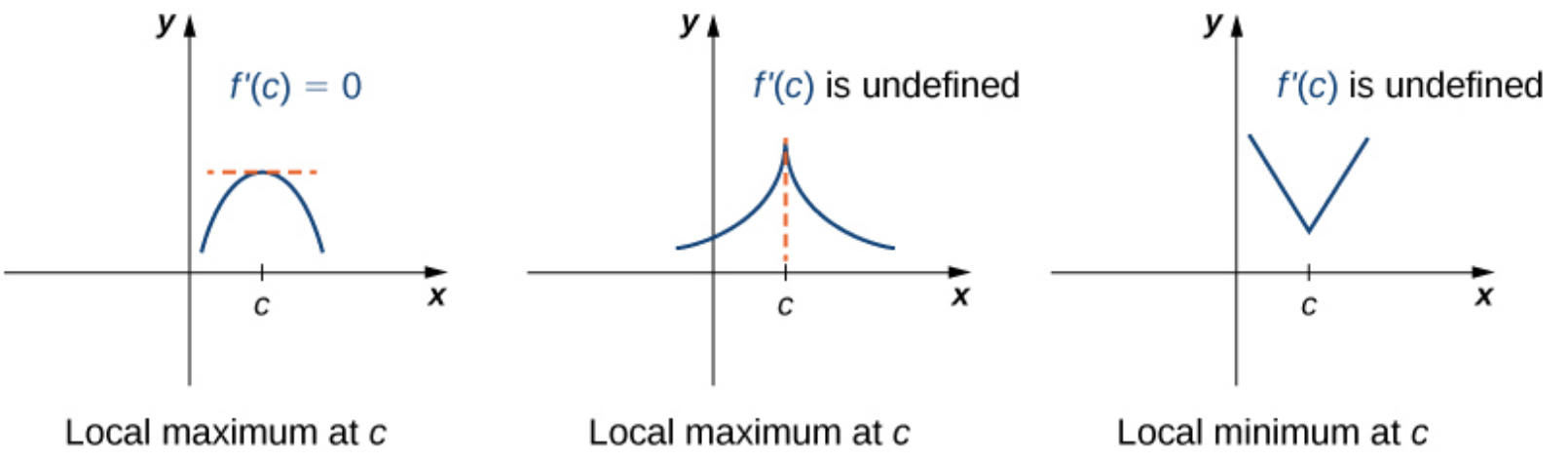
Examples
In the graphs below, the critical points $c$ correspond to maxima and minima.
Dire Warning
Just because a point is a critical point does not guarantee that it's an extremum.
The critical points of a function are merely candidates for extrema.
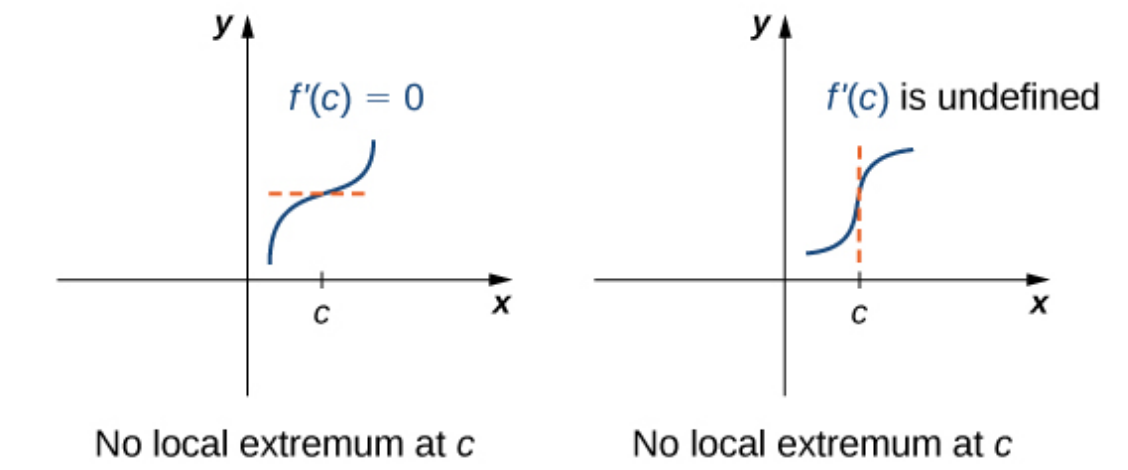
Example
In the graphs below, the critical points $c$ do not correspond to maxima and minima.
Example
Find the critical points in the domain of the function $\displaystyle y=\sqrt{4-x^2}.$
We compute the derivative $f'(x)$ to understand where it is either $0$ or undefined:
$$
\begin{array}{cc}
f'(x)&=\frac{d}{dx}\sqrt{4-x^2}\\
&=\displaystyle \frac{1}{2\sqrt{4-x^2}}\frac{d}{dx}(4-x^2)\\
&=\displaystyle \frac{1}{2\sqrt{4-x^2}}(-2x)\\
&=\displaystyle -\frac{x}{\sqrt{4-x^2}}\\
\end{array}
$$
Setting $f'(x)=0,$ we have
$$
-\frac{x}{\sqrt{4-x^2}}=0
$$
which, solving for $x,$ gives $x=0.$ Thus, $x=0$ is a critical point.
$f'(x)$ is undefined where the denominator is $0,$ that is, where $\sqrt{4-x^2}=0.$ Solving for $x$ we see that $x=-2$ and $x=2$ are critical points.
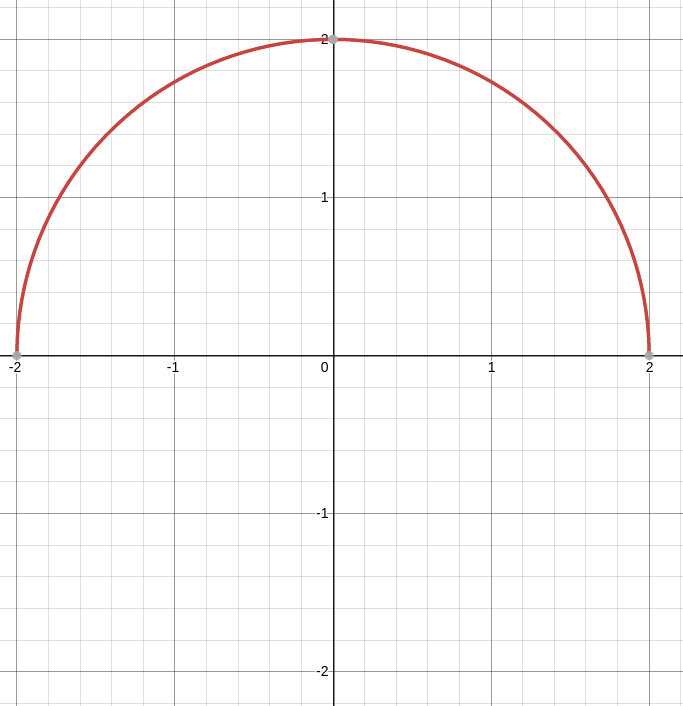
$f'(x)$ is undefined where the denominator is $0,$ that is, where $\sqrt{4-x^2}=0.$ Solving for $x$ we see that $x=-2$ and $x=2$ are critical points.

Locating Absolute Extrema
Theorem
Let $f$ be a continuous function over a closed and bounded interval $I.$
The absolute maximum of $f$ over $I$ and the absolute minimum of $f$ over $I$ must occur at endpoints of $I$ or at critical points of $f$ in $I.$
Example: Consider again $\displaystyle y=\sqrt{4-x^2}$ on its domain $[-2,2].$
We found the critical points are $x=0,$ $x=-2,$ and $x=2.$
The absolute maximum occurs at the critical point $x=0$ and the absolute minima over occur at the critical points $x=-2$ and $x=2.$ (Note that $x=-2$ and $x=2$ happen to be the endpoints as well.)

Example
Find the local and/or absolute maxima for the function over the specified domain. $$y= x^2+\frac{2}{x}\,\,\, \mbox{ over } \,\,\, [0.5,4]$$
We first find the critical points on $[0.5,4]$ by looking at $y':$
$$
y'=2x-\frac{2}{x^2}
$$
Now, since $y'$ is undefined at $x=0,$ we need not consider this point as a critical point since
we are only considering $0.5 \leq x \leq 4.$ Thus, we move on to finding where $y'=0:$
$$
\begin{array}{lll}
&y'=0&\\
\implies &\displaystyle 2x-\frac{2}{x^2}=0&\\
\implies &\displaystyle x-\frac{1}{x^2}=0&\mbox{}\\
\implies &x^3-1=0&\mbox{multiplying by $x^2$}\\
\implies &(x-1)(x^2+x+1)=0&\mbox{factoring a difference of cubes}\\
\implies &x-1=0 \mbox{ OR } x^2+x+1=0&\mbox{}\\
\implies &x=1&\mbox{since $x^2+x+1=0$ has no real solution}\\
\end{array}
$$
So, $x=1$ is the only critical point in the interval $[0.5,4].$
Thus, since absolute extrema occur at critical points and endpoints of a closed and bounded interval, we examine the function values at $x=0.5,$ $x=1,$ and $x=4:$ $$ f(0.5)=4.25, \,\,\,\,\,\,\, f(1)=3, \mbox{ and } \,\,\,\,\,\,\, f(4)=16.5 $$ We conclude that the absolute minimum of the $y$ occurs at $x=1$ and the absolute maximum of $y$ occurs at $x=4.$
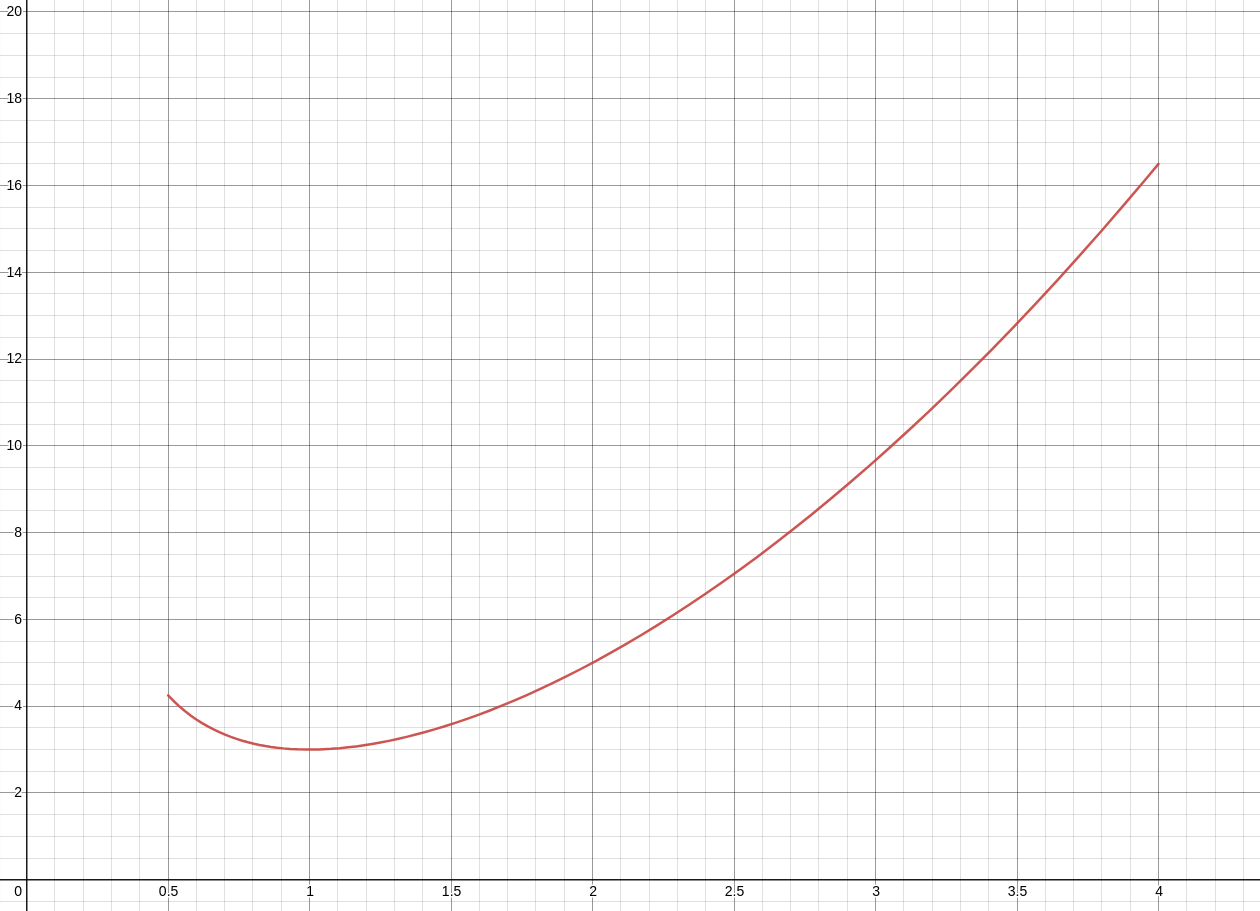
Thus, since absolute extrema occur at critical points and endpoints of a closed and bounded interval, we examine the function values at $x=0.5,$ $x=1,$ and $x=4:$ $$ f(0.5)=4.25, \,\,\,\,\,\,\, f(1)=3, \mbox{ and } \,\,\,\,\,\,\, f(4)=16.5 $$ We conclude that the absolute minimum of the $y$ occurs at $x=1$ and the absolute maximum of $y$ occurs at $x=4.$
