In applications it is very common to approximate an unknown function with a simpler function in order to make a prediction.
We do this by using the function value at a certain point, and then using the function's rate of change, we can make a prediction about the behavior of the unknown function near the known value.
Recall we have done a little bit of this already.
Linear Approximation and Local Linearity
Local Linear Approximations
Example: Use the linear approximation of $f(x)=\sqrt{x}$ at $x=4$ to approximate the value of $\sqrt{4.2}.$
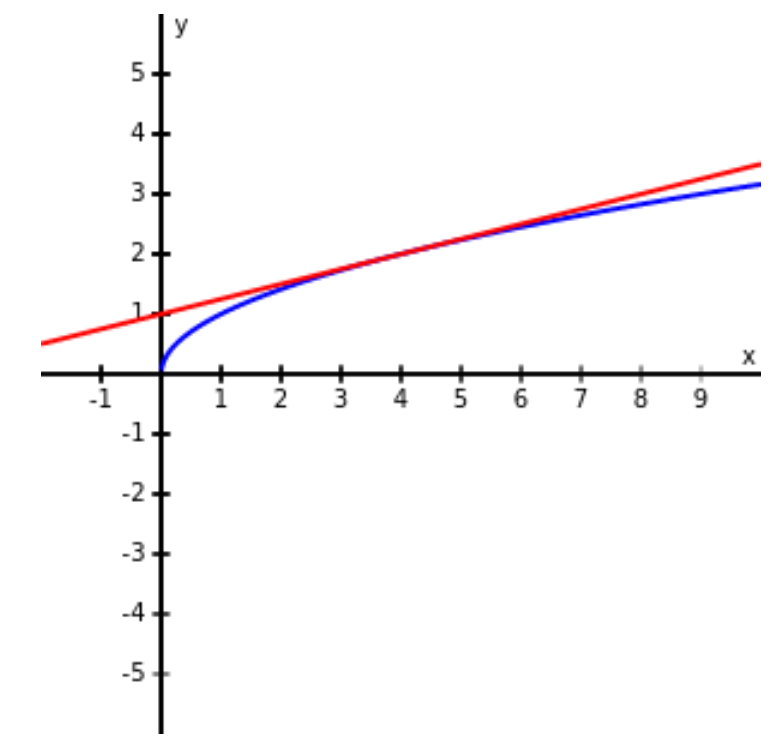
We will use the local linear approximation (the tangent line!) at $x=4$ to make the estimation.
To find the slope of the tangent line, we must compute $f'(4).$ Since $f'(x)=\displaystyle \frac{1}{2\sqrt{x}},$ we have that $f'(x)=\displaystyle \frac{1}{2\sqrt{4}}=\frac{1}{4}.$
Since our linearizatiion is at $(4,2),$ we may now find the tangent line: $$y-y_0=m(x-x_0),$$ or $$y-2=\frac{1}{4}(x-4),$$ which becomes, $$y=\frac{1}{4}x+1.$$ Thus, $$\sqrt{4.2}\approx \frac{1}{4}4.2+1=1.05+1=2.05.$$ For comparison, $\sqrt{4.2}=2.049390153...$
To find the slope of the tangent line, we must compute $f'(4).$ Since $f'(x)=\displaystyle \frac{1}{2\sqrt{x}},$ we have that $f'(x)=\displaystyle \frac{1}{2\sqrt{4}}=\frac{1}{4}.$
Since our linearizatiion is at $(4,2),$ we may now find the tangent line: $$y-y_0=m(x-x_0),$$ or $$y-2=\frac{1}{4}(x-4),$$ which becomes, $$y=\frac{1}{4}x+1.$$ Thus, $$\sqrt{4.2}\approx \frac{1}{4}4.2+1=1.05+1=2.05.$$ For comparison, $\sqrt{4.2}=2.049390153...$
Differentials
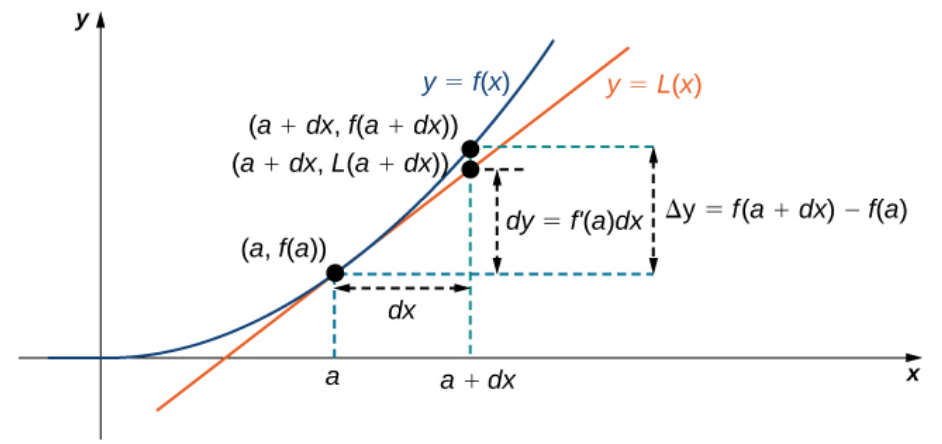
For a function $y=f(x),$ we may approximate $f(x)$ for values of $x$ near some fixed value $a$ by looking at the locally linear approximation $$y-f(a) = f'(a)(x-a).$$ Suppose we increase or decrease $a$ by a small amount, say $\Delta x.$ This produces a small change in $y,$ say $\Delta y.$ To approximate this change at $x=a+\Delta x$ we have $$f(a+\Delta x)-f(a) \approx f'(a)(a+\Delta x-a),$$ which is the same as saying $$\Delta y \approx f'(a)\Delta x.$$ It is this fact which inspires the notion of differentials.
Differentials
The differential of a function $y=f(x)$ is given by the equation $$dy=f'(x)dx.$$ The quantities $dy$ and $dx$ are called differentials.
The idea is that at any point along the curve, a "differential" (very small) change in $x,$ causes a "differential" change in $y.$
Differentials
The Big Deal: Differentials offer a nice way to approximate the change in a function. Going back to our original line of thinking, suppose we increase or decrease $x$ by a "differential" (small) amount $dx.$ This produces a small change in $y,$ say $\Delta y.$ To approximate this change at $x=a+dx$ we have $$\Delta y =f(a+dx)-f(a) \approx f'(a)(a+dx-a)=f'(a)dx=dy.$$ This is all to say that $$dy \approx \Delta y.$$
Example
Approximate $\Delta y$ by by finding the differential and evaluate for the given $x$ and $dx.$ $$y=f(x)=\sqrt{x}, \,\,\, x=4, \,\,\, dx=0.2$$ Compute the value $\Delta y$ directly and compare to $dy.$
For $y=f'(x)=\sqrt{x},$ the differential is $$\displaystyle dy=f'(x)dx=\frac{1}{2\sqrt{x}}dx.$$
Thus, increasing $x=4$ by $dx=0.2,$ $$\Delta y \approx dy = \frac{1}{2\sqrt{4}}0.2=0.05.$$
This is close to the actual value $$\Delta y=\sqrt{4.2}-\sqrt{4}=2.049390153...-2=0.049390153...$$
Example
Approximate $\Delta y$ by by finding the differential and evaluate for the given $x$ and $dx.$ $$y=f(x)=\tan x, \,\,\, x=0, \,\,\, dx=\frac{\pi}{10}$$ Compute the value $\Delta y$ directly and compare to $dy.$
For $y=f'(x)=\tan x,$ the differential is $$\displaystyle dy=f'(x)dx=\sec^2 x \, dx.$$
Thus, increasing $x=0$ by $\displaystyle dx=\frac{\pi}{10},$ $$\Delta y \approx dy = \sec^2(0)\cdot \frac{\pi}{10}=\frac{\pi}{10}=0.3141592654...$$
This is close to the actual value $$\Delta y=\tan\frac{\pi}{10}-\tan 0=0.3249196962...-0=0.3249196962$$
Example
Suppose a round balloon is being inflated as seen below.
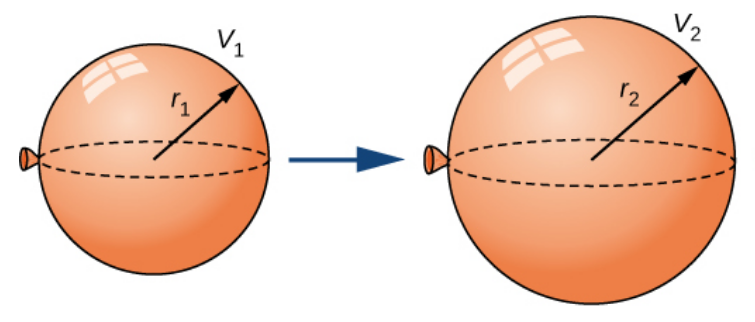
(a) Find the change in volume $dV$ if the radius of the balloon changes from $r_1=10$ inches to $r_1+dr=r_2=10.1$ inches.
Here $r=10$ and $dr=0.1.$
Since $\displaystyle V=V(r)=\frac{4}{3}\pi r^3,$ we have
$dV=V'(r)dr=4\pi r^2 \, dr.$
For $r=10$ and $dr=0.1,$
$$dV=4\pi \cdot 10^2 \cdot 0.1=125.663706144...$$
$$
\begin{array}{ll}
\Delta V&=V_2-V_1\\
&=V(r_2)-V(r_1)\\
&=V(10.1)-V(10)\\
&=\displaystyle\frac{4}{3}\pi \cdot 10.1^3-\frac{4}{3}\pi \cdot 10^3\\
&=\displaystyle\frac{4}{3}\pi (10.1^3-10^3)\\
&=\displaystyle\frac{4}{3}\pi \cdot 30.301\\
&=126.924532...\\
\end{array}
$$
Measurement Error
In measurement there will always be some error. That is, we can never measure something like a length exactly.
Errors in one quantity causes errors in others. For example, an error in measuring the side length of a cube will cause error in the volume of that cube.
Here, when we measure some value of $x,$ we shall treat the error in our measurement as a small difference $dx$ from the desired quantity.
If some quantity $y$ depends on $x$ in some way, say $y=f(x),$ we can use differentials to approximate the error in $y,$ that is $\Delta y,$ with $dy.$
Error versus Relative Error
The relative error in a quantity $Q$ is the comparison of the change to the quantity $\Delta Q$ from some value $Q.$ That is, $$\mbox{Relative Error}=\frac{\Delta Q}{Q}.$$ When this value is expressed as a percentage, it is called the percent error and is computed as $$\mbox{Percent Error}=100 \cdot \frac{\Delta Q}{Q}.$$
Example
A metal fabricator named Billy Bob needs to cut out a square which is $15$ cm by $15$ cm. Both side lengths must be measured with an accuracy of $\pm 0.2$ cm.
(a) Estimate the error in the computed area of a square.
The area of an $x$ cm by $x$ cm square is given by $A(x)=x^2$ in cm2.
The side lengths must be measured with an accuracy of $\pm 0.2$ cm. That is, $-0.2 \leq dx \leq 0.2.$
Then, $$ \begin{array}{lll} &A'(x) (-0.2) \leq A'(x) \, dx \leq A'(x) 0.2&\\ \implies & A'(x) (-0.2) \leq dA \leq A'(x) 0.2&\\ \implies & A'(15) (-0.2) \leq dA \leq A'(15) 0.2 &\mbox{since $x=15$ cm}\\ \implies & 2\cdot 15 \cdot (-0.2) \leq dA \leq 2\cdot 15 \cdot 0.2&\\ \implies &-6 \leq dA \leq 6&\\ \end{array} $$ That is, if the length of the side of the square can vary by $\pm 0.2$ cm, the area can vary within approximately $\pm 6$ cm2 from the desired area.
The side lengths must be measured with an accuracy of $\pm 0.2$ cm. That is, $-0.2 \leq dx \leq 0.2.$
Then, $$ \begin{array}{lll} &A'(x) (-0.2) \leq A'(x) \, dx \leq A'(x) 0.2&\\ \implies & A'(x) (-0.2) \leq dA \leq A'(x) 0.2&\\ \implies & A'(15) (-0.2) \leq dA \leq A'(15) 0.2 &\mbox{since $x=15$ cm}\\ \implies & 2\cdot 15 \cdot (-0.2) \leq dA \leq 2\cdot 15 \cdot 0.2&\\ \implies &-6 \leq dA \leq 6&\\ \end{array} $$ That is, if the length of the side of the square can vary by $\pm 0.2$ cm, the area can vary within approximately $\pm 6$ cm2 from the desired area.
(b) Estimate the relative error in the computed area of a square.
The relative error in area is $\displaystyle \frac{\Delta A}{A}$ which we will approximate using $\displaystyle \frac{dA}{A}:$
$$
\begin{array}{lll}
&-6 \leq dA \leq 6&\\
\implies &\displaystyle-\frac{6}{A} \leq \frac{dA}{A} \leq \frac{6}{A}&\\
\implies &\displaystyle-\frac{6}{15^2} \leq \frac{dA}{A} \leq \frac{6}{15^2}&\mbox{ since $A=15^2$ cm$^2$}\\
\implies &\displaystyle -0.02\overline{6} \leq \frac{dA}{A} \leq 0.02\overline{6}&\\
\implies &\displaystyle -2.\overline{6}\% \leq \frac{dA}{A} \leq 2.\overline{6}\%&\\
\end{array}
$$
That is, if the length of the side of the square can vary by $\pm 0.2$ cm,
the area can vary within approximately $\pm 2.\overline{6}\%$ of the desired area.
(c) Compute the exact error and the relative error in the area and compare to the estimate in part (a) and part (b).
Since $-0.2 \leq dx \leq 0.2,$ we have
$$
\begin{array}{rl}
&A(15-0.2)-A(15)\leq \Delta A \leq A(15+0.2)-A(15)\\
\implies &A(14.8)-A(15) \leq \Delta A \leq A(15.2)-A(15)\\
\implies & 14.8^2-15^2\leq \Delta A \leq 15.2^2-15^2\\
\implies & 219.04-225\leq \Delta A \leq 331.04-225\\
\implies & -5.96 \leq \Delta A \leq 6.04\\
\end{array}
$$
Thus, the exact error is $-5.96 \leq \Delta A \leq 6.04$ cm2.
That is, if the length of the side of the square can vary by $\pm 0.2$ cm, the true area will be off by an amount between $5.96$ cm2 below and $6.04$ cm2 above.
We may now calculate the relative error: $$ \begin{array}{lll} &-5.96 \leq \Delta A \leq 6.046&\\ \implies &\displaystyle-\frac{5.96}{A} \leq \frac{\Delta A}{A} \leq \frac{6.04}{A}&\\ \implies &\displaystyle-\frac{5.96}{15^2} \leq \frac{\Delta A}{A} \leq \frac{6.04}{15^2}&\mbox{ since $A=15^2$ cm$^2$}\\ \implies &\displaystyle -0.0264\overline{8} \leq \frac{\Delta A}{A} \leq 0.0268\overline{4}&\\ \implies &\displaystyle -2.64\overline{8}\% \leq \frac{\Delta A}{A} \leq 2.68\overline{4}\%&\\ \end{array} $$ That is, if the length of the side of the square can vary by $\pm 0.2$ cm, the true area will be within $\pm 2.64\overline{8}\%$ of the desired area.
That is, if the length of the side of the square can vary by $\pm 0.2$ cm, the true area will be off by an amount between $5.96$ cm2 below and $6.04$ cm2 above.
We may now calculate the relative error: $$ \begin{array}{lll} &-5.96 \leq \Delta A \leq 6.046&\\ \implies &\displaystyle-\frac{5.96}{A} \leq \frac{\Delta A}{A} \leq \frac{6.04}{A}&\\ \implies &\displaystyle-\frac{5.96}{15^2} \leq \frac{\Delta A}{A} \leq \frac{6.04}{15^2}&\mbox{ since $A=15^2$ cm$^2$}\\ \implies &\displaystyle -0.0264\overline{8} \leq \frac{\Delta A}{A} \leq 0.0268\overline{4}&\\ \implies &\displaystyle -2.64\overline{8}\% \leq \frac{\Delta A}{A} \leq 2.68\overline{4}\%&\\ \end{array} $$ That is, if the length of the side of the square can vary by $\pm 0.2$ cm, the true area will be within $\pm 2.64\overline{8}\%$ of the desired area.