Antiderivatives

Antiderivatives

If derivatives aren't your thing, you'll love antiderivatives!

Antiderivatives: The Big Idea

By this point we should be well aware of the fact that $\displaystyle \frac{d}{dx}x^2=2x.$

However, suppose that we were given the function $f(x)=2x$ and were asked to find a function $F(x)$ such that $F'(x)=2x.$

Then $F(x)=x^2$ would be a possibility since $F'(x)=2x.$

We say that $F(x)=x^2$ is an antiderivative of $f(x)=2x.$

Defintion: Antiderivative

We say that $F(x)$ is an antiderivative of $f(x)$ if $F'(x)=f(x).$

Antiderivatives: The Big Idea

We've seen that $F(x)=x^2$ is an antiderivative of $f(x)=2x.$

But what if I told you this isn't the only one. For example suppose $G(x)=x^2+5.$ Then, $G'(x)=2x$ too.

So antiderivatives aren't unique. $F(x)=x^2$ and $G(x)=x^2+5$ are both antderivatives of $f(x)=2x.$

Antiderivatives: The Big Idea

In fact, any function of the form $F(x)=x^2+C,$ where $C$ is a constant, is an antiderivative since $F'(x)=2x=f(x)$.

In this way, a function has infinitely many antiderivatives.

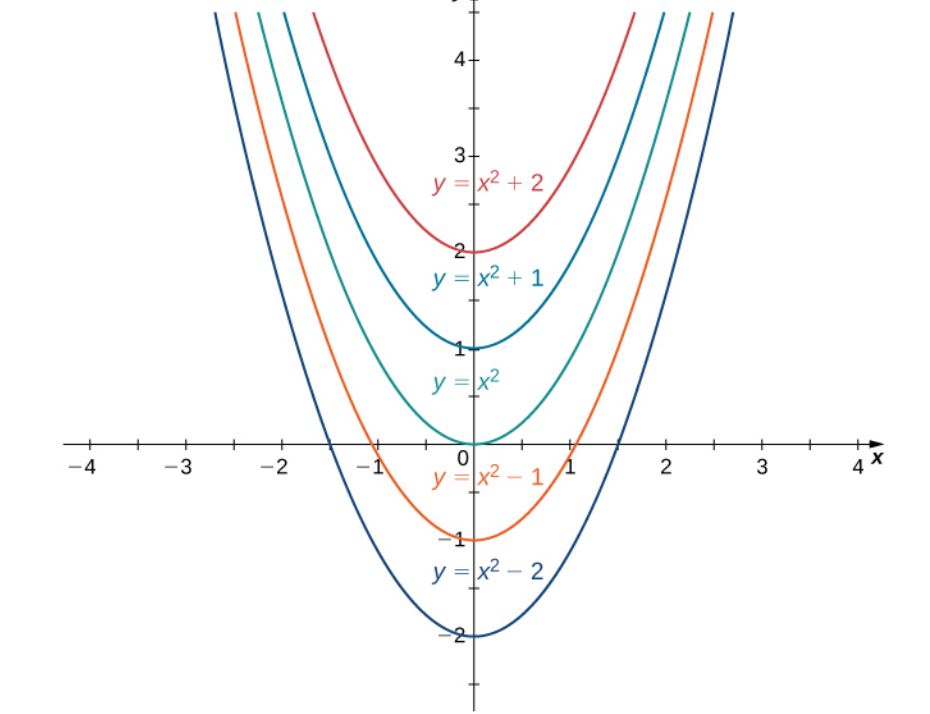
The big question at this point is: are these ALL of them?

Big Answer: Yes!

Theorem

Suppose $F(x)$ and $G(x)$ are both antiderivatives of the function $y=f(x).$

Then $F(x)=G(x)+C$ where $C$ is some constant.

In Other Words: Any two antiderivatives differ only by a constant.

Note: This fact follows from Corollary #2 of the MVT.

More Examples

Find the antiderivative family for the functions below.

$\displaystyle f(x)=3x^2$

$F(x)=x^3+C$

$\displaystyle f(x)=\frac{1}{x}$

$F(x)=\ln |x| +C$

$\displaystyle f(x)=\cos x$

$F(x)=\sin x +C$

$\displaystyle f(x)=e^x$

$F(x)=e^x+C$

A New Notation

We now introduce a new notation for antiderivatives. It may seem a little strange at first, but will begin make more sense next term in MTH 252.

As an example, to indicate that $F(x)=x^2+C$ is the family of antiderivatives of $f(x)=2x,$ we may write $$\int 2x \, dx =x^2+C.$$

Generally Speaking

If $F(x)+C$ is the family of antiderivatives of a function $f(x),$ then we may write $$\int f(x) \, dx=F(x)+C.$$

Note: Again, for reasons that will become clearer later in MTH 252, $\displaystyle \int f(x) \, dx$ is also called the indefinite integral of $f(x).$

The Power Rule

If $n\neq -1,$ then $$\int x^n \, dx=\frac{1}{n+1}x^{n+1}+C.$$

Example: Find $\displaystyle \int x^3 \, dx.$

More Examples

$\displaystyle \int x^3 \, dx = \frac{1}{4}x^4+C$ since $\displaystyle \frac{d}{dx}\left( \frac{1}{4}x^4+C\right)=x^3$

$\displaystyle \int \frac{1}{x} \, dx=\ln|x|+C$ since $\displaystyle \frac{d}{dx}\left(\ln|x|+C\right)=\frac{1}{x}$

$\displaystyle \int \cos x \, dx=\sin x+C$ since $\displaystyle \frac{d}{dx}\left(\sin x+C\right)=\cos x$

$\displaystyle \int e^x \, dx=e^x+C$ since $\displaystyle \frac{d}{dx} \left(e^x+C\right)=e^x$

In fact, every differentiation formula can be turned into a formula for the indefinite integral.

Properties of the Indefinite Integral

$\displaystyle \int [f(x)+g(x)] \, dx=\int f(x) \, dx+\int g(x) \, dx$

$\displaystyle \int [f(x)-g(x)] \, dx=\int f(x) \, dx-\int g(x) \, dx$

$\displaystyle \int cf(x) \, dx=c \int f(x) \, dx$

Example

Evaluate the definite integrals.

$\displaystyle \int (4x+\sqrt{x}) \, dx.$

$$ \begin{array}{lll} &\displaystyle \int (4x+\sqrt{x}) \, dx &\\ &=\displaystyle \int (4x+x^{1/2}) \, dx&\mbox{write in exponential form}\\ &=\displaystyle \int 4x \, dx + \int x^{1/2} \, dx&\mbox{integral of a sum is the sum of the integrals}\\ &=\displaystyle 4 \int x \, dx + \int x^{1/2} \, dx&\mbox{integral of a constant multiple is the constant multiple of the integrals}\\ &=\displaystyle 4 \cdot \frac{1}{1+1}x^{1+1} + C_1 + \frac{1}{1/2+1}x^{1/2+1} +C_2 &\mbox{by the power rule for integrals}\\ &=\displaystyle 4 \cdot \frac{1}{2}x^{2} + \frac{1}{3/2}x^{3/2}+ C_1+C_2 &\mbox{simplfying}\\ &=\displaystyle 2 x^{2} + \frac{2}{3}x^{3/2}+C &\mbox{$C_1+C_2$ is just another constant we'll call $C$}\\ \end{array} $$

$\displaystyle \int (\sec x \tan x -4x) dx.$

$$ \begin{array}{lll} & \displaystyle \int (\sec x \tan x -4x) \,dx &\mbox{integral of a difference is the difference of the integrals}\\ &= \displaystyle \int \sec x \tan x \,dx - \int 4x \,dx &\mbox{integral of a difference is the difference of the integrals}\\ &= \displaystyle \int \sec x \tan x \,dx - 4 \int x \,dx &\mbox{integral of a constant multiple is the constant multiple of the integrals}\\ &= \displaystyle \sec x +C_1 - 4 \cdot \frac{1}{2} x^2 +C_2 &\mbox{integral of a constant multiple is the constant multiple of the integrals}\\ &= \displaystyle \sec x - 2x^2 +C &\mbox{$C_1+C_2$ is just another constant we'll call $C$}\\ \end{array} $$

$\displaystyle \int \frac{14x^3+2x+1}{x^3} dx.$

$$ \begin{array}{ll} \displaystyle \int \frac{14x^3+2x+1}{x^3} dx &\mbox{}\\ =\displaystyle \int \left(\frac{14x^3}{x^3}+\frac{2x}{x^3}+\frac{1}{x^3} \right) \, dx &\mbox{divide each term in the numerator by $x^3$}\\ =\displaystyle \int \left(14+\frac{2}{x^2}+\frac{1}{x^3} \right) \, dx &\mbox{simplify}\\ =\displaystyle \int \left(14+2x^{-2}+x^{-3} \right) \, dx &\mbox{rewrite in exponential form}\\ =\displaystyle \int 14\,dx+\int 2x^{-2}\,dx+\int x^{-3}\, dx &\mbox{integral of a sum is the sum of the integrals}\\ =\displaystyle 14\int \,dx+ 2\int x^{-2}\,dx+\int x^{-3}\, dx &\mbox{integral of a constant multiple is the constant multiple of the integrals}\\ =\displaystyle 14x+C_1+ 2 \cdot \frac{1}{-2+1} x^{-2+1}+C_2+ \frac{1}{-3+1}x^{-3+1}+C_3&\mbox{by the power rule for integrals}\\ =\displaystyle 14x- 2 x^{-1}- \frac{1}{2}x^{-2}+C_1+C_2+C_3&\mbox{simplify}\\ =\displaystyle 14x- 2 x^{-1}- \frac{1}{2}x^{-2}+C&\mbox{$C_1+C_2+C_3$ is just another constant we'll call $C$}\\ \end{array} $$

Initial Value Problems

It is very common in applications to need to find an antiderivative that satisfies a certain condition.

Differential Equations

Many applied problems are stated as an equation involving some unknown function $y(x)$ its derivatives $\displaystyle \frac{dy}{dx},$ $\displaystyle \frac{d^2y}{dx^2},$ $\displaystyle \frac{d^3y}{dx^3},$ and so forth

An equation involving some unknown function $y(x)$ its derivatives is called a differential equation.

When we find antiderivatives we are solving a very basic differential equation $$\frac{dy}{dx}=f(x).$$

Example

The family of antiderivatives $\displaystyle y=\int 2x \,dx=x^2+C$ solves the differential equation $$\frac{dy}{dx}=2x.$$

Initial Value Problems

In applications, it is very common to find a solution to differential equation that satisfies a particular condition called an initial condition.

For example, it might be that we need a function which satisfies the differential $\displaystyle \frac{dy}{dx}=2x$ as well as an initial condition $y(0)=2.$

Initial Value Problems

Example: Solve the initial value problem $\displaystyle \frac{dy}{dx}=2x,$ $y(0)=2.$

We can see that the solution $y=x^2+2$ satisfies both the differential equation and the initial condition $y(0)=2.$

Example: Solve the initial value problem $\displaystyle \frac{dy}{dx}=3x^{-2},$ $y(1)=2.$

We first find the general solution to the equation by finding an antiderivative: $$ \begin{array}{ll} \displaystyle y=\int 3 x^{-2} \, dx & \\ \displaystyle =3 \int x^{-2} \, dx & \mbox{pull out constant multiple}\\ \displaystyle =3 (-x^{-1}+C & \mbox{use power rule for integrals}\\ \displaystyle =-3x^{-1}+C & \mbox{simplfy}\\ \end{array} $$ We now find the particular solution by imposing the initial condition: $$ \begin{array}{lll} &\displaystyle y(1)=2 & \\ \implies & \displaystyle-3(1)^{-1}+C =2 & \mbox{}\\ \implies & \displaystyle-3+C =2 & \mbox{}\\ \implies & \displaystyle C =5 & \mbox{}\\ \end{array} $$ Since, $y=-3x^{-1}+5$ satisfies the differential equation and the initial condition, it satisfies the initial value problem.

Position, Velocity, and Acceleration

Recall that velocity $v(t)$ is the derivative of position $s(t),$ and that acceleration $a(t)$ is the derivative of velocity $v(t).$

In several cases we were given a position function $s(t)$ and found the velocity function as $v(t)=s'(t)$ by taking a derivative, of the acceleration function $a(t)=v'(t)=s''(t)$ as the derivative of velocity or the second derivative of position.

What if we were given the velocity function or the acceleration function but not position?

How would we recover the position from the velocity or acceleration functions?

Answer: By solving an initial value problem! :D

Example

According to nacto.org, "if a street surface is dry, the average driver can safely decelerate an automobile or light truck with reasonably good tires at the rate of about 15 feet per second."

Suppose a car is being driven at a rate of $45$ mph when the brakes are applied. The car decelerates at a constant rate of $15$ ft/sec².

How long does it take for the car to stop?

We shall model the situation with a differential equation. Since acceleration is the derivative of the velocity function $v(t),$ a constant deceleration of $15$ feet per second is modelled by $$\displaystyle \frac{d v}{dt}=-15$$ Since the velocity at the moment the brakes we applied (when the clock starts) is $45$ miles per hour, we have an initial condition. However, we must state the velocity in feet per second: $$ \frac{45 \mbox{ mi}}{1 \mbox{ hr}}\cdot \frac{ 5280\mbox{ ft}}{ 1 \mbox{ mi}}\cdot \frac{ 1 \mbox{ hr}}{ 3600 \mbox{ sec}}=\frac{66 \mbox{ ft}}{1 \mbox{ sec}} $$ Thus, our initial condition is $v(0)=66.$

We will now solve the above initial value problem. First we find a general solution to the differential equation by finding an antiderivative: $$v(t)=\int (-15) \,dt =-15t+C.$$ Imposing the initial condition we have $$ \begin{array}{lll} &\displaystyle v(0)=66 & \\ \implies & \displaystyle-15\cdot 0+C =66 & \mbox{}\\ \implies & \displaystyle C =66 & \mbox{}\\ \end{array} $$ Thus, our velocity function is $v(t)=-15t+66.$

The car stops when the velocity is $0.$ Thus, we set $v(t)=0$ which gives $-15t+66=0.$ So, the car stops after $t=4.4$ seconds.

How far will the car travel from the time the brakes are applied to the time the vehicle stops?

To answer the question, we now need to find the position function $s(t).$ Since velocity is the derivative of position, we may use the above solution to write another differential equation: $$\frac{ds}{dt}=-15t+66.$$ We will say the $s(t)$ is the distance the car travels after the brakes are applied so that our initial condition is $s(0)=0.$

Again, we have a differential equation and an initial condition, that is, an initial value problem. And again, we find a general solution to the differential equation by finding an anti derivative: $$s(t)=\int (-15t+66) \,dt =-\frac{15}{2}t^2 +66 t + C.$$ Imposing the initial condition we have $$ \begin{array}{lll} &\displaystyle s(0)=0 & \\ \implies & \displaystyle -\frac{15}{2}0^2 +66 \cdot 0 + C=0 & \mbox{}\\ \implies & \displaystyle C =0 & \mbox{}\\ \end{array} $$ Thus, our position function is $\displaystyle s(t)=-\frac{15}{2}t^2 +66 t.$ Since the car will travel $t=4.4$ seconds before stopping, the car will go $\displaystyle s(4.4)=-\frac{15}{2}(4.4)^2 +66 \cdot 4.4= 145.2$ feet before stopping.