We begin our application of derivatives with the exceedingly useful technique of related rates.
When two or more quantities are related in some way, one can depend on the other, or both depend on some other quantity. From these, we can find related rates.
A spherical balloon is being filled with air at the constant rate of $2$ cm3/sec. How fast is the radius increasing when the radius is $3$ cm?
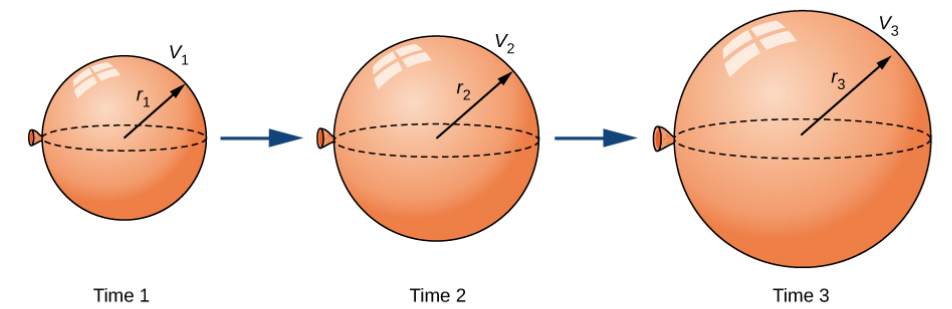
Volume and radius are two quantities which vary with one another; both vary with respect to time.
Although we won't solve this problem here, you may find this example on page 342 of the course textbook.
Example
A brush fire is burning in an approximately circular shape as seen below. If the radius of the burned area is $2.3$ miles, and the edge of the fire is proceeding at $0.5$ miles per hour, what is the rate at which the burned area is increasing?

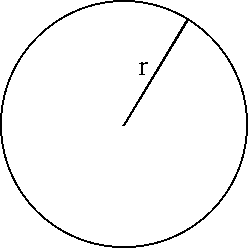
Area and radius vary with one another; both vary with respect to time.
We first consider the the formula which relates the area of a circle $A$ to the radius $r:$
$$
A=\pi r^2.
$$
Thinking of $A$ and $r$ explicitly as functions of time, we could also write
$A(t)=\pi r(t)^2.$
However, for the sake of simpler notation, let's stick with the first equation above.
We differentiate both sides with respect to time $t:$
$$
\begin{array}{lll}
&A=\pi r^2&\\
\implies & \displaystyle \frac{d}{dt}A=\frac{d}{dt}(\pi r^2)&\mbox{differentiate both sides with respect to $t$}\\
\implies & \displaystyle \frac{dA}{dt}=\pi \frac{d}{dt}r^2&\mbox{}\\
\implies & \displaystyle \frac{dA}{dt}=\pi \cdot 2r\frac{dr}{dt}&\mbox{by the Chain Rule}\\
\implies & \displaystyle \frac{dA}{dt}=2\pi r\frac{dr}{dt}&\mbox{}\\
\end{array}
$$
The above relates the rate at which the area is increasing to the rate at which the radius is increasing.
Thus, plugging in the known information we may find the rate at which $A$ is changing: $$\frac{dA}{dt}=2 \pi r\frac{dr}{dt}=2 \pi \cdot 2.3 \cdot 0.5\approx 7.23.$$ That is, at the moment described above, the burn area is increasing by about $7.23$ square miles per hour.
Thus, plugging in the known information we may find the rate at which $A$ is changing: $$\frac{dA}{dt}=2 \pi r\frac{dr}{dt}=2 \pi \cdot 2.3 \cdot 0.5\approx 7.23.$$ That is, at the moment described above, the burn area is increasing by about $7.23$ square miles per hour.
Strategy for Related Rates Problems
Step 1. Assign symbols to all variables involved in the problem. Draw a figure if applicable.
Step 2. State, in terms of the variables, the information that is given and the rate to be determined.
Step 3. Find an equation relating the variables introduced in Step 1.
Step 4. Using the chain rule, differentiate both sides of the equation found in Step 3 with respect to the independent variable. This new equation will relate the derivatives.
Step 5. Substitute all known values into the equation from Step 4, then solve for the unknown rate of change
Example
A $5.3$ foot tall person running at night casts a shadow from a lamppost which is $11$ feet tall.
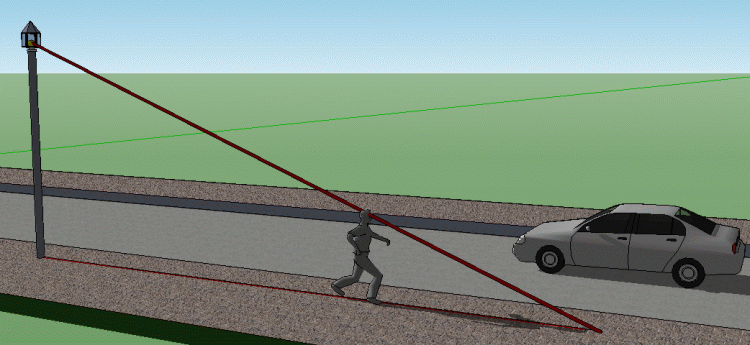
If the person is $13$ feet away from the lamppost and running at a speed of $17$ feet per second, how fast is the tip of the shadow moving away from the runner?
Step 1: Let $x$ be the runner's distance from the lamppost, and let $s$ be the length of the runner's shadow.
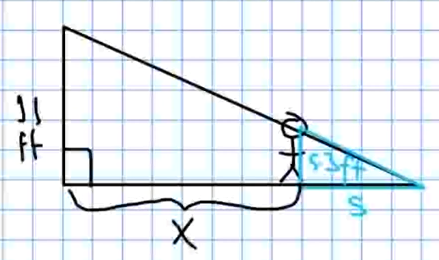
Step 2: The information we're given is $x=13$ feet, and $\displaystyle\frac{dx}{dt}=17$ feet per second. We want to find $\displaystyle\frac{dx}{dt}.$
Step 3: From the picture, we may relate $x$ and $s$ by using similar triangles: $$\frac{x+s}{11}=\frac{s}{5.3}$$ We may simplify the above: $$ \begin{array}{lll} &\displaystyle \frac{x+s}{11}=\frac{s}{5.3}&\\ \implies & \displaystyle 5.3(x+s)=11s &\mbox{}\\ \implies & 5.3x+5.3s=11s &\mbox{}\\ \implies & 5.3x=5.7s &\mbox{}\\ \end{array} $$ Thus, $x$ and $s$ are related more simply by $5.3x=5.7s.$ Step 4: We now differentiate both sides of the equation from Step 3: $$ \begin{array}{lll} & 5.3x=5.7s &\mbox{}\\ \implies & \displaystyle \frac{d}{dt}(5.3x)=\frac{d}{dt}(5.7s) &\mbox{}\\ \implies & \displaystyle 5.3\frac{dx}{dt}=5.7\frac{ds}{dt} &\mbox{}\\ \end{array} $$ Step 5: We now plug in all the known information given in Step 2: $$ \begin{array}{lll} & \displaystyle 5.3\frac{dx}{dt}=5.7\frac{ds}{dt} &\mbox{}\\ \implies & \displaystyle 5.3 \cdot 17=5.7\frac{ds}{dt} &\mbox{recall from Step 2 that $\displaystyle\frac{dx}{dt}=17$}\\ \implies & \displaystyle \frac{5.3 \cdot 17}{5.7}=\frac{ds}{dt} &\mbox{}\\ \end{array} $$ Thus, $\displaystyle \frac{ds}{dt}\approx 15.81.$
That is, the tip of the runner's shadow is moving away from them at a rate of about $15.81$ feet per second.

Step 2: The information we're given is $x=13$ feet, and $\displaystyle\frac{dx}{dt}=17$ feet per second. We want to find $\displaystyle\frac{dx}{dt}.$
Step 3: From the picture, we may relate $x$ and $s$ by using similar triangles: $$\frac{x+s}{11}=\frac{s}{5.3}$$ We may simplify the above: $$ \begin{array}{lll} &\displaystyle \frac{x+s}{11}=\frac{s}{5.3}&\\ \implies & \displaystyle 5.3(x+s)=11s &\mbox{}\\ \implies & 5.3x+5.3s=11s &\mbox{}\\ \implies & 5.3x=5.7s &\mbox{}\\ \end{array} $$ Thus, $x$ and $s$ are related more simply by $5.3x=5.7s.$ Step 4: We now differentiate both sides of the equation from Step 3: $$ \begin{array}{lll} & 5.3x=5.7s &\mbox{}\\ \implies & \displaystyle \frac{d}{dt}(5.3x)=\frac{d}{dt}(5.7s) &\mbox{}\\ \implies & \displaystyle 5.3\frac{dx}{dt}=5.7\frac{ds}{dt} &\mbox{}\\ \end{array} $$ Step 5: We now plug in all the known information given in Step 2: $$ \begin{array}{lll} & \displaystyle 5.3\frac{dx}{dt}=5.7\frac{ds}{dt} &\mbox{}\\ \implies & \displaystyle 5.3 \cdot 17=5.7\frac{ds}{dt} &\mbox{recall from Step 2 that $\displaystyle\frac{dx}{dt}=17$}\\ \implies & \displaystyle \frac{5.3 \cdot 17}{5.7}=\frac{ds}{dt} &\mbox{}\\ \end{array} $$ Thus, $\displaystyle \frac{ds}{dt}\approx 15.81.$
That is, the tip of the runner's shadow is moving away from them at a rate of about $15.81$ feet per second.
Example
Water is draining from the bottom of a cone-shaped funnel at the rate of $0.03$ ft3/sec. The height of the funnel is $2$ ft and the radius at the top of the funnel is $1$ ft. At what rate is the height of the water in the funnel changing when the height of the water is $\displaystyle \frac{1}{4}$ ft?
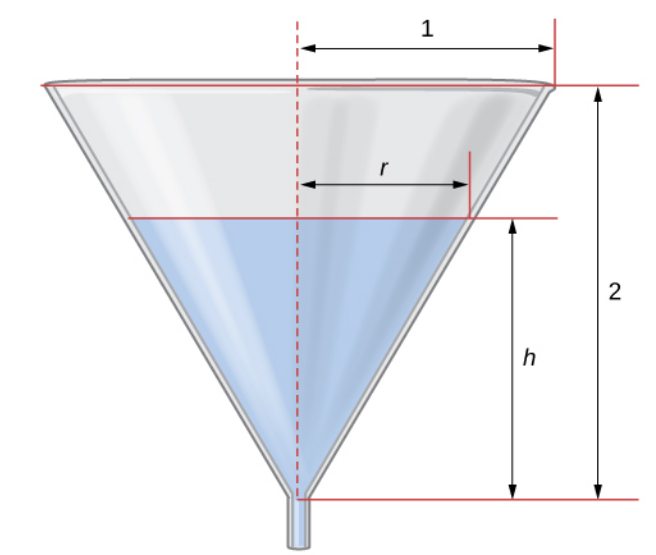
Step 1: The figure is drawn for us. We see that the volume $V,$ the height $h$ of the water, and the radius $r$ at the water's surface all vary with time.
Step 2: We are given that $\displaystyle \frac{dV}{dt}=-0.03$ cubic feet per second. We also know that the overall height and radius of the funnel are $2$ feet and $1$ foot. We are looking to find $\displaystyle \frac{dh}{dt}$ when $h=0.25$ feet.
Step 3: The formula for the volume of a cone relates all three variable given in Step 2: $\displaystyle V=\frac{1}{3}\pi r^2 h.$
We also know how $r$ and $h$ are related by similar triangles: $\displaystyle \frac{r}{h}=\frac{1}{2}.$
From this we have that $\displaystyle r=\frac{1}{2}h$ so that we may simplify our volume formula: $$ \begin{array}{lll} & \displaystyle V=\displaystyle \frac{1}{3}\pi \left(\frac{1}{2}h\right)^2 h &\mbox{}\\ \implies & \displaystyle V=\frac{1}{3}\pi \cdot\frac{1}{4}h^2 \cdot h &\mbox{}\\ \implies & \displaystyle V=\frac{\pi}{12}h^3 &\mbox{}\\ \end{array} $$ Step 4: We now differentiate both sides of the resulting equation with respect to $t:$ $$ \begin{array}{lll} & \displaystyle V=\frac{\pi}{12}h^3 &\mbox{}\\ \implies & \displaystyle \frac{d}{dt}V=\frac{d}{dt}\left(\frac{\pi}{12}h^3\right) &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}=\frac{\pi}{12}\frac{d}{dt}h^3 &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}=\frac{\pi}{12}\cdot 3h^2\frac{dh}{dt} &\mbox{by the Chain Rule}\\ \implies & \displaystyle \frac{dV}{dt}=\frac{\pi}{4}h^2\frac{dh}{dt} &\mbox{}\\ \end{array} $$ Step 5: We now plug in the known information and solve for $\displaystyle \frac{dh}{dt}:$ $$ \begin{array}{lll} & \displaystyle \frac{dV}{dt}=\frac{\pi}{4}h^2\frac{dh}{dt} &\mbox{}\\ \implies & \displaystyle -0.03=\frac{\pi}{4}(0.25)^2\frac{dh}{dt} &\mbox{from Step 2, $\frac{dV}{dt}=-0.03$ and $h=0.25$}\\ \implies & \displaystyle \frac{-0.03}{\frac{\pi}{4}(0.25)^2}=\frac{dh}{dt} &\mbox{solving for $\frac{dh}{dt}$}\\ \implies & \displaystyle \frac{dh}{dt}=\frac{-0.03\cdot 4}{\pi(0.25)^2} &\mbox{}\\ \implies & \displaystyle \frac{dh}{dt}\approx -0.61 &\mbox{}\\ \end{array} $$ We interpret the above to mean that at the moment in question, the height of the water will be decreasing by about $0.61$ feet per second.
Step 2: We are given that $\displaystyle \frac{dV}{dt}=-0.03$ cubic feet per second. We also know that the overall height and radius of the funnel are $2$ feet and $1$ foot. We are looking to find $\displaystyle \frac{dh}{dt}$ when $h=0.25$ feet.
Step 3: The formula for the volume of a cone relates all three variable given in Step 2: $\displaystyle V=\frac{1}{3}\pi r^2 h.$
We also know how $r$ and $h$ are related by similar triangles: $\displaystyle \frac{r}{h}=\frac{1}{2}.$
From this we have that $\displaystyle r=\frac{1}{2}h$ so that we may simplify our volume formula: $$ \begin{array}{lll} & \displaystyle V=\displaystyle \frac{1}{3}\pi \left(\frac{1}{2}h\right)^2 h &\mbox{}\\ \implies & \displaystyle V=\frac{1}{3}\pi \cdot\frac{1}{4}h^2 \cdot h &\mbox{}\\ \implies & \displaystyle V=\frac{\pi}{12}h^3 &\mbox{}\\ \end{array} $$ Step 4: We now differentiate both sides of the resulting equation with respect to $t:$ $$ \begin{array}{lll} & \displaystyle V=\frac{\pi}{12}h^3 &\mbox{}\\ \implies & \displaystyle \frac{d}{dt}V=\frac{d}{dt}\left(\frac{\pi}{12}h^3\right) &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}=\frac{\pi}{12}\frac{d}{dt}h^3 &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}=\frac{\pi}{12}\cdot 3h^2\frac{dh}{dt} &\mbox{by the Chain Rule}\\ \implies & \displaystyle \frac{dV}{dt}=\frac{\pi}{4}h^2\frac{dh}{dt} &\mbox{}\\ \end{array} $$ Step 5: We now plug in the known information and solve for $\displaystyle \frac{dh}{dt}:$ $$ \begin{array}{lll} & \displaystyle \frac{dV}{dt}=\frac{\pi}{4}h^2\frac{dh}{dt} &\mbox{}\\ \implies & \displaystyle -0.03=\frac{\pi}{4}(0.25)^2\frac{dh}{dt} &\mbox{from Step 2, $\frac{dV}{dt}=-0.03$ and $h=0.25$}\\ \implies & \displaystyle \frac{-0.03}{\frac{\pi}{4}(0.25)^2}=\frac{dh}{dt} &\mbox{solving for $\frac{dh}{dt}$}\\ \implies & \displaystyle \frac{dh}{dt}=\frac{-0.03\cdot 4}{\pi(0.25)^2} &\mbox{}\\ \implies & \displaystyle \frac{dh}{dt}\approx -0.61 &\mbox{}\\ \end{array} $$ We interpret the above to mean that at the moment in question, the height of the water will be decreasing by about $0.61$ feet per second.
Example: Billy Bob is sitting on his front porch playing the banjo watching the traffic go by. Billy Bob notices a truck passing by, and at that instant, the angle measure from his driveway to the truck is $\displaystyle \frac{\pi}{6}$ radians. If the angle of Billy Bob's gaze is changing at a rate of $\displaystyle \frac{1}{8}$ of a radian per second, and Billy Bob's driveway is $500$ feet long (perpendicular to the road), how fast is the truck moving?
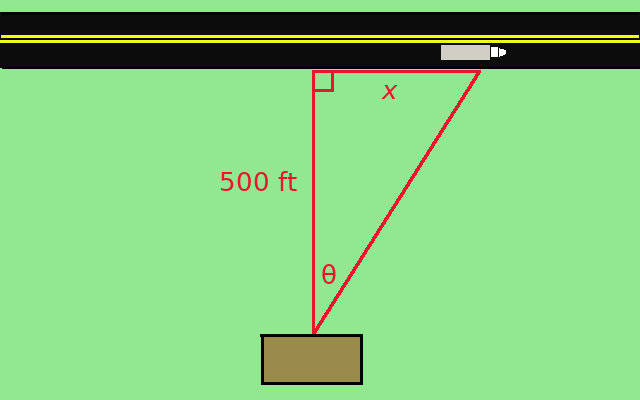
Step 1: We will let be $x$ be the truck's distance from Billy Bob's driveway and $\theta$ be the angle
formed from between Billy Bob's driveway and the line between Billy Bob and the truck.
Step 2: At the moment in question, $\displaystyle \theta=\frac{\pi}{6}$ radians, and $\displaystyle \frac{d\theta}{dt} =\frac{1}{8}.$ We also know that the length of the driveway is $500$ feet. We want to know the speed of the truck, $\displaystyle \frac{dx}{dt}.$
Step 3: From the figure, we see that $\displaystyle \tan \theta =\frac{x}{500}.$ Then, $$x=500\tan \theta.$$ Step 4: We now differentiate both sides of the resulting equation with respect to $t:$ $$ \begin{array}{lll} & \displaystyle x=500\tan \theta &\mbox{}\\ \implies & \displaystyle \frac{d}{dt}x=\frac{d}{dt}\left(500\tan \theta \right) &\mbox{}\\ \implies & \displaystyle \frac{dx}{dt}=500\frac{d}{dt}\tan \theta &\mbox{}\\ \implies & \displaystyle \frac{dx}{dt}=500\sec^2 \theta \frac{d\theta}{dt} &\mbox{by the Chain Rule}\\ \end{array} $$
Step 5: We now plug in the known information and find $\displaystyle \frac{dx}{dt}:$ $$ \begin{array}{lll} & \displaystyle \frac{dx}{dt}=500\sec^2 \theta \frac{d\theta}{dt} &\mbox{}\\ \implies & \displaystyle \frac{dx}{dt}=500\sec^2\left(\frac{\pi}{6}\right)\cdot \frac{1}{8} &\mbox{from Step 2, $\theta=\frac{\pi}{6}$ and $\frac{d\theta}{dt}=\frac{1}{8}$}\\ \implies & \displaystyle \frac{dx}{dt}\approx 83.33 &\mbox{}\\ \end{array} $$ We interpret this to mean that at the moment in question, the truck is travelling at about $83.33$ feet per second. We note that this is about $56.82$ miles per hour.
Step 2: At the moment in question, $\displaystyle \theta=\frac{\pi}{6}$ radians, and $\displaystyle \frac{d\theta}{dt} =\frac{1}{8}.$ We also know that the length of the driveway is $500$ feet. We want to know the speed of the truck, $\displaystyle \frac{dx}{dt}.$
Step 3: From the figure, we see that $\displaystyle \tan \theta =\frac{x}{500}.$ Then, $$x=500\tan \theta.$$ Step 4: We now differentiate both sides of the resulting equation with respect to $t:$ $$ \begin{array}{lll} & \displaystyle x=500\tan \theta &\mbox{}\\ \implies & \displaystyle \frac{d}{dt}x=\frac{d}{dt}\left(500\tan \theta \right) &\mbox{}\\ \implies & \displaystyle \frac{dx}{dt}=500\frac{d}{dt}\tan \theta &\mbox{}\\ \implies & \displaystyle \frac{dx}{dt}=500\sec^2 \theta \frac{d\theta}{dt} &\mbox{by the Chain Rule}\\ \end{array} $$
Step 5: We now plug in the known information and find $\displaystyle \frac{dx}{dt}:$ $$ \begin{array}{lll} & \displaystyle \frac{dx}{dt}=500\sec^2 \theta \frac{d\theta}{dt} &\mbox{}\\ \implies & \displaystyle \frac{dx}{dt}=500\sec^2\left(\frac{\pi}{6}\right)\cdot \frac{1}{8} &\mbox{from Step 2, $\theta=\frac{\pi}{6}$ and $\frac{d\theta}{dt}=\frac{1}{8}$}\\ \implies & \displaystyle \frac{dx}{dt}\approx 83.33 &\mbox{}\\ \end{array} $$ We interpret this to mean that at the moment in question, the truck is travelling at about $83.33$ feet per second. We note that this is about $56.82$ miles per hour.
Recall the Following Example
Suppose that the price $p$ (in dollars) and weekly sales $x$ (in thousands of units) of a certain commodity satisfy the demand equation $$2p^2+x^2=2572.$$ Determine the rate at which the weekly sales are changing at a time when $x=50,$ $p=6,$ and the price is changing at a rate of $-0.5$ dollars per week.
This is nothing more than a related-rates problem.
If you want to see this example again, please watch the last example in the video for Section 3.8.
We interrupt this lecture to bring you a super-applied example of related rates which involves the loudest sound ever made and is not for the faint of heart.
Viewer discretion is advised.
Krakatoa: Some Background
Krakatoa was a volcano in Indonesia.
In $1883$ Krakatoa erupted explosively. The final explosion was so powerful that:
- barographs around the world detected a pressure wave that circled the globe four times
- it created the loudest sound ever measured and was heard more than $3000$ miles away
- anyone within ten miles would have gone deaf
- it threw $5$ cubic miles of earth $50$ miles into the air
- two thirds of the island was destroyed
Enter Anak Krakatoa ("Child of Krakatoa")
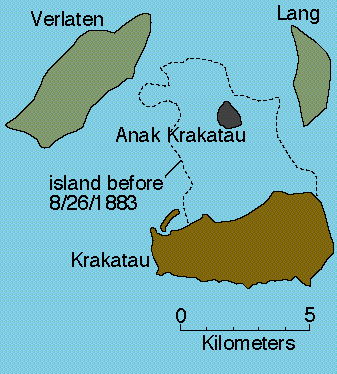
Anak Krakatoa Before $2018$

- For more than $60$ years Anak Krakatoa had been growing in height by about $6.8$ meters per year.
- In $2017,$ the height of Anak Krakatoa was more than $400$ meters.
- Anak Krakatoa and the surrounding islands are an interesting case study on how life re-populates after being wiped out.
Anak Krakatoa After $2018$

Related Rates Application: Using 1) the above information, 2) the formula for the volume of a cone, 3) a little guesswork about a cinder cone's angle of repose (between $30^{\circ}$ and $40^{\circ}$), and of course, 4) a little calculus, we can estimate the rate at which Anak Krakatoa's volume was growing before December $2018.$
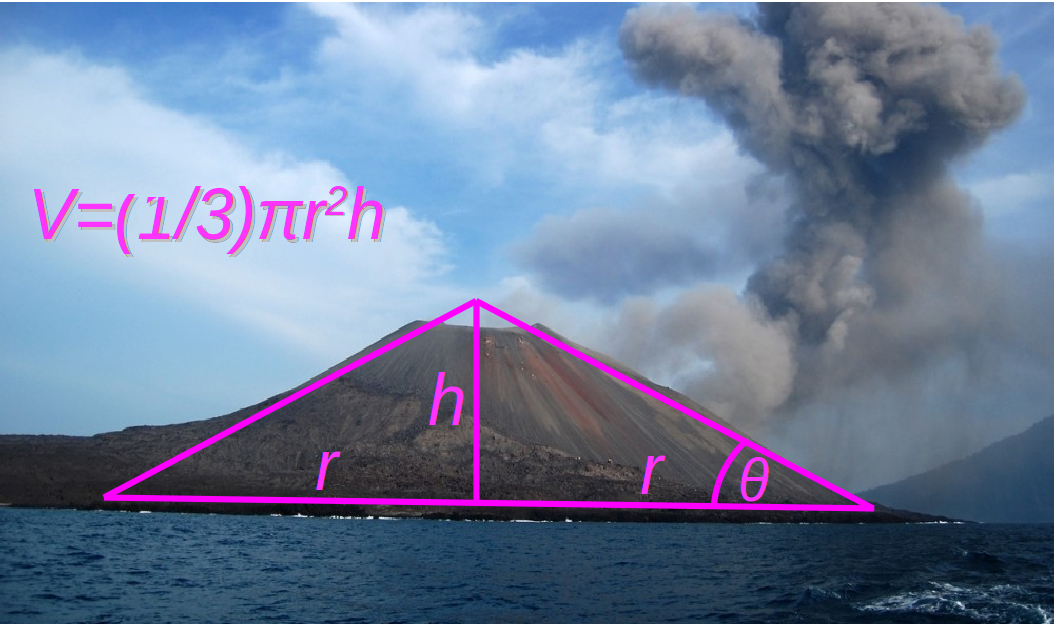
Step 1: From the figure, we see that $h$ and $r$ vary with respect to time $t.$ The angle of repose $\theta$ remains approximately constant,
so we will treat it as such.
Step 2: We know that in $2017$ that the height of Krakatoa was $400$ meters. That is, $h=400.$ We also know that the height was growing by about $6.8$ meters per year. So, $\displaystyle \frac{dh}{dt}=6.8.$ We also know that $30^{\circ} \leq \theta \leq 40^{\circ}.$ We will use this information later.
Based on this information, we want to estimate the rate of change in volume $\displaystyle \frac{dV}{dt}$ in cubic meters per year.
Step 3: The volume of a right circular cone relates all the variables listed in the previous steps: $$V=\frac{1}{3}\pi r^2 h$$ Since the the angle of repose is roughly constant, we know that $\tan \theta$ is roughly constant. From this, we may relate $r$ and $h:$ $$\tan \theta = \frac{h}{r}.$$ Thus, $\displaystyle r=\frac{h}{\tan \theta}.$ From this, we may state the volume directly in terms of the height: $$ \begin{array}{lll} & \displaystyle V=\frac{1}{3}\pi r^2 h &\mbox{}\\ \implies & \displaystyle V=\frac{1}{3}\pi \left(\frac{h}{\tan \theta}\right)^2 h &\mbox{ since $r=\frac{h}{\tan \theta}$}\\ \implies & \displaystyle V=\frac{1}{3}\pi \frac{h^2}{\tan^2 \theta}\cdot h &\mbox{}\\ \implies & \displaystyle V=\frac{\pi}{3\tan^2 \theta} h^3 &\mbox{}\\ \end{array} $$
Step 4: We now differentiate both sides of the resulting equation with respect to $t:$ $$ \begin{array}{lll} & \displaystyle V=\frac{\pi}{3\tan^2 \theta} h^3 &\mbox{}\\ \implies & \displaystyle \frac{d}{dt} V= \frac{d}{dt} \frac{\pi}{3\tan^2 \theta} h^3 &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}= \frac{\pi}{3\tan^2 \theta} \frac{d}{dt} h^3 &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}= \frac{\pi}{3\tan^2 \theta} 3h^2\frac{dh}{dt} &\mbox{by the Chain Rule}\\ \implies & \displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 \theta} h^2\frac{dh}{dt} &\mbox{}\\ \end{array} $$
Step 5: We now plug in the known information to get an estimate for $\displaystyle \frac{dV}{dt}:$ $$ \begin{array}{lll} & \displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 \theta} h^2\frac{dh}{dt} &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 \theta} 400^2\cdot 6.8 &\mbox{}\\ \end{array} $$ Now, according to our source, $30^{\circ} \leq \theta \leq 40^{\circ}.$ Thus, we'll plug in $\theta=30^{\circ}$ and $\theta=40^{\circ}$ to get an upper and lower bound on the rate at which the volume was changing.
For $\theta=30^{\circ}:$ $$\displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 30^{\circ}} 400^2 \cdot 6.8 \approx \mbox{10,254,158}$$ For $\theta=40^{\circ}:$ $$\displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 40^{\circ}} 400^2 \cdot 6.8 \approx \mbox{4,854,581}$$
Thus, we estimate that the rate of change of the volume of Anak Krakatoa before $2018$ was between about $\mbox{4,854,581}$ and $\mbox{10,254,158}$ cubic meters per year.
Step 2: We know that in $2017$ that the height of Krakatoa was $400$ meters. That is, $h=400.$ We also know that the height was growing by about $6.8$ meters per year. So, $\displaystyle \frac{dh}{dt}=6.8.$ We also know that $30^{\circ} \leq \theta \leq 40^{\circ}.$ We will use this information later.
Based on this information, we want to estimate the rate of change in volume $\displaystyle \frac{dV}{dt}$ in cubic meters per year.
Step 3: The volume of a right circular cone relates all the variables listed in the previous steps: $$V=\frac{1}{3}\pi r^2 h$$ Since the the angle of repose is roughly constant, we know that $\tan \theta$ is roughly constant. From this, we may relate $r$ and $h:$ $$\tan \theta = \frac{h}{r}.$$ Thus, $\displaystyle r=\frac{h}{\tan \theta}.$ From this, we may state the volume directly in terms of the height: $$ \begin{array}{lll} & \displaystyle V=\frac{1}{3}\pi r^2 h &\mbox{}\\ \implies & \displaystyle V=\frac{1}{3}\pi \left(\frac{h}{\tan \theta}\right)^2 h &\mbox{ since $r=\frac{h}{\tan \theta}$}\\ \implies & \displaystyle V=\frac{1}{3}\pi \frac{h^2}{\tan^2 \theta}\cdot h &\mbox{}\\ \implies & \displaystyle V=\frac{\pi}{3\tan^2 \theta} h^3 &\mbox{}\\ \end{array} $$
Step 4: We now differentiate both sides of the resulting equation with respect to $t:$ $$ \begin{array}{lll} & \displaystyle V=\frac{\pi}{3\tan^2 \theta} h^3 &\mbox{}\\ \implies & \displaystyle \frac{d}{dt} V= \frac{d}{dt} \frac{\pi}{3\tan^2 \theta} h^3 &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}= \frac{\pi}{3\tan^2 \theta} \frac{d}{dt} h^3 &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}= \frac{\pi}{3\tan^2 \theta} 3h^2\frac{dh}{dt} &\mbox{by the Chain Rule}\\ \implies & \displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 \theta} h^2\frac{dh}{dt} &\mbox{}\\ \end{array} $$
Step 5: We now plug in the known information to get an estimate for $\displaystyle \frac{dV}{dt}:$ $$ \begin{array}{lll} & \displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 \theta} h^2\frac{dh}{dt} &\mbox{}\\ \implies & \displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 \theta} 400^2\cdot 6.8 &\mbox{}\\ \end{array} $$ Now, according to our source, $30^{\circ} \leq \theta \leq 40^{\circ}.$ Thus, we'll plug in $\theta=30^{\circ}$ and $\theta=40^{\circ}$ to get an upper and lower bound on the rate at which the volume was changing.
For $\theta=30^{\circ}:$ $$\displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 30^{\circ}} 400^2 \cdot 6.8 \approx \mbox{10,254,158}$$ For $\theta=40^{\circ}:$ $$\displaystyle \frac{dV}{dt}= \frac{\pi}{\tan^2 40^{\circ}} 400^2 \cdot 6.8 \approx \mbox{4,854,581}$$
Thus, we estimate that the rate of change of the volume of Anak Krakatoa before $2018$ was between about $\mbox{4,854,581}$ and $\mbox{10,254,158}$ cubic meters per year.
How Good is Our Estimate?
"The height prior to the $2018$ collapse appears to have been a bit over $400$ meters after a growth spurt in the preceding decade. However, it was still very far from rebuilding the old island. The lava flow rates are not excessive: the island has grown by about $0.002 \mbox{ km}^3$ $(\mbox{2,000,000 m}^3)$ per year."
-From Volcano Cafe: The Rise and Fall of Anak Krakatoa