For any equation expressing a relationship between two or more quantities, we can imagine that one depends on the other even if one is cannot not be explicitly expressed in terms of the other.
Moreover, solving for one quantity in terms of another is not always possible.
A Classic Example: Circles
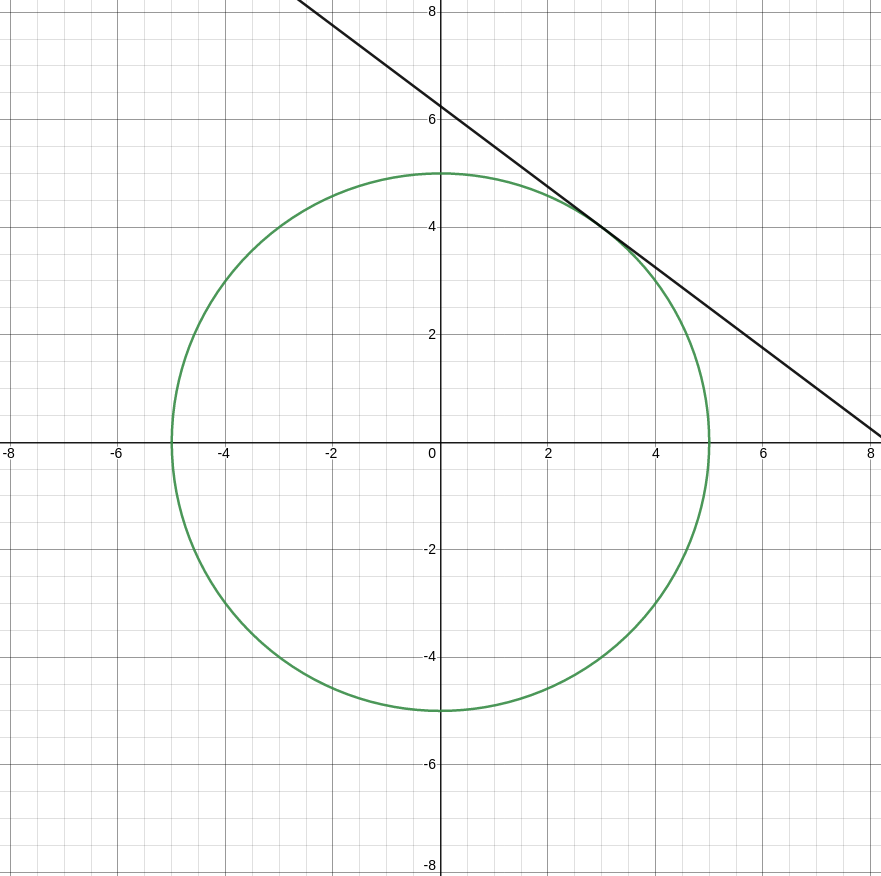
The equation for a circle of radius 5 is $x^2+y^2=25$ has the graph below.

A Classic Example: Circles
The equation for a circle of radius 5 is $x^2+y^2=25$ has the graph below

Example

(a) Find the slope of the tangent line of the circle $x^2+y^2=25$ at the point $(3,4)$ by implicit differentiation.
$$
\begin{array}{lll}
&x^2+y^2=25&\\
\implies & \displaystyle \frac{d}{dx}(x^2+y^2)=\frac{d}{dx}25&\mbox{differentiate both sides with respect to $x$}\\
\implies & \displaystyle \frac{d}{dx}x^2+\frac{d}{dx}y^2=0&\mbox{}\\
\implies & \displaystyle 2x+2y\frac{dy}{dx}=0&\mbox{by the Chain Rule ($y$ is a function of $x$)}\\
\implies & \displaystyle \frac{dy}{dx}=-\frac{x}{y}&\mbox{solving for $\frac{dy}{dx}$}\\
\end{array}
$$
Thus, the slope of the tangent line at $(x,y)=(3,4)$ is
$$
\frac{dy}{dx}=-\frac{x}{y}=-\frac{3}{4}
$$
(b) Find the equation of the tangent line of the circle $x^2+y^2=25$ at the point $(3,4).$
We shall call upon our old friend, the point-slope form. We know the tangent line is a line of slope $-\frac{3}{4}$ passing through the point $(3,4).$
Thus, out tangent line is
$$
\begin{array}{lll}
&y-y_0=m(x-x_0)&\\
\implies & \displaystyle y-4=-\frac{3}{4}(x-3)\\
\implies & \displaystyle y=-\frac{3}{4}x+\frac{3}{4}\cdot 3+4\\
\implies & \displaystyle y=-\frac{3}{4}x+\frac{9}{4}+\frac{16}{4}\\
\implies & \displaystyle y=-\frac{3}{4}x+\frac{25}{4}\\
\end{array}
$$

Implicit Differentiation: The General Process
1) Differentiate the equation with respect to $x$ while treating $y$ as a function of $x.$
2) Solve for $\displaystyle \frac{dy}{dx}.$ You should get an equation of the form $\displaystyle \frac{dy}{dx}=\mbox{Expression}(x,y).$
3) If necessary, to find the slope of the tangent line to the curve at the point $(a,b),$ plug $(a,b)$ into the $\mbox{Expression}$ above.
Example: The Folium of Descartes
The Folium of Descartes below has the equation $x^3+y^3=3xy.$
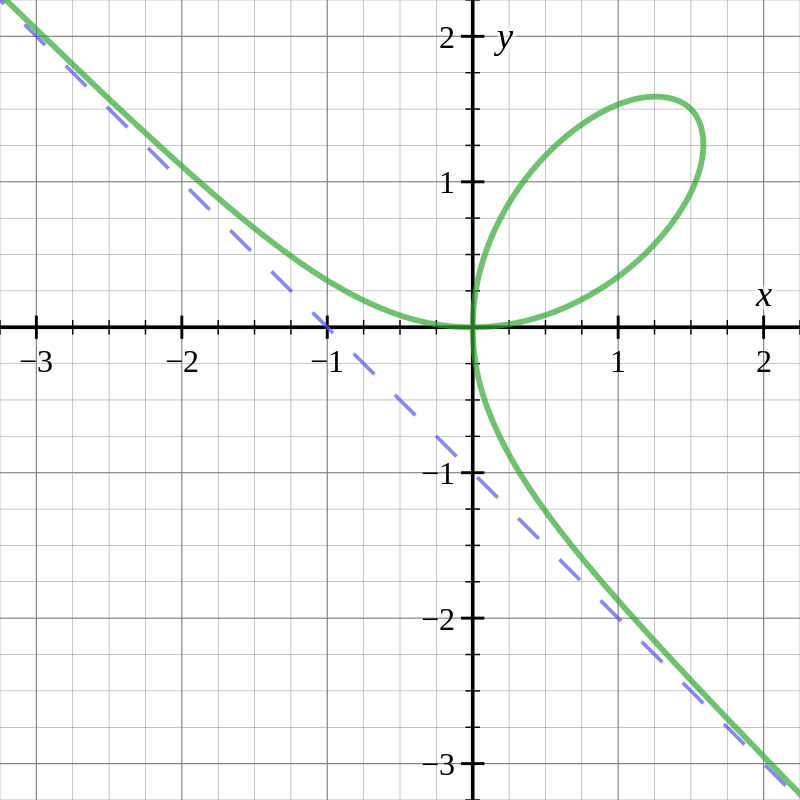
(a) Find the slope of the tangent line at the point $\displaystyle \left(\frac{3}{2},\frac{3}{2}\right)$ by implicit differentiation.
$$
\begin{array}{lll}
&x^3+y^3=3xy&\\
\implies & \displaystyle \frac{d}{dx}(x^3+y^3)=\frac{d}{dx}(3xy)&\mbox{differentiate both sides with respect to $x$}\\
\implies & \displaystyle \frac{d}{dx}x^3+\frac{d}{dx}y^3=3\frac{d}{dx}(xy)&\mbox{}\\
\implies & \displaystyle 3x^2+3y^2y'=3(x'y+xy')&\mbox{by the Chain Rule and Product Rule}\\
\implies & \displaystyle 3x^2+3y^2y'=3(y+xy')&\mbox{}\\
\implies & \displaystyle x^2+y^2y'=y+xy'&\mbox{divide out 3 on both sides}\\
\implies & \displaystyle y^2y'-xy'=-x^2+y&\mbox{get $y'$ terms on one side and everything else on the other}\\
\implies & \displaystyle (y^2-x)y'=y-x^2&\mbox{factor out $y'$}\\
\implies & \displaystyle y'=\frac{y-x^2}{y^2-x}&\mbox{solve for $y'$}\\
\end{array}
$$
Thus, the slope of the tangent line at $(x,y)=\displaystyle \left(\frac{3}{2},\frac{3}{2}\right)$ is
$$
\frac{dy}{dx}=y'=\frac{y-x^2}{y^2-x}=\frac{\displaystyle \frac{3}{2}-\left(\frac{3}{2}\right)^2}{\displaystyle \left(\frac{3}{2}\right)^2-\frac{3}{2}}=-1
$$
(b) Find the equation of the tangent line at the point $\displaystyle \left(\frac{3}{2},\frac{3}{2}\right).$
$$
\begin{array}{lll}
&y-y_0=m(x-x_0)&\\
\implies & \displaystyle y-\frac{3}{2}=-1\cdot (x-\frac{3}{2})\\
\implies & \displaystyle y=-x+\frac{3}{2}+\frac{3}{2}\\
\implies & \displaystyle y=-x+3\\
\end{array}
$$
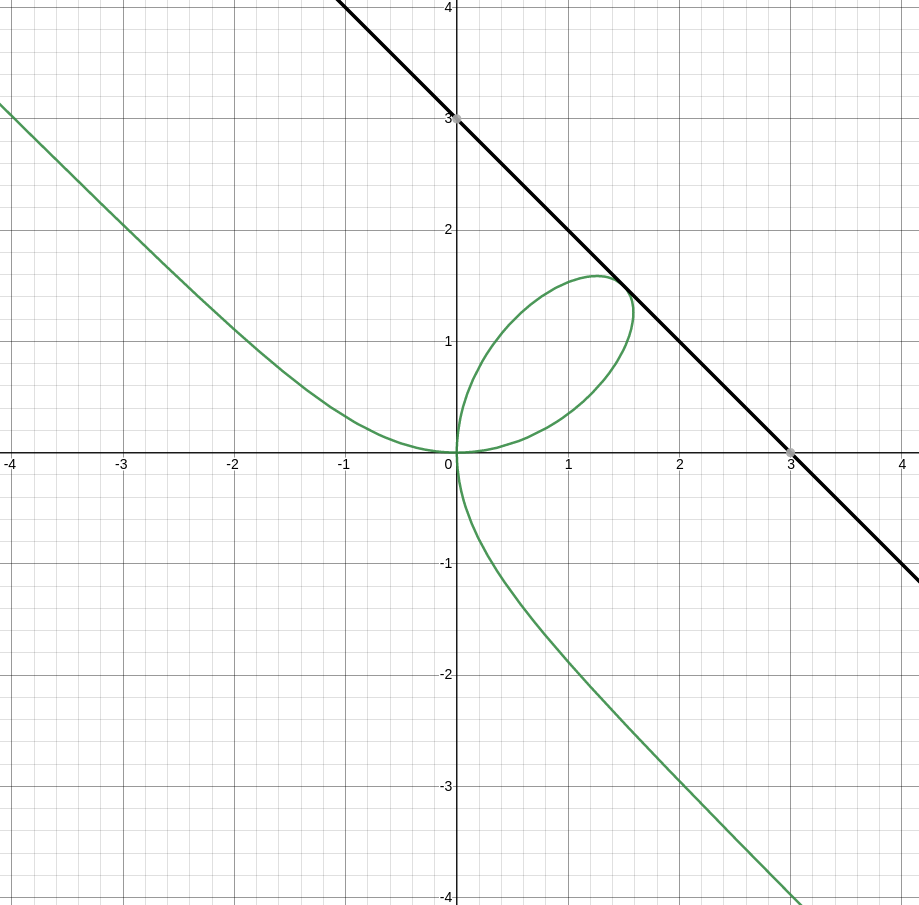

(c) Find the equation of the normal line at the point $\displaystyle \left(\frac{3}{2},\frac{3}{2}\right).$
The normal line is the line perpendicular to the tangent line. Since slopes of perpendicular lines are opposite reciprocals,
the slope of out normal line is $-\frac{1}{-1}=1.$
Thus,
$$
\begin{array}{lll}
&y-y_0=m(x-x_0)&\\
\implies & \displaystyle y-\frac{3}{2}=1\cdot (x-\frac{3}{2})\\
\implies & \displaystyle y=x-\frac{3}{2}+\frac{3}{2}\\
\implies & \displaystyle y=x\\
\end{array}
$$
The normal line is $y=x.$

Application: Demand Curves
Suppose that the price $p$ (in dollars) and weekly sales $x$ (in thousands of units) of a certain commodity satisfy the demand equation $$2p^2+x^2=2572.$$ Determine the rate at which the weekly sales are changing at a time when $x=50,$ $p=6,$ and the price is changing at a rate of $-0.50$ dollars per week.
The problem asks us to find "the rate at which the weekly sales are changing at [a point in time]."
This helps us to realize that both price $p$ and demand $x$ are both functions of time.
Thus, we take a derivative of both sides of the demand equation with respect to time $t:$ $$ \begin{array}{lll} &2p^2+x^2=2572&\\ \implies & \displaystyle \frac{d}{dt}(2p^2+x^2)=\frac{d}{dt}2572&\\ \implies & \displaystyle 2\frac{d}{dt}p^2+\frac{d}{dt}x^2=0&\\ \implies & \displaystyle 2 \cdot 2p\frac{dp}{dt}+2x\frac{dx}{dt}=0&\\ \implies & \displaystyle 2p\frac{dp}{dt}+x\frac{dx}{dt}=0&\mbox{dividing out 2}\\ \implies & \displaystyle x\frac{dx}{dt}=-2p\frac{dp}{dt}&\\ \implies & \displaystyle \frac{dx}{dt}=-\frac{2p}{x}\frac{dp}{dt}&\mbox{since $\frac{dx}{dt}$ is the desired quantity}\\ \end{array} $$ We may now use the given information: $x=50,$ $p=6,$ and $\frac{dp}{dx}=-0.50,$ $$ \frac{dx}{dt}=-\frac{2p}{x}\frac{dp}{dt}=-\frac{2\cdot 6 }{50}\cdot (-0.50)=0.12. $$ Now recall that $x$ is measured in thousands of units sold. So, the unit of the above answer is in thousands of units sold per week.
Thus, at this particular point in time, sales are increasing by $120$ units per week.
This helps us to realize that both price $p$ and demand $x$ are both functions of time.
Thus, we take a derivative of both sides of the demand equation with respect to time $t:$ $$ \begin{array}{lll} &2p^2+x^2=2572&\\ \implies & \displaystyle \frac{d}{dt}(2p^2+x^2)=\frac{d}{dt}2572&\\ \implies & \displaystyle 2\frac{d}{dt}p^2+\frac{d}{dt}x^2=0&\\ \implies & \displaystyle 2 \cdot 2p\frac{dp}{dt}+2x\frac{dx}{dt}=0&\\ \implies & \displaystyle 2p\frac{dp}{dt}+x\frac{dx}{dt}=0&\mbox{dividing out 2}\\ \implies & \displaystyle x\frac{dx}{dt}=-2p\frac{dp}{dt}&\\ \implies & \displaystyle \frac{dx}{dt}=-\frac{2p}{x}\frac{dp}{dt}&\mbox{since $\frac{dx}{dt}$ is the desired quantity}\\ \end{array} $$ We may now use the given information: $x=50,$ $p=6,$ and $\frac{dp}{dx}=-0.50,$ $$ \frac{dx}{dt}=-\frac{2p}{x}\frac{dp}{dt}=-\frac{2\cdot 6 }{50}\cdot (-0.50)=0.12. $$ Now recall that $x$ is measured in thousands of units sold. So, the unit of the above answer is in thousands of units sold per week.
Thus, at this particular point in time, sales are increasing by $120$ units per week.