Derivatives of Inverse Functions

Derivatives of Inverse Functions

Today, we shall learn how to differentiate inverse functions.

As we shall see, there are lots of useful functions that are inverses of other useful functions. For example, inverse trig functions appear often in applications.

Also, exponential functions and logarithmic functions are inverses of one another.

Derivatives of Inverse Functions

Suppose $y=f(x)$ has an inverse $f^{-1}.$

Then $x=f(f^{-1}(x)).$

We now take a derivative of both sides and use the chain rule.

Derivatives of Inverse Functions

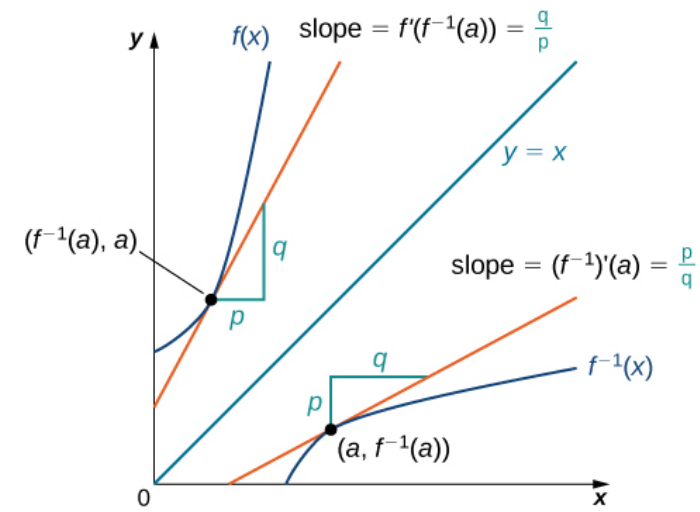
Inverse Function Theorem: Let $y=f(x)$ be a function that is both invertible and differentiable. Let$y=f^{-1}(x)$ be the inverse of $f(x).$ Then for all $x$ satisfying $f'(f^{-1}(x))\neq 0,$ $$(f^{-1})'(x)=\frac{1}{f'(f^{-1}(x))}.$$

Derivatives of Inverse Functions

$$(f^{-1})'(a)=\frac{1}{f'(f^{-1}(a))}.$$ Interpretation: The derivative of $f^{-1}$ at $(a,b)$ is the reciprocal of the derivative of $f$ at $(b,a).$

Derivatives of Inverse Functions

Using other notations for the derivative, we may also write $$\frac{df^{-1}}{dx}=\frac{d}{dx}f^{-1}(x)=(f^{-1})'(x)=\frac{1}{f'(f^{-1}(x))}.$$

Example: Consider the graph of $y = f (x)$ below.

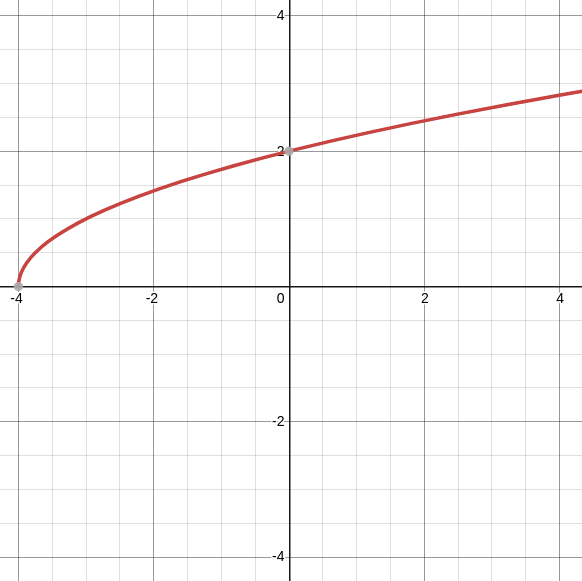
(a) On the above graph, sketch the graph of $y = f^{-1}(x),$ and

(b) Use part (a) to estimate $\left(f^{-1}\right)'(2).$

Power Rule for Rational Exponents

Being able to find derivatives of inverse functions also enables us to find derivatives of rational powers of $x,$ not just integer powers.

Example: Find the derivative of $g(x)=\sqrt[3]{x}.$

First, we express $g$ as $g(x)=x^{1/3}.$ Now clearly, $$ x=(x^{1/3})^3 $$ We then take a derivative of both sides. $$ \frac{d}{dx}x=\frac{d}{dx}(x^{1/3})^3 $$ Then, by the Chain Rule, $$ 1=3(x^{1/3})^2\frac{d}{dx}x^{1/3} $$ After simplifying, $$ 1=3x^{2/3}\frac{d}{dx}x^{1/3} $$ After isolating $\displaystyle \frac{d}{dx}x^{1/3},$ we've done it! $$ \displaystyle \frac{d}{dx}x^{1/3}= \displaystyle \frac{1}{3x^{2/3}} $$ Bonus: Also notice that $$ \begin{array}{ll} \displaystyle \frac{d}{dx}x^{1/3}&= \displaystyle \frac{1}{3x^{2/3}}\\ &=\displaystyle\frac{1}{3}x^{-2/3}\\ &=\displaystyle\frac{1}{3}x^{1/3-1}\\ \end{array} $$ Do you realize what this means?!

Power Rule for Rational Exponents

If $n$ is a positive integer and $m$ is an arbitrary integer, then $$\frac{d}{dx}x^{m/n}=\frac{m}{n}x^{m/n-1}$$

Example: Find the derivative of $$\displaystyle f(x)=\frac{1}{\sqrt[3]{(x^2-4)^2}}$$

We rewrite $f$ as $\displaystyle f(x)=(x^2-4)^{-2/3}.$ Then $$ \begin{array}{lll} \displaystyle f'(x)&=\displaystyle \frac{d}{dx}(x^2-4)^{-2/3}&\\ &=\displaystyle -\frac{2}{3}(x^2-4)^{-2/3-1}\frac{d}{dx}(x^2-4)& \mbox{ by the Chain Rule}\\ &=\displaystyle -\frac{2}{3}(x^2-4)^{-5/3}(2x)&\\ &=\displaystyle -\frac{4x}{3(x^2-4)^{5/3}}&\\ &=\displaystyle -\frac{4x}{3\sqrt[3]{(x^2-4)^5}}&\mbox{ optional step of writing in radical form}\\ \end{array} $$

Example

Use the function $f (x) = \sqrt{x+4}$ to find

(a) $\displaystyle \frac{df}{dx}$ at $x = 0.$

$$ \begin{array}{ll} \displaystyle \frac{df}{dx}&=\displaystyle\frac{d}{dx}\sqrt{x+4}\\ &=\displaystyle\frac{d}{dx}(x+4)^{1/2}\\ &=\displaystyle\frac{1}{2}(x+4)^{1/2-1}\frac{d}{dx}(x+4)\\ &=\displaystyle\frac{1}{2}(x+4)^{-1/2}\\ &=\displaystyle\frac{1}{2(x+4)^{1/2}}\\ &=\displaystyle\frac{1}{2\sqrt{x+4}}\\ \end{array} $$ Thus, $\displaystyle \frac{df}{dx}$ at $x=0$ is $\displaystyle\frac{1}{2\sqrt{0+4}}=\frac{1}{4}.$

(b) $x = f^{-1}(y).$

$$ \begin{array}{ll} &y=f(x)=\sqrt{x+4}\\ \implies & y^2=x+4\\ \implies & x=f^{-1}(y)=y^2-4\\ \end{array} $$

$\displaystyle \frac{df^{-1}}{dy}=\displaystyle\frac{d}{dy}(y^2-4)=2y.$

Thus, $\displaystyle \frac{df^{-1}}{dy}$ at $y=f(0)=2$ is $4.$

$$ f'(0)=\frac{1}{4}, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(f^{-1})'(2)=\frac{1}{f'(f^{-1}(2))}=\frac{1}{f'(0)}=\frac{1}{\frac{1}{4}}=4 $$

Example

For the function $\displaystyle f (x) = x-\frac{2}{x}$ defined on $x \lt 0,$ find $\left(f^{-1}\right)'(1).$

Using the Inverse Function Theorem, $$ \begin{array}{ll} \displaystyle \left(f^{-1}\right)'(1)&=\displaystyle\frac{1}{f'(f^{-1}(1))}\\ \end{array} $$ Thus, we must find the value $f^{-1}(1)$ as well as $f'(x).$

First we'll find $f^{-1}(1).$ Let's say that $x=f^{-1}(1).$ Then $$ \begin{array}{ll} &1=f(x)\\ \implies & 1=\displaystyle x-\frac{2}{x}\\ \implies & x=x^2-2\\ \implies & x^2-x-2=0\\ \implies & (x+1)(x-2)=0\\ \implies & x=-1 \mbox{ OR } x=2.\\ \end{array} $$ Since the domain has been restricted to $x \lt 0,$ we choose $x=-1.$

As for $f'(x):$ $$ \begin{array}{ll} \displaystyle f'(x)&=\displaystyle\frac{d}{dx}\left(x-\frac{2}{x}\right)\\ &=\displaystyle 1+\frac{2}{x^2}. \end{array} $$ Thus, we may continue the calculation started above: $$ \begin{array}{ll} \displaystyle \left(f^{-1}\right)'(1)&=\displaystyle\frac{1}{f'(f^{-1}(1))}\\ &=\displaystyle\frac{1}{f'(-1)}\\ &=\displaystyle\frac{1}{1+\frac{2}{(-1)^2}}\\ &=\displaystyle\frac{1}{1+2}\\ &=\displaystyle\frac{1}{3}\\ \end{array} $$

Example

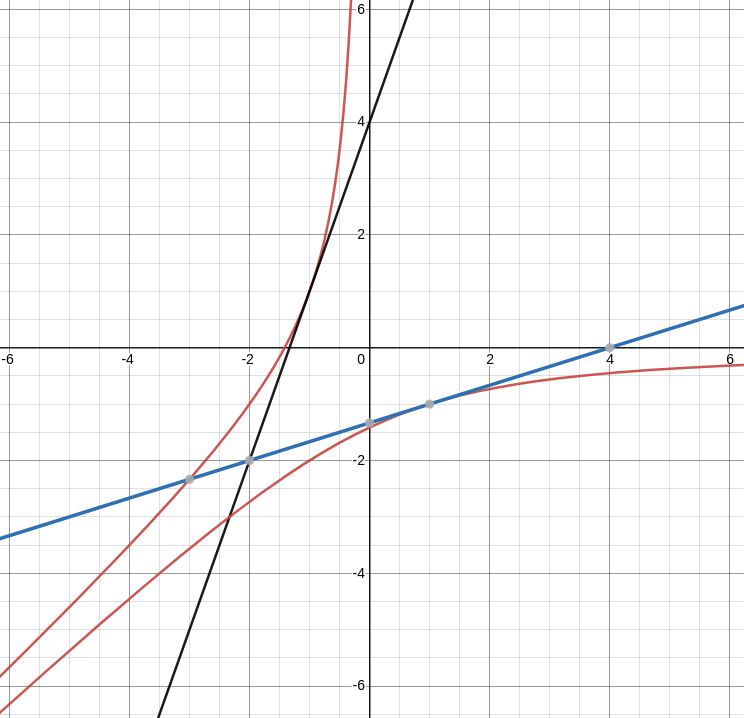
Consider the function $\displaystyle f (x) = x-\frac{2}{x}$ defined on $x \lt 0.$

(a) Find the slope of the tangent line to its inverse function $f^{-1}$ at the point $P(1,-1).$

Done! We did this above! $(f^{-1})'(1)=\displaystyle \frac{1}{3}.$

(b) Find the equation of the tangent line to the graph of $f^{-1}$ at the indicated point.

Since we have a point and a slope, we will use the old-school point-slope form of a line: $$ \begin{array}{ll} &y-y_0=m(x-x_0)\\ \implies & \displaystyle y-(-1)=\frac{1}{3}(x-1)\\ \implies & \displaystyle y+1=\frac{1}{3}x-\frac{1}{3}\\ \implies & \displaystyle y=\frac{1}{3}x-\frac{1}{3}-1\\ \implies & \displaystyle y=\frac{1}{3}x-\frac{4}{3}\\ \end{array} $$

$$ f'(-1)=3, \,\,\,\,\,\,\,\,\,\,\,\,(f^{-1})(1)=\frac{1}{3} $$

Derivatives of Inverse Trigonometric Functions

Suppose we want to find the derivative of $y=\sin^{-1} x.$

We can pull the same trick we did with a generic function by saying $$x=\sin(\sin^{-1} x)$$ and then differentiating both sides.

$$ \begin{array}{ll} &x=\sin(\sin^{-1} x)\\ \implies & \displaystyle \frac{d}{dx}x=\frac{d}{dx}\sin(\sin^{-1} x)\\ \implies & \displaystyle 1=\cos(\sin^{-1} x)\frac{d}{dx}\sin^{-1} x\\ \implies & \displaystyle \frac{d}{dx}\sin^{-1} x=\frac{1}{\cos(\sin^{-1} x)}\\ \end{array} $$ At this point we can still make things a bit simpler. We note that $\sin^{-1} x$ is an angle between $-\frac{\pi}{2}$ and $\frac{\pi}{2}.$ Thus, $$\sin^2(\sin^{-1} x)+\cos^2(\sin^{-1} x)=1.$$ But since $x=\sin(\sin^{-1} x),$ the above becomes $$x^2+\cos^2(\sin^{-1} x)=1.$$ Thus, solving for $\cos(\sin^{-1} x),$ $$\cos(\sin^{-1} x)=\sqrt{1-x^2}.$$ We take the positive root since $\cos \theta$ is non-negative for $-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}.$

We now have our derivative! $$\displaystyle \frac{d}{dx}\sin^{-1} x=\frac{1}{\sqrt{1-x^2}}$$

Derivatives of Inverse Trigonometric Functions $$\frac{d}{dx}\sin^{-1}(x)=\frac{1}{\sqrt{1-x^2}}$$ $$\frac{d}{dx}\cos^{-1}(x)=-\frac{1}{\sqrt{1-x^2}}$$ $$\frac{d}{dx}\tan^{-1}(x)=\frac{1}{1+x^2}$$ $$\frac{d}{dx}\cot^{-1}(x)=-\frac{1}{1+x^2}$$ $$\frac{d}{dx}\sec^{-1}(x)=\frac{1}{|x|\sqrt{x^2-1}}$$ $$\frac{d}{dx}\csc^{-1}(x)=-\frac{1}{|x|\sqrt{x^2-1}}$$

Example

Find $\displaystyle \frac{dy}{dx}$ for $\displaystyle y=\sec^{-1}\left(\frac{1}{x}\right).$

$$ \begin{array}{lll} \displaystyle \frac{dy}{dx}&=\displaystyle\frac{d}{dx}\sec^{-1}\left(\frac{1}{x}\right)&\\ &=\displaystyle \frac{1}{\left|\displaystyle\frac{1}{x}\right|\sqrt{\left(\displaystyle \frac{1}{x}\right)^2-1}}\frac{d}{dx}\frac{1}{x}&\mbox{by the Chain Rule}\\ &=\displaystyle \frac{1}{\displaystyle \frac{1}{|x|}\sqrt{\displaystyle\frac{1}{x^2}-1}}\left(-\frac{1}{x^2}\right)&\\ &=\displaystyle \frac{-|x|}{x^2\sqrt{\displaystyle \frac{1-x^2}{x^2}}}&\\ &=\displaystyle \frac{-|x|}{\displaystyle \frac{x^2\sqrt{1-x^2}}{\sqrt{x^2}}}&\\ &=\displaystyle \frac{-|x|}{\displaystyle \frac{x^2\sqrt{1-x^2}}{|x|}}&\\ &=\displaystyle \frac{-|x|\cdot |x|}{\displaystyle x^2\sqrt{1-x^2}}&\\ &=\displaystyle \frac{-x^2}{\displaystyle x^2\sqrt{1-x^2}}&\\ &=\displaystyle -\frac{1}{\displaystyle \sqrt{1-x^2}}&\\ \end{array} $$

Example

A pole stands $75$ feet tall. An angle $\theta$ is formed when wires of various lengths of $x$ feet are attached from the ground to the top of the pole, as shown in the following figure.

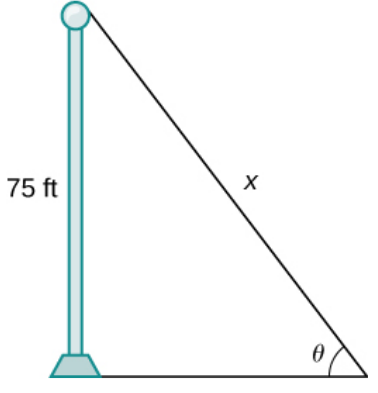
Find the rate of change of the angle $\displaystyle \frac{d \theta }{dx}$ when a wire of length $90$ feet is attached.

We begin with a trig ratio which involves $75,$ $x,$ and $\theta:$ $$\sin \theta = \frac{75}{x}.$$ Rearranging we have $$\theta = \sin^{-1}\left(\frac{75}{x}\right).$$ We may now find the derivative of $\theta$ with respect to $x:$ $$ \begin{array}{lll} \displaystyle \frac{d\theta}{dx}&=\displaystyle\frac{d}{dx}\sin^{-1}\left(\frac{75}{x}\right)&\\ &=\displaystyle\frac{1}{\sqrt{1-\left(\displaystyle \frac{75}{x}\right)^2}}\frac{d}{dx}\left(\frac{75}{x}\right)&\\ &=\displaystyle\frac{1}{\sqrt{1-\displaystyle \frac{75^2}{x^2}}}\left(-\frac{75}{x^2}\right)&\\ &=\displaystyle -\frac{75}{x^2\sqrt{\displaystyle \frac{x^2-75^2}{x^2}}}&\\ &=\displaystyle -\frac{75}{\displaystyle \frac{x^2\sqrt{x^2-75^2}}{\sqrt{x^2}}}&\\ &=\displaystyle -\frac{75}{\displaystyle \frac{x^2\sqrt{x^2-75^2}}{|x|}}&\\ &=\displaystyle -\frac{75|x|}{\displaystyle x^2\sqrt{x^2-75^2}}&\\ &=\displaystyle -\frac{75x}{\displaystyle x^2\sqrt{x^2-75^2}}&\mbox{since $x$ is a positive length}\\ &=\displaystyle -\frac{75}{\displaystyle x\sqrt{x^2-75^2}}&\\ \end{array} $$ Thus, when $x=90,$ $$ \begin{array}{ll} \displaystyle \frac{d\theta}{dx}&=\displaystyle -\frac{75}{\displaystyle 90\sqrt{90^2-75^2}}\\ &\approx -0.01675063025 \end{array} $$ That is, as the length of the wire $x$ increases, when the wire reaches $90$ feet, the angle $\theta$ is decreasing by about $0.0168$ radians per foot.