At this point we can find derivatives of lots of functions! This is awesome!
However... (gulp!)
What if this functions walked up to you and said: "differentiate me": $$f(x)=\left(\sin x+ \frac{1}{x}\right)^{10}$$ What would you do?
Today we learn the Chain Rule which will enable us to find this derivative with the greatest of ease.
The Chain Rule
The chain rule helps us differentiate functions which are compositions with other functions.
For example, the function $h(x)=\sin(x^2)$ is the composition of the functions $f(x)=\sin x$ and $g(x)=x^2.$
This is because $$h(x)=\sin(x^2)=f(x^2)=f(g(x))=(f \circ g)(x).$$ Notice there's an "outside function," $\sin x$, and an "inside function," $x^2.$
Once we can identify "outside" and "inside" functions, we can differentiate their composition with the Chain Rule.
The Chain Rule
Let $f$ and $g$ be functions. For all $x$ in the domain of $g$ for which $g$ is differentiable at $x$ and $f$ is differentiable at $g(x),$ the derivative of the composite function $h(x)=(f\circ g)(x) =f(g(x))$ is given by $$h'(x)=f'(g(x)) \cdot g'(x).$$ We may also write $$\frac{d}{dx}[f(g(x))]=f'(g(x)) \cdot g'(x).$$ The outside function is $f$ and the inside function is $g.$
Example
$$\frac{d}{dx}\sin(x^2)$$ The "outside function" is $\sin x$, and the "inside function" is $x^2.$
$$
\begin{array}{ll}
\displaystyle \frac{d}{dx}\sin(x^2)&\\
=\displaystyle \frac{d}{dx}f(g(x))& \mbox{outside: $f(x)=\sin x,$ inside: $g(x)=x^2$}\\
=\displaystyle f'(g(x))\cdot g'(x)& \mbox{by the chain rule}\\
=\displaystyle \cos(x^2)\cdot 2x& \mbox{since $f'(x)=\cos x$ and $g'(x)=2x$}\\
=\displaystyle 2x\cos(x^2)&\\
\end{array}
$$
Example
$$\frac{d}{dx}\left(\sin x+ \frac{1}{x}\right)^{10}$$ The "outside function" is _________, and the "inside function" is ____________.
$$
\begin{array}{ll}
\displaystyle \frac{d}{dx}\left(\sin x+ \frac{1}{x}\right)^{10}&\\
=\displaystyle \frac{d}{dx}f(g(x))& \mbox{outside: $f(x)=x^{10},$ inside: $\displaystyle g(x)=\sin x+ \frac{1}{x}$}\\
=\displaystyle f'(g(x))\cdot g'(x)& \mbox{by the chain rule}\\
=\displaystyle 10\left(\sin x+ \frac{1}{x}\right)^9\cdot \left(\cos x -\frac{1}{x^2}\right)& \mbox{since $f'(x)=10x^9$ and $\displaystyle g'(x)=\cos x -\frac{1}{x^2}$}\\
\end{array}
$$
The Chain Rule Redux
We can also write the chain rule in Leibniz notation. This is a fancy way to say $\frac{dy}{dx}$ notation which is sometimes called differential notation.
Let $y$ be a function of $u,$ and let $u$ be a function of $x,$ then $$\frac{dy}{dx}=\frac{dy}{du} \cdot \frac{du}{dx}$$
Example
$$\frac{d}{dx}\sin(x^2)$$
Here we can say $y=\sin u$ (outside function) and $u=x^2$ (inside function). Then $$ \begin{array}{ll} &\displaystyle \frac{dy}{dx}\\ =&\displaystyle \frac{dy}{du} \cdot \frac{du}{dx}\\ =&\cos u \cdot 2x \\ = &\cos(x^2)\cdot 2x\\ =&2x\cos(x^2).\\ \end{array} $$
A Handy Way of Writing the Chain Rule
Sometimes when dealing with complex-looking functions, it will be convenient to simply label the "outside function" as $O(x)$ and the "inside function" as $I(x).$ We may then write the chain rule as $$\frac{d}{dx}O(I(x))=O'(I(x))\cdot I'(x).$$ Such labeling will come in handy in the next example.
Example
Use the information in the following table to find $h'(a)$ at the given value for $a.$
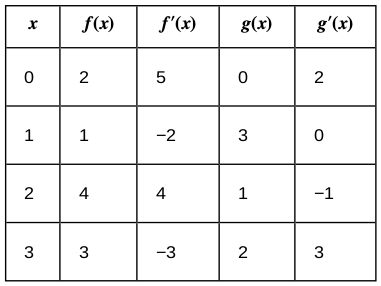
First we find the derivative function $h'(x):$
$$
\begin{array}{ll}
\displaystyle \frac{d}{dx}g \left( 2 + f ( x^2 )\right)&\\
=\displaystyle \frac{d}{dx}O(I(x))& \mbox{outside: $O(x)=g(x),$ inside: $\displaystyle I(x)=2 + f ( x^2 )$}\\
=\displaystyle O'(I(x))\cdot I'(x)& \mbox{by the chain rule}\\
=\displaystyle g'\left( 2 + f ( x^2 )\right)\cdot \frac{d}{dx}\left( 2 + f ( x^2 )\right)& \mbox{since $O'(x)=g'(x)$ and $\displaystyle I'(x)=\frac{d}{dx}\left( 2 + f ( x^2 )\right)$}\\
=\displaystyle g'\left( 2 + f ( x^2 )\right)\cdot \frac{d}{dx}f ( x^2 )&\\
\end{array}
$$
To find our derivative function, we must also find $\frac{d}{dx}f ( x^2 )$ which also requires the chain rule:
$$
\begin{array}{ll}
\displaystyle \frac{d}{dx}f(x^2)&\\
=\displaystyle \frac{d}{dx}O(I(x))& \mbox{outside: $O(x)=f(x)$ inside: $I(x)=x^2$}\\
=\displaystyle O'(I(x))\cdot I'(x)& \mbox{by the chain rule}\\
=\displaystyle f'(x^2)\cdot 2x& \mbox{since $O'(x)=f'(x)$ and $I'(x)=2x$}\\
=\displaystyle 2xf'(x^2)&\\
\end{array}
$$
Thus, we may now complete the original calculation:
$$
\begin{array}{ll}
h'(x)&\\
=\displaystyle g'\left( 2 + f ( x^2 )\right)\cdot f '( x^2 ) \cdot 2x&\\
=\displaystyle 2xf'(x^2)g'\left( 2 + f ( x^2 )\right)&\\
\end{array}
$$
From the above calculation and our table of values we have
$$
\begin{array}{ll}
h'(1)&\\
=\displaystyle 2\cdot 1\cdot f'(1^2)g'\left( 2 + f ( 1^2 )\right)&\\
=\displaystyle 2\cdot 1\cdot f'(1)g'\left(2 + f (1)\right)&\\
=\displaystyle 2\cdot 1\cdot (-2) \cdot g'\left(2 + f (1)\right)& \mbox{from the table $f'(1)=-2$}\\
=\displaystyle -4 g'\left(2 + 1\right)& \mbox{from the table $f(1)=1$}\\
=\displaystyle -4 g'\left(3 \right)& \mbox{}\\
=\displaystyle -4 \cdot 3& \mbox{from the table $g'(3)=3$}\\
=\displaystyle -12& \mbox{}\\
\end{array}
$$
Application
The graph below is a sinusoidal fit of the average-high-temperature data from my hometown. The red function $T(t)$ is given by $$T(t)= 19.5379 \cdot \sin(0.5236t-1.7337) + 72.9917$$ Use the function $T$ to estimate the time interval over which the average high temperature is increasing
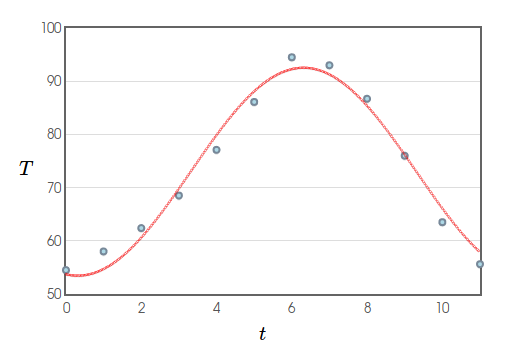
In general, a function is increasing on an interval when the derivative is positive on that interval.
Thus, the temperature increases when $T'(t) \gt 0.$ So, we must first calculate $T'(t):$ $$ \begin{array}{ll} T'(t)&\\ = \displaystyle \frac{d}{dt}\left(19.5379 \cdot \sin(0.5236t-1.7337) + 72.9917\right)&\\ = \displaystyle 19.5379 \frac{d}{dt} \sin(0.5236t-1.7337)&\\ = \displaystyle 19.5379 \frac{d}{dt} f(g(t))& \mbox{outside: $f(t)=\sin t,$ inside: $g(t)=0.5236t-1.7337$}\\ = \displaystyle 19.5379 f'(g(t))\cdot g'(t)& \mbox{by the chain rule}\\ = \displaystyle 19.5379 \cos(0.5236t-1.7337) \cdot 0.5236 & \mbox{since $f'(t)=\cos t,$ inside: $g'(t)=0.5236$}\\ = \displaystyle 10.23 \cos(0.5236t-1.7337) & \\ \end{array} $$ We now find where $T'(t)$ is positive: $$ \begin{array}{ll} T'(t) \gt 0&\\ \implies \displaystyle \displaystyle 10.23 \cos(0.5236t-1.7337) \gt 0&\\ \implies \displaystyle \displaystyle \cos(0.5236t-1.7337) \gt 0&\\ \end{array} $$ Now, $\cos x$ will be positive when $-\frac{\pi}{2}+2k\pi \lt x \lt \frac{\pi}{2}+2k\pi$ where $k \in \mathbb{Z}$ ($k$ is an integer).
Replacing $x$ with $0.5236t-1.7337$ in the above, we then have $$-\frac{\pi}{2}+2k\pi \lt 0.5236t-1.7337 \lt \frac{\pi}{2}+2k\pi.$$ Solving for $t$ we obtain $$\frac{-\frac{\pi}{2}+2k\pi +1.7337}{0.5236} \lt t \lt \frac{\frac{\pi}{2}+2k\pi+1.7337}{0.5236}.$$ From our model, we know that our $t$ interval must fit inside $[0,12).$ Trying different values of $k,$ we see that $k=0$ is the only value of $k$ which gives a valid interval. Thus, for $k=0,$ the above becomes $$\frac{-\frac{\pi}{2}+1.7337}{0.5236} \lt t \lt \frac{\frac{\pi}{2}+1.7337}{0.5236},$$ which can be written as approximately to four decimal places as $$0.3111 \lt t \lt 6.311.$$ Thus, we may now answer our question: the approximate time interval over which the average high temperature is increasing is from $t=0.3111$ to $t=6.311,$ or, from early January to early July.
Thus, the temperature increases when $T'(t) \gt 0.$ So, we must first calculate $T'(t):$ $$ \begin{array}{ll} T'(t)&\\ = \displaystyle \frac{d}{dt}\left(19.5379 \cdot \sin(0.5236t-1.7337) + 72.9917\right)&\\ = \displaystyle 19.5379 \frac{d}{dt} \sin(0.5236t-1.7337)&\\ = \displaystyle 19.5379 \frac{d}{dt} f(g(t))& \mbox{outside: $f(t)=\sin t,$ inside: $g(t)=0.5236t-1.7337$}\\ = \displaystyle 19.5379 f'(g(t))\cdot g'(t)& \mbox{by the chain rule}\\ = \displaystyle 19.5379 \cos(0.5236t-1.7337) \cdot 0.5236 & \mbox{since $f'(t)=\cos t,$ inside: $g'(t)=0.5236$}\\ = \displaystyle 10.23 \cos(0.5236t-1.7337) & \\ \end{array} $$ We now find where $T'(t)$ is positive: $$ \begin{array}{ll} T'(t) \gt 0&\\ \implies \displaystyle \displaystyle 10.23 \cos(0.5236t-1.7337) \gt 0&\\ \implies \displaystyle \displaystyle \cos(0.5236t-1.7337) \gt 0&\\ \end{array} $$ Now, $\cos x$ will be positive when $-\frac{\pi}{2}+2k\pi \lt x \lt \frac{\pi}{2}+2k\pi$ where $k \in \mathbb{Z}$ ($k$ is an integer).
Replacing $x$ with $0.5236t-1.7337$ in the above, we then have $$-\frac{\pi}{2}+2k\pi \lt 0.5236t-1.7337 \lt \frac{\pi}{2}+2k\pi.$$ Solving for $t$ we obtain $$\frac{-\frac{\pi}{2}+2k\pi +1.7337}{0.5236} \lt t \lt \frac{\frac{\pi}{2}+2k\pi+1.7337}{0.5236}.$$ From our model, we know that our $t$ interval must fit inside $[0,12).$ Trying different values of $k,$ we see that $k=0$ is the only value of $k$ which gives a valid interval. Thus, for $k=0,$ the above becomes $$\frac{-\frac{\pi}{2}+1.7337}{0.5236} \lt t \lt \frac{\frac{\pi}{2}+1.7337}{0.5236},$$ which can be written as approximately to four decimal places as $$0.3111 \lt t \lt 6.311.$$ Thus, we may now answer our question: the approximate time interval over which the average high temperature is increasing is from $t=0.3111$ to $t=6.311,$ or, from early January to early July.